Prediction of transonic wing buffet pressure based on deep learning

Abstract

In the present study, a deep learning approach based on a long short-term memory (LSTM) neural network is applied for the prediction of transonic wing buffet pressure. In particular, fluctuations in surface pressure over a certain time period as measured by a piezoresistive pressure sensor, are considered. As a test case, the generic XRF-1 aircraft configuration developed by Airbus is used. The XRF-1 configuration has been investigated at different transonic buffet conditions in the European Transonic Wind tunnel (ETW). During the ETW test campaign, sensor data has been obtained at different local span—and chordwise positions on the lower and upper surface of the wing and the horizontal tail plane. For the training of the neural network, a buffet flow condition with a fixed angle of attack $\alpha$ and a fixed sensor position on the upper wing surface is considered. Subsequent, the trained network is applied towards different angles of attack and sensor positions considering the flow condition applied for training the network. As a final step, the trained LSTM neural network is used for the prediction of pressure data at a flow condition different from the flow condition considered for training. By comparing the results of the wind tunnel experiment with the results obtained by the neural network, a good agreement is indicated.

1 Introduction and motivation

Transonic wing buffet represents an unsteady aerodynamic phenomenon, which is of paramount importance for the definition of safety and efficiency requirements of a civil aircraft. The buffet phenomenon, also commonly referred to as shock buffet, represents an instability including self-sustained shock-wave oscillations and intermittent boundary layer separation. Based on experimental studies by Koike et al. [1] and Paladini et al. [2], the wing shock motions are typically of lower amplitude and more broadband compared to two-dimensional buffet on airfoils, representing Strouhal numbers in the range of $\mathrm {Sr}$ = 0.2 – 0.6. However, the amplitude and frequency vary with the geometry of the wing (e.g. sweep, span) and other flight parameters. As a result of the shock-induced and separated flow, the aircraft structure is susceptible to excitations which lead to structural degradation and reduced passenger comfort during flight [3].

While numerical and experimental studies of transonic buffet on airfoils have been in focus in the recent past, the investigation of transonic wing buffet is still developing. Based on an early study by Sator and Timme [4] on the RBC12 aircraft configuration, it was shown that applying an unsteady Reynolds-averaged Navier-Stokes (URANS) simulation approach is sufficient for the reproduction of the dominant flow features of transonic buffet. In addition, their study revealed that the unsteady shock motions first become apparent at the wingtip and move in a spanwise direction towards the wing root. The increase in incidence further results in the development of more broadband frequencies, however, the dominant frequency decreases as the shock unsteadiness spreads to spanwise positions of a larger chord. Further, in comparison to two-dimensional buffet, the shock oscillations at developed buffet condition for three-dimensional geometries typically exhibit aperiodic [5].

To investigate the influence of geometry parameters on the buffet instability, in particular the wing sweep angle and the aspect ratio of the wing, Iovnovich and Raveh [7] performed several numerical simulations on an infinite-straight, an infinite-swept as well as a finite-swept wing. Based on their study, an increase in pressure disturbance propagation in spanwise direction with increasing sweep angle was observed. Further, the unsteady shock motions observed on the swept configurations are clearly distinctable from the two-dimensional buffet mechanism and are characterised by a periodic convection of so-called buffet cells in spanwise direction [5]. The outboard propagation of the buffet cells is thought to constitute the buffet instability and has been additionally observed in both experimental and numerical studies ( [4, 6]). Similar to the study of Iovnovich and Raveh [7], Crouch et al. [8] and Paladini et al. [2] investigated the effect of wing sweep on the buffet instability using modal analysis.

In addition to the description of the characteristic buffet mechanism as provided by Iovnovich and Raveh [7], a study by Timme and Thormann [9] revealed that the origins of the buffet instability might result in globally unstable aerodynamic modes. Further, Ohmichi et al. [10] applied modal identification techniques, in particular proper orthogonal decomposition (POD) and dynamic mode decomposition (DMD), in order to investigate the dominant modes.

Based on the aforementioned studies it is shown that capturing the characteristic flow features of the three-dimensional buffet instability requires extensive numerical and experimental effort, especially if industrial applications are considered. To solve for this issue, deep learning approaches, also often referred to as reduced-order models (ROMs), are developed and applied to some extent towards the computation of transonic buffet of industry-relevant configurations.

As already outlined in a previous study [11] by the authors, databased techniques such as POD and DMD have been applied by Timme [3] and Ohmichi et al. [10] in order to identify instability mechanisms and dominant flow modes of three-dimensional wing buffet. In addition, Candon et al. [12] investigated deterministic and non-deterministic ROM approaches for dynamic bending and torsion load spectra prediction resulting from the transonic buffet on a high-agility aircraft configuration. Another study conducted by Candon et al. [13] compared three deep learning architectures, namely a standard recurrent neural network (RNN), a long short-term memory (LSTM) neural network and a bidirectional LSTM concerning the prediction of buffet loads. Based on their investigations the bidirectional LSTM yields the best prediction capability regarding structural dynamic responses of a high-agility aircraft during buffet critical maneuvers.

However, none of the studies summarized above investigated the application of deep learning methods for the computation of buffet pressure loads on a realistic civil aircraft configuration. Further, the aforementioned studies considered numerical data, whereas in the present study experimental buffet data is applied for training a neural network. The experimental data is obtained during a wind tunnel test campaign in the European Transonic Wind tunnel (ETW) with the Airbus XRF-1 configuration as a test case. In particular, unsteady pressure-sensitive paint (iPSP) measurements are conducted by the German Aerospace Center (DLR). Further, the aircraft model is equipped with piezoresistive pressure sensors on the wing lower and upper surface and the horizontal tail plane (HTP) to establish reference data for the iPSP measurements. In the present study, only pressure data obtained on the wing upper surface is included in the investigation. The experiments in the ETW included the investigation of different buffet conditions on the Airbus XRF-1 configuration. Based on the data obtained by the unsteady pressure sensors, a deep learning model based on a LSTM neural network, is trained. Subsequent, the trained LSTM network is applied for the prediction of pressure data at angles of attack and sensor positions other than those of the training conditions. As a final step, the trained LSTM is also applied to varying flow conditions, including different angles of attack and sensor positions. By comparing the experimental data and the results obtained by the LSTM, a good agreement is indicated for all application cases. The buffet characteristic frequencies as well as the trends of both low and high-frequency content are captured by the proposed LSTM-ROM.

2 Test case: airbus XRF-1

Within this section, the Airbus XRF-1 test case applied for the following investigations, is introduced. Therefore, the experimental setup as well as the data acquisition method are briefly described. In the second part of the section, a flow characterization of the buffet instability on the wing upper surface is provided.

2.1 Wind tunnel model

As a test case for the following investigation, a wind tunnel model of the Airbus XRF-1 configuration is chosen. The configuration is provided by Airbus UK and represents a long-range twin-engine aircraft model. The XRF-1 wind tunnel model, as shown in Fig. 1, is equipped with horizontal and vertical stabilizers as well as adjustable ailerons. The experimental investigations, which have been obtained by the ETW and the German Aerospace Center (DLR), included both static and dynamic data acquisition.

Fig. 1

Front (top) and back (bottom) view of the Airbus XRF-1 wind tunnel model ($\copyright$Airbus/ETW)

In the following, the focus is on dynamic data, which includes unsteady pressure sensitive paint (iPSP) [14, 15] measurements. Besides the application of iPSP, the wind tunnel model is equipped with piezoresistive pressure sensors on the wing lower and upper surface and the horizontal tail plane (HTP) to establish reference data. Here, pressure data obtained by sensors positioned on the wing upper surface is included in the following investigations. In Fig. 2, an overview of the pressure sensors on the wing suction side, including their descriptions, is presented.

During the wind tunnel test campaign, different buffet flow conditions are considered for the iPSP measurements, characterized by freestream Mach numbers of $Ma_{\infty }$ = [0.84,0.9] and Reynolds numbers of Re = [12.9 Mio., 25 Mio.]. In addition, for each flow condition, pressure data at varying angles of attack $\alpha$ is measured. The pressure data is obtained individually by each sensor using a high-speed data acquisition system with a sampling rate of 10 kHz. The length of each sensor signal is defined by the duration of the corresponding iPSP measurements, which is defined by 3.86 s.

Fig. 2

Pressure sensor positions and names on the upper wing surface ($\copyright$Airbus/ETW)

2.2 Wing flow characterization

Based on the obtained iPSP data, the buffet flow field on the upper wing surface of the Airbus XRF-1 wind tunnel model is briefly discussed in the following. To provide a clear visualization, the results are provided by means of the mean (${\bar{c}}_{p}$) and root mean square ($c_{p,rms}$) distribution of the pressure coefficient. Due to visualization restrictions, axis notations are suppressed in all the following figures. In Fig. 3, the mean (left) and root mean square (right) of the pressure coefficient distribution are exemplary visualized, considering a Mach number of $Ma_{\infty }$ = 0.9, a Reynolds number of Re = 25 Mio. and an angle of attack of $\alpha$ = 4$^{\circ }$. As shown, a distinct $\lambda$-shaped shock pattern in spanwise direction is clearly visible. Close to the wing root, the shock is located near the trailing edge (TE), whereas in the mid-span and tip region, the shock position is shifted forward to the leading edge (LE).

Fig. 3

Mean (${\bar{c}}_{p}$, left) and root mean square ($c_{p,rms}$, right) pressure distribution on the wing upper surface ($Ma_{\infty }$ = 0.9, Re = 25 Mio., $\alpha$ = 4$^{\circ }$)

Fig. 4

Mean pressure distribution (${\bar{c}}_{p}$) representing a flow condition of $Ma_{\infty }$ = 0.9, Re = 25 Mio. and varying angles of attack $\alpha$ = [4$^{\circ }$,5$^{\circ }$,6$^{\circ }$]

With increasing angle of attack, as shown in Fig. 4, the inboard shock position moves towards the TE of the wing. In contrast, the shock position close to the wing tip shifts towards the LE. Further, the sweep angle of the inboard shock increases and the intersection of both shocks shifts closer to the wing root. In addition, the intensity of the shock increases with increasing $\alpha$.

In addition to the variation of the angle of attack, the change in surface pressure distribution due to a change in Mach and Reynolds number is visualized in Fig. 5.

Fig. 5

Mean pressure distribution (${\bar{c}}_{p}$) at an angle of attack of $\alpha$ = 5$^{\circ }$ and varying flow conditions

With decreasing Reynolds number, the supersonic flow area shifts from the wing root towards the wing tip. Further, considering the lower Reynolds number case (see Fig 5, middle), additional areas of supersonic flow arise at the TE of the wing. In contrast, by decreasing the Mach number the shock position at the wind root and wing tip moves towards the LE.

As shown, the investigated flow conditions develop distinct buffet characteristics. Due to the spanwise variation in the surface pressure distribution and the dynamics of the buffet instability, each sensor captures different spectral characteristics. Therefore, the trained LSTM neural network is applied towards the prediction of highly nonlinear flow characteristics, captured by each sensor at varying flow conditions and angle of attacks.

3 Nonlinear system identification

In the first part of the following section, the architecture of the applied LSTM neural network is introduced in detail. In the second subsection, the preprocessing steps applied to the experimental pressure data, are briefly outlined. Further, a detailed description of the choice of the LSTM hyperparameters and the network training process is provided in the third subsection. The section is concluded with an overview of error metrics used for quantifying the performance of the trained LSTM.

3.1 Long short-term memory (LSTM) neural network

The LSTM architecture as proposed by Hochreiter and Schmidhuber [16] represents a special type of a recurrent neural network (RNN), which has proven to be powerful for predicting both short- and long-term dependencies in time-series data. In contrast to a standard RNN architecture, the application of an LSTM solves for a problem known as vanishing gradient [17], in which the networks training process is susceptible to become insufficient after a certain number of training iterations. Further, time-delayed effects which must be accounted for in unsteady aerodynamic modeling, are already considered by the LSTM network architecture itself [18].

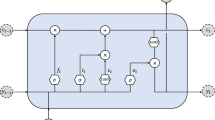
Compared to a standard RNN architecture, the hidden layer of an LSTM consists of a set of recurrently connected blocks, which are referred to as memory blocks or cells. Between the input layer (x) and the output layer (y), the LSTM memory cells are combined in an LSTM layer, as depicted in Fig. 6.

Fig. 6

Schematic of a RNN structure including a LSTM layer. Several inputs ${\varvec{x}}$ are connected to outputs ${\varvec{y}}$

Each cell is defined by a characteristics gate structure, which processes the incoming information. Using the gates, the LSTM is able to remove or add information to the cell state. In Fig. 7, the architecture of a single LSTM memory cell is illustrated in detail.

Fig. 7

Architecture of a single LSTM memory cell

As shown in Fig. 7, the LSTM cell is defined by three gates, defined as forget gate ${\varvec{f}}$, input gate ${\varvec{i}}$ and output gate ${\varvec{o}}$. The input of the current time step ${\varvec{x}}_{t}$ as well as the vector representing the output from the previous time step ${\varvec{h}}_{t-1}$ are processed within the forget gate ${\varvec{f}}$:

$$\begin{aligned} {\varvec{f}}_{t}=\sigma ({\varvec{W}}_{f}{\varvec{x}}_{t} + {\varvec{W}}_{f} {\varvec{h}}_{t-1} + {\varvec{b}}_{f}). \end{aligned}$$

(1)

The inputs are multiplied by the weight matrix of the forget gate ${\varvec{W}}_{f}$ and a bias ${\varvec{b}}_{f}$ is added. The output from the previous time step ${\varvec{h}}_{t-1}$ is also referred to as the hidden state of the LSTM cell. By means of an activation function, which is commonly implemented as a sigmoid ($\sigma$) function, a certain amount of the incoming information is discarded from the cell. Using a sigmoid activation, the values are defined between 0 and 1. If the activation is zero, all information is discarded, whereas for an activation equal to one, the information is further stored in the cell.

The input gate performs a similar operation to update the state of the cell. The current time step ${\varvec{x}}_{t}$ as well as the hidden state from the previous time step ${\varvec{h}}_{t-1}$ are processed by a sigmoid activation function:

$$\begin{aligned} {\varvec{i}}_{t}=\sigma ({\varvec{W}}_{i}{\varvec{x}}_{t} + {\varvec{W}}_{i}{\varvec{h}}_{t-1} + {\varvec{b}}_{i}), \end{aligned}$$

(2)

with ${\varvec{W}}_{i}$ and ${\varvec{b}}_{i}$ defining the weights and bias of the input gate, respectively. In the second step, both inputs are processed by an activation, implemented as a hyperbolic tangent ($\tanh$), which creates a new cell vector $\varvec{\tilde{c}}_{t}$:

$$\begin{aligned} \varvec{\tilde{c}}_{t}= tanh ({\varvec{W}}_{h}{\varvec{x}}_{t} + {\varvec{W}}_{h}{\varvec{h}}_{t-1} + {\varvec{b}}_{h}). \end{aligned}$$

(3)

Due to the $\tanh$ activation, the values will be rescaled between -1 and 1. Based on the newly created cell state $\varvec{\tilde{c}}_{t}$, new information is stored in the current cell state $\varvec{{c}}_{t}$. Therefore, the previous cell state $\varvec{{c}}_{t-1}$ is multiplied with the forget gate vector $\varvec{{f}}_{t}$ and the cell state is updated with the input gate vector $\varvec{{i}}_{t}$:

$$\begin{aligned} {\varvec{c}}_{t} = {\varvec{f}}_{t} {\varvec{c}}_{t-1} + {\varvec{i}}_{t} \varvec{\tilde{c}}_{t}. \end{aligned}$$

(4)

In the output gate, the values of the current state ${\varvec{x}}_{t}$, the previous hidden state ${\varvec{h}}_{t-1}$ as well as the current cell state $\varvec{{c}}_{t}$ are processed by a sigmoid and $\tanh$ activation:

$$\begin{aligned} \begin{aligned}&{\varvec{o}}_{t} = \sigma ({\varvec{W}}_{o}{\varvec{x}}_{t} + {\varvec{W}}_{o}{\varvec{h}}_{t-1} + {\varvec{b}}_{o}) \\&{\varvec{h}}_{t} = {\varvec{o}}_{t} \cdot tanh ({\varvec{c}}_{t}). \end{aligned} \end{aligned}$$

(5)

The information, which are stored in the updated hidden state ${\varvec{h}}_{t}$, are transferred to the next hidden layer or the dense and output layer to get the final prediction.

Based on the available experimental data set representing the characteristic buffet features, the weights (${\varvec{W}}_{f}$, ${\varvec{W}}_{i}$, ${\varvec{W}}_{o}$) and biases (${\varvec{b}}_{f}$, ${\varvec{b}}_{i}$, ${\varvec{b}}_{o}$) of each gate and the hidden state (${\varvec{W}}_{h}$, ${\varvec{b}}_{h}$) are computed and updated by applying gradient descent (GD) optimization with back-propagation through time (BPTT) [19]. More specifically, the adaptive moment estimation (ADAM) [20] algorithm is applied in the present study. To achieve an appropriate model performance, the mean squared error (MSE) (see Eq.(6)) between the prediction of the LSTM neural network and the reference experimental data is minimized.

$$\begin{aligned} MSE = \frac{1}{N_{S}}\displaystyle \sum _{i=1}^{N_{S}} ({\hat{y}}_{i}-y_{i})^2. \end{aligned}$$

(6)

In Eq.(6), ${\hat{y}}$ and y representing the data as obtained by the neural network and the experiment, respectively. $N_{S}$ equals the number of sample points of the predicted and measured data sets.

3.2 Data preprocessing

Prior to the training of the LSTM, the experimental data sets needs to be preprocessed. Based on the measurements in the ETW, the signals of each sensor are provided as a displacement series. Therefore, in the first step, the data is transferred into pressure data, using calibration coefficients provided by the ETW.

In the second preprocessing step, the pressure samples are transferred into pressure coefficient samples, measured at a location P and time t:

$$\begin{aligned} c_{p}(P,t) = \frac{p(P,t) - p_{\infty }}{\frac{1}{2} \rho _{\infty } U^{2}_{\infty }}, \end{aligned}$$

(7)

with pressure, density and flow velocity p, $\rho$ and U, respectively. Subsequent, the mean pressure ${\bar{c}}_{p}$ is subtracted from all samples, transferring the data into the fluctuations of the pressure coefficient $c{'}_{p}(P,t)$:

$$\begin{aligned} c{'}_{p}(P,t) = \frac{p{'}(P,t) - p{'}_{\infty }}{\frac{1}{2} \rho _{\infty } U^{2}_{\infty }}. \end{aligned}$$

(8)

In the last step, all data sets are normalized using the minimum and maximum values of the pressure fluctuations ($c{'}_{p,min}(P,t)$,$c{'}_{p,max}(P,t)$) as given in the training data set. Therefore, all data values are rescaled to [-1,1]. Since the minimum and maximum value of the training data set are applied for normalization, the value range of the test data set may slightly differ from [-1,1]. However, an information leak between the training and test data set is prevented.

3.3 Training of the LSTM

For the training of the LSTM neural network, a data set representing a single flow condition, is applied. Therefore, data obtained by the sensor KUP10802 (see Fig. 2) at a flow condition with Mach number of $Ma_{\infty }$ = 0.9, a Reynolds number of Re = 25 Mio. and an angle of attack of $\alpha$ = 4$^{\circ }$, is selected. Prior to the training, the available data set is splitted into two data sets. The first data set, including 80% of the data points, is used for training the LSTM, whereas the remaining data is used for monitoring the training process. This data set is referred to as the validation data set and is also used for hyperparameter tuning. In Fig. 8, the convergence trends of the training and validation loss of the LSTM training are visualized. Therefore, the decrease in MSE (see Eq. 6) is plotted over the number of training iterations. By evaluating the MSE during the training process and applying early stopping, the training process is terminated after 115 epochs.

Fig. 8

Convergence trends of training and validation losses

By conducting an extensive parameter study, the following network and training hyperparameters are identified for the LSTM. The number of hidden layers is varied between one and three, however, two hidden layers are chosen for the following application. Applying a single-layer LSTM indicates a lower performance quality compared to a stacked LSTM, however, the implementation of three hidden layers intensively increases the training time without any considerable performance improvement. For both hidden layers, the following number of neurons is considered: $N_{neurons}$ = [50,100,200]. Based on the results, a number of 200 neurons in each layer, is chosen. The data points are feed into the LSTM in batches, including 16 data points each. Increasing the batch size to 32 or higher slowed down the training without minimizing the training error. As already mentioned in Sect. 3.1, the LSTM is trained using BPTT with an initial learning rate of $\eta$ = 0.001. An increase of the learning rate to $\eta$ = 0.01 results in an acceleration of convergence, however, the training performance decreases. Reducing the learning rate to $\eta$ = 0.0001 leads to a deceleration of convergence and therefore an considerable increase in training time. As already stated in Sect. 3.1, a hyperbolic tangent (tanh) is selected as the state activation function, while the gate activation function is chosen as sigmoid ($\sigma$).

3.4 Error quantification

To quantify the error between the experimental results (y) and the results computed by the LSTM (${\hat{y}}$), an evaluation metric proposed by Russell [21] is applied in the present study. Instead of using a metric for a point-to-point comparison between the original and predicted data set, the data is compared in terms of amplitudes and phases of both signals. Following the definition of Russell [21], the amplitude error between two signals is evaluated as follows:

$$\begin{aligned} A_\mathrm {err} = \mathrm {sign(RME)}Log_{10}(1+|RME|), \end{aligned}$$

(9)

with the relative magnitude error (RME) defined as:

$$\begin{aligned} \mathrm {RME} = \frac{\displaystyle \sum _{i=1}^N {\hat{y}}_{i}^{2} - \displaystyle \sum _{i=1}^N y_{i}^{2}}{\sqrt{\displaystyle \sum _{i=1}^N {\hat{y}}_{i}^{2} \displaystyle \sum _{i=1}^N y_{i}^{2}}}. \end{aligned}$$

(10)

The length of both data sets including the number of measured and predicted data points N must be the same. The phase error between both data sets is computed as follows:

$$\begin{aligned} P_{err} = \frac{1}{\pi }cos^{-1}\left( \frac{\displaystyle \sum _{i=1}^N {\hat{y}}_{i}y_{i}}{\sqrt{\displaystyle \sum _{i=1}^N {\hat{y}}_{i}^{2} \displaystyle \sum _{i=1}^N y_{i}^{2}}}\right) . \end{aligned}$$

(11)

Finally, the amplitude ($A_{err}$) and phase error ($P_{err}$) are combined into a comprehensive error $C_{err}$:

$$\begin{aligned} C_{err} = \sqrt{\frac{\pi }{4}(A_{err}^2 - P_{err}^2}) \end{aligned}$$

(12)

If there is no disagreement between the experimental data and the data predicted by the LSTM-ROM, the computed comprehensive error will be zero. Therefore, the lower the error, the better is the prediction capability of the trained LSTM.

4 LSTM-ROM application

In the following section, the results of the application of the trained LSTM, are presented. Further, the computational effort of the LSTM-ROM application, compared to the experimental investigations, is outlined.

4.1 Multi-step prediction on the validation data set

Prior to applying the trained LSTM neural network towards the prediction of pressure characteristics as obtained by different sensor positions and different freestream parameter conditions, the LSTM is evaluated based on the validation data set by performing recurrent multi-step predictions. Therefore, the first 1000 pressure samples in the validation data set are applied. In Fig. 9, the data points as predicted by the LSTM are compared to the data obtained during the experiments. As it can be seen, the LSTM neural network is able to reproduce the general trends of the pressure data time series with sufficient accuracy. The good prediction capability is also highlighted by the corresponding errors as summarized in Table 1.

Table 1 Amplitude, phase and comprehensive error of LSTM application for multi-step predictions on the validation data ($Ma_{\infty }$ = 0.9, Re = 25 Mio., $\alpha$ = 4$^{\circ }$, sensor position: KUP10802)

Fig. 9

Comparison of experimental and predicted $c_{p}$ of the validation data set ($Ma_{\infty }$ = 0.9, Re = 25 Mio., $\alpha$ = 4$^{\circ }$, sensor position: KUP10802)

4.2 Prediction of pressure characteristics at varying angles of attack

Subsequent to the application of the trained LSTM-ROM on the validation data set, the trained LSTM is applied for the prediction of pressure data obtained at angles of attack which differ from the training condition ($\alpha _{train}$ = 4$^{\circ }$). However, the freestream Mach and Reynolds number ($Ma_{\infty }$ = 0.9, Re = 25 Mio.) as well as the position of the pressure sensor (KUP10802) remain unchanged. In particular, the following angles of attack are considered for performance evaluation: $\alpha$ = [2.5$^{\circ }$, 5$^{\circ }$, 6$^{\circ }$]. The trained LSTM is applied to the unknown data sets in a recurrent multi-step prediction mode. Therefore, an initial number of timesteps x is provided to the trained ROM to enable a prediction of future time steps y. For the following performance evaluation, the number of initial time steps is defined as x = 100, whereas for simplicity the time steps to be predicted ahead is defined as y = 1. As the prediction advances, the data obtained during the sensor measurement are successively substituted by the data points predicted by the LSTM-ROM. Therefore, with the exception of the initialization phase, no additional experimental data is used for the multi-step prediction mode.

To provide a clear visualization of the results, the data is presented by means of the power spectral density (PSD) of $c_{p}$, plotted over the reduced frequency $k_{red}$:

$$\begin{aligned} k_{red} = \omega \cdot \frac{MAC}{U_{\infty }}. \end{aligned}$$

(13)

In Eq.(13), $\omega$ is defined as the angular frequency, MAC as the mean aerodynamic chord of the wing and $U_{\infty }$ as the freestream velocity.

In Fig. 10, the mean of the pressure fluctuations on the wing suction side as well as the PSD of the sensor data are visualized. Based on the visualization of the pressure distribution it is shown that depending on the angle of attack, the sensor is exposed to a different flow behavior. The PSD of the results as obtained by the LSTM-ROM are compared to the experimental data. By comparing the results, an overall good agreement is indicated. In general, the trends of the experimental frequency spectra are correctly captured by the trained LSTM. Here, both the low and high frequency content, are sufficiently represented. Especially at an angle of attack $\alpha$ = 2.5$^{\circ }$ (see Fig. 10, top), a broadband, high frequency bump is clearly visible, which corresponds to a frequency range (0.4 < $k_{red}$ < 0.7) related to wing buffet [1, 3]. However, a small deviation in the frequency amplitudes is visible for the three test cases. By evaluating the corresponding errors for each $\alpha$, which are summarized in Table 2, the precise prediction performance is underlined. Although there is a shift in the amplitudes, the corresponding amplitude errors are not extremely high, compared to the predictions obtained using the validation data set (see Table 1).

Table 2 Amplitude, phase and comprehensive error of the LSTM application at different angles of attack $\alpha$ ($Ma_{\infty }$ = 0.9, Re = 25 Mio., sensor position: KUP10802)

Fig. 10

Comparison of experimental and predicted $c_{p}$ at different angles of attack $\alpha$ = [2.5$^{\circ }$,5$^{\circ }$,6$^{\circ }$] ($Ma_{\infty }$ = 0.9, Re = 25 Mio., sensor position: KUP10802)

4.3 Prediction of pressure characteristics at varying sensor positions

Besides different angles of attack, the trained LSTM-ROM is applied for the prediction of pressure data as obtained at different sensor positions. Therefore, sensors which are located at different spanwise positions closer to the wing root and wing tip, are considered. In particular, the following sensor positions are selected for performance evaluation: KUP10401, KUP11002, KUP11402, KUP11802 (from root to tip). The positions of the selected sensors in relation to the sensor training position are visualized in Fig. 2.

Analog to Sect. 4.2, data measured at a flow condition of $Ma_{\infty }$ = 0.9, Re = 25 Mio. and $\alpha$ = 4$^{\circ }$ is applied. In Figs. 11 and  12, the spectra of the experimental sensor signals as well as the signals predicted by the LSTM-ROM are comparatively visualized. In addition, the mean of the pressure distribution on the wing suction side is shown. On the wing, the position of the test sensors is marked in black, whereas the position of the training sensor is defined by a red marker. Therefore, it is indicated, that each sensor is exposed to a different flow behavior, which must be captured by the LSTM-ROM. By comparing the experimental results and the data predicted by the LSTM, it is shown that the LSTM is able to represent both the low and high frequencies with sufficient accuracy. As already indicated by the previous application (see Fig. 10), a slight shift in the frequency amplitude is indicated. The corresponding errors are summarized in Table 3.

Table 3 Amplitude, phase and comprehensive error of the LSTM application for different sensor positions ($Ma_{\infty }$ = 0.9, Re = 25 Mio., $\alpha$ = 4$^{\circ }$)

Fig. 11

Comparison of experimental and predicted $c_{p}$ at different sensor positions (black marker): KUP10401 (top), KUP11002 (bottom) ($Ma_{\infty }$ = 0.9, Re = 25 Mio., $\alpha$ = 4$^{\circ }$). The reference training sensor is marked in red

Fig. 12

Comparison of experimental and predicted $c_{p}$ at different sensor positions (black marker): KUP11402 (top), KUP11802 (bottom) ($Ma_{\infty }$ = 0.9, Re = 25 Mio., $\alpha$ = 4$^{\circ }$). The reference training sensor is marked in red

4.4 Prediction of pressure characteristics at different Mach and Reynolds numbers

For the final performance evaluation, the trained LSTM-ROM is applied for the prediction of pressure characteristics measured under different flow conditions. In the first step, a variation of the Reynolds number is considered, whereas in the second step, a different Mach number is selected.

The first flow condition is defined by a Mach number of $Ma_{\infty }~=~0.9$ and a Reynolds number of Re = 12.9 Mio., while the second flow condition is represented by a Mach number of $Ma_{\infty }~=~0.84$ and a Reynolds number of Re = 25 Mio.. In Fig. 13 and  14, the spectra of the experimental signals and the signals predicted by the LSTM for a variation of the angle of attack and the sensor position at $Ma_{\infty }~=~0.9$ and Re = 12.9 Mio are visualized, respectively. In contrast, Fig. 15 and  16 represent a comparative presentation of experimental and predicted results due to the angle of attack and sensor position variations at $Ma_{\infty }~=~0.84$ and Re = 25 Mio.

Analogous to the results discussed in Sect. 4.2 and Sect. 4.3, the LSTM-ROM achieves an accurate prediction for each test case, which is also emphasized by the corresponding errors summarized in Table 4 and  5. The shift in amplitude is still visible and the computed amplitude errors are slightly higher than for the other test cases. However, the general trend as well as the overall frequency content of the spectra are captured by the trained LSTM.

Table 4 Amplitude, phase and comprehensive error of the LSTM application for different flow conditions and $\alpha$ variations ( $Ma_{\infty }$ = [0.84, 0.9], Re = [ 12.9 , 25 ] Mio., sensor position: KUP10802)

Table 5 Amplitude, phase and comprehensive error of the LSTM application for different flow conditions and sensor variations ( $Ma_{\infty }$ = [0.84, 0.9], Re = [ 12.9 , 25 ] Mio., $\alpha$ = 5$^{\circ }$)

Fig. 13

Comparison of experimental and predicted $c_{p}$ at $\alpha$ = 5$^{\circ }$ (left) and $\alpha$ = 7$^{\circ }$ (right) ($Ma_{\infty }$ = 0.9, Re = 12.9 Mio., KUP10802)

Fig. 14

Comparison of experimental and predicted $c_{p}$ at different sensor positions: KUP11402 (left), KUP11802 (right) ($Ma_{\infty }$ = 0.9, Re = 12.9 Mio., $\alpha$ = 5$^{\circ }$)

Fig. 15

Comparison of experimental and predicted $c_{p}$ at $\alpha$ = 4$^{\circ }$ (left) and $\alpha$ = 5$^{\circ }$ (right) ($Ma_{\infty }$ = 0.84, Re = 25 Mio., KUP10802)

Fig. 16

Comparison of experimental and predicted $c_{p}$ at different sensor positions: KUP11402 (left), KUP11802 (right) ($Ma_{\infty }$ = 0.84, Re = 25 Mio., $\alpha$ = 4$^{\circ }$)

4.5 Computational effort

In the following, a comparison of the computational effort of the sensor measurements and the LSTM training and application process, is given. As already stated in Sect. 2.1, the acquisition of the pressure data at each sensor took 3.86 seconds.

All computations including the training and application of the LSTM have been performed on a workstation using a single Intel Xeon 2.3 GHz processor. The training of the LSTM, using the available amount of data points, took around two hours. The application of the LSTM for the prediction of the unknown pressure data took two to three minutes, depending on the amount of data points to be predicted ahead.

The trained LSTM can provide pressure data if measurement errors occur during a run or if sensors get damaged. For future application, the LSTM could also be applied for data interpolation, which enables the use of less sensors and the prediction of pressure data at different span - and chordwise positions.

5 Conclusion

In the present study, a deep learning approach based on a long short-term memory (LSTM) neural network has been applied to predict pressure data at transonic buffet condition as obtained by unsteady pressure sensors. For training and performance evaluation, experimental pressure data obtained during a test campaign of the Airbus XRF-1 configuration in the European Transonic Wind Tunnel (ETW), has been applied. For the training process, data measured at a flow condition of $Ma_{\infty }$ = 0.9, Re = 25 Mio. and $\alpha$ = 4$^{\circ }$ and a fixed sensor position has been chosen. After the training is finalized, the trained LSTM-ROM has been applied for the prediction of unknown pressure data considering different angles of attack and sensor positions measured at the training flow condition. Subsequent, flow conditions which differ from the training condition have been considered for performance evaluation. Therefore, both the angle of attack as well as the sensor position have been additionally varied. By comparing the experimental data with the predictions obtained by the trained LSTM-ROM for all test cases, a precise agreement is indicated. The LSTM is able to capture both the low- and high-frequency content, including characteristic buffet frequencies. A slight shift in the amplitude between the experimental data and the data predicted by the LSTM is visible, however, an overall good performance quality is indicated.