1 Introduction

According to the report of the World Health Organization (WHO), as of June 14, 2020, there have been a total of 7.855 million confirmed cases of coronavirus disease 2019 (COVID-19) across the globe. The outbreak of COVID-19 which is ravaging globally has severely affected the safety and the development around the world. The history of human coronavirus began in 1965 when a virus named B814 was found by Tyrrell [1]. Since 2003, at least five new human coronaviruses have been identified (such as the SARS pandemic and H1N1 influenza in 2009), which caused significant morbidity and mortality. On February 11, 2020, the WHO announced that the disease caused by this new coronavirus was a COVID-19 [2]. It concluded that the virus can be transmitted from human-to-human. Symptomatic people are the most common source of COVID-19 spreading, however, the possibility of transmission before the onset of symptoms cannot be excluded.

The propagation rules and predictions of various infectious diseases require theoretical analysis, quantitative analysis and simulations. The analysis is inseparable from the mathematical model established for various infectious diseases. Therefore, understanding diseases and modeling the spread of pandemic mathematically attract a lot of attention. As early as 1906, Hamer used a discrete mathematical model to study the pandemic pattern of measles [3]. In 1911, Ross established a differential equation model to study the spread of malaria [4]. In 1927, Kermack and Mckendrick established a compartment model with a bilinear incidence rate in order to analyze the spread of the Black Death in London [5]. Based on this work, many researches have studied the spread of infectious diseases in a population by compartmental models such as SIS, SIR, SIRS or SEIR [6,7,8,9]. The use of disease transmission models to generate short-term and long-term pandemic forecasts has increased as the number of infectious disease outbreaks has increased over the last decades [10]. To investigate the pandemic of COVID-19, some models have been made modifications based on the conventional “SEIR” model [11] and concluded that strictly controlled interventions are critically important to impede COVID-19 outbreak [12,13,14,15,16,17]. A few models established a stochastic transition model to evaluate the spread of COVID-19 and also emphasized the necessity for isolation and quarantine [18, 19]. Some other models have been developed to evaluate the role of coronavirus transmission based on asymptomatic cases [20, 21]. However, a crucial factor caused by asymptomatic cases or virus incubation period is not considered, that is the time delay. Because it is hard to find and confirm the infected cases in good time, there will be a time delay before the infected cases are quarantined. Then, bifurcation, chaos or fractal may occur in the pandemic dynamic system, which means the COVID-19 pandemic may outbreak over and over again. It will cause great difficulties to the prevention and control of the COVID-19 outbreak. Kissler et al. have given a similar projection by using estimates of seasonality, immunity and cross-immunity, that is, the recurrent wintertime outbreaks of COVID-19 will probably occur after the initial, most severe pandemic wave [46].

The study of complex dynamic evolutionary behavior of nonlinear dynamical systems may cover ecology, economics, computer science and many other fields. Li et al. discuss bifurcation and chaos of the discrete model about a physiological control system with delay [22]. The qualitative analysis of the discrete model including the boundedness of solutions and bifurcation is investigated in [23]. In order to reveal the effect of time delay on the stability and Hopf bifurcation, the fractional neural networks with delay were investigated in [24]. Dong et al. proposed a computer virus model with time delay, and they regard the time delay as bifurcating parameter to study the dynamical behaviors including Hopf bifurcation and local asymptotical stability [25]. Other studies in computer science show that the spread dynamic system of malware would be unstable and appear bifurcation and chaos [26,27,28]. These studies illustrate that time delay will cause unpredictable and complex influence on the dynamic system. This paper aims to analyze the impact caused by time delay on the dynamic of COVID-19 spreading and the effect of home isolation, hospital isolation, antibody failure and other factors on the pandemic prevention and control. We try to provide some suggestions to more effectively prevent the spread of COVID-19 through feasible measures.

This paper is organized as follows. In Sect. 2, I propose the SIDQR pandemic model with hierarchical quarantine and time delay. Section 3 analyzes the stability of equilibrium and deduces the threshold of Hopf bifurcation. In Sect. 4, based on the model, I carry out the numerical simulations for the dynamics and bifurcation phenomenon of the COVID-19 outbreak. Section 5 gives the discussion about the prevention of COVID-19 and the conclusion for this paper.

2 Pandemic Model with Hierarchical Quarantine and Time Delay

To effectively suppress the spread of the pandemic, many governments around the world have taken measures to extend vacations and quarantine. Practice has proved that quarantine is an effective measure in large-scale pandemic situation. In order to illustrate the importance of quarantine measures to restrain the propagation of the COVID-19, I propose a nonlinear pandemic model by considering hierarchical quarantine measures and time delay.

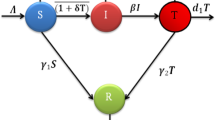
In order to show clearly, the transition diagram and frequently used notations of the model is given in Fig. 1 as follows.

Fig. 1
figure 1

State transition diagram of the pandemic model

Full size image

In the model, the population is partitioned into six compartments depending on the states. Susceptible state (\(S\), it denotes the population who are at risk of being infected by the COVID-19). Infected state (\(I\), it denotes the population who are infected by COVID-19). Delayed state (\(D\), it denotes the number of delayed population. In this case, if someone is infected by COVID-19, it will take some days to get a definite diagnosis and be quarantined in a hospital setting, and this state can be regarded as a transitional state). Home isolation state (\(Q_{1}\), it denotes the restriction of movement or isolation from the people who are susceptible to a contagious disease). Quarantine state (\(Q_{2}\), it denotes that the confirmed patients who are quarantined in a hospital setting) and Recovered state (\(R\), it denotes the population who are recovered from COVID-19). The notations and their explanations are listed as follows.

2.1 Some Hypotheses

In this paper, the pandemic models are based on the following hypothesis:

  1. (1)

    At every time step, the susceptible population will be infected by the infected population at a rate \(\beta_{1}\), and the susceptible population will be subjected to home isolation at a rate \(\varphi_{1}\). The value of \(\varphi_{1}\) depends on the management of the government and the degree of public compliance.

  2. (2)

    In reality, the population who is isolated at home still may be infected at a small risk, because it is unavoidable for the isolated people to contact the others. Some infected cases have been confirmed to be caused by family gatherings. Thus, the population at home isolation state will be infected at a rate \(\beta_{2}\) in the model.

  3. (3)

    For the infected population, a small number of confirmed patients will be self-healing at a rate \(\gamma\), others will be quarantined in a hospital at a rate \(\varphi_{2}\). However, the infected population will take some days to be confirmed and quarantined in the hospital. Then, there is a delayed state between infected state and quarantine state in this case.

  4. (4)

    The quarantined population in the hospital will get recovered at a rate \(\omega\).

  5. (5)

    Currently, there is no evidence that people can get permanent immunity, even the vaccine may be invalid after a period of time. In the model, the recovered population may be susceptible again at a rate \(\delta\), it is inversely related to the duration of the vaccine effect.

  6. (6)

    The total number of population is assumed as \(N\). To study the nonlinear dynamics of the pandemic model, the total number \(N\) in the system is fixed.

2.2 Model Formulation

Based on the hypothesis and the transition diagram of COVID-19 in human population as depicted in Fig. 1, the model can be expressed with the following equations (the source and explanations of the equations can be found in [45]):

$$ \left\{ \begin{gathered} \frac{dS\left( t \right)}{{dt}} = \delta R(t) - \frac{{\beta_{1} I\left( t \right)S\left( t \right)}}{N} - \varphi_{1} S\left( t \right), \hfill \\ \frac{dI\left( t \right)}{{dt}} = \frac{{\beta_{1} I\left( t \right)S\left( t \right)}}{N} + \frac{{\beta_{2} I\left( t \right)Q_{1} \left( t \right)}}{N} - \left( {\gamma + \varphi_{2} } \right)I\left( t \right), \hfill \\ \frac{dD\left( t \right)}{{dt}} = \varphi_{2} I\left( t \right) - \varphi_{2} I\left( {t - \tau } \right), \hfill \\ \frac{{dQ_{1} \left( t \right)}}{dt} = \varphi_{1} S\left( t \right) - \frac{{\beta_{2} I\left( t \right)Q_{1} \left( t \right)}}{N}, \hfill \\ \frac{{dQ_{2} \left( t \right)}}{dt} = \varphi_{2} I\left( {t - \tau } \right) - \omega Q_{2} (t), \hfill \\ \frac{dR(t)}{{dt}} = \gamma I(t) + \omega Q_{2} (t) - \delta R(t), \hfill \\ \end{gathered} \right. $$
(1)

and the total population is:

$$ N = S\left( t \right) + I\left( t \right) + D(t) + Q_{1} (t) + Q_{2} (t) + R\left( t \right) $$
(2)

In the model, the infection rates \(\beta_{1}\) and \(\beta_{2}\) are determined by three parameters: the successfully infecting rate of the virus (parameter b), the number of people that a virus carrier contacts each day (parameter k) and the average number of days that the infected population can spread the virus (parameter D). In order to calculate the value of this parameter, I use a simplified model (SIR model) to fit the real data. Assuming a person is infected at the beginning of the outbreak, according to the basic epidemic SIR model,

$$ \frac{dI\left( t \right)}{{dt}} = \frac{{\beta_{1} I\left( t \right)S\left( t \right)}}{N} - \gamma I(t) \approx \left( {\beta_{1} - \gamma } \right)I(t), $$
(3)

The solution of the above formula can be solved as the following equation:

$$ I(t) = e^{{\left( {kb - \gamma } \right)t}} $$
(4)

According to the existing confirmed data of COVID-19 released by WHO, it can be fitted that b = 0.04133. Assuming that a virus carrier closely contacts ten people every day, the infection rate is \(\beta_{1} = kb = 0.4133\) in this case (Tables 1 and 2).

Table 1 Notations and their explanations in this paper
Full size table
Table 2 Existing confirmed data of COVID-19 released by WHO [2]
Full size table

During the transmission of infected diseases, the basic regeneration number R0 is also a crucial factor. In pandemic dynamics, if no isolation measures are taken, Lipsitch et al. have given the simple expression of the basic regeneration number \(R_{0} = kbD\) [29]. According to the epidemiological survey results of [30], it is assumed that D = 8, and by using the case report before January 21, 2020, they estimated the basic regeneration number (R0) of 2019-nCoV to be 3.6–4.0 (95% confidence interval). Cao et al. incorporate human movement data to improve epidemiological estimates for 2019-nCoV, and they estimate the basic reproduction number to be 3.24 [31]. Basic reproduction number of some highly infectious disease is given in Table 3. Approximately, in this paper, according to the Lipsitch’s method [29], the basic regeneration number R0 can be calculated as \(R_{0} = kbD{ = }3.3064\).

Table 3 Values of R0 of well-known pandemic diseases
Full size table

3 Stability of Equilibrium and Bifurcation Analysis

The dynamical behaviors of model (1) proposed in Sect. 2 are studied in this section. An equilibrium of model (1) under which the virus remains pandemics is determined, that is, the equilibrium point. Then, the threshold value of Hopf bifurcation and the stability of the model are studied.

Theorem 1

System (1) has a unique positive equilibrium point \(E_{{}}^{*} = (S_{{}}^{*} ,I_{{}}^{*} ,D^{*} ,Q_{1}^{*} ,Q_{2}^{*} ,R^{*} )\), where

$$ S^{*} = \frac{{\left( {\gamma + \varphi_{2} } \right)NI^{*} }}{{\beta_{1} I^{*} + \varphi_{1} N}},D^{*} = \varphi_{2} \tau I^{*} ,Q_{1}^{*} = \frac{{N\left( {\gamma + \varphi_{2} } \right) - \beta_{1} S^{*} }}{{\beta_{2} }},Q_{2}^{*} = \frac{{\varphi_{2} I^{*} }}{\omega },R^{*} = \frac{{\left( {\gamma + \varphi_{2} } \right)I^{*} }}{\delta }. $$

Proof

When system (1) is stable, all the derivatives on the left of equal sign of the system are set to zero, which implies that the system becomes stable, it can be obtained:

$$ \left\{ \begin{gathered} \delta R(t) - \frac{{\beta_{1} I\left( t \right)S\left( t \right)}}{N} - \varphi_{1} S\left( t \right) = 0, \hfill \\ \frac{{\beta_{1} I\left( t \right)S\left( t \right)}}{N} + \frac{{\beta_{2} I\left( t \right)Q_{1} \left( t \right)}}{N} - \left( {\gamma + \varphi_{2} } \right)I\left( t \right) = 0, \hfill \\ \varphi_{2} I\left( t \right) - \varphi_{2} I\left( {t - \tau } \right) = 0, \hfill \\ \varphi_{1} S\left( t \right) - \frac{{\beta_{2} I\left( t \right)Q_{1} \left( t \right)}}{N} = 0, \hfill \\ \varphi_{2} I\left( {t - \tau } \right) - \omega Q_{2} (t) = 0, \hfill \\ \gamma I(t) + \omega Q_{2} (t) - \delta R(t) = 0, \hfill \\ \end{gathered} \right. $$
(5)

Since the total number of hosts in system (1) is \(N\), I can get the following equation of \(I\),

$$ S^{*} { + }I^{*} + \varphi_{2} \tau I^{*} + \frac{{N\left( {\gamma + \varphi_{2} } \right) - \beta_{1} S^{*} }}{{\beta_{2} }} + \frac{{\varphi_{2} }}{\omega }I^{*} + \frac{{\left( {\gamma + \varphi_{2} } \right)}}{\delta }I^{*} = N $$
(6)

Obviously, Eq. (5) has one unique positive root \(I\), there is one unique positive equilibrium point \(E_{{}}^{*} = (S_{{}}^{*} ,I_{{}}^{*} ,D^{*} ,Q_{1}^{*} ,Q_{2}^{*} ,R^{*} )\). The proof is completed.

According to (2), \(Q_{2} (t) = N - S\left( t \right) - I\left( t \right) - D(t) - Q_{1} (t) - R\left( t \right)\), thus system (1) can be simplified to

$$ \left\{ \begin{gathered} \frac{dS\left( t \right)}{{dt}} = \delta R(t) - \frac{{\beta_{1} I\left( t \right)S\left( t \right)}}{N} - \varphi_{1} S\left( t \right), \hfill \\ \frac{dI\left( t \right)}{{dt}} = \frac{{\beta_{1} I\left( t \right)S\left( t \right)}}{N} + \frac{{\beta_{2} I\left( t \right)Q_{1} \left( t \right)}}{N} - \left( {\gamma + \varphi_{2} } \right)I\left( t \right), \hfill \\ \frac{dD\left( t \right)}{{dt}} = \varphi_{2} I\left( t \right) - \varphi_{2} I\left( {t - \tau } \right), \hfill \\ \frac{{dQ_{1} \left( t \right)}}{dt} = \varphi_{1} S\left( t \right) - \frac{{\beta_{2} I\left( t \right)Q_{1} \left( t \right)}}{N}, \hfill \\ \frac{dR(t)}{{dt}} = \gamma I(t) + \omega \left[ {N - S\left( t \right) - I\left( t \right) - D(t) - Q_{1} (t) - R\left( t \right)} \right] - \delta R(t), \hfill \\ \end{gathered} \right. $$
(7)

The Jacobi matrix of system (5) about \(E_{{}}^{*} = (S_{{}}^{*} ,I_{{}}^{*} ,D^{*} ,Q_{1}^{*} ,Q_{2}^{*} ,R^{*} )\) is given by

$$ J(E^{*} ) = \left( {\begin{array}{*{20}c} { - \frac{{\beta_{1} I^{*} }}{N} - \varphi_{1} } & { - \frac{{\beta_{1} S^{*} }}{N}} & 0 & 0 & \delta \\ {\frac{{\beta_{1} I^{*} }}{N}} & {\frac{{\beta_{1} S^{*} }}{N} + \frac{{\beta_{2} Q_{1}^{*} }}{N} - \left( {\gamma + \varphi_{2} } \right)} & 0 & {\frac{{\beta_{2} I^{*} }}{N}} & 0 \\ 0 & {\theta_{2} - \theta_{2} e^{ - \lambda \tau } } & 0 & 0 & 0 \\ {\varphi_{1} } & { - \frac{{\beta_{2} Q_{1}^{*} }}{N}} & 0 & { - \frac{{\beta_{2} I^{*} }}{N}} & 0 \\ { - \omega } & {\gamma - \omega } & { - \omega } & { - \omega } & { - \omega - \delta } \\ \end{array} } \right) $$
(8)

To find the characteristic equation, I have

$$ \lambda {\mathbf{E}} - J(E^{*} ) = \left( {\begin{array}{*{20}c} {\lambda + \beta_{1} a_{1} + \varphi_{1} } & {\beta_{1} a_{2} } & 0 & 0 & { - \delta } \\ { - \beta_{1} a_{1} } & {\lambda - \beta_{1} a_{2} - \beta_{2} a_{3} + \gamma + \varphi_{2} } & 0 & { - \beta_{2} a_{1} } & 0 \\ 0 & { - \theta_{2} + \theta_{2} e^{ - \lambda \tau } } & \lambda & 0 & 0 \\ { - \varphi_{1} } & {\beta_{2} a_{3} } & 0 & {\lambda + \beta_{2} a_{1} } & 0 \\ \omega & { - \gamma + \omega } & \omega & \omega & {\lambda + \omega { + }\delta } \\ \end{array} } \right) $$

where

\(a_{1} = \frac{{I^{*} }}{N},a_{2} = \frac{{S^{*} }}{N},a_{3} = \frac{{Q_{1}^{*} }}{N}\).

The characteristic equation of that matrix (8) can be obtained by

$$ P(\lambda ) + Q(\lambda )e^{ - \lambda \tau } = 0 $$
(9)

The expressions of \(P(\lambda )\) and \(Q\left( \lambda \right)\) are

$$ P(\lambda ) = \lambda^{5} + p_{4} \lambda^{4} + p_{3} \lambda^{3} + p_{2} \lambda^{2} + p_{1} \lambda + p_{0} ,\;Q(\lambda ) = q_{1} \lambda + q_{0} $$
(10)

where

$$ \begin{gathered} p_{4} = \left( {\varphi_{1} + \omega { + }\delta + \beta_{1} a_{1} + \varphi_{2} + \beta_{2} a_{1} + \gamma - \beta_{1} a_{2} - \beta_{2} a_{3} } \right), \hfill \\ p_{3} = \left( \begin{gathered} \varphi_{1} \varphi_{2} + \omega \varphi_{2} { + }\delta \varphi_{2} + \varphi_{1} \gamma + \omega \gamma { + }\delta \gamma \hfill \\ + \beta_{1} \varphi_{2} a_{1} + \omega \beta_{1} a_{1} { + }\delta \beta_{1} a_{1} + \varphi_{1} \omega { + }\varphi_{1} \delta + \varphi_{1} \beta_{2} a_{1} \hfill \\ + \omega \beta_{2} a_{1} { + }\delta \beta_{2} a_{1} + \beta_{1} a_{1} \gamma + \beta_{2} a_{1} \gamma + \beta_{2} a_{1} \varphi_{2} + \beta_{1} a_{1} \beta_{2} a_{1} \hfill \\ - \beta_{2} \beta_{1} a_{1} a_{2} - 2\beta_{2} \beta_{2} a_{1} a_{3} - \beta_{1} \beta_{2} a_{1} a_{3} \hfill \\ - \varphi_{1} \beta_{1} a_{2} - \omega \beta_{1} a_{2} - \beta_{1} \delta a_{2} \hfill \\ - \varphi_{1} \beta_{2} a_{3} - \omega \beta_{2} a_{3} - \delta \beta_{2} a_{3} - \omega \delta \hfill \\ \end{gathered} \right), \hfill \\ p_{2} = \left[ \begin{gathered} \left( {\left( {\omega { + }\delta } \right)\beta_{1} + \beta_{2} \left( {\beta_{1} a_{1} + \varphi_{1} } \right)} \right)\beta_{1} a_{1} a_{2} \hfill \\ + \left( {\omega { + }\delta } \right)\left( {\beta_{1} a_{1} + \varphi_{1} } \right)\left( {\varphi_{2} + \gamma + \beta_{2} a_{1} - \beta_{1} a_{2} - \beta_{2} a_{3} } \right) \hfill \\ + \left( {\varphi_{1} + \omega { + }\delta + \beta_{1} a_{1} } \right)\left( {\varphi_{2} - \beta_{1} a_{2} - 2\beta_{2} a_{3} + \gamma } \right)\beta_{2} a_{1} \hfill \\ + \left( \begin{gathered} \varphi_{1} \omega + \beta_{1} a_{1} \gamma + \omega \beta_{1} a_{2} + \omega \beta_{2} a_{3} \hfill \\ - \omega \beta_{1} a_{1} - \beta_{2} a_{1} \omega - \omega \gamma - \omega \varphi_{2} \hfill \\ \end{gathered} \right)\delta \hfill \\ \end{gathered} \right], \hfill \\ p_{1} = \left[ \begin{gathered} \beta_{2} a_{1} \left( {\varphi_{2} - 2\beta_{2} a_{3} + \gamma } \right)\left( {\omega { + }\delta } \right)\left( {\beta_{1} a_{1} + \varphi_{1} } \right) \hfill \\ + \delta \beta_{2} a_{1} \left( {\omega \beta_{1} a_{2} + \gamma \varphi_{1} - \beta_{1} a_{3} \omega - \varphi_{1} \omega - \omega \gamma - \omega \varphi_{2} } \right) \hfill \\ + \left( {\beta_{1} a_{1} \theta_{2} + \gamma \varphi_{1} + \varphi_{1} \varphi_{2} - \beta_{1} a_{2} \varphi_{1} - \beta_{2} a_{3} \varphi_{1} } \right)\delta \omega \hfill \\ \end{gathered} \right], \hfill \\ p_{0} = \left( {\beta_{1} a_{1} \gamma + \beta_{1} a_{1} \omega \theta_{2} + \theta_{2} \varphi_{1} \omega - \beta_{1} a_{1} \omega } \right)\beta_{2} a_{1} \delta , \hfill \\ q_{1} = - \beta_{1} a_{1} \theta_{2} \omega \delta , \hfill \\ q_{0} = - \left( {\beta_{1} \beta_{2} a_{1} + \beta_{2} \varphi_{1} } \right)a_{1} \theta_{2} \omega \delta . \hfill \\ \end{gathered} $$

Theorem 2

If the following conditions \((H)\) hold, then the positive equilibrium \(E_{{}}^{*} = (S_{{}}^{*} ,I_{{}}^{*} ,D^{*} ,Q_{1}^{*} ,Q_{2}^{*} ,R^{*} )\) is locally asymptotically stable without time delay.

\((H)\):\(p_{4} > 0,p_{3} p_{4} - p_{2} > 0,p_{1} + q_{1} > 0,p_{2} \left( {p_{3} p_{4} - p_{2} } \right) - p_{4}^{2} \left( {p_{1} + q_{1} } \right) > 0\) (11).

Proof

When \(\tau = 0\), Eq. (9) simplifies to

$$ \lambda^{5} + p_{4} \lambda^{4} + p_{3} \lambda^{3} + p_{2} \lambda^{2} + (p_{1} + q_{1} )\lambda + (p_{0} + q_{0} ) = 0 $$
(12)

According to Routh-Hurwitz criterion, all the roots of Eq. (12) have negative real parts. Hence, I can deduce that the positive equilibrium point \(E_{{}}^{*} = (S_{{}}^{*} ,I_{{}}^{*} ,D^{*} ,Q_{1}^{*} ,Q_{2}^{*} ,R^{*} )\) is locally asymptotically stable without time delay. The proof is completed.

For Eq. (9), the root is \(\lambda = i\alpha \left( {\alpha > 0} \right)\), which was substituted into Eq. (9). After separating the real and imaginary parts, two equations were obtained:

$$ p_{4} \alpha^{4} - p_{2} \alpha^{2} + p_{0} + q_{1} \alpha \sin (\alpha \tau ) + q_{0} \cos (\alpha \tau ) = 0 $$
(13)
$$ \alpha^{5} - p_{3} \alpha^{3} + p_{1} \alpha + q_{1} \alpha \cos (\alpha \tau ) - q_{0} \sin (\alpha \tau ) = 0 $$
(14)

Uniting Eq. (13) and (14), Eq. (15) is obtained:

$$ q_{1}^{2} \alpha^{2} + q_{0}^{2} = (p_{4} \alpha^{4} - p_{2} \alpha^{2} + p_{0} )^{2} + (\alpha^{5} - p_{3} \alpha^{3} + p_{1} \alpha )^{2} $$
(15)

which implies

$$ \begin{gathered} \alpha^{10} + \left( {p_{4}^{2} - 2p_{3} } \right)\alpha^{8} + \left( {p_{3}^{2} + 2p_{1} - 2p_{2} p_{4} } \right)\alpha^{6} \hfill \\ + \left( {2p_{0} p_{4} + p_{2}^{2} - 2p_{1} p_{3} } \right)\alpha^{4} \hfill \\ + \left( {p_{1}^{2} - 2p_{0} p_{2} - q_{1}^{2} } \right)\alpha^{2} + p_{0}^{2} - q_{0}^{2} = 0, \hfill \\ \end{gathered} $$

that is

$$ \alpha^{10} + D_{4} \alpha^{8} + D_{3} \alpha^{6} + D_{2} \alpha^{4} + D_{1} \alpha^{2} + D_{0} = 0 $$
(16)

where

$$ \begin{gathered} D_{4} = p_{4}^{2} - 2p_{3} , \hfill \\ D_{3} = p_{3}^{2} + 2p_{1} - 2p_{2} p_{4} , \hfill \\ D_{2} = 2p_{0} p_{4} + p_{2}^{2} - 2p_{1} p_{3} , \hfill \\ D_{1} = p_{1}^{2} - 2p_{0} p_{2} - q_{1}^{2} , \hfill \\ D_{0} = p_{0}^{2} - q_{0}^{2} . \hfill \\ \end{gathered} $$
(17)

Let \(x = \alpha^{2}\), then Eq. (16) can be turned into:

$$ f(x) = x^{5} + D_{4} x^{4} + D_{3} x^{3} + D_{2} x^{2} + D_{1} x + D_{0} = 0 $$
(18)

Let us assume that the following conditions (\(H_{1}\)) hold: \(p_{4} > 0,d_{1} > 0,p_{1} > 0,p_{2} d_{1} - p_{4}^{2} p_{1} > 0\) is satisfied. From previous derivation, Eq. (18) has at least a positive root \(\alpha_{0}\) which also means Eq. (9) has a pair of purely imaginary roots \(\pm i\alpha_{0}\). By uniting Eq. (13) and Eq. (14), the corresponding threshold value \(\tau_{k} > 0\) can be gotten:

$$ \tau_{k} = \frac{1}{{\alpha_{0} }}\arccos \left[\frac{{q_{0} (p_{2} \alpha_{0}^{2} - p_{4} \alpha_{0}^{4} - p_{0} ) + q_{1} \alpha_{0} (p_{3} \alpha_{0}^{3} - \alpha_{0}^{5} - p_{1} \alpha_{0} )}}{{q_{0}^{2} + q_{1}^{2} \alpha_{0}^{2} }}\right] + \frac{2k\pi }{{\alpha_{0} }} $$
(19)

Let \(\lambda (\tau ) = v(\tau ) + i\omega (\tau )\) be the root of Eq. (9). It is satisfied that \(v(\tau_{k} ) = 0\), \(\omega (\tau_{k} ) = \alpha_{0}\) when \(\tau = \tau_{k}\).

Theorem 3

Supposing \(f^{\prime } (x_{0} ) \ne 0\). If \(\tau = \tau_{k}\), and \(\pm i\alpha_{0}\) is a pair of purely imaginary roots of Eq. (9), then \(\frac{{d{\text{Re}} \lambda (\tau_{k} )}}{d\tau } > 0\).

Proof

This means that there exists at least one eigenvalue with positive real part when \(\tau > \tau_{k}\). Differentiating on both sides of Eq. (9) with respect to \(\tau\), I can obtain:

$$ \begin{aligned} \left( {\frac{d\lambda }{{d\tau }}} \right)^{ - 1} &= \frac{{(5\lambda^{4} + 4p_{4} \lambda^{3} + 3p_{3} \lambda^{2} + 2p_{2} \lambda + p_{1} ) + q_{1} e^{ - \lambda \tau } - (q_{1} \lambda + q_{0} )\tau e^{ - \lambda \tau } }}{{(q_{1} \lambda + q_{0} )\lambda e^{ - \lambda \tau } }} \hfill \\ &= \frac{{(5\lambda^{4} + 4p_{4} \lambda^{3} + 3p_{3} \lambda^{2} + 2p_{2} \lambda + p_{1} )e^{\lambda \tau } }}{{(q_{1} \lambda + q_{0} )\lambda }} + \frac{{q_{1} }}{{(q_{1} \lambda + q_{0} )\lambda }} - \frac{\tau }{\lambda } \hfill \\ \end{aligned} $$
(20)

Then,

$$ \begin{gathered} {\text{sgn}} \left[ {\frac{{d{\text{Re}} \lambda }}{d\tau }} \right]_{{\tau = \tau_{k} }} = {\text{sgn}} \left[ {{\text{Re}} \left( {\frac{d\lambda }{{d\tau }}} \right)^{ - 1} } \right]_{{\lambda = i\alpha_{0} }} \hfill \\ = {\text{sgn}} \left[ {{\text{Re}} \left( {\frac{{(5\lambda^{4} + 4p_{4} \lambda^{3} + 3p_{3} \lambda^{2} + 2p_{2} \lambda + p_{1} )e^{\lambda \tau } }}{{(q_{1} \lambda + q_{0} )\lambda }} + \frac{{q_{1} }}{{(q_{1} \lambda + q_{0} )\lambda }} - \frac{\tau }{\lambda }} \right)} \right]_{{\lambda = i\alpha_{0} }} \hfill \\ = {\text{sgn}} \frac{{4\alpha_{0}^{6} + (3p_{4}^{2} - 6p_{3} )\alpha_{0}^{4} + (2p_{3}^{2} + 4p_{1} - 4p_{2} p_{4} )\alpha_{0}^{2} + (p_{2}^{2} + 2p_{0} p_{4} - 2p_{1} p_{3} )}}{{q_{1}^{2} \alpha_{0}^{2} + q_{0} }} \hfill \\ = {\text{sgn}} \left\{ {f^{\prime } (\alpha_{0}^{2} )} \right\} \hfill \\ \end{gathered} $$

It follows that \(f^{\prime } (x_{0} ) \ne 0\), therefore,

$$ \left. {\frac{{d({\text{Re}} \lambda )}}{d\tau }} \right|_{{\tau = \tau_{k} }} > 0. $$
(21)

According to Routh’s theorem [43], as \(\tau\) continuously varies from a value less than \(\tau_{k}\) to one greater than \(\tau_{k}\), the root of characteristic Eq. (9) crosses from left to right on the imaginary axis. Thus, the transverse condition holds and the conditions for Hopf bifurcation are satisfied at \(\tau = \tau_{k}\) according to Hopf bifurcation theorem. Therefore, the following conclusions can be obtained.

Theorem 4

Supposing that the conditions (\(H_{1}\)) are satisfied.

  1. (1)

    When \(0 \le \tau < \tau_{0}\), the positive equilibrium \(E_{{}}^{*} = (S_{{}}^{*} ,I_{{}}^{*} ,D^{*} ,Q_{1}^{*} ,Q_{2}^{*} ,R^{*} )\) of system (2) is locally asymptotically stable, and unstable when \(\tau \ge \tau_{0}\).

  2. (2)

    If Eq. (9) has a pair of purely imaginary roots \(\pm i\alpha_{0}\), the system undergoes a Hopf bifurcation at the positive equilibrium \(E_{{}}^{*} = (S_{{}}^{*} ,I_{{}}^{*} ,D^{*} ,Q_{1}^{*} ,Q_{2}^{*} ,R^{*} )\) when time delay \(\tau = \tau_{0}\).

This implies that when time delay \(\tau < \tau_{0}\), the system will stabilize at the equilibrium point, which is beneficial for us to implement a containment strategy; when the delay \(\tau \ge \tau_{0}\), the system will be unstable and the virus cannot be effectively controlled.

4 Numerical Simulations

In this section, numerical simulations are conducted to reveal the pandemic dynamics of COVID-19, and some nonlinear properties of the system are verified. In the following experiments, it is assumed that the total number of population is 10000000, at the beginning, the number of infected population is 10. And I will conduct experiments in two cases, with \(\tau < \tau_{0}\) and \(\tau \ge \tau_{0}\).

4.1 The Case of \(\tau < \tau_{0}\)

The value of parameters is listed as follows.

Because the population at home isolation state contact fewer people, the infection rate for home isolation population (\(\beta_{2}\)) is lower than the infection rate for susceptible population (\(\beta_{1}\)). Assuming that they contact eight people every day, the infection rate for home isolation population is \(\beta_{2} = kb = 0.33064\) in this case. Currently, the duration of medical observation before hospital quarantine is generally 14 days, it means that the delay time can be 14 days in this case. When \(\tau = 14 < \tau_{0}\), we can see the changes of the numbers of six states of population in Fig. 2. It can be found that the equilibrium point \(E_{{}}^{*} = (S_{{}}^{*} ,I_{{}}^{*} ,D^{*} ,Q_{1}^{*} ,Q_{2}^{*} ,R^{*} )\) is locally asymptotically stable.

Fig. 2
figure 2

Equilibrium for the pandemic mode when \(\tau = 14 < \tau_{0}\)

Full size image

The parameter \(\varphi_{2}\) indicates the intensity of isolation policy. In other words, larger parameters \(\varphi_{2}\) mean that the hospital can treat more patients. It has a direct impact on the number of infected population. Figure 3 shows the change of the infected population with different \(\varphi_{2}\) when \(\tau = 14 < \tau_{0}\). Obviously, increasing the intensity of hospital quarantine can significantly improve the effect of pandemic control. In other words, the government should increase the number of tested people with or without symptoms in order to identify early on clusters of infection which can be targeted with an isolation strategy.

Fig. 3
figure 3

The number of infected population \(I(t)\) with different \(\varphi_{2}\)

Full size image

4.2 The Case of \(\tau \ge \tau_{0}\)

The delay will increase as the incubation period increases. Once the delay exceeds the threshold value, the pandemic dynamic system is at risk of instability. The stability of equilibrium point is simulated when \(\tau { = }40 \ge \tau_{0}\) in Fig. 4. The values of parameters are the same as in Table 1 except \(\tau\). The equilibrium is unstable within 1000 days. To show the stability of equilibrium point when \(\tau { = }40\) more clearly, the number of infected population \(I(t)\) with different \(\beta_{2}\) is shown in Fig. 5 on a larger time scale. For the same virus (COVID-19), the change in infectious ability is very small. For \(\beta_{2} = kb\), the number of people that the population at home isolation state contact each day (k) is the key factor. In Fig. 5, three cases (\(k = 6,8,10\), correspondingly, \(\beta_{2} = 0.24798,0.33064,0.4133\)) are shown. When \(\beta_{2} = \beta_{1} { = }0.4133\), it can clearly find that the number of infected population will outburst after a short period of peace and repeat again and again. In this situation, the effect of home isolation fails. When the population at home isolation state contact two people less every day (\(\beta_{2} = 0.24798,0.33064\)), the effect of home isolation is very significant. This illustrates the importance of home isolation for pandemic control, it is crucial that residents restrain their daily behavior, and it is a feasible solution for pandemic prevention (Table 4).

Fig. 4
figure 4

Equilibrium for the pandemic mode when \(\tau = 40 \ge \tau_{0}\)

Full size image
Fig. 5
figure 5

The number of infected population \(I(t)\) with different \(\beta_{2}\) when \(\tau = 40\)

Full size image
Table 4 Parameters in the simulations
Full size table

The annual, biennial or sporadic COVID-19 outbreak is similar to the projection of the researchers in Harvard University which was published in Science. They project that if the immunity of the antibody maintains for 40 weeks or 104 weeks, it will favor annual COVID-19 outbreaks or biennial outbreaks [44]. Obviously, the term of immunity affects the parameters \(\delta\) in the model, then the simulation with different \(\delta\) is shown in Fig. 6.

Fig. 6
figure 6

The number of infected population \(I(t)\) with different \(\delta\) when \(\tau = 40,\beta_{2} = \beta_{1} = 0.4133\)

Full size image

In Figs. 6 and 7, the influence of the rate \(\delta\) and the self-healing rate \(\gamma\) on the spread of the virus is simulated, respectively. From the two figures, we can find that lower \(\delta\) and larger \(\gamma\) are more beneficial for the prevention of COVID-19. It means that we should improve the self-healing ability of infected population and maintain the immunity of the recovered population (vaccine may be the best method). In other words, the longer the vaccine effect lasts, the easier it is to limit the spread of the virus.

Fig. 7
figure 7

The number of infected population \(I(t)\) with different \(\gamma\) when \(\tau = 40,\beta_{2} = \beta_{1} = 0.4133\)

Full size image

4.3 Hopf Bifurcation of the Equilibrium

To show the bifurcation phenomenon of the equilibrium clearly in the model, the results of numerical experiment are shown in Figs. 8, 9, 10, 11 and 12. Figure 8 shows the projection of the phase portrait in \((I,Q,R)\)-space when \(\tau = 40\), the value of parameters is listed in Table 5. The curve radiates to a limit cycle which implies the system is unstable, and it corresponds to the curve (\(\beta_{2} = 0.4133\)) in Fig. 5. Then, let us observe the effect of \(\beta_{2}\) and \(\delta\) on the bifurcation phenomenon in Figs. 9 and 10, respectively. In Fig. 9, only the infection rate for home isolation population (\(\beta_{2}\)) is decreased, then it is found that the curve converges to a fixed point which implies the system is stable. In Fig. 10, only the rate \(\delta\) is decreased, and the curve converges to a fixed point which implies the system is stable as well. It means that the parameters \(\beta_{2}\) and \(\delta\) affect the threshold \(\tau_{0}\) of bifurcation.

Fig. 8
figure 8

The projection of the phase portrait in \((I,Q_{1} ,R)\)-space when \(\beta_{2} { = }0.4133,\delta = 0.04\)

Full size image
Fig. 9
figure 9

The projection of the phase portrait in \((I,Q_{1} ,R)\)-space when \(\beta_{2} = 0.33064,\delta = 0.04\)

Full size image
Fig. 10
figure 10

The phase portrait of \(Q_{1} (t)\) and \(I(t)\) when \(\beta_{2} { = }0.4133,\delta = 0.02\)

Full size image
Fig. 11
figure 11

Bifurcation diagram of the equilibrium with \(\beta_{2} { = }0.4133,\delta = 0.04\)

Full size image
Fig. 12
figure 12

Bifurcation diagram of the equilibrium with \(\beta_{2} { = }0.33064,\delta = 0.02\)

Full size image
Table 5 Parameters in Fig. 9
Full size table

Figure 11 gives the bifurcation diagram of the equilibrium with the parameters \(\beta_{2} { = }0.4133,\delta = 0.04\). It can be easily obtained that the Hopf bifurcation occurs at about \(\tau = \tau_{0} = 33\) which is similar to the results of theoretical derivation. Figure 12 gives the bifurcation diagram of the equilibrium with the parameters \(\beta_{2} { = }0.33064,\delta = 0.02\). The Hopf bifurcation occurs at about \(\tau = \tau_{0} = 43\). Comparing the two Figs, it shows that the parameters \(\beta_{2}\) and \(\delta\) have effect on the time that Hopf bifurcation occurs. As the parameters \(\beta_{2}\) and \(\delta\) decrease, the threshold value of the bifurcation increases, and the control of the pandemic is more effective. This confirms the importance of home isolation and the immunity of the population (or the vaccine effect) once again.

5 Discussion and Conclusion

In the proposed model, hierarchical quarantine strategy is deployed to prevent the COVID-19 outbreak, and home isolation is a feasible and crucial measure. To illuminate the role of home isolation in the pandemic prevention, a simplified model without the home isolation state is proposed to compare with the hierarchical quarantine strategy. The transition diagram is given in Fig. 13. And the value of the parameters is the same as that in Table 4. The case of \(\tau = 14 < \tau_{0}\) is conducted to show the comparison. The number of infected population is shown in Fig. 14. The effect of home isolation is clearly shown in Fig. 14. When the dynamic system reaches the equilibrium point, the number of infected population without home isolation is larger than that with hierarchical quarantine strategy. In addition, the peak in the model with hierarchical quarantine strategy is much lower than that without home isolation. The result indicates that the hierarchical quarantine strategy can inhibit the spread of COVID-19 effectively. The surveillance of COVID-19 should be maintained as normal and people should restrain their actions at this urgent time and try to avoid close contact with people as much as possible.

Fig. 13
figure 13

State transition diagram of the pandemic model without home isolation

Full size image
Fig. 14
figure 14

Comparison of the infected population for the two models

Full size image

In summary, a pandemic model with hierarchical quarantine and time delay is developed for the COVID-19 outbreak. Time delay caused by virus incubation period and the possibility of reinfection due to antibody failure are well considered in the model. The model gives a better description of the spread of COVID-19 and some suggestions worth considering for the COVID-19 prevention. For example, the government should increase the number of tested people with or without symptoms in order to identify early on clusters of infection which can be targeted with an isolation strategy. The stability of the equilibrium and the bifurcation phenomenon is analyzed in detail. The threshold value \(\tau_{k}\) of the bifurcation is deduced and quantitatively analyzed. When the time delay is low, i.e., \(\tau < \tau_{0}\), the system will stabilize at the equilibrium point, which is beneficial for us to implement a containment strategy of COVID-19; when the time delay is long, i.e., \(\tau \ge \tau_{0}\), the system will be unstable and the virus cannot be effectively controlled. Fortunately, the simulations show that the COVID-19 pandemic dynamic system is stable with \(\tau { = }14\) (at present, the latent observation period is usually two weeks), however, the trend of the COVID-19 pandemic may have some ups and downs in a period of time. In addition, the results of the numerical simulations show that lower \(\delta\) (larger self-healing rate) and larger \(\gamma\) (vaccine with better immunogenicity) are more beneficial for pandemic prevention of COVID-19, \(\delta\) means the rate that the recovered population lose immunity, and \(\gamma\) means the self-healing rate of infected population. If the immunity of recovered population lasts for a short time, the prevention of COVID-19 will be beset with difficulties. Evidently, home isolation is a more feasible and effective measure. The simulations show that a lower \(\beta_{2}\) can expand the threshold \(\tau_{0}\) of bifurcation, which leads a better effect of the COVID-19 prevention. For the public, just staying home and avoiding close contact with people will provide great support to prevent the COVID-19 outbreak.