Introduction

In all climatic areas across the globe, groundwater is a highly significant and stable water source. Groundwater resource is depleted because of overexploitation with other natural resources (Falkenmark et al. 2019). The agriculture for developing countries like Bangladesh relies on irrigation based on groundwater. Therefore, groundwater exploitation is higher, causing the loss of groundwater supplies, which is a significant cause of worry (Khan et al. 2021; Nzama et al. 2021). In Bangladesh, Groundwater provides around 79 percent of the water supply (Shahinuzzaman et al. 2021). Groundwater provides 95 percent of irrigation supplies in certain sections, like the northwest (Shahinuzzaman et al. 2021). Agriculture accounts for around 18 percent of Bangladesh’s GDP and provides jobs to about 48 percent of the workforce (Shahinuzzaman et al. 2021). As a result, the development of groundwater resources is critical to the country's social and economic growth. It is also critical for the agricultural policy of the government toward attaining food independence and poverty reduction (Salem et al. 2017).

Consequently, it is critical to design a tactical plan to properly evaluate and manage groundwater resources using an assimilated method that considers a variety of ecological, socioeconomic, and scientific aspects. For the extension of irrigation-based agriculture and the execution of government initiatives, a thorough understanding of the spatial distribution of groundwater accessibility is critical. In order to minimize overdraft, it is also critical to utilize groundwater wisely (Benjmel et al. 2020).

Delineation of the areas having groundwater is one of the most fundamental aspects of groundwater research. Recently, there has been a strong interest in potential groundwater mapping among the researchers, especially in dry places, where the shortage of safe freshwater is a significant issue, and the growth of irrigation, industry, and urbanization is nearly entirely dependent on groundwater (Portoghese et al. 2021; Zhu and Abdelkareem 2021). The geographic information systems (GISs) and remote sensing (RS) technology have been used recently to analyze large-scale spatial and temporal databases. These technologies help delineate the potential groundwater zones with high precision and very little time. These technologies have replaced the time-consuming and costly groundwater research methods, such as drilling and geological and geophysical procedures. Now, GIS is crucial for dealing with large geographic datasets, such as spring and qanat sites (Pham et al. 2021; Nwankwo et al. 2020). By integrating RS and GIS, many topographical, hydrological, climatic, pedogenic parameters for extensive areas can be extracted with very high precision (Arabameri et al. 2020, 2021) (Table 1). Also, these technologies help to assimilate multi-parameters and are able to produce highly accurate groundwater potential maps for large to a small areas within a short time (Dau et al. 2021; Namous et al. 2021). Therefore, these technologies have added a new dimension to groundwater research (Mallick et al. 2021c; Nguyen et al. 2020). The robust and effective models generally rely on the choice of conditioning variables and standard assimilation methods (Kumar et al. 2020). The proper parameters choice for GWP modeling is challenging because redundant parameters can produce the erroneous results (Malik and Bhagwat 2021). However, researchers have used several topographical, hydrological, climatic, pedogenic parameters for modeling (Tolche 2021; Zhu and Abdelkareem 2021). In the present study, we chose the conditioning variables for the modeling based on the literature survey (Table 2). We chose those variables, which many researchers have extensively used. In the plain regions, topographic and climatic parameters have been recognized as important variables, while in the mountains, along with topographic, geological variables have been described as critical variables for GWP mapping (Mallick et al. 2021c; Al-Djazouli et al. 2021; Pathak et al. 2021; Namous et al. 2021; Al-Abadi et al. 2021). For example, drainage density could be a valid variable in flood plains, not in mountainous regions (Bhattacharya et al. 2021; Fadhillah et al. 2021). Therefore, researchers should pay attention while choosing variables for modeling the spatial features of the study area (Pal et al. 2020b). Consequently, as shown in Table 1, the groundwater potentiality conditioning factors utilized in this study were determined after a comprehensive literature review.

Table 1 Literature review for groundwater potentiality conditioning parameters selection
Full size table
Table 2 Literature survey for hybrid models used to forecast groundwater potential zones
Full size table

Recently, researchers have found that just the assimilation of several parameters does not provide highly accurate and robust GWP maps; therefore, to achieve the accurate GWP maps, researchers have to use different methods, which can assimilate mathematically all parameters having different data patterns and direction (Hembram et al. 2019; Das et al. 2021). Therefore, researchers have been paid higher interest in developing such accurate GWP modeling methods (Nguyen et al. 2020). Several approaches have been developed and used for GWP modeling (Pande et al. 2020). Therefore, we classified all methods as per their operational background, such as (1) statistical approaches for zoning groundwater potential, which have a long history of use (Mallick et al. 2021c; Pham et al. 2021). Statistical procedures that are now in use include frequency ratio (Abd Manap et al. 2014; Guru et al. 2017), logistic regression (Rizeei et al. 2019), weight of evidence (Rane and Jayaraj 2021; Das et al. 2021), certainty factor (Razandi et al. 2015), and evidential belief function (Tahmassebipoor et al. 2016). However, they have several disadvantages, including a lack of precision (Chen et al. 2020). (2) Techniques for multi-criteria decision analysis (MCDA), such as the analytic hierarchy process (AHP) (Kumar et al. 2020; Murmu et al. 2019) and TOPSIS (Mandal et al. 2021; Zaree et al. 2019). Experts' judgment has tuned semiquantitative models (AHP), but for comparable geo-environmental elements or locations, the models need extensive understanding of groundwater and conditioning variables, which is seldom accessible (El Bilali et al. 2021; Mogaji et al. 2016). Statistical approaches have been widely regarded as the best way for GWP mapping at sizes of 1:20,000 to 1:50,000, as they can map springs and wells in detail (Mallick et al. 2021a; Arshad et al. 2020). Statistical models cannot account for nonlinear interactions. Therefore, machine learning (ML) models based on artificial intelligence have been created (Mallick et al. 2021a). The conditions necessary to enhance groundwater capacity have been established using machine learning algorithms based on data mining. (3) Machine learning (ML) models include CART (Gayen and Pourghasemi 2019), random forest (RF) (Golkarian et al. 2018), support vector machine (Panahi et al. 2020), artificial neural network (Nguyen et al. 2020; Naghibi et al. 2017; Mallick et al. 2021c), neuro-fuzzy (Termeh et al. 2019), and decision trees (Choubin et al. 2019). Each has the same goal: to discover the best cost-effective and efficient technique. It is also worth noting that utilizing field data in GIS-based models enhances outcomes (Phong et al. 2021; Zhao and Chen 2020).

The utilization of EML algorithms has been substantially increased for higher accuracy in GWP mapping (Al-Abadi and Shahid 2015). Ensemble modeling included two or more ML algorithms to enhance the prediction accuracy (Muavhi et al. 2021; Pham et al. 2021; Farzin et al. 2021). Ensemble modeling can mitigate the flaws of an individual model (Talukdar et al. 2020, 2021b; Rahmati et al. 2016). Susceptibility, vulnerability, hazards, potentiality, and other issues can now be studied using a multi-model approach and ensemble modeling (Talukdar and Pal, 2019; Islam et al., 2021; Mahato et al. 2021; Talukdar et al. 2021a). The ensemble models include AdaBoost (Ha et al. 2021), bagging (Yen et al. 2021), Reptree-bagging (Chen et al. 2019a), dagging (Talukdar et al. 2021a, b), and rotation forest (Mallick et al. 2021c). Therefore, to increase the model's resilience for GWP mapping, we utilized six ensemble machine learning techniques in the present study, including RF, RS, bagging, dagging, NBT, and stacking. The EML-based prediction approach is rarely utilized in the Teesta River Basin of Bangladesh for GWP mapping.

Experimental hybrid models for GWP mapping have now been investigated in recent years, as there is a necessity to investigate contemporary prediction methodologies and procedures to collect more scientific knowledge to make fair findings (Table 2). Several hybrid approaches have been effectively utilized for groundwater potentiality modeling, which has been produced by combining statistical techniques with machine learning approaches, such as bagging based linear discriminant function (Chen et al. 2019b), EML models with discriminant analysis (Ha et al. 2021), and adaptive neuro-fuzzy (Termeh et al. 2019).

To create hybrid models, six EML models were combined with four operators of fuzzy logic models and a ROC-based weighting technique in the current work. The hybrid models have a higher capacity to help researchers in future groundwater potentiality studies by increasing the popularity of this approach. Predictions of GWP utilizing contemporary hybrid techniques are significant since the models are more accurate in detecting and predicting than machine learning models.

Additionally, prior studies devoted minimal emphasis to thematic layer sensitivity analysis. This research has treated thematic layers with sensitivity tests following creating hybrid models. The most significant thematic layers have been determined utilizing several machine learning-based sensitivity studies to improve the model's predictive performance. This technique was utilized to minimize uncertainty in other research, such as gully erosion prediction, land subsidence prediction, and landslide susceptibility (Forkuor et al. 2017; Abdulkadir et al. 2019; Chen et al. 2018). In this study, RF-based sensitivity analyses were implemented to identify the model's significant thematic layer output. In addition, the model's efficiency was assessed using the ROC curve. Only a few researchers have used parametric and nonparametric ROC curves for validation. Therefore, to address the research as mentioned earlier gaps, the study's main objectives are to:

  1. 1.

    Develop hybrid algorithm-based GPMs by combining EMLs such as RF, RS, bagging, dagging, NBT, and stacking with four fuzzy logic operators;

  2. 2.

    Undertake sensitivity analysis; and

  3. 3.

    Apply eROC and bROC curves for validation.

This study will aid governments and scientists in effectively proposing plans for groundwater management.

Materials and methods

Description of the study area

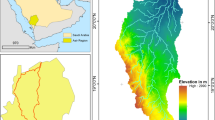
The Teesta River is originated from eastern Himalayas, flows across Bangladesh's northern area (Fig. 1), and is recognized as the lifeblood of Bangladesh's northern area. This river covers fourteen percent land, which provides direct and indirect livelihood for twenty-one million people of Bangladesh, which accounts for seven percent population of the Bangladesh (BBS 2016). The floodplain of this river is considered as the important geomorphic units, including fourteen northern districts. It flows across the five districts of Bangladesh (Gaibandha, Kurigram, Lalmonirhat, Nilphamari, and Rangpur districts). The basin area of this river is around 2,000 km2 and comprises alluvial floodplain having fine to medium sand.

Fig. 1
figure 1

The location of the study area

Full size image

This river is a vital supply of water in the northern drought-prone area, and millions of people rely on it for their lives. The study area is in a subtropical monsoon climatic zone where rainfall occurs only during monsoon months (June to September), dry for the rest of the year (Akter et al. 2019). Although the northern region stays dry throughout the post- and pre-monsoon seasons, the area receives over 1900 mm of annual rainfall on average. Summer and winter mean temperatures in the Teesta River basin are about 35 °C and 15 °C, respectively (Islam et al. 2014).

Preparation of groundwater inventory

In the present research, GWP was predicted using ML and EML algorithms with conditioning parameters. To create the inventory, we used well locations of the study area. The inventory map for the study area contains 230 well points gathered across multiple sources and a thorough field examination. First, non-groundwater data should be generated that is comparable to the groundwater data used in GWP modeling. The field survey has been used to make the selection, along with an equal quantity of non-groundwater data (230 points). All datasets have been separated into 80 percent (368): 20 percent (92 points) training and testing datasets based on arbitrary partitioning (Fig. 11). Groundwater and non-groundwater training data are used to calibrate the model, while groundwater and non-groundwater testing data are used to validate it (Mallick et al. 2021b).

Data preparation

In the present study, we selected 12 conditioning variables based literature review, availability of data, and technological setup (Table 1). Therefore, the variables are elevation, aspect, TWI, SPI, STI, LULC, TRI, distance to the river, curvature, soil condition, slope, and rainfall. Employing a resampling approach, all relevant factors have been converted to a spatial resolution of 30 m.

Topographic factors, derived from ASTER GDEM, are important for GWP modeling since they influence the study region's hydrological properties both directly and indirectly (Bui et al. 2020b).

Elevation

The elevation primarily shows surface terrain irregularity, crucial to groundwater potentiality. There is a reduced infiltration rate in locations connected with steep elevation due to increased surface runoff. In contrast, plain land with lower elevation has an extended water retention period, increasing the water infiltration rate for higher groundwater recharge (Arulbalaji et al. 2019). We created the elevation map of the research region using an SRTM-DEM. The research area's elevation ranges from 18 to 69 m (Fig. 2a). The majority of the region (about 70% of the total area) has elevations ranging from 18 to 40 m, while fewer than 10% of the entire area has elevations over 60 m.

Curvature

Curvature values describe the shape of regional topography (Ginesta Torcivia and Ros López 2020). A positive curvature indicates that the surface is convex, whereas a negative curvature indicates that it is concave (Costache and Tien Bui 2020). The value zero denotes a fat surface. Convex slopes, on the other hand, drain more runoff water than concave slopes. The concave down regions have been the most vulnerable to groundwater recharge (Fig. 2b).

TRI

Riley et al. (1999) created TRI (Fig. 2c) by computing the discrepancy between the elevation values of a given cell in a DEM (Arabameri et al. 2021). Each of the numbers is squared to keep them all positive, and then, the squares are averaged. To obtain the TRI, the square root of this average is calculated. The TRI value in the study area ranges 0–27.

Aspect

Aspect is the direction in which a slope faces, and it impacts the physical properties of a slope such as lineament, and exposure to sunlight (Masroor et al. 2021). DEM was used to construct aspect data (Fig. 2d), which were divided into nine categories: north, east, south, west, northeast, northwest, southeast, southwest, and flat.

Slope

Slope is the magnitude of inclination of a surface in reference to a horizontal plane that affects water flow under the influence of gravity, thereby determining subsurface lateral transmissivity rate (Bhattacharya et al. 2021; Al-Abadi et al. 2021). It controls the quantity of water that collects in a certain area, and hence plays an essential role in groundwater recharge. Lower slopes and flat regions define the research area, which contribute to good groundwater recharge. The study area belongs to flat regions, therefore, has a high probability of groundwater (Fig. 2e).

TWI

The topographic wetness index (TWI) was first established by Beven and Kirkby (1979) as part of the runoff model TOPMODEL (Arulbalaji et al. 2019). This index is an indicator of availability of water in an area as a result of topographic effects on water accumulation (Mokarram et al. 2015). This index represents the amount of water contained in the region at each pixel scale (Saha et al. 2021) and is calculated using Eq. (1):

$${\text{TWI}} = \frac{{\ln ({A_s})}}{\tan \beta }$$
(1)

As and β denote, respectively, the same catchment area (m2m1) and slope (in degrees). High TWI values and GWP have a strong association in general (Shit et al. 2020). TWI values range from − 1.54 to 7.72 in the research region (See Fig. 2f.)

SPI

The slope and contributing area are used to determine SPI, which is a measure of the erosive strength of flowing water (Namous et al. 2021). The SPI is calculated using Eq. 2.

$${\text{SPI}} = {A_s}\;\tan \beta$$
(2)

As indicates the catchment area, while \(\beta\) denotes the slope. The SPI in the study area ranges between 0 and > 3 (Fig. 3a).

Fig. 2
figure 2

Thematic parameters for GWP modeling such as a elevation, b curvature, c TRI and d aspect, e slope, and f TWI

Full size image

STI

The sediment transport index (STI) represents the quantity of erosion and depositions that might affect infiltration and recharging (Pham et al. 2021). The channel's bed alters owing to silt deposition, limiting the channel's capacity to retain water and creating groundwater potentiality. The STI is calculated from the DEM using Eq. 3.

$${\rm{STI}} = {\left( {\frac{{{A_s}}}{{22.13}}} \right)^{0.6}}{\left( {\frac{{\sin }}{{0.0896}}} \right)^{1.3}}$$
(3)

where each pixel of the slope of the upstream region is defined by As. The STI value in the study area varies between 0 and 140.64. (See Fig. 3b.)

Rainfall

Rainfall, collected from meteorological stations of Bangladesh, has been identified as a critical component in influencing the possibility for groundwater to be recharged (Arulbalaji et al. 2019). In part, an excessive amount of rain in a short period may cause a low groundwater potential (Fadhillah et al. 2021). The kriging interpolation method constructed a rainfall map in the ArcGIS software version 10.3 environment using recorded rainfall data from four Bangladesh meteorological stations. The data were imported into ArcGIS 10.3 and processed. Because of the tiny quantity of information available, this strategy is highly recommended (Zhu and Abdelkareem 2021). The yearly rainfall in the study region, on the other hand, varies from 361 to 550 mm each year (Das 2021; Das and Wahiduzzaman 2021) (Fig. 3c).

Soil types

Soil type affects the rainfall-runoff process (Tolche 2021). Soil qualities directly regulate water penetration, therefore affects rainfall-runoff production. If the degree of penetration seems to be high, groundwater incidents are more likely to happen. According to USDA soil classification, the research area comprises 12 different types of soil (Fig. 3d).

Land use/land cover

The influence of LULC on surface runoff and sediment flow has a substantial effect on the incidence of groundwater potentiality (Senapati and Das 2021). Usually, the LULC has a complete control over surface runoff production and penetration. The built-up regions prohibit water from accessing and creating surface water, and groundwater potentiality is quite low. The forest environment, on the other hand, favors water infiltration, resulting in lower groundwater potentiality (Elmahdy et al. 2020). The association between GWP and plant density is inverse when evaluating hydrological responses at different time scales (Senapati and Das 2021). We collected Landsat 8 OLI (path/row: 138/42) for LULC mapping. The ANN model was used to produce a LULC map in ENVI software (version 5.3). The LULC map was categorized into six classes: bare land, forest, sand bar, built-up, agricultural land, and water body (Fig. 3e).

Distance to the river

The majority of groundwater potentiality-inundation regions are often located around the river's edge. Because river distance effects groundwater potentiality and river flow to river aspect, it is an important factor for finding basin regions with high groundwater potential (Namous et al. 2021). The greater the distance between a place and a river, the less probable it is that the area has a big amount of groundwater capacity. The basin-scale storage of terrestrial water accounts for regional groundwater potentiality. In this investigation, we used a topographic map with a scale of 1: 50,000 and Google Earth to compute the distance to the river map (Fig. 3f).

Methods for information gain ratio and multicollinearity test

Before using ML models to measure GWP in this study, two preliminary tests have been executed, such as multicollinearity and feature selection. When two or more variables in an analysis have a linear correlation, multicollinearity arises. If there is multicollinearity, slight adjustments in the model or data might cause considerable variations in the multiple regression coefficient estimations. This circumstance may impair the precision of the generated models' predictions. The feature selection (FS) test is the other preliminary test, and it seeks to pick the appropriate characteristics for utilization in model creation. The FS minimizes the complexity of a model while also improving the predictors' effectiveness. It also allows for a deeper grasp of the underpinning mechanism that produced the data (Tien Bui et al. 2020). The information gain ratio (IGR) approach was employed in this investigation. IGR measures the information gain with regard to the class to determine the value of a feature. The IGR measures the value of a characteristic in relation to the class, with a larger information gain ratio indicating a stronger prediction power of the utilized models. Tien Bui et al. (2020) provide more information on this approach.

Method for groundwater potentiality modeling

RF

A random forest model is an ensemble machine learning approach that may build many decision trees to elucidate the spatial link between landslides. It operates by training many decision trees and then generating classes that represent the mode of classification or regression of individual trees (Breiman 2001). A decision tree is used to output the class in the classification process. The average of the findings is used to predict the dependent variable in the regression process. There are no preconceptions regarding the connection between explanatory factors and response variables in the random forest. This is an effective way to investigate hierarchical relationships and nonlinearities in big data. As a result, a random forest method may be used to anticipate new data cases more accurately.

Random subspace

Random subspace is a successful EML algorithm developed by Ho (1998) that uses a pseudo-randomly selected subset of characteristics to separate classifiers and combines their outputs via voting. RSS is a forest creation approach that uses an ensemble classifier to enhance the performance of individual classifiers that are underperforming (Kotsiantis 2011). The RS method includes selecting samples from the original training set at random to create a bootstrap sample, which would then be utilized to construct the decision tree (Kotsiantis 2011). A subset of features gets picked at random for each node of the decision tree, and the best split gets determined. Attributes, predictors, and independent variables are all included in an RS model. The correlation between estimators is reduced when randomly chosen features are used instead of the whole feature set. Ultimately, the tree is constructed to its full potential. As a result of leveraging random subspaces in both creation and aggregation, this strategy generates an effective hybrid model for minimizing over-fitting difficulties and managing datasets with a large number of repetitive variables. Ho (1998) has detailed information of the RS model.

Dagging

Ting and Witten (1997) pioneered the dagging technique. The dagging approach divides the training dataset into a number of disjoint, stratified folds and uses the given base learner to train each fold. Predictions are produced using a majority vote approach for classification issues and an averaging procedure for regression problems.

Bagging

The bagging (Bootstrap aggregating) EML algorithm is a fundamental group learning model to manufacture and aggregate (Quinlan 2006). It was offered as a way to reduce variation without raising bias error too much. Hong et al. (2019) found that bagging is a useful strategy for simulating a variety of environmental concerns. Bagging combines the bootstrap technique with the auxiliary approach to create several sets of samples, which are referred to as bootstrapped subsets. Each subgroup trains a base classifier on its own till the outputs get combined into a unified strong classifier via majority voting approach.

NBT

The machine learning classifier naive Bayes (NB) produces a probability-based model, which operates using the Bayes' theorem. The NB's structure is based on a decision tree (DT), and it arranges an NB model on each of the DT's leaf nodes (Jiang and Li 2011). The NBT performs well in terms of categorization and reliability (Arabameri et al. 2020).

The influence of a feature values on a given class throughout the NB process is independent of the value of another feature, which is referred to as class conditional independence. NB's conditional independence speeds up the training of datasets by treating all vectors as independent and using the Bayes rule.

Stacking

Stacking is an ensemble model in which the training data are utilized to generate a variety of algorithms. This method was developed by Wolpert (1992), and it works by computing the raw classifiers of the poor performance in relation to independent or bootstrapped reference data. Ensemble stacking is also known as blending since all of the statistics may be blended to create an estimation or classification. The stacking method increases the classifier's predictive power over the bagging and boosting procedures. Remote sensing, computer science, and finance are just a few of the fields where this ensemble method has shown potential. Table 3 shows the parameters that have been optimized.

Table 3 The optimization parameters of the EML algorithms employed for GWP mapping
Full size table

Validation of the models

The ROC curve has been employed to evaluate the precision GWP models. The ROC is a relative factor that indicates the probability of a class employing the Boolean method. The vertical axis of the ROC curve shows the actual positive proportion, while the horizontal axis represents the false positive percentage. AUC stands for the area under the ROC curve, and value ranges from 0 to 1. The high values indicate good performance of the models. If the value is close to 1.0, the predicted model's accuracy will be very high.

Both nonparametric and parametric methodologies were used to determine the area under the ROC curve. In this study, we applied nonparametric and nonparametric approaches for validation.

Proposing fuzzy logic-ROC weighting-based hybrid EML models for GWP mapping

We combined the fuzzy logic model with previously utilized EMLs to increase the accuracy of GPMs. A variety of procedures were taken to achieve this. The EML algorithms (six models) were utilized as parameters to build GPMs using a fuzzy logic model. Zadeh (1965) was the first to propose the concept of fuzzy sets. It makes it possible to grasp non-discrete natural events mathematically. The following are the specifics of fuzzy logic-based hybrid models:

We combined different operators of FL model with already developed six EML models to enhance the precision of the GWP models. To do so, we followed several steps, such as first we considered six EML models as input of the FL model. Then, we applied linear fuzzy membership function to the six EML models as the value of EML models showed the monotonic trend of potentiality like low potential to high potential.

We did not use conditioning factors directly in this investigation; instead, we used six GPMs that had already been created using conditioning variables. The concept behind using six GPMs is that each GPM was created using distinct ensemble machine learning models and numerous parameters. As a result, the GPM result revealed the intricate functioning of algorithms, conditioning parameters, and existing inventories. After converting the input variables (six EML models) into fuzzy crisp layers, the subsequent process is the integration of the parameters.

For integrating several input variables, fuzzy operators have been used. Five operators, such as AND, OR, SUM, PRODUCT, and GAMMA, have been extensively used (Chung and Fabbri 2001). To obtain very high precision prediction, a suitable operator should be selected for integration. In the present study, we used all the operators for combining the input variables. Based on the initial screening, we excluded the final output of AND and PRODUCT operators. The following formulas have been used to integrate the input variables using fuzzy operators:

$$[f{\text{AND}} = {\text{MIN}}\left[ {{f_{{\text{RF}}}},{f_{{\text{RS}}}},{f_{{\text{Bagging}}}},{f_{{\text{Dagging}}}},{f_{{\text{NBT}}}},{f_{{\text{Stacking}}}}} \right]$$
(4)
$${\text{fOR}} = {\text{MAX}}\left[ {{f_{{\text{RF}}}},{f_{{\text{RS}}}},{f_{{\text{Bagging}}}},{f_{{\text{Dagging}}}},{f_{{\text{NBT}}}},{f_{{\text{Stacking}}}}} \right]$$
(5)
$${\text{Fuzzy Algebraic Product}} = \prod\limits_{i = 1}^n {R_i}$$
(6)
$${\text{Fuzzy Algebraic Sum}} = 1 - \prod\limits_{i = 1}^n {(1 - {R_i})}$$
(7)
$${f_\gamma } = {({\text{Fuzzy Algebraic Sum}})^\gamma } \times {({\text{Fuzzy Algebraic Product}})^{1 - \gamma }})$$
(8)

where \({f_{{\text{RF}}}}\), \({f_{{\text{RS}}}}\), \({f_{{\text{Bagging}}}}\), \({f_{{\text{Dagging}}}}\), \({f_{{\text{NBT}}}}\), \({f_{{\text{Stacking}}}}\) are fuzzy crisp layers of RF, RS, bagging, dagging, NBT, and stacking, respectively. Also \({R_i}\) represents the fuzzy membership function of the \(ith\) map, \(i = 1,2,...,n\).

For GAMMA operator, we used six coefficients, such as 0.7, 0.75, 0.8, 0.85, 0.9, and 0.95. After screening, we excluded the final output of 0.7, 0.75, 0.8, and 0.85 coefficient. The value of final output after integration ranges from 0 to 1, where close to 1 indicates the higher potentiality. Then, we applied natural break algorithm to classify the models into five classes, such as very low, low, moderate, high, and very high potentiality.

Sensitivity analysis

In the present study, we performed machine learning algorithm (RF)-based sensitivity analysis to compute the relevancy of the conditioning variables. The mean decrease in accuracy (MDA) and mean decrease in Gini (MDG) coefficient are two measures based on RF for evaluating the sensitivity power of the input variables. To determine a variable's MDA, their values are permuted arbitrarily for the OOB data, whereas the other variables' values remain unchanged. The variable's relevance is determined through evaluating the resultant misclassification rate to the rate obtained without arbitrarily permuting the variable's values. This process is carried out for each parameter. Using the Gini splitting criteria, a variable's MDG is calculated considering the number of trees in the forest as a normalization factor. (For details of RF, see method section.)

The methodology of this research is summarized in Fig. 4.

Fig. 3
figure 3

Thematic layers for GWP conditioning variables such as a SPI, b STI, c rainfall d soil types, e LULC, and f distance to river

Full size image

Results

Computation of the multicollinearity analysis and importance of the parameters

In multicollinearity diagnostics tests, the highest VIF is discovered in elevation (2.71) and rainfall (2.67), followed by STI, SPI, and slope. The lowest VIF has been found in the case of aspect, curvature, and TWI (Table 4). The results also show that the variables have no collinearity among themselves; therefore, we can use them for modeling GWP.

Table 4 The multicollinearity test for computing the collinearity among the conditioning variables for GWP modeling
Full size table

Table 4 also provides the results of the tenfold cross-validation method used to calculate each parameter's InGR. The InGR data indicated that the LULC (0.516), distance to river (0.124), and elevation (0.114) have the high InGR value that indicates the most influential parameters for modeling GWP. The TRI (0.031), SPI (0.027), and STI (0.015) have just a slight impact on the GWP models. The TWI (0.008) and curvature (0.011) are all statistically insignificant. It is worth noting that the aspect factor has a value of InGR = 0.007, suggesting that it has the least impact on groundwater potential zones prediction.

GWP modeling and their validation

We created GWP models in Fig. 5 utilizing six EMLs, including RF, RS, bagging, dagging, NBT, and stacking. We classified GWP models into five classes, as illustrated in Fig. 5, as follows: very high to very low. The possible GWP areas follow the drainage route of the watershed, running northwest–southeast. Zones with high GWP dominate the south and southeast part of the study area, whereas zones with low GWP comprise the north and northwest part of the study area.

Fig. 4
figure 4

Flowchart shows the steps for preparing the hybrid GWP map

Full size image
Fig. 5
figure 5

The EML algorithms based GWP models, such as a RF, b RS, c bagging, d dagging, e NBT, and f stacking

Full size image

According to the RF model, 2.26 percent and 36.69 percent area predicted as very high GWP and high GWP zones (Table 5). While the RS, bagging, dagging, NBT, and stacking models categorized roughly thirty percent of the entire basin area as having a high GWP zone. The NBT model revealed the lowest area for extremely low class, whereas RF, bagging, and RS covered the maximum area (Table 5). All the models identified the river catchment region as possessing many possibilities for groundwater storage. However, since the size of the area varies, it is crucial to describe the most appropriate model.

Table 5 Calculation of area of five GWP zones using six EML models
Full size table

Using the obtained GPS coordinates, the AUC of ROC has been utilized to verify the GWP models (Meten et al. 2015; Nahayo et al. 2019). NBT (AUC: 0.892 and 0.928) seemed to be the best model for both ROC curves, preceded by stacking (AUC: 0.889 and 0.931), RS (AUC: 0.889 and 0.912), dagging (AUC: 0.87 and 0.882), RF (AUC: 0.882 and 0.936), and bagging (AUC: 0.861 and 0.87) (Fig. 6). However, according to the binormal ROC curve, RF was the finest model (bROC: 0.936), followed by stacking (bROC: 0.931), NBT (bROC: 0.928), RS (bROC: 0.912), dagging (bROC: 0.882), and bagging (bROC: 0.87) (Fig. 6).

Sensitivity analysis using machine learning algorithms

Advanced EML models showed the zonation of GWP areas for the present study area. Furthermore, none of these models include the influence of any variables to the prediction of GWP modeling. The problem emerges in developing and implementing management plans without a thorough grasp of the link between parameters and GWP models.

Fig. 6
figure 6

Validation of GWP models using eROC and bROC curves for a RF, b RS, c bagging, d dagging, e NBT, and f stacking

Full size image

If the influence of the conditioning variables is not possible to compute, it would be very unclear how management strategies would be developed and implemented. Identifying factors linked with GWP models could sometimes help reduce the exploitation of groundwater resources and formulation of groundwater management plans. As a consequence, determining which elements have the most influence is crucial. For this, we used RF-based two error matrices, such as MDG and MDA to compute the influence of the variables to the GWP models (Hollister et al. 2016). The results showed that the distance to the river, TWI, aspect, STI, slope, elevation, and rainfall were the most relevant parameters for GWP modeling (Fig. 7). The least significant factors in defining the relative importance of the 12 variables included in EML models were soil kinds, LULC, and SPI, with soil types, LULC, and SPI being the least important.

Development of FL and ROC weighting-based hybrid models and their validation

The GWP models must be very resilient and precise before providing sustainable management approaches. As a result, we attempted to increase the robustness and accuracy of EML-based GWP models to provide highly effective sustainable management strategies in this work. Integrating fuzzy logic and a ROC-based weighting technique has enhanced the EML models even further. Before using fuzzy logic, the ROC-based weighting technique was used to weight the EML-based GWP layers in this work. The rationale for using a ROC-based weighting method rather than an expert-based approach, AHP, or weighted linear combination is because the ROC measures how similar EML-based GWP models are to the ground truth or reality. Therefore, the value of ROC curve shows that the high value reflects the prediction of the models is quite similar with ground conditions. As a result, the model with the highest AUC value can be very appropriate and given a higher weight than other models. Hence, we utilized the AUC values of the ROC curve as the weighted value in this investigation. For the weighting technique, we used the AUC value of the binormal ROC curve. In this study, the RF model received the highest score of all the models, since it had higher AUC values than the other models. RF, stacking, NBT, RS, dagging, and bagging are the layers in the hierarchical sequence for allocating weights based on AUC values.

The fuzzy logic model was deployed after the EML-based GWP models were transformed into weighted layers. Before applying the weighted method, the models were normalized because the EML algorithms predicted GWP as 0–1 values. The data patterns of the layers reflect a similar tendency, such as monotonous growth, which shows a constant growing or declining trend. The data pattern in this investigation revealed a constant GW decreasing tendency. As a result, we used a linear fuzzy membership function to normalize all the GWP layers. After applying the fuzzy membership function, the fuzzy crisp layers of six EML-based GWP models are shown in Fig. 8a–f.

Fig. 7
figure 7

Sensitivity analyses of groundwater potential conditioning factors in terms of best GWP models using a MDG, and b MDA

Full size image

After converting the crisp fuzzy layers, we integrated all fuzzified layers using different fuzzy operators, such as AND, OR, SUM, PRODUCT, GAMMA 0.7, GAMMA 0.75, GAMMA 0.8, and GAMMA 0.9. Then, we inspected the generated output through visualization. Subsequently, we excluded the output generated from SUM, PRODUCT, GAMMA 0.7, and GAMMA 0.75, as these outputs seem not good enough. We considered the output from AND, OR, GAMMA 0.8, and GAMMA 0.9 as excellent results based on our inspection. After that, we classified the output into five classes as we did for previous EML models. Then, we validated the models using eROC and bROC curves (Fig. 9a–d). The area coverage for various GPW categories was calculated. According to all models, 1045–1200 km2 of the area were classified as very high GPW zones, whereas 780–895km2 of the area was projected as very-low GPW zones (Fig. 9a–d).

Fig. 8
figure 8

Conversion of EML models into crisp fuzzy layers, such as a RF, b RS, c bagging, d dagging, e NBT, and f stacking based on linear membership function,

Full size image
Fig. 9
figure 9

Novel hybrid models with the integration of EML models and ROC weighted fuzzy operators, a AND, b OR, c GAMMA 0.8, and d GAMMA 0.9

Full size image

Based on the AUC of ROC curve, GAMMA 0.9 appeared as best model (eAUC: 0.903 and bAUC: 0.932), followed by GAMMA 0.8 (eAUC: 0.902 and bAUC: 0.949), AND (eAUC: 0.899 and bAUC: 0.948), and OR (eAUC: 0.866 and bAUC: 0.919) models (see Fig. 9a–d). However, according to the bROC curve, GAMMA 0.8 was shown to be the superior model for prediction of natural hazards (bAUC: 0.949), followed by AND (bAUC: 0.948), GAMMA 0.9 (bAUC: 0.932), and bagging (bAUC: 0.919) (Fig. 10). All models are highly accurate and robust than the EML-based models. Therefore, it can be stated that after integrating ROC-based weighting approach and fuzzy logic, the efficiency of the GPW models is increased further.

Fig. 10
figure 10

Validation of novel hybrid models, such as a AND, b OR, c GAMMA 0.8, and d GAMMA 0.9 using empirical and binormal ROC curves

Full size image

Discussion

Delineation of GWP or other natural hazards using ML and EML algorithms is highly timely work since future circumstances should be known to professionals and governments to promote sustainable development. Decision-makers can suggest management plans based on this information. No model, however, is ideal for predicting GWP and natural hazards using ML and EML algorithms. As a result, researchers are constantly attempting to create and use new models for predicting occurrences through the complicated nonlinear process. Therefore, in the present study, we proposed six ROC weighting integrated ensemble machine learning models, such as RF, RS, bagging, dagging, and stacking, which had never been used before, were tested and coupled with fuzzy logic operators (AND, OR, GAMMA 0.8, and GAMMA 0.9), a widely employed advanced model, in the current study. The criteria that are beneficial for groundwater occurrence were initially detected for groundwater resource identification. The precision of the outputs entirely relies on the model's predictive capacity and the input data's quality. Therefore, the impact of these variables was evaluated (Table 1), and we eliminated the variables having less impact from modeling (Table 4). These less important variables could affect the prediction procedure (Maskooni et al. 2020; Muavhi et al. 2021).

Also, we applied machine learning technique like random forest for computing the importance of the GWP conditioning variables to the GWP models (Fig. 7). The results showed that the distance to the river and the TWI have the largest impact since water penetration is stronger near the river and in the higher TWI zone, resulting in larger GWP ability. Our work is quite identical to the findings of Pham et al. (2021) and Pal et al. (2020a). Rainfall ranks third in the MDA and seventh in the MDG (Fig. 7) because it has a moderate influence on the groundwater potentiality model. The relevance of the factors in potential groundwater mapping, on the other hand, is heavily determined by the study region's features and the research method used.

There have been several statistical, and ML models applied in GWP modeling, and many of these models have yielded excellent prediction results, as shown in the literature review (Mallick et al. 2021d). In recent years, hybrid models, on the other hand, have become more popular. For groundwater-related studies, the effectiveness of hybrid approaches could be helpful to researchers in the future (Farzin et al. 2021). Because of this, we proposed ROC weighting-based ensemble machine learning algorithms (RF, RS, bagging and dagging, NBT, and stacking) for groundwater potentiality modeling in the present study. We combined these algorithms with different operators of fuzzy logic (AND, OR, GAMMA 0.8, and GAMMA 0.9). In this way, we built hybrid models for GWP modeling.

The RS, bagging, and dagging models, together with the NBT and stacking models, categorized approximate thirty percent area of the total study area as considered high GWP zone. The NBT model predicted that the very low class would have the lowest coverage area, while the RF, bagging, and RS classes would have the maximum coverage area (Table 4). The river catchment region, in general, was identified by all the models as having a significant impact on GWP model. Furthermore, the six advanced EMLs were validated using the eROC and bROC curves and showed NBT model (eROC: 0.892; bROC: 0.928) appeared as best model, followed by stacking (eROC: 0.889; bROC: 0.931), RS (eROC: 0.889; bROC: 0.912), dagging (eROC: 0.87; bROC: 0.882), RF (eROC: 0.882; bROC: 0.936), and bagging (eROC: 0.861; bROC: 0.87). These six models performed better, with AUC values greater than 0.8. As a result, it is reasonable to conclude that NBT outperformed other models because it is a fast decision algorithm ensemble with naïve Bayes that has been successfully applied to achieving trustworthy findings for forecasting natural disasters and other environmental factors (Pham et al. 2021; Phong et al. 2021).

Finally, to the best of the authors' knowledge, the fuzzy logic-ROC weighted integrated hybrid EML models were proposed for the first time. The outputs were found to be very high rather than standalone ML and EML, such as AND-hybrid (eROC: 0.899; bROC: 0.948), OR-hybrid (eROC: 0.866; bROC: 0.919), GAMMA 0.8 (eROC: 0.902; bROC: 0.949), and GAMMA 0.9 (eROC: 0.903; bROC: 0.932) can improve the accuracy and robustness of advanced machine learning models.

We concluded that hybrid EML models outperformed other EML models and ML models for GWP modeling based on the above discussion and results. Therefore, the present study recommends using hybrid EML models to predict natural hazards and other natural resource predictions in different regions. These models would yield high precision prediction results.

Conclusion

Specifically, the present work is concerned with creating fuzzy logic, and EML integrated hybrid models to predict groundwater potentiality models. We summarized the main findings below:

  1. (i)

    Using six EML models and four fuzzy-based hybrid models, researchers determined that the extremely high groundwater potential zone encompasses an area ranging from 830 to 21200km2.

  2. (ii)

    The NBT model performed as superior for GWP modeling (eROC = 0.892; bROC: 0.928). It was followed by stacking, RS, dagging, RF, and bagging. However, the suggested FL-based hybrid models, such as GAMMA 0.9 (eROC − 0.903; bROC: 0.932), outperformed all other models in terms of AUC. The best models, according to binormal ROC, would be GAMMA 0.8 (bROC: 0.949), followed by AND (bROC: 0.948), GAMMA 0.9 (bROC: 0.932), and OR (bROC: 0.919), respectively. All four models outperformed the six EML models by a significant margin.

  3. (iii)

    We performed machine learning algorithm like random forest for sensitivity analysis to compute the influence of the parameters for GWP modeling. The results showed that the distance to the river, elevation, and slope are mostly sensitive parameters for GWP.

Among GWP models, hybrid models beat EML-based models in accuracy and sensitivity. These findings encourage the researchers to adopt the hybrid EML-based models for integrating multi-parameters for any predictive model. In addition, we recommend using more numbers of conditioning variables for generating the high precision predictive models. Also, the application and integration of hybrid models with deep learning algorithms may produce very high precision findings. The present study also recommends proper management of the conditioning variables, reducing groundwater exploitation, and increasing groundwater recharge. Consequently, the maintenance of forest cover will help in the recharging of groundwater. For a scientific evaluation of groundwater in different potential zones, more research is required to provide more accurate advice on how much water may be taken from each prospective zone.