Introduction

The concept of highly dispersive (HD) solitons was conceived just a few years ago [1,2,3]. It is out of extreme necessity that the concept of highly dispersive solitons has emerged [4,5,6]. Solitons are the outcome of a delicate balance that exists between chromatic dispersion (CD) and self-phase modulation (SPM) effect [7,8,9]. Occasionally during intercontinental transmission, CD can run low and thus the balance is compromised [10,11,12]. This can lead to catastrophic situations. Thus, to replenish the low count of CD, one needs to introduce higher-order dispersive effects [13,14,15]. This would enable the balance between CD and SPM to be maintained, which in turn would ensure the stable transmission of pulses across intercontinental distances [16,17,18]. The additional dispersive effects that are typically taken into account stem from inter-modal dispersion (IMD), third-order (3OD), fourth-order (4OD), fifth-order (5OD), and sixth-order (6OD) dispersions and were consequently included [19,20,21]. These dispersive effects collectively form the HD optical solitons [22,23,24]. A couple of negatively impacted features are inevitable with the presence of the higher-order dispersion terms [25,26,27]. The soliton velocity drastically slows down with such higher-order dispersive effects [28,29,30,31]. The other aspect of negativity is the heavy soliton radiation. This paper addresses the highly dispersive optical solitons after neglecting the effects of soliton velocity and the soliton radiation. The governing model is the nonlinear Schrödinger's equation (NLSE), which is considered with the generalized quadratic-cubic (QC) form of SPM. The model with the QC form of SPM has been recently studied [1]. The paper focuses on the retrieval of optical soliton solutions to the model with the generalized form of the QC form of SPM by the aid of Sardar’s sub-equation scheme. This would lead to the recovery of optical solitons and complexitons that are enumerated in the work. The existence criteria of such solitons are also presented.

Governing model

Within the context of [1], the HD-NLSE is characterized by its generalized QC nonlinearity:

$$i{q}_{t}+i{a}_{1}{q}_{x}+{a}_{2}{q}_{xx}+i {a}_{3}{q}_{xxx}+{a}_{4}{q}_{xxxx}+i{a}_{5}{q}_{xxxxx}+{a}_{6}{q}_{xxxxxx}+\left({b}_{1}{\left|q\right|}^{n}+{b}_{2}{\left|q\right|}^{2n}\right)q=0.$$
(1)

Equation (1) introduces \(q=q(x,t)\), a complex-valued function representing the optical wave. Here, \(x\) signifies the propagation distance along the optical medium, while \(t\) denotes the time variable. The refractive index structure adheres to a generalized QC form, with SPM effects stemming from the coefficients of \({b}_{j}\) for \(j=\mathrm{1,2}\), thereby introducing quadratic and cubic effects sequentially. The power-law nonlinearity parameter is denoted by \(n\). The term \(i{q}_{t}\) illustrates the optical wave's temporal evolution within the nonlinear medium. Additionally, the coefficients of \({a}_{j}\) for \(j=1-6\) contribute to inter-modal dispersion, chromatic dispersion, third-order, fourth-order, fifth-order, and sixth-order dispersions, respectively.

Travelling wave solution

The solutions to Eq. (1) are considered as:

$$q\left(x,t\right)= u\left(\xi \right) {e}^{i \theta (x,t)}$$
(2)

Here, \(\xi = x-\gamma t\) represents the wave variable, and \(\theta (x,t)=-kx+\omega t+{\theta }_{0}\) stands for the phase component of the soliton. The amplitude component of the soliton is denoted by \(u\left(\xi \right)\), with \(\gamma\) representing its speed. Furthermore, \(k\) refers to the soliton frequency, \(\omega\) signifies its wavenumber, and \({\theta }_{0}\) is the phase constant. By utilizing Eq. (2) and its derivatives, Eq. (1) undergoes transformation to:

$$\left({a}_{2}+3{a}_{3} k -6{k}^{2}{a}_{4} -10{k}^{3} {a}_{5}+15{k}^{4}{a}_{6}\right) {u}^{{\prime}{\prime}}+i \left({a}_{1}-\gamma -2{a}_{2} k -3{a}_{3}{k}^{2} +4{a}_{4}{k}^{3} +5{k}^{4}{a}_{5} -6{k}^{5}{a}_{6}\right) {u}^{\prime}-\left(\omega -k{a}_{1}+{k}^{2}{a}_{2}+{k}^{3}{a}_{3}-{a}_{4}{k}^{4}-{k}^{5} {a}_{5}+{k}^{6}{a}_{6}\right) u+i\left({a}_{3}-4{a}_{4} k -10{k}^{2}{a}_{5}+20 i{k}^{3}{a}_{6} \right) {u}^{\left(3\right)}+\left({a}_{4}+5k{a}_{5} -15{k}^{2}{a}_{6}\right) {u}^{\left(4\right)}+i\left({a}_{5}-6 {a}_{6} k\right) {u}^{\left(5\right)}+{a}_{6}{u}^{\left(6\right)}+{b}_{1}{u}^{n+1}+{b}_{2}{u}^{2n+1}=0.$$
(3)

Equation (3) can be decomposed into its real and imaginary parts, expressed as follows:

$$\left({a}_{2}+3{a}_{3} k -6{k}^{2}{a}_{4} -10{k}^{3} {a}_{5}+15{k}^{4}{a}_{6}\right) {u}^{{\prime}{\prime}}-\left(\omega -k{a}_{1}+{k}^{2}{a}_{2}+{k}^{3}{a}_{3}-{a}_{4}{k}^{4}-{k}^{5} {a}_{5}+{k}^{6}{a}_{6}\right) u+\left({a}_{4}+5k{a}_{5} -15{k}^{2}{a}_{6}\right) {u}^{\left(4\right)}+{a}_{6}{u}^{\left(6\right)}+{b}_{1}{u}^{n+1}+{b}_{2}{u}^{2n+1}=0,$$
(4)

and

$$\left({a}_{1}-\gamma -2{a}_{2} k -3{a}_{3}{k}^{2} +4{a}_{4}{k}^{3} +5{k}^{4}{a}_{5} -6{k}^{5}{a}_{6}\right) {u}{\prime}+\left({a}_{3}-4{a}_{4} k -10{k}^{2}{a}_{5}+20 i{k}^{3}{a}_{6} \right) {u}^{\left(3\right)}+\left({a}_{5}-6 {a}_{6} k\right) {u}^{(5)}=0.$$
(5)

From Eq. (5), we get

$$\gamma ={a}_{1}-2 k {a}_{2}-8 {a}_{4}{k}^{3}-96{a}_{6}{k}^{5}$$
(6)

whenever

$${a}_{3}=\left(4{a}_{4} k+40 {a}_{6}{k}^{3}\right)$$
(7)

and

$${a}_{5}=\left(6 {a}_{6} k\right)$$
(8)

Equation (4) can be written as:

$${c}_{3} {u}^{\left(4\right)}+{a}_{6}{u}^{\left(6\right)}+\left({b}_{1}{u}^{n+1}+{b}_{2}{u}^{2n+1}\right)=0$$
(9)

where

$$\omega =k{a}_{1}-3 {a}_{4} {k}^{4}-40{a}_{6}{k}^{6}$$
(10)
$${a}_{2}=- {k}^{2}\left(6{a}_{4}+75{a}_{6}{k}^{2}\right)$$
(11)

and

$${c}_{3}=\left({a}_{4}+15{a}_{6}{k}^{2}\right)$$
(12)

Setting

$$u={v}^\frac{1}{n}$$
(13)

Equation (4) becomes:

$${c}_{3} \lceil{v}^{5} {v}^{(4)}+4\frac{1-n}{n}{v}^{4} {v}^{\prime} {v}^{(3)}+6{\frac{1-n}{n}\frac{1-2n}{n}v}^{3} {{v}^{\prime}}^{2} {v}^{{\prime}{\prime}}+3{\frac{1-n}{n}v}^{4} {v}^{{\prime}{\prime}2}+{ \frac{1-n}{n}\frac{1-2n}{n}\frac{1-3n}{n} v}^{2} {v}^{{\prime}4}\rceil+{a}_{6}\lceil{v}^{5} {v}^{(6)}+6\frac{1-n}{n}{v}^{4}{v}^{\prime} {v}^{(5)}+15\frac{1-n}{n}{v}^{4} {v}^{{\prime}{\prime}}{v}^{(4)}+15\frac{1-n}{n}\frac{1-2n}{n}{v}^{3} {{v}^{\prime}}^{2}{v}^{(4)} ++10\frac{1-n}{n}{v}^{4} {{v}^{{\prime}{\prime}{\prime}}}^{2}+60\frac{1-n}{n}\frac{1-2n}{n}{v}^{3} {v}^{\prime} {v}^{{\prime}{\prime}}{v}^{(3)}+20\frac{1-n}{n}\frac{1-2n}{n}\frac{1-3n}{n}{v}^{2}{{v}^{\prime}}^{3}{v}^{(3)}+15\frac{1-n}{n}\frac{1-2n}{n}{v}^{3} {{v}^{{\prime}{\prime}}}^{3}+45\frac{1-n}{n}\frac{1-2n}{n}\frac{1-3n}{n}{v}^{2} {{v}^{\prime}}^{2}{{v}^{{\prime}{\prime}}}^{2}+15\frac{1-n}{n}\frac{1-2n}{n}\frac{1-3n}{n}\frac{1-4n}{n}v {v}^{{\prime}{\prime}} {{v}^{\prime}}^{4} +\frac{1-n}{n}\frac{1-2n}{n}\frac{1-3n}{n}\frac{1-4n}{n}\frac{1-5n}{n} {v}^{{\prime}6}\rceil+n\left({b}_{1}{v}^{7}+{b}_{2}{v}^{8}\right)=0.$$
(14)

Sardar sub-equation method (SSEM)

The SSEM offers a significant advantage in its ability to generate a wide array of soliton solutions, ranging from dark and bright to singular forms, as well as more intricate combinations like mixed dark-bright, dark-singular, bright-singular, and mixed singular solutions. Furthermore, it extends its utility by providing rational, periodic, trigonometric, and various other solution types.

In this approach, to address Eq. (14), we adopt the assumption that the solution follows the format proposed in references [14, 15]:

$$v\left(\xi \right)=\sum_{n=0}^{{\text{N}}}{\lambda }_{n}{\Psi }^{n}(\xi ) , { \lambda }_{{\text{N}}} \ne 0.$$
(15)

Here, \({\lambda }_{n}\) (\(n=0, 1, \dots , N)\) represents constants to be determined subsequently. The integer \(N\) is established using the homogeneous balance method, balancing the nonlinear term and the highest-order derivative in Eq. (15). Additionally, the function \({\Psi }^{n}(\xi )\) in Eq. (15) must fulfill the following equation:

$${\Psi }^{\mathrm{^{\prime}}}\left(\xi \right)=\sqrt{{\eta }_{2}{\Psi \left(\xi \right)}^{4}+{\eta }_{1}{\Psi \left(\xi \right)}^{2}+{\eta }_{0}},$$
(16)

where \({\eta }_{l}\) (\(l=0, 1, 2\)) are constant values.

Based on the parameters \({\eta }_{l}\), Eq. (16) yields different known solutions, as outlined below [12, 13]:

Case I: \({\eta }_{0}=0.\)

If \({\eta }_{1}>0\) and \({\eta }_{2}\ne 0\), then we get:

$$\Psi_1^\pm\left(\xi\right)=\pm\sqrt{-pq\frac{\eta_1}{\eta_2}}{\text{sech}}_\text{pq}\left(\sqrt{\eta_1}\xi\right),\eta_2<0$$
(17)

and

$$\Psi_2^\pm\left(\xi\right)=\pm\sqrt{-pq\frac{\eta_1}{\eta_2}}{\text{csch}}_\text{pq}\left(\sqrt{\eta_1}\xi\right),\eta_2>0$$
(18)

where

$${{\text{sech}}}_{\mathit{pq}}\left(\sqrt{{\eta }_{1}}\xi \right)=\frac{2}{p {e}^{\sqrt{{\eta }_{1}}\xi }+q {e}^{-\sqrt{{\eta }_{1}}\xi } } , {{\text{csch}}}_{\mathit{pq}}\left(\sqrt{{\eta }_{1}}\xi \right)=\frac{2}{p {e}^{\sqrt{{\eta }_{1}}\xi }-q {e}^{-\sqrt{{\eta }_{1}}\xi }}$$
(19)

Case II: \({\eta }_{0}=\frac{1}{4}\frac{{\eta }_{1}^{2}}{{\eta }_{2}}\) and \({\eta }_{2}>0\).

If \({\eta }_{1}<0\), then we arrive at:

$$\Psi_3^\pm\left(\xi\right)=\pm\sqrt{-\frac{\eta_1}{2\eta_2}}{\text{tanh}}_\text{pq}\left(\sqrt{-\frac{\eta_1}2}\xi\right)$$
(20)
$$\Psi_4^\pm\left(\xi\right)=\pm\sqrt{-\frac{\eta_1}{2\eta_2}}{\text{coth}}_\text{pq}\left(\sqrt{-\frac{\eta_1}2}\xi\right)$$
(21)
$$\Psi_5^\pm\left(\xi\right)=\pm\sqrt{-\frac{\eta_1}{2\eta_2}}\left({\text{tanh}}_{\mathit{pq}}\left(\sqrt{-2\eta_1}\xi\right)\pm i\sqrt{pq}{\text{sech}}_{\mathit{pq}}\left(\sqrt{{-2\eta}_1}\xi\right)\right)$$
(22)
$$\Psi_6^\pm\left(\xi\right)=\pm\sqrt{-\frac{\eta_1}{2\eta_2}}\left({\text{coth}}_{\mathit{pq}}\left(\sqrt{-2\eta_1}\xi\right)\pm\sqrt{pq}{\text{csch}}_{\mathit{pq}}\left(\sqrt{{-2\eta}_1}\xi\right)\right)$$
(23)

and

$$\Psi_7^\pm\left(\xi\right)=\pm\frac12\sqrt{-\frac{\eta_1}{2\eta_2}}\left({\text{tanh}}_{\mathit{pq}}\left(\sqrt{-\frac{\eta_1}8}\xi\right)\pm{\text{coth}}_{\mathit{pq}}\left(\sqrt{\frac{{-\eta}_1}8}\xi\right)\right)$$
(24)

where

$${{\text{tanh}}}_{\mathit{pq}}\left(\sqrt{{\eta }_{1}}\xi \right)=\frac{p {e}^{\sqrt{{\eta }_{1}}\xi }-q {e}^{-\sqrt{{\eta }_{1}}\xi }}{p {e}^{\sqrt{{\eta }_{1}}\xi }+q {e}^{-\sqrt{{\eta }_{1}}\xi } } , {{\text{coth}}}_{\mathit{pq}}\left(\sqrt{{\eta }_{1}}\xi \right)=\frac{p {e}^{\sqrt{{\eta }_{1}}\xi }+q {e}^{-\sqrt{{\eta }_{1}}\xi }}{p {e}^{\sqrt{{\eta }_{1}}\xi }-q {e}^{-\sqrt{{\eta }_{1}}\xi }}$$
(25)

Application of the modified sardar sub-equation method

We initiated our analysis by applying the principle of the homogeneous balance method, balancing the nonlinear term \({v}^{{\prime}6}\) with the nonlinear linear term \({v}^{8}\) in Eq. (14). This yields \(6N+6=8N\), resulting in \(N=\) 3. Consequently, Eq. (15) transforms to:

$$v\left(\xi \right)=\left({\lambda }_{0}+{\lambda }_{1}\Psi +{\lambda }_{2}{\Psi }^{2}+{\lambda }_{3}{\Psi }^{3}\right)$$
(26)

For \({\lambda }_{0}={\lambda }_{1}={\lambda }_{2}=0\), we get:

$$v\left(\xi \right)={\lambda }_{3}{\Psi }^{3}$$
(27)

By substituting Eq. (27) and its derivatives, along with Eq. (16), into Eq. (14), we derive:

$$54 {a}_{6}\frac{1-n}{n}{\Psi }^{14} \left({\eta }_{2}{\Psi }^{4}+{\eta }_{1}{\Psi }^{2}+{\eta }_{0}\right) \left(840 {{\eta }_{2}}^{2}{\Psi }^{6}+680{\eta }_{2}{\eta }_{1}{\Psi }^{4}+\left(252{\eta }_{0}{\eta }_{2}+81{{\eta }_{1}}^{2}\right){ \Psi }^{2}+20 {\eta }_{0}{\eta }_{1}\right)+3 \left(4\frac{1-n}{n}{\Psi }^{12} 3{\Psi }^{2} {c}_{3}+60 {a}_{6}\frac{1-n}{n}\frac{1-2n}{n}{\Psi }^{9} 3{\Psi }^{2} \left[3\left(4{\eta }_{2}{\Psi }^{5}+3{\eta }_{1}{\Psi }^{3}+2{\eta }_{0}\Psi \right)\right]+20{a}_{6}\frac{1-n}{n}\frac{1-2n}{n}\frac{1-3n}{n}{\Psi }^{6}\left(9{\Psi }^{4} \left({\eta }_{2}{\Psi }^{4}+{\eta }_{1}{\Psi }^{2}+{\eta }_{0}\right)\right)3{\Psi }^{2} \right)\left(20 {\eta }_{2}{\Psi }^{4}+9{\eta }_{1}{\Psi }^{2}+2{\eta }_{0}\right) \left({\eta }_{2}{\Psi }^{4}+{\eta }_{1}{\Psi }^{2}+{\eta }_{0}\right)+{c}_{3}\lceil162{\frac{1-n}{n}\frac{1-2n}{n}}^{3}{\Psi }^{13}\left({\eta }_{2}{\Psi }^{4}+{\eta }_{1}{\Psi }^{2}+{\eta }_{0}\right) \left(4{\eta }_{2}{\Psi }^{5}+3{\eta }_{1}{\Psi }^{3}+2{\eta }_{0}\Psi \right)+27\frac{1-n}{n} {\Psi }^{12} {\left[\left(4{\eta }_{2}{\Psi }^{5}+3{\eta }_{1}{\Psi }^{3}+2{\eta }_{0}\Psi \right)\right]}^{2}+81\frac{1-n}{n}\frac{1-2n}{n}\frac{1-3n}{n} {\Psi }^{14}{\left({\eta }_{2}{\Psi }^{4}+{\eta }_{1}{\Psi }^{2}+{\eta }_{0}\right)}^{2}\rceil+{a}_{6}\lceil10\frac{1-n}{n}{\Psi }^{12} 9{\left(20 {\eta }_{2}{\Psi }^{4}+9{\eta }_{1}{\Psi }^{2}+2{\eta }_{0}\right)}^{2} \left({\eta }_{2}{\Psi }^{4}+{\eta }_{1}{\Psi }^{2}+{\eta }_{0}\right)+15\frac{1-n}{n}\frac{1-2n}{n}{\Psi }^{9} {\left[3\left(4{\eta }_{2}{\Psi }^{5}+3{\eta }_{1}{\Psi }^{3}+2{\eta }_{0}\Psi \right)\right]}^{3}+45\frac{1-n}{n}\frac{1-2n}{n}\frac{1-3n}{n}{\Psi }^{6} \left(9{\Psi }^{4} \left({\eta }_{2}{\Psi }^{4}+{\eta }_{1}{\Psi }^{2}+{\eta }_{0}\right)\right){\left[3\left(4{\eta }_{2}{\Psi }^{5}+3{\eta }_{1}{\Psi }^{3}+2{\eta }_{0}\Psi \right)\right]}^{2}+15\frac{1-n}{n}\frac{1-2n}{n}\frac{1-3n}{n}\frac{1-4n}{n}{\Psi }^{3}\left[3\left(4{\eta }_{2}{\Psi }^{5}+3{\eta }_{1}{\Psi }^{3}+2{\eta }_{0}\Psi \right)\right] \left(9{\Psi }^{4} \left({\eta }_{2}{\Psi }^{4}+{\eta }_{1}{\Psi }^{2}+{\eta }_{0}\right)\right)\left(9{\Psi }^{4} \left({\eta }_{2}{\Psi }^{4}+{\eta }_{1}{\Psi }^{2}+{\eta }_{0}\right)\right) +\frac{1-n}{n}\frac{1-2n}{n}\frac{1-3n}{n}\frac{1-4n}{n}\frac{1-5n}{n} \left(9{\Psi }^{4} \left({\eta }_{2}{\Psi }^{4}+{\eta }_{1}{\Psi }^{2}+{\eta }_{0}\right)\right)\left(9{\Psi }^{4} \left({\eta }_{2}{\Psi }^{4}+{\eta }_{1}{\Psi }^{2}+{\eta }_{0}\right)\right)\left(9{\Psi }^{4} \left({\eta }_{2}{\Psi }^{4}+{\eta }_{1}{\Psi }^{2}+{\eta }_{0}\right)\right)\rceil+n\left({b}_{1}{\lambda }_{3}{\Psi }^{21}+{b}_{2}{{\lambda }_{3}}^{2}{\Psi }^{24}\right)=0.$$
(28)

Through collecting and setting the coefficients of the independent functions \({\Psi }^{j}\left(\xi \right)\) in Eq. (28) to zero, we deduce the following scenarios:

Case I: \({\eta }_{0}=0\), \({\lambda }_{0}=0\), \({\lambda }_{1}=0\), \({\lambda }_{2}=0\), \({\eta }_{2}<0\).

Thus, Eq. (28) reduces to the following equation:

$$54 {a}_{6}\frac{1-n}{n} \left( 840 {{\eta }_{2}}^{3}{\Psi }^{21}+1520 {\eta }_{1}{{\eta }_{2}}^{2}{\Psi }^{19}+761{{\eta }_{1}}^{2}{\eta }_{2}{\Psi }^{17}+81{{\eta }_{1}}^{3}{\Psi }^{15}\right)+3\left({c}_{3}\left(120 {{\eta }_{2}}^{2}{\Psi }^{19}+136{\eta }_{2}{\eta }_{1}{\Psi }^{17}+27{{\eta }_{1}}^{2}{ \Psi }^{15}\right)+135\frac{1-n}{n}\frac{1-2n}{n}\left( 120{{\eta }_{2}}^{3}{\Psi }^{21}+256{\eta }_{1}{{\eta }_{2}}^{2}{\Psi }^{19}+163{{\eta }_{1}}^{2}{\eta }_{2}{\Psi }^{17}+27{{\eta }_{1}}^{3}{\Psi }^{15}\right) {a}_{6}\right)+36 \frac{1-n}{n}\left( {c}_{3}\left(20{{\eta }_{2}}^{2}{\Psi }^{19}+29{\eta }_{1}{\eta }_{2}{\Psi }^{17}+9{{\eta }_{1}}^{2}{\Psi }^{15}\right) +45 {a}_{6}\frac{1-2n}{n}\left(80{{\eta }_{2}}^{3}{\Psi }^{21}+176{\eta }_{1}{{\eta }_{2}}^{2}{\Psi }^{19}+123{{\eta }_{1}}^{2}{\eta }_{2}{\Psi }^{17}+27{{\eta }_{1}}^{3}{\Psi }^{15}\right)+45{a}_{6}\frac{1-2n}{n}\frac{1-3n}{n}\left(20{{\eta }_{2}}^{3}{\Psi }^{21}+49{\eta }_{1}{{\eta }_{2}}^{2}{\Psi }^{19}+38{{\eta }_{1}}^{2}{\eta }_{2}{\Psi }^{17}+9{{\eta }_{1}}^{3}{\Psi }^{15}\right) \right) +\frac{1-n}{n}{c}_{3}\lceil162\frac{1-2n}{n}\left(4{{\eta }_{2}}^{2}{\Psi }^{19}+7{\eta }_{1}{\eta }_{2}{\Psi }^{17}+3{{\eta }_{1}}^{2}{\Psi }^{15}\right) +27 \left(16{{\eta }_{2}}^{2}{\Psi }^{19}+24{\eta }_{1}{\eta }_{2}{\Psi }^{17}+9{{\eta }_{1}}^{2}{\Psi }^{15}\right)+81\frac{1-2n}{n}\frac{1-3n}{n} \left({{\eta }_{2}}^{2}{\Psi }^{19}+2{\eta }_{1}{\eta }_{2}{\Psi }^{17}+{{\eta }_{1}}^{2}{\Psi }^{15}\right)\rceil+9\frac{1-n}{n}{a}_{6}\lceil10\left(400{ {\eta }_{2}}^{3}{\Psi }^{21}+760{\eta }_{1}{ {\eta }_{2}}^{2}{\Psi }^{19}+441 {{\eta }_{1}}^{2}{\eta }_{2}{\Psi }^{17}+81 {{\eta }_{1}}^{3}{\Psi }^{15}\right) +455\frac{1-2n}{n} \left(64{{\eta }_{2}}^{3}{\Psi }^{21}+144 {{\eta }_{2}}^{2}{\eta }_{1}{\Psi }^{19}+108 {\eta }_{2}{{\eta }_{1}}^{2}{\Psi }^{17}+27{{\eta }_{1}}^{3}{\Psi }^{15}\right)+405\frac{1-2n}{n}\frac{1-3n}{n} \left( 16{{\eta }_{2}}^{3}{\Psi }^{21}+40{\eta }_{1}{{\eta }_{2}}^{2}{\Psi }^{19}+33{{\eta }_{1}}^{2}{\eta }_{2}{\Psi }^{17}+9{{\eta }_{1}}^{3}{\Psi }^{15}\right)+405\frac{1-2n}{n}\frac{1-3n}{n}\frac{1-4n}{n} \left(4{{\eta }_{2}}^{3}{\Psi }^{21}+11{\eta }_{1}{{\eta }_{2}}^{2}{\Psi }^{19}+10{{\eta }_{1}}^{2}{\eta }_{2}{\Psi }^{17}+3{{\eta }_{1}}^{3}{\Psi }^{15}\right) +81\frac{1-2n}{n}\frac{1-3n}{n}\frac{1-4n}{n}\frac{1-5n}{n} \left({{\eta }_{2}}^{3}{\Psi }^{21}+3{\eta }_{1}{{\eta }_{2}}^{2}{\Psi }^{19}+3{{\eta }_{1}}^{2}{\eta }_{2}{\Psi }^{17}+{{\eta }_{1}}^{3}{\Psi }^{15}\right)\rceil+n\left({b}_{1}{\lambda }_{3}{\Psi }^{18}+{b}_{2}{{\lambda }_{3}}^{2}{\Psi }^{21}\right)=0.$$
(29)

For \({\Psi }^{j}\) with \(j=\) 15, 17, 19, 21, we derive the following system of algebraic equations:

$$\begin{array}{c}{b}_{1}=0,\\ {\Psi }^{21}: \frac{1}{{n}^{2}{b}_{2}} {a}_{6} {M}_{0}\left(n\right) {{\eta }_{2}}^{3}+ {{\lambda }_{3}}^{2}=0,\\ \begin{array}{c}{\Psi }^{19}: {a}_{6} {M}_{1}(n) {\eta }_{1}+n{N}_{1}(n){c}_{3}=0,\\ {\Psi }^{17}: {a}_{6}{\eta }_{1}{M}_{2}\left(n\right)+n{N}_{2}\left(n\right) {c}_{3}=0,\\ {{\Psi }^{15}: a}_{6}{\eta }_{1}{M}_{3}\left(n\right)+n{N}_{3}\left(n\right){c}_{3}=0,\end{array}\end{array}$$
(30)

where

$${M}_{0}\left(n\right)=9\left[\frac{1}{n}9040+\frac{1-n}{n}\left( 227120 \frac{1-2n}{n}+1080\frac{1-2n}{n}\frac{1-3n}{n} +1620\frac{1-2n}{n}\frac{1-3n}{n}\frac{1-4n}{n} +81\frac{1-2n}{n}\frac{1-3n}{n}\frac{1-4n}{n}\frac{1-5n}{n}\right)\right]$$
(31)
$${M}_{1}\left(n\right)=\lceil27360 +119600\frac{1-2n}{n} +26460 \frac{1-2n}{n}\frac{1-3n}{n}+3\left(7600 +65520\frac{1-2n}{n} +16200\frac{1-2n}{n}\frac{1-3n}{n} +4455\frac{1-2n}{n}\frac{1-3n}{n}\frac{1-4n}{n} +243\frac{1-2n}{n}\frac{1-3n}{n}\frac{1-4n}{n}\frac{1-5n}{n}\right)\rceil$$
(32)
$${M}_{2}\left(n\right)=9\lceil8976 +78615\frac{1-2n}{n}+20205\frac{1-2n}{n}\frac{1-3n}{n}+4050\frac{1-2n}{n}\frac{1-3n}{n}\frac{1-4n}{n} +243\frac{1-2n}{n}\frac{1-3n}{n}\frac{1-4n}{n}\frac{1-5n}{n}\rceil$$
(33)
$${M}_{3}\left(n\right)=\lceil11564+165312\frac{1-2n}{n}+47385 \frac{1-2n}{n}\frac{1-3n}{n} +10935\frac{1-2n}{n}\frac{1-3n}{n}\frac{1-4n}{n} +729\frac{1-3n}{n}\frac{1-4n}{n}\frac{1-5n}{n}\rceil$$
(34)
$${N}_{1}\left(n\right)=\lceil120 +384\frac{1-n}{n}+216\frac{1-2n}{n} \frac{1-n}{n}+27\frac{1-2n}{n}\frac{1-3n}{n} \frac{1-n}{n}\rceil$$
(35)
$${N}_{2}\left(n\right)=\lceil408 +\frac{1-n}{n}\left(1692+1134\frac{1-2n}{n} +162\frac{1-2n}{n}\frac{1-3n}{n}\right)\rceil$$
(36)
$${N}_{3}\left(n\right)=\lceil81+\frac{1-n}{n}\left(+567+486\frac{1-2n}{n} +81\frac{1-2n}{n}\frac{1-3n}{n}\right)\rceil$$
(37)

Upon solving the system of algebraic Eqs. (30), we obtain:

$${\lambda }_{3}=\mp \frac{1}{n}\sqrt{-\frac{{M}_{0}\left(n\right){a}_{6} {\eta }_{2}}{{b}_{2}} } {\eta }_{2},$$
(38)
$${\upeta }_{1,{\text{j}}}=-\frac{{\mathrm{n N}}_{{\text{j}}}\left({\text{n}}\right){{\text{C}}}_{{\text{a}}}}{{{\text{a}}}_{6}{{\text{M}}}_{{\text{j}}}\left({\text{n}}\right)}\bullet ,\bullet \bullet \mathrm{for j}=1. 2. 3$$
(39)

Thus, bright and singular soliton solutions come out as:

$${q}_{1,j}\left(x,t\right)=\left(-pq\frac{{\eta }_{1,j}}{{\eta }_{2}}\right){\lceil{\lambda }_{3}\sqrt{\left(-pq\frac{{\eta }_{1,j}}{{\eta }_{2}}\right)}{{{\text{sech}}}^{3}}_{\mathit{pq}}\left(\sqrt{{\eta }_{1,j}}\left(x-\gamma t\right)\right)\rceil}^\frac{1}{n}exp\left[i\left(-\kappa x+\omega t+{\theta }_{0}\right)\right],$$
(40)

and

$${q}_{2,j}\left(x,t\right)=\left(-pq\frac{{\eta }_{1,j}}{{\eta }_{2}}\right){\lceil{\lambda }_{3}\sqrt{\left(-pq\frac{{\eta }_{1,j}}{{\eta }_{2}}\right)}{{{\text{csh}}}^{3}}_{\mathit{pq}}\left(\sqrt{{\eta }_{1,j}}\left(x-\gamma t\right)\right)\rceil}^\frac{1}{n}exp\left[i\left(-\kappa x+\omega t+{\theta }_{0}\right)\right]$$
(41)

respectively.

Case II: \({\eta }_{0}=\frac{1}{4}\frac{{\eta }_{1}^{2}}{{\eta }_{2}}\), \({\lambda }_{0}=0\), \({\lambda }_{1}=0\), \({\lambda }_{2}=0\), \({\eta }_{2}>0\).

Thus, Eq. (28) is reduced to the following equation:

(42)

For \({\Psi }^{j}\) with \(j=2, 4, 6, 8, 10, 12\), we obtain the following system of algebraic equations:

$$\begin{array}{c}{b}_{1}=0,\\ {{\Psi }^{12}: {\eta }_{2}}^{3}{a}_{6} {K}_{0}\left(n\right)+\frac{{n}^{2}}{1-n}{b}_{2}{{\lambda }_{3}}^{2}=0,\\ \begin{array}{c}{\Psi }^{10}: {a}_{6} {\eta }_{1}{K}_{1}\left(n\right)+{c}_{3}\lceil1152+\frac{1-2n}{n}\left(648+81\frac{1-3n}{n}\right) \rceil=0,\\ {\Psi }^{8}: {a}_{6} {\eta }_{1}{K}_{2}\left(n\right)+{c}_{3}\lceil1692+\frac{1-2n}{n}\left(1134+162\frac{1-3n}{n}\right)\rceil=0,\\ \begin{array}{c}{\Psi }^{6}: {a}_{6} {\eta }_{1}{K}_{3}\left(n\right)+{c}_{3}\lceil873+\frac{1-2n}{n}\left(364+121\frac{1-3n}{n}\right) \rceil=0,\\ {\Psi }^{4}: {a}_{6} {\eta }_{1}{K}_{4}\left(n\right)+{c}_{3}\lceil180+\frac{1-2n}{n}\left(202+40\frac{1-3n}{n}\right) \rceil=0,\\ {\Psi }^{2}: {a}_{6} {\eta }_{1}{K}_{5}\left(n\right)+{c}_{3}\lceil11+\frac{1-2n}{n}\left(20+5\frac{1-3n}{n}\right) \rceil=0,\end{array}\end{array}\end{array}$$
(43)

where

$${K}_{0}\left(n\right)=\left(90 840 +\frac{1-2n}{n}\left(155520 +\frac{1-3n}{n}\left(90720 +\frac{1-4n}{n}\left(14580+729\frac{1-5n}{n}\right)\right)\right)\right)$$
(44)
$${K}_{1}\left(n\right)=\left( 136800 +\frac{1-2n}{n}\left(343440 \frac{1-3n}{n}\left(+225180 +\frac{1-4n}{n}\left(40095 +2187\frac{1-5n}{n}\right)\right)\right)\right)$$
(45)
$${K}_{2}\left(n\right)=\left(106326+\frac{1-2n}{n}\left(251505 +\frac{1-3n}{n}\left(195210 +\frac{1-4n}{n}\left(45562+2733\frac{1-5n}{n}\right)\right)\right)\right)$$
(46)
$${K}_{3}\left(n\right)=\left(32355+\frac{1-2n}{n}\left(126360 +\frac{1-3n}{n}\left(95276+\frac{1-4n}{n}\left(27337+1822\frac{1-5n}{n}\right)\right)\right)\right)$$
(47)
$${K}_{4}\left(n\right)=\left(5319+\frac{1-2n}{n}\left(28350 +\frac{1-3n}{n}\left(30121+\frac{1-4n}{n}\left(9112+683\frac{1-5n}{n}\right)\right)\right)\right)$$
(48)

and

$${K}_{5}\left(n\right)=\left(292+\frac{1-2n}{n}\left(4455 +\frac{1-3n}{n}\left(4961 +\frac{1-4n}{n}\left(1594+13\frac{1-5n}{n}\right)\right)\right)\right)$$
(49)

Upon solving the system of algebraic Eqs. (43), we arrive at:

$${\eta }_{0}= \frac{1}{4}\frac{{\eta }_{1}^{2}}{{\eta }_{2}}, {\lambda }_{3}=\mp \frac{1}{n}\sqrt{- \frac{\left(1-n\right){a}_{6} {K}_{0}\left(n\right){\eta }_{2}}{{b}_{2}} }{\eta }_{2}$$
(50)
$${\eta }_{\mathrm{1,1}}=- \frac{{c}_{3}\lceil1152+648\frac{1-2n}{n}+81\frac{1-2n}{n}\frac{1-3n}{n} \rceil}{{a}_{6} {K}_{1}\left(n\right)}$$
(51)
$${\eta }_{\mathrm{1,2}}=- \frac{{c}_{3}\lceil1692+1134\frac{1-2n}{n}+162\frac{1-2n}{n}\frac{1-3n}{n}\rceil}{{a}_{6} {K}_{2}\left(n\right)}$$
(52)
$${\eta }_{\mathrm{1,3}}=- \frac{{c}_{3}\lceil873+364\frac{1-2n}{n}+121\frac{1-2n}{n}\frac{1-3n}{n} \rceil}{{a}_{6} {K}_{3}\left(n\right)}$$
(53)
$${\eta }_{\mathrm{1,4}}=- \frac{{c}_{3}\lceil180+202{\frac{1-2n}{n}}^{3}+40\frac{1-2n}{n}\frac{1-3n}{n} \rceil}{{a}_{6} {K}_{4}\left(n\right)}$$
(54)

and

$${\eta }_{\mathrm{1,5}}=- \frac{{c}_{3}\lceil11+20\frac{1-2n}{n}+5\frac{1-2n}{n}\frac{1-3n}{n} \rceil}{{a}_{6} {K}_{5}\left(n\right)}$$
(55)

Therefore, for \(j=1, 2, 3, 4, 5\), soliton solutions come out as.

Dark soliton solution:

$$q_{3,j}\left(x,t\right)=\sqrt{\left(-\frac{\eta_{1,j}}{2\eta_2}\right)^\frac3n}{\lambda_3^\frac1n\lceil{\text{tanh}^3}_{\mathit{pq}}\left(\sqrt{-\frac{\eta_{1,j}}2}\left(x-\gamma t\right)\right)\rceil}^\frac1nexp\left[i\left(-\kappa x+\omega t+\theta_0\right)\right]$$
(56)

Singular soliton solution:

$$q_{4,j}\left(x,t\right)=\sqrt{\left(-\frac{\eta_{1,j}}{2\eta_2}\right)^\frac3n}{\lambda_3^\frac1n\lceil{\text{coth}^3}_{\mathit{pq}}\left(\sqrt{-\frac{\eta_{1,j}}2}\left(x-\gamma t\right)\right)\rceil}^\frac1nexp\left[i\left(-\kappa x+\omega t+\theta_0\right)\right]$$
(57)

Straddled dark-bright soliton solution:

$$q_{5,j}\left(x,t\right)=\sqrt{\left(\frac{-\eta_{1,j}}{2\eta_2}\right)^\frac3n}\lambda_3^\frac1n{\lceil\begin{array}{c}{\text{tanh}}_{\mathit{pq}}\left(\sqrt{-2\eta_{1,j}}\left(x-\gamma t\right)\right)\\\pm\sqrt{-pq}{\text{sech}}_{\mathit{pq}}\left(\sqrt{{-2\eta}_{1,j}}\left(x-\gamma t\right)\right)\end{array}\rceil}^\frac3nexp\left[i\left(-\kappa x+\omega t+\theta_0\right)\right]$$
(58)

Straddled singular-singular soliton solution:

$$q_{6,j}\left(x,t\right)=\sqrt{\left(-\frac{\eta_{1,j}}{2\eta_2}\right)^\frac3n}\lambda_3^\frac1n{\lceil\begin{array}{c}{\text{coth}}_{\mathit{pq}}\left(\sqrt{-2\eta_{1,j}}\left(x-\gamma t\right)\right)\\\pm\sqrt{-pq}{\text{csch}}_{\mathit{pq}}\left(\sqrt{{-2\eta}_{1,j}}\left(x-\gamma t\right)\right)\end{array}\rceil}^3exp\left[i\left(-\kappa x+\omega t+\theta_0\right)\right]$$
(59)

Straddled dark-singular soliton solution:

$$q_{7,j}\left(x,t\right)={\sqrt{\left(-\frac{\eta_{1,j}}{2\eta_2}\right)^\frac3n}\lambda_3^\frac1n\lceil{\text{tanh}}_{\mathit{pq}}\left(\sqrt{-\frac{\eta_{1,j}}8}\xi\right)\pm{\text{coth}}_{\mathit{pq}}\left(\sqrt{\frac{{-\eta}_{1,j}}8}\xi\right)\rceil}^\frac3nexp\left[i\left(-\kappa x+\omega t+\theta_0\right)\right]$$
(60)

Results and discussion

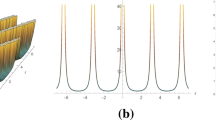
Figures 1, 2 and 3 explore the characteristics and evolution of an optical bright soliton solution described by Eq. (40) with specific parameter values: \(\kappa =1.1\), \({\theta }_{0}=1.7\), \(p=1.4\), \(q=1.8\), \({\eta }_{2}=-1.7\), \({b}_{2}=3.2\), \({a}_{1}=1.8\), \({a}_{2}=2.2\), \({a}_{6}=-1.5\), \({a}_{4}=4.3\), and \(k=1.\) These parameters are crucial in determining the behavior of the bright soliton solutions. The results are presented through surface plots, contour plots, and 2D plots. These figures offer insights into the behavior of the bright soliton solution under different conditions. Figures 1(a), 2(a), and 3(a) depict surface plots showcasing the spatial–temporal dynamics of the bright soliton solution. These plots reveal the amplitude and shape of the soliton as it propagates through the medium. The bright soliton maintains its characteristic intensity profile over time, indicative of its stable propagation behavior. In Figs. 1(b), 2(b), and 3(b), contour plots illustrate the contours of constant intensity of the bright soliton solution. These plots provide a detailed view of the soliton's shape and intensity distribution. The contour plots demonstrate the robustness of the soliton structure, which remains well-defined even as it travels through the medium. Figures 1(c) to 3 (c) display 2D plots illustrating the evolution of the bright soliton solution under the influence of the Kerr law of nonlinearity (n = 1). These plots reveal how the soliton's profile changes over time, with the soliton maintaining its characteristic shape and intensity as it propagates. By varying the time variable, the plots provide insights into the temporal evolution of the bright soliton solution. Figures 1(d) to 3 (d) investigate the impact of the power-law nonlinearity parameter (n) on the evolution of the bright soliton solution. By varying n from 1 to 2.1, these plots examine how the soliton's behavior is influenced by changes in the nonlinearity parameter. The results highlight the sensitivity of the soliton dynamics to variations in the nonlinearity parameter, with different values of n leading to distinct evolution patterns.

Fig. 1
figure 1

Profile of a bright soliton solution

Full size image
Fig. 2
figure 2

Profile of a bright soliton solution

Full size image
Fig. 3
figure 3

Profile of a bright soliton solution

Full size image

Figures 4, 5 and 6 focus on the properties and evolution of an optical dark soliton solution described by Eq. (56) with the specific parameter values: \(\kappa =1.1\), \({\theta }_{0}=1.7\), \(p=1.4\), \(q=1.8\), \({\eta }_{2}=-1.7\), \({b}_{2}=3.2\), \({a}_{1}=1.8\), \({a}_{2}=2.2\), \({a}_{6}=-1.5\), \({a}_{4}=4.3\), and \(k=1.\) These parameter values play a crucial role in shaping the behavior of dark soliton solutions. Similar to the bright soliton analysis, these figures utilize surface plots, contour plots, and 2D plots to characterize the behavior of the dark soliton solution. Figures 4(a), 5(a), and 6(a) present surface plots illustrating the spatiotemporal dynamics of the dark soliton solution. These plots depict the evolution of the soliton's amplitude and shape as it propagates through the medium. Unlike bright solitons, dark solitons exhibit localized intensity minima, maintaining their characteristic dark profile over time. In Figs. 4(b), 5(b), and 6(b), contour plots are used to visualize the intensity contours of the dark soliton solution. These plots provide detailed information about the soliton's shape and intensity distribution, emphasizing the presence of the dark notch within the soliton profile. The contour plots demonstrate the stability of the dark soliton structure during propagation. Figures 4(c) to 6(c) depict 2D plots showing the evolution of the dark soliton solution under the Kerr law of nonlinearity (n = 1). These plots demonstrate how the dark soliton maintains its characteristic profile over time, exhibiting stable propagation behavior. Additionally, Figs. 4(d) to 6(d) examine the influence of the nonlinearity parameter (n) on the dark soliton's evolution. By varying n, these plots highlight the sensitivity of the dark soliton dynamics to changes in the nonlinearity parameter, with different values of n leading to distinct evolution patterns.

Fig. 4
figure 4

Profile of a dark soliton solution

Full size image
Fig. 5
figure 5

Profile of a dark soliton solution

Full size image
Fig. 6
figure 6

Profile of a dark soliton solution

Full size image

As a result, the results presented in Figs. 1, 2, 3, 4, 5 and 6 offer comprehensive insights into the properties and behavior of both bright and dark soliton solutions under various conditions, providing valuable information for the understanding and manipulation of soliton-based optical systems.

Conclusions

This paper presents the recovery of highly dispersive optical soliton solutions to the NLSE with a generalized quadratic-cubic form of SPM using Sardar’s sub-equation approach. A wide range of soliton solutions has been recovered and exhibited. Additionally, complexiton solutions emerged as a byproduct of the integration scheme. The soliton solutions encompass single solitons as well as straddled solitons. Consequently, the results provide an exhaustive display of soliton solutions stemming from the model, retrievable through the utilization of Sardar’s sub-equation approach.

The paper holds significant promise. The integration scheme will next be applied to the NLSE with additional forms of SPM, offering new perspectives to the model not reported earlier. Subsequently, the model will be extended to include differential group delay and, ultimately, dispersion-flattened fibers. These awaited results will be sequentially reported once organized, following the structure of the cited works [32,33,34,35,36,37,38,39,40,41,42,43].