Longtime behaviour and bursting frequency, via a simple formula, of FitzHugh–Rinzel neurons

Abstract

The longtime behaviour of the FitzHugh–Rinzel (FHR) neurons and the transition to instability of the FHR steady states, are investigated. Criteria guaranteeing solutions boundedness, absorbing sets, in the energy phase space, existence and steady states instability via oscillatory bifurcations, are obtained. Denoting by $\lambda ^{3} + \sum\nolimits_{{k = 1}}^{3} {A_{k} } (R)\lambda ^{{3 - k}} = 0$, with R bifurcation parameter, the spectrum equation of a steady state $m_0$, linearly asymptotically stable at certain value of R, the frequency f of an oscillatory destabilizing bifurcation (neuron bursting frequency), is shown to be $f=\displaystyle \frac{\sqrt{A_2(R_\mathrm{H})}}{2\pi }$ with $R_\mathrm{H}$ location of R at which the bifurcation occurs. The instability coefficient power (ICP) (Rionero in Rend Fis Acc Lincei 31:985–997, 2020; Fluids 6(2):57, 2021) for the onset of oscillatory bifurcations, is introduced, proved and applied, in a new version.

1 Introduction

The brain contains many millions of neurons which trasmit the electrochemicals signals via the following mechanism. Any neuron has a central region (soma), the dendrites three and the axon. The dendrites are thin fibers around the soma while the axon is a long cylinder—starting from soma and ending in contact with other neurons (via the structures called synapses)—is constituted by long fibers. Each neuron performs a relative simple activity: the dendrites receive input from other neurons or external sources and elaborate an output signal which is propagated along the axon branchies, to thousands of other neurons (the branchies terminate on the dendrites or cell bodies of other neurons). Along the years, starting from about the second half of the past century Gerstener et al. (2014), various mathematical models have been introduced for modeling the bio-physical activity of neurons (Hodgin 1948; Hodgin and Huxley 1952; Izhikevich 2007; Ermentrant and Temam 2010; Gerstener et al. 2014). The FitzHugh–Rinzel model is given by Rinzel (1981, 1987), Rinzel and Ermentrout (1989), Izhikevich (2004), FitzHugh (1955, 1961)

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\mathrm{d}v}{\mathrm{d}t}=v-\displaystyle \frac{v^3}{3}-w+y+I,\\ \\ \displaystyle \frac{\mathrm{d}w}{\mathrm{d}t}=\delta (a+v-bw),\\ \\ \displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}=\mu (c-v-\mathrm{d}y) \end{array}\right. }\end{aligned}$$

(1)

with $I,\delta ,a,b,\mu ,c,d$ real constants and

$$\begin{aligned} \left\{ \begin{array}{ll} v=&{} \text{ difference } \text{ of } \text{ potential } \text{ between } \text{ the } \text{ dentritic }\\ &{} \text{ spine } \text{ head } \text{ and } \text{ the } \text{ surrounding } \text{ medium },\\ y=&{} \text{ slowly } \text{ moving } \text{ current } \text{ in } \text{ the } \text{ dentrite },\\ w=&{} \text{ recovery } \text{ variable }, I= \text{ applied } \text{ external } \text{ current },\\ \mu =&{} \text{ small } \text{ parameter } \text{ determining } \text{ the } \text{ pace } \text{ of } \text{ the } \text{ slow }. \end{array}\right. \end{aligned}$$

In the absence of third equation and $y=0$, (1) reduces to the FitzHugh–Nagumo binary model which contains—as special case for $\delta =1,a=b=0$—the celebrated Van der Pol oscillator (Van der Pol 1926; Hale and Kocak 1991). The variable y, introduced by Rinzel, represents the bursting behaviour of neurons: alternance between brief bursts of oscillator activity and quiescent period. In the present paper, we investigate the longtime behaviour of (1) solutions, the instability of steady states and the oscillatory bifurcations onset via the Instability Coefficients Power (ICP) approach (Rionero 2020, 2021a, b). Because of the neurons oscillatory activity, the onset of oscillatory bifurcation has attracted the attention of many scientists $\{$see Wojcik and Shilnikov 2011; Yadav et al. 2016; Alidousti and Khoshsiar Ghaziani 2017; Xie et al. 2018; Temam 1988 and the references therein$\}$, but the results obtained—although of sure interest—with respect to the rich dynamics of (1) generated by the seven parameters $(I,\delta ,a,b,\mu ,c,d)$—appear to be longely partial. Our aim is to obtain—via the instability coefficient power (ICP) approach (Rionero 2020, 2021a, b)—general criteria guaranteeing the existence of oscillatory Hopf bifurcations and an estimate of their locations (in order to obtain—via a simple closed form—the neurons activity frequency). The plane of the paper is as follows. Section 2 is devoted to boundedness and longtime behaviour of (1) solutions. In particular, the existence of absorbing sets is put in evidence. The critical points are investigated in Sect. 3 while their linear stability/instability conditions are considered in Sect. 4. The subsequent Sect. 5 is dedicated to the bifurcation power of the spectrum equation coefficients. Successively, in Sects. 6–8 the transition to instability via Hopf bifurcations driven by the growing of the bifurcating paramters ${\bar{v}},\bar{\alpha },\bar{\beta }$, respectively, is analyzed. In Sect. 9, the case $\{\alpha ^2<\frac{\mu +\delta }{3},\,\bar{\gamma }>0\}$ is investigated while the operativity of conditions (3) is checked in Sect. 10. The paper ends with: discussion, final remarks and perspectives (Sect. 11).

2 Boundedness and longtime dynamics

Setting

$$\begin{aligned} \alpha =b\delta ,\quad \beta =\mu d,\end{aligned}$$

(2)

in view of (1)$_2$-(1)$_3$ one immediately realizes that $\alpha >0$ and $\beta >0$ play the role of “viscosity coefficients”. The following properties hold.

Property 1

Let

$$\begin{aligned} |b|>\displaystyle \frac{|1-\delta |}{2|\delta |}>0,\qquad |d|>\displaystyle \frac{|1-\mu |}{2|\mu |}>0.\end{aligned}$$

(3)

Then the solutions of (1) are bounded.

Proof

In view of (2), (1) can be written

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\mathrm{d}v}{\mathrm{d}t}=-(\alpha +\beta )v+y-w+I+\left[ (\alpha +\beta +1)-\displaystyle \frac{v^2}{3}\right] v,\\ \\ \displaystyle \frac{\mathrm{d}w}{\mathrm{d}t}=-\alpha w+\delta (a+v),\\ \\ \displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}=-\beta y+\mu (c-v). \end{array}\right. }\end{aligned}$$

(4)

Introducing the “energy”

$$\begin{aligned} {\mathcal {E}}=\displaystyle \frac{1}{2}\left( v^2+w^2+y^2 \right) ,\end{aligned}$$

(5)

one has

$$\begin{aligned} \begin{array}{ll} \displaystyle \frac{\mathrm{d}{\mathcal {E}}}{\mathrm{d}t}=&{} -\left[ (\alpha +\beta )v^2+\alpha w^2+\beta y^2\right] +v(y-w+I)+ \left[ (\alpha +\beta +1)-\displaystyle \frac{v^2}{3}\right] v^2\\ \\ &{}+\delta w(a+v)+\mu y(c-v). \end{array}\end{aligned}$$

(6)

In view of

$$\begin{aligned} (\alpha +\beta +1)v^2= \,\,& {} (\alpha +\beta +1)\sqrt{\displaystyle \frac{3}{2}}\sqrt{\displaystyle \frac{2}{3}} v^2\nonumber \\\le \,\,& {} \displaystyle \frac{3}{4}(\alpha +\beta +1)^2+\displaystyle \frac{v^4}{3},\end{aligned}$$

(7)

one has

$$\begin{aligned} \begin{array}{ll} \displaystyle \frac{\mathrm{d}{\mathcal {E}}}{\mathrm{d}t}\le &{}-\left[ (\alpha +\beta )v^2+\alpha w^2+\beta y^2\right] +(\delta -1)wv+(1-\mu )yv\\ \\ &{}+(\mu c y+\delta aw+Iv)+\displaystyle \frac{3}{4}(\alpha +\beta +1)^2. \end{array}\end{aligned}$$

(8)

But

$$\begin{aligned} {\left\{ \begin{array}{ll} (\delta -1)wv\le \displaystyle \frac{|\delta -1|}{2}\left( w^2+v^2 \right) ,\,\,\,\, \delta a w\le \displaystyle \frac{(\delta a)^2}{2\varepsilon }+\displaystyle \frac{\varepsilon }{2 }w^2,\\ \\ (1-\mu )yv\le \displaystyle \frac{|\mu -1|}{2}\left( y^2+v^2 \right) ,\,\,\,\, \mu c y\le \displaystyle \frac{(\mu c)^2}{2\varepsilon }+\displaystyle \frac{\varepsilon y^2}{2},\\ \\ Iv\le \displaystyle \frac{I^2}{2\varepsilon }+\displaystyle \frac{\varepsilon v^2}{2} \end{array}\right. }\end{aligned}$$

(9)

with $\varepsilon$ positive constant, implies

$$\begin{aligned} \begin{array}{ll} \displaystyle \frac{\mathrm{d}{\mathcal {E}}}{\mathrm{d}t}\le &{}-\left\{ \left[ (\alpha +\beta )-\displaystyle \frac{1}{2}(|1-\delta |+|1-\mu |+\varepsilon )\right] v^2\right. \\ \\ &{}+\left. \left[ \alpha -\displaystyle \frac{1}{2}(|1-\delta |+\varepsilon )\right] w^2+\left[ \beta -\displaystyle \frac{1}{2}(|1-\mu |+\varepsilon )\right] y^2\right\} \\ \\ &{}+\left\{ \displaystyle \frac{3}{4}(\alpha +\beta +1)^2+\displaystyle \frac{1}{2\varepsilon }\left[ I^2+(\delta a)^2+(\mu c)^2\right] \right\} \end{array}\end{aligned}$$

(10)

and choosing the constant $\varepsilon$ such that

$$\begin{aligned} {\left\{ \begin{array}{ll} \bar{\alpha }=\displaystyle \frac{1}{2}\left[ 2\alpha -(|1-\delta |+\varepsilon )\right] >0,\\ \\ \bar{\beta }=\displaystyle \frac{1}{2}\left[ 2\beta -(|1-\mu |+\varepsilon )\right] \end{array}\right. }\end{aligned}$$

(11)

then (10) implies

$$\begin{aligned} \displaystyle \frac{\mathrm{d}\mathrm{d}{{\mathcal {E}}}}{\mathrm{d}t}\le -h{\mathcal {E}}+ h_1\end{aligned}$$

(12)

with

$$\begin{aligned} {\left\{ \begin{array}{ll} h=\min (\bar{\alpha },\bar{\beta }),\\ \\ h_1=\displaystyle \frac{3}{4}(\alpha +\beta +1)^2+\displaystyle \frac{1}{2\varepsilon }\left[ I^2+(\delta a)^2+(\mu c)^2\right] . \end{array}\right. }\end{aligned}$$

(13)

In view of (12), one easily obtains

$$\begin{aligned} {\mathcal {E}}\le {{\mathcal {E}}}_0 e^{-ht}+\displaystyle \frac{h_1}{h}(1-e^{-ht})\end{aligned}$$

(14)

and hence

$$\begin{aligned} {\mathcal {E}}\le {{\mathcal {E}}}_0+\displaystyle \frac{h_1}{h}.\end{aligned}$$

(15)

$\square$

Remark 1

We remark that, case by case, according to the values of the parameters contained in (1), the existence of the positive constants appearing in (11), has to be verified. Only then properties 1–2 hold. We underline that (11) equivalently can be written

$$\begin{aligned} {\left\{ \begin{array}{ll} 2\alpha>|1-\delta |+\varepsilon ,\\ 2\beta >|1-\mu |+\varepsilon \end{array}\right. }\end{aligned}$$

(16)

for at least a positive $\varepsilon$, i.e. equivalently

$$\begin{aligned} {\left\{ \begin{array}{ll} 2\alpha>|1-\delta |,\\ 2\beta >|1-\mu |. \end{array}\right. }\end{aligned}$$

(17)

In fact, (16) is implied by (17) and

$$\begin{aligned} {\left\{ \begin{array}{ll} 2\alpha =|1-\delta |,\\ 2\beta =|1-\mu | \end{array}\right. }\end{aligned}$$

(18)

is not allowed by (13)$_1$.

Property 2

Let (3) holds. Then, in the phase space $\{v,w,y\}$, any sphere S centered at the origin of radius r bigger than $\left( \displaystyle \frac{2h_1}{h}\right) ^{\frac{1}{2}}$, is an absorbing set.

Proof

Let ${\bar{r}}>\left( \displaystyle \frac{2h_1}{h}\right) ^{1/2}$ and let ${{\mathcal {E}}}_0<\displaystyle \frac{h_1}{h}$. Then (12) implies

$$\begin{aligned} \left( \displaystyle \frac{d{\mathcal {E}}}{dt}\right) _{(t=0)}<0,\end{aligned}$$

(19)

i.e. $S({\bar{r}})$ is invariant. Further if

$$\begin{aligned} \bar{{\mathcal {E}}}_0=\displaystyle \max _{{\mathcal {I}}}{\mathcal {E}}_0 \end{aligned}$$

with ${\mathcal {I}}$ bounded region of the phase space, all the solutions with the initial data in ${\mathcal {I}}$, at the time ${\bar{t}}$ given by

$$\begin{aligned} \displaystyle \frac{h_1}{h}+\left| \bar{{\mathcal {E}}}_0-\displaystyle \frac{h_1}{h}\right| e^{-h{\bar{t}}}={{\bar{r}}}^2 \end{aligned}$$

i.e. at

$$\begin{aligned} {\bar{t}}=\displaystyle \frac{1}{h}\ln \displaystyle \frac{\left| \bar{{\mathcal {E}}}_0-\displaystyle \frac{h_1}{h}\right| }{\left| {{\bar{r}}}^2-\displaystyle \frac{h_1}{h}\right| }>0 \end{aligned}$$

are in $S({\bar{r}})$. Therefore $S({\bar{r}})$ is an absorbing set and the longtime dynamics happens in $S({\bar{r}})$. $\square$

3 Critical points

In view of (1), one has

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\mathrm{d}v}{\mathrm{d}t}=v-w+y-\displaystyle \frac{v^3}{3}+I,\\ \\ \displaystyle \frac{\mathrm{d}w}{\mathrm{d}t}=-\alpha w+\delta v+a\delta ,\\ \\ \displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}=-\beta y-\mu v+\mu c \end{array}\right. }\end{aligned}$$

(20)

and the critical points are the roots of

$$\begin{aligned} {\left\{ \begin{array}{ll} {\bar{v}}-{\bar{w}}+{\bar{y}}-\displaystyle \frac{{\bar{v}}^3}{3}+I=0,\\ \\ {\bar{w}}=\displaystyle \frac{\delta }{\alpha }({\bar{v}}+a),\,\, {\bar{y}}=\displaystyle \frac{\mu }{\beta }(c-{\bar{v}}). \end{array}\right. }\end{aligned}$$

(21)

One has

$$\begin{aligned} {\bar{v}}^3-3\left[ {\bar{v}}-\displaystyle \frac{\delta }{\alpha }({\bar{v}}+a)+\displaystyle \frac{\mu }{\beta }(c-{\bar{v}})+I\right] =0\end{aligned}$$

(22)

and hence it follows

$$\begin{aligned} {\left\{ \begin{array}{ll} {\bar{v}}^3-3\left( 1-\displaystyle \frac{\delta \beta +\mu \alpha }{\alpha \beta }\right) {\bar{v}}-3\displaystyle \frac{\alpha \beta I-a\beta \delta +\mu \alpha c}{\alpha \beta }=0,\\ \\ {\bar{w}}=\displaystyle \frac{\delta }{\alpha }({\bar{v}}+a),\,\, {\bar{y}}=\displaystyle \frac{\mu }{\beta }(c-{\bar{v}}). \end{array}\right. }\end{aligned}$$

(23)

Setting

$$\begin{aligned} A=\displaystyle \frac{3(\delta \beta +\mu \alpha -\alpha \beta )}{\alpha \beta },\qquad B=\displaystyle \frac{3(a\delta \beta -\mu \alpha c-I\alpha \beta )}{\alpha \beta },\end{aligned}$$

(24)

one has

$$\begin{aligned} {\left\{ \begin{array}{ll} {\bar{v}}^3+A{\bar{v}}+B=0,\\ \\ {\bar{w}}=\displaystyle \frac{\delta }{\beta }({\bar{v}}+a),\\ \\ {\bar{y}}=\displaystyle \frac{\mu }{\beta }(c-{\bar{v}}). \end{array}\right. }\end{aligned}$$

(25)

Remark 2

We remark that

• 1. The DS (1)—depending on seven real parameters—has a very rich dynamics;

• 2. A, B—being real constants—(25)$_1$ admits at least one real root for any value of the parameters—given by the celebrated Cardano formula—and therefore at least $\infty ^7$ critical points are admissible;

• 3. $\{I=\displaystyle \frac{a\beta \delta -\mu \alpha c}{\alpha \beta },\,\beta \ne 0\}$ implies the existence of the critical point $E=\left( 0,\displaystyle \frac{a\delta }{\mu },\displaystyle \frac{\mu c}{\beta }\right)$;

• 4. $\{\delta \beta +\mu \alpha =\alpha \beta ,\,\beta \ne 0\}\Rightarrow A=0$ and (23)$_1$ reduces to ${\bar{v}}^3_e+B=0$ and one has the critical points $\{{\bar{v}}_e=|B|^\frac{1}{3},\,\bar{\omega }_e=\displaystyle \frac{\delta }{\alpha }(|B|^\frac{1}{3}-a), {\bar{y}}_e=\displaystyle \frac{\mu }{\beta }(c-|B|^\frac{1}{3})\}$ for $B<0$, while $B>0$ implies the existence of $\{{\bar{v}}_e=-B^\frac{1}{3},\,\bar{\omega }_e=\displaystyle \frac{\delta }{\alpha }(a-B^\frac{1}{3}), {\bar{y}}_e=\displaystyle \frac{\mu }{\beta }(c+B^\frac{1}{3})\}$;

• 5. $\{I=\displaystyle \frac{a\beta \delta -\mu \alpha c}{\alpha \beta },\,\delta \beta +\mu \alpha <\alpha \beta \}$ implies the existence of the real critical points ${\bar{v}}_e=\pm \left( 3\displaystyle \frac{\alpha \beta -\delta \beta -\mu \alpha }{\alpha \beta }\right) ^\frac{1}{2},\,\bar{\omega }_e=\displaystyle \frac{\delta }{\alpha }\left[ \pm \left( \displaystyle \frac{\alpha \beta -\delta \beta -\mu \alpha }{\alpha \beta }\right) ^\frac{1}{2}+a\right] ,$ ${\bar{y}}_e=\displaystyle \frac{\mu }{\beta }\left[ c\mp \left( \displaystyle \frac{\alpha \beta -\delta \beta -\mu \alpha }{\alpha \beta }\right) ^\frac{1}{2}\right]$;

• 6. Real steady states, via (26), are not admissible

  $$\begin{aligned} {\left\{ \begin{array}{ll} {\bar{v}}^2_e-\root 3 \of {B}{\bar{v}}_e+\root 3 \of {B^2}=0, \text{ for } B>0,\\ {\bar{v}}^2_e+\root 3 \of {|B|}{\bar{v}}_e+\root 3 \of {|B|^2}, \text{ for } B<0. \end{array}\right. } \end{aligned}$$

  (26)

4 Linear stability, spectrum equation and its coefficients properties

Let $E=({\bar{v}},{\bar{w}},{\bar{y}})$ be an admissible critical point. Setting

$$\begin{aligned} V=v-{\bar{v}},\quad W=w-{\bar{w}},\quad Y=y-{\bar{y}},\end{aligned}$$

(27)

it follows that

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \frac{\mathrm{d}V}{\mathrm{d}t}=V-\displaystyle \frac{V^3}{3}-{\bar{v}} V^2-{\bar{v}}^2 V-W+Y,\\ \\ \displaystyle \frac{\mathrm{d}W}{\mathrm{d}t}=\delta V-\alpha W,\\ \\ \displaystyle \frac{\mathrm{d}Y}{\mathrm{d}t}=-\mu V-\beta Y. \end{array}\right. }\end{aligned}$$

(28)

Linearizing about E one has

$$\begin{aligned} \displaystyle \frac{d}{dt}\left( \begin{array}{c} V\\ W\\ Y \end{array}\right) =L\left( \begin{array}{c} V\\ W\\ Y \end{array}\right) \end{aligned}$$

(29)

with

$$\begin{aligned} L=\left( \begin{array}{ccc} 1-{\bar{v}}^2&{}-1&{}1\\ \delta &{}-\alpha &{}0\\ -\mu &{}0&{}-\beta \end{array}\right) \end{aligned}$$

(30)

The spectrum equation is

$$\begin{aligned} {\mathcal {P}}(\lambda )=\lambda ^3+A_1\lambda ^2+A_2\lambda +A_3=0,\end{aligned}$$

(31)

with

$$\begin{aligned} A_1=-I_1,\quad A_2=I_2,\quad A_3=-I_3,\end{aligned}$$

(32)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} I_1=\text{ trace } \text{ of } L,\,\,\,\,I_3=\text{ det } \text{ of } L,\\ \\ I_2=\left| \begin{array}{cc} 1-{\bar{v}}^2&{}-1\\ \delta &{}-\alpha \end{array}\right| + \left| \begin{array}{cc} 1-{\bar{v}}^2&{}1\\ -\mu &{}-\beta \end{array}\right| +\left| \begin{array}{cc} -\alpha &{}0\\ 0&{}-\beta \end{array}\right| \end{array}\right. }\end{aligned}$$

(33)

i.e.

$$\begin{aligned} {\left\{ \begin{array}{ll} I_1=1-{\bar{v}}^2-(\alpha +\beta ),\,\,\,\, I_2=\mu +\alpha \beta +\delta -(\alpha +\beta )(1-{\bar{v}}^2),\\ \\ I_3=\beta \left[ \alpha (1-{\bar{v}}^2)-\delta \right] -\mu \alpha . \end{array}\right. }\end{aligned}$$

(34)

Let $\sigma$ be the spectrum of L, i.e. the set of the roots of (31) and recall that

• (i) $E=({\bar{v}},{\bar{w}},{\bar{y}})$ is linearly (asymptotically) stable if and only if all the eigenvalues of the spectrum equation have negative real part (Rionero 2012);

• (ii) only if

  $$\begin{aligned} A_k>0,\qquad \forall k\in (1,2,3),\end{aligned}$$

  (35)

  all the eigenvalues can have negative real part;

• (iii) if and only if

  $$\begin{aligned} A_1>0,\quad A_3>0,\quad A_1A_2-A_3>0,\end{aligned}$$

  (36)

  all the eigenvalues have negative real part (Routh-Hurwitz conditions) (Rionero 2019a). If the problem at stake depends on a positive parameter R (bifurcation parameter) at the growing of R, E can become unstable. Then (31) becomes

  $$\begin{aligned} {\mathcal {P}}(\lambda ,R)=\lambda ^3+A_1(R)\lambda ^2+A_2(R)\lambda +A_3(R)=0.\end{aligned}$$

  (37)

  Denoting by $R_{\rm S}$ the lowest root of

  $$\begin{aligned} A_3(R)=0\end{aligned}$$

  (38)

  and by $R_{\rm H}$ the lowest positive root of

  $$\begin{aligned} {\mathcal {P}}(i\omega , R)=0\end{aligned}$$

  (39)

  with i imaginary unit and $\omega$ real number, then—since the instability case occurs via a zero or via a pure imaginary eigenvalues—one has

  $$\begin{aligned} \left\{ \begin{array}{lll} R_{\rm S}<R_{\rm H}&{}\Leftrightarrow &{} \text{ steady } \text{ bifurcation },\\ \\ R_{\rm S}>R_{\rm H}&{}\Leftrightarrow &{} \text{ oscillatory } \text{ Hopf } \text{ bifurcation },\\ \\ R_{\rm S}=R_{\rm H}&{}\Leftrightarrow &{} \text{ coupled } \text{ steady-Hopf } \text{ bifurcation } \end{array}\right. \end{aligned}$$

  (40)

5 The instability coefficient power method for ternary DS

We call “auxiliary coefficient” of the spectrum equation (31) the coefficient $A_0$ given by

$$\begin{aligned} A_0(R)=A_1(R)A_2(R)-A_3(R),\end{aligned}$$

(41)

and remark that properties (ii) and (iii) of Sect. 4 give to the coefficients $A_k, k\in \{0,1,2,3\}$, via their becoming zero at certain values of the bifurcation parameter R, the power of driving the location and the type of the occurring bifurcation. The following property holds.

Property 3

Let a critical point $m_0$ be linearly, asymptotically stable at certain value ${\bar{R}}$ of the bifurcation parameter R and let $R_{c_k}$ be the lowest root of $A_k(R)=0$, at the increasing (decreasing) of R from $R={\bar{R}}$. Measuring the instability power of $A_k$ via the (ICP) index given by

$$\begin{aligned} (ICP)=(R_{c_k})^{-1},\quad k\in \{0,1,2,3\}\end{aligned}$$

(42)

then the coefficient with the biggest (ICP) drives the occurring of a steady bifurcation for $k=3$, while $k<3$ implies the occurring of an Hopf bifurcation at $R_0$, lowest root of $A_0(R)=0$ and the estimates $R_0\in ]{\bar{R}}, R_{c_k}[$ at the increasing of R ($R_0\in ]R_{c_k},{\bar{R}}[$ at the decreasing of R) hold.

Proof

Property 3 is implied by the following properties 4–5. $\square$

Property 4

At a value ${\bar{R}}$ of the bifurcation parameter R, an Hopf bifurcation occurs if and only if

$$\begin{aligned} A_0({\bar{R}})=0,\quad A_k({\bar{R}})>0,\quad k\in \{1,2,3\}.\end{aligned}$$

(43)

Proof

(43)$_1$ is necessary. Let an oscillatory bifurcation arises. Then the eigenvalues of the spectrum equation are of type

$$\begin{aligned} \lambda _1=\delta ,\,\,\,\lambda _{3,4}=\pm i\varphi ,\,(\delta ,\varphi \in {\mathbb {R}})\end{aligned}$$

(44)

and hence

$$\begin{aligned} (\lambda ^2+\varphi ^2)(\lambda -\delta )=\lambda ^3-\delta \lambda ^2+\varphi ^2\lambda -\delta \varphi ^2=0\end{aligned}$$

(45)

and one has

$$\begin{aligned} A_1=-\delta ,\quad A_2=\varphi ^2,\quad A_3-\delta \varphi ^2,\quad A_0=A_3-A_1A_2=0.\end{aligned}$$

(46)

Viceversa (43) is sufficient. In fact, (37) in view of (43)$_1$ becomes

$$\begin{aligned} (\lambda +A_1)(\lambda ^2+A_2)=0\end{aligned}$$

(47)

and the eigenvalues

$$\begin{aligned} \lambda _{1,2}=\pm i\sqrt{A_2},\quad \lambda _3=-A_1,\end{aligned}$$

(48)

are immediately obtained. Since the general integral of the spectrum equation implies

$$\begin{aligned}&\left( \begin{array}{l} v\\ \omega \\ y \end{array}\right) =c_1e^{-A_1 t}+c_2\cos \varphi t+c_3\sin \varphi t,\nonumber \\&\quad (c_n=\text{ constant },\, n\in \{1,2,3\}),\end{aligned}$$

(49)

one has that, $A_1>0$ implies the existence of a simple Hopf bifurcation (SHB) of frequency

$$\begin{aligned} f=\displaystyle \frac{1}{2\pi }\sqrt{A_2({\bar{R}})}\end{aligned}$$

(50)

coupled to a time exponentially decreasing perturbation, while $A_1=0$ implies that the Hopf bifurcation is coupled to a steady one (steady-Hopf bifurcation). $\square$

Property 5

Let $A_k(R), k\in \{1,2,3\}$ be smooth functions of the bifurcation parameter R and let a steady state $m_0$ be asymptotically stable at $R={\bar{R}}$. Then, at the increasing (decreasing) of R from $R={\bar{R}}$, a SHB occurrs if and only if exists only one coefficient $A_k, k\in \{1,2\}$, such that

$$\begin{aligned} (ICP)_k>(ICP)_3.\end{aligned}$$

(51)

Proof

(51) is obviously necessary. On the other hand—by assumptions, one has

$$\begin{aligned} A_k({\bar{R}})>0,\qquad \forall k\in \{0,1,2,3\},\end{aligned}$$

(52)

$\square$

and, in view of proeprty 5,

$$\begin{aligned} A_0(R_{c,k})=(A_1A_2-A_3)_{(R=R_{c_k})}<0.\end{aligned}$$

(53)

Therefore, at the increasing (decreasing) of R from ${\bar{R}}$ to $R_{c_k}$, one has

$$\begin{aligned} A_0({\bar{R}})>0,\quad A_0(R_{c_k})<0\end{aligned}$$

(54)

which implies the existence of a $R_*\in ]{\bar{R}}, R_{c_k}[$ ($R_*\in ] R_{c_k},{\bar{R}}[$), lowest root of $A_0=0$, at which the SHB occurs.

Remark 3

The cases

$$\begin{aligned} R_{c_2}=R_{c_3},\end{aligned}$$

(55)

and

$$\begin{aligned} R_{c_1}=R_{c_3},\end{aligned}$$

(56)

since implies $A_0(R_{c_k})=0, (k=1,2)$, are governed by property 5.

5.1 The ICP method for a bifurcation parameter $R\in ]-\infty , \infty [$

Since the parameters appearing in (1) have only to be real numbers, it appears necessary a formulation of the ICP method for a bifurcation parameter $\zeta \in ]-\infty ,\infty [$.

Let at a value $\zeta \in ]-\infty ,\infty [$ of R exists a steady state $m_0$. Then the following formulation of the ICP method holds.

Property 6

If, at $R=\zeta$, the steady state $m_0$ is linearly asymptotically stable, then, at the increasing (decreasing) of R from $R=\zeta$, the coefficient $A_k$ of the spectrum equation of $m_0$, first becoming zero, drives not only the transition to instability but also the type and location of the occurring bifurcation which is a SHB if $k<3$, a steady one if $k=3$, and a Hopf bifurcation coupled to a steady one if $R_{c_k}=R_{c_3}$, $k=1$ or $k=3$.

Proof

Introducing the parameters ${\mathcal {R}}, \bar{{\mathcal {R}}}$ such that

$$\begin{aligned} \begin{array}{ll} {\mathcal {R}}=R-\zeta ,&{}\quad \text{ for } R\ge \zeta ,\\ \bar{{\mathcal {R}}}=\zeta -R,&{}\quad \text{ for } R\le \zeta \end{array} \end{aligned}$$

it follows that ${\mathcal {R}}\ge 0,\bar{{\mathcal {R}}}\ge 0$ respectively and the formulation of the ICP method given in property 4 can be applied with ${\bar{R}}=0$. $\square$

6 Hopf bifurcations driven by ${\bar{v}}$

Property 7

Let

$$\begin{aligned} \inf (b, \mu ,\delta )>0.\end{aligned}$$

(57)

Then only the critical points $E=({\bar{v}},\bar{\omega },{\bar{y}})$ with $({\bar{v}})^2\le 1$ can bifurcate via Hopf bifurcations.

Proof

In vire of (32)–(34), the coefficients of the spectrum equation can be written

$$\begin{aligned} \left\{ \begin{array}{l} A_1=\alpha +\beta +\gamma ,\\ A_2=\mu +\delta +\alpha \beta +(\alpha +\beta )\gamma ,\\ A_3=\mu \alpha +\beta (\delta +\alpha \gamma ), \end{array}\right. \end{aligned}$$

(58)

with

$$\begin{aligned} \gamma =({\bar{v}})^2-1,\quad \inf (\alpha ,\beta )>0\end{aligned}$$

(59)

and are—in view of (57)—increasing functions of $\gamma$. It follows that

$$\begin{aligned} \gamma \ge 0\Leftrightarrow \left\{ \begin{array}{l} A_k>0,\,\forall k\in \{1,2,3\},\\ (A_1A_2-A_3)_{(\gamma =0)}=A_2+A_1(\alpha +\beta )-\alpha \beta>A_1(\alpha \beta )>0. \end{array}\right. \end{aligned}$$

(60)

On the other hand

$$\begin{aligned} (A_1A_2-A_3)_{(\gamma =0)}=(\alpha +\beta )(\mu +\delta +\alpha \beta )-(\mu \alpha +\beta \delta )>0\end{aligned}$$

(61)

and the linear stability conditions (36) are verified $\forall \gamma \ge 0,$ i.e. $\forall \bar{v}\ge 1$. $\square$

On setting

$$\begin{aligned} \bar{\gamma }=1-{\bar{v}}^2=-\gamma \end{aligned}$$

(62)

(58) becomes

$$\begin{aligned} \left\{ \begin{array}{l} A_1=\alpha +\beta -\bar{\gamma },\\ A_2=\mu +\delta +\alpha \beta -(\alpha +\beta )\bar{\gamma },\\ A_3=\mu \alpha +\beta \delta -\alpha \beta \bar{\gamma }\end{array}\right. \end{aligned}$$

(63)

and at the decreasing of ${\bar{v}}^2$ from ${\bar{v}}^2=1$, the $A_k$ are decreasing functions of $\bar{\gamma }$.

Denoting by $\bar{\gamma }_{ck}$ the lowest root of $A_k(\bar{\gamma })$ and letting (57) holds, one has

$$\begin{aligned} {\left\{ \begin{array}{ll} \bar{\gamma }_{c1}=\alpha +\beta ,\\ \bar{\gamma }_{c2}=\displaystyle \frac{\mu +\delta +\alpha \beta }{\alpha +\beta },\\ \bar{\gamma }_{c3}=\displaystyle \frac{\mu \alpha +\beta \delta }{\alpha \beta } \end{array}\right. }\end{aligned}$$

(64)

and it follows that

$$\begin{aligned} {\left\{ \begin{array}{ll} \bar{\gamma }_{c1}\le (\ge )\bar{\gamma }_{c2} \Leftrightarrow (\alpha +\beta )^2\le (\ge ) \mu +\delta +\alpha \beta ,\\ \bar{\gamma }_{c2}\le (\ge )\bar{\gamma }_{c3} \Leftrightarrow (\alpha \beta ) (\mu +\delta +\alpha \beta )\le (\ge ) (\alpha +\beta )(\mu \alpha +\beta \delta ),\\ \bar{\gamma }_{c1}\le (\ge )\bar{\gamma }_{c3} \Leftrightarrow (\alpha \beta )(\alpha +\beta )\le (\ge ) \mu \alpha +\beta \delta \end{array}\right. }\end{aligned}$$

(65)

Property 8

Let (57) holds with

$$\begin{aligned} \inf (\alpha ,\bar{\gamma })>0.\end{aligned}$$

(66)

Then, at the growing of $\bar{\gamma }$ from $\bar{\gamma }=0$,

$$\begin{aligned} \alpha \beta (\alpha +\beta )<\mu \alpha +\beta \delta ,\end{aligned}$$

(67)

guarantees the existence of a $\bar{\gamma }_c\in ]0,\bar{\gamma }_{c3}[$ at which an oscillatory bifurcation occurs, while

$$\begin{aligned} \alpha \beta (\alpha +\beta )=\mu \alpha +\beta ^2,\end{aligned}$$

(68)

guarantees that at $\bar{\gamma }_{c1}=\bar{\gamma }_{c3}$ an oscillatory bifurcation, coupled with a steady one, occurs.

Proof

In fact, (67)–(68) are—according to (65)$_3$—respectively equivalent to $\bar{\gamma }_{c1}<\bar{\gamma }_{c3}$ and to $\bar{\gamma }_{c1}=\bar{\gamma }_{c3}$. Then the proof is implied by properties 3-4 and by

$$\begin{aligned} \bar{\gamma }_{c1}=\bar{\gamma }_{c3}\Rightarrow \left[ (A_1A_2-A_3)\right] _{\bar{\gamma }_{c1}=\bar{\gamma }_{c3}=0}^{\bar{\gamma }=0}=0. \end{aligned}$$

$\square$

Property 9

Let (57), (66) hold. Then at the growing of $\bar{\gamma }$ from $\bar{\gamma }=0$

$$\begin{aligned} \alpha \beta (\mu +\delta +\alpha \beta )<(\alpha +\beta )(\mu \alpha +\beta \delta ),\end{aligned}$$

(69)

guarantees the existence of a $\bar{\gamma }_c\in ]0,\bar{\gamma }_{c3}[$ at which an Hopf bifurcation occurs while

$$\begin{aligned} \alpha \beta (\mu +\delta +\alpha \beta )=(\alpha +\beta )(\mu \alpha +\beta \delta ),\end{aligned}$$

(70)

guarantees that at $\bar{\gamma }_{c2}=\bar{\gamma }_{c3}$, an Hopf bifurcation, coupled with a steady one, occurs.

Proof

(69) implies $\bar{\gamma }_{c2}<\bar{\gamma }_{c3}$. Then the proof is implied by properties 3–4. $\square$

7 Hopf bifurcations driven by $\bar{\alpha }=-\alpha$ growing

The bifurcations criteria obtained in the previous section, all require $\gamma \le 0$. In the present section, we obtain that decreasing $\alpha$ as bifurcating parameter and letting $\alpha \le 0$, the Hopf bifurcation can arise with $\gamma \ge 0$.

Property 10

Let

$$\begin{aligned} \alpha \le 0,\quad \inf (\beta ,\mu ,\delta ,\gamma )>0,\end{aligned}$$

(71)

and set

$$\begin{aligned}&\bar{\alpha }=-\alpha ,\quad \bar{\alpha }_{c1}=\beta +\gamma ,\,\,\, \bar{\alpha }_{c2}=\displaystyle \frac{\mu \delta +\beta \gamma }{\beta +\gamma },\nonumber \\&\quad \bar{\alpha }_{c3}=\displaystyle \frac{\beta \delta }{\mu +\beta \gamma }.\end{aligned}$$

(72)

Then at the growing of $\bar{\alpha }$ from $\bar{\alpha }=0,$ one has that

$$\begin{aligned} \bar{\alpha }_{c1}<\bar{\alpha }_{c3}\le \bar{\alpha }_{c2}, \end{aligned}$$

(73)

$$\begin{aligned} \bar{\alpha }_{c1}=\bar{\alpha }_{c3}< \bar{\alpha }_{c2}, \end{aligned}$$

(74)

$$\begin{aligned} \bar{\alpha }_{c12}<\bar{\alpha }_{c3}\le \bar{\alpha }_{c1},\end{aligned}$$

(75)

guarantee respectively the existence of

• (i) an $\bar{\alpha }\in ]0,\bar{\alpha }_{c1}[$ in which a SHB occurs;

• (ii) an Hopf bifurcation of frequency $\varphi =\displaystyle \frac{1}{2\pi }\sqrt{A_2(\bar{\alpha }_{c1})}$, coupled to a steady state, at $\bar{\alpha }=\bar{\alpha }_{c2}$;

• (iii) an $\bar{\alpha }\in ]0,\bar{\alpha }_{c2}[$ in which a simple Hopf bifurcation occurs.

Proof

At $\bar{\alpha }=0$, in view of (58), one has

$$\begin{aligned} {\left\{ \begin{array}{ll} A_1=\beta +\gamma>0,\,\,A_2=\mu +\delta +\beta \gamma>0,\,\,A_3=\beta \delta>0,\\ A_1A_2-A_3=(\beta +\gamma )(\mu +\delta +\beta \gamma )-\beta \delta =\beta (\mu +\beta \gamma )+\gamma (\mu +\delta +\beta \gamma )>0 \end{array}\right. }\end{aligned}$$

(76)

and $E=({\bar{v}},{\bar{w}},{\bar{y}})$ is linearly stable at $\bar{\alpha }=0$. On the other hand, being $\bar{\alpha }_{ck}$ the lowest positive root of $A_k(\bar{\alpha })=0, k\in \{1,2,3\}$, property 10 is implied by property 3. $\square$

Remark 4

We remark that

$$\begin{aligned} \alpha =b\delta \le 0,\qquad \delta >0,\end{aligned}$$

(77)

implies that b is a bifurcating parameter.

8 Hopf bifurcations driven by $\bar{\beta }=-\beta$ growing

A criterion analogous to the which one of property 10 can be easily obtained.

Property 11

Let

$$\begin{aligned} -\alpha \gamma<\mu <0,\quad \inf (b,\delta ,\gamma )>0,\quad \delta =1\end{aligned}$$

(78)

and set

$$\begin{aligned}&\bar{\beta }=-\beta ,\,\,\,\bar{\beta }_{c1}=\alpha +\gamma ,\,\,\, \bar{\beta }_{c2}=\displaystyle \frac{\mu \delta +\alpha \gamma }{\alpha +\gamma },\nonumber \\&\quad \bar{\beta }_{c3}=\displaystyle \frac{\alpha \delta }{\mu +\alpha \gamma }.\end{aligned}$$

(79)

Then at the growing of $\bar{\beta }$ form $\bar{\beta }=0$, one has that

$$\begin{aligned} {\left\{ \begin{array}{ll} \bar{\beta }_{c1}<\bar{\beta }_{c3}\le \bar{\beta }_{c_2},\\ \bar{\beta }_{c1}=\bar{\beta }_{c3}\le \bar{\beta }_{c_2},\\ \bar{\beta }_{c2}<\bar{\beta }_{c3}= \bar{\beta }_{c1} \end{array}\right. }\end{aligned}$$

(80)

guarantee, respectively, the existence of

• (i) an $\bar{\beta }\in ]0,\bar{\beta }_{c1}[$ in which a SHB occurs;

• (ii) an Hopf bifurcation of frequency $f=\displaystyle \frac{\sqrt{A_2(\bar{\beta }_{c1})}}{2\pi }$, coupled to a steady state, at $\bar{\alpha }=\bar{\beta }_{c2}$;

• (iii) an $\bar{\beta }\in ]0,\bar{\beta }_{c2}[$ in which a SHB occurs.

Proof

In view of (58) one has

$$\begin{aligned}&A_1=\alpha -\bar{\beta }+\gamma ,\,\,A_2=\mu +\delta -\alpha \bar{\beta }+(\alpha -\bar{\beta })\gamma ,\nonumber \\&\quad A_3=\mu \alpha -\bar{\beta }(\delta +\alpha \gamma ),\end{aligned}$$

(81)

and immediately follows that $\bar{\beta }_{ck}$ is the lowest root of $A_k(\bar{\beta })$. On the other hand at $\bar{\beta }=0$ one has

$$\begin{aligned} {\left\{ \begin{array}{ll} A_k>0,\,\,k\in \{1,2,3\},\\ A_1A_2-A_3=(\alpha +\gamma )(\mu +\delta +\alpha \gamma )-\mu \alpha >0 \end{array}\right. } \end{aligned}$$

(82)

$\square$

i.e. the linear asymptotic stability of $E=({\bar{v}},{\bar{w}},{\bar{y}})$ at $\bar{\beta }=0$. Since (80) can be obtained from (79) via the substitution

$$\begin{aligned} \left( \begin{array}{ccc} \delta &{}\mu &{}\beta \\ \mu &{}\delta &{}\alpha \end{array}\right) \end{aligned}$$

(83)

one easily verifies that (73)–(75) with $\bar{\beta }_{ck}$ at the place of $\bar{\alpha }_{ck}$ implies (i)–(iii) of property 11.

9 A criterion of existence, location of bifurcations in the case $\{\alpha =\beta ,\delta >0,\gamma \ge 0\}$

Let

$$\begin{aligned} \bar{\gamma }=1-{\bar{v}}^2,\quad \inf (b,\mu ,\delta )>0.\end{aligned}$$

(84)

Then (63)–(65) reduce to

$$\begin{aligned}&A_1=2\alpha -\bar{\gamma },\quad A_2=\mu +\delta +\alpha ^2-2\alpha \bar{\gamma },\nonumber \\&\quad A_3=\alpha (\mu +\delta -\alpha \bar{\gamma }),\end{aligned}$$

(85)

and setting

$$\begin{aligned} \bar{\gamma }_{c_1}=2\alpha ,\quad \bar{\gamma }_{c_2}=\displaystyle \frac{\mu +\delta +\alpha ^2}{2\alpha },\quad \bar{\gamma }_{c_3}=\displaystyle \frac{\mu +\delta }{\alpha ^2}\end{aligned}$$

(86)

one has

$$\begin{aligned} A_k(\bar{\gamma }_{c_k})=0.\end{aligned}$$

(87)

It follows that

$$\begin{aligned} {\left\{ \begin{array}{ll} \bar{\gamma }_{c_1}\le (\ge ) \bar{\gamma }_{c_3}\Leftrightarrow \alpha ^2\le (\ge ) \displaystyle \frac{\mu +\delta }{2},\\ \bar{\gamma }_{c_1}\le (\ge ) \bar{\gamma }_{c_2}\Leftrightarrow \alpha ^2\le (\ge ) \displaystyle \frac{\mu +\delta }{3},\\ \\ \bar{\gamma }_{c_2}\le (\ge ) \bar{\gamma }_{c_3}\Leftrightarrow \alpha ^2\le (\ge ) \mu +\delta , \end{array}\right. } \end{aligned}$$

(88)

Since

$$\begin{aligned} \mu +\delta >0\end{aligned}$$

(89)

implies that at $\bar{\gamma }=0$ one has

$$\begin{aligned} {\left\{ \begin{array}{ll} A_k>0,\quad \forall k\in \{1,2,3\},\\ \\ (A_1A_2-A_3)_{(\bar{\gamma }=0)}=\alpha \left[ (\mu +\delta )+2\alpha ^2\right] >0 \end{array}\right. }\end{aligned}$$

(90)

i.e. the linear asymptotic stability holds.

Property 12

Let (84), (89) hold. Then

$$\begin{aligned} \alpha ^2<\displaystyle \frac{\mu +\delta }{3},\quad \bar{\gamma }>0,\end{aligned}$$

(91)

at the growing of $\bar{\gamma }$ from $\bar{\gamma }=0$, implies the existence of a $(\bar{\gamma })^*\in ]0,\bar{\gamma }_{c_1}[$ at which a SHB occurs and its frequency is given by

$$\begin{aligned} f=\displaystyle \frac{\varphi }{2\pi },\end{aligned}$$

(92)

with

$$\begin{aligned} \varphi ^2=A_2[(\bar{\gamma })^*],\end{aligned}$$

(93)

and $(\bar{\gamma })^*$ lowest root of

$$\begin{aligned} A_1A_2-A_3=(\bar{\gamma }-\alpha )[2\alpha \bar{\gamma }-(2\alpha ^2+\mu +\delta )]=0.\end{aligned}$$

(94)

Proof

The proof, via property 3, is easily obtained. $\square$

9.1 Steady bifurcations

In view of

$$\begin{aligned} {\left\{ \begin{array}{ll} \bar{\gamma }_{c_3}<\bar{\gamma }_{c_1}\Leftrightarrow \alpha ^2>\displaystyle \frac{\mu +\delta }{3},\\ \\ \bar{\gamma }_{c_3}<\bar{\gamma }_{c_2}\Leftrightarrow \alpha ^2>\mu +\delta \end{array}\right. }\end{aligned}$$

(95)

it follows that

$$\begin{aligned} \alpha ^2>\mu +\delta \end{aligned}$$

(96)

implies the onset of steady bifurcations.

9.2 Absence of SHB for $\bar{\gamma }\in [0,\bar{\gamma }_{c_2}]$

In view of

$$\begin{aligned} {\left\{ \begin{array}{ll} \bar{\gamma }_{c_2}<\bar{\gamma }_{c_3}\Leftrightarrow \alpha ^2>\mu +\delta ,\\ \\ \bar{\gamma }_{c_2}<\bar{\gamma }_{c_1}\Leftrightarrow \alpha ^2>\mu +\delta \end{array}\right. }\end{aligned}$$

(97)

the non existence of $\bar{\gamma }\in [0,\bar{\gamma }_{c_2}]$ immediately follows.

10 Applications

The boundedness and existence of absorbing sets have a basic importance for the longtime behaviour of any DS Izhikovich (2000a). Their existence for the solutions of the FHR model (1) appears to be—as far as we know—new in the existing literature, at least in the formulation given in Sect. 2. Therefore, a check on the operativity of properties 1,2 could be of relevant interest. We return on the conditions (3) and remark that are equivalent to

$$\begin{aligned} |b|>\displaystyle \frac{|1-\delta |^2}{2|\delta |},\quad |\delta |>\displaystyle \frac{|1-\mu |^2}{2|\mu |},\end{aligned}$$

(98)

and consider as prototypes of a general case, the following two cases

$$\begin{aligned} {\left\{ \begin{array}{ll} a=0.2,\quad b=0.08,\quad d=1,\\ I=0.3125,\quad \delta =0.8,\quad \mu =0,5\\ c= \text{ bifurcation } \text{ parameter } \end{array}\right. }\end{aligned}$$

(99)

$$\begin{aligned} {\left\{ \begin{array}{ll} a=0.2,\quad b=0.08,\quad d=1,\\ I=0.3125,\quad \delta =0.8,\quad c=-0,775\\ \mu = \text{ bifurcation } \text{ parameter } \end{array}\right. }\end{aligned}$$

(100)

In view of remark 1, we have to check on the existence of a positive value of $\varepsilon$, such that (11) holds. In both the cases (98), (99) one has

$$\begin{aligned} {\left\{ \begin{array}{ll} |1-\delta |^2=|1-0.8|^2=0.04,\\ \alpha =b\delta =(0.008)(0.8)=0.064,\,\,2\alpha =0.128. \end{array}\right. } \end{aligned}$$

(101)

10.1 Check on the operativity of conditions (3) in the case (99)

In the case (99), one has

$$\begin{aligned} \beta =\mu \delta =(0.5)(0.8)=0.4,\quad 2\beta =0.8.\end{aligned}$$

(102)

Therefore, in the case (99), one has

$$\begin{aligned} {\left\{ \begin{array}{ll} \varepsilon<2\alpha -|1-\delta |^2=0.128-0.04=0.088,\\ \varepsilon <2\beta -|1-\mu |^2=0.8-0.25=0.55, \end{array}\right. }\end{aligned}$$

(103)

which implies that boundedness and existence of absorbing sets, according to properties 1–2, is guaranteed for $\varepsilon <0.088$.

10.2 Check on the operativity of conditions (3) in the case (100)

In the case (100), since (103)$_1$ is verified for $r<0.088$, the boundedness and existence of absorbing sets are guaranteed by the values of the bifurcation parameter $\mu$ such that

$$\begin{aligned} |1-\mu |^2<2\beta -\varepsilon =0.8-0.088=0.712,\end{aligned}$$

(104)

i.e.

$$\begin{aligned} |1-\mu |<0.8438\end{aligned}$$

(105)

and hence

$$\begin{aligned} 0.15\le \mu \le 1.8438.\end{aligned}$$

(106)

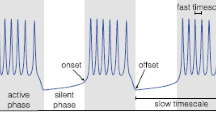
The case (99), with $\{b=0.8,\delta =0.08, \mu =0.002\}$ has been investigated in Yadav et al. (2016) and the case (100), with the same b and $\delta$, has been investigated in Alidousti and Khoshsiar Ghaziani (2017). The procedures applied in Yadav et al. (2016), Alidousti and Khoshsiar Ghaziani (2017), are completely different of the which ones of the present paper. In particular, boundedness and existence of absorbing sets are not considered (Fig. 1).

Remark 5

Let $b,\delta ,\mu$ be known and verify (98). Denoting by $R\notin \{b,\delta ,\mu \}$ a bifurcation parameter, it follows that

• 1. the properties 1–2 hold;

• 2. a bifurcation parameter $R\in \{I,a,c,d\}$ has influence via h and $h_1$, given by (13), only on the radius of the attraction bacin of the energy.

Fig. 1

Plot of $|z|=\frac{|1-x|^2}{2|x|}, \, x\in {\mathbb {R}}$. If, via (98), b and $\delta$ go over of it, then boundedness and absorbing sets of FHR solution are guaranteed by properties 1–2

11 Discussion, final remarks and perspectives

• (I) The paper is addressed to boundedness, longtime behaviour of FHR solutions and onset of Hopf bifurcations;

• (II) Conditions guaranteeing boundedness of FHR solutions and existence of absorbing sets in the energy phase space, are furnished;

• (III) Criteria guaranteeing the occurring of Hopf bifurcations, destabilizing steady states of FHR, are obtained;

• (IV) The power of each coefficient of the spectrum equation (37) to drive instability, location of the bifurcating parameter and the type of the occurring bifurcation, via a new version of the ICP method, is shown;

• (V) The FHR neurons bursting frequency is shown to be given by

  $$\begin{aligned} f=\displaystyle \frac{1}{2\pi }\sqrt{A_2(R_k)} \end{aligned}$$

  (107)

  with $A_2$ coefficient of $\lambda ^2$ of (37) and $R_k$ lowest positive zero of $A_0=A_1A_2-A_3$, location of a bifurcation parameter R at which the Hopf bifurcation occurs;

• (VI) (107), in the existing literature—as far as we know—is a completely new result;

• (VII) The looking for conditions necessary and/or sufficient for guaranteeing the:

• 1. existence of sequences of FHR steady states destabilized by sequences of Hopf bifurcations with variable frequencies, to contribure to characterize the neuron recurrent passage from a steady state to a ripetitive firing state (Izhikovich 2000b; Wang and Wang 2001; Varin 2011) similar and/or analogous to Feigenbaum cascades {see Izhikovich (2000a), p.5, Varin (2011) and the references therein};

• 2. transfer to the FHR-PDEs model the criteria for the onset of Hopf bifurcations, the associate neuron bursting frequency and the result of longtime dynamics,

is under investigation.