1 Introduction

Let’s say that \({\mathbb {N}}_0\) is the set of all nonnegative integers, \({\mathbb {N}}\) is the set of all natural numbers, \({\mathbb {Z}}\) is the set of all integers, \({\mathbb {R}}\) is the set of all real numbers, and for \(k \in {\mathbb {Z}} \) the notation \({\mathbb {N}}_{k}\) denotes the set of \(\{n \in {\mathbb {Z}}:n\ge k \}\).

A popular area of study in applied sciences is nonlinear difference equations or systems of difference equations with order greater than one. In nature, these equations or systems also exist as discrete analogues of numerical solutions of delay differential equations, which represent various phenomena in fields such as biology, geometry, probability theory, stochastic time series, physics, ecology, neural networks and engineering. The behavior of solutions to concrete difference equations or systems of difference equations with orders greater than one, as well as the asymptotic stability of their equilibrium points, have caught the attention of numerous authors recently. For example, in [1], Bešo et al. considered the following nonlinear second order difference equation

$$\begin{aligned} u_{n+1}=\gamma +\delta \frac{u_{n}}{u_{n-1}^2}, \quad n\in {\mathbb {N}}_0, \end{aligned}$$
(1)

where the parameters \(\gamma \), \(\delta \) and the initial conditions \(u_{-i},\) \(i\in \{0,1\},\) are positive real numbers. Boundedness, global attractivity and Neimark-Sacker bifurcation results were obtained. Subsequently, Tasdemir, in [2], generalized some results of Eq. (1) to the following higher-order difference equation

$$\begin{aligned} u_{n+1}=\mu +\eta \frac{u_{n}}{u_{n-m}^2}, \quad n\in {\mathbb {N}}_0, \end{aligned}$$
(2)

where the parameters \(\mu ,\) \(\eta \) and the initial conditions \(u_{-i},\) \(i\in \{0,1,\dots ,m\},\) are positive real numbers. Also, in [3], the equation in (1) was extended to the following discrete two-dimensional system of difference equations

$$\begin{aligned} u_{n+1}=\mu +\eta \frac{v_{n}}{v^2_{n-1}}, \quad v_{n+1}=\mu +\eta \frac{u_{n}}{u^2_{n-1}}, \quad n\in {\mathbb {N}}_0, \end{aligned}$$
(3)

where the parameters \(\mu ,\) \(\eta \) and the initial conditions \(u_{-i},\) \(v_{-i},\) \(i\in \{0,1\},\) are positive real numbers. Further, Khan, in [4], studied the asymptotic proporties of the following discrete difference equations system

$$\begin{aligned} u_{n+1}={\mathcal {B}}_1+{\mathcal {B}}_2\frac{v_{n}}{v_{n-1}^2}, \quad v_{n+1}={\mathcal {B}}_3+{\mathcal {B}}_4\frac{u_{n}}{u_{n-1}^2}, \quad n\in {\mathbb {N}}_0, \end{aligned}$$
(4)

where \({\mathcal {B}}_i,\) for \(i\in \{1,2,3,4\},\) are positive real numbers and the initial conditions \(u_{-j},\) \(v_{-j},\) for \(j\in \{0,1\}\) may be positive or negative real numbers, is a natural generalization of both the equation given in (1) and the system given in (2). Motivated by aforementioned studies, we consider the following nonlinear three-dimensional system of difference equations with quadratic terms

$$\begin{aligned} x_{n+1}={\mathcal {A}}_1+{\mathcal {B}}_1\frac{y_{n}}{y^2_{n-1}}, \quad y_{n+1}={\mathcal {A}}_2+{\mathcal {B}}_2\frac{z_{n}}{z^2_{n-1}}, \quad z_{n+1}={\mathcal {A}}_3+{\mathcal {B}}_3\frac{x_{n}}{x^2_{n-1}}, \quad n\in {\mathbb {N}}_0, \nonumber \\ \end{aligned}$$
(5)

where the parameters \({\mathcal {A}}_i,\) \({\mathcal {B}}_i\), \(i\in \{1,2,3\},\) and the initial conditions \(x_{-j},\) \(y_{-j},\) \(z_{-j},\) \(j\in \{0,1\},\) are positive real numbers. In this paper we study the equilibrium point, the boundedness character, local asymptotic stability and global behavior of equilibrium point of system (5), the rate of convergences of the solutions and confirmation of theoretical results of mentioned system numerically. It is important to note that the results derived from this article are a generalization and extension of above mentioned articles. Other related difference equations and systems of difference equations can be found in references [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24].

Let us consider a three-dimensional discrete dynamical system with second-order of the following form

$$\begin{aligned} {\left\{ \begin{array}{ll} u_{n+1}&{}=f_1\left( v_n,v_{n-1}\right) , \\ v_{n+1}&{}=f_2\left( w_n,w_{n-1}\right) , \\ w_{n+1}&{}=f_3\left( u_n,u_{n-1}\right) , \end{array}\right. } \quad n\in {\mathbb {N}}_0, \end{aligned}$$
(6)

where \(f_1:I_{2}\times I_{2}\rightarrow I_1, \) \(f_2:I_{3}\times I_{3} \rightarrow I_2\) and \(f_3:I_{1}\times I_{1} \rightarrow I_3, \) are continuously differentiable functions and \(I_j,\) \(j\in \{1,2,3\},\) are some intervals of real numbers. Moreover, the solution \(\{\left( u_n,v_n,w_n\right) \}_{n=-1}^{\infty }\) of corresponding system is uniquely determined by certain initial conditions.

Definition 1

[25] Let \(f_{i},\) \(i\in \{1,2,3\},\) be continuously differentiable functions at the equilibrium \(\left( \bar{u},\bar{v},\bar{w}\right) \) that is an equilibrium point of the map \(\Phi .\) The linearized system of (6) about the equilibrium point \(\left( \bar{u},\bar{v},\bar{w}\right) \) is

$$\begin{aligned} U_{n+1}=\Phi \left( U_n\right) ={\mathcal {F}}_{J}U_n, \quad n \in {\mathbb {N}}_0, \end{aligned}$$
(7)

where \(U_n=\left( u_n,u_{n-1},v_n,v_{n-1},w_n,w_{n-1}\right) ^{T}\) and \({\mathcal {F}}_{J}\) is a Jacobian matrix of system (6) related to equilibrium point \(\bar{U}=\left( \bar{u},\bar{v},\bar{w}\right) \).

Theorem 1

[17] Consider system (7), where \(\bar{U}\) is a fixed point of \(\Phi \). If all eigenvalues of the Jacobian matrix \({\mathcal {F}}_J\) about \(\bar{U}\) lie inside the open unit disk \(\Vert \rho \Vert <1,\) that is, if all of them have absolute value less than one, then \(\bar{U}\) is locally asymptotically stable. If at least one of the eigenvalues has a modulus greater than 1, than \(\bar{U}\) is unstable.

2 Linearized stability system

First of all, by employing the change of variables \(\alpha _{n}=\frac{x_{n}}{{\mathcal {A}}_1},\ \beta _{n}=\frac{y_{n}}{{\mathcal {A}}_2}, \ \gamma _{n}=\frac{z_{n}}{{\mathcal {A}}_3}\), for \(n\ge -1\), system (5) becomes

$$\begin{aligned} \alpha _{n+1}=1+p\frac{\beta _{n}}{\beta ^2_{n-1}},\quad \beta _{n+1}=1+q\frac{\gamma _{n}}{\gamma ^2_{n-1}},\quad \gamma _{n+1}=1+r\frac{\alpha _{n}}{\alpha ^2_{n-1}},\quad n \in {\mathbb {N}}_0, \end{aligned}$$
(8)

where

$$\begin{aligned} p=\frac{{\mathcal {B}}_1}{{\mathcal {A}}_1{\mathcal {A}}_2}>0, \quad q=\frac{{\mathcal {B}}_2}{{\mathcal {A}}_2{\mathcal {A}}_3}>0, \quad r=\frac{{\mathcal {B}}_3}{{\mathcal {A}}_1{\mathcal {A}}_3}>0. \end{aligned}$$
(9)

From here on, we will study on the equivalent system (8).

Lemma 1

System (8) has two equilibrium points \(\Gamma _1=\left( \xi _{11},\xi _{12},\xi _{13}\right) \) and \(\Gamma _2=\left( \xi _{21},\xi _{22},\xi _{23}\right) \), where

$$\begin{aligned} {\left\{ \begin{array}{ll} \xi _{11}=\frac{1+p+q-r+\sqrt{\left( 1+p+q-r\right) ^2+4\left( 1+p\right) \left( 1+q\right) r}}{2\left( 1+q\right) }, \\ \xi _{12}=\frac{1-p+q+r+\sqrt{\left( 1+p+q-r\right) ^2+4\left( 1+p\right) \left( 1+q\right) r}}{2\left( 1+r\right) }, \\ \xi _{13}= \frac{1+p-q+r+\sqrt{\left( 1+p+q-r\right) ^2+4\left( 1+p\right) \left( 1+q\right) r}}{2\left( 1+p\right) }, \end{array}\right. } \end{aligned}$$
(10)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} \xi _{21}=\frac{1+p+q-r-\sqrt{\left( 1+p+q-r\right) ^2+4\left( 1+p\right) \left( 1+q\right) r}}{2\left( 1+q\right) }, \\ \xi _{22}= \frac{1-p+q+r-\sqrt{\left( 1+p+q-r\right) ^2+4\left( 1+p\right) \left( 1+q\right) r}}{2\left( 1+r\right) },\\ \xi _{23}= \frac{1+p-q+r-\sqrt{\left( 1+p+q-r\right) ^2+4\left( 1+p\right) \left( 1+q\right) r}}{2\left( 1+p\right) }. \end{array}\right. } \end{aligned}$$
(11)

Proof

Let \(\Gamma =\left( \bar{\alpha },\bar{\beta },\bar{\gamma }\right) \) be equilibrium point of system (8). Then, from system (8), we have

$$\begin{aligned} \bar{\alpha }=1+p\frac{\bar{\beta }}{\bar{\beta }^2},\quad \bar{\beta }=1+q\frac{\bar{\gamma }}{\bar{\gamma }^2},\quad \bar{\gamma }=1+r\frac{\bar{\alpha }}{\bar{\alpha }^2}, \end{aligned}$$
(12)

from which it follows that

$$\begin{aligned} \bar{\beta }=\frac{p}{\bar{\alpha }-1}, \quad \bar{\gamma }=\frac{q}{\bar{\beta }-1}, \quad \bar{\alpha }=\frac{r}{\bar{\gamma }-1}. \end{aligned}$$
(13)

By substituting the second equation in (13) into the third one in (13) and then the first equation in (13) into the third one in (13), it follows that

$$\begin{aligned} \left( q+1\right) \bar{\alpha }^2-\left( p+q-r+1\right) \bar{\alpha }-r\left( p+1\right) =0, \end{aligned}$$
(14)

whose roots are

$$\begin{aligned} \bar{\alpha }_{1,2}= \frac{1+p+q-r\pm \sqrt{\left( 1+p+q-r\right) ^2+4\left( 1+p\right) \left( 1+q\right) r}}{2\left( 1+q\right) }, \end{aligned}$$
(15)

where \(p=\frac{{\mathcal {B}}_1}{{\mathcal {A}}_1{\mathcal {A}}_2}>0\), \(q=\frac{{\mathcal {B}}_2}{{\mathcal {A}}_2{\mathcal {A}}_3}>0\) and \(r=\frac{{\mathcal {B}}_3}{{\mathcal {A}}_1{\mathcal {A}}_3}>0\). Similarly, by substituting the third equation in (13) into the first one in (13) and then the second equation in (13) into the first one in (13), by keeping in mind the truth of (9) and after manipulation, we get

$$\begin{aligned} \left( r+1\right) \bar{\beta }^2-\left( -p+q+r+1\right) \bar{\beta }-p\left( q+1\right) =0, \end{aligned}$$
(16)

whose roots are

$$\begin{aligned} \bar{\beta }_{1,2}= \frac{1-p+q+r \pm \sqrt{\left( 1+p+q-r\right) ^2+4\left( 1+p\right) \left( 1+q\right) r}}{2\left( 1+r\right) }, \end{aligned}$$
(17)

where \(p=\frac{{\mathcal {B}}_1}{{\mathcal {A}}_1{\mathcal {A}}_2}>0\), \(q=\frac{{\mathcal {B}}_2}{{\mathcal {A}}_2{\mathcal {A}}_3}>0\) and \(r=\frac{{\mathcal {B}}_3}{{\mathcal {A}}_1{\mathcal {A}}_3}>0\). Analogously, by substituting the first equation in (13) into the second equation in (13) and the third equation in (13) into the second equation in (13), later by keeping in mind the truth of (9) and, finally, after manipulation, we have

$$\begin{aligned} \left( p+1\right) \bar{\gamma }^2-\left( p-q+r+1\right) \bar{\gamma }-q\left( r+1\right) =0, \end{aligned}$$
(18)

whose roots are

$$\begin{aligned} \bar{\gamma }_{1,2}= \frac{1+p-q+r \pm \sqrt{\left( 1+p+q-r\right) ^2+4\left( 1+p\right) \left( 1+q\right) r}}{2\left( 1+p\right) }, \end{aligned}$$
(19)

where \(p=\frac{{\mathcal {B}}_1}{{\mathcal {A}}_1{\mathcal {A}}_2}>0\), \(q=\frac{{\mathcal {B}}_2}{{\mathcal {A}}_2{\mathcal {A}}_3}>0\) and \(r=\frac{{\mathcal {B}}_3}{{\mathcal {A}}_1{\mathcal {A}}_3}>0\). From (15), (17) and (19), one deduces that system (8) has two equilibrium points such as \(\Gamma _1=\left( \bar{\alpha },\bar{\beta },\bar{\gamma }\right) =\left( \xi _{11},\xi _{12},\xi _{13}\right) \) and \(\Gamma _2=\left( \bar{\alpha },\bar{\beta },\bar{\gamma }\right) =\left( \xi _{21},\xi _{22},\xi _{23}\right) \), where is described in (10) and (11). \(\square \)

Now, we will carry out the linearized form of system (8) related to the equilibrium point \(\Gamma _1=\left( \xi _{11},\xi _{12},\xi _{13}\right) \). Firstly, we will write system (8) in vectorial form. To do this, we define the function \({\mathcal {F}}:\left( 0,\infty \right) ^{6}\rightarrow \left( 0,\infty \right) ^{6}\) by

$$\begin{aligned} {\mathcal {F}}\left( X\right) =\left( g_1\left( X\right) ,u_2,g_2\left( X\right) ,v_2,g_3\left( X\right) ,w_2\right) , \end{aligned}$$
(20)

where \(X=\left( u_1,u_2,v_1,v_2,w_1,w_2\right) ,\) \(g_1\left( X\right) =1+p\frac{v_1}{v_2^{2}},\) \(g_2\left( X\right) =1+q\frac{w_1}{w_2^{2}}\) and \(g_3\left( X\right) =1+r\frac{u_1}{u_2^{2}}.\) From (20), one can write the vector form and linearized form of system (8) as follows

$$\begin{aligned} X_{n+1}={\mathcal {F}}\left( X_n\right) ={\mathcal {J}}\mid _{\Gamma }X_n, \end{aligned}$$
(21)

where \(X_n=\left( u_n,u_{n-1},v_n,v_{n-1},w_n,w_{n-1}\right) ^{T}\) and \({\mathcal {J}}\mid _{\Gamma }\) is a Jacobian matrix of the system (8) about equilibirum point \(\Gamma _1=\left( \xi _{11},\xi _{12},\xi _{13}\right) \), which is given by

$$\begin{aligned} {\mathcal {J}}\mid _{\Gamma }= \begin{pmatrix} 0 &{} 0 &{} \frac{p}{\xi _{12}^2} &{} \frac{-2p}{\xi _{12}^2} &{} 0 &{} 0\\ 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} \frac{q}{\xi _{13}^2} &{} \frac{-2q}{\xi _{13}^2}\\ 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0\\ \frac{r}{\xi _{11}^2} &{} \frac{-2r}{\xi _{11}^2} &{} 0 \ {} &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 \end{pmatrix}. \end{aligned}$$
(22)

3 Boundedness and persistence of system (8)

In the following result, we prove that system (8) is bounded and persists.

Theorem 2

If \(pqr<1,\) then the solution \(\{\left( \alpha _n,\beta _n,\gamma _n\right) \}_{n=-1}^{\infty }\) of system (8) is bounded and persists.

Proof

Let \(\{\left( \alpha _n,\beta _n,\gamma _n\right) \}_{n=-1}^{\infty }\) be a positive solution of system (8). Then, from (8) we have

$$\begin{aligned} \alpha _n\ge 1, \quad \beta _n \ge 1, \quad \gamma _n \ge 1, \quad n\in {\mathbb {N}}. \end{aligned}$$
(23)

Further, from (23) and system (8), the following inequalities can be easily obtained

$$\begin{aligned} {\left\{ \begin{array}{ll} \alpha _{n+1} \le 1+p+pq+pqr\alpha _{n-2},\\ \beta _{n+1} \le 1+q+qr+pqr\beta _{n-2}, \\ \gamma _{n+1} \le 1+r+pr+pqr\gamma _{n-2}. \end{array}\right. } \end{aligned}$$
(24)

From the first inequality in (24) one has

$$\begin{aligned} {\hat{\alpha }}_{n+1}=1+p+pq+pqr{\hat{\alpha }}_{n-2}, \end{aligned}$$
(25)

such that \({\hat{\alpha }}_{j}=\alpha _{j}\), \(j\in \{-1,0,\dots ,3\},\) whose solution is

$$\begin{aligned} {\hat{\alpha }}_{n}=\frac{1+p+pq}{1-pqr} + \left( \root 3 \of {pqr}\right) ^{n}\left( C_{11}+C_{12} \cos \left( \frac{2\pi }{3}n\right) +C_{13}\sin \left( \frac{2\pi }{3}n\right) \right) , \nonumber \\ \end{aligned}$$
(26)

where \(C_{1i}\), for \(i \in \{1,2,3\}\), are bounded up with \({\hat{\alpha }}_{-j}\), for \(j \in \{-1,0,1\}\). From the second inequality in (24) one gets

$$\begin{aligned} {\hat{\beta }}_{n+1}=1+q+qr+pqr{\hat{\beta }}_{n-2}, \end{aligned}$$
(27)

such that \({\hat{\beta }}_{j}=\beta _{j}\), \(j\in \{-1,0,\dots ,3\},\) whose solution is

$$\begin{aligned} {\hat{\beta }}_{n}=\frac{1+q+qr}{1-pqr} + \left( \root 3 \of {pqr}\right) ^{n}\left( C_{21}+C_{22} \cos \left( \frac{2\pi }{3}n\right) +C_{23}\sin \left( \frac{2\pi }{3}n\right) \right) , \nonumber \\ \end{aligned}$$
(28)

where \(C_{2i}\), for \(i \in \{1,2,3\}\), are bounded up with \({\hat{\beta }}_{-j}\), for \(j \in \{-1,0,1\}\). Similarly, from the third equality in (24) one obtains

$$\begin{aligned} {\hat{\gamma }}_{n+1}=1+r+pr+pqr{\hat{\gamma }}_{n-2}, \end{aligned}$$
(29)

such that \({\hat{\gamma }}_{j}=\gamma _{j}\), \(j\in \{-1,0,\dots ,3\},\) whose solution is

$$\begin{aligned} {\hat{\gamma }}_{n}=\frac{1+r+pr}{1-pqr} + \left( \root 3 \of {pqr}\right) ^{n}\left( C_{31}+C_{32} \cos \left( \frac{2\pi }{3}n\right) +C_{33}\sin \left( \frac{2\pi }{3}n\right) \right) , \nonumber \\ \end{aligned}$$
(30)

where \(C_{3i}\), for \(i \in \{1,2,3\}\), are depicted in \({\hat{\gamma }}_{-j}\), for \(j \in \{-1,0,1\}\). By considering \({\hat{\alpha }}_{j}=\alpha _{j}\), \({\hat{\beta }}_{j}=\beta _{j}\), and \({\hat{\gamma }}_{j}=\gamma _{j}\), for \(j\in \{-1,0,\dots ,3\},\) and from the assumption \(pqr<1\), then one has the following inequalities

$$\begin{aligned} \alpha _n\le \frac{1+p+pq}{1-pqr}, \quad \beta _n \le \frac{1+q+qr}{1-pqr}, \quad \gamma _{n} \le \frac{1+r+pr}{1-pqr}, \end{aligned}$$
(31)

from which along with (23), it follows that

$$\begin{aligned} 1\le \alpha _n\le \frac{1+p+pq}{1-pqr}, \quad 1\le \beta _n \le \frac{1+q+qr}{1-pqr}, \quad 1\le \gamma _{n} \le \frac{1+r+pr}{1-pqr}. \end{aligned}$$
(32)

\(\square \)

Theorem 3

System (8) has an invariant interval when \(0<pqr<1.\) Further the set \([1,\frac{1+p+pq}{1-pqr}]\times [1,\frac{1+q+qr}{1-pqr}]\times [1,\frac{1+r+pr}{1-pqr}]\) is an invariant.

Proof

Assume that \(\{\left( \alpha _n,\beta _n,\gamma _n\right) \}_{n=-1}^{\infty }\) is the solution of system (8) such that \(\alpha _{-i} \in [1,\frac{1+p+pq}{1-pqr}], \) \(\beta _{-i} \in [1,\frac{1+q+qr}{1-pqr}] \) and \(\gamma _{-i}\in [1,\frac{1+r+pr}{1-pqr}]\), for \(i\in \{ 0,1\}.\) Then, from system (8) and equalities in (23) one gets

$$\begin{aligned} {\left\{ \begin{array}{ll} 1\le \alpha _1=1+p\frac{\beta _{0}}{\beta ^2_{-1}} \le \frac{1+p+pq}{1-pqr}, \\ 1\le \beta _1=1+q\frac{\gamma _{0}}{\gamma ^2_{-1}} \le \frac{1+q+qr}{1-pqr}, \\ 1\le \gamma _1=1+r\frac{\alpha _{0}}{\alpha ^2_{-1}} \le \frac{1+r+pr}{1-pqr}, \end{array}\right. } \end{aligned}$$
(33)

from which deduce that \(\alpha _1 \in [1,\frac{1+p+pq}{1-pqr}], \) \(\beta _1 \in [1,\frac{1+q+qr}{1-pqr}] \) and \(\gamma _1 \in [1,\frac{1+r+pr}{1-pqr}].\) Finally, by using induction method, one easily shows that \(\alpha _{k+1} \in [1,\frac{1+p+pq}{1-pqr}], \) \(\beta _{k+1} \in [1,\frac{1+q+qr}{1-pqr}] \) and \(\gamma _{k+1} \in [1,\frac{1+r+pr}{1-pqr}] \) if \(\alpha _{k} \in [1,\frac{1+p+pq}{1-pqr}], \) \(\beta _{k} \in [1,\frac{1+q+qr}{1-pqr}] \) and \(\gamma _{k} \in [1,\frac{1+r+pr}{1-pqr}]. \) \(\square \)

4 Stability analysis of system (8)

The global attractivity and the local asymptotic stability of the equilibrium point given in (10) of system (8) will be addressed in this section. Also, the globally asymptotic result will be presented by using the gained results.

Theorem 4

If the following condition

$$\begin{aligned} \max \left\{ \frac{12r\left( 1+q\right) ^2}{\left( 1+p+q-r+\sqrt{\Delta }\right) ^2}, \frac{12p\left( 1+r\right) ^2}{\left( 1-p+q+r+\sqrt{\Delta }\right) ^2}, \frac{12q\left( 1+p\right) ^2}{\left( 1+p-q+r+\sqrt{\Delta }\right) ^2}\right\} <1, \end{aligned}$$
(34)

where \(\Delta =\left( 1+p+q-r\right) ^2+4\left( 1+p\right) \left( 1+q\right) r\), holds, then the equilibrium point \(\Gamma _1=\left( \xi _{11},\xi _{12},\xi _{13}\right) \) of system (8) is locally asymptotically stable.

Proof

From (21), the linearized equation of system (8) about equilibrium point \(\Gamma _1=\left( \xi _{11},\xi _{12},\xi _{13}\right) \) is

$$\begin{aligned} X_{n+1}={\mathcal {J}}\mid _{\Gamma _1}X_n, \end{aligned}$$
(35)

where \(X_n=\left( u_n,u_{n-1},v_n,v_{n-1},w_n,w_{n-1}\right) ^{T}\) and

$$\begin{aligned}&{\mathcal {J}}\mid _{\Gamma _1}= \begin{pmatrix} 0 &{} 0 &{} \frac{4p\left( 1+r\right) ^2}{\left( 1-p+q+r+\sqrt{\Delta }\right) ^2} &{} \frac{-8p\left( 1+r\right) ^2}{\left( 1-p+q+r+\sqrt{\Delta }\right) ^2} &{} 0 &{} 0\\ 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} \frac{4q\left( 1+p\right) ^2}{\left( 1+p-q+r+\sqrt{\Delta }\right) ^2} &{} \frac{-8q\left( 1+p\right) ^2}{\left( 1+p-q+r+\sqrt{\Delta }\right) ^2}\\ 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0\\ \frac{4r\left( 1+q\right) ^2}{\left( 1+p+q-r+\sqrt{\Delta }\right) ^2} &{} \frac{-8r\left( 1+q\right) ^2}{\left( 1+p+q-r+\sqrt{\Delta }\right) ^2}&{} 0 \ {} &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} \end{pmatrix}, \nonumber \\ \end{aligned}$$
(36)

where \(\Delta =\left( 1+p+q-r\right) ^2+4\left( 1+p\right) \left( 1+q\right) r.\) Let \(\lambda _{i},\) for \(i\in \{1,2,\dots ,6\},\) be the eigenvalues of \({\mathcal {J}}\mid _{\Gamma _1}\). From (34) we can choose an \(\epsilon >0\) such that

$$\begin{aligned} \max&\left\{ \root 3 \of { \frac{12p\left( 1+r\right) ^2}{\left( 1-p+q+r+\sqrt{\Delta }\right) ^2}},\root 3 \of {\frac{12q\left( 1+p\right) ^2}{\left( 1+p-q+r+\sqrt{\Delta }\right) ^2}},\right. \nonumber \\&\left. \root 3 \of {\frac{12r\left( 1+q\right) ^2}{\left( 1+p+q-r+\sqrt{\Delta }\right) ^2}} \right\}<\epsilon <1, \end{aligned}$$
(37)

where \(\Delta =\left( 1+p+q-r\right) ^2+4\left( 1+p\right) \left( 1+q\right) r.\) If

$$\begin{aligned} {\mathcal {D}}=diag\left( 1,\epsilon ,\epsilon ^{-1},\epsilon ^{-2},\epsilon ^{-3},\epsilon ^{-4},\epsilon ^{-5}\right) , \end{aligned}$$
(38)

then

$$\begin{aligned}&{\mathcal {D}}^{-1}{\mathcal {J}}\mid _{\Gamma _1}{\mathcal {D}}&\nonumber \\&= \begin{pmatrix} 0&{} 0 &{}\frac{4p(1+r)^2\epsilon ^{-2}}{\left( 1-p+q+r+\sqrt{\Delta }\right) ^2}&{} \frac{-8p\left( 1+r\right) ^2\epsilon ^{-3}}{\left( 1-p+q+r+\sqrt{\Delta }\right) ^2} &{} 0 &{} 0 \\ \epsilon &{} 0 &{} 0&{} 0 &{} 0 &{} 0 \\ 0&{} 0 &{} 0 &{} 0 &{} \frac{4q\left( 1+p\right) ^2\epsilon ^{-2}}{\left( 1+p-q+r+\sqrt{\Delta }\right) ^2} &{} \frac{-8q\left( 1+p\right) ^2\epsilon ^{-3}}{\left( 1+p-q+r+\sqrt{\Delta }\right) ^2}\\ 0 &{} 0 &{} 0 &{} \epsilon &{} 0 &{} 0 \\ \frac{4r\left( 1+q\right) ^2\epsilon ^{4} }{\left( 1+p+q-r+\sqrt{\Delta }\right) ^2}&{}\frac{-8r\left( 1+q\right) ^2 \epsilon ^{3}}{\left( 1+p-q-r+\sqrt{\Delta }\right) ^2} &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} \epsilon &{} 0 \end{pmatrix}&\nonumber \\ \end{aligned}$$
(39)

where \(\Delta =\left( 1+p+q-r\right) ^2+4\left( 1+p\right) \left( 1+q\right) r.\) Then, we can obtain the next norm of the matrix \({\mathcal {D}}^{-1}{\mathcal {J}}\mid _{\Gamma _1}{\mathcal {D}}\) as

$$\begin{aligned} \Vert {{\mathcal {D}}^{-1}{\mathcal {J}}\mid _{\Gamma _1}{\mathcal {D}}} \Vert&=\max \left\{ \frac{4p(1+r)^2\epsilon ^{-2}}{\left( 1-p+q+r+\sqrt{\Delta }\right) ^2} +\frac{8p\left( 1+r\right) ^2\epsilon ^{-3}}{\left( 1-p+q+r+\sqrt{\Delta }\right) ^2}, \right. \nonumber \\&\qquad \quad \left. \frac{4q\left( 1+p\right) ^2\epsilon ^{-2}}{\left( 1+p-q+r+\sqrt{\Delta }\right) ^2}+ \frac{8q\left( 1+p\right) ^2\epsilon ^{-3}}{\left( 1+p-q+r+\sqrt{\Delta }\right) ^2}, \right. \nonumber \\&\qquad \quad \left. \frac{4r\left( 1+q\right) ^2\epsilon ^{4} }{\left( 1+p+q-r+\sqrt{\Delta }\right) ^2}+\frac{8r\left( 1+q\right) ^2 \epsilon ^{3}}{\left( 1+p-q-r+\sqrt{\Delta }\right) ^2}, \epsilon \right\} . \end{aligned}$$
(40)

Since \(\epsilon <1\) and the inequality in (37) satisfies, we can write the following inequalities

$$\begin{aligned} \Vert {{\mathcal {D}}^{-1}{\mathcal {J}}\mid _{\Gamma _1}{\mathcal {D}}} \Vert \le \max&\left\{ \frac{12p\left( 1+r\right) ^2\epsilon ^{-3}}{\left( 1-p+q+r+\sqrt{\Delta }\right) ^2}, \frac{12q\left( 1+p\right) ^2\epsilon ^{-3}}{\left( 1+p-q+r+\sqrt{\Delta }\right) ^2}, \right. \nonumber \\&\qquad \quad \left. \frac{12r\left( 1+q\right) ^2 \epsilon ^{-3}}{\left( 1+p-q-r+\sqrt{\Delta }\right) ^2}, \epsilon \right\} <1. \end{aligned}$$
(41)

Since \({\mathcal {J}}\mid _{\Gamma _1}\) possesses the same eigenvalues as \({\mathcal {D}}^{-1}{\mathcal {J}}\mid _{\Gamma _1}{\mathcal {D}},\) we have that \(|\lambda _i|\le \Vert {{\mathcal {D}}^{-1}{\mathcal {J}}\mid _{\Gamma _1}{\mathcal {D}}} \Vert <1,\) where \(\lambda _i,\) for \(i\in \{1,2,\dots ,6\},\) are the eigenvalues of \({\mathcal {J}}\mid _{\Gamma _1}\). From Theorem (1), the equilibrium point given in (10) of system (8) is locally asymptotically stable, which is desired. \(\square \)

Theorem 5

Assume that \(p,q,r \in \left( 0,\frac{1}{2}\right) \). Then, the equilibrium point \(\Gamma _1\) of system (8) is global attractor.

Proof

Let \(\{\left( \alpha _n,\beta _n,\gamma _n\right) \}_{n=-1}^{\infty }\) be a positive solution of system (8) and be \(p,q,r \in \left( 0,\frac{1}{2}\right) \). From Theorem (2), there exists

$$\begin{aligned} \begin{array}{c c c} \lim _{n\rightarrow \infty }\sup {\alpha _n}=U_1, &{} \lim _{n\rightarrow \infty }\sup {\beta _n}=U_2, &{} \lim _{n\rightarrow \infty }\sup {\gamma _n}=U_3,\\ \lim _{n\rightarrow \infty }\inf {\alpha _n}=l_1, &{} \lim _{n\rightarrow \infty }\inf {\beta _n}=l_2, &{} \lim _{n\rightarrow \infty }\inf {\gamma _n}=l_3, \end{array} \end{aligned}$$
(42)

where \(U_1,U_2, U_3, l_1, l_2, l_3 \in \left( 0,\infty \right) . \) Then, from system (8) and the relations in (42), one gets the following inequalities

$$\begin{aligned} \begin{array}{c c c} U_1\le 1+p\frac{U_2}{l_2^{2}}, &{} U_2\le 1+q\frac{U_3}{l_3^{2}}, &{} U_3\le 1+r\frac{U_1}{l_1^{2}}, \\ l_1\ge 1+p\frac{l_2}{U_2^{2}}, &{} l_2\ge 1+q\frac{l_3}{U_3^{2}}, &{} l_3\ge 1+r\frac{l_1}{U_1^{2}}, \end{array} \end{aligned}$$
(43)

from which it follows that

$$\begin{aligned}{} & {} U_2+p\frac{l_2}{U_2}\le l_1U_2, \end{aligned}$$
(44)
$$\begin{aligned}{} & {} U_3+q\frac{l_3}{U_3}\le l_2U_3, \end{aligned}$$
(45)
$$\begin{aligned}{} & {} U_1+r\frac{l_1}{U_1}\le l_3U_1, \end{aligned}$$
(46)
$$\begin{aligned}{} & {} U_1l_2\le l_2+p\frac{U_2}{l_2}, \end{aligned}$$
(47)
$$\begin{aligned}{} & {} U_2l_3\le l_3+q\frac{U_3}{l_3}, \end{aligned}$$
(48)
$$\begin{aligned}{} & {} U_3l_1\le l_1+r\frac{U_1}{l_1}. \end{aligned}$$
(49)

By multiplying both sides of inequality in (44) by \(U_3\) and both sides of inequality in (49) by \(U_2\), one has

$$\begin{aligned} U_3l_1U_2\ge U_2U_3+p\frac{l_2U_3}{U_2},\quad U_2U_3l_1\le U_2l_1+r\frac{U_2U_1}{l_1}, \end{aligned}$$

from which it follows that

$$\begin{aligned} U_2U_3+p\frac{l_2U_3}{U_2}\le U_2l_1+r\frac{U_2U_1}{l_1}. \end{aligned}$$
(50)

Similarly, multiplying both sides of inequality in (45) by \(U_1\) and both sides of inequality in (47) by \(U_3\), one gets

$$\begin{aligned} U_1U_3l_2\ge U_1U_3+q\frac{l_3U_1}{U_3},\quad U_1U_3l_2\le U_3l_2+p\frac{U_2U_3}{l_2} \end{aligned}$$

from which it follows that

$$\begin{aligned} U_1U_3+q\frac{l_3U_1}{U_3}\le U_3l_2+p\frac{U_2U_3}{l_2}. \end{aligned}$$
(51)

Analogously, multiplying both sides of inequality in (46) by \(U_2\) and both sides of inequality in (48) by \(U_1\), one obtains

$$\begin{aligned} U_1U_2l_3\ge U_1U_2+r\frac{l_1U_2}{U_1},\quad U_2l_3U_1\le l_3U_1+q\frac{U_1U_3}{l_3}, \end{aligned}$$

from which it follows that

$$\begin{aligned} U_1U_2+r\frac{l_1U_2}{U_1}\le l_3U_1+q\frac{U_1U_3}{l_3}. \end{aligned}$$
(52)

From (50), (51) and (52), one can write

$$\begin{aligned}{} & {} U_2U_3+p\frac{l_2U_3}{U_2} +U_1U_3+q\frac{l_3U_1}{U_3}+U_1U_2+r\frac{l_1U_2}{U_1}\le U_2l_1+r\frac{U_1U_2}{l_1}+U_3l_2+p\frac{U_2U_3}{l_2}+l_3U_1\nonumber \\{} & {} \quad +q\frac{U_1U_3}{l_3}, \end{aligned}$$
(53)

which implies that

$$\begin{aligned}&U_2U_3+p\frac{l_2U_3}{U_2} +U_1U_3+q\frac{l_3U_1}{U_3}+U_1U_2+r\frac{l_1U_2}{U_1}- U_2l_1-r\frac{U_1U_2}{l_1}-U_3l_2-p\frac{U_2U_3}{l_2}-l_3U_1\nonumber \\&\quad -q\frac{U_1U_3}{l_3}\le 0 \end{aligned}$$
(54)

and consequently

$$\begin{aligned}&U_3(U_2-l_2)+U_2(U_1-l_1)+U_1(U_3-l_3)+pU_3(\frac{l_2}{U_2}-\frac{U_2}{l_2})+qU_1(\frac{l_3}{U_3} -\frac{U_3}{l_3})\nonumber \\&\quad +rU_2(\frac{l_1}{U_1}-\frac{U_1}{l_1})\le 0. \end{aligned}$$
(55)

From (55) and after some basic calculation, one has

$$\begin{aligned}&U_3(U_2-l_2)\left( 1-p(\frac{1}{l_2}+\frac{1}{U_2})\right) +U_2(U_1-l_1)\left( 1-r(\frac{1}{l_1} +\frac{1}{U_1})\right) \nonumber \\&\quad +U_1(U_3-l_3)\left( 1-q(\frac{1}{l_3}+\frac{1}{U_3})\right) \le 0. \end{aligned}$$
(56)

From the fact that \(1\le l_1,\) \(1\le l_2,\) \(1\le l_3\) and from the assumption \(p,q,r \in \left( 0,\frac{1}{2}\right) \), then one gets

$$\begin{aligned} 1-p\left( \frac{1}{l_2}+\frac{1}{U_2}\right)>0,\quad 1-r\left( \frac{1}{l_1}+\frac{1}{U_1}\right)>0,\quad 1-q\left( \frac{1}{l_3}+\frac{1}{U_3}\right) >0, \end{aligned}$$
(57)

from which it follows that

$$\begin{aligned} U_1-l_1=0,\quad U_2-l_2=0,\quad U_3-l_3=0, \end{aligned}$$
(58)

and so, \(U_1=l_1\), \( U_2=l_2\) and \(U_3=l_3\), which completes the proof. \(\square \)

Taking into account Theorem (4) and Theorem (5), the following theorem gives the main result of this article.

Theorem 6

If the condition in (34) and \(p,q,r \in \left( 0,\frac{1}{2}\right) \) are hold, then the equilibrium point given in (10) of system (8) is globally asymptotically stable.

5 Rate of convergence

In this section, we study the rate of convergence of a solutions which converges to the equilibrium point \(\Gamma _1=\left( \xi _{11},\xi _{12},\xi _{13}\right) \) of the system (8) in the region of parameters described by \(p,q,r \in \left( 0,\infty \right) .\) The following result gives the rate of convergence of solutions of difference equations system

$$\begin{aligned} \Psi _{n+1}=[M+N{(n)}]\Psi _n \end{aligned}$$
(59)

where \(\Psi _n\) is a k-dimensional vector, \(M\in C^{k\times k}\) is a constant matrix and \(N:{\mathbb {Z}}^+\rightarrow C^{k\times k}\) is a matrix function with

$$\begin{aligned} \Vert N{(n)}\Vert \rightarrow 0,\quad \text {as}\quad n\rightarrow \infty , \end{aligned}$$
(60)

where \(\Vert .\Vert \) denotes any matrix norm.

Theorem 7

(Perron’s Theorem, see, [26]) Assume that condition in (60) holds. If \(\Psi _n\) is a solution of (59), then either \(\Psi _n=0\) for all large n or

$$\begin{aligned} \vartheta =\lim _{n\rightarrow \infty }\frac{\Vert \Psi _{n+1}\Vert }{\Vert \Psi _n\Vert } \end{aligned}$$

or

$$\begin{aligned} \vartheta =\lim _{n\rightarrow \infty }\left( \Vert \Psi _n \Vert \right) ^{\frac{1}{n}} \end{aligned}$$

exists and \(\vartheta \) is equal to the modulus of one of the eigenvalues of matrix M.

Theorem 8

Assume that \(p,q,r \in \left( 0,\frac{1}{2}\right) \) and the solution \(\{\left( \alpha _n,\beta _n,\gamma _n\right) \}_{n=-1}^{\infty }\) of system (8) tends to \(\Gamma _1=\left( \xi _{11},\xi _{12},\xi _{13}\right) \). Then, the error vector

$$\begin{aligned} {\mathcal {E}}_n= \begin{pmatrix} e^1_n\\ e^1_{n-1}\\ e^2_n\\ e^2_{n-1}\\ e^3_n\\ e^3_{n-1}\\ \end{pmatrix} =\begin{pmatrix} \alpha _n-\xi _{11}\\ \alpha _{n-1}-\xi _{11}\\ \beta _n-\xi _{12}\\ \beta _{n-1}-\xi _{12}\\ \gamma _n-\xi _{13}\\ \gamma _{n-1}-\xi _{13}\\ \end{pmatrix} \end{aligned}$$

of every solution of system (8) satisfies both of the asymptotic relations

$$\begin{aligned} \vartheta&=\lim _{n\rightarrow \infty }(||\Psi _n||)^{\frac{1}{n}}=|\lambda _{1,2,3,4,5,6}J_F\left( \xi _{11},\xi _{12},\xi _{13}\right) |, \quad \\ \vartheta&=\lim _{n\rightarrow \infty }\frac{||\Psi _{n+1}||}{||\Psi _n||}=|\lambda _{1,2,3,4,5,6}J_F\left( \xi _{11},\xi _{12},\xi _{13}\right) |, \end{aligned}$$

where \(\vartheta \) is equal to the modulus of one of the eigenvalues of \(\mathcal {J_F}\) about \(\left( \xi _{11},\xi _{12},\xi _{13}\right) \). and \(\lambda _{1,2,3,4,5,6}J_F\left( \xi _{11},\xi _{12},\xi _{13}\right) \) are the characteristic roots of the Jacobian matrix \(\mathcal {J_F}\left( \xi _{11},\xi _{12},\xi _{13}\right) \).

Proof

Let \(\{\left( \alpha _n,\beta _n,\gamma _n\right) \}_{n=-1}^{\infty }\) be a positive solution of system (8) such that the following conditions hold

$$\begin{aligned} \lim _{n\rightarrow \infty }\alpha _n=\xi _{11}, \quad \lim _{n\rightarrow \infty } \beta _n=\xi _{12}, \quad \lim _{n\rightarrow \infty }\gamma _n=\xi _{13}. \end{aligned}$$
(61)

In order for the error terms of system, from (12) with depicting on \(\Gamma _1= \left( \bar{\alpha },\bar{\beta },\bar{\gamma }\right) =\left( \xi _{11},\xi _{12},\xi _{13}\right) \), one has

$$\begin{aligned} {\left\{ \begin{array}{ll} \alpha _{n+1}-\xi _{11}&{}=p\frac{\beta _n}{\beta _{n-1}^2}- \frac{p}{\xi _{12}} =\frac{p}{\beta _{n-1}^2}\Big (\beta _n-\xi _{12}\Big )-\frac{p\left( \beta _{n-1} +\xi _{12}\right) }{\xi _{12}\beta _{n-1}^2}\big (\beta _{n-1}-\xi _{12}\Big ), \\ \beta _{n+1}-\xi _{12}&{}=q\frac{\gamma _n}{\gamma _{n-1}^2}- \frac{q}{\xi _{13}} =\frac{q}{\gamma _{n-1}^2}\Big (\gamma _n-\xi _{13}\Big )-\frac{q\left( \gamma _{n-1}+\xi _{13}\right) }{\xi _{13}\gamma _{n-1}^2} \big (\gamma _{n-1}-\xi _{13}\Big ),\\ \gamma _{n+1}-\xi _{13}&{}=r\frac{\alpha _n}{\alpha _{n-1}^2}- \frac{r}{\xi _{11}}=\frac{r}{\alpha _{n-1}^2}\Big (\alpha _n-\xi _{11}\Big ) -\frac{r\left( \alpha _{n-1}+\xi _{11}\right) }{\xi _{11}\alpha _{n-1}^2}\big (\alpha _{n-1}-\xi _{11}\Big ). \end{array}\right. } \end{aligned}$$
(62)

Set

$$\begin{aligned} e^1_n=\alpha _n-\xi _{11},\quad e^2_n=\beta _n-\xi _{12}, \quad e^3_n=\gamma _n-\xi _{13}. \end{aligned}$$
(63)

From (62) and (63), one gets

$$\begin{aligned} {\left\{ \begin{array}{ll} e_{n+1}^1=a_{11}e_{n}^2+a_{12}e_{n-1}^2, \\ e_{n+1}^2=a_{21}e_{n}^3+a_{22}e_{n-1}^3, \\ e_{n+1}^3=a_{31}e_{n}^1+a_{32}e_{n-1}^1, \\ \end{array}\right. } \end{aligned}$$
(64)

where \(a_{11}=\frac{p}{\beta _{n-1}^2},\) \(a_{12}=-\frac{p\left( \beta _{n-1}+\xi _{12}\right) }{\xi _{12}\beta _{n-1}^2},\) \(a_{21}=\frac{q}{\gamma _{n-1}^2},\) \(a_{22}=-\frac{q\left( \gamma _{n-1}+\xi _{13}\right) }{\xi _{13}\gamma _{n-1}^2},\) \(a_{31}=\frac{r}{\alpha _{n-1}^2}\) and \(a_{32}=-\frac{r\left( \alpha _{n-1}+\xi _{11}\right) }{\xi _{11}\alpha _{n-1}^2},\) from which it follows that

$$\begin{aligned} {\left\{ \begin{array}{ll} \lim _{n\rightarrow \infty }a_{11}=\frac{p}{\xi _{12}^2}, \quad \lim _{n\rightarrow \infty }a_{12}=\frac{-2p}{\xi _{12}^2}, \\ \lim _{n\rightarrow \infty }a_{21}=\frac{q}{\xi _{13}^2}, \quad \lim _{n\rightarrow \infty }a_{22}=\frac{-2q}{\xi _{13}^2}, \\ \lim _{n\rightarrow \infty }a_{31}=\frac{r}{\xi _{11}^2}, \quad \lim _{n\rightarrow \infty }a_{32}=\frac{-2r}{\xi _{11}^2}. \end{array}\right. } \end{aligned}$$
(65)

That is,

$$\begin{aligned} {\left\{ \begin{array}{ll} a_{11}=\frac{p}{\xi _{12}^2}+\rho _{11}, \quad a_{12}=\frac{-2p}{\xi _{12}^2}+\rho _{12}, \\ a_{21}=\frac{q}{\xi _{13}^2}+\rho _{21}, \quad a_{22}=\frac{-2q}{\xi _{13}^2}+\rho _{22}, \\ a_{31}=\frac{r}{\xi _{11}^2}+\rho _{31}, \quad a_{32}=\frac{-2r}{\xi _{11}^2}+\rho _{32}, \end{array}\right. } \end{aligned}$$
(66)

where \(\rho _{ij}\rightarrow 0\) as \(n \rightarrow \infty .\) Then, one possesses the following system of the form in (59)

$$\begin{aligned} {\mathcal {E}}_{n+1}=\left( M+N(n)\right) {\mathcal {E}}_n, \end{aligned}$$
(67)

where \({\mathcal {E}}_n=\left( e_n^1,e_{n-1}^1,e_n^2,e_{n-1}^2,e_n^3,e_{n-1}^3\right) ^T\) and

$$\begin{aligned} M= \begin{pmatrix} 0\hspace{0.5em}&{}0\hspace{0.5em}&{}\frac{p}{\xi _{12}^{2}}\hspace{0.5em}\hspace{0.5em}&{}\frac{-2p}{\xi _{12}^{2}} \hspace{0.5em}&{} 0\hspace{0.5em}&{}0\\ 1\hspace{0.5em}&{}0\hspace{0.5em}&{} 0\hspace{0.5em}\hspace{0.5em}&{}0 \hspace{0.5em}&{} 0\hspace{0.5em}&{}0\\ 0\hspace{0.5em}&{}0\hspace{0.5em}&{}0\hspace{0.5em}\hspace{0.5em}&{}0\hspace{0.5em}&{} \frac{q}{\xi _{13}^{2}}\hspace{0.5em}&{}\frac{-2q}{\xi _{13}^{2}}\\ 0\hspace{0.5em}&{}0\hspace{0.5em}&{} 1\hspace{0.5em}\hspace{0.5em}&{}0 \hspace{0.5em}&{} 0\hspace{0.5em}&{}0\\ \frac{r}{\xi _{11}^{2}}\hspace{0.5em}&{}\frac{-2r}{\xi _{11}^{2}}\hspace{0.5em}&{} 0\hspace{0.5em}\hspace{0.5em}&{}0 \hspace{0.5em}&{} 0\hspace{0.5em}&{}0\\ 0\hspace{0.5em}&{}0\hspace{0.5em}&{} 0\hspace{0.5em}\hspace{0.5em}&{}0 \hspace{0.5em}&{} 1\hspace{0.5em}&{}0 \end{pmatrix}, \ N(n)= \begin{pmatrix} 0\hspace{0.5em}&{}0\hspace{0.5em}&{}\rho _{11}\hspace{0.5em}\hspace{0.5em}&{}\rho _{12} \hspace{0.5em}&{} 0\hspace{0.5em}&{}0\\ 1\hspace{0.5em}&{}0\hspace{0.5em}&{} 0\hspace{0.5em}\hspace{0.5em}&{}0 \hspace{0.5em}&{} 0\hspace{0.5em}&{}0\\ 0\hspace{0.5em}&{}0\hspace{0.5em}&{}0\hspace{0.5em}\hspace{0.5em}&{}0\hspace{0.5em}&{} \rho _{21}\hspace{0.5em}&{}\rho _{22}\\ 0\hspace{0.5em}&{}0\hspace{0.5em}&{} 1\hspace{0.5em}\hspace{0.5em}&{}0 \hspace{0.5em}&{} 0\hspace{0.5em}&{}0\\ \rho _{31}\hspace{0.5em}&{}\rho _{32}\hspace{0.5em}&{} 0\hspace{0.5em}\hspace{0.5em}&{}0 \hspace{0.5em}&{} 0\hspace{0.5em}&{}0\\ 0\hspace{0.5em}&{}0\hspace{0.5em}&{} 0\hspace{0.5em}\hspace{0.5em}&{}0 \hspace{0.5em}&{} 1\hspace{0.5em}&{}0 \end{pmatrix}, \end{aligned}$$
(68)

where \( \Vert N(n)\Vert \rightarrow 0\) as \(n\rightarrow \infty \). The matrix M is equal to \(\mathcal {J_F}\left( \xi _{11},\xi _{12},\xi _{13}\right) \). So, by using Theorem (7) to system (8), the result easily follows. \(\square \)

6 Numerical simulations

In this section, we verify the above mathematical discussion and represent some interesting dynamical properties of system (8) through numerical simulations. For this, certain parametric values are taken into account for system (8).

Example 1

Consider system (8) with \(p=0.49,\) \(q=0.48,\) \(r=0.41\). Then, system (8) can be written as

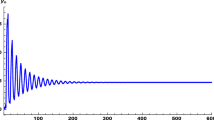
$$\begin{aligned}{} & {} \alpha _{n+1}=1+0.49\frac{\beta _{n}}{\beta ^2_{n-1}},\quad \beta _{n+1}=1+0.48\frac{\gamma _{n}}{\gamma ^2_{n-1}}, \nonumber \\{} & {} \quad \gamma _{n+1}=1+0.41\frac{\alpha _{n}}{\alpha ^2_{n-1}},\quad n \in {\mathbb {N}}_0, \end{aligned}$$
(69)

with the initial conditions \(x_{-1}=21.2,\) \(x_{0}=0.8,\) \(y_{-1}=9.2,\) \(y_{0}=7.3,\) \(z_{-1}=2.71,\) \(z_{0}=6.47.\) From Theorem (5), one easily sees that every positive solution of system (8) is bounded and the equilibrium point \(\Gamma _1=\left( 1.35801,1.36869,1.30191\right) \) of system (69) is global attractor (See, Figs. 1 and 2).

Fig. 1
figure 1

Plot of \(\alpha _n,\) \(\beta _n\) and \(\gamma _n\) in system (69) with \(p,q,r\in \left( 0,\frac{1}{2}\right) .\)

Full size image
Fig. 2
figure 2

Plot of attractor of system (69) with \(p,q,r\in \left( 0,\frac{1}{2}\right) .\)

Full size image

Example 2

Consider system (8) with \(p=1.7,\) \(q=0.6,\) \(r=3.4\). Then, system (8) can be written as

$$\begin{aligned}{} & {} \alpha _{n+1}=1+1.7\frac{\beta _{n}}{\beta ^2_{n-1}},\quad \beta _{n+1}=1+0.6\frac{\gamma _{n}}{\gamma ^2_{n-1}}, \nonumber \\{} & {} \quad \gamma _{n+1}=1+3.4\frac{\alpha _{n}}{\alpha ^2_{n-1}},\quad n \in {\mathbb {N}}_0, \end{aligned}$$
(70)

with the initial conditions \(x_{-1}=4.2,\) \(x_{0}=5.1,\) \(y_{-1}=0.6,\) \(y_{0}=3.1,\) \(z_{-1}=0.6,\) \(z_{0}=14.6.\) The the positive equilibrium point \(\Gamma _1=\left( 2.36426,1.2461,2.43808\right) \) of system (70) is not global attractor. (See, Figs. 3 and 4).

Fig. 3
figure 3

Plot of \(\alpha _n,\) \(\beta _n\) and \(\gamma _n\) in system (70)

Full size image
Fig. 4
figure 4

The plot of system (70) with \(p,r\notin \left( 0,\frac{1}{2}\right) \) and \(q\in \left( 0,\frac{1}{2}\right) \)

Full size image

7 Conclusion

This study represents a contribution to the analysis of three-dimensional concrete nonlinear system of difference equations, with arbitrary constant and different parameters. This paper mainly discusses the dynamic properties of a class of second-order system of difference equations by utilizing stability theory and rate of convergence. The main results are as follows.

  1. i.

    When \(pqr<1\), then the solution of system (8) is bounded and persists. Further for under this condition, system (8) has an invariant interval.

  2. ii.

    When \( \frac{12r\left( 1+q\right) ^2}{\left( 1+p+q-r+\sqrt{\Delta }\right) ^2}<1,\) \(\frac{12p\left( 1+r\right) ^2}{\left( 1-p+q+r+\sqrt{\Delta }\right) ^2}<1\) and \(\frac{12q\left( 1+p\right) ^2}{\left( 1+p-q+r+\sqrt{\Delta }\right) ^2}<1\), where \(\Delta =\left( 1+p+q-r\right) ^2+4\left( 1+p\right) \left( 1+q\right) r\), then the equilibrium point \(\Gamma _1=\left( \xi _{11},\xi _{12},\xi _{13}\right) \) of system (8) is locally asymptotic stable.

  3. iii.

    When \(p,q,r \in \left( 0,\frac{1}{2}\right) \), then the equilibrium point \(\Gamma _1\) of system (8) is global attractor.

The results imply that this approach might also be helpfully expanded to \(k-\)dimensional system of difference equations, or to system of difference equations with higher-order, or to system of difference equations with arbitrary powers. Thereby, we are going to offer a significant unresolved problem for scholars studying difference equations theory.

Open Problem. One can study the dynamical proporties of the following \(k-\)dimesional system of difference equations with quadratic terms

$$\begin{aligned} x_{n+1}^{\left( 1\right) }={\mathcal {A}}_1+{\mathcal {B}}_1\frac{x_{n}^{\left( 2\right) }}{\left( x_{n-1}^{\left( 2\right) }\right) ^2}, \ x_{n+1}^{\left( 2\right) }={\mathcal {A}}_2+{\mathcal {B}}_2\frac{x_{n}^{\left( 3\right) }}{\left( x_{n-1}^{\left( 3\right) }\right) ^2}, \dots , x_{n+1}^{\left( k\right) }={\mathcal {A}}_k+{\mathcal {B}}_k\frac{x_{n}^{\left( 1\right) }}{\left( x_{n-1}^{\left( 1\right) }\right) ^2}, \end{aligned}$$

where \(n\in {\mathbb {N}}_0,\) \(k\in {\mathbb {N}}_4,\) the parameters \({\mathcal {A}}_i,\) \({\mathcal {B}}_i,\) for \(i\in \{1,2,\dots ,k\},\) and the initial conditions \(x_{-j}^{\left( i\right) },\) for \(i\in \{1,2,\dots ,k\}\) and \(j\in \{0,1\},\) are positive real numbers.