An energetic approach to the evolution of growth curve plasticity

Abstract

Growth in individual body size amongst different species can to a greater or lesser extent depend on environmental factors such as resource availability. Individual growth curves can therefore be largely fixed or more plastic. Classic theory about phenotypic plasticity assumes that such plasticity has associated costs. In contrast, according to dynamic energy budget theory, maintaining a fixed growth rate in the face of variable resource availability would incur additional energetic costs. In this article, we explore the simultaneous evolution of the degree of plasticity in individual growth curves and the rate of non-plastic, environment-independent individual growth. We explore different relations between possible additional energetic costs and the degree of growth curve plasticity. To do so, we use adaptive dynamics to analyze a size-structured population model that is based on dynamic energy budget theory to account for the energetic trade-offs within an individual. We show that simultaneous evolution of the degree of growth curve plasticity and the rate of non-plastic individual growth will drive these traits to intermediate values at first. Afterwards, the degree of growth curve plasticity might evolve slowly towards extreme values depending on whether energetic costs increase or decrease with the degree of plasticity. In addition, the analysis shows that it is unlikely to encounter species in which individual growth is entirely fixed or entirely plastic, opposing general assumptions in dynamic energy budget theory.

Introduction

Individual body size strongly affects the physiology, morphology and life history of an individual (Calder 1996; LaBarbera 1989; Peters 1983). For example, body size is positively correlated with stress tolerance, fecundity, mating success and survival (Hone and Benton 2005; Kingsolver and Pfennig 2004; Blanckenhorn 2000; Peters 1983). This suggests that fitness increases with body size, and therefore, body size should be under strong selective pressure (Kingsolver and Huey 2008). Comparison between taxa indeed shows an increase in species body size throughout the history of life, a pattern that is known as Cope’s rule (Smith et al. 2016; Stanley 1973). However, this interspecific trend of increasing body size does not imply that intraspecific selection pressure always results in directional selection towards faster growth rates (Gotanda et al. 2015). On the contrary, trade-off relations between individual growth rates and other life history processes such as fecundity and senescence often result in opposing selection forces (Rollinson and Rowe 2015; Dmitriew 2011; Blanckenhorn 2000). This is likely to result in balancing selection towards an optimal growth rate and body size. The optimal growth rate is likely to be species and population-specific as it strongly depends on the environment and could shift with human impact or climate change (Gardner et al. 2011; Allendorf and Hard 2009).

Individual growth curves, that is the relationship between individual body size and age, are not only determined by genetic components, but in many species also show a strong plastic response to the environment. Environment-dependent changes in individual growth curves are observed in a wide range of ectothermic species ranging from Daphnia (McCauley et al. 1990) and fish (Zimmermann et al. 2018; Lorenzen and Enberg 2002) to amphibians and reptiles (Halliday and Verrell 1988), but it is even suggested that some large fossil mammals were growing in body size at flexible rates (Köhler and Moyà-Solà 2009). This suggests that the growth curves of most ectotherms and early endotherms are or were at least partly plastic. In contrast, modern-day endotherms (e.g. birds and mammals) might be able to sustain a more constant growth curve due to the ability to maintain a strong homeostasis (Kooijman 2010). For example, female mice stop ovulating but maintain growth in body size if food is scarce (Perrigo 1990). Overall, this suggests that taxa not only differ in their growth rate but also differ strongly in the degree of plasticity in the individual growth curves. In this paper, we will explore a mechanistic way to study the simultaneous evolution of the degree of plasticity in individual growth curves.

The evolution of a trait and the plasticity herein is often considered in the context of a dynamic environment with a certain degree of unpredictability. As a consequence, phenotypic plasticity is argued to be able to both hamper and accelerate evolutionary change in a trait, while plasticity itself might be subject to selection as well (Perry et al. 2018; Levis and Pfennig 2016; Fusco and Minelli 2010). Plasticity decouples the phenotypic expression of a trait from the genotype of an individual and increases its dependence on the environment. Yet, the mechanisms that link a life history trait to the environment are often unknown and are likely to have a genetic basis as well. As a consequence, plasticity and evolution of a trait are found to influence each other in several ways (Pfennig et al. 2010; Crispo 2007). Plasticity could, for example, enable species to survive in new environmental conditions encountered through environmental change or radiation and in this way grant species more time to adapt to new environments (Levis and Pfennig 2016; Moczek et al. 2011; Price et al. 2003). On the other hand, canalization could cause a species to lose plasticity in a trait if the environment is relatively constant (Crispo 2007). Simultaneously, plasticity may also mask genotypes from selective forces which could reduce the total genetic change in a trait (Crispo 2007). In general, it is suggested that an intermediate degree of plasticity is expected to favour the evolution of a trait, while fluctuating environments favour a higher degree of plasticity (Levis and Pfennig 2016; Moczek et al. 2011; Fusco and Minelli 2010; Price et al. 2003). Although it is clear that the environment plays an important role in the evolution of plasticity, the mechanistic link between the environment and a trait often remains vague and unconsidered.

A way to obtain a more mechanistic underpinning of the evolution of phenotypic plasticity is to consider the energy expenses or costs that are associated with phenotypic plasticity (Pigliucci 2005). The energetic costs of plasticity could arise from numerous mechanisms and processes and strongly depend on the trait (DeWitt et al. 1998). A useful way to disentangle the energetic expenses of expressing a plastic trait is to split these expenses into the costs of expressing the trait itself and the costs of maintaining plasticity in the trait (Murren et al. 2015). Energetic costs of expressing the trait itself can be considered the expenses that are needed to express a specific phenotype and are only paid when a phenotype is actually expressed. In contrast, energetic costs of maintaining plasticity in a trait are expenses that are always paid even if a phenotype is not expressed. This would for example include costs of monitoring the environment or costs of maintaining a complex genetic or chemical pathway to facilitate plasticity in a trait. Although maintaining plasticity in a trait might bring additional expenses, plasticity can still increase the fitness of an individual as the benefits of plasticity can outweigh the costs for maintaining plasticity. It is generally assumed that costs of maintaining plasticity are low or have a very small impact on the evolution of plasticity (Auld et al. 2010), even though it is often difficult to disentangle the different costs of a plastic trait.

Dynamic energy budget (DEB) theory offers a useful way to formulate a mechanistic model about the energetic expenses regarding phenotypic plasticity in individual growth. DEB theory describes the allocation of assimilated energy to growth, reproduction and somatic maintenance costs within an individual and in this way links important life history processes (Jager et al. 2013; Kooijman 2010). DEB models inherently incorporate the costs of expressing a specific growth rate and include a trade-off with fecundity, because assimilated energy can only be spent once. Most DEB models use a $\kappa$-rule, in which a fraction $\kappa$ of the assimilated energy is allocated to somatic growth and somatic maintenance, while a fraction $1-\kappa$ is allocated to reproduction (Jager et al. 2013; Kooijman 2010), which implies that both the individual growth curve and individual fecundity depend on the food availability in the environment and are therefore entirely plastic. It is clear that most endothermic species deviate from the $\kappa$-rule as these species maintain a relatively constant growth curve, which is prioritized over reproduction. This fundamental trade-off between growth and reproduction becomes especially apparent if individuals maintain a fixed growth rate under extreme conditions. This trade-off is very clear in ungulates which show delayed reproduction and decreased fecundity under reduced food conditions (Albon et al. 2000; Coulson et al. 2000; Clutton-Brock et al. 1987; Festa-Bianchet et al. 1995; Skogland 1986). DEB theory assumes that the $\kappa$-rule is a fundamental mechanism in individual energy allocation and that deviating from this rule requires additional mechanisms such as monitoring the environment and adaptive behaviour as well as more complex genetic and chemical systems to regulate energy allocation (Kooijman 2010). These additional mechanisms are argued to induce additional costs for deviating from the simpler and more straightforward $\kappa$-rule to maintain a more constant growth rate. This assumption contrasts with the general assumption that plasticity in a trait is costly, such that an increase in the degree of plasticity implies higher costs (Pigliucci 2005). Whether costs increase or decrease with plasticity might, in the end, strongly depend on the type of costs and their link to the underlying chemical structure for energy allocation. Here, we therefore explore both the situation in which additional costs increase with plasticity and the situation in which costs decrease with plasticity.

In this research, we use a size-structured population model formulated by Croll and De Roos (2022) based on a DEB model describing growth and reproduction to explore the simultaneous evolution of the degree of plasticity in the individual growth curve and the rate of the non-plastic part of individual growth. The DEB model provides a mechanistic way to incorporate the energy expenses and costs linked to plasticity in individual growth on an individual level. The translation of the individual energetic model to a size-structured population model allows us to analyze the model at the population level. Because we are interested in how the individual energetic model affects the evolution of plasticity, we study the model in an artificial and closed condition without external influences. As a consequence, fluctuations in the environment only arise due to changes in the structure of the consumer population, for example due to evolution of the individual traits or population dynamic cycles. In this way, individuals are able to use plasticity in growth to optimize their energy allocation schemes. With this model, we will explore the situation in which costs decrease with plasticity, which is in line with DEB theory, and contrast this with the scenario in which costs increase with plasticity, which is in line with general theory about plasticity.

Methods

Model formulation

In this study, we use a physiologically structured population model to describe the dynamics of a consumer population structured by age (a) and size (length $\ell$). The individuals of the consumer population compete for a shared, unstructured resource (R). The energetics of individual consumers is modelled with a DEB model that forms the core of the population model. The details of this DEB model for individual energetics are presented by Croll and De Roos (2022), and here, we provide a concise overview of its main features.

In the underlying DEB model, consumer individuals are characterized by the energy stored in lean mass. In DEB theory, it is assumed that energy in lean mass scales with the mass of an individual. Likewise, the mass is assumed to scale with the volume, and the volume can be related to the cubed length (Kooijman 2010). As a consequence, energy in lean mass scales with length cubed ($\ell ^3$).

We assume that individuals feed on a resource community that follows semi-chemostat dynamics with a maximum density K and a turn-over rate $\nu$. Consumption of the resource scales with the surface area of an individual, which is assumed to be proportional to length squared ($\ell ^2$). In addition, the consumption rate scales with the resource density following a scaled type II functional response ($f(R) = \frac{R}{R_h+R}$, with a half saturation constant $R_h$) and an ingestion scalar ($I_{max}$).

$$\begin{aligned} \frac{d R}{d t} = \nu \left( K-R\right) \;-\; \int _0^{a_{max}} I_{max} f(R) \ell (t,a)^2 n(t,a) da \end{aligned}$$

(1)

In which n(t, a) represents the number of individuals at time t with age a. Consumed resources are assimilated in the guts, and the ingestion rate times the assimilation rate is given by $\alpha$. Assimilated energy is divided between somatic processes and reproductive processes. Somatic processes include growth in body size and somatic maintenance costs, which are costs for maintaining the current individual state. Reproductive processes include the maturation of juveniles and the production of offspring by adults.

The model follows DEB theory in assuming that total energy allocation to somatic processes scales with individual surface area ($\ell ^2$). This energy allocation rate to somatic processes is furthermore assumed to be a combination of a fixed energy allocation rate and an ingestion-dependent energy allocation rate. The fixed energy allocation rate is determined by a fixed scalar ($\zeta$) and is therefore non-plastic. In contrast, for the ingestion-dependent allocation rate, we follow DEB theory by assuming that a fixed fraction $\kappa$ of assimilated energy is channelled to somatic processes. Since ingestion depends on the resource availability in the environment (following f(R)), this ingestion-dependent allocation is plastic. In other words, allocation to growth consists of a non-plastic part scaling with $\zeta$ and a plastic part scaling with the energy availability in the environment (f(R)). The balance between these two energy flows determines the level of plasticity in the energy allocation to somatic processes. We introduce the parameter $\phi$ to vary this balance from entirely fixed growth ($\phi =0$) to entirely plastic growth ($\phi =1$). Energy allocated to somatic processes is first used to pay somatic maintenance costs because these costs are essential for the functioning of an individual (Kooijman 2010). The somatic maintenance costs are independent of the environment and scale with the energy stored in lean mass and therefore with length cubed ($\ell ^3$) and a maintenance scalar (b). The remainder of the energy allocated to somatic processes is used for somatic growth. When there are no additional costs for plasticity, we assume that energy is converted to mass with a constant efficiency ($\gamma _m$):

$$\begin{aligned} \frac{d \ell ^3}{dt} = \gamma _m \left( \kappa \alpha \left( \phi f(R) + (1-\phi ) \zeta \right) \ell ^2 - b \ell ^3 \right) \end{aligned}$$

(2)

Note that the parameter $\phi$ itself is constant and in particular does not depend on resource availability. This parameter provides, however, a mechanistic basis for varying levels of plasticity in the growth rate in body size and thus the growth curve of individuals, as it influences to what extent somatic growth depends on resource availability. The value of $\phi$ varies between 0 and 1. Without growth curve plasticity ($\phi = 0$), energy allocation to somatic growth is determined by a fixed parameter ($\zeta$) and is therefore independent of the environment. With full growth curve plasticity ($\phi = 1$), this energetic model simplifies to the DEB model described by Jager et al. (2013), and energy allocation to somatic growth is entirely determined by the resource density in the environment (f(R)).

The assimilated energy not allocated to somatic processes is allocated to maturation in juveniles and reproduction in adults. In our model, consumer individuals eventually mature when reaching a predefined size ($\ell _J$). Adult consumers convert the energy not used for somatic processes to reproductive energy ($E_r$) with a constant conversion efficiency ($\gamma _r$):

$$\begin{aligned} \frac{d E_r}{d t} = {\left\{ \begin{array}{ll} \gamma _r \left( \alpha f(R)\ell ^2 - \kappa \alpha \left( \phi f(R) + (1-\phi ) \zeta \right) \ell ^2 \right) &{} \quad \text {if } \ell > \ell _J \\ 0 &{} \quad \text {if } \ell < \ell _J \end{array}\right. } \end{aligned}$$

(3)

From Eqs. (2) and (3), it is clear that assimilated energy might become insufficient to cover the energy required for somatic maintenance or non-plastic growth resulting in starvation. Under these conditions, individuals are forced to change their energy allocation scheme, which unavoidably results in additional plasticity. The DEB model assumes that individuals will first prioritize somatic maintenance and then non-plastic growth over other processes. To do so, individuals have to reallocate energy from reproduction to somatic processes under starvation conditions. In addition, we assume that individuals will experience starvation mortality ($\mu _s$) on top of the fixed background mortality ($\mu _b$). We assume that the starvation mortality increases with the energy deficit scaled with a starvation scalar ($q_s$). Starvation mortality ranges from 0 under normal conditions to immediate death ($\mu _s = \infty$) if individuals fail to pay all somatic maintenance costs. Previous implementations of the model showed that starvation conditions do not arise under equilibrium conditions. The population dynamic cycles in which starvation conditions arise only emerge in a limited parameter space and are driven by other mechanisms (De Roos et al. 1990; Croll and De Roos 2022). As a consequence, the specific formulation of the starvation conditions plays a minor role in the ecological and evolutionary dynamics of the model. The equations for the energy dynamics and mortality under starvation conditions are therefore outlined in more detail in the supplementary materials.

We reformulate the equation for growth (2) to describe the growth in length rather than the growth in length cubed. In addition, we use a conversion factor to translate the reproductive energy into the number of offspring. To express this model more succinctly, we use three composite parameters representing the ultimate asymptotic size under unlimited resource conditions ($\ell _\infty = \frac{\alpha \kappa }{b}$), the time constant of growth ($r_B = \frac{\gamma _m b}{3}$) and the time constant of reproduction ($r_F = \frac{\gamma _r b}{\ell _b^3}$). Interesting to note is that $\left( \phi f(R) + (1-\phi ) \zeta \right) \ell _\infty$ is the actual asymptotic size of an individual taking into account the energy allocation strategy and environment of an individual. Individuals grow towards this asymptotic size with a rate $r_B$.

The physiologically structured population model describes the dynamics at the level of the population (Table 1). At the core of the population model are three equations describing the energy surplus or deficit in growth ($F_g(R,\ell )$), in reproduction ($F_r(R)$) and these two combined in terms of length ($F_t(R,\ell )$). These terms indicate the amount of energy available for growth and reproduction and the amount of energy not used for somatic maintenance. As long as these terms are positive, individuals have sufficient energy to grow and reproduce. As soon as one of these terms becomes negative, individuals do not have sufficient energy to grow, reproduce or cover somatic maintenance costs and experience starvation conditions. Although most equations in the population model are expressed in these terms for energetic surpluses or deficits, we have to derive some additional expressions to complete the model. Integrating the individual fecundity ($\beta (R,\ell )$) at a given time (t) over the entire population results in the number of individuals at birth (n(t, 0)). The dynamics of the number of individuals at a given time and age (n(t, a)) is determined by the background mortality ($\mu _b$) and starvation mortality ($\mu _s(R,\ell )$). For computational reasons, we also assume that individuals die when reaching a maximum age ($a_{max}$), which might be a realistic assumption for some species. In general, this assumption barely affects the dynamics as it is set such that almost no individual reaches this age. Individuals are born with a fixed size ($\ell _b$) and grow towards an asymptotic size determined by the energy assimilation to somatic processes ($(\phi f(R) + (1-\phi ) \zeta ) \ell _\infty$). If the energy allocation to somatic processes is highly plastic (high $\phi$), the asymptotic size largely depends on the resource availability in the environment ($f(R) \ell _\infty$) and is therefore largely plastic. This then directly results in a plastic individual growth curve. In contrast, if the energy allocation to somatic processes is largely fixed (low $\phi$), the asymptotic size is largely fixed ($\zeta \ell _\infty$) and the growth rate is largely independent of the environment.

Table 1 Equations describing the population dynamics based on the model by Croll and De Roos (2022)

Besides the situation without additional costs associated with plasticity, we explore the situation in which additional costs are associated with growth curve plasticity. We assume that these costs reduce the efficiency with which energy allocated to growth is converted into lean mass. We explore both the situation in which costs increase with individual growth curve plasticity and the situation in which costs decrease with growth curve plasticity. We introduce a separate parameter ($c_g$) to switch between these two situations ($c_g=1$ and $c_g=0$ respectively). In addition, we use the parameter $c_p$ to scale the costs with the level of growth curve plasticity ($\phi$). This results in an expression for the total costs of plasticity:

$$\begin{aligned} c_t = \left( c_g \phi + (1-c_g) (1-\phi ) \right) c_p \end{aligned}$$

(4)

From this expression, it follows that the costs for plasticity ($c_t$) will increase ($c_g=1$) from 0 to $c_p$ or decrease ($c_g=0$) from $c_p$ to 0 if plasticity in the growth curve ($\phi$) changes from 0 to 1. In other words, $c_t$ indicates the fraction of energy allocated to growth that is used to cover additional costs for plasticity. This results in a reduction of the growth rate scalar from $r_B$ to $r_B(1 - c_t)$.

Adaptive dynamics

We analyze the evolution of growth curve plasticity ($\phi$) and the non-plastic growth scalar ($\zeta$) in the described model using the adaptive dynamics framework (Brännström et al. 2013). This framework considers the invasion fitness of a rare mutant, which has a slightly different trait value compared to resident individuals, in an environment determined by the resident population in equilibrium. Because the population is in equilibrium, the environment only changes over evolutionary time and is therefore constant throughout the lifetime of an individual. As a consequence, growth curve plasticity in individual growth is not visible during the lifetime of an individual, but still affects the energy allocation of an individual. Mutant trait values that yield a positive invasion fitness can spread and take over the population, which results in a stepwise change in the trait throughout the population. Using this framework results in a fitness landscape which predicts the evolutionary trajectories towards and away from evolutionary singular strategies.

The adaptive dynamics framework assumes that the evolutionary timescale can be separated from the ecological timescale. The derivation of the invasion fitness function therefore starts with defining the ecological equilibrium of a resident population with a given trait value ($\phi$, $\zeta$). In physiologically structured population models, the equilibrium conditions can be derived using the expression for the lifetime reproductive output of an individual (De Roos 1997). The lifetime reproductive output represents the average number of offspring an individual produces during its lifetime. In equilibrium, the resource density is constant, and individuals therefore do not experience starvation conditions. As a consequence, the lifetime reproductive output of an individual in equilibrium ($LRO(\tilde{R})$) is given by an expression in which only the scaled resource density ($f(\tilde{R})$) is unknown (derivation in the Supplementary materials and Croll and De Roos (2022)):

$$\begin{aligned} \begin{aligned} LRO(\tilde{R})&= r_F F_r(\tilde{R}) \int _{\tilde{a_J}}^{a_{max}} \tilde{\ell }(a)^2 e^{-\mu _b a} da \\ \tilde{\ell }(a)&= \ell _b e^{-r_B (1 - c_t) a} + \left( \phi f(\tilde{R}) + (1-\phi ) \zeta \right) \left( 1-e^{-r_B (1 - c_t) a}\right) \ell _\infty \\ \tilde{a_J}&= \frac{1}{r_B (1 - c_t)} \ln \left( \frac{\left( \phi f(\tilde{R}) + (1-\phi ) \zeta \right) \ell _\infty - \ell _b}{ \left( \phi f(\tilde{R}) + (1-\phi ) \zeta \right) \ell _\infty - \ell _J} \right) \end{aligned} \end{aligned}$$

(5)

Herein, we denoted the equilibrium value of a variable with a tilde. In equilibrium, every individual should exactly replace itself and the lifetime reproductive output should therefore be equal to one. This can be used to numerically compute the resource density in equilibrium ($\tilde{R}$). We refrain from calculating the consumer density in equilibrium as is done by Croll and De Roos (2022) because this is not necessary to compute the invasion fitness of a mutant individual.

To calculate the invasion fitness of a mutant, we consider the lifetime reproductive output of a mutant individual in an environment set by the resident population in equilibrium. We assume that the difference between the mutant trait value and the resident trait value is sufficiently small to prevent mutant individuals from experiencing starvation mortality in an environment set by the resident population in equilibrium. We can therefore use the same expression for the lifetime reproductive output for mutant and resident individuals (Eq. 5). A mutant trait value can spread through the population if the lifetime reproductive output of a mutant individual ($LRO_m(\tilde{R})$) exceeds the lifetime reproductive output of a resident individual in equilibrium ($LRO_r(\tilde{R})$), which is always equal to one. The invasion fitness of a mutant can therefore be closely approximated by the natural logarithm of the lifetime reproductive output of the mutant in an environment set by the resident population in equilibrium, scaled by the average age at reproduction of a resident individual in equilibrium ($T_r$) (Metz and Leimar 2011):

$$\begin{aligned} \begin{aligned} S_m(\tilde{R}) =&\frac{\ln \left( LRO_m(\tilde{R}) \right) }{T_r(\tilde{R})} \\ T_r(\tilde{R}) =&\int _0^{a_{max}} a \beta (\tilde{R},\tilde{\ell }) e^{-\mu _b a} da \end{aligned} \end{aligned}$$

(6)

Note that the average age at reproduction of a resident individual in equilibrium ($T_r$) is always positive and therefore never affects the qualitative form of the fitness landscape. The local selection gradient represents the direction and rate of evolutionary change in a trait (Geritz et al. 1998). For the degree of growth curve plasticity ($\phi$) and the non-plastic growth rate scalar ($\zeta$), these selection gradients are therefore given as follows:

$$\begin{aligned} D_\phi (\tilde{R}) =&\frac{1}{T_r} \left[ \frac{\partial }{\partial \phi _m} \ln \left( LRO_m(\tilde{R}) \right) \right] _{\phi _m = \phi _r} \end{aligned}$$

(7a)

$$\begin{aligned} D_\zeta (\tilde{R}) =&\frac{1}{T_r} \left[ \frac{\partial }{\partial \zeta _m} \ln \left( LRO_m(\tilde{R}) \right) \right] _{\zeta _m = \zeta _r} \end{aligned}$$

(7b)

The full expression for the selection gradients is given in the Supplementary material (Eqs. 16 and 17).

We refer to the collection of points at which one of the selection gradients is equal to zero as an evolutionary isocline ($D_\phi (\tilde{R}) = 0$ or $D_\zeta (\tilde{R})=0$). A singular strategy occurs if both selection gradients are equal to zero, which is at the intersection of an evolutionary isocline for the growth curve plasticity and an evolutionary isocline for the non-plastic growth scalar. In this article, we explore the fitness landscape around these singular strategies without additional costs for growth curve plasticity ($c_p=0$), if costs increase with growth curve plasticity ($c_g=1$) and if costs decrease with growth curve plasticity ($c_g=0$). We use general root finding and curve continuation procedures implemented in C (De Roos 2021) for the continuation of the isoclines ($LRO = 1$ and $D_\phi = 0$ or $D_\zeta = 0$) with respect to the growth curve plasticity ($\phi$) and the non-plastic growth scalar ($\zeta$). In addition, we perform this analysis for two values of the somatic energy allocation scalar ($\kappa$) because this parameter strongly influences the configuration of the fitness landscape. Bifurcation over other parameters showed that the presented fitness landscapes cover all biologically relevant scenarios. In addition, we verify the evolutionary behaviour of the traits around the evolutionary isoclines in terms of convergence and evolutionary stability by plotting the sign of the invasion fitness for combinations of resident and mutant trait values in so-called pairwise invasibility plots (PIPs) (Geritz et al. 1998). An evolutionary isocline is convergence stable if evolution drives a trait value towards the isocline and evolutionary stable if evolution cannot drive the trait value away from the isocline in any direction. For the model analysis, we will use a parameter set for Daphnia feeding on algae adapted from De Roos et al. (1990) (Table 2).

Table 2 Parameters used in the structured population model for Daphnia magna feeding on algae, derived from De Roos et al. (1990)

Dynamic simulations

To corroborate the evolutionary analysis using adaptive dynamics, we also carry out numerical simulations of both the ecological and evolutionary dynamics using the escalator-boxcar-train method (EBT) (De Roos 1988), a numerical method specifically designed to study the dynamics of structured population models. During these simulations, the ecological dynamics and evolutionary dynamics occur at the same timescale, because every day new mutations occur during a reproductive event. As a consequence, the composition of the consumer population changes constantly and is not in equilibrium. Similarly, the resource density therefore is not in equilibrium and changes due to the changes in the structure of the consumer population as well as population dynamic cycles (Croll and De Roos 2022). This results in more realistic conditions in which individuals have to deal with a constantly changing environment, which could affect the evolution of the level of growth curve plasticity.

In the EBT method, the population is subdivided into cohorts consisting of individuals born at approximately the same time. In our simulations, a new cohort will be formed once a day, and all offspring are always born with age 0 and length $\ell _b$. We split a cohort into multiple sub-cohorts consisting of genetically identical individuals such that the differential equations can be solved separately for every sub-cohort. When a new cohort is formed based on the reproductive output of the current population, we assume that a mutation occurs with probability $p_m$ for each trait and that this mutation has an effect of size $d_m$ on either the growth curve plasticity ($\phi$) or the non-plastic growth scalar ($\zeta$). We assume that mutations can affect traits in both directions, resulting in either an increase or decrease in growth curve plasticity or an increase or decrease in non-plastic growth rate, such that selection can drive these trait values in both directions. As a result, a fraction $1-4 p_m$ of the offspring will have the same trait values as the parent cohort. In addition, four sub-cohorts with mutants are produced, which differ from the parent cohort in either the growth curve plasticity ($\phi - d_m$ or $\phi + d_m$) or the non-plastic growth scalar ($\zeta - d_m$ or $\zeta + d_m$). A fraction $p_m$ of the offspring is allocated to each of the mutant sub-cohorts. If the trait values of a mutant cohort fall outside the range of the allowed trait values ($0 \le \phi \le 1$, $0\le \zeta \le 1$), the trait values of the mutant sub-cohort are reset to the trait values of the parent cohort. Simulations are started from a population dynamic attractor for the resident population, obtained by running the model 5000 time steps with a given parameter set and a mutation probability of zero. Afterwards, simulations are continued with a non-zero mutation probability until the number of cohorts, the average trait values and the resource density become constant with a precision of $10^{-6}$, which indicates that the population has reached an evolutionary and ecological attractor (which took at least 5000 time steps). We will depict the evolving trait values of the simulated trajectories using black solid lines in the same graphs as the fitness landscapes computed with adaptive dynamics.

Results

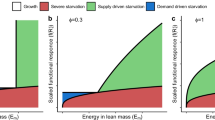
We first consider the situation in which maintaining a plastic or non-plastic growth curve does not incur additional costs in the form of a reduced conversion efficiency ($c_p = 0$, Fig. 1). We found two evolutionary isoclines for the degree of growth curve plasticity ($D_\phi (\tilde{R}) = 0$) and two evolutionary isoclines for the non-plastic growth scalar ($D_\zeta (\tilde{R})=0$). The first isocline for the growth curve plasticity ($D_\phi (\tilde{R}) = 0$) occurs when the non-plastic growth scalar is equal to the scaled resource density in the environment ($\zeta = f(\tilde{R})$, Fig. 1, blue dashed line). At this isocline, the plastic growth rate is equal to the non-plastic growth rate and as a consequence, a mutation in growth curve plasticity does not affect the fitness of an individual. Selection in the non-plastic growth scalar will drive the population away from this evolutionary isocline for growth curve plasticity. We will therefore refer to this isocline as the trivial evolutionary isocline for growth curve plasticity ($\phi$). The direction of the selection gradient for growth curve plasticity is opposite at different sides of this trivial isocline for growth curve plasticity.

Similarly, an evolutionary isocline for the non-plastic growth scalar ($D_\zeta (\tilde{R}) = 0$) occurs if growth is entirely plastic ($\phi = 1$, Fig. 1 red dashed line). At this isocline, the life history and fitness of an individual are not affected by the non-plastic growth scalar. Evolution in growth curve plasticity will drive the population away from this evolutionary isocline for some values of the non-plastic growth scalar. We therefore refer to this isocline as the trivial evolutionary isocline for the non-plastic growth scalar ($\zeta$).

The second evolutionary isocline for the growth curve plasticity and the non-plastic growth scalar ($D_\phi (\tilde{R})=0$, $D_\zeta (\tilde{R})=0$) occur on the same manifold in the parameter space in absence of additional costs for growth curve plasticity (Fig. 1, purple line; see Eqs. 16 and 17 for corroboration that these isoclines coincide when $c_p = 0$). This manifold represents a collection of singular points. All combinations of trait values on this manifold have the same fitness which results in evolutionary neutrality on the manifold. Nonetheless, the singular points on the manifold are invasion and convergence stable against mutants with trait values which are not on the manifold (Figs. 6 and 7). The manifold therefore forms a collection of evolutionary endpoints with the same fitness. We will refer to this manifold as the main ESS-manifold. Time simulations revealed two different evolutionary trajectories towards this main ESS-manifold (Fig. 1, black lines). If the initial point of the trajectory and the main manifold occur at the same side of the trivial evolutionary isocline for growth curve plasticity, selection will drive the growth curve plasticity and the non-plastic growth scalar directly towards the main manifold. On the other hand, if the initial point of the trajectory and the main ESS-manifold occur at opposite sides of the trivial evolutionary isocline for growth curve plasticity, selection will first drive the growth curve plasticity and non-plastic growth scalar towards the trivial isocline for growth curve plasticity. At this isocline, the direction of selection for the growth curve plasticity changes and selection drives the growth curve plasticity and the non-plastic growth scalar towards the main ESS-manifold.

Fig. 1

Selection gradients and evolutionary trajectories for the evolution of the growth curve plasticity ($\phi$) and the non-plastic growth scalar ($\zeta$) without additional costs for plasticity ($c_p=0$) for $\kappa =0.3$ (left) and $\kappa =0.9$ (right). Blue, red and purple arrows show the selection gradient for the growth curve plasticity ($\phi$), non-plastic growth scalar ($\zeta$) and combination of both respectively. Blue, red and purple lines indicate evolutionary isoclines for the growth curve plasticity ($\phi$), non-plastic growth scalar ($\zeta$) and overlapping instances of these isoclines. Solid lines represent evolutionary isoclines which are convergence and evolutionary stable for the parameter under consideration. Because these isoclines overlap in this situation, these lines form a manifold that is evolutionary neutral for all parameter combinations on the manifold and evolutionary stable against invasion of mutants with parameter combinations not on the manifold. Dashed lines represent evolutionary isoclines which are evolutionary neutral for the parameter under consideration. Black lines show the average trait values from time simulations of evolutionary trajectories starting at the parameter values marked with a dot

Fig. 2

Selection gradient and evolutionary trajectories for the evolution of the growth curve plasticity ($\phi$) and the non-plastic growth scalar ($\zeta$) with costs increasing with growth curve plasticity ($c_g=1, c_p=0.4$) for $\kappa =0.3$ (left) and $\kappa =0.9$ (right). Blue, red and purple arrows show the selection gradient for the growth curve plasticity ($\phi$), non-plastic growth scalar ($\zeta$) and combination of both respectively. Blue and red lines indicate evolutionary isoclines for the growth curve plasticity ($\phi$) and the non-plastic growth scalar ($\zeta$). Solid lines represent evolutionary isoclines that are convergence and evolutionary stable for the parameter under consideration. Dashed lines represent evolutionary isoclines that are evolutionary neutral for the parameter under consideration. Black lines show the average trait values from time simulations of evolutionary trajectories starting at the parameter values marked with a dot

Introducing a cost increasing with growth curve plasticity ($c_g = 1, c_p=0.4$) changes the location of the evolutionary isoclines in the parameter space relatively little but does so differently for the evolutionary isoclines of the growth curve plasticity and the non-plastic growth scalar (Fig. 2). First of all, the trivial evolutionary isocline for growth curve plasticity (Fig. 2, almost horizontal blue line) slightly curves when growth is not entirely non-plastic ($\phi > 0$), which makes this evolutionary isocline an evolutionary attractor when only considering the evolution in growth curve plasticity (Figs. 6 and 7). In addition, the main isocline for growth curve plasticity shifts away from the main isocline for the non-plastic growth scalar (Fig. 2, red and blue curved lines). As a consequence, selection on the non-plastic growth scalar will drive the population away from the main isocline for growth curve plasticity, while close to the main isocline for the non-plastic growth scalar, the selection gradient for the growth curve plasticity is negative. As a result, the growth curve plasticity and the non-plastic growth scalar will first evolve towards the main isoclines, similar to the situation without additional costs for growth curve plasticity (Fig. 2, black lines). But as soon as the population trait values are between these main isoclines, the trait values will remain between these isoclines and slowly evolve towards lower growth curve plasticity. Interestingly, selection gradients and the time series reveal that the initial evolution towards the main isoclines is much faster compared to the evolution towards low growth curve plasticity between the main isoclines (length of arrows in Fig. 2 and Supplementary videos).

Fig. 3

Selection gradient and evolutionary trajectories for the evolution of the growth curve plasticity ($\phi$) and the non-plastic growth scalar ($\zeta$) with costs decreasing with growth curve plasticity ($c_g=0, c_p=0.4$) for $\kappa =0.3$ (left) and $\kappa =0.9$ (right). Blue, red and purple arrows show the selection gradient for the growth curve plasticity ($\phi$), non-plastic growth scalar ($\zeta$) and combination of both respectively. Blue and red lines indicate evolutionary isoclines for the growth curve plasticity ($\phi$) and the non-plastic growth scalar ($\zeta$). Solid lines represent evolutionary isoclines that are convergent and evolutionary stable for the parameter under consideration. Dashed lines represent evolutionary isoclines that are evolutionary neutral for the parameter under consideration. Black lines show the average trait values from time simulations of evolutionary trajectories starting at the parameter values marked with a dot

Introducing a cost decreasing with growth curve plasticity ($c_g = 0$, $c_p=0.4$) shifts the location of the isoclines in the opposite direction compared to the situation in which costs increase with growth curve plasticity (Fig. 3). The trivial isocline for growth curve plasticity remains an evolutionary attractor when only considering the evolution of growth curve plasticity (Figs. 6 and 7). Although sometimes very slightly, costs decreasing with plasticity decreases the distance between the trivial and the main isoclines for growth curve plasticity if growth is not entirely plastic ($\phi <1$, blue lines Fig. 3). For some parameter settings, this can even cause these isoclines to collide and form a single isocline in the relevant parameter space (Fig. 3b). In this situation, evolution always drives the population towards a relatively high degree of growth curve plasticity. Furthermore, we see again that the evolution of the non-plastic growth scalar drives the population away from the main isocline for growth curve plasticity, but this time, the selection gradient for growth curve plasticity is positive around the main isocline for the non-plastic growth scalar. As a consequence, evolution will drive the population first towards the main isoclines, from which the population evolves between these isoclines towards a higher level of growth curve plasticity. The directional evolution between the main isoclines will eventually stop when the non-plastic growth scalar reaches a physiological maximum or minimum value. Again, the evolution towards the main isoclines is relatively fast compared to the evolution between the main isoclines (length of arrows in Fig. 3 and Supplementary videos).

Discussion

We studied the combined evolution of plasticity in individual growth curves and the non-plastic growth rate. To do so, we modelled a size-structured consumer population feeding on a single shared resource. In this model, plasticity in individual growth curves ($\phi$) determines the fraction of the individual growth rate that depends on the scaled resource availability in the environment (f(R)), while the non-plastic growth rate is determined by an environment-independent scalar ($\zeta$). Additional costs scaling with plasticity ($c_t$) were incorporated as a reduction in the conversion efficiency from energy to lean mass. This might be plausible under the assumption that these costs result from an increase in the chemical complexity of the regulatory mechanism, but other costs associated with plasticity, such as additional monitoring of the environment, are more likely to increase the somatic maintenance costs of an individual. This would result in a more complex equation for individual growth in which the growth scalar ($r_B$) and the asymptotic size ($\ell _\infty$) respond in opposite directions to a change in additional costs. The implementation of costs as increased somatic maintenance costs results in the same evolutionary patters as costs incorporated as a decreased conversion efficiency (Supplementary information).

We analyzed the model using the adaptive dynamics framework (Brännström et al. 2013) by defining an expression for the invasion fitness based on the lifetime reproductive output of mutant individuals in an equilibrium of the resident population. We furthermore corroborated the results of the adaptive dynamics approach using numerical simulations of the ecological and evolutionary dynamics. Evolution will always drive the population uphill towards a peak in the invasion fitness, which is a singular strategy. Because we consider the consumer population in a one-dimensional environment consisting of a single resource community, a peak in the invasion fitness corresponds to a minimum in the resource density (Supplementary materials, Eqs. 18–20). In our model, a decrease in resource density can only be caused by an increase in consumption by the entire population, from which it follows that evolution on the growth curve plasticity and the non-plastic growth scalar actually optimize the resource consumption by the consumer population. Individuals with a degree of growth curve plasticity and non-plastic growth rate closer to the singular strategy also have a higher lifetime reproductive output in an environment without competition (Croll and De Roos 2022). This shows that evolution not only optimizes the energy consumption of the population but also the efficiency of energy allocation at an individual level.

In our model, evolution always ends on the main evolutionary isoclines. These main evolutionary isoclines occur when a trait value yields the most optimal energy allocation scheme, when only considering evolution in that specific trait. At these main isoclines, individuals most optimally divide the assimilated energy between growth and reproduction (Croll and De Roos 2022), and these isoclines are always convergence and evolutionary stable in our model when considering the evolution in only one trait (Figs. 6 and 7). The main isoclines for the growth curve plasticity and the non-plastic growth scalar occur at the same combinations of parameter values if no additional costs for maintaining a plastic or non-plastic growth curve are included (Fig. 1). As a consequence, the strategies on this main ESS-manifold are invasion stable against strategies outside the manifold but evolutionary neutral for points on the manifold. As a consequence, combined evolution will drive both the growth curve plasticity and the non-plastic growth scalar towards this main ESS-manifold, and evolution can end in a wide range of strategies on this main ESS-manifold depending on the strategies present in the population at the start of the trajectory. The incorporation of costs that increase or decrease with growth curve plasticity slightly shifts the location of the main isoclines such that combined evolution will eventually drive the population towards one of the extreme ends of these isoclines (Figs. 2 and 3). Logically, if costs increase with growth curve plasticity, the population will end up between the main isoclines at the side with the lowest degree of growth curve plasticity. If costs decrease with growth curve plasticity, the population will end up between the main isoclines at the side with the highest degree of growth curve plasticity. General theory about plasticity assumes that energetic costs for maintaining plasticity increase with the degree of plasticity, which limits the evolution of plasticity (Pigliucci 2005). This corresponds with the evolution towards a low level of growth curve plasticity if energetic costs increase with plasticity. In contrast, DEB theory assumes that the $\kappa$-rule is a fundamental mechanism in all organisms and that a deviation from this rule is costly (Kooijman 2010). Under this assumption, growth curves are entirely plastic, and a decrease in growth curve plasticity would result in an increase in energetic costs. This corresponds with the evolution towards a high degree of growth curve plasticity if energetic costs decrease with plasticity found in our model. In other words, assumptions about the energetic costs for maintaining plasticity based on DEB theory and classic theory about plasticity result in contradicting conclusions about the evolution of plasticity in individual growth curves.

Our model clearly shows the contribution of different types of expenses scaling with plasticity to the evolution of growth curve plasticity. In our model, the expenses of expressing a plastic growth curve are determined by the individual energy allocation schemes, which depend amongst others on the plastic growth energy allocation constant ($\kappa$). The individual energy allocation schemes determine the global location for the main isoclines in the parameter space. For example, at low values of the plastic growth energy allocation constant ($\kappa$), the main isoclines occur at relatively high values of the non-plastic growth scalar (Figs. 1a, 2a and 3a). In this situation, the non-plastic growth rate exceeds the plastic growth rate. In contrast, at high values of the somatic energy allocation scalar ($\kappa$), the main isoclines occur at relatively low values of the non-plastic growth scalar (Figs. 1b, 2b and 3b). In this situation, the plastic growth rate exceeds the non-plastic growth rate. We could therefore state that the individual energy assimilation schemes and therewith the expenses for expressing a specific growth rate determine the global position of the main isoclines. In addition, the simulated trajectories show that evolution towards these main isoclines is relatively fast. In contrast, costs that are directly linked to the degree of growth curve plasticity determine the final destination of the evolutionary process. For example, if additional costs increase with plasticity, the population will evolve towards lower plasticity, while if costs decrease with plasticity, the population will evolve towards a higher degree of growth curve plasticity (Figs. 2 and 3). In addition, the selection gradient and the simulated trajectories show that evolution along these main isoclines is much slower than evolution towards the main isoclines. We could therefore argue that individual energy allocation schemes and expenses for expressing a specific growth rate determine the global evolutionary trajectory for growth curve plasticity, while the exact way additional costs scale with the growth curve plasticity determines the precise endpoint of evolution. This adds to the general hypothesis that costs for maintaining plasticity only play a minor role compared to costs for expressing a trait in the evolution of plasticity because a major part of the evolutionary trajectory is determined by the energy trade-off within an individual (Auld et al. 2010).

Several energetic costs might be involved in maintaining growth curve plasticity. We assumed a linear relationship between the costs for maintaining growth curve plasticity and the degree of growth curve plasticity. As a consequence, evolution drives the growth curve plasticity to one of the extreme values along the main isoclines. A non-monotonic relation between the costs for maintaining growth curve plasticity and the degree of growth curve plasticity is likely to alter the relative location of the main isoclines. For example, if costs for plasticity would increase towards extreme values of the growth curve plasticity, we expect balancing selection along the main isoclines to drive the growth curve plasticity towards intermediate values. In contrast, if costs for plasticity would decrease towards extreme values of the growth curve plasticity, we expect disruptive selection along the main isoclines to drive the growth curve plasticity towards one of the extreme values depending on the starting conditions.

We also found two trivial evolutionary isoclines that occur at very specific conditions in our model. Such an isocline occurs for the growth curve plasticity ($\phi$) if the plastic growth rate and the non-plastic growth rate are equal ($f(\tilde{R})=\zeta$, Fig. 1), because in this case, a shift in growth curve plasticity does not affect the total growth rate of an individual. As a consequence, individuals with different degrees of growth curve plasticity have the same fitness, and growth curve plasticity will not change due to selection. This trivial isocline for growth curve plasticity is not an evolutionary endpoint, because evolution of other traits such as the non-plastic growth scalar could easily drive the population away from these strategies. Nonetheless, the occurrence of this trivial manifold for growth curve plasticity suggests that the selection pressure on the level of phenotypic plasticity becomes stronger if a change in growth curve plasticity has a larger impact on the phenotype of an individual.

It is also suggested that phenotypic plasticity can mask genotypes from selective forces and therefore hamper the evolution of a trait (Crispo 2007; Price et al. 2003). It could be argued that this occurs at the trivial isocline for the non-plastic growth scalar ($\zeta$). This trivial isocline occurs if growth is entirely plastic ($\phi =1$, Figs. 1, 2 and 3). As a consequence, the individual growth rate does not have a non-plastic component that is scaled by the non-plastic growth scalar and selection does not affect the non-plastic growth scalar. This only occurs at an extreme condition in the model, and it is likely that evolution in another trait such as the degree of growth curve plasticity will drive natural populations away from this trivial isocline. It is therefore unlikely that growth curve plasticity will entirely mask a non-plastic part of growth from evolutionary pressure. Nonetheless, the occurrence of this trivial isocline for the non-plastic growth scalar suggests that the selection pressure on the non-plastic growth rate decreases with an increasing degree of growth curve plasticity.

In this study, we focused on the effect of an individual energetic mechanism on the evolution of growth curve plasticity. We therefore chose to consider a structured consumer population feeding on a single resource in closed conditions. In the adaptive dynamics analysis, the resource is in population dynamic equilibrium and therefore does not fluctuate during the lifetime of an individual. As a consequence, evolution results in the optimization of individual life histories through optimization of the individual energy allocation scheme. Interestingly, this suggests that plasticity in growth might evolve even when the environment is constant, although the same optimal energy allocation scheme could arguably be achieved through the evolution of other individual traits such as the plastic energy allocation constant ($\kappa$) as well. During the dynamic simulations, the resources were not in equilibrium and followed transient dynamics. Changes in the resource density occur through population dynamic cycles (Croll and De Roos 2022) as well as changes in the structure of the consumer population. It is generally expected that fluctuations in the environment would favour a more plastic life history strategy (Levis and Pfennig 2016; Moczek et al. 2011; Fusco and Minelli 2010; Price et al. 2003). Surprisingly, the results from the dynamic simulations seem to barely differ from the predictions from the adaptive dynamics framework. This might suggest that optimization of the individual life histories is a stronger selective force for the level of growth curve plasticity than environmental fluctuations. It is important to note that in our model, all fluctuations in the environment are generated by the system itself. It is likely that externally driven fluctuations in the environment have a stronger effect on the level of growth curve plasticity. These fluctuations could for example cause different types of starvation dynamics depending on the underlying energy allocation schemes of an individual (Croll and De Roos 2022). Whether and how external environmental fluctuations would affect the evolution of growth curve plasticity in combination with a mechanistic description of individual energy allocation is still an open question, and our model offers a suitable framework to study this.

This study can at least inform us about the evolution of plasticity in the light of the optimization of individual energy allocation dynamics. Our model supports the suggestion that taxa are likely to strongly differ in the plasticity in their growth curves and the non-plastic growth rate. It is generally suggested that growth curves of ectotherms are largely plastic while growth curves of endotherms are largely static (McCauley et al. 1990; Lorenzen and Enberg 2002; Zimmermann et al. 2018; Halliday and Verrell 1988; Köhler and Moyà-Solà 2009; Kooijman 2010). An explanation of this could be that costs decrease with plasticity in ectotherms, because they need additional chemical or genetic mechanisms to maintain a constant growth curve. In contrast, endotherms have strong homeostasis and therefore might need additional mechanisms to monitor the environment (Kooijman 2010). If these mechanisms are costly, costs might increase with plasticity, which could explain evolution towards lower plasticity in growth curves. Interestingly, our model suggests that it is possible for a population to evolve towards entirely non-plastic growth curves, while a strategy with entirely plastic growth curves is not evolutionary stable. This contrasts with DEB theory which argues that a $\kappa$-rule mechanism for energy allocation is most efficient for individuals (Kooijman 2010). Independent of this, our model suggests that it is unlikely that growth curves are entirely plastic or entirely non-plastic in most species, because even if maintaining a plastic or non-plastic growth curve induces additional costs, evolution is likely to drive plasticity towards intermediate values at first, after which the evolution towards extreme values is very slow. It is more likely to find species with an intermediate degree of growth curve plasticity on the trajectory towards more extreme values. Similarly, the total growth rate of individuals is most likely at intermediate values, due to the trade-off with other life history characteristics such as reproduction in this model (Gardner et al. 2011; Allendorf and Hard 2009). Unfortunately, it is hard to disentangle the plastic and non-plastic components of individual growth curves and the evolution herein for a specific species as the difference between plastic and non-plastic growth only becomes visible under extreme conditions. Therefore, there might even be more variation in individual growth rates and the plasticity herein than we currently expect.

Appendices

Appendix A: Additional analysis

Energy dynamics under starvation

From Eqs. (2) and (3), it is clear that the energy flow can become insufficient to cover demand-driven processes such as maintenance costs and growth. This would lead to starvation conditions which require a rechannelling of the assimilated energy. Three different types of starvation conditions can be distinguished.

Under supply-driven starvation, the energy supplied to somatic processes is insufficient to cover somatic maintenance costs ($\kappa \alpha \left( \phi f(R) + (1-\phi ) \zeta \right) \ell ^2 < b \ell ^3$). Under this condition some of the energy is reallocated from reproductive processes to cover somatic maintenance costs. As a consequence, somatic growth stops and reproduction is reduced. In contrast, under demand-driven starvation the assimilated energy is insufficient to cover the energy demand by non-plastic growth and somatic maintenance ($\alpha f(R) \ell ^2 < \kappa \alpha \left( \phi f(R) + (1-\phi ) \zeta \right) \ell ^2$). Under this condition we assume that all energy is used to cover the energy demand by non-plastic growth and somatic maintenance as these are both demand-driven processes determined by the internal state of an individual. As a consequence reproduction stops and growth is reduced. Under severe starvation conditions, assimilated energy is insufficient to cover somatic maintenance costs ($\alpha f(R) \ell ^2 < b \ell ^3$) and both growth and reproduction stop immediately. This results in the following equations for energy allocation to growth and reproduction:

$$\begin{aligned} \frac{d \ell ^3}{dt} = {\left\{ \begin{array}{ll} \gamma _m (1-c_t) \left( \kappa \alpha \left( \phi f(R) + (1-\phi ) \zeta \right) \ell ^2 - b \ell ^3\right) & \text { if } b \ell ^3< \kappa \alpha \left( \phi f(R) + (1-\phi ) \zeta \right) \ell ^2< \alpha f(R) \ell ^2 \\ \gamma _m (1-c_t) \left( \alpha f(R) \ell ^2 - b \ell ^3 \right) & \text { if } b \ell ^3< \alpha f(R) \ell ^2 < \kappa \alpha \left( \phi f(R) + (1-\phi ) \zeta \right) \ell ^2 \\ 0 & \text { otherwise} \end{array}\right. } \end{aligned}$$

(8a)

$$\begin{aligned} \frac{d E_r}{dt} = {\left\{ \begin{array}{ll} \gamma _r \alpha \left( (1-\kappa ) f(R) + (f(R)-\kappa \zeta ) \right) \ell ^2 & \text { if } b \ell ^3< \kappa \alpha \left( \phi f(R) + (1-\phi ) \zeta \right) \ell ^2< \alpha f(R) \ell ^2 \\ \gamma _r \left( \alpha f(R) \ell ^2 - b \ell ^3\right) & \text { if } \kappa \alpha \left( \phi f(R) + (1-\phi ) \zeta \right) \ell ^2< b \ell ^3 < \alpha f(R) \ell ^2 \\ 0 & \text { otherwise} \end{array}\right. } \end{aligned}$$

(8b)

Additionally, we assume that starvation conditions lead to an increase in mortality. We assume that starvation mortality scales with the energy deficit of an individual and a starvation mortality scalar ($q_s$). Under extreme conditions it can even occur that the assimilated energy is insufficient to cover somatic maintenance costs ($\alpha f(R) \ell ^2 < b \ell ^3$). We assume that individuals will starve instantaneously under these extreme starvation conditions. This results in the following expressions for the starvation mortality:

$$\begin{aligned} \mu _s = {\left\{ \begin{array}{ll} 0 & \text { if } b \ell ^3< \kappa \alpha \left( \phi f(R) + (1-\phi ) \zeta \right) \ell ^2< \alpha f(R) \ell ^2 \\ q_s \frac{b \ell ^3 - \kappa \alpha \left( \phi f(R) + (1-\phi ) \zeta \right) \ell ^2 }{ \alpha f(R) \ell ^2 - b \ell ^2} & \text { if } \kappa \alpha \left( \phi f(R) + (1-\phi ) \zeta \right) \ell ^2< b \ell ^3< \alpha f(R) \ell ^2 \\ q_s \frac{\kappa \alpha \left( \phi f(R) + (1-\phi ) \zeta \right) \ell ^2 - \alpha f(R) \ell ^2}{\alpha f(R) \ell ^2 - b \ell ^3} & \text { if } b \ell ^3< \alpha f(R) \ell ^2< \kappa \alpha \left( \phi f(R) + (1-\phi ) \zeta \right) \ell ^2 \\ \infty & \text { if } \alpha f(R) \ell ^2 < b \ell ^3 \end{array}\right. } \end{aligned}$$

(9)

Together this results in the formulation of the population dynamics under supply-driven ($F_g(R,\ell ) < 0$), demand-driven ($F_r(R) < 0$) and severe ($F_t(R,\ell )<0$) starvation conditions in Eq. (1) in the main text.

Derivation of ecological equilibrium

In equilibrium the density of the resource is constant ($\tilde{R}$). As a consequence, starvation conditions can not occur in equilibrium (Croll and De Roos 2022). Therefore, we can simplify the differential equation for the number of individual at a given age in equilibrium ($\tilde{n}(a)$):

$$\begin{aligned} \frac{\partial n}{\partial a} = - \mu _b \tilde{n}(a) \end{aligned}$$

(10)

Because the number of individuals at birth in equilibrium ($\tilde{n}(0)$) is constant, this equation can be solved explicitly:

$$\begin{aligned} \tilde{n}(a) = \tilde{n}(0) e^{-\mu _b a} \end{aligned}$$

(11)

Similarly, the differential equation of the growth rate in equilibrium simplifies to:

$$\begin{aligned} \frac{\partial \ell }{\partial a} = r_B \left( 1 - c_t\right) \left( \left( \phi f(\tilde{R}) - (1 - \phi ) \zeta \right) \ell _\infty - \ell \right) \end{aligned}$$

(12)

We solve this differential condition by using the boundary condition of the length at birth ($\ell (0) = \ell _b$):

$$\begin{aligned} \tilde{\ell }(a) = \ell _b e^{-r_B (1 - c_t) a} + \left( \phi f(\tilde{R}) + (1-\phi ) \zeta \right) \left( 1-e^{-r_B (1 - c_t) a}\right) \ell _\infty \end{aligned}$$

(13)

By substituting the length at maturation ($\ell _J$) in this equation, we can rearrange the equation to express the age at maturation ($a_J$):

$$\begin{aligned} \tilde{a_J} = \frac{1}{r_B (1 - c_t)} \ln \left( \frac{\left( \phi f(\tilde{R}) + (1-\phi ) \zeta \right) \ell _\infty - \ell _b}{ \left( \phi f(\tilde{R}) + (1-\phi ) \zeta \right) \ell _\infty - \ell _J} \right) \end{aligned}$$

(14)

With an explicit expression for the density at age, the size at age and the age at maturation, we can evaluate the integral of the individual fecundity to sum the reproductive rate of all adults resulting in the number of individuals at birth:

$$\begin{aligned} \tilde{n}(0) = \int _0^{a_{max}} \beta (\tilde{R},\tilde{\ell }(a)) \tilde{n}(t,a) da = \int _{a_J}^{a_{max}} r_F F_r(\tilde{R}) \tilde{n}(0) e^{-\mu a} da \end{aligned}$$

(15)

We can divide both sides of this expression by the number of individuals at birth in equilibrium ($\tilde{n}(0)$). This yield the expression for the lifetime reproductive output in equilibrium given in Eq. 5.

Mathematical expressions of the selection gradients

The explicit expressions for the selection gradients are derived by differentiating the function $LRO(\tilde{R})$ (Eq. 5) with respect to $\phi$ and $\zeta$, respectively, resulting in:

$$\begin{aligned} D_\phi (\tilde{R}) = & \frac{r_F \left( f(\tilde{R}) - \zeta \right) \ell _\infty }{T_r (\tilde{R}) LRO_m(\tilde{R})} \left[ \int _{\tilde{a_J}}^{a_{max}} \left( 2 \left( 1-e^{-r_B (1 - c_t) a}\right) F_r(\tilde{R}) - \tilde{\ell }(a) \right) \tilde{\ell }(a) e^{-\mu _b a} da + \frac{ \left( \ell _J-\ell _b \right) F_r(\tilde{R}) \ell _J^2 e^{-\mu _b \tilde{a_J}}}{r_B (1 - c_t) \left( \left( \phi f(\tilde{R}) + (1-\phi ) \zeta \right) \ell _\infty -\ell _b \right) \left( \left( \phi f(\tilde{R}) + (1-\phi ) \zeta \right) \ell _\infty -\ell _J \right) } \right] \\& - \frac{ (2 c_g - 1) c_p r_F F_r(\tilde{R})}{T_r (\tilde{R}) LRO_m(\tilde{R})} \left( \frac{ \ell _J^2 \tilde{a_J} e^{-\mu _b \tilde{a_J}}}{ (1-c_t)} + 2 r_B \left( \left( \phi f(\tilde{R}) + (1-\phi ) \zeta \right) \ell _\infty -\ell _b\right) \int _{\tilde{a_J}}^{a_{max}} \tilde{\ell }(a) e^{-\mu _b a} e^{-r_B (1-c_t) a} a da \right) \end{aligned}$$

(16)

$$\begin{aligned}D_\zeta (\tilde{R}) = &\frac{r_F \left( 1 - \phi \right) \ell _\infty }{T_r (\tilde{R}) LRO_m(\tilde{R})} \left[ \int _{\tilde{a_J}}^{a_{max}} \left( 2 \left( 1-e^{-r_B (1 - c_t) a}\right) F_r(\tilde{R}) - \tilde{\ell }(a) \right) \tilde{\ell }(a) e^{-\mu _b a} da + \frac{ \left( \ell _J-\ell _b \right) F_r(\tilde{R}) \ell _J^2 e^{-\mu _b \tilde{a_J}}}{r_B (1 - c_t) \left( \left( \phi f(\tilde{R}) + (1-\phi ) \zeta \right) \ell _\infty -\ell _b \right) \left( \left( \phi f(\tilde{R}) + (1-\phi ) \zeta \right) \ell _\infty -\ell _J \right) } \right] \end{aligned}$$

(17)

The lifetime reproductive output of the resident in equilibrium ($LRO_r(\tilde{R})$) is always equal to one and therefore cancels out in these equations. The numerator of the fraction before the squared brackets represents the effect of a change in $\phi$ or $\zeta$ on the asymptotic size of an individual. The term between the squared brackets represents the effect of a change of the asymptotic size on the fecundity, size and age at maturation of an individual. Note that the terms between squared brackets in both selection gradients are equal. The second term of the selection gradient for the growth curve plasticity deals with the additional costs scaling with plasticity and only occurs if there is a cost for maintaining a plastic or non-plastic growth curve ($c_p \ne 0$). An isocline arises if the selection gradient is equal to zero. If there are no additional costs scaling with plasticity ($c_p=0$) the second term of the selection gradient for growth curve plasticity is equal to zero. In this case it is clear that the selection gradient for growth curve plasticity is equal to zero ($D_\phi (\tilde{R})=0$) if the non-plastic growth scalar is equal to the scaled resource density ($\zeta = f(\tilde{R})$) or if the term between square brackets is equal to zero. Similarly, the selection gradient for the non-plastic growth scalar is zero ($D_\zeta (\tilde{R})$=0) if the growth curve plasticity is equal to one ($\phi =1$) or if the term between squared brackets is equal to zero. Setting the term between square brackets equal to zero thus yields a manifold at which the isoclines for the growth curve plasticity and non-plastic growth scalar overlap as long as there are no additional costs for maintaining a plastic or non-plastic growth rate.

Deriving the isoclines becomes somewhat more complicated if additional costs for maintaining a plastic or a non-plastic growth curve are involved ($c_p \ne 0$). It is at least clear that costs increasing with plasticity ($c_g=1$) decrease the selection gradient for growth curve plasticity ($D_\phi (\tilde{R})$), while costs decreasing with growth curve plasticity ($c_p<0$) increase the selection gradient for growth curve plasticity ($D_\phi (\tilde{R})$).

We can also derive the derivative of the lifetime reproductive output with respect to the resource density:

$$\begin{aligned}\frac{\partial LRO(\tilde{R})}{\partial \tilde{R}} = &\frac{\partial LRO(\tilde{R})}{\partial f(\tilde{R})} \frac{\partial f(\tilde{R})}{\partial \tilde{R}} \\ \frac{\partial LRO(\tilde{R})}{\partial f(\tilde{R})} = &\frac{r_F \ell _\infty }{\kappa } \int _{\tilde{a_J}}^{a_{max}} \left( 2 \phi \kappa \left( 1-e^{-r_B (1 - c_t) a}\right) F_r(\tilde{R}) + (1-\phi \kappa ) \tilde{\ell }(a) \right) \tilde{\ell }(a) e^{-\mu _b a} da + \frac{ r_F \phi \ell _\infty \left( \ell _J - \ell _b\right) F_r(\tilde{R}) \ell _J^2 e^{-\mu _b a_J} }{ r_B (1 - c_t) \left( \left( \phi f(\tilde{R}) + (1-\phi ) \zeta \right) \ell _\infty - \ell _b \right) \left( \left( \phi f(\tilde{R}) + (1-\phi ) \zeta \right) \ell _\infty - \ell _J \right) } \\ \frac{\partial f(\tilde{R})}{\partial \tilde{R}} = & \frac{R_h}{\left( \tilde{R} + R_h\right) ^2} \end{aligned}$$

(18)

All terms in the derivative of the lifetime reproductive output with respect to the resource density in equilibrium are positive. This shows that an increase in resource density will always result in an increase in the lifetime reproductive output of an individual.

Now we will consider the change in resource density ($\tilde{R}$), growth curve plasticity ($\phi$) and non-plastic growth scalar ($\zeta$) over evolutionary time ($\tau$). We assume that ecological time is relatively fast compared to evolutionary time and therefore assume that the population is always in ecological equilibrium and therefore the lifetime reproductive output is always equal to one ($\tilde{LRO} = 1$). As a consequence, the lifetime reproductive output does not change over evolutionary time and changes in the resource density, growth curve plasticity and non-plastic growth scalar are always due to evolutionary change:

$$\begin{aligned} \begin{aligned} \frac{d \tilde{LRO}}{d \tau } =&\frac{\partial LRO(\tilde{R})}{\partial \tilde{R}} \frac{d \tilde{R}}{d\tau } + \frac{\partial LRO(\tilde{R})}{\partial \phi } \frac{d \phi }{d\tau } =0 \\ \frac{d \tilde{LRO}}{d \tau } =&\frac{\partial LRO(\tilde{R})}{\partial \tilde{R}} \frac{d \tilde{R}}{d\tau } + \frac{\partial LRO(\tilde{R})}{\partial \zeta } \frac{d \zeta }{d\tau } =0 \end{aligned} \end{aligned}$$

(19)

We can rearrange these expressions using the chain rule and the inverse function theorem:

$$\begin{aligned} \begin{aligned} \frac{d \tilde{R}}{d \phi } =&\frac{\frac{d \tilde{R}}{d \tau }}{\frac{d \phi }{d\tau }} = - \frac{1}{\frac{\partial LRO(\tilde{R})}{\partial \tilde{R}}} \frac{\partial LRO(\tilde{R})}{\partial \phi } \\ \frac{d \tilde{R}}{d \zeta } =&\frac{\frac{d \tilde{R}}{d \tau }}{\frac{d \zeta }{d\tau }} = - \frac{1}{\frac{\partial LRO(\tilde{R})}{\partial \tilde{R}}} \frac{\partial LRO(\tilde{R})}{\partial \zeta } \end{aligned} \end{aligned}$$

(20)

Because the derivative of the lifetime reproductive output with respect to the resource density is always positive, these expressions show that a change in resource density due to a shift in a trait value is opposite to the change in lifetime reproductive output. The isoclines studied in this article occur at a maximum of the lifetime reproductive output with respect to the trait value of interest. This maximum in lifetime reproductive output thus corresponds with a minimum in resource density. This shows that evolution in this system minimizes the resource density in the system which can only occur through maximizing the consumption by the consumer population.

Costs as part of the somatic maintenance

Fig. 4

Isoclines for the evolution of the growth curve plasticity ($\phi$) and the non-plastic growth scalar ($\zeta$) with costs increasing with growth curve plasticity ($c_g=1, c_p=0.4$), incorporated as an increase in somatic maintenance costs. Blue and red lines represent evolutionary isoclines for the growth curve plasticity ($\phi$) and the non-plastic growth scalar ($\zeta$) respectively. Solid lines represent evolutionary isoclines that are convergent and evolutionary stable for the parameter under consideration. Dashed lines represent evolutionary isoclines that are evolutionary neutral for the parameter under consideration. Incorporating costs as an increase in somatic maintenance results in the same evolutionary patterns as costs incorporated as decreased conversion efficiency (Fig. 2)

Fig. 5

Isoclines for the evolution of the growth curve plasticity ($\phi$) and the non-plastic growth scalar ($\zeta$) with costs decreasing with growth curve plasticity ($c_g=0, c_p=0.4$), incorporated as an increase in somatic maintenance costs. Blue and red lines represent evolutionary isoclines for the growth curve plasticity ($\phi$) and the non-plastic growth scalar ($\zeta$) respectively. Solid lines represent evolutionary isoclines that are convergent and evolutionary stable for the parameter under consideration. Dashed lines represent evolutionary isoclines that are evolutionary neutral for the parameter under consideration. Incorporating costs as an increase in somatic maintenance results in the same evolutionary patterns as costs incorporated as decreased conversion efficiency (Fig. 3)

It could be argued that costs for plasticity scale with individual body mass and therefore arise as a part of the somatic maintenance costs. The energy dynamics without starvation could then be described as:

$$\begin{aligned} \frac{d \ell ^3}{dt} = \gamma _m \left( \kappa \alpha \left( \phi f(R) + (1-\phi ) \zeta \right) \ell ^2 - b (1+c_t) \ell ^3 \right) \end{aligned}$$

(21)

This incorporation of additional costs for plasticity results in a less intuitive implementation of the costs in the individual growth functions, as the maintenance costs both affect the asymptotic size as well as the time constant for growth.

$$\begin{aligned} \frac{d \ell }{d a} = (1+c_t) r_B \left( \left( \phi f(R) + (1-\phi ) \zeta \right) \frac{\ell _\infty }{(1+c_t) } - \ell \right) \end{aligned}$$

(22)

This results in the following equation for the length at age in equilibrium:

$$\begin{aligned} \tilde{\ell }(a) = \ell _b e^{-(1+c_t) r_B a} + \left( \phi f(R) + (1-\phi ) \zeta \right) \left( 1- e^{-(1+c_t) r_B a} \right) \frac{\ell _\infty }{1+c_t} \end{aligned}$$

(23)

From this expression we can also derive the new expression for the age at maturation under equilibrium conditions:

$$\begin{aligned} \tilde{a_J} = \frac{1}{(1 + c_t) r_B} \ln \left( \frac{\left( \phi f(\tilde{R}) + (1-\phi ) \zeta \right) \ell _\infty - (1 + c_t) \ell _b}{ \left( \phi f(\tilde{R}) + (1-\phi ) \zeta \right) \ell _\infty - (1 + c_t) \ell _J} \right) \end{aligned}$$

(24)

Because maintenance costs are only paid after the division of energy between somatic processes and reproduction, the equation for the energy surplus of reproduction remains the same:

$$\begin{aligned} F_r(\tilde{R})= \left( \phi \frac{(1-\kappa ) f(\tilde{R})}{\kappa } + (1-\phi ) \left( \frac{f(\tilde{R})}{\kappa } - \zeta \right) \right) \ell _\infty \end{aligned}$$

(25)

This again can be combined with the expression for the lifetime reproductive output:

$$\begin{aligned} LRO(\tilde{R}) = r_F F_r(\tilde{R}) \int _{\tilde{a_J}}^{a_{max}} \tilde{\ell }(a)^2 e^{-\mu _b a} da \end{aligned}$$

(26)

From this model we can derive a new expression for the selection gradient of the degree of growth curve plasticity ($\phi$) and the non-plastic growth scalar ($\zeta$) (Eqs. 27 and 28).

If we compare these selection gradients to the selection gradients for the situation in which additional costs for maintaining plasticity only affect the growth scalar (Eq. 17), it is clear that the selection gradient for the non-plastic growth scalar is the same except for the new incorporation of the plasticity costs ($c_t$). Similarly, the first term in the selection gradient for the level of growth curve plasticity is the same except for the new location of the plasticity costs (16). The second term from the selection gradient for growth curve plasticity has an opposite sign compared to the selection gradient in the main article, because the effect of the plasticity costs on the growth scalar changed sign. This new formulation adds a third term, which incorporates the effects of costs for growth curve plasticity on the asymptotic size.

We can create the analogues of Figs. 2 and 3 with this alternative model formulation (see Figs. 4 and 5). Comparison shows that costs incorporated as increased somatic maintenance costs show the same evolutionary patterns as costs incorporated as decreased conversion efficiency.

$$\begin{aligned} D_\phi (\tilde{R}) = &\frac{ r_F \left( f(\tilde{R}) - \zeta \right) \ell _\infty }{ T_r(\tilde{R}) (1+c_t) LRO_m(\tilde{R})} \left[ \int _{\tilde{a_J}}^{a_{max}} \left( 2 \left( 1 - e^{-(1+c) r_B a} \right) F_r(\tilde{R}) - (1+c_t) \tilde{\ell }(a) \right) \tilde{\ell }(a) e^{-\mu _b a} da + \frac{ (1+c_t) \left( \ell _J - \ell _b \right) F_r(\tilde{R}) \ell _J^2 e^{-\mu \tilde{a_J}} }{ r_B \left( \left( \phi f(\tilde{R}) + (1-\phi ) \zeta \right) \ell _\infty - (1 + c_t) \ell _b \right) \left( \left( \phi f(\tilde{R}) + (1-\phi ) \zeta \right) \ell _\infty - (1 + c_t) \ell _J \right) } \right] \\ & + \frac{\left( 2 c_g - 1 \right) c_p r_F F_r(\tilde{R})}{ T_r(\tilde{R}) LRO_m(\tilde{R})} \left( \frac{\ell _J^2 \tilde{a_J} e^{-\mu \tilde{a_J} }}{(1 + c_t)} + 2 r_B \int _{\tilde{a_J}}^{a_{max}} \left( \left( \phi f(\tilde{R)} + (1-\phi ) \zeta \right) \frac{\ell _\infty }{(1+c_t)} - \ell _b \right) \tilde{\ell }(a) e^{-\mu a} e^{-(1+c) r_B a} a da \right) \\& - \frac{ \left( 2 c_g - 1 \right) c_p r_F F_r(\tilde{R}) \left( \phi f(\tilde{R)} + (1-\phi ) \zeta \right) \ell _\infty }{ T_r(\tilde{R}) (1+c_t)^2 LRO_m(\tilde{R})} \left[ \int _{\tilde{a_J}}^{a_{max}} 2 \left( 1 - e^{-(1+c) r_B a} \right) \tilde{\ell }(a) e^{-\mu a} da + \frac{ (1 + c_t) \left( \ell _J - \ell _b \right) \ell _J^2 e^{-\mu \tilde{a_J}} }{ r_B \left( \left( \phi f(\tilde{R}) + (1-\phi ) \zeta \right) \ell _\infty - (1 + c_t) \ell _b \right) \left( \left( \phi f(\tilde{R}) + (1-\phi ) \zeta \right) \ell _\infty - (1 + c_t) \ell _J \right) } \right] \end{aligned}$$

(27)

$$\begin{aligned} D_\zeta (\tilde{R})= & \frac{r_F \left( 1 - \phi \right) \ell _\infty }{ T_r(\tilde{R}) (1+c_t) LRO_m(\tilde{R})} \left[ \int _{\tilde{a_J}}^{a_{max}} \left( 2 \left( 1-e^{-r_B (1 + c_t) a}\right) F_r(\tilde{R}) - (1+c_t) \tilde{\ell }(a) \right) \tilde{\ell }(a) e^{-\mu _b a} da + \frac{ (1+c_t) \left( \ell _J-\ell _b \right) F_r(\tilde{R}) \ell _J^2 e^{-\mu _b \tilde{a_J}}}{r_B \left( \left( \phi f(\tilde{R}) + (1-\phi ) \zeta \right) \ell _\infty -\ell _b \right) \left( \left( \phi f(\tilde{R}) + (1-\phi ) \zeta \right) \ell _\infty -\ell _J \right) } \right] \end{aligned}$$

(28)

Appendix B: Additional figures

Fig. 6

Pairwise Invasibility Plots (PIPs) for the non-plastic growth scalar ($\zeta$) at different parameter combinations on the isoclines for growth curve plasticity in Figs. 1 to 3. These PIPs only consider evolution for the non-plastic growth scalar and assume a constant value for the growth curve plasticity ($\phi$). Grey lines indicate instances at which the invasion fitness of the mutation is equal to zero ($S_m(\tilde{R})=0$), while the invasion fitness is positive ($S_m(\tilde{R})>0$) in black areas and negative ($S_m(\tilde{R})<0$) in white areas. In all PIPs a singular strategy arises at the intersection of the grey lines. The positive invasion fitness just to the left and right of the singular strategies indicates that the singular strategy can invade a resident population. The negative invasion fitness just above and below the singular strategy indicates that the singular strategy is invasion stable and is therefore an evolutionary endpoint

Fig. 7

Pairwise Invasibility Plots (PIPs) for the growth curve plasticity ($\phi$) at different parameter combinations on the isoclines for growth curve plasticity in Figs. 1 to 3. These PIPs only consider evolution for the growth curve plasticity and assume a constant value for the non-plastic growth scalar ($\zeta$). Grey lines and areas indicate instances at which the invasion fitness of the mutation is equal to zero ($S_m(\tilde{R})=0$), while the invasion fitness is positive ($S_m(\tilde{R})>0$) in black areas and negative ($S_m(\tilde{R})<0$) in white areas. In the two entirely grey PIPs, all strategies have the same fitness and the trait value in the population might change due to drift. In all other PIPs a singular strategy arises at the intersection of the grey lines. The positive invasion fitness just to the left and right of the singular strategies indicates that the singular strategy can invade a resident population. The negative invasion fitness just above and below the singular strategy indicates that the singular strategy is invasion stable and is therefore an evolutionary endpoint