Exact and numerical solutions of higher-order fractional partial differential equations: A new analytical method and some applications

Abstract

In this paper, the solution methodology of higher-order linear fractional partial deferential equations (FPDEs) as mentioned in eqs (1) and (2) below in Caputo definition relies on a new analytical method which is called the Laplace-residual power series method (L-RPSM). The main idea of our proposed technique is to convert the original FPDE in Laplace space, and then apply the residual power series method (RPSM) by using the concept of limit to obtain the solution. Some interesting and important numerical test applications are given and discussed to illustrate the procedure of our method, and also to confirm that this method is simple, understandable and very fast for obtaining the exact and approximate solutions (ASs) of FPDEs compared with other methods such as RPSM, variational iteration method (VIM), homotopy perturbation method (HPM) and Adomian decomposition method (ADM). The main advantage of the proposed method is its simplicity in computing the coefficients of terms of series solution by using only the concept of limit at infinity and not as the other well-known analytical method such as, RPSM that need to obtain the fractional derivative (FD) each time to determine the unknown coefficients in series solutions, and VIM, ADM, or HPM that need the integration operators which is difficult in fractional case.

1 Introduction and basic concepts

The fractional differential equations (FDEs) and fractional partial differential equations (FPDEs) have become more popular nowadays due to their numerous applications in areas of physics and engineering. Additionally, most of the solutions of FPDEs and FDEs do not have exact solutions (ESs), and therefore approximate solutions (ASs) are used extensively.

In recent decades, FDEs have been focussing on several models and applications such as in signal processing, biological population, space–time, dynamical systems, electrical circuits, control theory etc [1,2,3,4]. Many researchers have used various methods to solve FPDEs, for example, Zhang and Zhang [3] proposed a new direct algebraic method named fractional subequation method for solving FPDEs based on the homogeneous balance principle. Meng [4] proposed a new approach for solving time biological population and ($4+1$)-dimensional space–time Fokas FPDEs based on a nonlinear fractional complex transformation and the general Riccati equation. Behzad et al [5] applied an analytical generalised exponential rational function technique to acquire wave solutions of a PDE involving a local fractional derivative (FD). Khalid et al [6] used a computational approach for solving time-fractional differential equation via spline functions and Bonyah et al [7] established the existence and uniqueness of solution of the fractional corona virus model by using the Banach fixed point theorem approach. Variational iteration method (VIM) [8, 9], homotopy perturbation method (HPM) [10,11,12,13,14,15], Adomian decomposition method (ADM) [9] and residual power series method (RPSM) [16,17,18,19,20,21,22] are also applied to solve problems in science and engineering.

In our previous work [23], we proposed the Laplace-residual power series method (L-RPSM), which is an analytical method, to increase the efficiency of the RPSM and to solve linear and nonlinear FDEs. The L-RPSM is based on employing the Laplace transform (LT) on the specific equation and then applying a particular expansion to indicate the solution of the FDE in the new space. Lastly, the obtained solution is transformed into the original space by employing the inverse LT to exhibit the solution of the required FDE. This new method (L-RPS) is guaranteed to have higher efficiency and more simplicity than RPSM for creating the ESs and ASs to the linear and nonlinear neutral FDEs [23], a class of hyperbolic system of time-FPDEs with variable coefficients [24], nonlinear time-dispersive FPDEs [25], time-fractional nonlinear water wave PDE [26] and fuzzy quadratic Riccati differential equations [27].

The main aims of this work can be summarised as follows: First, we propose a new L-RPSM to solve the following linear FPDE [9, 10, 28]:

$$\begin{aligned} \begin{aligned}&\frac{\partial ^\alpha u(x,t)}{\partial t^\alpha } +\sum _{c=0}^{z}{a_c(x)\frac{\partial ^c u(x,t)}{\partial x^c}}=g(x,t), \end{aligned} \end{aligned}$$

(1)

subject to:

$$\begin{aligned} \frac{\partial ^j u(x,0)}{\partial t^j}=\phi _j(x),\ j=0,1,\ldots , m-1, \end{aligned}$$

(2)

where $x\in {\mathbb {R}},\ 0\le m-1 < \alpha \le m,\ m \in {\mathbb {N}}$, $\alpha$ is the order of the Caputo FD, $a_i (i=0,1,2,\ldots , z)$ all are continuous function, and $\phi _j(x),\ g(x,t)$ are the analytic functions on ${\mathbb {R}}$. Secondly, several attractive numerical test applications such as are given: time-fractional wave (T-FW), space-fractional telegraph (S-FT), time-fractional vibration (T-FV), time-fractional Swift–Hohenberg (T-FSH) and time-fractional Navier–Stokes (T-FNS) equations. Finally, we analyse the solutions of eqs (1) and (2) by comparing our suggested method with other methods such as HPM, VIM and ADM and we show that our method is simple, understandable and very fast for obtaining the ESs and ASs for FPDEs with higher orders.

Now, we introduce some basic concepts and theories related to the FDs and LT that are used to construct the L-RPS solution for the FPDEs. For a more detailed discussion, the reader is referred to [29,30,31,32,33,34].

DEFINITION 1

The Caputo $\alpha$-derivative of the multivariable function u(x, t) is defined as [20, 22, 23]

$$\begin{aligned}&D_t^\alpha u(x,t) \nonumber \\&\quad =\frac{\partial ^\alpha u(x,t)}{\partial t^\alpha }\nonumber \\&\quad ={\left\{ \begin{array}{ll} J_t^{m-\alpha } \left( \dfrac{\partial ^m u(x,t)}{\partial t^m } \right) ,&{} m-1< \alpha <m,\\ \dfrac{\partial ^m u(x,t)}{\partial t^m }, &{} \alpha =m \in {\mathbb {N}}, \end{array}\right. } \end{aligned}$$

(3)

where $\alpha \in (m-1,m], m \in {\mathbb {N}}$ and $J^\beta _t$ is the Riemann–Liouville with $\beta$ order that is defined as [20, 22, 23]

$$\begin{aligned}&J^{\beta }_tu = \frac{\mathrm {1}}{{\varGamma }\left( \beta \right) }\int ^t_{t_0}{{\left( t\mathrm {-}\tau \right) }^{\beta \mathrm {-}\mathrm {1}}}u\left( x,\tau \right) \mathrm {d}\tau \mathrm {,\ } \quad \nonumber \\&\quad t> \tau \ge t_0 \ge 0{,\ } \beta >0, \nonumber \\&J^{0 }_tu = u\left( x,t \right) . \end{aligned}$$

(4)

The following lemma includes some properties related to the $D^\alpha _t$ operator.

Lemma 1

For $t \ge 0 , \gamma >-1$, $\alpha \in (m-1,m], m \in {\mathbb {N}}$ and $c \in {\mathbb {R}}$. Then

• 1. $D^\alpha _t t^\gamma$=$\dfrac{\Gamma {(\gamma +1)}}{\Gamma {(\gamma +1-\alpha )}}t^{\gamma -\alpha }$.

• 2. $D^\alpha _t c= 0$.

• 3. $D^\alpha _t J^\alpha _t u(x,t)= u(x,t)$.

• 4. $J^\alpha _t D^\alpha _t u(x,t) = u(x,t)- \sum \limits _{j=0}^{m-1}{u_t^{(j)}(x,0^+){\dfrac{t^j}{j!}}}$.

DEFINITION 2

Let u(x, t) be a multivariable function on $I_1 \times I_2 \times [0, \infty$) and of exponential order (EO) $\delta$, then the LT of u(x, t) is

$$\begin{aligned} U(x,s)={\mathcal {L}}[u(x,t)]:=\int ^\infty _0{e^{-st} u(x,t) \mathrm {d}t},\quad s > \delta ,\nonumber \\ \end{aligned}$$

(5)

and the inverse LT of U(x, y, s) is given by

$$\begin{aligned}&u(x,t)={\mathcal {L}}^{-1}[U(x,s)]:=\int ^{c-i\infty }_{c+i\infty }{e^{st} U(x,s)\mathrm {d}s},\nonumber \\&c = Re(s)>c_0. \end{aligned}$$

(6)

The next lemma illustrates some basic and important properties of our workers related to the LT.

Lemma 2

Suppose that u(x, t) and v(x, t) are multivariable functions on $[0,\infty )$ and of EO $\delta$, $U(x,s)={\mathcal {L}}[u(x,t)]$, $V(x,s)={\mathcal {L}}[v(x,t)]$, $\alpha \in (m-1,m], k, m \in {\mathbb {N}}$ and $D^{n\alpha }_t$ means $D^\alpha _t . D^\alpha _t \ldots D^\alpha _t$ (n times). Then

• 1. $\underset{s\rightarrow \infty }{lim}sU(x,s)=u(x,0)$.

• 2. $\begin{aligned}{\mathcal {L}}[D^k_t u(x,t)]&=s^k U(x,s)\\ {}&\quad -\sum _{j=0}^{k-1}{s^{k-j-1}}D^j_tu(x,0).\end{aligned}$

• 3. $\begin{aligned}{\mathcal {L}}[D^\alpha _t u(x,t)]&=s^\alpha U(x,s)\\ {}&\quad -\sum _{j=0}^{m-1}{s^{\alpha -j-1}}D^j_tu(x,0).\end{aligned}$

• 4. $\begin{aligned} {\mathcal {L}}[D^k_tD^{\alpha }_t u(x,t)]&=s^{\alpha +k} U(x,s)\\ {}&\quad -\sum _{j=0}^{m-1}{s^{\alpha +k-j-1}}D^{j}_tu(x,0)\\ {}&\quad -\sum _{j=0}^{k-1}{s^{k-j-1}}D^j_tD^{\alpha }_tu(x,0). \end{aligned}$

• 5. $\begin{aligned} {\mathcal {L}}[D^k_tD^{2\alpha }_t u(x,t)]&=s^{2\alpha +k} U(x,s)\\ {}&\quad -\sum _{j=0}^{m-1}{s^{2\alpha +k-j-1}}D^j_tu(x,0)\\ {}&\quad -\sum _{j=0}^{m-1}{s^{\alpha +k-j-1}}D^{j}_tD^\alpha _tu(x,0)\\ {}&\quad -\sum _{j=0}^{k-1}{s^{k-j-1}}D^j_tD^{2\alpha }_tu(x,0). \end{aligned}$

We can find the proofs of the parts from (1) to (3) in refs [23, 30,31,32,33,34,35]. The proof of parts (4) and (5) are trivial by using the parts (2) and (3) in the above lemma.

Theorem 1

[36]. Assume that u(x, t) has a multiple fractional power series (FPS) representation at $t=t_0$ of the following form:

$$\begin{aligned}&u(x,t)=\sum ^{\infty }_{n=0}\sum ^{m-1}_{j=0}f_{nj}(x)(t-t_ 0)^{j+n\alpha },\ \nonumber \\&t_0\le t < t_0+R. \end{aligned}$$

(7)

If $u(x,t)\in C[t_0,t_0+R), D^{n\alpha }_{t_0} u(x,t)\in C(t_0,t_0+R)$, and $D^{n\alpha }_{t_0}u(x,t)$ can be differentiated $(m-1)$ times on $(t_0, t_0+R)$ for $n=0,1,2,\ldots$, where $0\le m-1 < \alpha \le m$. Then the coefficients $f_{nj}(x)$ of eq. (7) are given by the formula

$$\begin{aligned} f_{nj}(x)= & {} \frac{D^j_{t_0}D^{n\alpha }_{t_0}u(x,t_0)}{\Gamma (j+n\alpha +1)},\quad n=0,1,\ldots , j\nonumber \\= & {} 0,1,\ldots ,m-1. \end{aligned}$$

(8)

Remark 1

Different from classical (or integer-order) derivative, there are several kinds of definitions for FDs. These definitions are generally not equivalent with each other, among which the Riemann—Liouville and the Caputo FDs are two of the most important ones in applications [37]. The Risez FD is a linear representation of the left Riemann–Liouville FD and right Riemann–Liouville FD. A close relationship exists between the Riemann–Liouville FD and the Caputo FD. The Riemann–Liouville FD can be converted to the Caputo FD under some regularity assumptions of the function [31, 37]. In FPDEs, the time-FDs are commonly defined using the Caputo FD. The main reason lies in that the Riemann–Liouville approach needs initial conditions containing the limit values of Riemann–Liouville FD at the origin of time $t = 0$, whose physical meanings are not very clear. However, in cases with the time-fractional Caputo derivative, the initial conditions take the same form as that for integer-order differential equations, namely, the initial values of integer-order derivatives of functions at the origin of time $t = 0$ [28, 37, 38]. In other words, comparing Caputo fractional definition with the Riemann–Liouville one, functions which are derivable in the Caputo sense are much fewer than those which are derivable in the Riemann–Liouville sense. In general, the main advantage of derivatives and integrals of fractional order is modelling of the physical system with full memory effect [39]. Also, real world problems associated with fractional operators are able to give better physical description of the model than the derivatives and integrals of classical nature. The fractional model represents the system with more efficient, complex nonlinear phenomena with high-order dynamics. It happens mainly due to three reasons: (i) There is freedom to select any arbitrary order of fractional operators whereas it is not applicable to standard order derivative, (ii) since classical order derivative is local in characteristics, it does not describe the whole memory and physical aspects of the model whereas fractional-order derivative is non-local in nature, and hence it narrates the complete memory and physical behaviour of the system and (iii) useful analysis of fractional blood alcohol model with composite FD [39].

2 Fractional multiple of new form of Taylor’s series

In this section, we introduce a fractional multiple new form of Taylor’s series in Laplace space that will be used to build a series solution for the linear FPDEs in §3.

Theorem 2

Assume that $U(x,s)={\mathcal {L}}[u(x,t)]$ has a multiple FPS as follows:

$$\begin{aligned} U(x,s)= & {} \sum _{n=0}^{\infty } {\sum _{k=0}^{m-1} {\frac{f_{nk}(x)}{s^{k+n\alpha +1}}}},\quad 0\le m-1 < \alpha \le m, \nonumber \\&m \in {\mathbb {N}}. \end{aligned}$$

(9)

Then, the coefficients, $f_{nk}(x)$ of eq. (9) are given by the formula

$$\begin{aligned}&f_{nk}(x) \nonumber \\&= {\left\{ \begin{array}{ll} D^k_tu(x,0), &{} k=0,1, \ldots , m-1, n=0 ,\\ D^k_tD^{n\alpha }_tu(x,0), &{} k=0,1, \ldots , \\ {} &{} m-1,n=1,2,\ldots \end{array}\right. } \end{aligned}$$

(10)

where $D^{n\alpha }_t$ means $D^\alpha _t . D^\alpha _t \ldots D^\alpha _t$ (n times).

Proof

Let U(x, s) be a function that can be presented as in eq. (9). If we multiply both sides of eq. (9) by s and take the limit as $s \rightarrow \infty$, we get $f_{00}(x)=\lim _{s \rightarrow \infty } sU(x,s)=u(x,0)$.

Now, multiplying eq. (9) by $s^2$ leads to the following equation of $f_{01}(x)$:

$$\begin{aligned}&f_{01}(x)\nonumber \\&\quad =s^2U(x,s)-su(x,0)-\frac{f_{02}}{s}\nonumber \\&\qquad -\frac{f_{03}}{s^2}- \cdots -\frac{f_{0(m-1)}}{s^{m-2}}\nonumber \\&\qquad -\sum _{n=1}^{\infty } {\sum _{k=0}^{m-1} {\frac{f_{nk}(x)}{s^{k+n\alpha -1}}}}. \end{aligned}$$

(11)

Take the limit as $s \rightarrow \infty$ to eq. (11). Through part (2) of Lemma 2, it is clear that

$$\begin{aligned} f_{01}(x)= & {} \underset{s\rightarrow \infty }{\mathrm{lim}}( s^2U(x,s)-su(x,0))\nonumber \\= & {} \underset{s\rightarrow \infty }{\mathrm{lim}}s( sU(x,s)-u(x,0))\nonumber \\= & {} \underset{s\rightarrow \infty }{\mathrm{lim}}s({\mathcal {L}}[D_tu(x,t)])=D_tu(x,0). \end{aligned}$$

(12)

Now, by multiplying eq. (9) by $s^3$ and taking the limit as $s \rightarrow \infty$, we have

$$\begin{aligned} f_{02}(x)= & {} \underset{s\rightarrow \infty }{\mathrm{lim}}( s^3U(x,s)-s^2u(x,0)-sD_tu(x,0))\nonumber \\ {}= & {} \underset{s\rightarrow \infty }{\mathrm{lim}}s(s^2U(x,s)-su(x,0)-D_tu(x,0))\nonumber \\ {}= & {} \underset{s\rightarrow \infty }{\mathrm{lim}}s({\mathcal {L}}[D^2_tu(x,t)])=D^2_tu(x,0). \end{aligned}$$

(13)

The pattern is clear, if we multiply $s^k$ on the series in eq. (9) and take the limit as $s \rightarrow \infty$ in the resulting equation, then we obtain

$$\begin{aligned} f_{0k}(x)=D^k_tu(x,0). \end{aligned}$$

(14)

Back to eq. (9), multiplying $s^{\alpha +1}$ on both sides, we get

$$\begin{aligned} s^{\alpha +1}U(x,s)= & {} \sum _{k=0}^{m-1}{s^{\alpha -k}D^k_tu(x,0)}+f_{10}(x)+\frac{f_{11}(x)}{s} \nonumber \\&+\frac{f_{12}(x)}{s^2}+\cdots +\frac{f_{1(m-1)}(x)}{s^{m-1}}\nonumber \\&+\sum _{n=2}^{\infty } {\sum _{k=0}^{m-1} {\frac{f_{nk}(x)}{s^{k+(n-1)\alpha }}}}. \end{aligned}$$

(15)

By taking the limit as $s \rightarrow \infty$ in eq. (15), then according to part (3) of Lemma 2, we get

$$\begin{aligned} f_{10}(x)= & {} \underset{s \rightarrow \infty }{\mathrm{lim}}\left( s^{\alpha +1}U(x,s)-\sum _{k=0}^{m-1}{s^{\alpha -k}D^k_tu(x,0)}\right) \nonumber \\ {}= & {} \underset{s \rightarrow \infty }{\mathrm{lim}}s\left( s^{\alpha }U(x,s)-\sum _{k=0}^{m-1}{s^{\alpha -k-1}D^k_tu(x,0)}\right) \nonumber \\ {}= & {} \underset{s \rightarrow \infty }{\mathrm{lim}}s({\mathcal {L}}[D^\alpha _t u(x,t)])=D^\alpha _t u(x,0). \end{aligned}$$

(16)

On the other hand, multiplying eq. (9) by $s^{\alpha +2}$, and taking the limit as $s \rightarrow \infty$, according to part (4) of Lemma 2, we have

$$\begin{aligned} f_{11}(x)= & {} \underset{s \rightarrow \infty }{\mathrm{lim}}\Bigg (s^{\alpha +2}U(x,s)-\sum _{k=0}^{m-1}{s^{\alpha -k+1}D^k_t u(x,0)}\nonumber \\&-sD^\alpha _t u(x,0)\Bigg )\nonumber \\ {}= & {} \underset{s \rightarrow \infty }{\mathrm{lim}} s\Bigg (s^{\alpha +1}U(x,s)-\sum _{k=0}^{m-1}{s^{\alpha -k}D^k_t u(x,0)}\nonumber \\&-D^\alpha _t u(x,0)\Bigg )\nonumber \\ {}= & {} \underset{s \rightarrow \infty }{\mathrm{lim}} s({\mathcal {L}}[D_t D^\alpha _t u(x,t)])=D_t D^\alpha _t u(x,0).\nonumber \\ \end{aligned}$$

(17)

In the same manner, by multiplying eq. (9) by $s^{\alpha +3}$ and taking the limit as $s \rightarrow \infty$, we have

$$\begin{aligned} f_{12}(x)= & {} \underset{s \rightarrow \infty }{\mathrm{lim}} \Bigg (s^{\alpha +3}U(x,s)-\sum _{k=0}^{m-1}{s^{\alpha -k+2}D^k_t u(x,0)}\nonumber \\&-s^2D^\alpha _t u(x,0)-sD_tD^\alpha _tu(x,0)\Bigg )\nonumber \\ {}= & {} \underset{s \rightarrow \infty }{\mathrm{lim}} s\Bigg (s^{\alpha +2}U(x,s)-\sum _{k=0}^{m-1}{s^{\alpha -k+1}D^k_t u(x,0)}\nonumber \\&-sD^\alpha _t u(x,0)-D_tD^\alpha _tu(x,0)\Bigg )\nonumber \\ {}= & {} \underset{s \rightarrow \infty }{\mathrm{lim}} s({\mathcal {L}}[D^2_t D^\alpha _t u(x,t)])=D^2_t D^\alpha _t u(x,0).\nonumber \\ \end{aligned}$$

(18)

Similar to the previous pattern, we can obtain

$$\begin{aligned} \begin{aligned} f_{1k}(x)=D^k_t D^\alpha _t u(x,0). \end{aligned} \end{aligned}$$

(19)

Multiplying $s^{2\alpha +1}$ on the series expansion in eq. (9), one can get

$$\begin{aligned}&s^{2\alpha +1}U(x,s)\nonumber \\&\quad =\sum _{k=0}^{m-1}{s^{2\alpha -k}D^k_tu(x,0)}+\sum _{k=0}^{m-1}{s^{\alpha -k}D^k_tD^\alpha _tu(x,0)}\nonumber \\&\qquad +f_{20}(x)+\frac{f_{21}(x)}{s}+\cdots +\frac{f_{2(m-1)}(x)}{s^{m-1}}\nonumber \\&\qquad +\sum _{n=3}^{\infty } {\sum _{k=0}^{m-1} {\frac{f_{nk}(x)}{s^{k+(n-2)\alpha }}}}. \end{aligned}$$

(20)

The limit as $s \rightarrow \infty$ into eq. (20) gives

$$\begin{aligned} f_{20}(x)= & {} \underset{s \rightarrow \infty }{\mathrm{lim}} \Bigg (s^{2\alpha +1}U(x,s)-\sum _{k=0}^{m-1}{s^{2\alpha -k}D^k_tu(x,0)}\nonumber \\&-\sum _{k=0}^{m-1}{s^{\alpha -k}D^k_tD^\alpha _tu(x,0)}\Bigg )\nonumber \\ {}= & {} \underset{s \rightarrow \infty }{\mathrm{lim}} s\Bigg (s^{2\alpha }U(x,s)-\sum _{k=0}^{m-1}{s^{2\alpha -k-1}D^k_tu(x,0)}\nonumber \\&-\sum _{k=0}^{m-1}{s^{\alpha -k-1}D^k_tD^\alpha _tu(x,0)}\Bigg )\nonumber \\ {}= & {} \underset{s \rightarrow \infty }{\mathrm{lim}} s({\mathcal {L}}[D^{2\alpha }_tu(x,t)])=D^{2\alpha }_tu(x,0). \end{aligned}$$

(21)

Again, by multiplying eq. (9) by $s^{2\alpha +2}$ and taking limit as $s \rightarrow \infty$, we get

$$\begin{aligned} \begin{aligned} f_{21}(x)&=\!\underset{s \rightarrow \infty }{\mathrm{lim}} \Bigg (s^{2\alpha +2}U(x,s)-\!\sum _{k=0}^{m-1}{s^{2\alpha -k+1}D^k_tu(x,0)}\\ {}&\quad -\sum _{k=0}^{m-1}{s^{\alpha -k+1}D^k_tD^\alpha _tu(x,0)}-sD^{2\alpha }_tu(x,0)\Bigg )\\ {}&=\underset{s \rightarrow \infty }{\mathrm{lim}} s\Bigg (s^{2\alpha +1}U(x,s)-\sum _{k=0}^{m-1}{s^{2\alpha -k}D^k_tu(x,0)}\\ {}&\quad -\sum _{k=0}^{m-1}{s^{\alpha -k}D^k_tD^\alpha _tu(x,0)}-D^{2\alpha }_tu(x,0)\Bigg )\\ {}&=\underset{s \rightarrow \infty }{\mathrm{lim}} s({\mathcal {L}}[D_tD^{2\alpha }_tu(x,t)])=D_tD^{2\alpha }_tu(x,0). \end{aligned}\nonumber \\ \end{aligned}$$

(22)

If we multiply $s^{2\alpha +k+1}$ by eq. (9) and take the limit as $s \rightarrow \infty$, we can have the coefficients $f_{2k}(x), k=0,1,2, \ldots , m-1$ of eq. (9) as the following expansion:

$$\begin{aligned} \begin{aligned} f_{2k}(x)&=D^k_tD^{2\alpha }_tu(x,0). \end{aligned} \end{aligned}$$

(23)

Now we can see the pattern completely. However, if we multiply $s^{n\alpha +k+1}$ by both sides of eq. (9) and take the limit as $s \rightarrow \infty$ on the resulting equation, then we get the formula of the coefficients, $f_{nk}(x)$ as in eq. (10).

By substituting the formula of $f_{nk}(x)$ into the series as in eq. (9), we see that if U(x, s) has a multiple FPS expansion, then it must be of the following form:

$$\begin{aligned} U(x,s)=\sum _{n=0}^{\infty } {\sum _{k=0}^{m-1} {\frac{D^k_tD^{n\alpha }_tu(x,0)}{s^{k+n\alpha +1}}}}, \end{aligned}$$

(24)

which is a fractional multiple new form of the Taylor’s series. $\square$

Remark 2

If we take the inverse LT of the multiple FPS as in eq. (9), then we have

$$\begin{aligned} u(x,t)=\sum _{n=0}^{\infty } {\sum _{k=0}^{m-1} {\frac{D^k_tD^{n\alpha }_tu(x,0)}{\Gamma (n\alpha +k+1)}}}t^{n\alpha +k}, \end{aligned}$$

(25)

which corresponds to eq. (7) at $t_0=0$.

Theorem 3

Let $U(x,s)={\mathcal {L}}[u(x,t)]$ be the multiple FPS as in eq. (9). If $|s{\mathcal {L}}[D^{(n+1)\alpha }_t u(x,t)]| \le M(x)$ on $I \times (\delta ,\gamma ]$, then

$$\begin{aligned} |{\mathfrak {R}}_n(x,s)|\le \frac{M(x)}{s^{1+(n+1)\alpha }},\qquad x\in I, \delta <s\le \gamma , \end{aligned}$$

(26)

where ${\mathfrak {R}}_n(x,s)$ is the reminder of the multiple FPE (9).

Proof

Suppose that ${\mathcal {L}}[D^{k\alpha }_t u(x,t)](s)$ is on $I \times (\delta ,\gamma ]$ for $k = 0, 1,\ldots ,n+1$ and

$$\begin{aligned} |s{\mathcal {L}}[D^{(n+1)\alpha }_t u(x,t)]|\le {M(x)}, x\in I, \delta <s\le \gamma .\nonumber \\ \end{aligned}$$

(27)

The definition of the remainder, ${\mathfrak {R}}_n(x,s)$, is

$$\begin{aligned} {\mathfrak {R}}_n(x,s)=U(x,s)-\sum ^{n}_{k=0}\frac{D^{k\alpha }_t u(x,0)}{s^{1+k\alpha }}. \end{aligned}$$

(28)

Multiply both sides of eq. (28) by $s^{1+(n+1)\alpha }$ we get

$$\begin{aligned} s^{1+(n+1)\alpha }{\mathfrak {R}}_n(x,s)= & {} s^{1+(n+1)\alpha }U(x,t)\nonumber \\&\quad -\sum ^{n}_{k=0}{{s^{(n+1-k)\alpha }}D^{k\alpha }_t u(x,0)}\nonumber \\= & {} s\Bigg (s^{(n+1)\alpha }U(x,t)\nonumber \\&\quad -\sum ^{n}_{k=0}{{s^{(n+1-k)\alpha -1}}D^{k\alpha }_t u(x,0)}\Bigg )\nonumber \\= & {} s{\mathcal {L}}[D^{(n+1)\alpha }_t u(x,t)]. \end{aligned}$$

(29)

From eqs (27) and (29) we have $|s^{1+(n+1)\alpha }{\mathfrak {R}}_n(x,s)| \le M(x)$. Hence,

$$\begin{aligned}&-M(x) \le s^{1+(n+1)\alpha }{\mathfrak {R}}_n(x,s) \le M(x), x\in I,\nonumber \\ \quad&\delta <s\le \gamma . \end{aligned}$$

(30)

Thus, we can rewrite eq. (30) to obtain the result as in eq. (26). $\square$

3 Constructing the L-RPSM solution for the linear FPDE

In this section, we use the new L-RPSM to build the solutions of the initial value problem (IVP) as in eqs (1) and (2). According to [23], we first start by applying LT on eq. (1) and using eq. (2), to get

$$\begin{aligned}&s^\alpha U(x,s)-\sum _{j=0}^{m-1}s^{\alpha -j-1}\phi _j(x)\nonumber \\&\quad +\sum _{c=0}^{z}{a_c(x)\frac{\partial ^c U(x,s)}{\partial x^c}}=G(x,s), \end{aligned}$$

(31)

where $U(x,s)={\mathcal {L}}[u(x,t)]$ and $G(x,s)={\mathcal {L}}[g(x,t)]$.

We can rewrite eq. (31) as

$$\begin{aligned}&U(x,s)-\sum _{j=0}^{m-1}\frac{\phi _j(x)}{s^{j+1}}\nonumber \\&\quad +\sum _{c=0}^{z}{s^{-\alpha }a_c(x)\frac{\partial ^c U(x,s)}{\partial x^c}}-\frac{G(x,s)}{s^{\alpha }}=0. \end{aligned}$$

(32)

The L-RPSM expresses the solution of eq. (32) as a multiple FPS expansion as follows:

$$\begin{aligned} U(x,s)=\sum _{j=0}^{m-1}{\frac{f_{0j}(x)}{s^{j+1}}}+\sum _{i=1}^{\infty } {\sum _{j=0}^{m-1} {\frac{f_{ij}(x)}{s^{i\alpha +j+1}}}}, \quad s>0.\nonumber \\ \end{aligned}$$

(33)

By using initial conditions in eq. (2) and referring to eq. (33), one can get $f_{0j}(x)=D^j_tu(x,0)=\phi _j(x), j=0,1,\ldots , m-1$. Hence, the multiple FPS expansion in eq. (33) becomes

$$\begin{aligned} U(x,s)=\sum _{j=0}^{m-1}{\frac{\phi _j(x)}{s^{j+1}}}+\sum _{i=1}^{\infty } {\sum _{j=0}^{m-1} {\frac{f_{ij}(x)}{s^{i\alpha +j+1}}}}, \quad s>0.\nonumber \\ \end{aligned}$$

(34)

Now, let $U_k(x,s)$ be the kth-truncated series of U(x, s). That is

$$\begin{aligned} U_k(x,s)=\sum _{j=0}^{m-1}{\frac{\phi _j(x)}{s^{j+1}}}+\sum _{i=1}^{k} {\sum _{j=0}^{m-1} {\frac{f_{ij}(x)}{s^{i\alpha +j+1}}}}, \quad s>0.\nonumber \\ \end{aligned}$$

(35)

Before applying the L-RPSM for obtaining the form of coefficients $f_{ij}(x)$ in eq. (35), we must define the Laplace residual (LR) function for eq. (32) as follows:

$$\begin{aligned} LRes(x,s)= & {} U(x,s)\nonumber \\&-\sum _{j=0}^{m-1}s^{-j-1}\phi _j(x)-s^{-\alpha }G(x,s)\nonumber \\&+\sum _{c=0}^{z}{s^{-\alpha }a_c(x)\frac{\partial ^c U(x,s)}{\partial x^c}}, s>0 \end{aligned}$$

(36)

and the following kth-truncated LR function:

$$\begin{aligned} LRes_k(x,s)= & {} U_k(x,s)\nonumber \\&-\sum _{j=0}^{m-1}s^{-j-1}\phi _j(x)-s^{-\alpha }G(x,s)\nonumber \\&+\sum _{c=0}^{z}{s^{-\alpha }a_c(x)\frac{\partial ^c U_k(x,s)}{\partial x^c}}. \end{aligned}$$

(37)

As in [23], it is clear that $LRes(x,s)=0$ and $\lim \nolimits _{s\rightarrow \infty } sLRes(x,s)=\lim \nolimits _{s\rightarrow \infty } sLRes_k(x,s)$. In fact, this shows that $\lim \nolimits _{s\rightarrow \infty } s^{i\alpha +j+1}LRes(x,s)=0$ and one can write

$$\begin{aligned} \begin{aligned}&\underset{s \rightarrow \infty }{\mathrm{lim}} s^{i\alpha +j+1}LRes(x,s)=\underset{s \rightarrow \infty }{\mathrm{lim}} s^{i\alpha +j+1}LRes_k(x,s)\\&\quad =0, i=1,2,3,\ldots ,k, j=0,1,\ldots ,m-1. \end{aligned}\nonumber \\ \end{aligned}$$

(38)

To find out the form of the unknown coefficients $f_{ij}(x)$ in eq. (35) for $i=1,\ldots ,k$ and $j=0,1,\ldots ,m-1$, we substitute kth-truncated series of U(x, s) into eq. (37), multiply the resulting function by $s^{i\alpha +j+1}$, take the limit as $s \rightarrow \infty$ and solve the obtained equation for $f_{ij}(x)$.

On other aspects as well, to obtain the form of the first unknown coefficients, $f_{1j}(x), j=0,1,\ldots ,m-1$ in eq. (35), we substitute the first-truncated series, $U_1(x,s)$, into the first-LR function, $LRes_1(x,s)$, to get

$$\begin{aligned} LRes_1(x,s)= & {} U_1(x,s)\nonumber \\&-\sum _{j=0}^{m-1}s^{-j-1}\phi _j(x)-s^{-\alpha }G(x,s)\nonumber \\&+\sum _{c=0}^{z}{s^{-\alpha }a_c(x)\frac{\partial ^c U_1(x,s)}{\partial x^c}}. \end{aligned}$$

(39)

Since

$$\begin{aligned} U_1(x,s)=\sum _{j=0}^{m-1}{\phi _j(x)/{s^{j+1}}}+\sum _{j=0}^{m-1}{f_{1j}(x)/s^{\alpha +j+1}}, \end{aligned}$$

then eq. (39) can be formulated as

$$\begin{aligned} LRes_1(x,s)= & {} \sum _{j=0}^{m-1}s^{-\alpha -j-1}f_{1j}(x)-s^{-\alpha }G(x,s)\nonumber \\&+\sum _{c=0}^{z}{a_c(x)\frac{\partial ^c }{\partial x^c}}\Bigg (\sum _{j=0}^{m-1}s^{-\alpha -j-1}\phi _j(x)\nonumber \\&+\sum _{j=0}^{m-1}s^{-2\alpha -j-1}f_{1j}(x)\Bigg ). \end{aligned}$$

(40)

To find the form of $f_{10}(x)$, we multiply eq. (40) by $s^{\alpha +1}$ to get

$$\begin{aligned} s^{\alpha +1}LRes_1(x,s)= & {} f_{10}(x)\!+\!\sum _{j=1}^{m-1}s^{-j}f_{1j}(x)-sG(x,s)\nonumber \\&+\sum _{c=0}^{z}{a_c(x)\frac{\partial ^c }{\partial x^c}}\Bigg (\sum _{j=0}^{m-1}s^{-j}\phi _j(x)\nonumber \\&+\sum _{j=0}^{m-1}s^{-\alpha -j}f_{1j}(x)\Bigg ). \end{aligned}$$

(41)

Applying limit on both sides of eq. (41) as $s \rightarrow \infty$, we get

$$\begin{aligned}&\underset{s \rightarrow \infty }{\mathrm{lim}} s^{\alpha +1}LRes_1(x,s)=f_{10}(x)\nonumber \\&\quad +\sum _{c=0}^{z}{a_c(x)}D^c_x\phi _0(x)-g(x,0). \end{aligned}$$

(42)

Refer to eq. (38) for $k=1$ and $j=0$ and solve eq. (42) for $f_{10}(x)$, we have

$$\begin{aligned} f_{10}(x)=g(x,0)-\sum _{c=0}^{z}{a_c(x)D^c_x\phi _0(x)}. \end{aligned}$$

(43)

To find the form of $f_{11}(x)$, we multiply both sides of eq. (40) by $s^{\alpha +2}$, to get

$$\begin{aligned}&s^{\alpha +2}LRes_1(x,s)\nonumber \\&\quad =f_{11}(x)+\sum _{j=2}^{m-1}s^{1-j}f_{1j}(x)\nonumber \\&\qquad -s(sG(x,s)-g(x,0))\nonumber \\&\qquad +\sum _{c=0}^{z}{a_c(x)\frac{\partial ^c }{\partial x^c}}\Bigg (\phi _1(x)+\sum _{j=2}^{m-1}s^{1-j}\phi _j(x)\nonumber \\&\qquad +\sum _{j=0}^{m-1}s^{1-\alpha -j}f_{1j}(x)\Bigg ). \end{aligned}$$

(44)

Again, applying limit on both sides of eq. (44) as $s \rightarrow \infty$ and using the fact in eq. (38) for $k=1$ and $j=1$, then the form of $f_{11}(x)$ is

$$\begin{aligned} f_{11}(x)=\left( D_tg\right) (x,0)-\sum _{c=0}^{z}{a_c(x)D^c_x\phi _1(x)}. \end{aligned}$$

(45)

We can find the form of $f_{12}(x)$, by multiplying eq. (44) by s to get the following equation:

$$\begin{aligned}&s^{\alpha +3}LRes_1(x,s)\nonumber \\&\quad =f_{12}(x)+\sum _{j=3}^{m-1}s^{1-j}f_{1j}(x)\nonumber \\&\qquad +\sum _{c=0}^{z}{a_c(x)\frac{\partial ^c }{\partial x^c}}\Bigg (\phi _2(x)+\sum _{j=3}^{m-1}s^{2-j}\phi _j(x)\nonumber \\&\qquad +\sum _{j=0}^{m-1}s^{2-\alpha -j}f_{1j}(x)\Bigg )\nonumber \\&\qquad -s(s^2G(x,s)-sg(x,0)-\left( D_tg\right) (x,0)). \end{aligned}$$

(46)

Refer to the facts in eq. (38) that $\lim \nolimits _{s\rightarrow \infty } s^{k\alpha +j+1}LRes_k(x,s)=0$ for $k=1, j=2$ and solving the obtained algebraic equation for $f_{12}(x)$, to get

$$\begin{aligned} f_{12}(x)=(D^2_tg)(x,0)-\sum _{c=0}^{z}{a_c(x)D^c_x\phi _2(x)}. \end{aligned}$$

(47)

We have a pattern in the form of the unknown coefficients $f_{1j}(x), j=1,2,\ldots ,m-1$. Therefore, the general form of $f_{1j}(x)$ can be predicted and given in the following relation:

$$\begin{aligned} f_{1j}(x)=(D^j_tg)(x,0)-\sum _{c=0}^{z}{a_c(x)D^c_x\phi _j(x)}. \end{aligned}$$

(48)

Again, to determine the form of the unknown coefficients, $f_{2j}(x), j=0,1,\ldots ,m-1$, we substitute the second-truncated series $U_2(x,s)$ in the second-LR function $LRes_2(x,s)$, to get the following form:

$$\begin{aligned}&LRes_2(x,s)\nonumber \\&=\sum _{j=0}^{m-1}s^{-\alpha -j-1}f_{1j}(x)+\sum _{j=0}^{m-1}s^{-2\alpha -j-1}f_{2j}(x)\nonumber \\&\qquad +\sum _{c=0}^{z}{a_c(x)\frac{\partial ^c }{\partial x^c}}\Bigg (\sum _{j=0}^{m-1}s^{-\alpha -j-1}\phi _j(x)\nonumber \\&\qquad +\sum _{j=0}^{m-1}s^{-2\alpha -j-1}f_{1j}(x)+\sum _{j=0}^{m-1}s^{-3\alpha -j-1}f_{2j}(x)\Bigg )\nonumber \\&\qquad -\frac{G(x,s)}{s^\alpha }. \end{aligned}$$

(49)

Now, to find the form of $f_{20}(x)$ we will multiply both sides of eq. (49) by $s^{2\alpha +1}$ to get the following expansion:

$$\begin{aligned}&s^{2\alpha +1}LRes_2(x,s)\nonumber \\&\quad =f_{20}(x)+\sum _{j=1}^{m-1}s^{-j}f_{2j}(x)\nonumber \\&\qquad +\sum _{c=0}^{z}{a_c(x)\frac{\partial ^c }{\partial x^c}}\Bigg (f_{10}(x)+\sum _{j=1}^{m-1}s^{-j}f_{1j}(x)\nonumber \\&\qquad +\sum _{j=0}^{m-1}s^{-\alpha -j}f_{2j}(x)\Bigg )-s\Bigg (s^{\alpha }G(x,s)\nonumber \\&\qquad -\sum _{j=0}^{m-1}s^{\alpha -j-1}(D^j_tg)(x,0)\Bigg ). \end{aligned}$$

(50)

Using the fact in eq. (38) for $k=2, j=0$ and solving the obtained equation for $f_{20}(x)$, we get

$$\begin{aligned} f_{20}(x)=\left( D^\alpha _tg\right) (x,0)-\sum _{c=0}^{z}{a_c(x)D^c_xf_{10}(x)}. \end{aligned}$$

(51)

Again, to find the form of $f_{21}(x)$ we will multiply eq. (49) by $s^{2\alpha +2}$ to get the following expansion:

$$\begin{aligned}&S^{2\alpha +2}LRes_2(x,s)\nonumber \\&\quad =f_{21}(x)+\sum _{j=2}^{m-1}s^{1-j}f_{2j}(x)\nonumber \\&\qquad +\sum _{c=0}^{z}{a_c(x)\frac{\partial ^c }{\partial x^c}}\Bigg (f_{11}(x)\nonumber \\&\qquad +\sum _{j=2}^{m-1}s^{1-j}f_{1j}(x)+\sum _{j=0}^{m-1}s^{1-\alpha -j}f_{2j}(x)\Bigg )\nonumber \\&\qquad -s\Bigg (s^{\alpha +1}G(x,s)-\sum _{j=0}^{m-1}s^{\alpha -j}\left( D^j_tg\right) (x,0)\nonumber \\&\qquad -\left( D^\alpha _tg\right) (x,0)\Bigg ). \end{aligned}$$

(52)

By using the fact in eq. (38) for $k=2, j=1$ and solving the obtained equation for $f_{21}(x)$, we get

$$\begin{aligned} f_{21}(x)=\left( D_tD^\alpha _tg\right) (x,0)-\sum _{c=0}^{z}{a_c(x)D^c_xf_{11}(x)}. \end{aligned}$$

(53)

In the same manner, multiply both sides of eq. (52) by s, then using the fact in eq. (38) for $k=2, j=2$ and solving the equation, $\lim _{s \rightarrow \infty } s^{2\alpha +3}LRes_k(x,s)=0$, for $f_{21}(x)$, one can get

$$\begin{aligned} f_{22}(x)=(D^2_tD^\alpha _tg)(x,0)-\sum _{c=0}^{z}{a_c(x)D^c_xf_{12}(x)}. \end{aligned}$$

(54)

Therefore, we can give the general form of the coefficients $f_{2j}(x)$ as follows:

$$\begin{aligned} f_{2j}(x)=(D^j_tD^\alpha _tg)(x,0)-\sum _{c=0}^{z}{a_c(x)D^c_xf_{1j}(x)}. \end{aligned}$$

(55)

We can notice that there is an obvious pattern in the form of the unknown coefficients in the series expansion as in eq. (33). Thus, the general form of the coefficients $f_{ij}(x), j=0,1,2,\ldots ,m-1$ can be obtained as:

$$\begin{aligned}&f_{ij}(x) = {\left\{ \begin{array}{ll} \phi _j(x), &{} i=0\\ (D^j_tD^{(i-1)\alpha }_tg)(x,0)-\sum _{c=0}^{z}{a_c(x)D^c_xf_{(i-1)j}(x)}, &{} i>0 \end{array}\right. }\nonumber \\ \end{aligned}$$

(56)

Therefore, the kth-AS of eq. (32) can be given as follows:

$$\begin{aligned} U_k(x,s)= & {} \sum ^{m-1}_{j=0}\frac{\phi _j(x)}{s^{j+1}}+\sum ^{k}_{i=1}\sum ^{m-1}_{j=0}\Bigg (\frac{(D^j_tD^{(i-1)\alpha }_tg)(x,0)}{s^{i\alpha +j+1}}\nonumber \\&-\frac{\sum _{c=0}^{z}{a_c(x)D^c_xf_{(i-1)j}(x)}}{s^{i\alpha +j+1}}\Bigg ). \end{aligned}$$

(57)

Finally, apply the inverse LT onto eq. (57) to return the solution in eq. (57) to the original space. Thus, the kth-AS of the linear FPDE in eqs (1) and (2) can be given as follows:

$$\begin{aligned}&u_k(x,t)\nonumber \\&\quad =\sum ^{m-1}_{j=0}\frac{t^j}{j!}\phi _j(x)+\sum ^{k}_{i=1}\sum ^{m-1}_{j=0}\Bigg (\frac{(D^j_tD^{(i-1)\alpha }_tg)(x,0)}{\Gamma ({i\alpha +j+1})}\nonumber \\&\qquad -\frac{\sum _{c=0}^{z}{a_c(x)D^c_xf_{(i-1)j}(x)}}{\Gamma ({i\alpha +j+1})}\Bigg )t^{i\alpha +j}, \quad k=1,2,\ldots .\nonumber \\ \end{aligned}$$

(58)

4 Some applications

To validate our new approach, we considered six attractive and important applications. The MATHEMATICA 11 and MAPLE 2018 are applied in our computational process.

Application 1

Consider the homogeneous T-FW equation:

$$\begin{aligned} \frac{\partial ^\alpha u(x,t)}{\partial t^\alpha }=\frac{1}{2}x^2 \frac{\partial ^2 u(x,t)}{\partial x^2}, x\in {\mathbb {R}}, t \ge 0, 1<\alpha \le 2,\nonumber \\ \end{aligned}$$

(59)

subject to

$$\begin{aligned} u(x,0)=x, u_t(x,0)=x^2. \end{aligned}$$

(60)

By comparing the T-FW as in IVP (59) and (60) with the general form as in IVP (1) and (2), we have $m=2,\ \phi _0(x)=x,\ \phi _1(x)=x^2,\ a_2(x)=-\frac{1}{2}x^2$ and $g(x,t)=a_c(x)=0,\ c=0,1,3,4,\ldots ,z$. Thus, according to eq. (56), we can easily find the forms of $f_{ij}(x), i=0,1,2,3,\ j=0,1$, respectively:

$$\begin{aligned} f_{00}(x)= & {} x, f_{01}(x)=x^2,\nonumber \\ f_{10}(x)= & {} 0, f_{11}(x)=x^2,\nonumber \\ f_{20}(x)= & {} 0, f_{21}(x)=x^2,\nonumber \\ f_{30}(x)= & {} 0, f_{31}(x)=x^2. \end{aligned}$$

(61)

Therefore, according to eq. (33), the third-AS of the LT of eqs (59) and (60) can be written as

$$\begin{aligned} U_3(x,s)=\frac{x}{s}+x^2\Bigg (\frac{1}{s^2}+\frac{1}{s^{\alpha +2}}+\frac{1}{s^{2\alpha +2}}+\frac{1}{s^{3\alpha +2}}\Bigg ).\nonumber \\ \end{aligned}$$

(62)

The inverse LT of eq. (62) represents the third-AS of eqs (59) and (60) as

$$\begin{aligned}&u_3(x,t)=x\nonumber \\&\quad +x^2\Bigg (t+\frac{t^{\alpha +1}}{\Gamma (\alpha +2)}+\frac{t^{2\alpha +1}}{\Gamma (2\alpha +2)}+\frac{t^{3\alpha +1}}{\Gamma (3\alpha +2)}\Bigg ).\nonumber \\ \end{aligned}$$

(63)

There are patterns between the terms of the series solution. Thus, the ES of the IVP (59) and (60) can be given as follows:

$$\begin{aligned} u(x,t)=x+x^2\sum ^{\infty }_{i=0}\frac{t^{i\alpha +1}}{\Gamma (i\alpha +2)}. \end{aligned}$$

(64)

When $\alpha =2$, the solution of eq. (59) becomes

$$\begin{aligned} u(x,t)=x+x^2\Bigg (t+\frac{t^3}{3!}+\frac{t^5}{5!}+\frac{t^7}{7!}+\cdots \Bigg ). \end{aligned}$$

(65)

So, the ES of IVP (59) and (60) will be $u(x,t)=x+x^2\sinh {t}$.

We noted that the third-truncated solution by L-RPSM as in eq. (63) is the same as (3,1)-truncated series solution that was obtained by RPSM [40] and as the third-AS that was obtained by ADM [9], whereas the fourth term AS for IVP (59) and (60) that were obtained by the HPM [10] and the VIM [9] are the same and are given as

$$\begin{aligned} \begin{aligned}&u_4(x,t)\\&\quad =x+x^2\Bigg (t+\frac{t^3}{2}+\frac{t^5}{40}+\frac{t^7}{7!}+\frac{3t^{5-\alpha }}{\Gamma (6-\alpha )}\\&\qquad +\frac{2t^{7-\alpha }}{\Gamma (8-\alpha )}+\frac{t^{7-2\alpha }}{\Gamma (8-2\alpha )}\Bigg ). \end{aligned} \end{aligned}$$

(66)

Tables 1–3 show the values of the residual error (Re. Err) when $\alpha =1.5,\ 1.75,\ 2$, respectively, and for different values of x and t. Those values are obtained from the third-AS for the L-RPSM and the fourth term AS for the VIM, HPM, ADM and RPSM of eqs (59) and (60), where the Re. Err of $u_3(x,t)$ of eq. (59) is

$$\begin{aligned} \mathrm {Re. Err}(x,t)=\Bigg |\frac{\partial ^\alpha u_3(x,t)}{\partial t^\alpha }-\frac{1}{2}x^2\frac{\partial ^2u_3(x,t)}{\partial x^2}\Bigg |. \end{aligned}$$

(67)

From tables 1–3, we can conclude that the L-RPSM provides us with the accurate AS and clarify the rapid convergence in AS of the IVP (59) and (60) from the other methods such as the VIM and HPM. Furthermore, the results show that the L-RPSM is simple, understandable and very fast to obtain ASs compared with other methods such as the HPM, VIM, ADM and RPSM.

Table 1 The numerical results of Re. Err for Application 1 when $\alpha =1.5$.

Table 2 The numerical results of Re. Err for Application 1 when $\alpha =1.75$.

Table 3 The numerical results of Re. Err for Application 1 when $\alpha =2$.

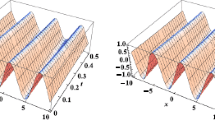
Figure 1 shows the surface graphs of the third-AS obtained by L-RPSM and ES of Application 1 for different values of $\alpha$. It is clear from the subfigures that the L-RPSM solution of Application 1 is in very good agreement with ES.

Fig. 1

The surface graphs of the AS and ES of Application 1: (a) $u_3(x,t)$ when $\alpha =4/3$, (b) $u_3(x,t)$ when $\alpha =5/3$, (c) $u_3(x,t)$ when $\alpha =2$, (d) $u(x,t)=x+x^2 \sinh {t}$ (the ES).

Application 2

Consider the following homogeneous S-FT equation:

$$\begin{aligned}&\frac{\partial ^\alpha u(x,t)}{\partial x^\alpha }= \frac{\partial ^2 u(x,t)}{\partial t^2}+\frac{\partial u(x,t)}{\partial t}+u(x,t),\nonumber \\&0<x<1, t \ge 0, 1<\alpha \le 2, \end{aligned}$$

(68)

with the non-homogeneous initial conditions

$$\begin{aligned} u(0,t)=u_x(0,t)=\mathrm {e}^{-t}. \end{aligned}$$

(69)

For the space-fractional applications, we will replace x by t and t by x in the equations in previous sections.

So, by referring to the general form as in the IVP (1) and (2) and comparing it with the S-FT equation as in the IVP (68) and (69), we obtain that $m=2,\ \phi _0(t)=\phi _1(t)=\mathrm {e}^{-t},\ a_0(t)=a_1(t)=a_2(t)=-1$ and $g(x,t)=a_c(t)=0,\ c=3,4,5,\ldots ,z$.

Equation (56) leads to $f_{ij}(t)=\mathrm {e}^{-t},\ j=0,1,\ i=0,1,2,\ldots$. Therefore, according to eq. (33), the AS of the LT of eqs (68) and (69) can be given as

$$\begin{aligned} U(s,t)= & {} \mathrm {e}^{-t}\Bigg (\frac{1}{s}+\frac{1}{s^{2}}+\frac{1}{s^{\alpha +1}}+\frac{1}{s^{\alpha +2}}+\frac{1}{s^{2\alpha +1}}\nonumber \\&+\frac{1}{s^{2\alpha +2}}+\cdots \Bigg ). \end{aligned}$$

(70)

The inverse LT of eq. (70) represents the infinite series L-RPSM solution of the S-FT equation as in IVP (68) and (69) as follows:

$$\begin{aligned}&u(x,t)\nonumber \\&\quad =\mathrm{e}^{-t}\Bigg (1+x+\frac{x^\alpha }{\Gamma ({\alpha +1})}+\frac{x^{\alpha +1}}{\Gamma ({\alpha +2})}+\frac{x^{2\alpha }}{\Gamma ({2\alpha +1})}\nonumber \\&\qquad +\frac{x^{2\alpha +1}}{\Gamma ({2\alpha +2})}+\cdots \Bigg ), \end{aligned}$$

(71)

the above equation are exactly the same as those given by LT and homotopy analysis method (HATM) [41], Decomposition method [42] and RPSM [40].

When $\alpha =2$, the L-RPSM solution of S-FT equation as in IVP (68) and (69) has the general pattern which tend to the ES of the following series:

$$\begin{aligned} u(x,t)=\mathrm {e}^{-t}\Bigg (1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+\frac{x^5}{5!}+\cdots \Bigg ),\nonumber \\ \end{aligned}$$

(72)

which is equivalent to the exact form $u(x,t)=\mathrm{e}^{x-t}$.

Table 4 shows the values of the third-approximate L-RPSM solution when $\alpha =1.25,\ 1.5,\ 1.75,\ 2$ and the ES of S-FT equation as in IVP (68) and (69) for different values of x and t on the domain $(0,1) \times [0,1]$. From the results, we conclude that the L-RPSM is a simple and attractive method for finding the solution.

Table 4 The numerical results of the AS and ES for Application 2.

Application 3

Consider the following non-homogeneous S-FT equation:

$$\begin{aligned}&\frac{\partial ^\alpha u(x,t)}{\partial x^\alpha }= \frac{\partial ^2 u(x,t)}{\partial t^2}+\frac{\partial u(x,t)}{\partial t}+u(x,t)-x^\alpha \nonumber \\&-t+1, x\ge 0,\ t \ge 0,\ 1<\alpha \le 2, \end{aligned}$$

(73)

subject to

$$\begin{aligned} u(0,t)=t,\quad u_x(0,t)=0. \end{aligned}$$

(74)

We noted that this application is an extension of the third example in [41], where it was converted to the general form that is suggested in (1) by replacing $x^2$ by $x^\alpha$ since $x^2$ is of a power 2 which must be of the form $j+i\alpha ,\ j=0,1,\ldots ,m-1,\ i=0,1,2,\ldots ,$ that is either of the form $i\alpha$ or $i\alpha +1$ since $m=2$.

By referring to the general form as in the IVP (1) and (2) and comparing it with the S-FT equation as in the IVP (73) and (74), we obtain that $m=2,\ \phi _0(t)=t,\ \phi _1(t)=0,\ a_0(t)=a_1(t)=a_2(t)=-1,a_c(t)=0,\ c=3,4,5,\ldots ,z$ and $g(x,t)=-x^\alpha -t+1$ (recall that in the space applications, we replace x by t and t by x).

To determine the form of the coefficients $f_{ij}(t),\ j=0,1,\ i=0,1,2,\ldots$, we need to use eq. (56). To facilitate and accelerate the calculations we compute the value of the term $(D^j_xD^{(i-1)\alpha }_xg)(0,t),\ j=0,1,$ $i=1,2,\ldots$. Hence

$$\begin{aligned}&g(0,t)=-t+1,\nonumber \\&\left( D_xg\right) (0,t)=0,\nonumber \\&\left( D^{\alpha }_xg\right) (0,t)=-\Gamma (\alpha +1),\nonumber \\&\left( D_xD^{\alpha }_xg\right) (0,t)=0,\nonumber \\&(D^j_xD^{(i-1)\alpha }_xg)(0,t)=0,\quad j=0,1,i=3,4,5,\ldots .\nonumber \\ \end{aligned}$$

(75)

Returning to eq. (56), after simple calculations we find the forms of $f_{ij}(t),\ j=0,1,\ i=0,1,2,\ldots$, respectively as

$$\begin{aligned} f_{00}(t)= & {} t,\nonumber \\ f_{10}(t)= & {} 2,\nonumber \\ f_{i0}(t)= & {} 2-\Gamma (\alpha +1),\quad i=2,3,4,\ldots \nonumber \\ f_{i1}(t)= & {} 0,\quad i=0,1,2,3,4,\ldots \end{aligned}$$

(76)

Hence, by using eq. (58) we obtained the AS for IVP (73) and (74) as follows:

$$\begin{aligned}&u_k(x,t)=t+\frac{2 x^{\alpha }}{\Gamma (\alpha +1)}\nonumber \\&\quad +\sum ^{k}_{i=2}\frac{2-\Gamma (\alpha +1)}{\Gamma ({i\alpha +1})}x^{i\alpha }, \quad k=2,3,\ldots \end{aligned}$$

(77)

When $\alpha =2$ as $k \rightarrow \infty$, we have $u(x,t)=t+x^2$, which is the ES of the IVP (73) and (74).

Application 4

Consider the following T-FV equation of large membranes:

$$\begin{aligned}&\frac{\partial ^\alpha u(x,t)}{\partial t^\alpha }=w^2\Bigg (\frac{\partial ^2 u(x,t)}{\partial x^2}+\frac{1}{x}\frac{\partial u(x,t)}{\partial x}\Bigg ),\nonumber \\&x,t \ge 0, 1<\alpha \le 2, \end{aligned}$$

(78)

with the non-homogeneous initial conditions

$$\begin{aligned} u(x,0)=\xi (x),\quad u_t(x,0)=w\psi (x), \end{aligned}$$

(79)

where u(x, t) represents the probability density function of finding a particle at position x at time t and w is the wave velocity of free vibration.

By referring to the T-FV equation as in the IVP (1) and (2) and comparing it with the general form as in the IVP (78) and (79), we obtain $m=2,\ \phi _0(x)=\xi (x),\ \phi _1(t)=w\psi (x),\ a_1(x)={-w^2}/{x},\ a_2(x)=-w^2,\ a_c(x)=0,\ c=0,3,4,5,\ldots ,z$ and $g(x,t)=0$.

To determine the form of the coefficients $f_{ij}(t),\ j=0,1,\ i=0,1,2,\ldots$., we need to use eq. (56), which after easy calculations, leads to

$$\begin{aligned} f_{00}(x)= & {} \xi (x),\nonumber \\ f_{01}(x)= & {} w\psi (x),\nonumber \\ f_{10}(x)= & {} w^2\Bigg (D^2_x\xi (x)+\frac{1}{x}D_x\xi (x)\Bigg ),\nonumber \\ f_{11}(x)= & {} w^3\Bigg (D^2_x\psi (x)+\frac{1}{x}D_x\psi (x)\Bigg ),\nonumber \\ f_{20}(x)= & {} w^4\Bigg (D^4_x\xi (x)+\frac{2}{x}D^3_x\xi (x)-\frac{1}{x^2}D^2_x\xi (x)\nonumber \\&+\frac{1}{x^3}D_x\xi (x)\Bigg ),\nonumber \\ f_{21}(x)= & {} w^5\Bigg (D^4_x\psi (x)+\frac{2}{x}D^3_x\psi (x)-\frac{1}{x^2}D^2_x\psi (x)\nonumber \\&+\frac{1}{x^3}D_x\psi (x)\Bigg ),\nonumber \\ f_{30}(x)= & {} w^6\Bigg (D^6_x\xi (x)+\frac{3}{x}D^5_x\xi (x)-\frac{3}{x^2}D^4_x\xi (x)\nonumber \\&+\frac{6}{x^3}D^3_x\xi (x)-\frac{9}{x^4}D^2_x\xi (x)+\frac{9}{x^5}D_x\xi (x)\Bigg ),\nonumber \\ f_{31}(x)= & {} w^6\Bigg (D^6_x\psi (x)+\frac{3}{x}D^5_x\psi (x)-\frac{3}{x^2}D^4_x\psi (x)\nonumber \\&+\frac{6}{x^3}D^3_x\psi (x)-\frac{9}{x^4}D^2_x\psi (x)+\frac{9}{x^5}D_x\psi (x)\Bigg ).\nonumber \\ \end{aligned}$$

(80)

Hence, by using eq. (58) we have obtained the infinite series solution for IVP (78) and (79) as follows:

$$\begin{aligned}&u(x,t)\nonumber \\&\quad =\xi (x)+w\psi (x)t+w^2\Bigg (D^2_x\xi (x)+\frac{1}{x}D_x\xi (x)\Bigg )\nonumber \\&\qquad \times \frac{t^\alpha }{\Gamma (\alpha +1)}+w^3\Bigg (D^2_x\psi (x)+\frac{1}{x}D_x\psi (x)\Bigg )\frac{t^{\alpha +1}}{\Gamma (\alpha +2)}\nonumber \\&\qquad +w^4\Bigg (D^4_x\xi (x)+\frac{2}{x}D^3_x\xi (x)-\frac{1}{x^2}D^2_x\xi (x)\nonumber \\&\qquad +\frac{1}{x^3}D_x\xi (x)\Bigg )\frac{t^{2\alpha }}{\Gamma (2\alpha +1)}+w^5\Bigg (D^4_x\psi (x)\nonumber \\&\qquad +\frac{2}{x}D^3_x\psi (x)-\frac{1}{x^2}D^2_x\psi (x)+\frac{1}{x^3}D_x\psi (x)\Bigg )\nonumber \\&\qquad \times \frac{t^{2\alpha +1}}{\Gamma (2\alpha +2)}+\cdots . \end{aligned}$$

(81)

Case 1: If $\xi (x)=x^2$ and $\psi (x)=x$, then eq. (81) can be reduced to

$$\begin{aligned} u(x,t)=x^2+\frac{4w^2t^\alpha }{\Gamma (1+\alpha )}+wtxE_{\alpha ,2}\Bigg (\frac{w^2}{x^2}Mt^\alpha \Bigg ). \end{aligned}$$

(82)

Case 2: If $\xi (x)=x$ and $\psi (x)=x$, then eq. (81) can be reduced to

$$\begin{aligned} u(x,t)=xE_\alpha \Bigg (\frac{w^2}{x^2}Mt^\alpha \Bigg )+wtxE_{\alpha ,2}\Bigg (\frac{w^2}{x^2}Mt^\alpha \Bigg ), \end{aligned}$$

(83)

where

$$\begin{aligned} E_\alpha (t)=\sum ^\infty _{n=0}\frac{t^n}{\Gamma (n\alpha +1)}, \end{aligned}$$

$$\begin{aligned} E_{\alpha ,\beta }(t)=\sum ^\infty _{n=0}\frac{t^n}{\Gamma (n\alpha +\beta )} \end{aligned}$$

are Mittag–Leffler function and generalised Mittag–Leffler function respectively, and $M^n=[1.3.5\ldots (2n-1)]^2$.

Case 3: If $\xi (x)=x^2$ and $\psi (x)=x^2$, then eq. (81) gives

$$\begin{aligned} u(x,t)=x^2+wtx^2+\frac{4w^2t^{\alpha }}{\Gamma (\alpha +1)}+\frac{4w^3t^{\alpha +1}}{\Gamma (\alpha +2)}. \end{aligned}$$

(84)

Fig. 2

(a) u(x, t) when $w=5$ and $\alpha =3/2$ for Case 1 and (b) u(x, t) for various values of $\alpha$ when $w=5$ and $x=6$ for Case 1.

Fig. 3

(a) u(x, t) a when $w=5$ and $\alpha =3/2$ for Case 2 and (b) u(x, t) for various values of $\alpha$ when $w=5$ and $x=6$ for Case 2.

Fig. 4

(a) u(x, t) when $w=5$ and $\alpha =3/2$ for Case 3 and (b) u(x, t) for various values of $\alpha$ when $w=5$ and $x=6$ for Case 3.

Table 5 The numerical result of the AS and ES for Application 5.

Fig. 5

The surface graphs of the AS of Application 5: (a) $u_8(x,t)$ when $\alpha =0.25$, (b) $u_8(x,t)$ when $\alpha =0.5$, (c) $u_8(x,t)$ when $\alpha =0.75$, (d) $u_8(x,t)$ when $\alpha =1$.

The results in eqs (82)–(84) are the same results which are obtained by [43, 44].

Figures 2–4 show the values of u(x, t) for different values of radii of the membrane and time in three different cases. It seen from figures 2(a), 3(a) and 4(a) that the values of u(x, t) increase with the increase of t for $w=5$. It is also seen from figures 2(b), 3(b) and 4(b) that the values of u(x, t) increase with the increase of t for wave velocity $w=5$ and $x=6$, but decrease with the increase of values of $\alpha$ which confirms the exponential decay of the regular Brownian motion. It is also observed that the rate of change of u(x, t) in Case 3 is more than the rate of change in Cases 1 and 2, which means that the rate of change of the values of u(x, t) when $\xi (x)$ and $\psi (x)$ are nonlinear in nature is more than when $\xi (x)$ and $\psi (x)$ are linear in nature.

Application 5

Consider the following T-FSH equation:

$$\begin{aligned}&\frac{\partial ^\alpha u(x,t)}{\partial t^\alpha }+(1-r)u(x,t)+2\frac{\partial ^2 u(x,t)}{\partial x^2}\nonumber \\&+\frac{\partial ^3 u(x,t)}{\partial x^3}=0, 0<\alpha \le 1, \end{aligned}$$

(85)

with the initial conditions

$$\begin{aligned} u(x,0)=\mathrm {e}^x, \end{aligned}$$

(86)

where r is the real bifurcation parameter, u(x, t) is the scalar valued function defined on the line or the plane. In this application $\alpha \in (0,1]$; that is $m=1$. Therefore, the solution of the Laplace form of the IVP (85) and (86) have the following expansion:

$$\begin{aligned} U(x,s)=\sum _{i=0}^{\infty } { {\frac{f_{i}(x)}{s^{i\alpha +1}}}}. \end{aligned}$$

(87)

Depending on the general form of the IVP (1) and (2) and comparing it with the T-FSH equation as in the IVP (85) and (86), we can obtain values of elements to the solution of IVP (85) and (86), which are $\phi _0(x)=\mathrm {e}^x,\ a_0(x)=(1-r),\ a_2(x)=2,\ a_3(x)=1,\ a_c(x)=0,\ c=1,4,5,\ldots ,z$ and $g(x,t)=0$. According to eq. (56), we find $f_i(x)=(r-4)^i \mathrm {e}^x,\ i=0,1,2,\ldots$. Therefore, the solution of the Laplace form of the IVP (85) and (86) will be

$$\begin{aligned} U(x,s)=\sum _{i=0}^{\infty } { {\frac{(r-4)^i \mathrm {e}^x}{s^{i\alpha +1}}}}. \end{aligned}$$

(88)

Employ inverse LT for eq. (88) to get the AS of the IVP (85) and (86) as

$$\begin{aligned} u(x,t)=\sum _{i=0}^{\infty } { {\frac{(r-4)^i \mathrm {e}^x}{\Gamma ({i\alpha +1})}}t^{i\alpha }}, \end{aligned}$$

(89)

which is the same results as that obtained by RPSM [45]. The AS of the IVP (85) and (86) has general pattern form which is coinciding well with the ES for $\alpha =1$ as:

$$\begin{aligned}&u(x,t)\nonumber \\&\quad =\mathrm {e}^x \Bigg (1+(r-4)t+\frac{(r-4)^2}{2}t^2+\frac{(r-4)^3}{3!}t^3+\cdots \Bigg )\nonumber \\&\quad =\mathrm {e}^{x+(r-4)t}. \end{aligned}$$

(90)

Table 5 shows numerical result and absolute error of AS, $u_8(x,t)$ of T-FSH equation as in (85) and (86) for various values of $\alpha$ when $r=3$. Figure 5 shows the surface graph of the eighth-AS by L-RPSM for T-FSH equation as in (85) and (86) for various values of $\alpha$ and $r=3$ when $x \in [-2,2]$ and $t \in [0,1]$.

Application 6

Consider the non-homogeneous T-FNS equation:

$$\begin{aligned}&\frac{\partial ^\alpha u(x,t)}{\partial t^\alpha }=\lambda +\frac{\partial ^2 u(x,t)}{\partial x^2}+\frac{1}{x}\frac{\partial u(x,t)}{\partial x},\nonumber \\&\lambda \in {\mathbb {R}},\ x>0,\ t\ge 0,\ 0<\alpha \le 1, \end{aligned}$$

(91)

with the following non-homogeneous initial condition

$$\begin{aligned} u(x,0)=1-x^2. \end{aligned}$$

(92)

Since $m=1$ as the previous application, we let the solution of the Laplace form of the T-FNS equation (91) and (92) as

$$\begin{aligned} U(x,s)=\sum _{i=0}^{\infty } { {\frac{f_{i}(x)}{s^{i\alpha +1}}}}. \end{aligned}$$

(93)

Depending on eqs (1) and (2), we can conclude that: $\phi _0(x)=1-x^2,\ a_1(x)=-1/x,\ a_2(x)=-1,\ a_c(x)=0,\ c=0,3,4,5,\ldots ,z$ and $g(x,t)=\lambda$. According to eq. (56), we find $f_0(x)=1-x^2,\ f_1(x)=\lambda -4$ and $f_i(x)=0,\ i=2,3,4,\ldots$. Therefore, the solution of the Laplace form of the T-FNS (91) and (92) will be as follows:

$$\begin{aligned} U(x,s)=\frac{1-x^2}{s}+\frac{\lambda -4}{s^{\alpha +1}}. \end{aligned}$$

(94)

Therefore, by taking inverse LT on eq. (94), we get the ES of the T-FNS (91) and (92) as follows:

$$\begin{aligned} u(x,t)=1-x^2+(\lambda -4)\frac{t^\alpha }{\Gamma {(\alpha +1)}}, \end{aligned}$$

(95)

which is the same solution that is obtained by the ADM [46] and RPSM [40]. When $\alpha =1$, the solutions of the T-FNS (91) and (92) has the general pattern form which is coinciding with the ES in terms of the following polynomial: $u(x,t)=1-x^2+(\lambda -4)t$.

5 Conclusion

In this paper, we developed a new analytical method, the so-called L-RPSM, to solve high-order linear FPDEs in Caputo sense. The merit of our method is that we can convert the FDE to algebraic equation using LT operator which reduces the size of the computational work needed to find the solution in a successive algebraic steps. The main advantage of the proposed method is the simplicity in computing the coefficients of terms of series solution by using the concept of limit at infinity only. Other well-known analytical method such as RPSM need to obtain the FD each time to determine the unknown coefficients in series solutions, and VIM, ADM or HPM need the integration operators which is difficult in fractional case. Our proposed method has been tested in six important applications to reveal accuracy, speed, simplicity and applicability in finding the ES and accurate ASs to linear FPDEs. These applications dealt with five types of linear FPDEs, namely the T-FW, S-FT, T-FV, T-FSH and T-FSH equations. The results obtained indicated their conformity with easy calculation steps and less complexity compared to the results obtained in other methods. It is worth noting that the proposed method can be applied for obtaining ES and ASs for other important types of linear and non-linear FPDEs.