Skip to main content
SpringerLink
Log in

Series and closed form solution of Caputo time-fractional wave and heat problems with the variable coefficients by a novel approach

  • Published:
Optical and Quantum Electronics Aims and scope Submit manuscript

Abstract

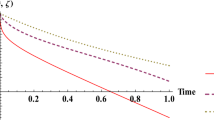
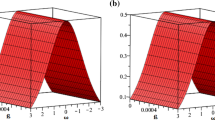
The mathematical efficiency of fractional-order differential equations in modeling real systems has been established. The first-order and second-order time derivatives are substituted in integer-order problems by a fractional derivative of order \(0 < \omega \le 1\), resulting in time-fractional heat and wave problems with variable coefficients. In this research, we analyze fractional-order wave and heat problems with variable coefficients within the framework of a Caputo derivative (CD) using the Elzaki residual power series method (ERPSM), which is a coupling of the residual power series method (RPSM) and the Elzaki transform (E-T). It relies on a novel form of fractional power series (FPS), which provides a convergent series as a solution. The accuracy and convergence rates have been proven by the relative, absolute, and recurrence error analyses, demonstrating the validity of the recommended approach. By employing the simple limit principle at zero, the ERPSM excels at calculating the coefficients of terms in a FPS, but other well-known approaches such as Adomian decomposition, variational iteration, and homotopy perturbation need integration, while the RPSM needs the derivative, both of which are challenging in fractional contexts. ERPSM is also more effective than various series solution methods due to the avoidance of Adomian’s and He’s polynomials to solve nonlinear problems. The results obtained using the ERPSM show excellent agreement with the natural transform decomposition method and homotopy analysis transform method, demonstrating that the ERPSM is an effective approach for obtaining the approximate and closed-form solutions of fractional models. We established that our approach for fractional models is accurate and straightforward and researcher can use this approach to solve various problems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

Data availability

No data were generated or analyzed during the current study.

References

  • Ahmed, I., Akgül, A., Jarad, F., Kumam, P., Nonlaopon, K.: A Caputo-Fabrizio fractional-order cholera model and its sensitivity analysis. Math Model Numer Simulat Appl 3, 170–187 (2023)

    Google Scholar 

  • Akgül, A., Baleanu, D.: Analysis and applications of the proportional Caputo derivative. Adv. Differ. Eq. pp. 1–12. (2021)

  • Alharbi, R., Alshaery, A.A., Bakodah, H.O., Nuruddeen, R.I., Gómez-Aguilar, J.F.: Revisiting (2+1)-dimensional Burgers’ dynamical equations: analytical approach and Reynolds number examination. Phys. Scr. 98, 085225 (2023)

    Article  ADS  Google Scholar 

  • Barros, L.C.D., Lopes, M.M., Pedro, F.S., Esmi, E., Santos, J.P.C.D., Sánchez, D.E.: The memory effect on fractional calculus: an application in the spread of COVID-19. Comput. Appl. Math. 40, 1–21 (2021)

    Article  MathSciNet  Google Scholar 

  • Evirgen, F., Esmehan, U.Ç.A.R., Sümeyra, U.Ç.A.R., Özdemir, N.: Modelling influenza a disease dynamics under Caputo-Fabrizio fractional derivative with distinct contact rates. Math Model Numer Simulat Appl 3, 58–72 (2023)

    Google Scholar 

  • Filali, D., Ali, A., Ali, Z., Akram, M., Dilshad, M., Agarwal, P.: Problem on piecewise Caputo-Fabrizio fractional delay differential equation under anti-periodic boundary conditions. Phys. Scr. 98, 034001 (2023)

    Article  ADS  Google Scholar 

  • He, J.H.: Approximate analytical solution for seepage flow with fractional derivatives porous media. Comput. Methods Appl. Mech. Eng. 167, 57–68 (1998)

    Article  MathSciNet  ADS  Google Scholar 

  • Hristov, J.: Magnetic field diffusion in ferromagnetic materials: fractional calculus approaches. Int J Optimizat Contr: Theor Appl (IJOCTA) 11, 1–15 (2021)

    MathSciNet  Google Scholar 

  • Khalouta, A.: A novel iterative method to solve nonlinear wave-like equations of fractional order with variable coefficients. Revista Colombiana De Matemáticas 56, 13–34 (2022)

    Article  MathSciNet  Google Scholar 

  • Khalouta, A., Kadem, A.B.: A new technique for finding exact solutions of nonlinear time-fractional wave-like equations with variable coefficients. InProc. Inst. Math. Mech. Natl. Acad. Sci. Azerb 45, 167–180 (2019)

    MathSciNet  Google Scholar 

  • Khalouta, A., Kadem, A.: Solutions of nonlinear time-fractional wave-like equations with variable coefficients in the form of Mittag-Leffler functions. Thai J. Math. 18, 411–424 (2020a)

    MathSciNet  Google Scholar 

  • Khalouta, A., Kadem, A.: A new iterative natural transform method for solving nonlinear Caputo time-fractional partial differential equations. Jordan J Math Statist 13, 459–476 (2020b)

    MathSciNet  Google Scholar 

  • Khalouta, A., Kadem, A.: A comparative study of Shehu variational iteration method and Shehu decomposition method for solving nonlinear Caputo time-fractional wave-like equations with variable coefficients. Appl. App. Math.: An Int. J. (AAM) 15, p 24 (2020)

  • Khan, H., Shah, R., Kumam, P., Arif, M.: Analytical solutions of fractional-order heat and wave equations by the natural transform decomposition method. Entropy 21, 597 (2019)

    Article  MathSciNet  PubMed  PubMed Central  ADS  Google Scholar 

  • Khan, A., Liaqat, M.I., Alqudah, M.A., Abdeljawad, T.: Analysis of the conformable temporal-fractional swift–hohenberg equation using a novel computational technique. Fractals 31, 1–17 (2023)

    Article  Google Scholar 

  • Khan, A., Liaqat, M. I., Younis, M., Alam, A.: Approximate and exact solutions to fractional order Cauchy reaction-diffusion equations by new combine techniques. J. Math., pp. 1–12 (2021)

  • Koca, I., Atangana, A.: Theoretical and numerical analysis of a chaotic model with nonlocal and stochastic differential operators. Int J Optimizat Contr: Theor Appl (IJOCTA) 13, 181–192 (2023)

    MathSciNet  Google Scholar 

  • Kumar, D., Singh, J., Purohit, S.D., Swroop, R.: A hybrid analytical algorithm for nonlinear fractional wave-like equations. Math Model Nat Phenom 14, 304 (2019)

    Article  MathSciNet  Google Scholar 

  • Liaqat, M.I., Khan, A., Alqudah, M.A., Abdeljawad, T.: Adapted homotopy perturbation method with shehu transform for solving conformable fractional nonlinear partial differential equations. Fractals 31, 2340027 (2023)

    Article  ADS  Google Scholar 

  • Liaqat, M. I., Khan, A., Alam, M. A., Pandit, M. K., Etemad, S., Rezapour, S.: Approximate and closed-form solutions of Newell-Whitehead-Segel equations via modified conformable Shehu transform decomposition method. Math. Probl. Eng. (2022)

  • Liaqat, M. I., Khan, A., Akgül, A., Ali, M. S.: A novel numerical technique for fractional ordinary differential equations with proportional delay. J. Fun. Spaces, (2022)

  • Molliq, Y., Noorani, M.S.M., Hashim, I.: Variational iteration method for fractional heat-and wave-like equations. Nonlinear Anal. Real World Appl. 10, 1854–1869 (2009)

    Article  MathSciNet  Google Scholar 

  • Momani, S.: Analytical approximate solution for fractional heat-like and wave-like equations with variable coefficients using the decomposition method. Appl. Math. Comput. 165, 459–472 (2005)

    MathSciNet  Google Scholar 

  • Morales-Delgado, V.F., Taneco-Hernández, M.A., Vargas-De-León, C., Gómez-Aguilar, J.F.: Exact solutions to fractional pharmacokinetic models using multivariate Mittag-Leffler functions. Chaos Solitons Fractals 168, 113164 (2023)

    Article  MathSciNet  Google Scholar 

  • Mubaraki, A.M., Nuruddeen, R.I., Gómez-Aguilar, J.F.: Modeling the dispersion of waves on a loaded bi-elastic cylindrical tube with variable material constituents. Res Phys 53, 106927 (2023)

    Google Scholar 

  • Nikan, O., Avazzadeh, Z., Machado, J.T.: A local stabilized approach for approximating the modified time-fractional diffusion problem arising in heat and mass transfer. J. Adv. Res. 32, 45–60 (2021)

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  • Nuruddeen, R.I., Gómez-Aguilar, J.F., Razo-Hernández, J.R.: Fractionalizing, coupling and methods for the coupled system of two-dimensional heat diffusion models. AIMS Math 8, 11180–11201 (2023)

    Article  MathSciNet  Google Scholar 

  • Qiu, L., Wang, F., Lin, J.: A meshless singular boundary method for transient heat conduction problems in layered materials. Comput. Math. Appl. 78, 3544–3562 (2019)

    Article  MathSciNet  Google Scholar 

  • Rashid, S., Kubra, K.T., Sultana, S., Agarwal, P., Osman, M.S.: An approximate analytical view of physical and biological models in the setting of Caputo operator via Elzaki transform decomposition method. J. Comput. Appl. Math. 413, 114378 (2022)

    Article  MathSciNet  Google Scholar 

  • Shams, M., Kausar, N., Agarwal, P., Jain, S., Salman, M.A., Shah, M.A.: On family of the Caputo-type fractional numerical scheme for solving polynomial equations. Appl Math Sci Eng 31, 2181959 (2023a)

    Article  MathSciNet  Google Scholar 

  • Shams, M., Kausar, N., Samaniego, C., Agarwal, P., Ahmed, S.F., Momani, S.: On efficient fractional Caputo-Type simultaneous scheme for finding all roots of polynomial equations with biomedical engineering applications. Fractals 15, 2340075 (2023b)

    Article  Google Scholar 

  • Shi, L., Tayebi, S., Arqub, O.A., Osman, M.S., Agarwal, P., Mahamoud, W., Alhodaly, M.: The novel cubic B-spline method for fractional Painleve and Bagley-Trovik equations in the Caputo, Caputo-Fabrizio, and conformable fractional sense. Alex. Eng. J. 65, 413–426 (2023)

    Article  Google Scholar 

  • Srivastava, H.M., Günerhan, H.: Analytical and approximate solutions of fractional-order susceptible-infected-recovered epidemic model of childhood disease. Math. Methods Appl. Sci. 42, 935–941 (2019)

    Article  MathSciNet  ADS  Google Scholar 

  • Subramanian, M., Manigandan, M., Tunç, C., Gopal, T.N., Alzabut, J.: On system of nonlinear coupled differential equations and inclusions involving Caputo-type sequential derivatives of fractional order. J Taibah Univ Sci 16, 1–23 (2022)

    Article  Google Scholar 

  • Wazwaz, A.M., Gorguis, A.: Exact solutions of heat-like and wave-like equations with variable coefficients. Appl. Math. Comput. 149, 15–29 (2004)

    MathSciNet  Google Scholar 

  • Wu, F., Zhang, H., Zou, Q., Li, C., Chen, J., Gao, R.: Viscoelastic-plastic damage creep model for salt rock based on fractional derivative theory. Mech. Mater. 150, 103600 (2020)

    Article  Google Scholar 

  • Xia, Y., Guo, P.: A time discontinuous Galerkin isogeometric analysis method for non-Fourier thermal wave propagation problem. Eng. Comput. 36, 2240–2259 (2019)

    Google Scholar 

  • Xu, H., Cang, J.: Analysis of a time fractional wave-like equation with the homotopy analysis method. Phys. Lett. A 372, 1250–1255 (2008)

    Article  MathSciNet  CAS  ADS  Google Scholar 

Download references

Funding

No funds were received.

Author information

Authors and Affiliations

  1. Abdus Salam School of Mathematical Sciences, Government College University, 68-B, New MuslimTown, Lahore, 54600, Pakistan

    Muhammad Imran Liaqat

  2. National College of Business Administration & Economics, Lahore, Pakistan

    Muhammad Imran Liaqat

  3. Department of Computer Science and Mathematics, Lebanese American University, Beirut, Lebanon

    Ali Akgül

  4. Art and Science Faculty, Department of Mathematics, Siirt University, 56100, Siirt, Turkey

    Ali Akgül

  5. Mathematics Research Center, Department of Mathematics, Near East University, Near East Boulevard, PC: 99138, Nicosia/Mersin 10, Turkey

    Ali Akgül

  6. Department of Computer Engineering, Biruni University, 34010, Topkapı, Istanbul, Turkey

    Mustafa Bayram

Authors
  1. Muhammad Imran Liaqat
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ali Akgül
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mustafa Bayram
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

The authors declare that the study was realized in collaboration with equal responsibility. All authors read and approved the final manuscript.

Corresponding authors

Correspondence to Muhammad Imran Liaqat or Ali Akgül.

Ethics declarations

Conflict of interest

The authors declare that they have no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liaqat, M.I., Akgül, A. & Bayram, M. Series and closed form solution of Caputo time-fractional wave and heat problems with the variable coefficients by a novel approach. Opt Quant Electron 56, 203 (2024). https://doi.org/10.1007/s11082-023-05751-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11082-023-05751-3

Keywords

Search

Navigation