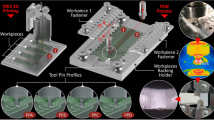
Abstract
The forming tools are conventionally manufactured from alloy steels. These tools can be designed to be light weight and cost effective without compromising performance characteristics. In this research, a fundamental forming tool (pressure die) of ‘rotary draw bending processes’ is topology optimized and 3D printed by using polymeric material. An accurate FE-simulation model of a rotary draw bending process is developed and topology optimization of the pressure die is carried out on the basis of contact stresses provided by FE-simulation results. The topology optimized pressure die is compared with its conventional metal made counter-part in terms of contact forces, contact normal stresses, effective area in-contact and cost performance index. This manuscript demonstrates that topology optimized lightweight 3D printed polymeric forming tools are a cost effective alternative to comparatively heavy alloy steels. This research contributes to widen the avenue of cost effective manufacturing by incorporating topology optimization regimes into existing production setups.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Rotary Draw Bending (RDB) process is a cold form metal bending process. Presently, it is considered as one of the most common tube bending industrial process for metal tubes [1]. The forming tools used in the RDB process are critically important because these tools are in-contact with the tube during bending operations. All forming forces and pressures are withstood or applied through these tools [2]. The positions of forming tools used in a RDB process are shown in Fig. 1. The pressure die (Pd) is a fundamental forming tool in a RDB process. It is mainly used to counter act the bending moments during bending operations [3]. Conventionally, pressure dies are made according to the size of the tube. Larger pressure dies are made for tubes with higher diameters and vice versa [4]. The circumferential surface of the Pd must be the same as that of outer diameter of the tube. For medium scale tube bending operations, a standard length of 160 mm is used for Pd [5]. Most of the tube bending industries are presently using this length as standard for medium sized tube bending operations. Significant research work has already been done to investigate the effect of forming tools on the quality of bent tubes in RDB processes. Heftrich et al. demonstrated that the complete circumferential surface area of forming tools do not come in-contact with the tube during a bending operation. He demonstrated that only certain portions on the surface of bend die come in contact with the tube and hence all the stresses are localized on these portions [6]. Kaleem et al. [7] demonstrated that the increasing magnitude of contact forces between forming tools and tube indirectly effect the tube’s ovality. Borchmann et al. [8] identified that specific process parameters are required to produce wrinkle free tubes. She presented the influence of forming tools positions on the bending process. It was shown that wrinkle free tubes are produced when the collet speed is in a ratio of 1.0 with the tube speed. It was also demonstrated that Pd must remain in-contact with the tube or a maximum clearance of 0.4 mm is tolerated before emergence of wrinkles on the tube. A Pd is typically manufactured for only large scale productions. It is conventionally made from alloy steels using conventional/subtractive manufacturing techniques. This makes them substantially expensive for individualized productions. Frohn-Sörensen et al. [9] demonstrated the possibility of manufacturing forming tools using polymeric materials. He compared the mechanical properties of various polymers suitable for additive tooling and their subsequent use in rubber pad forming of sheet metals. It was concluded that PLA is a suitable material for fabricating forming tools. However, an in-depth study of process conditions is necessary before incorporating polymeric tools in forming processes. Presently, FE-simulations are widely used to carry out an in-depth process analysis of RDB processes [6]. A high level of accuracy in FE-simulations results is necessary to identify high-stressed areas on surfaces of the forming tools. The identification of high-stressed area in forming tools provides a sound basis to re-design these tools for better performance in terms of flexibility and cost-effectiveness.
2 Literature review
In the past few years, a state of the art progress has been made in the domain of topology and shape optimization methods. Allaire et al. [10] proposed shape optimization method based on classical shape derivative and level set methods. He demonstrated that his method could handle mechanical models having non-linear elasticity and design dependent loads. Sigmund et al. [11] conducted a brief review on topology optimization approaches. He identified that most of the evolutionary methods in topology optimization are converging towards discrete SIMP schemes and density projection methods are similar to parameterized level set approaches. He highlighted that most of the commercial codes are tightly linked to commercially available FE solver softwares. In his opinion, the ‘Ease of Use’ is a challenge when one tries to understand the algorithms of topology optimization. Recently, substantial progress is done in the field of CAD compatibility with topology optimization based on non-uniform rational basis entities (NURBS). Montemurro et al. [12] integrated Huber Hencky von mises criterion specific for isotropic material into a density based algorithm for topology optimization. He studied the influence of stress and problem formulation on the topology optimization. It was concluded that substantial care should be taken on the step of problem formulation. In another study, Montemurro et al. [13] conducted experiments in which topological descriptor (pseudo-density field) is represented through NURBS hyper surface. He observed that since descriptor at each scale is NURBS entity therefore final outcome does not depend on the quality of mesh in FE-simulation. In case of RDB processes, significant research is done to identify the outcomes of RDB processes through FE-simulations. Simonetto et al. [14] investigated the springback in RDB process using FE simulations. Tronvoll et al. [15] compared the processes of compression bending and RDB process using FE-based stress analysis. On the other hand, topology optimization of tools in forming processes is a novel concept. So far, a very few research articles are found in this context. Engelhardt et al. [16] highlighted the possibility of optimizing die designs based on FE-simulations. Geueke et al. [17] demonstrated the possibility of structural optimization of tools for flexible sheet metal forming processes. These research articles highlighted the possibility of manufacturing topology optimized forming tools, however from an industrial perspective, the topology optimized forming tools are not yet designed for application in metal forming processes till to-date. The advantage of topology optimization entails development of light weight and cost effective forming tools particularly designed for individualized or small scale productions.
The tremendous advancement in the field of topology optimization warrants its application in the existing industrial processes. In order to design topology optimized forming tools for RDB processes, a multi-disciplinary approach is needed. An understanding of three discrete disciplines is deemed necessary. These are: first, an identification of process conditions of the understudy manufacturing process; second, an accurate FE-simulation to identify constraints particularly high stressed and in-contact surfaces of tools and third, basic understanding of topology optimization methods. Recent versions of many commercially available FE-solver softwares have incorporated topology optimization module in their processing database. This has made it convenient to inter-link process conditions of industrial processes with topology optimization requirements of the softwares. Autodesk-INVENTOR uses a combination of SIMP and Level-Set methods for topology optimization [18]. In INVENTOR, the meshing is done in AUTOMESH module therefore only process constraints, material properties and pre-processing boundary conditions are required to be fed to the software. In this paper, a combination of two FE-solver softwares are used for tool analysis. The topology optimization of a forming tool (Pd) is done in INVENTOR and a FE-simulation of a RDB process is conducted in a specialized tube forming software PAMSTAMP. The CAD models are transported from INVENTOR to PAMSTAMP and vice versa.
This research paper contributes to incorporate and apply topology optimization in existing production setups. The manuscript demonstrates that the topology optimized lightweight 3D printed polymeric forming tools are a cost effective alternative to comparatively heavy alloy steels. As a test case, a forming tool (Pd) is designed by using topology optimization and tested in an industrial tube bending process. The FE-simulation results serve as the basis to conduct topology optimization of Pd. The performance of topology optimized pressure die is compared with its conventional counterpart. In the end, a cost comparison is made between conventional (metallic) pressure die and topology optimized (polymeric) pressure die using cost performance index.
The block diagram presenting the work flow of this research paper is shown in Fig. 2. Sections 1 and 2 include introduction and literature review. Section 3 includes the development of an accurate FE-simulation model of a RDB process with conventional Pd, material selection, topology optimization and 3D printing of topology optimized Pd. Section 4 shows the performance results after use of topology optimized Pd in a RDB process and cost comparison via cost performance index. Sections 5 and 6 are discussions and conclusion.
3 Methodology
3.1 FE-Simulation model of RDB process
A RDB process is a forming process used for bending metallic tubes [2]. Unlike typical manufacturing processes, a RDB process depends largely on the process parameters. Bending factor (B) and wall factor (W) are the two fundamental process parameters which must be selected before conducting a RDB process [15]. In this research, the standard values of B = 1.5 and W = 22 are used as these values are commonly seen in most of the tube bending operations. B and W are numerically calculated by using Eqs. (1 and 2) respectively:
A list of process parameters used in this research is shown in Table 1. These parameters produce wrinkle free tubes as identified by Borchmann [8]. Here, the FE-simulation of the RDB process is conducted in the software PAMSTAMP. A mesh size of 1.00 is selected. A total number of 28,429 shell elements, 27,583 nodes and 56,002 edges are created. Hill plasticity law and Krupkowsky strain hardening curves are used. The criteria used for FE-simulation are chosen according to the sensitivity analysis conducted by Borchmann [19]. The standard coefficients of friction (COFs) of each forming tool are used for FE-simulation (see Model-1 in Table 1). The ovality obtained from FE-simulation at a radial angle ϴ = 45° is shown in Fig. 3 (red). The ovality of bent portion of tube can be calculated numerically by using Eq. (3) below:
For comparison, a RDB process with identical process parameters is practically conducted on a RDB machine. The ovality of the practically bent tubes is shown in Fig. 3 (blue). A noticeable difference is observed in the FE-simulation and practically bent tubes. In order to enhance the accuracy of FE-simulation, the COFs of forming tools are slightly modified (as shown in model-2, Table 1) [20]. This is done because sliding surfaces of forming tools are more polished as compared to other surfaces and therefore offer less friction as compared to standard material COFs provided by the material manufacturers [21]. Moreover, there is some grease left on tubes after manufacturing which is not completely removed even after cleaning. The slight presence of grease also contribute to decrease in COF values. The FE-simulation is run again with the modified COFs. The ovality of the bent portions of the tube obtained from modified COFs is shown in Fig. 3 (green). The values of initial COFs (Model-1) and modified COFs (Model-2) are shown in Table 1.
The accuracy of FE-simulation has a paramount importance in this research paper. This is because the stressed areas on the surface of Pd are provided by FE-simulations and further topology optimization is conducted on the basis of high stressed areas. In order to obtain an in-depth comparison of FE-simulations and practical experiments, an ‘Accuracy-Meter’ is designed which provides a comprehensive quality analysis of the bent tubes. Here, two model of FE-simulations (as mentioned in Table 1) are compared with the practically bent tubes in the Accuracy-Meter. Three tube samples are practically with consistency. The comparison results of initial FE-simulation (model-1), the modified FE-simulation (model-2) and practically bent tubes are shown by the Accuracy-Meter in Fig. 4. Model-2 showed enhanced accuracy of FE simulation as compared to model-1. Hence, the COF values of model-2 are used for further analysis in this paper.
3.2 Material selection
Few recently published research papers have suggested the possibility of manufacturing forming tools by polymeric materials. Frohn-Sörensen et al. [22] demonstrated the possibility of using polymeric forming tools for small scale productions. He conducted experiments on comparatively stiff polymeric materials and found out that mechanical properties of some polymeric materials are quite suitable for 3D printing and subsequent use in forming processes like RPF process (Rubber Pad Forming). It was demonstrated that PLA is a suitable material for additive tooling at a compression strength of 75 MPa and an ultimate flexural strength of 105 MPa and layer thickness of 0.2 mm [23]. The material selected for 3D printing of topology optimized Pd is ecoPLA. The material is commercially available at local and online platforms. In this research paper, the material has been procured by a private materials manufacturing company 3DJAKE GmBH. The material ecoPLA is available in black filaments with material properties: young’s modulus = 3.2 GPa, yield strength = 78 MPa and poisson’s ratio = 0.35 [24]. The material of the tube is standard stainless steel AISI 304 or EN-1.4301(X5CrNi18-10) having young’s modulus = 210 GPa, yield strength = 505 MPa and poisson’s ratio = 0.3.
3.3 Stress pattern on surface of conventional pressure die (Pdmetal)
The contact stress distribution on the surface of Pdmetal is provided by the FE-simulation. The shell elements of Pdmetal are replaced by volume elements [25, 26]. This is done so as to incorporate accurate material behaviour in the simulation. A total of 56,705 volume elements are created. The FE-simulation criteria is the same as mentioned in Sect. 3.1 and Table 1. The material properties of the alloy steel are: young’s modulus = 210 GPa, yield strength = 1750 MPa, poisson’s ration = 0.3 and density = 7.72 × 10−6 kg/mm3. The pressure pattern on the surface of Pdmetal (at a bending angle of α = 45° in RDB) is shown in Fig. 5.
The Pd made from the polymeric material ecoPLA is mentioned here as Pdpolymer. In FE-simulation model, the material of Pdmetal is replaced by thermoplastic polymer ecoPLA. The material properties of ecoPLA are fed to the software (young’s modulus = 3.25 GPa, yield strength = 78 MPa, poison’s ratio = 0.35 and a density = 1.24 × 10−6 kg/mm3). The geometric dimensions of Pdpolymer are kept exactly the same as that of Pdmetal so that a response exhibited by polymeric material can be observed. The FE-simulation showed that the pattern of the contact stresses on the surface of Pdpolymer are almost the same as that of the Pdmetal. However, the magnitude of pressures and contact forces are increased. The contact stress pattern experienced by the Pdpolymer at radial angle of ϴ = 45° is shown in Fig. 6.
3.4 Topology optimization of pressure die
Topology optimization can be conducted by different approaches. Some of the fundamental approaches used for topology optimization are level-set, density, phase-field, topological-derivative, evolutionary approach etc. Each approach is aimed to place required material within a pre-set design in order to obtain best performance from a pre-set design [10]. Presently, a combination of these approaches generally known as hybrid approach is used for topology optimization [10]. Due to substantial computational complexity associated with every approach (and particularly hybrid approach), many industrial FE-solver softwares have provided an in-built module of topology optimization at the interface. Autodesk-INVENTOR uses a combination of two significant approaches to conduct topology optimization. These are density (SIMP) and level set approaches [18]. SIMP is versatile in terms of additive design. It provides an option to introduce holes at any time during optimization process and the results are insensitive to starting volume fraction [18]. The penalization criteria of different vectors and tensors involved during the analysis is automatically selected be the software. On the other hand level-set approach provide explicit constraints formulation on the boundary. Hence, it provides convenience to integrate shape with the topology optimization algorithm. In nutshell, the software uses the combination of density and level set approaches in such an adroit way that an efficient convergence criteria is selected. It is also worth mentioning that there is a difference between shape optimization and topology optimization. Although both these terms are sometimes used interchangeably yet in case of shape optimization, the topology is mostly maintained and only the dimensions are changed. In case of topology optimization, layouts are modified based on dimensional constraints. This implies that spaces may be created within the object and the topology of the design is changed along with its exterior geometry.
In this study, the FE-simulation results (shown in Sect. 3.3) highlighted that the front portion on circumferential surfaces of the pressure die experience contact normal stresses whereas the rear portion is almost entirely un-used. Therefore, the rear portion of Pd is removed in the CAD model and the length of conventional Pd is reduced to half of its original value (i.e., 160 mm is reduced to 80 mm). The circumferential area, width and height of the Pd are kept the same at this stage (see Step 4 in Fig. 7). The CAD model of shortened Pd is then subjected to topology optimization in the software Inventor. The constraints of stress locations and magnitudes on the surface are added. The software generates a new topology based on provided constraints and pre-processing boundary conditions (mentioned in Table 1 as process conditions). The material properties of ecoPLA are fed to the software. Meshing is done using the auto-mesh module. The software carried out the topology optimization of Pd in less than 20 min. After topology optimization, external dimensions of the CAD model of shortened Pd are modified manually according to geometry provided by topology optimization (see step 7 in Fig. 7). This is done to keep margins of safety. The new design after topology optimization and subsequent modification is called herein as PdTOpolymer. The whole process of topology optimization of Pd along with respective stepwise descriptions is appended below in Fig. 7.
-
Step 1: Obtaining contact normal pressure distribution on the surface of Pdmetal using FE-simulation.
-
Step 2: Making CAD model of Pdpolymer with identical dimensions.
-
Step 3: Obtaining contact normal pressure distribution on the surface of Pdpolymer using FE-simulation.
-
Step 4: Shortening the length of Pdpolymer from 160 to 80 mm. Length with unused surfaces is omitted.
-
Step 5: Topology Optimization using combination of SIMP (Solid Isotropic Material Penalization) and Level-Set methods in the software Autodesk Inventor.
-
Step 6: Shape Comparison of topology optimized Pd with shortened Pd.
-
Step 7: Modifying the dimensions of shortened Pdpolymer according to the dictates of topology optimization results while leaving the safety margins. The final model is called PdTOpolymer.
-
Step 8: Testing the CAD model of PdTOpolymer in RDB process using FE-simulation and PAMSTAMP and obtaining the contact pressure distribution pattern on the surface of PdTOpolymer.
-
Step 9: Fabrication of PdTOpolymer by additive manufacturing (Fused Deposition Modelling) for subsequent experimental tests.
3.5 3D Printing and practical testing of PdTOpolymer
The PdTOpolymer is practically 3D printed by ecoPLA using the FDM (Prusa MK-4) 3D Printer [24, 27]. The print parameters used for 3D printing of PdTOpolymer are mentioned in Table 2. The 3D printed PdTOpolymer is installed and practically tested on an industrial RDB machine (RBV-35 by WAFIOS). The process parameters are mentioned in Table 1. The bending angle is 90° which means that the tube is bent from 0° to 90°. Three tube samples are bent. The practical experiment yielded wrinkle free tubes with identical quality aspects. The process setup is shown in Fig. 8.
4 Results
4.1 Contact forces
The PdTOpolymer is used successfully in the RDB process without any noticeable failure during or after the process. No cracks or geometric deviations were noticed either. In a typical RDB process, the contact forces experienced by a Pd are larger than the combined contact forces experienced by the mandrel and the wiper die [28]. In other words, the Pd counteracts the bending forces applied by the wiper die and the mandrel [29]. Here, the contact forces in a RDB process using conventional Pd (Pdmetal) and topology optimized Pd (PdTOpolymer) are compared as shown in Fig. 9. For simple visualization, the surface normals of Pd are reversed so that the magnitude of contact forces of all forming tools lie in same XY plane [30]. In both the cases, pressure die effectively counteracts the contact forces applied by other forming tools (mandrel and wiper die). Hence, it is manifested that the process is conducted smoothly.
4.2 Contact stresses on surface
The contact stress pattern (or pressure distribution pattern) on the circumferential surfaces of pressure dies are obtained from FE-simulation. The stress pattern obtained on the mating surfaces of both pressure dies (Pdmetal and PdTOpolymer) is shown in Fig. 7 (step 1 and step 8). An average stress is obtained by taking the average of all pressure ranges manifested in a particular stress pattern [31]. A comparison of an average stress exerted on the surfaces of a conventional pressure die (Pdmetal) and topology optimized pressure die (PdTOpolymer) is shown in Fig. 10. The average stresses are plotted against bending angles from 0° to 90°. It can be seen that almost a constant value of stresses is experienced by conventional pressure die (Pdmetal) whereas a sinusoidal pattern of stresses is experienced by topology optimized pressure die (PdTOpolymer).
4.3 Effective areas of pressure dies
The contact forces (Fig. 9) and stress magnitudes (Fig. 10) on the surface of Pd are identified by FE-simulations. The effective area can be calculated numerically by using Eq. (4). [32]. The effective and total circumferential areas of the under investigation pressure dies (Pdmetal and PdTOpolymer) are calculated by using Eqs. (5 and 6) mentioned below:
An effective area is the circumferential area which experiences any stress/pressure (or force) during the entire bending operation [33]. The effective and total circumferential areas of Pdmetal and PdTOpolymer are shown in Fig. 11. The total area of the pressure dies is constant throughout the bending operation and is shown by dashed lines. The unused areas of both pressure dies are shown by double sided hollow arrows.
4.4 Computational complexity
Topology optimization approaches are often associated with computational complexities [34]. One of the common problem associated with most of the approaches is that these methods are applied only for minimization problems whereas an arbitrary physical problems are sometimes not addressed by the algorithm [10]. Mesh convergence is also considered a significant challenge in the optimization processes. In case of mesh convergence, the number of iterations in optimization process should be independent of mesh refinement used in a particular approach [10]. Likewise, in case of an asymptotic behaviour of algorithms some approaches are quite in-efficient to starting guesses however they get efficient in later stages of design process. Particularly, SIMP methods have difficulties in defining objective and constraints on the boundaries, they need an extra process to integrate shape/topology and they need filtering to prevent checker boarding [18]. On the other hand, level set methods are restricted to generate geometry from existing boundaries, they have problems to introduce new holes, their results strongly depend on the starting guesses and they need special arrangements on the boundary to prevent oscillations and too fast growth. The problems associated by each of these approaches (SIMP and level set) are addresses by using a hybrid approach which utilize the benefits of each of these two approaches and address the complexities in a comparatively wholesome way [18, 35]. For the understudy process in this paper, topology optimization is carried out by using the hybrid approach (SIMP and level set method). The algorithm is automatically adopted and adjusted by the software (see Sect. 3.4). The pre-processing boundary conditions (Table 1) and stress constrains (Sect. 3.3) are relatively simple in problem definition. The overall processing time of topology optimization is less than 20 min. This processing time is however only relevant to the understudy design of the Pd in a RDB process. The processing time will increase with an increase in the complexity of the process and design.
4.5 Cost performance index
The geometric dimensions of Pdmetal and PdTOpolymer are shown in Table 3. A significant decrease in the weight and volume is observed between Pdmetal and PdTOpolymer.
The Ashby chart is widely used to conduct cost comparison of designed parts made from different materials [36]. It provides a cost performance index based on the stiffness of materials. A higher cost performance index represent better stiffness to weight performance and vice versa [37]. Table 4 represents the cost performance index of Pdmetal and PdTOpolymer. The cost per part is calculated by multiplying the cost/kg with respective volume of the Pd. Here, only the material costs are considered.
5 Discussions
The fluctuating magnitude of stresses manifested by topology optimized polymeric pressure die (as seen in Fig. 10) is attributed to the comparatively low stiffness value of PLA. Although the young’s modulus of ecoPLA (3.25 GPa) is considerably high when compared with other polymeric materials [38], yet it is far less than that of metals (alloy steel = 210 GPa). Hence, the softer polymer provides a springiness effect which absorbs and releases the applied pressure in an alternating way and hence a fluctuating and sinusoidal pattern of stress magnitudes is manifested [39]. This reason is complemented by the fact that counter acting forces (contact forces) provided the PdTOpolymer are significantly higher in response as compared to highly stiff Pdmetal (see Fig. 9 in which contact forces of PdTOpolymer are significantly more than Pdmetal). The less stiff polymeric material with comparatively high springiness effect generates more counteracting forces as compared to highly stiff (almost non deformable in this case) metallic material [40]. The fluctuating stresses have not affected the understudy RDB process, however owing to low yield strength of polymeric materials it is envisaged that in case of large scale bending operations, these fluctuating stresses can cause significant problems and hence polymeric materials would not be able to withstand high stresses.
In Fig. 9, it is observed that the contact forces experienced by PdTOpolymer are substantially greater than the forces experienced by Pdmetal. This is also attributed to comparatively low stiffness of polymeric materials. The polymeric material is compressed and released in a regular pattern and therefore high contact forces result due to greater inertia of larger released material. In other words, it is the sinusoidal counteraction of polymeric material. This is also the reason that the contact forces manifested by PdTOpolymer show a fluctuating increase as compared to static increase of contact forces experienced by Pdmetal (see Fig. 10). On the other hand, the increase in contact forces of wiper die used with PdTOpolymer is manifested due to counter acting of forces [41]. Since it is known that the wiper die and the mandrel counteract the contact force of the pressure die, therefore an increase in contact forces on the pressure die will be accompanied by an increase in the contact forces of the wiper die [42]. Another reason which contributes to this effect is the difference in COF values. The COF of PLA is 0.3 whereas the COF of polished surfaces of tool steel ranges around 0.1 [43]. A high friction impedes the movement of tube and mated surfaces remain in contact for larger durations thereby causing an increase in contact forces [44]. Although the frictional forces act in tangential direction with respect to the motion of the tube, yet the impeding friction force causes minute time delays during mating contact and hence more opportunity for the tube to affect the contact surface of PdTOpolymer.
The effective area of PdTOpolymer also represents a sinusoidal curve. However, this sinusoidal curve is less prominent as compared to the sinusoidal curve of the contact normal stresses. This is mainly due to the increased contact forces applied by PdTOpolymer. For a particular area, forces and pressures are directly proportional to each other [45]. Therefore, the increase in contact forces applied by PdTOpolymer is partly compensated by increasing stresses and vice versa. A sinusoidal pattern of effective area means that mated contact between tube and PdTOpolymer increase and decrease in an alternating manner. These alternating sinusoidal fluctuations of stresses are insignificant for the under investigated process. However, for RDB processes with extreme values of B and W, the sinusoidal fluctuations of stresses may pose problems leading to an increased sensitivity towards wrinkling or ovality.
A cost comparison based on the material volume used in each Pd (Pdmetal and PdTOpolymer) manifest that topology optimized Pd is significantly better than conventional Pd. The cost comparison is carried out by taking material performance into account. The manufacturing costs are not considered. On the other hand, modern polymer based 3D printers commonly known as FDM printers are also widely known to be less expensive as compared to conventional CNC milling or subtractive metal cutting machines.
6 Conclusion
A Pd is a fundamental forming tool used in RDB processes. It is conventionally made from alloy steels. This research demonstrates the successful use of a light weight and cost effective polymer made Pd in a RDB process. It is shown that the surface area of a conventional Pd made from an alloy steel is not utilized to a full extent during the bending operation. Therefore, the length of Pd is shortened to include only those areas which are effectively used during the bending operation. The topology of Pd is optimized by FE-solver software Inventor which uses a combination of SIMP and Level-Set methods. The final design obtained after topology optimization and is herein called as PdTOpolymer. The PdTOpolymer is 3D printed by polymeric filaments of PLA. The 3D printed PdTOpolymer is practically tested on an industrial RDB machine. The tubes bent by practical experiments show flawless consistency without failure. Hence, it is demonstrated that polymer made 3D printed pressure die is as effective in performance as is its metallic counterpart. The advantage of using PdTOpolymer is that it is substantially light in weight, compact in volume and significantly cost effective. The cost performance index of PdTOpolymer is substantially high as compared to Pdmetal (PdTOpolymer = 3.45 and Pdmetal = 0.20). On the other hand, a fluctuating pattern of applied stresses is experienced by PdTOpolymer. The fluctuating stresses do not disturb the outcomes of the understudy RDB process. However, it is envisaged that problems may occur if bending operations with larger bending radii (B > 3) are conducted by using polymeric forming tools. Moreover, polymeric forming tools are only recommended to be used for small scale and individualized productions.
This research is conducted to incorporate state of the art regime of topology optimization in industrial forming processes. The intention is to widen the avenue of cost-effective manufacturing by designing and testing forming tools made from cost effective materials.
Abbreviations
- RDB:
-
Rotary draw bending
- TO:
-
Topology optimization
- Pd:
-
Pressure die
- Pdpolymer :
-
Polymeric pressure die
- Pdmetal :
-
Metallic pressure die
- PdTOpolymer :
-
Topology optimized polymeric pressure die
- Vtube :
-
Tube velocity
- B:
-
Bending factor
- W:
-
Wall factor
- PLA:
-
Polylactide acid
- FDM:
-
Fused deposition modelling
- FC :
-
Contact force
- PCN :
-
Contact normal pressure/contact normal stress
- SIMP :
-
Solid Isotropic material penalization
- COF:
-
Coefficient of friction
- bR :
-
Base of radial curve of pressure die
- hR :
-
Height of radial curve of pressure die
- lpd :
-
Length of conventional pressure die
- ltpd :
-
Length of topology optimized polymeric pressure die
- Atotal :
-
Total surface area
- Aeffective :
-
Effective area on the surface
References
Kaleem, M.A., Frohn-Sörensen, P., Nebeling, D., Engel, B.: Refinement of process parameters in rotary draw bending processes. In: International conference on the technology of plasticity, pp. 359–370. Springer, Cham (2023)
Safdarian, R., Kord, A.: Experimental investigation of effective parameters in the tube rotary draw bending process. Mater. Res. Express 6(6), 066531 (2019)
Borchmann, L., Frohn-Sörensen, P., Engel, B.: In situ detection and control of wrinkle formation during rotary draw bending. Proc. Manuf. 50, 589–596 (2020)
Engel, B., Hassan, H.R.: Investigation of neutral axis shifting in rotary draw bending processes for tubes. Steel Res. Int. 85(7), 1209–1214 (2014)
Engel, B., Hassan, H.: Advanced model for calculation of the neutral axis shifting and the wall thickness distribution in rotary draw bending processes. Int. J. Mater. Metall. Eng. 9(2), 239–243 (2015)
Heftrich, C., Steinheimer, R., Engel, B.: Rotary-draw-bending using tools with reduced geometries. Proc. Manuf. 15, 804–811 (2018)
Kaleem, M.A., Frohn-Sörensen, P., Geueke, M., Engel, B.: The way forward in rotary draw bending: a review. (2023)
Borchmann, L., Heftrich, C., Engel, B.: Influence of the stiffness of machine axes on the formation of wrinkles during rotary draw bending. SN Appl. Sci. 2, 3 (2020)
Frohn-Sörensen, P., Geueke, M., Tuli, T.B., Kuhnhen, C., Manns, M., Engel, B.: 3D printed prototyping tools for flexible sheet metal drawing. Int. J. Adv.Manuf. Technol. 115(7–8), 2624 (2021)
Allaire, G., Jouve, F., Toader, A.M.: Structural optimization using sensitivity analysis and a level-set method. J. Comput. Phys. 194(1), 363–393 (2004)
Sigmund, O., Maute, K.: Topology optimization approaches: A comparative review. Struct. Multidiscip. Optim.. Multidiscip. Optim. 48(6), 1031–1055 (2013)
Roiné, T., Montemurro, M., Pailhès, J.: Stress-based topology optimization through non-uniform rational basis spline hyper-surfaces. Mech. Adv. Mater. Struct. 29(23), 3387–3407 (2022)
Montemurro, M., Bertolino, G., Panettieri, E.: Topology optimisation of architected cellular materials from additive manufacturing: analysis, design, and experiments. Structures 47, 2220–2239 (2023)
Simonetto, E., Ghiotti, A., Bruschi, S.: In-process measurement of springback in tube rotary draw bending. Int. J. Adv. Manuf. Technol. 112, 2485–2496 (2021)
Tronvoll, S.A., Ma, J., Welo, T.: Deformation behavior in tube bending: a comparative study of compression bending and rotary draw bending. Int. J. Adv. Manuf. Technol. 124(3–4), 801–816 (2023)
Engelhardt, M., Kurmajev, S., Maier, J., Becker, C., Hora, P.: The application of FEA for optimization of die design. Mater. Today Proc. 10, 226–233 (2019)
Geueke, M., Frohn-Sörensen, P., Reuter, J., Padavu, N., Reinicke, T., Engel, B.: Structural optimization of additively manufactured polymer tools for flexible sheet metal forming. Proc. CIRP 104, 1345–1350 (2021)
https://www.autodesk.com/autodesk-university/class/Topology-Optimization-Autodesk-Nastran-CAD-2017#presentation (slide 14). Accessed 15 April 2024
Borchmann, L., Kuhnhen, C., Frohn, P., Engel, B.: Sensitivity analysis of the rotary draw bending process as a database of digital equipping support. Proc. Manuf. 29, 592–599 (2019)
Sadeghi, S.H., Peters, T.: Adjusted friction correction factors for center-pivots with an end-gun. Irrig. Sci.. Sci. 31, 351–358 (2013)
Podgornik, B., Hogmark, S.: Surface modification to improve friction and galling properties of forming tools. J. Mater. Process. Technol. 174(1–3), 334–341 (2006)
Frohn-Sörensen, P., Geueke, M., Tuli, T.B., Kuhnhen, C., Manns, M., Engel, B.: 3D printed prototyping tools for flexible sheet metal drawing. Int. J. Adv. Manuf. Technol. 115(7–8), 2630 (2021)
Frohn-Sörensen, P., Geueke, M., Engel, B., Löffler, B., Bickendorf, P., Asimi, A., Schuh, G.: Design for 3D printed tools: mechanical material properties for direct polymer additive tooling. Polymers 14(9), 1694 (2022)
https://3d.nice-cdn.com/upload/file/TDS_ecoPLA_v1.4.pdf. Accessed 15 April 2024.
Mikihito, H., Yoshito, I.: A simplified FE simulation method with shell element for welding deformation and residual stress generated by multi-pass butt welding. Int. J. Steel Struct. 16, 51–58 (2016)
Parente, M.P.L., Valente, R.F., Jorge, R.N., Cardoso, R.P.R., de Sousa, R.A.: Sheet metal forming simulation using EAS solid-shell finite elements. Finite Elem. Anal. Des. 42(13), 1137–1149 (2006)
https://www.prusa3d.com/product/original-prusa-mk4-2. Accessed 15 April 2024
Safdarian, R.: Investigation of tube fracture in the rotary draw bending process using experimental and numerical methods. Int.J. Mater. Form.. Mater. Form. 13(4), 493–516 (2020)
Wu, W., Zhang, P., Zeng, X., Jin, L., Yao, S., Luo, A.A.: Bendability of the wrought magnesium alloy AM30 tubes using a rotary draw bender. Mater. Sci. Eng. A 486(1–2), 596–601 (2008)
Irving, G., Teran, J., Fedkiw, R.: Invertible finite elements for robust simulation of large deformation. In: Proceedings of the 2004 ACM SIGGRAPH/Eurographics symposium on computer animation, pp. 131–140 (2004)
Frink, L.J.D., van Swol, F.: A common theoretical basis for surface forces apparatus, osmotic stress, and beam bending measurements of surface forces. Colloids Surf. A 162(1–3), 25–36 (2000)
Bachus, K.N., DeMarco, A.L., Judd, K.T., Horwitz, D.S., Brodke, D.S.: Measuring contact area, force, and pressure for bioengineering applications: using Fuji Film and TekScan systems. Med. Eng. Phys. 28(5), 483–488 (2006)
Kersting, P., Gröbel, D., Merklein, M., Sieczkarek, P., Wernicke, S., Tekkaya, A.E., Willner, K.: Experimental and numerical analysis of tribological effective surfaces for forming tools in sheet-bulk metal forming. Prod. Eng. 10, 37–50 (2016)
Christiansen, A.N., Bærentzen, J.A., Nobel-Jørgensen, M., Aage, N., Sigmund, O.: Combined shape and topology optimization of 3D structures. Comput. Graph.. Graph. 46, 25–35 (2015)
Jansen, M., Pierard, O.: A hybrid density/level set formulation for topology optimization of functionally graded lattice structures. Comput. Struct. 231, 106205 (2020)
Ashby, M.F., Johnson, K.: Materials and design: the art and science of material selection in product design. Butterworth-Heinemann (2013)
Ashby, M., Cope, E., Cebon, D.: Materials selection for engineering design. In: Informatics for materials science and engineering, pp. 219–244. Butterworth-Heinemann, (2013)
Lin, S., Cao, C., Wang, Q., Gonzalez, M., Dolbow, J.E., Zhao, X.: Design of stiff, tough and stretchy hydrogel composites via nanoscale hybrid crosslinking and macroscale fiber reinforcement. Soft Matter 10(38), 7519–7527 (2014)
Wool, R.P.: Morphological mechanics of springy polymers. J. Polym. Sci. Polym. Phys. Ed. 14(4), 603–618 (1976)
Şirin, Ş, Aslan, E., Akincioğlu, G.: Effects of 3D-printed PLA material with different filling densities on coefficient of friction performance. Rapid Prototyp. J. 29(1), 157–165 (2023)
Okude, Y., Sakaki, S., Yoshihara, S., MacDonald, B.J.: Increasing the working limit of extruded aluminum tubes during draw bending by introducing a wiper die. Mater. Trans. 53(5), 875–878 (2012)
Xue, X., Liao, J., Vincze, G., Gracio, J.J.: Modelling of mandrel rotary draw bending for accurate twist springback prediction of an asymmetric thin-walled tube. J. Mater. Process. Technol. 216, 405–417 (2015)
Baumgart, E.: Stiffness—an unknown world of mechanical science. Injury 31(Suppl 2), B14-23 (2000)
Popov, V.L.: Contact mechanics and friction, pp. 231–253. Springer, Berlin (2010)
Middleton, J., Sinclair, P., Patton, R.: Accuracy of centre of pressure measurement using a piezoelectric force platform. Clin. Biomech.. Biomech. 14(5), 357–360 (1999)
Acknowledgements
The authors are thankful to DAAD (Deutscher Akademischer Austauschdienst) – Germany and the institute of Forming Technology, UTS – Siegen, for providing the funding and resources to conduct this study.
Funding
Open Access funding enabled and organized by Projekt DEAL. Funding was provided by Universität Siegen (Grant number: 1673610).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
Open access publication costs are provided by the ‘University of Siegen’. The authors have no competing interests to declare that are relevant to the content of this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kaleem, M.A., Steinheimer, R., Frohn-Sörensen, P. et al. Topology optimization of forming tools: pressure die in rotary draw bending process. Int J Interact Des Manuf (2024). https://doi.org/10.1007/s12008-024-01932-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12008-024-01932-w