1 Introduction

The expansion of drive concepts in the automotive industry is increasingly necessitating smaller batch sizes. Due to customer demands for a variety of variants and different vehicle types, product individualization will increase Kuhnhen et al. [1].

Individual products require set-up procedures at ever shorter intervals to adjust the forming process Borchmann et al. [2]. The set-up processes are made more difficult by the fact that the size progression and influence of variables such as axis displacements, structural inhomogeneities and fluctuations in material properties cannot be predicted Tekkaya et al. [3]. In order to investigate the effects of axis displacements on the quality of bending components, FE simulations were carried out in this paper. Results of investigations on the influence of axis displacements on the quality characteristic wrinkle formation according to VDI 3431 [4] are presented.

The influences on wrinkle formation in RDB can be divided into the areas semi-finished product, tool and machine as well as process control. The positioning of the wiper die and the pressure die is important, since the force transmission between pressure die, tube and wiper die that occurs during bending has a decisive influence on the height of wrinkles. Changes in the tool positions can be caused by bending up and deformation of the tools and the machine. The stiffness of each tool and each machine axis is therefore of great importance for the bending result.

The paper is divided into eleven chapters. Chapters 2–4 describe the state of the art and the preparatory work carried out. Chapters 5 and 6 explain the FE simulations conducted, the results of which are described and discussed in chapters 7 and 8. Chapter 9 shows the measurement of the axis stiffnesses at the machine. The comparison of results of FE simulation and practical bending test is presented in chapter 10. The summary and the outlook are given in chapter 11.

2 Rotary draw bending

The rotary draw bending was developed from a workshop technique and adapted to the requirements of series production. The extension of the applicability with simultaneous increase of the repetition accuracy was achieved in particular by programmable logic controls and the attachment of additional elements such as wiper die and controllable pressure die Kuhnhen et al. [1].

As a result, the machines used today have been developed to a standard with which it is possible to produce complex bending tasks for tubes and profiles even in highly automated lines.

To compare bending tasks, the wall thickness factor W is used for semi-finished product description as the quotient of the profile height H in the bending direction and the wall thickness s. The bending factor B is used as the quotient of the bending radius R in relation to the profile height H. With appropriate tool and machine technology, bending ratios of less than 1 can be bent Burkhard and Albrecht [5].

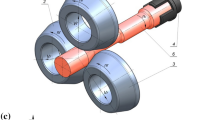
The tool design of the RDB is shown in Fig. 1. The tools bend die (1), clamp dies (2.1, 2.2) and pressure die (3) are necessary for the bending. Bending mandrel (4), wiper die (5) and collet (6) are used optionally.

Fig. 1
figure 1

a and b Tools of the rotary draw bending process Borchmann et al. [2]

Full size image

For bending, according to Hinkel [6], the tube is first clamped between the inner (2.1) and outer (2.2) clamp die in order to transfer the rotation from the machine to the tube. The bending moment is applied by supporting the tube on the pressure die (3). In addition to this main function, the pressure die can also influence the reduction in wall thickness and cross-sectional deformation of the tube by moving in longitudinal direction of the tube. According to Schulte et al. [7] and Borchmann et al. [2], the collet (6), which usually clamps the tube at its end, can also counteract the reduction in wall thickness at the outer bend by running along or pushing forward. The bending mandrel (4) supports the inner wall of the outer bend and thus reduces the cross-sectional deformation in the bend Hassan [8], Fang et al. [9]. The compressive stress on the inside of the tube can lead to the formation of wrinkles on the inside bend perpendicular to the longitudinal axis of the tube. To counteract this, a wiper die (5) can be used in addition to the bending mandrel. Engel and Mathes [10] The wiper die is in contact with the cavity of the bend die and supports the tube.

3 Quality characteristic wrinkle formation

3.1 Formation of wrinkles during rotary draw bending

Bending processes can be designed in advance against crack formation Kuhnhen et al. [1]. The process design against wrinkle formation is much more difficult because a large number of influencing factors are responsible for this error pattern (Fig. 2).

Fig. 2
figure 2

Influence on wrinkle formation Engel and Mathes [10]

Full size image

In addition to the positioning of the individual components, the alignments of the wiper die and the pressure die is of particular importance Simonetto et al. [11]. Further variables influencing the process are bends of the tool and the machine, therefore the stiffness of each tool and each machine axis is important.

To calculate the probability of wrinkling, Zhang et al. [12] examined titanium tubes (CP-Ti) with large diameters and small wall thicknesses. In order to predict the wrinkles more accurately, Liu et al. [13] developed an FE model for bending thin-walled tubes. A greatly simplified determination of the wrinkle formation probability is provided by Strano [14], who has developed software for faster design of bending processes. The influence of parameter variations when bending tubes with outside diameters of 20 mm made of the materials 1Cr18Ni9Ti (AISI 304) and 5A06 was investigated by Chen et al. [15] in FE simulations. Liewald et al. [16] are developing a method for the automated detection of sidewall wrinkles using finite element analysis on deep-drawn car body components. All investigations show that fluctuations to which a bending process is subject have a negative effect on the quality of the bending component. The more robust the process can be designed against its influencing factors, the more reproducible the quality criteria of the bending component can be achieved. Due to the tool contours tied to the product geometry and the adjustable lever arms for force transmission, only small position deviations in RDB process trigger all the major geometric deviations at the tube bend, which cause an increase in the tolerance range of the end component. This is shown, for example, by the bending tests described in Sect. 4, in which a 0.2 mm change in the pressure die in feed makes the difference between a wrinkle-free and a wrinkled component.

3.2 Quantification of wrinkles

The wrinkle formation on the inner arc is quantified by means of the evaluation factor Ω according to Eq. (1) and Fig. 3.

$$\begin{aligned} \varOmega & = \frac{2}{N}\mathop \sum \limits_{i} \left| {\frac{{\Delta A_{i} }}{{H_{i} \cdot \Delta L_{i} }} \cdot \sin \varsigma_{i} } \right| \cdot n_{i} \\ {\text{with}}\quad n_{i} & = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {\varsigma_{i} \ge 0.1} \hfill \\ {0,} \hfill & {\varsigma_{i} < 0.1} \hfill \\ \end{array} } \right.\quad {\text{and}}\quad N = \mathop \sum \limits_{i} n_{i} \\ \end{aligned}$$
(1)

∆Ai is the delta surface between the nominal and actual contour between two nodes. The distance of the Nodes is ∆Li. Nodes are, for example, points from a surface scan of a wrinkled surface, or node points from the mesh of an FE simulated wrinkled component. Two successive nodes are always compared with each other.

Fig. 3
figure 3

Quantification of wrinkles Kuhnhen [17]

Full size image

The factor increases if the angle of inclination ςi (radiant) between two nodes is higher than 0.1 (radiant) Kuhnhen [17]. In this way, the influence of the length of the tube side pieces can be eliminated. Each tube bend has a bend area and two straight tube ends (side pieces). If the wrinkle evaluation factor is determined in each surface node, there are many pairs of points in the straight side areas that do not have a wrinkled contour. The more pairs of points that do not have a wrinkled contour, the smaller the evaluation factor becomes. This is unintentional because the length of the side pieces should not be decisive for the wrinkle evaluation factor. Therefore, the point pairs that have an inclination angle smaller than 0.1 are set to zero, see Eq. (1). In the area of the wrinkle-free side pieces, no surface deviating from the nominal contour is stretched between two points. The angle of inclination in this range is less than 0.1 (radiant). If these points were taken into account in the calculation, the evaluation factor would improve, since little surface would be added up, but would be divided by a large number of points N. This would result in a decrease of the evaluation factor. The length of the side pieces depends on the simulation and in practical tests on the scanning of the tube bend. In order to be able to evaluate tube bends independently of their length, the restriction of the inclination angle in Eq. (1) was taken into account. In addition the influence of measurement noise can be eliminated. A disadvantage of this restriction is that a possible difference in the wrinkle length has no influence on the wrinkle evaluation factor.

Both, primary wrinkles in the side pieces of the tube bend and secondary wrinkles in the actual bend area are taken into account in the evaluation factor Engel and Mathes [10].

3.3 Characteristic of wrinkles in FE simulations

The formation of wrinkles on the tube is caused by compressive stresses only after the tube wall has thickened. The boundary between thickening and bulging of the tube wall depends on influencing variables such as structural inhomogeneities, hardening processes, moduli of elasticity, frictional changes and wall thickness changes. As there is not sufficient knowledge about the size progression and influence of these variables, calculation results for wrinkle formation deviate from practical experiments. Hoffmann et al. [18] and Schapitz [19] The wrinkles depicted in FE simulations are smaller than those of practical tests, which is confirmed by the results of this paper.

The deviation of the simulation is caused by ideal boundary conditions. The displacement of the tool axes is ignored in the simulations. As rigid bodies, the simulated tools are ideally kept rigid in their position.

4 Sensitivity analysis of wrinkle-relevant parameters

Practical experiments were carried out with the TN120 bending machine from Tracto Technik GmbH to investigate the wrinkle characteristics at different actuating variable combinations. Borchmann et al. [2] Tubes made of the material X5CrNi18-10 (material number 1.4301) with an outer diameter of 40 mm and a wall thickness of 2 mm were bent. The bending radius is 75 mm with a bending angle of 90°. The pressure die was moved in transverse direction to contact the tube and was fixed in transverse and longitudinal direction. The wiper die was positioned conventionally. The tube end was fixed in the collet. This allowed a superposition of tensile or compressive stress during forming. The other tube end was clamped in the inner and outer clamp dies. The speed of the collet vcollet was set equal to the theoretical unwinding speed of the tube vtube.

First the infeed of the pressure die axis was varied. The wrinkle height increases as the pressure die axis is moved away from the tube, see Fig. 4. The pressure die position for a wrinkle-free tube bend was called 0 mm. From this position the pressure die axis was moved away from the tube in 0.2 mm steps. While no wrinkles are visible at 0 mm and 0.4 mm, clearly visible wrinkles form at 0.6 mm. Even higher wrinkles are observed at a pressure die infeed of 0.8 mm.

Fig. 4
figure 4

Influence of the variation of the pressure die infeed and the collet speed on the formation of wrinkles

Full size image

In a next step, the speed of the collet was varied in the longitudinal direction of the tube. Figure 4 shows how reducing the collet speed to 0.89 times the tube speed results in a wrinkle-free tube.

The tests show that the process parameters pressure die infeed and collet speed have a significant influence on the wrinkles. This fact suggests that the stiffness of the pressure die, as well as the bend die and wiper die also plays a major role in wrinkle formation.

The aim of this study is to find out how large the influence of tool axis stiffness is on wrinkle formation. This offers the possibility to gain new knowledge about the material flow of formed tubes and to improve FE simulations of rotary draw bending by reducing the difference between the bending results of FE simulations and practical tests.

5 Tool stiffness and machine axis stiffness

According to Doege and Behrens [20], the stiffness of the machine axes is of decisive importance in investigations of the material flow. Kersten [21] measured the stiffness of three machine axes of the TN120 bending machine of Tracto Technik GmbH of the Chair of Forming Technology during Three-Roll-Pushbending.

The spring rate of the deflection roll axis is 30.39 kN/mm, the spring rate of the bending roll axis is 142.86 kN/mm and the spring rate of the support roll axis is 161.94 kN/mm. The deflection roll axis of the Three-Roll-Pushbending corresponds to the bend die axis of the RDB, the bending roll axis corresponds to the outer clamp die axis and the support roll axis corresponds to the pressure die axis. The directions of force of this free-form bending tool and of the rotary draw bending tool differ during the respective bending process, therefore the stiffnesses cannot be transferred. But they should be of the same order of magnitude.

In contrast to machine axis stiffness, tool stiffness refers to the compressibility of the tools. Depending on the modulus of elasticity, the tools are compressed under compressive stress, resulting in displacements of the tube contact surfaces and additional clearance between the tools and the tube during the bending process. The compressibility of the tools has not been considered in the following FE simulations. The elastic deformation of the tool material is smaller than the axis shift, so that the FE simulations focus on the tool displacement caused by the axis shift. The axis shift represents the unintentional movement of the tools during the process. This is caused by a setting behaviour of the components, such as tool holders or guides which are located between the tool and the axis drive. The tools therefore do not receive an elastic modulus. But by measuring the axis stiffness from the leading edge of a tool to its drive, part of the measured displacement is caused by the compressibility of the tool. In this paper the influence of the shifting of machine axes in the form of built-in spring elements is investigated.

Kersten [21] has performed stiffness measurements on the same bending machine as the one described in this paper. He investigated a free-form bending process in which the axis stiffness is of particular importance because the kinematic process is very sensitive to tool movements. Since Kersten [21] measured spring stiffness in the range of 30–160 kN/mm on the bending machine, parameter adjustments in a similar range were made in this paper. In order to emphasize the sensitivity of the axis stiffness and thus to create better equivalence, the same stiffness was applied to all axes. From this value, stiffness variations are performed at higher and lower spring rates.

6 Structure of the FE simulations

6.1 FE simulation setup

FE simulated bending tests were carried out with tubes made of the material 1.4301 with a bending factor of B = 1.5 and a wall thickness factor of W = 40. The specimen has an outer diameter of 40 mm and a wall thickness of 1 mm. The bending angle at the bend die was set to 90°. The FE simulation setup is shown in Fig. 5. The thickness curve of a tube bend with wrinkles is shown as an example.

Fig. 5
figure 5

FE simulation setup

Full size image

The material properties yield strength Rp0,2 = 390 N/mm2, tensile strength Rm = 690 N/mm2 and uniform elongation Ag = 50% were entered and the yield curve was calculated according to Swift [22]. The Young’s modulus was set to 200 GPa. An isotropic behaviour according to von Mises as a special case of Hill 48 was assumed. The FE simulation program PAM STAMP Professional 2019.0 of the ESI-Group, Neu-Isenburg Germany, was used. The used subroutine PAM-TUBE is specialized in tube bending simulations of complex components with small bending ratios.

The semi-finished product in the simulation has a length of 504 mm, was cross-linked with 62 shell elements in circumferential direction and 248 shell elements in longitudinal direction. The net size is thus 2.033 mm. The mid surface of the tube is modeled with deformable square shell elements of the Belytschko–Tsay type and the tools with rigid body elements. The friction between tools and tube is described according to COULOMB. The coefficient of friction was set to 0.15 except for the outer clamp die, which was assigned a coefficient of 0.3. The coefficients were selected according to the measurements of the friction tests for RDB according to Hinkel [6]. The mandrel was designed as a multi body system. The movement between the mandrel balls and the mandrel shaft is therefore kinematically restricted by joints.

In the investigations, a wrinkle-free tube bend with a pressure die distance of 0 mm was regarded as the reference bend. In addition, an already wrinkled tube bend with a pressure die distance of 1 mm was considered as a reference bend. Both tube bends were examined with regard to the influence of the machine axis stiffness on the formation of wrinkles.

6.2 Implementation of spring elements

In contrast to ideally fixed tools, six spring elements were built into the FE simulations to which the tool nodes were attached. If a tool is loaded with a force during the bending process, it springs back according to the entered spring rate. In PAM STAMP the spring element is modeled with bar elements. There the spring rate is defined over a force–displacement-curve. The pressure die and the wiper die were attached to two spring elements transverse to the tube. Both tools are free to rotate. The mandrel was attached to a spring element in the longitudinal direction and the bend die was attached to a spring element in the transverse direction. For the parameter variations, all spring elements were assigned the same spring rate and varied by the same values to investigate the influence of the machine axes with low stiffness compared to the machine axes with high stiffness. The bend die was fixed in the longitudinal direction to the tube because the machine is particularly stiff on this axis and no large displacements are to be expected, as would occur with low stiffness. Figure 6 shows the arrangement of the tools and the spring elements.

Fig. 6
figure 6

Arrangement of tools and spring elements in FE simulations

Full size image

The spring rate is entered by means of a diagram in which the spring displacement is shown on the horizontal axis and the spring force on the vertical axis. Figure 7 shows an example of the spring rate 100 kN/mm.

Fig. 7
figure 7

Entering the spring rate in Pam Stamp Professional 2019.0

Full size image

The FE simulations consist of four stages, see Fig. 8. The first stage corresponds to a preprocess in which the outer clamp die moves outwards so that a distance to the outer wall of the tube is created. The second stage corresponds to the clamping process, in which two spring elements are activated at the ends of the outer clamp die and pull it against the tube with a force of 70 kN. This is followed by the bending process as the third stage, in which all spring elements of the tool are activated and the bend die rotates until a bending angle of 90° is achieved under load. The last stage is the springback process. The springback of the tube bend is simulated after bending. All FE simulations were performed with the same solver of the software PAM STAMP.

Fig. 8
figure 8

Four stages of FE simulations

Full size image

With a clamp die length of 140 mm, the tube is not plasticized by the clamping force. The spring elements of the clamp die have the same spring rate in all simulations in order to guarantee a sufficient clamping force. It is therefore necessary to connect the clamp die with spring elements, since the spring-loaded bend die moves during bending, see Fig. 9.

Fig. 9
figure 9

Clamping the tube with the centre of rotation shifted

Full size image

Until now, the clamp die was given the coordinate of the center of rotation in order to let it rotate around this point during the entire bend. Since the center of rotation now shifts during bending and its coordinates change, the clamp die is pulled against the tube with spring elements (between the bend die and the clamp die), see “direction of movement” in Fig. 9. This ensures a sufficient clamping force independent of the position of the bending form and the center of rotation.

6.3 Evaluation by means of wrinkle evaluation factor

To evaluate the wrinkles of the simulated tube bends, the mesh of the springback process is exported in the STL file format. The mesh of the tube bend is then imported into the Poly-Works 2016 software as a polygon model. Points are selected at the two side pieces by which a cylinder is created on each side using a best-fit function, see Fig. 10. The cylinder points and the loaded polygon model is exported in the form of a point cloud.

Fig. 10
figure 10

Contour of the FE simulation in Poly-Works 2016

Full size image

Further processing of the point cloud takes place with the MATLAB R2016b software from developer The MathWorks, Inc. A projection plane is created from the end points of the cylinder center lines. The Matlab program filters out the contour points in the projection plane. These are the bases for approximate the contour by a spline. In a final step, the inner target contour of the tube is placed over the spline, with the ends of the side pieces superimposed. This corresponds to the contour comparison in Fig. 3.

The output size is the distance between the simulated tube bend contour and the target contour, which is expressed by the wrinkle evaluation factor, calculated according to Eq. (1).

7 Results

In the results described below, the influence of machine axis stiffness on wrinkle formation was investigated. Figure 11 shows the wrinkle evaluation factor over the spring stiffness of the axes. Only small wrinkles were formed with a pressure die distance of 0 mm and an axis stiffness of 1000 kN/mm. The wrinkle evaluation factor here is 0.001. By reducing the stiffness to 100 kN/mm and 50 kN/mm, the wrinkle evaluation factor and thus the size of the wrinkles increases slightly. With a reduction to stiffnesses of 10 kN/mm and 2 kN/mm, the wrinkle evaluation factor rises sharply with values above 0.013.

Fig. 11
figure 11

Influence of axis stiffness on wrinkle formation in RDB

Full size image

The extent of wrinkle formation is also illustrated in Fig. 12.

Fig. 12
figure 12

Influence of axis stiffness on wrinkle formation in RDB

Full size image

With a pressure die distance of 1 mm and an axial rigidity of 1000 kN/mm, wrinkles can already be seen with a wrinkle evaluation factor of 0.004. Figure 12 shows that the wrinkle formation of this wrinkled tube bend is increased by reducing the axial stiffness. The increase in the wrinkle evaluation factor is flatter than with a pressure die distance of 0 mm.

In addition to the wrinkle evaluation factors, the axial displacements were measured in the FE simulations. The mesh points that were measured were located at the points of load of the spring elements, see also Fig. 6. Each spring element represents one axis of the machine. For example, the drive of the pressure die axis (hydraulic cylinder) transmits the force to the holder of the pressure die and this holder transmits the force to the pressure die at two points. In the FE simulations, the spring elements of the pressure die were placed at these two points. The displacements of these two points and of the other points of load were measured. The positions at a bending angle of 0° were compared with the positions at a bending angle of 90°.

Table 1 shows the axial displacements with a pressure die distance of 0 mm. Table 2 shows the axial displacements at a pressure die distance of 1 mm.

Table 1 Axis shifting with a pressure die distance of 0 mm
Full size table
Table 2 Axis shifting with a pressure die distance of 1 mm
Full size table

In both diagrams, a reduction in axis stiffness leads to an increase in axis displacements. In Table 1 the pressure die is displaced by a maximum of 0.71 mm at the front and by a maximum of 0.67 mm at the back. In Table 2 the pressure die shifts by a maximum of 0.94 mm at the front and by a maximum of 0.19 mm at the back. The wiper die shifts equally at the front and at the back and is therefore only listed once. It achieves displacements up to 0.53 mm (Table 1) and 0.77 mm (Table 2). With an axis stiffness of 2 kN/mm the bend die shifts particularly strongly with 1.48 mm (Table 1) and 2.44 mm (Table 2). The mandrel shift in longitudinal direction is also very pronounced with values up to 5.70 mm (Table 1) and 4.68 mm (Table 2).

8 Discussion

In rotary draw bending, even small wrinkles can be significant for the further use of the component. The shape-bound process is used due to its extensive force transmission if only small shape deviations on the component are permissible. In fluid technology, for example, small wrinkles can cause undesired turbulence when using hydraulic tubes.

The calculated wrinkles are particularly high between stiffness values of 10 kN/mm and 50 kN/mm for rotary draw bending. But also the occurring wrinkle reinforcement between 50 and 100 kN/mm should not be underestimated. The formation of wrinkles is, as described in Sect. 3.3, an instability. As Fig. 4 shows, an axis travel of 0.2 mm can decide whether wrinkles occur or not. The distance the tool travels is even smaller. At an axis stiffness of 100 kN/mm, a displacement of 0.07 mm is measured at the pressure die and at 50 kN/mm a displacement of 0.18 mm is measured. These displacements are large enough to cause or reinforce wrinkles.

9 Stiffness measurements on the bending machine

In preparation for practical tests, the axes stiffnesses were measured on the bending machine TN 120 from Tracto Technik GmbH. The axes stiffnesses are calculated from the displacements of the tools and the tool forces. Each tool was individually loaded with force and measured.

9.1 Pressure die

Two stiffnesses are determined for the pressure die, one at the front end and one at the back, see Fig. 13. If the stiffnesses differ, the pressure die may tilt in practical tests. This is to be represented in the same way in the FE simulations by entering two stiffnesses.

Fig. 13
figure 13

Experimental setup for stiffness measurement on the pressure die axis

Full size image

In the stiffness measurement, care was taken to ensure that the forces at the front and back of the pressure die do not differ too much from each other for better comparability. The plate against which the pressure die has driven was aligned accordingly.

To measure the force, two load cells (301.100 kN, measurement uncertainty ≤ ± 0.08%) of the Test GmbH were integrated into the pressure die holder. For displacement measurement two precision feelers SM222.4 from Schreiber Messtechnik GmbH with a measuring accuracy of ± 0.5% were mounted at the front and back end. In addition, the total travel distance was measured at the drive cylinder of the pressure die axis using a precision feeler. The measured travel of the pressure die is smaller than the travel measured on the cylinder. The difference between the two corresponds to the spring deflection of the pressure die.

Figure 14 shows the total travel distance, the travel distance at the front end of the pressure die and the difference between the two (spring deflection path as a function of the force measured at the front).

Fig. 14
figure 14

Axis shifting of the pressure die, front

Full size image

The course of the stiffness can only be approximated conditionally by a straight line, see y = 0.0106× in Fig. 14. In the FE simulations, the approximation by means of a power series is selected for all stiffnesses.

Figure 15 shows the spring deflection path of the back end as a function of the force measured at the back. This stiffness is also approximated using a power series for the FE simulations.

Fig. 15
figure 15

Axis shifting of the pressure die, back

Full size image

The stiffnesses at the front and back of the pressure die differ slightly. This will cause the tool to tilt, even if the force acting on the front and back of the pressure die is the same.

9.2 Bend die

To measure stiffness in the transverse direction of the bend die, a hardened solid bar was placed against the bend die and the pressure die was moved up to the solid bar. The spring deflection path of the bend die was measured by means of a precision feeler, see Fig. 16.

Fig. 16
figure 16

Experimental setup for stiffness measurement on the bend die

Full size image

The acting force was calculated from the sum of the forces of the two load cells on the pressure die. The following stiffness of the bend die in transverse direction is obtained, see Fig. 17.

Fig. 17
figure 17

Axis shifting of the bend die

Full size image

The axial stiffness of the bend die is similar to the stiffness of the pressure die.

9.3 Wiper die

The wiper die is supported at the front of the bend die. At the back it is attached to the wiper die holder. The stiffness of the wiper die holder was measured by closing the pressure die, see Fig. 18. The spring deflection path was measured by means of a precision feeler. The transverse force of the wiper die was measured with a load cell (301.20 kN, measurement uncertainty ≤ ± 0.08%) of the Test GmbH.

Fig. 18
figure 18

Experimental setup for stiffness measurement on the wiper die

Full size image

Figure 19 shows that the stiffness of the wiper die axis can be approximated by a linear function. During bending, most of the force is transmitted to the bend die, so it is sufficient to measure the stiffness on the wiper die up to 12 kN.

Fig. 19
figure 19

Axis shifting of the wiper die

Full size image

In summary, Table 3 lists the spring stiffnesses of the axes. The values correspond to the straight line gradients of the linear approximations. In the following FE simulations, the approximations were entered using a power series.

Table 3 Axis shifting of the RDB tools (linear approximation)
Full size table

The spring stiffnesses show that the variations selected in Sect. 7 in terms of magnitude match the actual stiffnesses on the machine. In the following, the actual stiffnesses will be stored in FE-simulations and the results will be compared with a practical test.

10 Comparison of wrinkle formation in FE simulations with a practical test

10.1 Experimental setup and FE simulation setup

The axis stiffnesses measured in Sect. 9 are inserted into the FE simulation at the respective spring elements, see Fig. 6. The spring elements pressure die front, pressure die back, wiper die back and bend die get the indicated values. The spring element wiper die front gets the same stiffness as the bend die. A stiffness of 1000 kN/mm is used on the mandrel. Since the stiffness is almost exclusively the result of the elastic deformation of the mandrel bar in the longitudinal direction, this axis has a high stiffness in comparison.

Practical bending tests were carried out with tubes made of the material 1.4301 with a bending factor of B = 1.5 and a wall thickness factor of W = 40. The specimen has an outer diameter of 40 mm and a wall thickness of 1 mm. The bending angle at the bend die was set to 90°. The pressure die moves in longitudinal direction to minimize the relative speed to the tube and thus reduce the longitudinal expansion at the outer bend. The wiper die is positioned conventionally. The tube end is not fixed in the collet and can follow freely. The other tube end is clamped in the inner and outer clamp dies. The experimental setup is shown in Fig. 20a and b.

Fig. 20
figure 20

a and b Experimental setup of practical RDB tests

Full size image

10.2 Execution of experiments

In the bending tests, different wrinkle heights are created by varying the pressure die infeed. The pressure die cylinder is moved towards the tube in 0.2 mm steps.

A similar procedure is used in the FE-simulations. The holder of the two spring elements pressure die front and pressure die back are moved towards the tube in 0.2 mm steps, see the spring travel in Fig. 21.

Fig. 21
figure 21

Spring travel at the pressure die

Full size image

10.3 Results

With a spring travel of 0 mm the pressure die is applied to the tube, i.e. the pressure die distance, see Fig. 1, is 0 mm. But the pressure die does not exert any force on the tube (at a bending angle of 0°). Only when the spring travel is increased does the force on the tube rise. The pressure die distance remains 0 mm.

In order to be able to compare the result of the FE simulation with that of the practical test, the pressure die forces are compared. The FE simulation and the practical test, which show similar forces at the beginning, are compared and their wrinkle evaluation factors are compared.

Figure 22 shows the curves of the pressure die forces at the front and back end. The diagram shows a tube bend calculated by means of FEM and its counterpart produced in the practical test. The force curves of the practical test were recorded from a bending angle of 3°.

Fig. 22
figure 22

Pressure die forces in FE simulation and practical test

Full size image

As described in Sect. 10.1, the pressure die moves with the tube, therefore the force at the front load point decreases with increasing bending angle. The force at the back load point increases. The calculated force curve of the front load point corresponds well with the curve of the practical test. The calculated force curve of the back load point has the same gradient up to half of the bend. Towards the end it rises more flatly.

Since the curves at the beginning of the bend < 5° differ significantly from each other, tube bends were compared which show similar forces at a bending angle of 15°. The initial difference in the curves may have been caused by a contact between the pressure die and the bend die at the beginning of the bend.

Table 4 lists the wrinkle evaluation factors of the tube bends. The comparable tube bends from the practical test and the FE simulation are listed in one line. For comparison the forces of the front end of the pressure die at a bending angle of 15° and the spring deflections are also listed.

Table 4 Comparison of the wrinkle evaluation factors of FE simulation and practical experiment
Full size table

In practical tests, a spring travel of 1.2 mm produces a pressure die force of 12.5 kN and wrinkles with an evaluation factor of 0.0031. In the FE simulation, the same spring travel produces a force of 11.3 kN and an evaluation factor of 0.0006. With a spring travel of 1.0 mm and a force of 9.7 kN wrinkles with an evaluation factor of 0.0029 appear.

The results of FE simulations, which do not take the axis stiffness into account, do not show any wrinkles for the range given in Table 4. However, the results are not directly comparable. Different force curves are produced on the pressure die. In addition, with the same spring travel (or axis travel), the ideally stiff axes produce larger forces overall. For example, with a spring travel of 0.8 mm, the pressure die distance with an ideally rigid axis is − 0.8 mm and the pressure die force is already 95.9 kN.

11 Conclusion and outlook

The shifting of machine axes under load has an influence on the formation of wrinkles during rotary draw bending, as the variation of axis stiffnesses in FE simulations shows. The lower the axial stiffnesses, the larger the wrinkles occur during the bending process. A nearly wrinkle-free tube bend was considered, where the wrinkle formation increases due to a reduction of the axis stiffness. A wrinkle-free tube bend was also considered where the wrinkling increases to a lesser extent when the axis stiffness is reduced. The wrinkling is caused by larger shifts of the axes and thus more distance between the tools.

Using the stiffnesses measured on a bending machine in FE simulations leads to wrinkle sizes that are slightly smaller than those determined in practical tests. Compared to FE simulations, which do not take the axis stiffnesses into account, the wrinkle sizes are closer to the results of the practical tests. The wrinkle evaluation factor determined according to VDI 3431 and Kuhnhen [17] has the advantage that both a point cloud from FE simulation and a surface scan of a bent tube can be processed and directly compared.

Wrinkle formation is an instability that can only be calculated approximately. A prediction of wrinkling using FE simulations, which has been improved by this study, can lead to less rejects and more efficient bending processes.

In a next step, the results of the FE simulations are to be brought even closer to those of practical tests by measuring the friction coefficients of the tools in a tube pulling test. In addition, the shell elements used will be replaced by solid elements and the results will be compared.

The aim of these investigations is the prediction of wrinkles by FE calculations and the control of the RDB process by automatic adjustment of the process parameters during bending. This makes it possible to react to machine-specific axis displacements in the form of process control.