Introduction

China has abundant reserves of vanadium titanomagnetite in Panzhihua, Sichuan, with titanium resources being the largest and the vanadium resources being the third largest.1,2 These abundant resources hold significant strategic importance to China, as they serve as invaluable assets that fuel the nation's economic growth and development.3,4 Currently, the predominant approaches for exploiting vanadium titanomagnetite involve blast furnace techniques and direct reduction electric furnace smelting processes.5,6,7 In both blast furnace smelting and direct reduction electric furnace smelting, the key premise of the process is to establish an optimal slag system. The phase diagram is a geometric description of the relationship between the components of a substance in equilibrium, the phases, and the external conditions, which facilitates the choice of the slag regime for the vanadium titanomagnetite smelting process.8,9,10 To ensure accuracy in the phase diagram prediction, it is imperative to make adjustments to the prediction by incorporating the outcomes of phase equilibrium experiments.

Studying the equilibrium phase relationships of titanium slag using a phase diagram is challenging, due to formation of complex oxide components mainly produced by reactions of TiO2, MgO, CaO, Al2O3, and SiO2. Previous studies have identified rutile,11 anosovite,12 perovskite,13 and sphene14 as possible phases for Ti enrichment. However, practical applications have shown preference for only rutile, anosovite, and perovskite due to their higher TiO2 content and ease of separation. The perovskite phase in the CaO-MgO-SiO2-Al2O3-TiO2 system is present in the titanium slag produced by the blast furnace process, and its equilibrium phase relationships have been extensively studied by many academics over the past few decades. Zhao et al. and McRae et al.15,16,17 have investigated the equilibrium phase relationships, carbon saturation, and liquidus temperature in the CaO-SiO2-MgO-Al2O3-TiO2 system under an argon atmosphere for Ti-bearing slag (20–25 wt.% TiO2). The study considered the w(Al2O3)/w(SiO2) ratios ranging from 0.4 to 0.6 and the w(MgO)/w(Al2O3) ratios ranging from 0.2 to 0.72. The findings revealed that the major phases are pseudobrookite and CaTiO3, and the realistic isotherms are also given. In addition, Wang et al. and Ma et al.18,19,20 have reported on the effect of the (CaO + SiO2)-Al2O3-MgO system with CaO/SiO2 ratios of 0.9 and 1.3. The results show that the primary phase area of dicalcium silicate expands significantly towards the Al2O3 corner, and that the liquid area is reduced as the CaO/SiO2 ratio increases from 0.9 to 1.3 in an argon atmosphere. It can be seen that the w(Al2O3)/w(SiO2) ratios, w(MgO)/w(Al2O3) ratios, and w(CaO)/w(SiO2) ratios have a great influence on the equilibrium relationships in the CaO-SiO2-MgO-Al2O3-TiO2 system. Sun et al. and Shi et al. also reported a series of equilibrium relationships in the CaO-SiO2-MgO-Al2O3-TiO2 system in air and different oxygen partial pressure, including the CaO-SiO2-5%MgO-Al2O3-TiO2 slag system at 1300°C and 1400°C, the CaO-SiO2-5%MgO-20%Al2O3-TiO2 system at 1300°C and 1400°C,21 the CaO-5%MgO-SiO2-Al2O3-TiO2 system in high Al2O3 content with w(CaO)/w(SiO2)ratio of 1.5,22 as well as the CaO-MgO-SiO2-Al2O3-TiO2 system at 1250–1400°C,23 and the CaO-SiO2-TiO2 system at 1400°C and oxygen partial pressure of 10−10atm.24 These results found that the presence of a liquid phase, melilite solid solution phase, CaTiO3 phase, and Al-Ti diopside phase, and pseudobrookite solid solution, were present, and that the corresponding liquidus lines and phase diagram were constructed, and a lower oxygen partial pressure led to the shrinkage of the rutile and wollastonite primary phase areas. The equilibrium relationships mentioned above for the CaO-SiO2-MgO-Al2O3-TiO2 system with low TiO2 contents ranging from 20 wt.% to 25 wt.% in air or different oxygen partial pressure have some guiding significance. As a result, the reported phase diagrams may not be adequate for accurately estimating the primary phase region of anosovite and the liquidus temperatures of titanium slags with higher TiO2 contents (45–60 wt.%). It is necessary to further investigate and obtain more comprehensive phase diagrams and thermodynamic data for titanium slags with higher TiO2 contents. Currently, equilibrium phase relationships in the CaO-MgO-SiO2-Al2O3-TiO2 system with higher TiO2 contents (45–60 wt.%) have recently been reported by Wang et al.25,26 The results indicated that the isothermal section contains one liquidus region and five solid–liquid coexistence regions, and the primary phase region of anosovite was found. It appears that the available data are not enough to determine the composition ranges needed for the crystallization of anosovite in Ti-bearing electric furnace slag with higher TiO2 contents (45–60 wt.%). In addition, Wang et al.27 systematically compared the experimental results, FactSage predicted the results, and experimental data from the literature were from the CaO-SiO2-MgO-Al2O3- “50% TiO2” system. This report shows that the predicted primary phases in the CaTiO3 and TiO2 primary phase fields were consistent with the experimental results, but a number of inconsistent results were found in other primary phase fields, including M3O5 and spinel. Ohno and Ross28,29 measured the phase diagrams of the CaO-SiO2-TiO2-Al2O3 systems at 10 wt.% and 20 wt.% Al2O3 level, respectively, to adequately depict the smelting processes of titaniferous ores. This study covered a wide range of compositions with TiO2 being from 0 to nearly 50 wt.%, but the phase equilibria data at a TiO2 content higher than 45 wt.% are still very limited. So, the fundamental data are far from sufficient to obtain the composition ranges for the anosovite crystallization in the current Ti-bearing slag. It is therefore necessary to obtain a better understanding of the composition ranges required for anosovite crystallization in Ti-bearing electric furnace slag.

This study aims to provide a fundamental understanding of equilibrium phase relationships in the CaO-MgO-SiO2-13%Al2O3-50%TiO2 system, and the relationships were experimental determined from 1400°C to 1500°C in air using a high-temperature equilibration and quenching method. SEM analysis and phase identification by EDS were performed on all the quenched samples. Equilibrium results were calculated using Factsage 8.1, and were compared with the experimental results. The findings from this work not only offer valuable guidance for the development of titanium recovery methods from Ti-bearing electric furnace slag but also provide essential data for upgrading the existing thermodynamic oxide databases.

Experimental

Sample Preparation

In this study, only pure chemical reagents were used as raw materials, including CaCO3 (≥ 99.9%), Al2O3 (≥ 99.999%), MgO (≥ 99.9%), SiO2 (≥ 99.99%), and TiO2 (≥ 99.8%). To ensure accuracy in the ratios, all the reagents underwent pre-firing at 1000°C for 12 h to prevent any interference from moisture and impurities present in the samples. Following the predetermined ratio, 1 g of the sample was thoroughly ground for 30 min in an agate mortar. After weighing 0.2 g of the mixed sample, it was pressed into pellets measuring Φ10 mm × 2 mm, serving as raw materials for the experiment.

Experimental Process

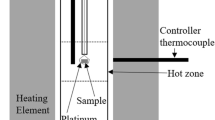
The phase equilibrium experiments were carried out in a high-temperature tube quenching furnace, and the corresponding equipment schematic is shown in Fig. 1. The temperature of the furnace was controlled by an KSY intelligent temperature controller, which has an overall accuracy of ± 2°C. Temperature calibration of the equipment is required before the start of the experiment. A standardized B-type Pt/Pt-10%Rh thermocouple was used to calibrate the constant temperature zone. To begin with, high-purity platinum flakes with a purity of 99.99% were used to wrap the prepared samples. Following that, the samples that had been wrapped were carefully positioned in a cylindrical corundum crucible with a diameter of 10 mm. The crucible was then heated using a platinum wire that was suspended within the quench furnace's constant temperature zone. The samples were pre-melted at a temperature 100°C higher than the equilibrium temperature for 60 min and then lowered to the required temperatures (1400°C, 1450°C, and 1500°C) for equilibration for 10 h. Upon completion of the experiment, pressing the electromagnetic button resulted in the sample being immersed in cold water (25°C) for quenching within a 2-s timeframe. Following the quenching process, the samples were dried, mounted, and polished for a series of SEM-EDS analyses.

Fig. 1
figure 1

Schematic of high-temperature quenching furnace.

Full size image

Analysis

Scanning electron microscopy (SEM; MIRA3 LMH; TESCAN) images combined with energy dispersive spectroscopy (EDS; Ultim Max 20) were used to observe the microstructure and distribution of the elements in the quenched samples. The accelerating voltage and beam current were 15 kv and 20 nA, respectively. For statistical reliability, at least 15 analysis points were chosen at random from each phase. The typical compositions of rutile, anosovite (M3O5), perovskite, and spinel are listed in Table I, combined with EDS to determine the specific phase type. In this investigation, Factsage 8.1 was employed. The modules "Phase" and "Equilibrium " were employed, the databases were selected in "FactPS" and "FToxid.", and the solutions species selected in the calculations were "FToxide-SLAGA", "FToxide-SPINA", "FToxide-RUTILE", and "FToxide-Mel".

Table I Equilibrium compositions of the phases, wt.%
Full size table

Results and Discussion

Equilibria Phase Relationships at 1400°C

In air at 1400°C, Table S1 (refer to online supplementary material) shows the equilibrium phase relationships of the CaO-MgO-SiO2-13%Al2O3-50%TiO2 system. It is important to note that, apart from the liquid phase, over six equilibria phase relationships were found. Figure 2a shows the SEM images of sample M4, where a coexistence of liquid and rutile phases has been identified in the relationships. The bright gray flakes in the sample are rutile, while the remaining dark gray is the glassy phase. As shown in Fig. 2b, sample M15, another two-phase field of liquid coexisting with anosovite is observed. The bright gray stripes are the anosovite phase, and the remaining light gray is the glass phase. Figure 2c shows a typical equilibrium phase relationship: liquid coexisting with two solid phases (anosovite and rutile) in sample M5, the bright gray flakes are rutile, the gray stripes are the anosovite phase, and the remaining light gray is the glass phase. The sample M8 has an equilibrium phase relationship in which liquid coexists with anosovite and spinel (as shown in Fig. 2d), the SEM images show that the bright gray stripes are anosovite, the black dots are the spinel phase, and the remaining light gray is the glass phase. It can be seen that sample M18 in Fig. 2e indicates an equilibrium phase relationship of liquid coexisting with CaTiO3 and spinel, the black dots representing the spinel phase, the bright white masses representing the CaTiO3 phase, and the remaining light gray representing the glass phase. Figure 2f presents an equilibrium phase relationship of liquid coexisting with CaTiO3 in sample M19, the bright white masses are the CaTiO3 phase and the remaining light gray is the glass phase.

Fig. 2
figure 2

Typical SEM images showing the microstructure of an equilibrium phase obtained at 1400°C, (a) sample M4, (b) sample M15, (c) sample M5, (d) sample M8, (e) sample M18, (f) sample M19.

Full size image

Equilibria Phase Relationships at 1450°C

The compositions of the equilibrium phase at 1450°C in air are collected in Table S2 (refer to online supplementary material), and the corresponding microstructures are displayed in Fig. 3. The representative SEM micrograph of sample W50 is shown in Fig. 3a, and the phase equilibrium relationship indicates a single liquid phase. Figure 3b shows the equilibrium phase relationship of the liquid coexisting with rutile (TiO2) in sample W18. The typical sample W20 presents an equilibrium phase relationship of liquid coexisting with anosovite (M3O5), as shown in Fig. 3c. Figure 3d, e, and f shows the SEM micrographs of samples W12, W49, and W6, depicting three equilibrium phase relationships: liquid coexisting with anosovite (M3O5) and rutile (TiO2), liquid coexisting with anosovite (M3O5) and spinel, and liquid coexisting with perovskite (CaTiO3) and spinel. In addition, two equilibrium phase relationships of liquid coexisting with perovskite (CaTiO3) can be seen in Fig. 3g, in sample W46, the bright white masses representing the CaTiO3 phase and the remaining light gray is the glass phase. Figure 3h shows the SEM micrographs of sample W48, revealing two additional equilibrium phase relationships of liquid coexisting with spinel. The black dots in the micrograph represent the spinel phase, while the remaining light gray areas correspond to the glass phase.

Fig. 3
figure 3

Typical SEM images showing the microstructure of the equilibrium phase obtained at 1450°C, (a) sample W50, (b) sample W18, (c) sample W20, (d) sample W12, (e) sample W49, (f) sample W6, (g) sample W46, (h) sample W48.

Full size image

Equilibria Phase Relationships at 1500°C

A total of 11 samples were used to demonstrate the phase equilibrium relationships in the primary phase of liquid-rutile. Table S3 (refer to online supplementary material) lists the experimental sample compositions, quenched glass compositions obtained by EDS, and the phase equilibrium relationships are shown in Fig. 4. The phase equilibrium relationships were compared with those at 1400°C and 1450°C. Figure 4a shows a single liquid phase in sample B23. The typical sample B34 presents an equilibrium phase relationship of liquid coexisting with rutile (TiO2), as shown in Fig. 4b. A SEM image of a typical sample of B36 illustrating the coexistence of liquid and M3O5 at equilibrium at 1500°C is shown in Fig. 4c. Based on the atomic ratios and mass percentages in the EDS results, it can be determined that the bright gray long stripes represent the anosovite phase, and the remaining gray is the liquid phase. Sample B38 has been found to have a phase equilibrium relationship between the liquid phase and perovskite (CaTiO3), as shown in Fig. 4d, the bright white chunks in the sample corresponding to the perovskite phase, while the remaining gray areas indicate the presence of the liquid phase.

Fig. 4
figure 4

Typical SEM images showing the microstructure of the equilibrium phase obtained at 1500°C, (a) sample B23, (b) sample B34, (c) sample B36, (d) sample B38.

Full size image

Projections of the 1400°C, 1450°C, and 1500°C Isotherms

Based on the above phase equilibrium relationships, the compositions obtained from Tables S1, S2, and S3 were projected onto the phase diagram to obtain the actual isotherms and phase boundary lines. Figure 5 shows the comparisons of boundaries and liquidus temperatures between the FactSage 8.1 calculations and the results obtained in the present study. The thick and thin solid lines represent the physical phase boundary lines and isotherms, respectively, and this result was calculated by the FactSage 8.1. The thick and thin dashed lines are the object phase boundary lines and isotherms, respectively, and these results were obtained through experimental studies. As can be seen, the experimental results align with the predictions made by FactSage 8.1, having the same primary phase field types. However, the difference in range between the anosovite (M3O5) phase region obtained from the experimental results and the predicted results, are attributed to the solid solution of Mg, Al, and other elements in the anosovite phase.27 In the primary phase of the spinel area, the composition range obtained from the experimental results was smaller than from the predicted results. In addition, the composition range obtained from the experimental results was also smaller compared to the predicted results in the primary phase of CaTiO3 and the rutile area.

Fig. 5
figure 5

Comparisons of boundaries and liquidus temperatures between FactSage 8.1 calculations and the present results.

Full size image

Figure 6 demonstrates the effect of MgO% in liquid on the liquidus temperature. It can be observed that both the experimental results and the predicted results exhibit a consistent pattern. With an increase in MgO content, the liquid phase temperature initially decreases and then starts to increase. However, it is worth noting that the predicted results of the minimum melting temperature by FactSage8.1 indicated a higher content of MgO compared to that obtained from the experimental results. The results of the phase equilibrium experiments indicate that, when the MgO content exceeds 5%, the corresponding liquid phase temperature shows an increasing trend with an increase in MgO content.

Fig. 6
figure 6

The effect of “MgO% in liquid” on the liquidus temperature.

Full size image

Figure 7 illustrates the maximum deviation between the predicted liquid temperature and the experimentally obtained liquid temperature at various temperatures. Observations reveal that the predicted liquidus temperatures exhibit minimum deviations of 146.71°C, 123.26°C, and 170.05°C, respectively, indicating values lower than the experimentally determined liquidus temperatures.

Fig. 7
figure 7

The deviation of the liquidus temperatures from the present work and the corresponding melting temperatures predicted by Factsage.

Full size image

Conclusion

In order to establish a fundamental understanding of equilibrium phase relationships within the Ti-bearing electric furnace slag system, we conducted experimental determinations ranging from 1400°C to 1500°C in air conditions, employing a high-temperature equilibration and quenching method. We found that a single liquid phase area, liquid-rutile (TiO2), liquid-anosovite (M3O5), liquid phase coexisting with anosovite and rutile, liquid phase coexisting with anosovite and spinel, liquid phase coexisting with perovskite and spinel, and liquid-perovskite (CaTiO3), a total of seven phase equilibrium relationships existed at 1400°C. At 1450°C, the phase equilibrium relationship of liquid-spinel was increased compared to 1400°C. At 1500°C, only four equilibrium relationships exist in this system: a single liquid phase area, liquid-rutile (TiO2), liquid-anosovite (M3O5), and liquid-perovskite (CaTiO3). According to the experimental results, realistic 1400°C, 1450°C, and 1500°C isotherms were obtained, which then confirmed the phase boundary lines. The experimental results reveal a notably broader phase region in the primary area of anosovite (M3O5) compared to the predicted results, due to the solid solution of Mg, Al, and other elements in the anosovite phase. The predicted liquidus temperatures have minimum deviations of 146.71°C, 123.26°C, and 170.05°C, respectively, which are lower than the experimentally determined liquidus temperatures. According to the effect of MgO% in liquid on the liquidus temperature, we found that, when the MgO content exceeds 5%, the corresponding liquid phase temperature increases with the increase of MgO content.