Introduction

Recently, ABO2 delafossite-oxides [A is monovalent = silver (Ag), B is trivalent = chromium (Cr) or iron (Fe)] have been paid great attention due to several potential applications, such as water purification, conductors, antimicrobials, chemical sensors, and solar cells.1,2,3,4,5,6,7,8,9,10,11 Moreover, it is known that silver (Ag) nanoparticles has high resistance against oxidation and high thermal and electrical conductivity that can be used in a wide range of useful applications.12,13,14,15,16,17,18,19,20 In this work, the study of elastic properties and high-frequency applications is discussed for the first time for AgCrO2 and AgFeO2 delafossite; there is no previous literature on this subject. Fourier-transform infrared (FTIR) analysis was determined to study the ordering phenomena of the samples. Moreover, the absorption bands assigned from the FTIR analysis were due to the oxygen cations and ions vibration at different frequencies.21 The elastic constants estimated from the FTIR analysis have a great interest due to their help in understanding the thermal properties of the samples.21 Industrialists need to study different properties in detail for different materials to be able to choose the right materials for the right applications. Thus, it is important to illustrate various properties in detail, such as the elastic constants, optical parameters, switching field, and high-frequency responses. It is known that these parameters are strongly dependent on the materials' structure and preparation methods. Many methods are used for preparing nanoparticles, such as ceramic and wet methods.22,23,24,25,26,27,28 The most effective methods that prepare the nanoparticles with s small size are wet methods, such as citrate, oxalate, flash, sol–gel, and co-precipitation. Flash auto-combustion is used in the present work and has many advantages such as saving time, giving a high yield, and being an effective method. Moreover, flash auto-combustion used to prepare AgFeO2 and AgCrO2 delafossite is simple and low-cost, which can have potential applications in electromagnetic composites.29,30,31,32 In addition, the characterization of the investigated samples has been discussed in detail in previous literature33,34,35,36 to assure their formation. Finally, the novelty of the present work is the illustration of the elastic properties estimated from FTIR analysis, as well as the optical properties of AgFeO2 and AgCrO2 delafossite. Also, high-frequency applications estimated from the magnetic measurements were studied for both samples. Moreover, to the authors’ knowledge, this is the first time that the elastic properties from FTIR analysis and high-frequency applications for the investigated samples have been explained.

Experimental Details

Preparation and Characterization

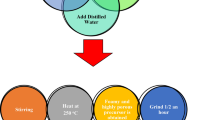
Figure 1a shows a schematic of the preparation of AgFeO2 and AgCrO2 delafossite by the flash method. The starting ingredients were silver, iron III, or chromium III nitrates. They were mixed in stoichiometric ratios after adding a small amount of distilled water. Next, urea was added to the mixture in a stoichiometric ratio. Then, the mixture was heated at 250°C until a fine powder was produced. The powder was ground for half an hour to be ready for analysis. The FTIR analysis was investigated using a Jasco FTIR 300 E spectrometer apparatus. Moreover, the magnetic properties were measured by a vibrating sample magnetometer (Lake Shore 7410). The optical properties were measured using a Jasco-V-570 spectrophotometer (Japan).

Fig. 1
figure 1

(a) Schematic of the synthesis of AgCrO2 and AgFeO2 delafossite. b FTIR spectra of AgCrO2 and AgFeO2 delafossite

Full size image

Results and Discussion

FTIR Analysis

Figure 1b and Table I show the FTIR analysis of AgFeO2 and AgCrO2 delafossite in the range 400–4000 cm−1. Two main absorption peaks, 1 and 2, appeared for both samples, which indicated the bond vibration of Cr–O or Fe–O in octahedral and tetrahedral sites, respectively. Moreover, peak 3 was assigned to the stretching vibration of water. However, peak 4 appeared due to the C=N group estimated from urea and metal nitrate.19,37 Peaks 5 and 6 were assigned to the carboxyl group, while peak 7 was due to the O–H stretching vibration. Finally, peak 8 was strong due to the presence of the NH group and the water molecules. As a result, FTIR analysis assured the formation of AgFeO2 and AgCrO2 delafossite.

Table I The peak values of FTIR analysis of AgCrO2 and AgFeO2 delafossite
Full size table

Elastic Study

The study of the elastic properties was calculated from the FTIR analysis for AgFeO2 and AgCrO2 delafossite. It is known that the cation distribution of both samples is important for calculating the force constants.38 The distribution of the cations was as follows:

$${\left({\mathrm{Ag}}_{0.5 }{\mathrm{Fe}}_{0.5}\right)}_{\mathrm{tet}}{ \left[{\mathrm{Ag}}_{0.5} {\mathrm{Fe}}_{0.5}\right]}_{\mathrm{oct} }{\mathrm{O}}_{4} \;\;\mathrm{for\;\;AgFeO}_{2}\;\;\mathrm{ delafossite}$$
(1)
$${\left({\mathrm{Ag}}_{1}\right)}_{\mathrm{tet}}{ \left[{\mathrm{Cr}}_{1}\right]}_{\mathrm{oct}}{\mathrm{O}}_{4}\; \mathrm{for\; AgCrO}2\;\mathrm{ delafossite}$$
(2)

Moreover, the force constants were calculated as follows:39

$${K}_{t}=7.62 \times {M}_{A} \times {\nu }_{1}^{2} \times {10}^{-7} \mathrm{N}/\mathrm{m}$$
(3)
$${K}_{o}=10.62 \times {M}_{B} \times {\nu }_{2}^{2} \times {10}^{-7} \mathrm{N}/\mathrm{m}$$
(4)

where Kt is the force constant in the tetrahedral site, Ko is the force constant in the octahedral site, and MA and MB are the molecular weights for tetrahedral and octahedral sites, respectively. Tables II and III show the elastic constants for both samples. It can be seen that the values of the force constant at the tetrahedral site (Kt) for both samples were larger than those for the octahedral site (Ko). This was due to the bond length in the tetrahedral structure being shorter than that in the octahedral site.39 It is known that the calculations of the bulk modulus (B), longitudinal elastic velocity (Vl), transverse or shear elastic velocity (Vt = Vs), and the mean elastic velocity (Vm) were as follows:40,41,42

$$B= \frac{1}{3} [ {C}_{11}+2 {C}_{12} ]$$
(5)
$$K=a {C}_{11}$$
(6)
$${V}_{l}= {\left(\frac{{C}_{11}}{{D}_{x}}\right)}^{1/2}$$
(7)
$${V}_{t}= \frac{{V}_{l}}{\sqrt{3}}$$
(8)
$${V}_{m}= \frac{1}{3} {\left[\frac{1}{{V}_{l}^{3}}+\frac{2}{{V}_{s}^{3}}\right]}^{1/3}$$
(9)

where C11 and C12 are the constants of stiffness, K is the force constant, Dx is the x-ray density, and a is the lattice parameter. In addition to knowing more details about the elasticity of the investigated samples, important parameters were calculated as follows:43

$$L={D}_{x} {V}_{l}^{2}$$
(10)
$$G= {D}_{x} {V}_{s}^{2}$$
(11)
$$\sigma = \frac{L-2 G}{2 (L-G)}$$
(12)
$$E=\left({C}_{11}- {C}_{12}\right)({C}_{11}+2 {C}_{12})$$
(13)

where L is the longitudinal modulus, E is Young’s modulus, G is the rigidity modulus, and σ is Poisson’s ratio. It can be seen from Tables II and III that these elastic parameters were larger for AgCrO2 delafossite than for AgFeO2 delafossite due to the interatomic bonding of the atoms. In addition, the bond strength of the Young’s modulus increased in AgCrO2 delafossite due to the increase of its rigidity. Thus, AgCrO2 delafossite has more strength than has AgFeO2 delafossite.

Table II The elastic parameters of AgCrO2 and AgFeO2 delafossite
Full size table
Table III The elastic parameters of AgCrO2 and AgFeO2 delafossite
Full size table

It is known from the theory of isotropic elasticity that Poisson’s ratio was in the range from −1 to 0.5. Thus, in the present study, Poisson’s ratio is 0.25, which is in good agreement with the theory, indicating that the investigated samples were not brittle.

The calculation of Debye temperature is important to know the conduction mechanism of the investigated sample, and can be calculated from Waldron’s equation as follows:38

$${\theta }_{D}= \frac{{\hslash c }{\nu }_{av}}{{k}_{B}}$$
(14)
$$\hslash= \frac{h}{2\pi }$$
(15)
$${\nu }_{av}= \frac{{\nu }_{t}+ {\nu }_{o}}{2}$$
(16)

where h is the Planck constant, c is the velocity of light, νav is the average frequency, kB is the Boltzmann constant, and νt and νo are the tetrahedral and octahedral frequencies, respectively. Table II shows that ϴD is larger for AgCrO2 delafossite than for o AgFeO2 delafossite due to the larger values of the octahedral and tetrahedral frequencies of AgCrO2 compared with AgFeO2 delafossite. Moreover, Anderson’s formula for the Debye temperature calculation \({\theta }_{D}^{^{\prime}}\) was as follows:44

$${\theta }_{D}^{^{\prime}}= \frac{h}{{k}_{B}} \times {\left(\frac{3 {N}_{A}}{4\pi {V}_{A}}\right)}^\frac{1}{3} \times {V}_{m}$$
(17)
$${V}_{A}={\left(\frac{M}{{D}_{x}}\right)}/{q}$$
(18)

where NA is the Avogadro number, VA is the mean atomic volume, and q is the number of atoms in the ABO2 formula (= 4). One can observe from the result of the \({\theta }_{D}^{^{\prime}}\) of both samples that the conduction mechanism of AgFeO2 was due to electrons (n-type).

Optical Properties

Optical properties have attracted attention from researchers because they are very useful in electronic devices.45,46,47 Figure 2a and Table IV illustrate the refractive index n2 and the wavelength λ2 of AgFeO2 and AgCrO2 delafossite. Based on the following equation, the lattice dielectric constant (εl) was obtained as follows:48

$${n}^{2}= {\varepsilon }_{l}- \left[\frac{{e}^{2}}{ {\pi } {c}^{2}}\right] \left(\frac{N}{{m}^{*}}\right) {\lambda }^{2}$$
(19)

where c is the velocity of light, (N/m*) is the ratio of the free carrier concentration to the effective mass, and e is the electronic charge. It can be seen from Fig. 2a that, at a longer wavelength (λ), the dependence of n2 versus λ2 is linear, and the dielectric constant (εl) is estimated from the extrapolation of the linear part to zero λ. Moreover, the values of (e2 N/π c2 m*) were also estimated from this linear part and are reported in Table IV. Generally, the increase of the charge carriers decreases the crystallinity of the material.49,50 Thus, AgCrO2 is more crystalline than AgFeO2 delafossite due to the (N/m*) of the AgCrO2 delafossite being smaller than that of AgFeO2 delafossite.

Fig. 2
figure 2

a The refractive index n2 versus the wavelength λ2 of AgCrO2 and AgFeO2 delafossite. b The refractive index (n2 -1)-1 versus the photon energy (hν)2 of AgCrO2 and AgFeO2 delafossite. c The refractive index (n2 -1)-1 versus the wavelength λ-2 of AgCrO2 and AgFeO2 delafossite

Full size image
Table IV The operating frequency and the optical parameters of AgCrO2 and AgFeO2 delafossite
Full size table

Figure 2b shows the relationship between (n2 − 1)−1 versus (hν2) for AgFeO2 and AgCrO2 delafossite. At low optical frequencies, the dispersion parameters (Eo and Ed) of the investigated samples can be obtained from the following equation:51

$${\left({n}^{2}-1\right)}^{-1}= -\frac{1}{{E}_{o} {E}_{d}} {\left(h \nu \right)}^{2}+ \frac{{E}_{o}}{{E}_{d}}$$
(20)

where Eo is the single oscillator energy and Ed is the dispersion energy. Table IV shows the values of Ed and Eo estimated from the intercept of the linear part of the graph, and they give information about the measure of the strength of the interband optical transition and the average excitation for the electronic transition, respectively.

Moreover, Fig. 2c shows the variation of (n2 − 1)−1 versus λ-2 of AgCrO2 and AgFeO2 delafossite and can be expressed from the following relationship:52

$$\frac{{n}_{\infty }^{2}-1}{{n}^{2}-1}=1- {\left(\frac{{\lambda }_{o}}{\lambda }\right)}^{2}$$
(21)

where λo is the average wavelength of the interband oscillator and \(n_{\infty}\) is the refractive index of the long wavelength. The average oscillator strength, So, was estimated from the slope and the intercept of the graph of Fig. 2c. Based on these results, all these optical parameters may help in tailoring the construction of optical devices.

Figure 3a shows the variation of the third-order nonlinear optical susceptibility versus the photon energy (hν) for AgCrO2 and AgFeO2 delafossite. The equation of the third-order nonlinear susceptibility, χ, (3) was expressed as follows:53

$${\chi }^{(3)}=A= {\left[\frac{{E}_{o }{E}_{d}}{4\pi \left({E}_{o}^{2}- {\left(h\nu \right)}^{2}\right)}\right]}^{4}$$
(22)

where A is 1.7 × 10-10. It can be seen from Fig. 3a and Table IV that χ (3) of AgCrO2 delafossite is higher than that of AgFeO2. As a result, AgCrO2 delafossite is a more promising material for applying in optical devices than AgFeO2 delafossite.

Fig. 3
figure 3

a The third-order nonlinear susceptibility versus the photon energy of AgCrO2 and AgFeO2 delafossite. b The switching field distribution of AgCrO2 and AgFeO2 delafossite

Full size image

Switching Field Distribution and High-Frequency Applications

Figure 3b shows the switching field distribution estimated from the first derivative of the magnetization of AgFeO2 and AgCrO2 delafossite. The magnetic properties of the investigated samples have been illustrated in detail in previous studies.33,34,35,36 It can be seen that AgFeO2 delafossite had a strong switching field distribution more than 9-fold that of AgCrO2 delafossite. This may be due to the strong magnetic interaction of the AgFeO2 cations. As a result, AgFeO2 delafossite is a promising material to be applied in magnetic applications.

Figure 4 and Table IV show the high microwave operating frequency response of the investigated samples. It is important to calculate the microwave operating frequency to use a certain frequency band to avoid the interference of the frequency.54 The microwave operating frequency was calculated from the following relationship:55

$$\omega =8{\pi }^{2}\gamma M$$
(23)

where γ = 2.8 (MHz/G) which is the gyromagnetic ratio and M is the magnetization of AgFeO2 and AgCrO2 delafossite. It can be seen that the operating frequency of AgFeO2 delafossite is larger by 5-fold than that of AgCrO2 delafossite, as shown in Table IV. This means that AgFeO2 could be applied in the microwave ultra-high frequency L band because it has the ω at 2.49 GHz. However, the AgCrO2 delafossite could be applied in the microwave ultrahigh-frequency P band because it has the ω at 420 MHz.

Fig. 4
figure 4

The operating frequency versus the applied field of AgCrO2 and AgFeO2 delafossite

Full size image

Conclusion

AgFeO2 and AgCrO2 delafossite were successfully prepared by the flash auto-combustion method. The main peaks of the FTIR analysis assured the formation of the investigated samples. In addition, the elastic properties were estimated from the FTIR analysis and showed that AgCrO2 delafossite has more strength than AgFeO2 delafossite. The optical properties were studied and showed that AgCrO2 delafossite is a more promising material for applying in optical devices. In addition, the switching field distribution was studied and showed that AgFeO2 is larger by 9-fold than that of AgCrO2 delafossite. Thus, AgFeO2 delafossite is a promising material in magnetic applications. Moreover, high-frequency applications were studied by magnetic analysis and showed that AgFeO2 could be applied in the microwave ultra-high frequency L band and AgCrO2 delafossite could be applied in the microwave ultrahigh-frequency P band. For the future, the authors suggest improving this work by studying the investigated samples using citrate or sol–gel methods.