Abstract
The constitutive equations for the irreversible mechanical phenomena, e.g. the plastic deformation and the sliding between solids with the friction have been studied over the several centuries. Especially, they have been studied for the description of the cyclic loading behaviors in the last half century in order to respond to the high developments of the mechanical, the civil and the structural industries. Then, various constitutive models for these phenomena during the cyclic loading have been proposed hitherto. In this article, the mechanical features and the advantages/disadvantages of the constitutive models which are adopted widely for mechanical design and installed into a lot of commercial software will be clarified by the critical review for the further developments of the research on the plastic deformation/sliding phenomena and the engineering design of solids and structures, since plural different models are not necessary to these ends for the analyses of identical deformation/sliding behaviors. Eventually, it will be described that the irrational formulations involved in the past formulations can be solved out thoroughly by the recent formulations of the subloading-overstress model and subloading-overstress friction model for the monotonic and cyclic loadings under the general rate of deformation/sliding from the quasi-static to the impact loadings in unified equations, disusing the rate-independent plastic/sliding constitutive models.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The study on the irreversible mechanical phenomena, i.e. the plastic/viscoplastic deformation/sliding of solids has the long history over the several centuries. Then, various plastic and viscoplastic models have been proposed in the last half century. Then, a new proposition of these models seems to be exhausted already twenty years ago. Therefore, it would be of importance to unify these models to a rational model, clarifying their mechanical features and the advantages/disadvantages, for the research study of plasticity and viscoplasticity and the engineering design of solids and structures, since plural models are not necessary for the analysis of identical deformation behaviors. The elastoplastic models proposed so far are shown as follows:
-
1.
Multi surface model proposed by Mróz [84] and Iwan [71], which is explained in the books (Lemaitre and Chaboche [78], Khan and Huang [74], Lubarda [80], Wu [114], Murakami [86]),
-
2.
Two surface model proposed by Dafalias and Popov [27] and Krieg [77], which is explained in the books (Khan and Huang [74], Murakami [86]),
-
3.
Subloading surface model proposed by Hashiguchi [39, 40, 43, 49], which is explained in the books (Hashiguchi [51, 53, 55]),
-
4.
Chaboche model proposed by Chaboche et al. [16], which is explained in the books (Lemaitre and Chaboche [78], Ellyin [31], Murakami [86], Kang and Kan [73]),
-
5.
Yoshida–Uemori model proposed by Yoshida and Uemori [119, 120] and Yoshida et al. [121] (see also Yoshida and Amaishi [117], Yoshida et al. [118]) with the modification of the two surface model,
while the Chaboche model is classified to the conventional model assuming that the interior of the yield surface is the elastic domain in the classification of the elastoplastic models by Drucker [29]. However, its mechanical features and the advantages/disadvantages have not been clarified hitherto. Nevertheless, the Chaboche model and the Yoshida–Uemori model are often quoted in literatures and installed into many commercial software.
Further, various viscoplastic models based on the creep model have been proposed or described by Lemaitre and Chaboche [78], Abel-Karim and Ohno [1], Betten [8], Asaro and Lubarda [6], Ohno et al. [91], de Souza Neto et al. [28], etc. In addition, various viscoplastic models based on the overstress concept have been proposed so far by Bingham [9], Prager [101], Perzyna [99, 100], Krempl et al. [76], Chaboche [12, 14, 15], Lubliner [81], Arnold and Saleeb [5], Simo [105], Simo and Hughes [106], Ho and Krempl [70], Lubarda [80], Ottosen and Ristinmaa [96], Saleeb and Arnold [102], Mayama et al. [83], de Souza Neto et al. [28], Chaboche et al. [17], Guo et al. [38], Chen and Feng [20], Chen et al. [21], etc.
Further, various constitutive models for the sliding with friction between solid surfaces have been proposed, since all bodies in the natural world are exposed to the friction phenomena, contacting with other bodies, except for bodies floating in a vacuum without any mechanical support. Nevertheless, only the classical Coulomb friction law is described in most literatures except for the papers/books by the present authors and is installed as the fundamental friction model in the commercial FEM software, e.g. Abaqus, Marc, Nastran, ANSYS, LS-DYNA, etc.
Under the above-mentioned present background on the constitutive equations for the irreversible mechanical phenomena of solids, the present article is composed of the following fundamental detections based on the exact examinations.
-
1.
The Chaboche model [16] and the Yoshida–Uemori model [119,120,121] widely adopted for the engineering analyses are incapable of describing the plastic deformation in the unloading process and thus of describing the plastic strain accumulation under the cyclic loading process below the yield stress. These shortcomings can be solved out by the extended subloading surface model (Hashiguchi [55]), in which the similarity-center of the subloading surface to the yield surface translates with the plastic deformation.
-
2.
The past overstress models are incapable of describing the cyclic loading behavior and the deformation behavior in a high stress or strain rate as the infinitely high stress is described in the impact loading. The monotonic/cyclic loading behavior at the general rate ranging from the quasi-static to the impact loading can be described by the subloading-overstress model (Hashiguchi [55, 64]) based on the extended subloading surface model.
-
3.
The Coulomb-friction law is incapable of describing the transition from the static friction coefficient to the kinetic friction coefficient, the plastic sliding by the variation of the tangential contact stress below the Coulomb friction condition and the saturation of the tangential contact stress with the increase of the contact normal stress. All these fundamental friction characteristics can be successfully described by the subloading friction model (Hashiguchi [52, 55, 63]).
Eventually, the subloading surface model is regarded as the governing law for the irreversible mechanical phenomena of solids. Then, the basic concept and the formulations in the subloading surface model for the elastoplastic deformation, the subloading-overstress model for the general viscoplastic deformation and the subloading-overstress friction model for the general sliding are reviewed and explained concisely and comprehensively in this article.
2 Elastoplastic Constitutive Models
Among the various elastoplastic models, the Chaboche model [16], the Yoshida–Uemori model [119,120,121] and the subloading surface model [51] are installed into the commercial FEM software and used widely for the engineering designs of solids and structures. The mechanical features of these models will be analyzed in this section.
The infinitesimal strain tensor
where \({\mathbf{x}} \cong {\mathbf{X}}\) and \({\mathbf{u}}\) are the position vector and the displacement vector, respectively, of the material particle is additively decomposed into the elastic strain tensor \({{\varvec{\upvarepsilon}}}^{e}\) and the plastic strain tensor \({{\varvec{\upvarepsilon}}}^{p}\) as follows:
Let the stress tensor \({{\varvec{\upsigma}}}\) be given by
where the elastic modulus tensor \({\mathbf{\mathbb{E}}}\) for the Hooke’s law is given as follows:
where \(E\) and \(\nu\) are Young’s modulus and Poisson’s ratio, respectively. The rate form of Eq. (3) is given for the constant elastic modulus tensor, i.e. \({\mathbf{\mathbb{E}}} = \text{const.}\) by
2.1 Chaboche Model
Chaboche et al. [16] have modified the conventional elastoplastic model with the yield surface enclosing the purely-elastic domain by the following methods in order to smooth the stress–strain curve in the first monotonic loading process.
-
1.
The yield surface is down-sized to 80–90% of the size of the conventional yield surface,
-
2.
The following evolution rule of the nonlinear kinematic hardening variable \({{\varvec{\upalpha}}}\) is adopted.
$$\mathop {{\varvec{\upalpha}}}\limits^{ \bullet } = \sum\limits_{{i = {1}}}^{n} {\mathop {{\varvec{\upalpha}}}\limits^{ \bullet }}_{i},$$(6)$$\mathop {{\varvec{\upalpha}}}\limits^{ \bullet }{}_{i} = a_{i} {\mathop {{\varvec{\upvarepsilon}}}\limits^{ \bullet }}{}^{p} - \sqrt{\frac{2}{3}} b_{i} \Vert {\mathop {{\varvec{\upvarepsilon}}}\limits^{ \bullet }}{}^{p} \Vert{{\varvec{\upalpha}}}_{i},$$(7)
where \(a_{i}\) and \(b_{i}\) \((i = 1, \, 2, \cdots , \, n)\) are the material constants, which is the superposition of the Armstrong–Frederick kinematic hardening rules (Armstrong and Frederick [4]):
where \(c_{k}\) and \(\bar{b}_{k}\) are the material constants. Equation (8) is reduced to the following equation for the uniaxial loading process for the Mises metals exhibiting the plastically-incompressibility.
where \({\mathop \varepsilon \limits^{ \bullet }}{}_{a}^{p}\) and \({\mathop \varepsilon \limits^{ \bullet }}{}_{l}^{p}\) are the axial and the lateral plastic strain rate, respectively. The variation of the axial component \(\alpha_{a}\) is shown in Fig. 1.
The stress–strain curve described by the Chaboche model with the above-mentioned modifications by the superposition of various nonlinear kinematic hardening rules is illustrated in Fig. 2, which is quoted from Lemaitre and Chaboche [78]. The smooth stress–strain curves are depicted in the cyclic loading with the large stress amplitude reaching the yield state as shown in Fig. 3 where the smooth stress–strain curve is depicted by superposing the highly-nonlinear and the moderate kinematic hardening equations.

(Source of this figure: Lemaitre and Chaboche [78])
Stress–strain curve described by Chaboche model
Stress–strain curve in forward and reverse loading processes described by Chaboche model [16]
However, the following various serious defects in the Chaboche model [16] are recognized for the description of plastic deformation.
-
1.
The plastic deformation cannot be described in the unloading process as shown in Fig. 4, since the interior of the yield surface is assumed to be the purely-elastic domain. Therefore, the plastic strain accumulation in the pulsating loading of stress and the spring-back phenomenon cannot be described at all.
-
2.
The reloading stress–strain curve does not return to the preceding stress–strain curve, exhibiting the large overshooting as shown Fig. 5. Therefore, the cyclic loading behavior cannot be described appropriately, predicting the excessively large strain accumulation under the constant stress amplitude.
Stress–strain curve in unloading process described by Chaboche model [16]
Overshooting of reloading stress–strain curve described by Chaboche model [16]
The Ohno–Wang model (Ohno and Wang [92, 93]) is the worsening of the Chaboche model in both aspects of the description of mechanical behavior and the simplicity of the mathematical expression by the piecewise of the Armstrong–Frederick nonlinear kinematic hardening rule, requiring the judgment on which surface the stress lies.
However, unfortunately, Chaboche and Ohno have shown only the prediction of the complete tension–compression alternating loading test, represented by the constant strain amplitude test as seen in Fig. 6 (quoted from Chaboche et al. [16] or Lemaitre and Chaboche [78]), in which the incomplete saturation of the kinematic hardening shown in Fig. 5 is not included.
A lot of papers on the modifications of the Chaboche model have been reported by Chaboche [11, 13], Chaboche and Rousselier [18, 19], Hassan et al. [69], Dafalias and Feigenbaum [25], Dafalias et al. [26], Okorokov et al. [95], etc. during nearly half century after the proposition (Chaboche et al. [16]) for the modification of the Chaboche model on the above-mentioned defects. However, all these repeated trials have failed definitely. It is quite natural consequence caused from the above-mentioned serious defect in the basic structure of this model.
The pertinent description of the cyclic loading behavior under the general stress or strain amplitude including partial-unloading processes can never be attained by the Chaboche model. On the other hand, it can be attained by the extended subloading surface model as will be verified in detail in the later Sect. 2.4.
2.2 Yoshida–Uemori Model
Consider the Yoshida–Uemori model [119,120,121] (see also Yoshida and Amaishi [117], Yoshida et al. [118]), which is the modification of the two surface model (Dafalias and Popov [27]), incorporating the chord modulus \(\bar{E}\) defined by the following equation is incorporated:
shown in Fig. 7, where \(\varepsilon^{\text{eqp}} \; ( = \sqrt {2/3} \int \Vert {\mathop {{\varvec{\upvarepsilon}}}\limits^{ \bullet }}{}^{p} \Vert \mathrm{d}t )\) is the equivalent plastic strain. \(E\) and \(\bar{E}_{\text{min}}\) are the initial chord modulus (true Young’s modulus) and the final lowest chord modulus, respectively, and \(\xi\) is the material constant.
Chord modulus incorporated in ad hoc Yoshida–Uemori model [119,120,121], which is incapable of describing strain accumulation under constant stress amplitude, where \(E\) is the true Young's modulus which is constant, \(\bar{E}\) is the chord Young's modulus and \(\bar{E}_{\text{min}}\) is its minimum value
However, the incorporation of the chord modulus by Yoshida–Uemori model [119,120,121] (see also Yoshida and Amaishi [117], Yoshida et al. [118]) contradicts to the real material behavior as known from the following various fundamental facts:
-
1.
The elastic deformation is induced by the elastic deformations of material particles themselves composing the solid. Therefore, the elastic deformation characteristics does not change as far as the material particles do not deform or break inelastically. Therefore, the elastic deformation property including Young’s modulus does not change in the small strain range (several percent strain) to which the spring-back is concerned.
-
2.
Then, the purely elastic deformation is observed at the beginning of the initial loading and at the moments of the stress reversal, i.e. the unloading and the reloading, in which the mutual slip of material particles causing the plastic strain rate is not induced but only the elastic deformation of material particles occurs as shown in Fig. 7.
-
3.
During the unloading process to the stress-free state, however, the compressive plastic deformation in the direction opposite to the preceding extension is induced, which is caused by the returning of the elongated shapes of material particles to the original shape due to the elastic deformation as shown in Fig. 7. This fact is not considered in the Yoshida–Uemori model.
-
4.
Physically, the reduction in Young’ modulus is induced by the generations of the small cracks and their extensions and thus it decreases acceleratingly under the monotonic loading process for the strain far larger than the strain concerning the spring-back phenomenon. This basic knowledge in the continuum damage mechanics is ignored in Yoshida and Uemori [119, 120] and Yoshida et al. [121] (see also Yoshida and Amaishi [117], Yoshida et al. [118]).
Eventually, the spring-back phenomenon cannot be described by the plasticity models incorporating the yield surface enclosing the purely-elastic domain, i.e. the Chaboche model [16] and the two surface model [27] without resorting to the irrational method adopted by Yoshida and Uemori [119, 120] and Yoshida et al. [121] (see also Yoshida and Amaishi [117], Yoshida et al. [118]).
2.3 Initial Subloading Surface Model
The Chaboche model [16] modified the conventional plasticity model so as to describe the smooth transition from the elastic to plastic state by the complex methods: (1) the reduction of the size of the yield surface and (2) the superposition of the nonlinear kinematic hardening rules. However, the smooth transition cannot be described in the partial unloading–reloading process by this model as described in detail in Sect. 2.1. On the other hand, the smooth elastic–plastic transition can be described always by the subloading surface model based on the subloading concept (Hashiguchi [39, 40]).
The concept of the subloading surface insisting that the plastic strain rate is induced as the stress approaches the yield surface is incorporated in the subloading surface model based on the physical fact: The plastic deformation is induced by the mutual slips between the solid particles in soils, the dislocation in crystals in metals, etc. which are not induced at the moment when the stress reaches the yield stress but induced gradually as the stress approaches the yield stress, while the elastic deformation is induced by the elastic deformation of material particles themselves.
Now, we describe the yield surface as follows (Fig. 8):
where \(f({\hat{\varvec{\sigma }}})\) is the homogeneous function of the variable
in degree-one and \(H\) is the isotropic hardening variable.
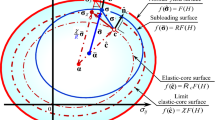
Now, we incorporate the subloading surface, which always passes through the current stress point and has similar shape and orientation to the yield surface with respect to a similarity-center in the stress space. The subloading surface for the yield surface in Eq. (11) is described as follows (Fig. 8):
where \(R \; (0 \le R \le 1)\) is the yield ratio designating the ratio of the size of the subloading surface to that of the yield surface, meaning the approaching-degree of the stress to the yield surface, while the similarity-center is chosen at the center of the yield surface, i.e. the back stress \({{\varvec{\upalpha}}}\).
Now, we adopt the associated flow rule
where \(\mathop \lambda \limits^{ \bullet }\) is the positive proportionality factor and \({\hat{\mathbf{n}}}\) is the normalized outward-normal of the subloading surface at a current stress point, i.e.
noting
The isotropic hardening function \(F(H)\) for metals is given by
where \(F_{{0}}\) is the initial value of \(F\), and \(s_{r}\) and \(c_{H}\) are the material constants. Further, the following nonlinear-kinematic hardening rule (Hashiguchi [53]) is adopted.
where \(c_{k}\) and \(b_{k} \; ( \le \sqrt {3/2} )\) are the material constants. Equation (17) is modified from the Armstrong–Frederick’s kinematic hardening rule in Eq. (8) such that the saturation value of the movement of the yield surface depends on the size of the yield surface \(F\) by the modification \(\bar{b}_{k} \to b_{k} F\).
The consistency condition of the subloading surface on which the current stress always lies is given as follows:
noting
The evolution rule of the yield ratio \(R\) is formulated by the subloading surface concept as follows:
-
1.
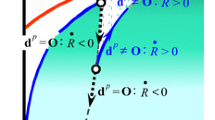
The purely-elastic deformation is induced at the similarity-center of the yield and the subloading surfaces, i.e. the back-stress (\({{\varvec{\upsigma}}} = {{\varvec{\upalpha}}}\)). Therefore, the stress increases so that the yield ratio \(R\) increases in the infinite rate with the plastic strain rate at that stress, i.e. \(\mathop R\limits^{ \bullet } \to \infty \text{ for }R = 0 .\)
-
2.
The stress approaches the yield surface so that the yield ratio increases with the plastic strain rate in the general stress state, i.e. \(\mathop R\limits^{ \bullet } > 0\text{ for }0 < R < 1\).
-
3.
The stress changes along the yield surface so that the yield ratio does not change with the plastic strain rate in the yield state, i.e. \(\mathop R\limits^{ \bullet } = 0\text{ for } R = 1\).
-
4.
The stress decreases towards the yield surface with the plastic strain rate in the over yield state, i.e. \(\mathop R\limits^{ \bullet } < 0\text{ for } R > 1\).
Then, the rate of the yield ratio must satisfy the following conditions.
Then, we formulate the evolution rule of the yield ratio as follows:
where \(U(R)\) is the monotonically decreasing function of \(R\) fulfilling the following conditions (see Fig. 9a).
A specific form of the function \(U(R)\) satisfying Eq. (21) is given by
where \(u\) is the dimensionless material parameter regulating the increase of the yield ratio \(R\) for a certain plastic strain increment. The gentler elastic–plastic transition is depicted for the smaller value of the material parameter \(u\), while the abrupt change from the elastic to the plastic state is described for \(u \to \infty\) as done in the conventional elastoplastic constitutive equation.
However, we note that there exist a lot of materials including usual metals in which the plastic strain rate is hardly induced below a certain value of the yield ratio. Then, let Eq. (21) be modified to the following equation, by which the plastic strain rate is not induced until the yield ratio \(R\) reaches a certain value of the material parameter \(R_{e} \; ( < 1)\) (see Fig. 9b).
The material parameter \(R_{e}\) is interpreted as the ratio of the (half) stress amplitude \(\sigma_{{\text{fl}}}\) at the fatigue (or endurance) limit, i.e. the ratio of the fatigue limit stress to the yield stress \(\sigma_{y}\) under the zero value of average stress \(\overline{\sigma }\), i.e. \(R_{e} = ( \sigma_{{\text{fl}}} /\sigma_{y} ) \big|_{{\overline{\sigma } = 0}}\). The fatigue limit is observed in steels, titanium, etc. but it is not observed in other materials involving non-ferrous metals. The explicit form of the function \(U(R)\) satisfying Eq. (23) is given by
where \(\langle \, \rangle\) is the Macaulay’s bracket defined by \(\langle s\rangle = (s + |s|)/2\), i.e. \(\langle s\rangle = 0\) for \(s < 0\) and \(\langle s\rangle = s\) for \(s \ge 0\) (\(s\): arbitrary scalar variable).
The following relation holds by virtue of the homogeneity of the function \(f({\hat{\varvec{\sigma }}})\) in degree-one.
by which one has
Equation (18) with Eq. (26) results in
Substituting the associated flow rule in Eq. (14) with Eqs. (16) and (17) into Eq. (27), one has
The positive proportionality factor \(\mathop \lambda \limits^{ \bullet }\) is directly derived from Eq. (28), and by noting Eq. (14), the plastic strain rate \({\mathop {{\varvec{\upvarepsilon}}}\limits^{ \bullet }}^{p}\) is formulated as follows:
where
which is reduced to the following plastic modulus in the conventional elastoplasticity based on the assumption that the interior of the yield surface is the purely-elastic domain.
which holds in the yield state \((R = 1 \leadsto U(R) = 0)\) or by choosing the material constant \(u\) to be infinite, i.e. \(u \to \infty\).
The strain rate is given by
noting Eq. (2). The magnitude of plastic strain \(\mathop \lambda \limits^{ \bullet }\) in terms of strain rate, denoted by the symbol \(\mathop \Lambda \limits^{ \bullet }\), is derived from Eq. (32) and then the plastic strain rate \({\mathop {{\varvec{\upvarepsilon}}}\limits^{ \bullet }}^{p}\) is given by noting Eq. (14) as follows:
Then, the stress rate, i.e. the inverse relation of Eq. (32) is given by
The loading criterion is given as follows (Hashiguchi [46, 48]):
noting \(\hat{M}{}^{p} + {\mathbf{\hat{n}}:{\mathbf{\mathbb{E}}}:{\mathbf{\hat{n}}}} > 0\) because of the positive-definiteness of the elastic modulus tensor \({\mathbf{\mathbb{E}}}\) and the stress decrease in an infinite rate for \(\hat{M}{}^{p} + {\mathbf{\hat{n}}:{\mathbf{{\mathbb{E}}}}:{\mathbf{\hat{n}}}} \to {0}\), where the judgment whether the stress reaches the yield surface is not required since the plastic strain rate is induced continuously as the stress approaches the yield surface in the subloading surface model. Equation (35) is applicable not only to the hardening state but also to the perfectly-plastic and softening states, while the loading criterion in terms of the stress rate \(\mathop {{\varvec{\upsigma}}}\limits^{ \bullet }\), which is often used for metals, holds only for the hardening state.
The subloading surface model possesses the following distinguished advantages:
-
1.
The smooth transition from elastic to plastic state is always described as observed in real material behavior. On the other hand, the smooth transition cannot be described by Chaboche et al. [16] except for the particular loading process without the partial unloading and the reloading processes, although the quite complex method by the superposition of the nonlinear kinematic hardening equations is incorporated.
-
2.
Plastic strain rate can be described even for low stress level and for cyclic loading process under small stress amplitudes since a purely-elastic domain is not assumed anywhere.
-
3.
The yield-judgment whether or not the stress reaches the yield surface is not required since the plastic strain rate develops continuously as the stress approaches the yield surface. In contrast, the yield judgment is required in all of the other elastoplastic models including the Chaboche model, since they assume a surface enclosing a purely-elastic domain.
-
4.
The stress is automatically pulled back onto the yield surface when it goes over the surface in numerical calculation because of \(\mathop R\limits^{ \bullet } < 0\) for \(R > 1\) from Eq. (19) with Eq. (21)4 as seen in Fig. 10. In contrast, the stress deviates finitely from the yield surface resulting in the decrease in the calculation accuracy in all of the other plastic models unless laborious treatment of return-mapping is adopted.
The subloading surface model possesses a lot of the above-mentioned distinguished advantages. It can be formulated only by incorporating only one material constant \(u\) into the conventional plastic constitutive equation. Here, note that the stress–strain curve described by the conventional elastoplastic model with the yield surface enclosing the purely-elastic domain is described by setting \(u \to \infty\) in the subloading surface model. Therefore, the drastic improvements can be attained merely by adding only one martial constant \(u\) in the evolution rule of the yield ratio \(R\). Then, the description of the deformation behavior is improved drastically and the efficiency of the numerical calculation is also improved drastically by the automatic controlling function to attract the stress to the yield surface in the subloading surface model. Therefore, the cost and the time required for the industrial design and development can be reduced tremendously even if we input irresponsible proper large value, e.g. \(U = 1000\) for the material constant \(u\), which is 300–1,000 for metals, 50–300 for soils and 20–70 for glass, noting that the deformation behavior by the conventional elastoplastic constitutive equation is calculated for \(u \to \infty\).
Eventually, the subloading surface model is the mathematical model which is capable of describing the overall real elastoplastic deformation behaviors of solids based on the physical facts.
2.4 Extended Subloading Surface Model
The initial subloading surface model described in the preceding section is incapable of describing the plastic strain rate in the unloading process, since the subloading surface is similar to the yield surface with respect to the origin of the stress space and thus it shrinks until the stress returns to the stress-free state. Then, let it be assumed that the similarity-center of the subloading surface to the yield surface moves with the plastic strain rate so that the subloading surface shrinks to the similarity-center until the stress is reduced to the similarity-center but it expands again until the stress is reduced to the stress-free state, leading to the description of the plastic strain rate in the unloading process. This assumption is necessary to describe the closed hysteresis loop in the unloading–reloading process. The subloading surface model in which the translation of the similarity-center is incorporated is called the extended subloading surface model.
Now, we extend the subloading surface so as to be similar to the yield surface with respect to the similarity-center \({\mathbf{c}}\) and thus it is described as follows (see Fig. 11).
where
\({\overline{\mathbf{\alpha }}}\) stands for the conjugate (similar) point in the subloading surface to the point \({{\varvec{\upalpha}}}\) representing the back-stress, i.e. the kinematic hardening variable in the yield surface. Here, note that the purely-elastic behavior is induced when the stress coincides with the similarity-center \(({{\varvec{\upsigma}}} = {\mathbf{c}})\) and thus the yield ratio becomes zero \((R = 0)\). Then, let the similarity-center \({\mathbf{c}}\) be called the elastic-core. Here, the following relation holds by virtue of the similarity (see Fig. 11).
which yields
where
Besides, \({{\varvec{\upsigma}}}_{y}\) in Fig. 11 is the conjugate stress on the yield surface to the current stress \({{\varvec{\upsigma}}}\) on the yield surface, fulfilling \({{\varvec{\upsigma}}} - {\overline{\varvec{\upalpha }}} = R({{\varvec{\upsigma}}}_{y} - {{\varvec{\upalpha}}})\). The time-derivative of \({\overline{\mathbf{\alpha }}}\) is described from Eq. (38) as
The subloading surface in Eq. (36) is rewritten by Eq. (40) as follows:
\(R\) is calculated by solving Eq. (43) in the elastic loading process \({\mathop {{\varvec{\upvarepsilon}}}\limits^{ \bullet }}{}^{e} \ne {\mathbf{O}}, \;{\mathop {{\varvec{\upvarepsilon}}}\limits^{ \bullet }}{}^{p} = {\mathbf{O}}\) by substituting the updated values of \({{\varvec{\upsigma}}}, \, {{\varvec{\upalpha}}}, {\mathbf{c}}\) and \(F\).
We adopt the associated flow rule for the subloading surface:
where
noting
The rate of the isotropic hardening variable is described by using the function \(f_{{H\overline{n}}}\) based on Eqs. (16) and (44) with the replacement of \({\hat{\mathbf{n}}}\) to \({\overline{\mathbf{n}}}\) as follows:
The rate of the kinematic hardening variable is given based on Eqs. (17) and (44)with the replacement of \({\hat{\mathbf{n}}}\) to \({\overline{\mathbf{n}}}\) as follows:
The elastic-core \({\mathbf{c}}\) is not allowed to approach the yield surface closely, because the purely elastic deformation is induced when the stress lies on the elastic-core but the apparent plastic deformation is induced when the stress lies on the yield surface. In addition, it should be noted that a smooth elastic–plastic transition leading to the continuous variation of the tangent stiffness modulus tensor is not described violating the continuity condition in the large, i.e. the smoothness condition (Hashiguchi [44, 45]), if the elastic-core lies on the yield surface. On the other hand, the other plasticity models, i.e. the cylindrical superposed kinematic hardening model, i.e. the Chaboche model (Chaboche et al. [16], Ohno and Wang [92, 93], Hassan et al. [69], etc.), the multi surface model (Mróz [84], Iwan [71]) and the two surface model (Dafalias and Popov [27], Krieg [77], Hashiguchi [42], Yoshida et al. [121], etc.) violate the smoothness condition leading to the remarkably discontinuous variation of the tangent stiffness modulus, since the purely-elastic domain contacts directly to the yield surface in which the remarkable plastic deformation is induced.
Now, we introduce the following elastic-core surface, which always passes through the elastic-core \({\mathbf{c}}\) and maintains a similarity to the yield surface with respect to the kinematic-hardening variable \({{\varvec{\upalpha}}}\).
where \(\Re_{c}\) designates the ratio of the size of the elastic-core surface to the normal-yield surface (see Fig. 11) so that let it be called the elastic-core yield ratio. The normalized outward-normal \({\hat{\mathbf{n}}}_{c}\) of the elastic-core surface is given as follows (Fig. 11):
Now, let it be postulated that the elastic-core can never reach the yield surface designating the fully-plastic stress state so that the elastic-core does not go out from the following limit elastic-core surface.
where \(\chi \;{( < 1)}\) is the material constant designating the maximum value of \(\Re_{c}\) and the following inequality must be satisfied.
The material-time derivative of Eq. (51) at the limit state that \({\mathbf{c}}\) lies on the limit elastic-core surface in Eq. (50) yields:
Here, noting
on account of the Euler’s homogeneous function \(f({\hat{\mathbf{c}}})\) in degree-one for the variable \({\hat{\mathbf{c}}}\), the substitution of Eq. (53) to Eq. (52) leads to
The inequality (51) is called the enclosing condition of elastic-core and Eq. (54) is its rate form.
Now, assume the equation (Hashiguchi [51]).
where \(c_{e}\) is the dimensionless material constant. Here, it holds for Eq. (55) that
and thus it holds that
Thus, it is recognized that the elastic-core never goes out from the limit elastic-core surface for the convex yield surface.
Then, the evolution rule of the elastic-core is given from Eq. (55) as follows:
which leads to
noting Eqs. (46) and (47), where
The material-time derivative of Eq. (36) leads to the consistency condition of the subloading surface as follows:
noting
Here, one has
based on the homogeneous function \(f({\overline{\varvec{\sigma }}})\) of \({\overline{\varvec{\sigma }}}\) in degree-one by the Euler’s theorem. Then, it follows that
The substitution of Eq. (62) into Eq. (60) leads to
The substitution of Eq. (42) into Eq. (63) leads to
Nothing the relation
it follows from Eq. (64) that
The substitutions of Eq. (65) with Eqs. (20), (46), (47) and (58) into Eq. (66) leads to
from which the plastic multiplier \(\mathop {\overline{\lambda }}\limits^{ \bullet }\) and the plastic strain rate \({\mathop {{\varvec{\upvarepsilon}}}\limits^{ \bullet }}{}^{p}\) are given as follows:
where
The plastic modulus \(\overline{M}{}^{p}\) in Eq. (69) is reduced to Eq. (31) for the conventional model in the yield state by setting \(R = 1\) leading to \(U = 0\).
The strain rate is given by substituting Eqs. (5) and (68)\(_{2}\) into Eq. (5)\(_{3}\) as follows:
from which the magnitude of plastic strain rate described in terms of the strain rate, denoted by \(\mathop \Lambda \limits^{ \bullet }\) instead of \(\mathop \lambda \limits^{ \bullet }\), in the flow rule of Eq. (44) is given as follows:
The stress rate is given from Eq. (5) with Eq. (71) as follows:
The loading criterion is given as follows (Hashiguchi [46, 48, 50]):
Now, we extend the material parameter \(u\) to the following function for the extended subloading surface model, in which the elastic-core, i.e. the similarity-center \({\mathbf{c}}\) moves with the plastic deformation, introducing the variables \(\Re_{c}\) and \(C_{n}\).
leading to the replacement
where \(u\) and \(u_{c}\) are the material constants and
Then, the plastic positive proportionality factor \(\mathop \lambda \limits^{ \bullet }\) is replaced to the following equation by Eq. (75), noting Eq. (20) with Eq. (24).
The prompt returning of the reloading curve to the preceding curve can be described by the above-mentioned modification of the material parameter \(u\) as illustrated in Fig. 12.
The overshooting of stress–strain curve is predicted unavoidably in the unloading–reloading process by the Chaboche model [16] as was described in detail in Sect. 2.1. This serious defect is solved out in the above-mentioned formulation of the extended subloading surface model.
2.5 Isotropic Hardening Stagnation
The isotropic hardening stagnates temporarily after the stress reversal, because the pilling-up of dislocation obstacles or the formation of various networks causing the isotropic hardening are released. The concept of the stagnation of the isotropic hardening has been proposed by Chaboche et al. [16] (see also Chaboche [13]), insisting that the isotropic hardening does not proceed when the plastic strain lies inside the nonhardening region. Based on this proposition, the following surface defined in the space of plastic strain, called the isotropic hardening surface, be introduced.
where
choosing \(g({\tilde{\varvec{\upvarepsilon }}}{}^{p} )\) be the homogeneous degree-one of the variable \({\tilde{\varvec{\upvarepsilon }}}{}^{p}\) (Hashiguchi [55]). The variables \(\tilde{K}\) and \({{\varvec{\uprho}}}\) are the size and the center, respectively, of the isotropic hardening surface. Further, we introduce the surface, called the sub-isotropic hardening surface, which always passes through the current plastic strain \({{\varvec{\upvarepsilon}}}^{p}\) and which has a similar shape and a same orientation to the isotropic hardening surface.
The sub-isotropic stagnation surface is described by the following equation.
where \(\tilde{R} = g({\tilde{\varvec{\upvarepsilon }}}{}^{p} )/\tilde{K} \; (0 \le \tilde{R} \le 1)\) is referred to as the isotropic hardening ratio designating the ratio of the size of sub-isotropic hardening surface to that of the isotropic hardening surface. The isotropic hardening and the sub-isotropic hardening stagnation surfaces are shown in Fig. 13.
The consistency condition of the sub-isotropic hardening surface is given from Eq. (80) as follows:
which is reduced to the following relation when the plastic strain just lies on the isotropic hardening surface.
where
which is the normalized outward-normal of the sub-isotropic stagnation surface.
Then, let the following evolution equations from Eq. (82) be assumed.
where \(0 \le C \le 1\) and \(\varsigma \; ( \ge 1)\) are the material constants.
The internal variables \(\tilde{K}\) and \({{\varvec{\uprho}}}\) evolve so as to enclose the plastic strain \({{\varvec{\upvarepsilon}}}^{p}\) by Eqs. (84) and (85). This fact can be verified by the following equation which is derived by substituting these equations into the consistency condition in Eq. (81) for the sub-isotropic hardening surface.
leading to \(1 - \tilde{R}^{\varsigma } + C\tilde{R}^{\varsigma } (1 - \tilde{R}) < 0\), and thus, \(\mathop {\tilde{R}}\limits^{ \bullet } < 0\) for \(\tilde{R} > 1\). Needless to say, the judgment whether the plastic strain reaches the isotropic hardening (stagnation) surface is unnecessary.
In contrast, the judgment whether the plastic strain or the back-stress reaches the isotropic hardening (stagnation) surface is required and the input loading increments must be infinitesimal such that the plastic strain or the back-stress does not deviates finitely from the isotropic stagnation surface in all other models (Chaboche et al. [16], Chaboche [12, 13], Ohno [89], Ohno and Kachi [90], Ohno et al. [91], Yoshida and Amaishi [117], Yoshida et al. [118, 121] and Yoshida and Uemori [119, 120], in which the kinematic hardening variable is used instead of the plastic strain, although the physical mechanism of isotropic hardening would be different from that of the kinematic hardening).
Then, the evolution rule of isotropic hardening in Eq. (46) is extended as follows:
where \(\upsilon \; ( \ge 1)\) is the material constant.
Adopting the extended isotropic hardening rule in Eq. (87) instead of Eq. (46) into Eq. (69), the plastic modulus is extended as follows:
The plastic strain rate is updated by Eq. (68) with Eq. (88).
We adopt the following simplest equation for the isotropic hardening function \(g({\tilde{\varvec{\upvarepsilon }}}{}^{p} )\).
It is described in Sect. 2.2 that the spring-back phenomenon of sheet metal can never be described pertinently by the Chaboche model [16] and the Yoshida–Uemori model [119,120,121] (see also Yoshida and Amaishi [117], Yoshida et al. [118]), which are incapable of describing the plastic deformation in the unloading process. On the other hand, the extended subloading surface model is capable of describing the plastic deformation in the unloading process. The measurement result of the spring-back phenomenon by Suzuki et al. [108] using the test apparatus in Fig. 14a is shown in Fig. 14b. The simulation result (Tateishi and Hashiguchi [109]) using the commercial FEM software Marc, in which the extended subloading surface model is installed as the standard material model for all Marc contractors, is shown in Fig. 14(b), choosing the material parameters as follows:
Material constants:
Initial values:
The spring-back is simulated accurately by the extended subloading surface model, which is induced by the plastic deformation in the stress-releasing process by virtue of the advantage of this model describing the plastic strain rate in the unloading process. In contrast, the smaller spring-back induced only by the elastic deformation during the stress-releasing process is described by the conventional elastoplastic model, which is calculated by adopting the arbitrary large value for the material constant in the evolution of the yield ratio, e.g. \(u = 100{,}000\) leading to \({\mathop {{\varvec{\upvarepsilon}}}\limits^{ \bullet }}{}^{p} \cong \mathbf{O} \text{ for } R < 1\) in the subloading surface model. It is also identical to the descriptions of the spring-back by the Chaboche model and the two surface model without resorting to the irrational method as done in the Yoshida–Uemori model [119,120,121], since the plastic deformation in the unloading process cannot be described by the Chaboche model and the two surface model as was explained in Sect. 2.1.
The subloading surface model has been applied for the constitutive equations of various materials, e.g. metals (Hashiguchi and Yoshimaru [68], Hashiguchi and Ueno [62], Hashiguchi et al. [66], Shoda et al. [104], Toluei and Kharazi [110], etc.), soils (Hashiguchi and Chen [56], Hashiguchi and Tsutsumi [61], Hashiguchi et al. [57, 60], Farias et al. [32], Khojastehpour and Hashiguchi [75], Yamakawa et al. [115, 116], Wang et al. [111], etc.), rocks (Zhou et al. [122], Zhu et al. [123]), etc., while all of the revised formulations described in this article have not yet been adopted in them at this time. Besides, the highly efficient determination method of the material parameters for metals in the subloading surface model has been proposed by Liu et al. [79] applying the artificial neural network. However, the elastoplastic constitutive equation can be disused by adopting the subloading-overstress model, which will be described in the subsequent sections.
3 Elasto-viscoplastic Constitutive Models
The strain is decomposed into the elastic and the viscoplastic strains, i.e.
The stress \({{\varvec{\upsigma}}}\) is given by
the rate forms of which are given by
3.1 Irrational Creep Model and Rational Overstress Model
The creep model is regarded as the simple nonlinearization of the resistance of the dash-pot in the Maxwell model for the viscoelastic deformation so that the creep strain rate is induced in any stress level lower than the yield stress. Therefore, the response of the creep model is not reduced to the elastoplastic model in the quasi-static rate of deformation. On the other hand, the overstress model (Bingham [9]) is the incorporation of a slider exhibiting the yield condition into the dashpot in parallel. This extends the creep model such that there exists a threshold value for the generation of the viscoplastic deformation. Therefore, the viscoplastic deformation is induced by the overstress from the yield stress but it is not induced for the stress lower than the yield stress. Then, the response of the creep model is not reduced to that of the elastoplastic constitutive equation but that of the overstress model is reduced to the elastoplastic constitutive equation for the quasi-static deformation process. Eventually, the creep model is not acceptable, although it is used widely (e.g. Lemaitre and Chaboche [78], Abdel-Karim and Ohno [1], Betten [8], Chaboche [15], Ohno et al. [94], de Souza Neto et al. [28]) regardless to this serious defect. On the other hand, the overstress model is acceptable and thus it will be adopted for the description of the viscoplastic deformation in the following.
3.2 Initial Subloading-Overstress Model
The static subloading and the limit subloading surfaces (see Fig. 15) are incorporated in the subloading-overstress model in addition to the subloading and the yield surfaces in the rate-independent subloading surface model for the elastoplastic deformation, which has been described in Sect. 2. Here, the subloading surface, on which the current stress always lies, may become larger than the yield surface in general.
The viscoplastic strain rate is induced by the overstress from the static subloading surface expressed by the following equation, which is given by replacing the yield ratio \(R\) to the static yield ratio \(R_{s} \; ( \le 1)\) in the subloading surface in Eq. (36) for the elastoplastic deformation.
with
where \({{\varvec{\upsigma}}}_{s}\) is the conjugate stress to the current stress \({{\varvec{\upsigma}}}\) by the similarity and \(R_{s}\) evolves by the following equation which is identical to Eq. (20) with Eq. (24) with the replacement of the plastic strain rate \({\mathop {{\varvec{\upvarepsilon}}}\limits^{ \bullet }}{}^{p}\) to the viscoplastic strain rate \({\mathop {{\varvec{\upvarepsilon}}}\limits^{ \bullet }}{}^{vp}\) (Fig. 16).
with
\(R_{s} \; ( \le 1)\) is called the static yield ratio because the quasi-static deformation proceeds in the state \(R \cong R_{s}\). On the other hand, the value of \(R_{s}\) is determined to satisfy Eq. (13) for the initial subloading surface in the elastic unloading process \(R = R_{s}\).
Now, let the flow rule of the viscoplastic strain rate be given by incorporating the crucially important variable in the subloading surface model, i.e. the yield ratio \(R\) into the overstress model as follows:
where \(\hat{\Gamma }\) is the positive viscoplastic multiplier given by
\(\mu_{v}\) (viscoplastic coefficient) and \(n \; ( > 1 )\) are the material constants. \(R\) is calculated by solving Eq. (13) for the subloading surface. Note that \(R\) may take a larger value than unity in an overstress state, unlike the rate-independent elastoplastic model in Sect. 2. The smooth elastic–viscoplastic transition is described by adopting the overstress due to \(R - R_{s}\) instead of \(R - 1\), while all the other past overstress models (Perzyna [99, 100], Chaboche [14], etc.) correspond to the state in which the value of \(R_{s}\) is fixed to \(R_{s} = 1\) in the subloading surface model so that the smooth elastic–viscoplastic transition cannot be described.
Further, let Eq. (98) be extended such that the infinite viscoplastic strain rate is induced for \(R \to c_{m} R_{s}\) (\(c_{m} \; ( \gg 1)\): material constant) leading to \(\hat{\Gamma } \to \infty\) in the impact loading process as follows:
The variable \(c_{m} R_{s} \; ( R < c_{m} R_{s} \le c_{m} )\) is called the viscoplastic limit yield ratio. Here, the surface to which the stress can reach at most in an impact loading is given by setting \(R = c_{m} R_{s}\) in the subloading surface in Eq. (36) is called the limit subloading surface. On the other hand, the elastic response is described unrealistically for the impact loading in the past overstress models (Perzyna [99, 100], Chaboche [14, 15], de Souza Neto et al. [28], Lemaitre and Chaboche [78], etc.). The rational description of deformation in the general rate ranging from the quasi-static to the impact loading is attained by the above-mentioned subloading-overstress model, in which the crucially-important variables, i.e. the yield ratio \(R\) is incorporated into \(\hat{\Gamma }\).
The rates of the internal variables \(H\) and \({{\varvec{\upalpha}}}\) are given from Eqs. (16) and (17) with the replacement of \({\mathop {{\varvec{\upvarepsilon}}}\limits^{ \bullet }}{}^{p}\) to \({\mathop {{\varvec{\upvarepsilon}}}\limits^{ \bullet }}{}^{vp} \; ( = \Gamma {\hat{\mathbf{n}}})\) as follows:
The isotropic hardening stagnation can be incorporated by the identical equations formulated in Sect. 2.5 with the replacement of the plastic strain rate \({\mathop {{\varvec{\upvarepsilon}}}\limits^{ \bullet }}{}^{p}\) to the viscoplastic strain rate \({\mathop {{\varvec{\upvarepsilon}}}\limits^{ \bullet }}{}^{vp}\).
The strain rate vs. stress rate relations are given from Eq. (92) with Eq. (97) as follows:
from which it follows that
in the quasi-static deformation process so that the stress changes along the static subloading surface given by Eq. (93). Consequently, the response of the subloading-overstress model is reduced to that of the subloading surface model for the rate-independent elastoplastic deformation behavior described in Sect. 2. The stress–strain curve described by the subloading-overstress model is illustrated in Fig. 17. The smooth elastic–viscoplastic transition is described. However, the closed hysteresis loop cannot be described in the unloading–reloading process inside the yield surface, because the plastic deformation is not described in the unloading process. This defect will be remedied by the extended subloading-overstress model which will be described in the next section.
3.3 Extended Subloading-Overstress Model
The initial subloading-overstress model based on the initial subloading surface model formulated in Sect. 3.2 is capable of describing the smooth elastic–viscoplastic transition but incapable of describing the viscoplastic strain rate in the unloading process as shown in Fig. 17. Then, it has been extended by adopting the extended subloading surface model described in Sect. 2.4 by Hashiguchi [55]. Analogously to Sect. 2.4, the elastic-core and the limit elastic-core surfaces are incorporated in addition to the limit subloading, the subloading, the yield, the static-subloading surfaces in the initial subloading-overstress model as shown in Fig. 18.
The viscoplastic strain rate is induced by the overstress from the static subloading surface expressed in the following equation, which is given by replacing the current stress \({{\varvec{\upsigma}}}\), the center \({\overline{\varvec{\upalpha}}}\) and the yield ratio \(R\) to their conjugate points \({{\varvec{\upsigma}}}_{s}\), \({\overline{\varvec{\upalpha}}}_{s}\) and the static yield ratio \(R_{s} \; ( \le 1)\), respectively, in the subloading surface in Eq. (36) for the elastoplastic deformation.
with
where \(R_{s}\) evolves according to Eq. (95) with the replacement of \(U_{s} (R_{s})\) in Eq. (96) to
Let the viscoplastic strain rate be given by
where \(\overline{\Gamma} \; ( \ge 0)\) is the positive viscoplastic multiplier and \({\overline{\mathbf{n}}}\) is the normalized outward-normal of the subloading surface as shown in Eq. (36).
The function \(U\) for the evolution rule of the yield ratio \(R\) and the non-negative proportionality factor (plastic multiplier) \(\mathop {\overline{\lambda }}\limits^{ \bullet }\) are modified to Eqs. (75) and (77), respectively, by incorporating the variables \(\Re_{c} \; ( \equiv f({\hat{\mathbf{c}}})/F )\) and \(C_{n} \; ( \equiv {\hat{\mathbf{n}}}_{c} : {\mathbf{\overline{n}}} )\) in the extended subloading surface model for the rate-independent elastoplastic deformation. Analogously, for the rate-dependent deformation, the viscoplastic multiplier in Eq. (99) is modified to
where \(\overline{u}_{c}\) is the material constant. \(R\) is calculated by solving Eq. (36) for the extended subloading surface model. Then, the rising and the lowering of the stress due to the decrease and the increase in strain rate are enforced in the state \(\Re_{c} C_{n} > 0\) and \(\Re_{c} C_{n} < 0\), respectively. This modification enables the description of the Masing effect [82] leading to the pertinent description of the cyclic loading behavior in the viscoplastic deformation process. The concise interpretation of the above-mentioned improvement of the viscoplastic multiplier is described for the uniaxial deformation in Hashiguchi [55].
The rational description of deformation in the general rate ranging from the quasi-static to the impact loading is attained by the above-mentioned subloading-overstress model, in which the crucially-important variables, i.e. the yield ratio \(R\), the static yield ratio \(R_{s}\), \(\Re_{c}\), \(C_{n}\) and the limit yield ratio \(c_{m} R_{s}\) are incorporated.
The rates of the internal variables \(H\), \({{\varvec{\upalpha}}}\) and \({\mathbf{c}}\) are given from Eqs. (46), (47) and (58) with the replacement of \({\mathop {{\varvec{\varepsilon}}}\limits^{ \bullet }}{}^{p}\) to \({\mathop {{\varvec{\varepsilon}}}\limits^{ \bullet }}{}^{vp}\) as follows:
The isotropic hardening stagnation can be incorporated by the identical equations formulated in Sect. 2.5 with the replacement of the plastic strain rate \({\mathop {{\varvec{\upvarepsilon}}}\limits^{ \bullet }}{}^{p}\) to the viscoplastic strain rate \({\mathop {{\varvec{\upvarepsilon}}}\limits^{ \bullet }}{}^{vp}\).
The strain rate vs. stress rate relations are given from Eq. (92) with Eq. (106) as follows:
The stress–strain relation by the extended subloading-overstress model is shown in Fig. 19, while the closed hysteresis loop is described by the extensions of Eqs. (96) and (99) to Eqs. (105) and (107).
The exact simulations of various test data from the static to the impact loading processes by the extended subloading-overstress model are shown in detail by Hashiguchi et al. [64]. It is noticeable that the test data published as the elastoplastic deformation in past relevant papers can be described more accurately by the extended subloading-overstress model than by the rate-independent subloading elastoplastic model as shown by Hashiguchi et al. [64], since any test data is measured in certain strain rate, noting that purely quasi-static experiment requiring an infinite time is impossible actually. The constitutive models for describing the general deformation behavior in the static to the impact loading is unified to the subloading-overstress model, disusing the rate-independent elastoplastic model.
Various test data of the elasto-viscoplastic deformation, i.e. the monotonic loading behaviors at various strain rates, the stress variation under a variable strain rate, the stress relaxation under a fixed strain, the strain variation for a stress cycle, the strain variation under a pulsating stress cycle and the stress variation under a constant strain amplitude have been simulated successfully by the subloading-overstress model in Hashiguchi et al. [64]. Only two examples among them will be shown here. First, the monotonic loading behavior at various constant strain rates at 550 °C in the test data for Modified 9 Cr–1 Mo steel after Abel-Karim and Ohno [1] is shown in Fig. 20, where the material parameters are chosen as follows:
Simulation of uniaxial loading behavior of Modified 9 Cr–1 Mo steel under various axial strain rates at 550 °C (Test data after Abdel-Karim and Ohno [1])
Material constants:
Initial values:
In addition, the simulation of the pulsating loading behavior between 0 MPa and + 830 MPa at room temperature after Jiang and Zhang [72] reported as the elastoplastic deformation is shown in Fig. 21, where the material parameters are chosen as shown in the following, while the axial strain rate is chosen to be quite low, i.e. \(\mathop \varepsilon \limits^{ \bullet }{}_{a} = 10^{ - 7} /\text{s}\), although the strain rate is not reported in their paper regarding merely the quasi-static deformation.
Simulation of mechanical ratcheting during pulsating loading between 0 and + 850 MPa of 1070 steel at room temperature (Test data after Jiang and Zhang [72]): The stress–strain curves are shown continuously up to the 10th cycle and then at the 16th, 32nd, 64th, 128th, 256th and 512th cycles for clarity
Material constants:
Initial values:
Then, it is noticeable that the simulation by the extended subloading-overstress model is more accurate than the simulation by the subloading elastoplastic model (Hashiguchi and Ueno [62]), since the test data reported as the elastoplastic deformation behavior are not measured at the infinitely slow (quasi-static) rate but measured at a low strain rate actually. Eventually, the elastoplastic constitutive equation can be unified to the subloading-overstress model and thus the former can be disused. The subloading-overstress model is no more than the generalization of the subloading surface model to the description of the elastoplastic deformation in the general strain rate ranging from static to impact loading. Eventually, the elastoplastic constitutive equation with the plastic modulus, which possesses often a complex mathematical expression as seen in Eq. (88), can be disused by adopting only the subloading-overstress model, while we have only to perform the update calculation of the viscoplastic internal variables involving the positive viscoplastic multiplier \(\overline{\Gamma }\) by Eq. (107).
4 Constitutive Equation of Friction: Subloading-Friction Model
All bodies in the natural world are exposed to the friction phenomena, contacting with other bodies, except for bodies without any mechanical support and it is the typical irreversible phenomenon connected directly to the second law of thermodynamics. Therefore, it has been studied by numerous natural scientists since ancient times. Aristotle in the ancient Greek has recognized the difference between the static friction and the kinetic friction. The term “Friction” was used first by Isaac Newton. The term “radiation friction” was coined by Albert Einstein. Thus, the friction phenomena have been studied extensively over the long years from the ancient Greek period. Then, the terms “static friction” and “kinetic friction” are described even in textbooks in middle and high schools. However, their mathematical expressions have to be waited until the proposition of the subloading-friction model by Hashiguchi and Ozaki [58]. Here, note that the intermittent occurrence of earthquakes is closely associated with the reduction of friction coefficient from the static friction to the kinetic friction coefficient and the recovery from the kinetic friction to the static friction. Therefore, the subloading-friction model would be effective for the precise prediction of the occurrence of earthquakes. Still now, however, only the classical Coulomb friction is described in literatures except for the book by the present author and installed in the commercial FEM software, e.g. Abaqus, Marc, Nastran, LS-DYNA, etc. The recent history of the research studies on the constitutive equation for friction will be reviewed in the following.
Constitutive equations of friction within the framework of elastoplasticity were formulated as the rigid-plasticity (Seguchi et al. [103], Fredriksson [36]). Subsequently, they were extended to elasto-perfect-plasticity (Oden and Martines [88], Curnier [24], Cheng and Kikuchi [22], Perić and Owen [98], Mróz and Stupkiewicz [85], Wriggers [112]). Further, isotropic hardening was introduced by Oden and Martines [88] to describe the test results (cf. e.g. Courtney-Pratt and Eisner [23]). However, the interior of the sliding-yield surface was assumed as an elastic domain. Therefore, the plastic sliding velocity induced by the rate of contact stress inside the sliding-yield surface cannot be described. Needless to say, the accumulation of plastic (irreversible) sliding displacement induced by the cyclic loading of contact stress within the sliding-yield surface cannot be described by these models. Therefore, they are incapable of describing an accumulation of sliding displacement during cyclic loading of contact stress inside the friction yield surface in addition to the incapability of describing the transition from the static to the kinetic friction and the recovery of the static friction.
The subloading friction model (Hashiguchi [54] and Hashiguchi and Ueno [63]) will be explained in this section.
4.1 Sliding Displacement and Contact Stress
The sliding displacement vector \({\overline{\mathbf{u}}}\), which is defined as the sliding displacement of the counter (slave) body relative to the main (master) body, is orthogonally decomposed into the normal sliding displacement vector \({\overline{\mathbf{u}}}_{n}\) and the tangential sliding displacement vector \({\overline{\mathbf{u}}}_{t}\) to the contact surface as follows:
where
\({\mathbf{n}}\) being the unit outward-normal vector of the surface of main body. The minus sign is added for \(\overline{u}_{n}\) to be positive when the counter body approaches the main body.
The sliding is induced by the elastic deflections of the surface asperities themselves and the mutual slips between the surface asperities, while the former and the latter are regarded to cause the elastic sliding and the plastic sliding, respectively. The sliding displacement vector \({\overline{\mathbf{u}}}\) can be exactly decomposed into the elastic (reversible) sliding displacement \({\overline{\mathbf{u}}}{}^{e}\) and the plastic (irreversible) sliding displacement \({\overline{\mathbf{u}}}{}^{p}\) in the additive form even for the finite sliding displacement, i.e.
where
setting
The elastic sliding displacement vector \({\overline{\mathbf{u}}}{}^{e}\) is formulated by the hyperelastic relation to the current contact stress vector \({\mathbf{f}}\), where \({\overline{\mathbf{u}}}{}^{e}\) is calculated by subtracting the plastic sliding displacement \({\overline{\mathbf{u}}}{}^{p}\) from the total sliding displacement vector \({\overline{\mathbf{u}}}\).
The contact stress vector \({\mathbf{f}}\) acting on the main body is additively decomposed into the normal stress vector \({\mathbf{f}}_{n}\) and the tangential stress vector \({\mathbf{f}}_{t}\) as follows:
where
The minus sign is added for \(f_{n}\) to be positive when the compressive stress acts to the main body by the counter body.
The contact stress vector \({\mathbf{f}}\), \({\mathbf{f}}_{n}\) and \({\mathbf{f}}_{t}\) can be calculated from the Cauchy stress \({{\varvec{\upsigma}}}\) applied in the contact bodies by virtue of the Cauchy’s fundamental theorem (cf. Hashiguchi [51]) as follows:
4.2 Elastic Sliding Displacement
Let the contact stress vector \({\mathbf{f}}\) be given by the hyperelastic relation with the elastic sliding energy function \(\varphi ({\overline{\mathbf{u}}}{}^{e} )\) as follows:
The simplest function \(\varphi ({\overline{\mathbf{u}}}{}^{e} )\) is given by the quadratic form:
where the second-order tensor \({\overline{\text{E}}}\) designates the elastic tangent contact stiffness modulus. The substitution of Eq. (123) into Eq. (122) leads to
Assuming the isotropy on the contact surface, i.e. the independence of frictional property to a sliding direction on the contact surface, and introducing the normalized rectangular coordinate system \(({\overline{\mathbf{e}}}_{{1}}, {\overline{\mathbf{e}}}_{{2}}, {\overline{\mathbf{e}}}_{{3}} ) = ({\overline{\mathbf{e}}}_{{1}}, {\overline{\mathbf{e}}}_{{2}}, {\mathbf{n}})\) fixed to the contact surface, the elastic contact tangent stiffness modulus tensor \({\overline{\mathbf{E}}}\) is given as follows:
where \(\alpha_{n}\) and \(\alpha_{t}\) are the material constants specifying the normal and tangential contact elastic moduli, respectively, which are determined by the surface asperities of the contact materials. Equation (124) with Eq. (125) leads to
4.3 Sliding Yield and Subloading Surfaces
The Coulomb friction condition is written as \(f_{t} /f_{n} = \overline{\mu }\) forming the conical surface in the stress vector space, while the dimensionless variable \(\overline{\mu }\) is called the friction coefficient.
Now, we assume the following sliding-yield surface with the isotropic hardening/softening, which describes the sliding-yield condition.
\(\mu\) designates the expansion (hardening) or the contraction (softening) of the sliding yield surface, possessing the dimension of stress and is called the sliding hardening function.
Now, incorporate the subloading surface concept: The plastic sliding velocity develops as the contact stress approaches the sliding yield surface, renamed the sliding yield surface. Then, introduce the sliding-subloading surface, which is similar to the sliding yield surface and passes through the current contact stress. Further, introduce the sliding yield ratio defined by the ratio of the size of the sliding-subloading surface to that of the sliding yield surface, which plays the role to designate the approaching degree of the contact stress to the sliding yield surface. The sliding subloading surface is represented by the following equation.
where \(r \; (0 \le r \le 1)\) is the sliding yield ratio.
The sliding yield and the sliding-subloading surfaces are schematically represented in Fig. 22 (Hashiguchi and Ueno [63]).
Sliding yield and subloading-sliding surfaces (Hashiguchi and Ueno [63])
The time-differentiation of Eq. (128) leads to the consistency condition for the sliding subloading surface:
Here, it is required to formulate the evolution rules of the sliding hardening/softening function \(\mu\) and the sliding yield ratio \(r\), which will be formulated in the following. The following facts are recognized for the evolution of the sliding hardening function \(\mu\) from the experiments.
-
(i)
The sliding hardening function first reaches the maximum value of static-friction and then decreases to the minimum stationary value of kinetic-friction. Physically, this phenomenon might be interpreted to result from separations of the adhesions of surface asperities between contact bodies due to the sliding (cf. Bowden and Tabor [10]). Note here that a real contact area between tips of asperities is far smaller than apparent contact area between bodies (cf. e.g. Bay and Wanheim [7]). Then, we assume that the plastic sliding causes the decrease in the friction coefficient, i.e. the plastic softening.
-
(ii)
The sliding hardening function recovers gradually with the elapse of time and the identical behavior as the initial sliding behavior exhibiting the static friction is reproduced if sufficient time elapses after the sliding ceases. Physically, this phenomenon might be interpreted to result from the reconstructions of the adhesions of surface asperities during the elapsed time under quite high contact pressures between edges of surface asperities. Then, let it be assumed that the time-elapse causes the increase in the sliding hardening function, i.e. the viscoplastic hardening.
Taking account of these facts, we assume the evolution rule of the isotropic sliding hardening function \(\mu\) as follows:
where \(\mu_{s}\) and \(\mu_{k }\) are the material constants designating the maximum and the minimum values of \(\mu\) for the static friction and the kinetic friction, respectively. \(\kappa\) is the material constant specifying the decrease in the sliding hardening function \(\mu\) by the plastic sliding displacement rate, and \(\xi\) is the material constant specifying the increase (recovery) in \(\mu\) by the elapsed time increment. The first and second terms in Eq. (130) are relevant to the destruction and reconstruction, respectively, of the adhesion between surface asperities. The variable \(\mu\) is regarded as the hardening variable, i.e. the size of the sliding yield surface. Equation (130) is revised from the past formulation (Hashiguchi and Ozaki [58]). The variation of the sliding hardening function \(\mu\) based on Eq. (130) is shown in Fig. 23.
4.4 Evolution Rule of Sliding Yield Ratio
On the basis of the above-mentioned fundamental postulate of elastoplastic sliding, the rate of the sliding-yield ratio \(r\) must satisfy the following conditions:
Then, it follows that
where \(\overline{U}(r)\) is the monotonically decreasing function of \(r\) fulfilling the conditions:
which can be given similarly to Eq. (22) by
where \(\tilde{u}\) is the material constant designating the increment of the sliding yield ratio \(r\), i.e. \(\mathrm{d}r\), for a certain plastic sliding increment \(\Vert \mathrm{d} {\overline{\mathbf{u}}}{}^{p} \Vert\). The curvature of the contact stress versus the sliding displacement curve is lower for the smaller value of \(\tilde{u}\), while the abrupt elastic–plastic transition is described for \(\tilde{u} \to \infty\).
The contact stress is automatically attracted to the sliding yield surface in the plastic sliding process and it is pulled back to the surface even when it happens to go over the surface in a numerical calculation because of \(\mathop r\limits^{ \bullet } < 0\) for \(r > 1\) from Eq. (132) with Eq. (133)4.
The partial derivative of the sliding yield stress function is derived as
noting
and it follows from Eq. (120) that
The substitution of Eqs. (130) and (132) into Eq. (129) leads to
Now, assume that the direction of plastic sliding velocity is tangential to the contact plane and outward-normal to the curve generated by the intersection of the sliding subloading surface and the constant normal stress plane \({\mathbf{f}}_{n} = \text{const.}\), leading to the tangential associated flow rule (see Fig. 22):
where
with
where \(\mathop {\overline{\lambda }}\limits^{ \bullet }\) and \({\mathbf{n}}_{t}\) are the magnitude and the direction, respectively, of the plastic sliding velocity.
The substitution of Eq. (139) into Eq. (138) reads:
where
are relevant to the plastic and the creep sliding velocity, respectively.
It is obtained from Eqs. (139) and (142) that
Substituting the rate form of Eq. (124) and Eq. (144) into the rate form of Eq. (113), the sliding velocity is given by
from which the plastic multiplier in terms of the sliding velocity, denoted by the symbol \({\mathop {\overline{\Lambda }}\limits^{ \bullet }}\), is given as follows:
The inverse relation of Eq. (145) is derived by substituting the rate form of Eq. (113) with Eq. (146) into the rate form of Eq. (124) as follows:
The loading criterion for the plastic sliding displacement rate is given as follows (Hashiguchi [51]):
because of \(m^{p} + \big( \partial f({\mathbf{f}}) / \partial {\mathbf{f}} \big) \bullet {\overline{\mathbf{E}} \mathbf{n}}_{t} > 0\), noting that the stress decrease in an infinite rate for \(m^{p} + \big( \partial f({\mathbf{f}}) / \partial {\mathbf{f}} \big) \bullet {\overline{\mathbf{E}} \mathbf{n}}_{t} \to 0\). Here, the judgment whether the stress reaches the sliding-yield surface is not required since the plastic sliding displacement rate is induced continuously as the stress approaches the sliding-yield surface in the sliding-subloading surface model.
The contact stress function for the isotropic sliding-yield surface is described by
for which the following partial derivative holds, noting Eq. (137).
It follows by substituting Eq. (150) into Eq. (140) that
Therefore, the direction of the plastic sliding displacement rate coincides with the direction of the tangential contact stress.
4.5 Friction Condition with Saturation of Tangential Contact Stress
It is recognized from experiments (cf. Bay and Wanheim [7], Dunkin and Kim [30], Stupkiewicz and Mróz [107], Gearing et al. [37]) that the friction coefficient decreases with the increase in normal contact stress. However, this property cannot be described by the Coulomb sliding-yield surface, in which the tangential contact stress increases linearly with the normal contact stress, resulting in the constant friction coefficient. Actually, the calculation adopting the Coulomb sliding-yield surface results in an unrealistic result that a tangential contact stress higher than the shear yield stress of the base materials applies under a high normal contact stress and thus the base materials adhere to each other, resulting in their peeling-off by the sliding. Actually, this problem may occur in the tightening of bolts and nuts and the friction between the landward plate and the seaward plate during the submerge of the seaward plate, which is essential for predicting earthquake occurrence. Then, the concrete formulations of the subloading-friction model taken account of this property have been proposed by Hashiguchi et al. [59] and Ozaki et al. [97]. The former formulation (Hashiguchi et al. [59]) involves the physical irrationality that the tangent friction coefficient becomes minus in a high normal contact stress region. The latter formulation (Ozaki et al. [97]) is concerned with soft material as the rubbers. The reasonable subloading-friction model incorporating the sliding-yield stress function \(f({\mathbf{f}})\) by which the tangential contact stress saturates with the increase in the normal contact stress will be shown in the following (Hashiguchi [54], Hashiguchi and Ueno [63]).
The following sliding yield stress function \(f({\mathbf{f}}) = f ( f_{t}, f_{n} )\) in the sliding-yield condition in Eq. (127), i.e. \(f(f_{t}, f_{n} ) = \mu\) is incorporated (Hashiguchi [54])
leading to the sliding yield surface:
where \(g_{n} \; ( 0 \le g_{n} \le 1)\) is the function of \(f_{n}\) satisfying the conditions
leading to
\(c_{n}\) is the material constant with the inverse dimension of stress. Equation (153) represents the sliding yield surface with the fusiform shape which expands from the origin to the positive direction of the normal contact stress \(f_{n}\) in the three-dimensional contact stress space \((f_{t1}, f_{t2}, f_{n})\).
The magnitude of the tangential contact stress \(f_{t}\) on the sliding yield surface increases with the normal contact stress \(f_{n}\) and saturates at \(f_{t} = \mu\), while it approaches faster to the saturation (maximum) value \(\mu\) for a larger value of \(c_{n}\) as shown in Fig. 24a, which is depicted for \(\mu = \text{const.}\) The sliding yield and the sliding subloading surfaces satisfying Eqs. (154) and (155) are shown in Fig. 24b. The Coulomb friction-yield condition can be realized approximately by setting \(\mu \to \infty\) (large value) and \(c_{n} \cong 0\) (small value) leading to \(c_{n} \mu \cong \text{const.}\) for \(f_{n} \ll \infty\).
The following differentiations hold for Eq. (152).
Now, we have
noting Eq. (150) with Eq. (157).
Further, we have
The substitutions of Eqs. (158)–(162) into Eqs. (145) and (147) with Eq. (151) lead to
with
Let the explicit function satisfying Eqs. (154) and (155) be given by the exponential function:
As mentioned before, the Coulomb friction condition is expressed approximately by giving a large and a small value to \(\mu\) and \(c_{n}\), respectively.
The simulations of the test data (Gearing et al [37].) for the monotonic sliding behaviors in the various normal contact stresses are shown by the solid curves in Fig. 25, where the material parameters are chosen as follows:
while the tangential sliding velocity \(\mathop {\overline{u}}\limits^{ \bullet }{}_{t}\) is \(1 \, \text{mm} \cdot \text{s}^{-1}\) in the test data. The variations of the tangential contact stress are closely simulated by the present friction model.
Simulations of test data (Gearing et al. [37]) for tangential contact stress vs. sliding displacement relations for six levels of normal contact stress
4.6 Subloading-Overstress (Viscoplastic) Friction Model
The subloading-friction model is concerned with the dry friction exhibiting the negative rate-sensitivity, i.e. the decrease in the friction resistance with the sliding velocity. On the other hand, the positive rate-sensitivity, i.e. the increase in the friction resistance with the sliding velocity, is observed in lubricated frictions. The subloading friction model described in the former sections has been extended to the subloading-overstress friction model (Hashiguchi [65]), which is capable of describing the friction behavior for the general sliding displacement rate exhibiting both the positive and the negative sensitivities as will be delineated in the following.
First, we introduce the viscoplastic sliding displacement vector \({\overline{\mathbf{u}}}{}^{vp}\) instead of the plastic sliding displacement vector \({\overline{\mathbf{u}}}{}^{p}\) in Eq. (113), i.e.
The viscoplastic strain rate is given by
leading to
The explicit function of \(\overline{\Gamma }\) is given by the exponential function
where \(\overline{\eta}_{v}\) is the material constant specifying the time required for the occurrence of a unit viscoplastic strain rate, \(n\) is the material constant and \(\hat{r} \; ( \gg 1)\) is the material constant specifying the maximum value of the sliding-yield ratio which is realized in the impact sliding process \(( \Vert {\mathop {{\overline{\mathbf{u}}}}\limits^{ \bullet }}{}^{vp} \Vert \to \infty )\). \(r_{s} \; (0 \le r_{s} \le 1)\) is the static sliding-yield ratio calculated using Eq. (132) by replacing the plastic sliding velocity \({\mathop {{\overline{\mathbf{u}}}}\limits^{ \bullet }}{}^{p}\) with the viscoplastic sliding velocity \({\mathop {{\overline{\mathbf{u}}}}\limits^{ \bullet }}{}^{vp}\) in Eq. (132), i.e.,
with
Thus, the viscoplastic sliding displacement rate is induced by overstress \(f({\mathbf{f}}) - r_{s} \mu\) from the static subloading friction surface:
so that a smooth elastic–viscoplastic transition is described.
The evolution rate of the sliding-hardening function \(\mu\) is given by replacing the plastic sliding displacement rate \({\mathop {{\overline{\mathbf{u}}}}\limits^{ \bullet }}{}^{p}\) to the viscoplastic sliding displacement rate \({\mathop {{\overline{\mathbf{u}}}}\limits^{ \bullet }}{}^{vp}\) in Eq. (130) as follows:
The dry friction exhibiting the negative rate-sensitivity is also described by the present subloading overstress model, since \(r = r_{s}\) holds in the quasi-static sliding state.
The simulation of test data for the lubricated friction behavior under the five levels of the sliding displacement rates by the subloading-overstress friction model with the Coulomb friction condition is shown in Fig. 26, using the following values of the material constants (Hashiguchi et al. [65]).
5 Discussions and Concluding Remarks
The development of the constitutive models for the irreversible mechanical phenomena of solids has been reviewed comprehensively and the state-of-arts are provided in this article.
The subloading surface model (Hashiguchi [40, 41]) has been proposed to describe the elastoplastic deformation behavior with the smooth transition from the elastic state to the elastoplastic state and it has been extended to describe the cyclic loading behavior (Hashiguchi [43, 53]). Further, it has been extended to describe the rate-dependent, i.e. viscoplastic deformation behavior (Hashiguchi [55], Hashiguchi et al. [64]). It is verified that the subloading-overstress model is capable of describing the viscoplastic deformation behavior under the monotonic and the cyclic loading processes in the general rate from the quasi-static to the impact loading. Therefore, the rate-independent elastoplastic model involving the complex formulation of the plastic modulus can be disused leading to the unification of the elastoplastic and the elasto-viscoplastic constitutive models. Further, the friction behavior during the monotonic and the cyclic sliding processes for the finite sliding with the transition from the static to the kinetic friction in the general rate from the quasi-static to the impact sliding can be described rigorously by the subloading-friction model as shown in Sect. 4.
Unfortunately, however, the Chaboche model [18, 19], the Ohno–Wang model [92, 93] and the Yoshida–Uemori model [119,120,121] are widely used still now, which exhibit various mechanical defects as revealed in detail in Sects. 2.1 and 2.2. Unfortunately, further, only the Coulomb friction law with the constant friction coefficient but without the static and the kinetic frictions is adopted widely to the analysis of boundary value problem involving friction phenomena as seen in almost all of the commercial finite element software.
The distinguished features in the formulation of the subloading surface model basically different from the formulations of the other elasto-plastic and elasto-viscoplastic models are summarized in the following.
-
1.
A purely-elastic domain is not assumed so that the plastic strain rate can be described for any small stress amplitude as observed in fatigue phenomenon. On the other hand, it is incorporated in all other models (Mróz [84], Iwan [71], Dafalias and Popov [27], Krieg [77], Chaboche et al. [18, 19], Ohno–Wang [92, 93] and Yoshida–Uemori [119,120,121]) so that the smooth elastic–plastic transition and a plastic strain rate under the cyclic loading with small stress amplitudes cannot be described.
-
2.
The subloading surface, which passes through the current stress point and is similar to the yield surface is incorporated.
-
3.
The yield ratio \(R\), which is the ratio of the size of the subloading surface to that of the yield surface, is incorporated. It is inevitable for the description of the smooth transition from the elastic to the irreversible state, satisfying the smoothness condition (Hashiguchi [44, 45]) so that the tangent stiffness modulus changes continuously. Then, loading judgment whether the stress reaches the yield surface is not required in the loading criterion. This feature leads to the improvement of the efficiency in the numerical calculation, while it is required in all other models. The yield ratio \(R\) plays the crucially important basic variable for the description of the irreversible mechanical phenomena of solids.
-
4.
The movement of the similarity-center \({\mathbf{c}}\) of the yield and the subloading surfaces with the plastic deformation is incorporated in order to describe the cyclic loading behavior. On the other hand, the plastic strain cannot be described under the pulsating loading process by the Chaboche model [16], the Ohno–Wang model [92, 93] and the Yoshida–Uemori model [119,120,121] assuming the yield surface enclosing the purely elastic domain, which could result in an engineering design on the dangerous side. Further, the large overshooting stress–strain curve is described under the partial unloading–reloading process and thus the excessively large plastic strain accumulation is described under the general cyclic loading process by these models as reviewed in Sect. 2.1.
-
5.
The positive plastic multiplier \(\mathop \lambda \limits^{ \bullet }\) and the positive viscoplastic multiplier \(\overline{\Gamma }\) are extended to describe the cyclic loading behavior by incorporating the variable \(\Re_{c} = f({\hat{\mathbf{c}}})/F(H)\), which describes the approaching degree of the similarity-center \({\mathbf{c}}\) to the yield surface, and the variable \(C_{n} \equiv {\hat{\mathbf{n}}}_{c} : {\mathbf{\overline{n}}} \; ( - 1 \le C_{n} \le 1 )\), which describes the proximity of the outward-normal \({\overline{\mathbf{n}}}\) of the direction of the plastic strain rate to the outward-normal of the elastic-core surface. \(C_{n}\) is larger and smaller in the reloading and the reverse loading, respectively. In addition, the static yield ratio \(R_{s}\) is incorporated in order to describe the smooth elastic–viscoplastic transition.
-
6.
The cyclic loading behavior can be described appropriately by the extended subloading surface model, in which the similarity-center of the subloading and the yield surfaces translates with the plastic deformation. Further, the isotropic hardening stagnation (Chaboche et al. [16]) is modified such that the isotropic hardening develops continuously as the plastic stain develops. Besides, the spring-back phenomenon can be described reasonably without resorting to the irrational method proposed by Yoshida–Uemori model [119,120,121] (see also Yoshida and Amaishi [117], Yoshida et al. [118]) ignoring the elementary knowledge in the damage mechanics. The analyses using these irrational models bring about the dangerous mechanical design of the mechanical elements subjected to the cyclic loading.
-
7.
The elastoplastic and the elasto-viscoplastic deformation behaviors can be described by the subloading-overstress model in the unified form, so that the elastoplastic constitutive equation can be disused hereinafter.
-
8.
The rate-independent and the rate-dependent sliding phenomena of solids with the transition from the static to the kinetic friction and the saturation of the tangential contact stress with the increase of the normal contact stress can be described by the subloading-overstress friction model in the unified formulation.
The subloading surface model has been applied to the wide classes of materials, e.g. metals, soils, rocks, concrete, polymers, and further the crystal plasticity, the phase-transformation, damage phenomenon (Hashiguchi [55]), the friction phenomenon, etc. Eventually, the wide classes of the irreversible mechanical phenomena in the general rate of deformation/sliding of solids can be described by the subloading surface model in the unified form. In other words, the subloading surface model is inevitable for the description of the irreversible mechanical phenomena of solids. Eventually, the subloading surface model is regarded as the governing law for the irreversible mechanical phenomena of solids. It is desirable for the subloading surface model to be used widely to the mechanical designs of solids and structures for the further great developments of the engineering science and the industrial technology.
The subloading surface models for the deformation/sliding behaviors are comprehensively reviewed from the viewpoint of the constitutive properties in this article. The implicit numerical calculation methods by use of the rigorous subloading surface models described in this article will be reviewed comprehensively in a future paper, although they have been studied for the past subloading surface models with the various incomplete formulations (cf. e.g. [2, 3, 33,34,35, 51, 53, 116]).
References
Abdel-Karim M, Ohno N (2000) Kinematic hardening model suitable for ratcheting with steady-state. Int J Plasticity 16(3–4):225–240. https://doi.org/10.1016/S0749-6419(99)00052-2
Anjiki T, Hashiguchi K (2022) Extended overstress model and its implicit stress integration algorithm: Formulations, experiments and simulations. Int J Numer Methods Eng 123(1):291–303. https://doi.org/10.1002/nme.6848
Anjiki T, Oka M, Hashiguchi K (2020) Complete implicit stress integration algorithm with extended subloading surface model for elastoplastic deformation analysis. Int J Numer Methods Eng 121(5):945–966. https://doi.org/10.1002/nme.6252
Armstrong PJ, Frederick CO (1966) A mathematical representation of the multiaxial Bauschinger effect. Central Electricity Generating Board and Berkeley Nuclear Laboratories, Research & Development Dept., Technical Report RD/B/N 731. (Frederick CO, Armstrong PJ (2007) A mathematical representation of the multiaxial Bauschinger effect. Mater High Temp 24(1):1–26). https://doi.org/10.1179/096034007X207589
Arnold SM, Saleeb AF (1994) On the thermodynamic framework of generalized coupled thermoelastic–viscoplastic–damage modeling. Int J Plasticity 10(3):263–278. https://doi.org/10.1016/0749-6419(94)90003-5
Asaro RJ, Lubarda V (2006) Mechanics of solids and materials. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511755514
Bay N, Wanheim T (1976) Real area of contact and friction stresses at high pressure sliding contact. Wear 38(2):201–209. https://doi.org/10.1016/0043-1648(76)90069-7
Betten J (2005) Creep mechanics, 2nd edn. Springer, Berlin. https://doi.org/10.1007/978-3-540-85051-9
Bingham EC (1922) Fluidity and plasticity. McGraw-Hill, New York.
Bowden FP, Tabor D (1958) The friction and lubrication of solids. Clarendon Press, Oxford.
Chaboche JL (1986) Time-independent constitutive theories for cyclic plasticity. Int J Plasticity 2(2):149–188. https://doi.org/10.1016/0749-6419(86)90010-0
Chaboche JL (1989) Constitutive equations for cyclic plasticity and cyclic viscoplasticity. Int J Plasticity 5(3):247–302. https://doi.org/10.1016/0749-6419(89)90015-6
Chaboche JL (1991) On some modifications of kinematic hardening to improve the description of ratcheting effects. Int J Plasticity 7(7):661–678. https://doi.org/10.1016/0749-6419(91)90050-9
Chaboche JL (1997) Thermodynamic formulation of constitutive equations and application to the viscoplasticity and viscoelasticity of metals and polymers. Int J Solids Struct 34(18):2239–2254. https://doi.org/10.1016/S0020-7683(96)00162-X
Chaboche JL (2008) A review of some plasticity and viscoplasticity constitutive theories. Int J Plasticity 24(10):1642–1693. https://doi.org/10.1016/j.ijplas.2008.03.009
Chaboche JL, Dang Van K, Cordier G (1979) Modelization of the strain memory effect on the cyclic hardening of 316 stainless steel. Trans. 5th Int. Conf. SMiRT, Berlin, Division L., Paper No. L 11/3.
Chaboche JL, Gaubert A, Kanouté P, Longuet A, Azzouz F, Mazière M (2013) Viscoplastic constitutive equations of combustion chamber materials including cyclic hardening and dynamic strain aging. Int J Plasticity 46:1–22. https://doi.org/10.1016/j.ijplas.2012.09.011
Chaboche JL, Rousselier G (1983) On the plastic and viscoplastic constitutive equations—Part I: rules developed with internal variable concept. J Press Vessel Technol (ASME) 105(2):153–158. https://doi.org/10.1115/1.3264257
Chaboche JL, Rousselier G (1983) On the plastic and viscoplastic constitutive equations—Part II: application of internal variable concepts to the 316 stainless steel. J Press Vessel Technol (ASME) 105(2):159–164. https://doi.org/10.1115/1.3264258
Chen W, Feng M (2015) A study of a cyclic viscoplasticity model based on hyperbolic sine form for the inelastic strain rate. Int J Mech Sci 101–102:155–160. https://doi.org/10.1016/j.ijmecsci.2015.07.028
Chen W, Wang F, Kitamura T, Feng M (2017) A modified unified viscoplasticity model considering time-dependent kinematic hardening for stress relaxation with effect of loading history. Int J Mech Sci 133:883–892. https://doi.org/10.1016/j.ijmecsci.2017.09.048
Cheng JH, Kikuchi N (1985) An incremental constitutive relation of uniaxial contact friction for large deformation analysis. J Appl Mech (ASME) 52(3):639–648. https://doi.org/10.1115/1.3169114
Courtney-Pratt JS, Eisner E (1957) The effect of a tangential force on the contact metallic bodies. Proc R Soc A 238(1215):529–550. https://doi.org/10.1098/rspa.1957.0016
Curnier A (1984) A theory of friction. Int J Solids Struct 20(7):637–647. https://doi.org/10.1016/0020-7683(84)90021-0
Dafalias YF, Feigenbaum HP (2011) Biaxial ratchetting with novel variations of kinematic hardening. Int J Plasticity 27(4):479–491. https://doi.org/10.1016/j.ijplas.2010.06.002
Dafalias YF, Kourousis KI, Saridis GJ (2008) Multiplicative AF kinematic hardening in plasticity. Int J Solids Struct 45(10):2861–2880. https://doi.org/10.1016/j.ijsolstr.2008.01.001
Dafalias YF, Popov EP (1975) A model of nonlinearly hardening materials for complex loading. Acta Mech 21:173–192. https://doi.org/10.1007/BF01181053
de Souza Neto EA, Perić D, Owen DRJ (2008) Computational methods for plasticity: theory and applications. John-Wiley, Chichester. https://doi.org/10.1002/9780470694626
Drucker DC (1988) Conventional and unconventional plastic response and representation. Appl Mech Rev (ASME) 41(4):151–167. https://doi.org/10.1115/1.3151888
Dunkin JE, Kim DE (1996) Measurement of static friction coefficient between flat surfaces. Wear 193(2):186–192. https://doi.org/10.1016/0043-1648(95)06706-X
Ellyin F (1997) Fracture damage, crack growth and life prediction. Chapman & Hall, London. https://doi.org/10.1007/978-94-009-1509-1
Farias MM, Pedroso DM, Nakai T (2009) Automatic substepping integration of the subloading tij model with stress path dependent hardening. Comput Geotech 36(4):537–548. https://doi.org/10.1016/j.compgeo.2008.11.003
Fincato R, Tsutsumi S (2017) Closest-point projection method for the extended subloading surface model. Acta Mech 228:4213–4233. https://doi.org/10.1007/s00707-017-1926-0
Fincato R, Tsutsumi S (2018) A return mapping algorithm for elastoplastic and ductile damage constitutive equations using the subloading surface method. Int J Numer Methods Eng 113(11):1729–1754. https://doi.org/10.1002/nme.5718
Fincato R, Tsutsumi S (2022) Numerical implementation of the multiplicative hyperelastic-based extended subloading surface plasticity model. Comput Methods Appl Mech Eng 401(B):115612. https://doi.org/10.1016/j.cma.2022.115612
Fredriksson B (1976) Finite element solution of surface nonlinearities in structural mechanics with special emphasis to contact and fracture mechanics problems. Comput Struct 6(4–5):281–290. https://doi.org/10.1016/0045-7949(76)90003-1
Gearing BP, Moon HS, Anand L (2001) A plasticity model for interface friction: application to sheet metal forming. Int J Plasticity 17(2):237–271. https://doi.org/10.1016/S0749-6419(00)00034-6
Guo S, Kang G, Zhang J (2013) A cyclic visco-plastic constitutive model for time-dependent ratchetting of particle-reinforced metal matrix composites. Int J Plasticity 40:101–125. https://doi.org/10.1016/j.ijplas.2012.07.006
Hashiguchi K (1978) Plastic constitutive equations of granular materials. In: Proc. US–Japan Seminar on Continuum Mech. Stast. Appr. Mech. Granular Materials (eds. Cowin SC and Satake M), Sendai, pp 321–329. https://cir.nii.ac.jp/crid/1571698600020803584
Hashiguchi K (1980) Constitutive equations of elastoplastic materials with elastic–plastic transition. J Appl Mech (ASME) 47(2):266–272. https://doi.org/10.1115/1.3153653
Hashiguchi K (1981) Constitutive equations of elastoplastic materials with anisotropic hardening and elastic–plastic transition. J Appl Mech (ASME) 48(2):297–301. https://doi.org/10.1115/1.3157612
Hashiguchi K (1988) A mathematical modification of two surface model formulation in plasticity. Int J Solids Struct 24(10):987–1001. https://doi.org/10.1016/0020-7683(88)90103-5
Hashiguchi K (1989) Subloading surface model in unconventional plasticity. Int J Solids Struct 25(8):917–945. https://doi.org/10.1016/0020-7683(89)90038-3
Hashiguchi K (1993) Fundamental requirements and formulation of elastoplastic constitutive equations with tangential plasticity. Int J Plasticity 9(5):525–549. https://doi.org/10.1016/0749-6419(93)90018-L
Hashiguchi K (1993) Mechanical requirements and structures of cyclic plasticity models. Int J Plasticity 9(6):721–748. https://doi.org/10.1016/0749-6419(93)90035-O
Hashiguchi K (1994) On the loading criterion. Int J Plasticity 10(8):871–878. https://doi.org/10.1016/0749-6419(94)90018-3
Hashiguchi K (1997) The extended flow rule in plasticity. Int J Plasticity 13(1–2):37–58. https://doi.org/10.1016/S0749-6419(96)00052-6
Hashiguchi K (2000) Fundamentals in constitutive equation: continuity and smoothness conditions and loading criterion. Soils Found 40(4):155–161. https://doi.org/10.3208/sandf.40.4_155
Hashiguchi K (2013) General description of elastoplastic deformation/sliding phenomena of solids in high accuracy and numerical efficiency: subloading surface concept. Arch Comput Methods Eng 20(4):367–417. https://doi.org/10.1007/s11831-013-9089-1
Hashiguchi K (2016) Exact formulation of subloading surface model: unified constitutive law for irreversible mechanical phenomena in solids. Arch Comput Methods Eng 23(3):417–447. https://doi.org/10.1007/s11831-015-9148-x
Hashiguchi K (2017) Foundations of elastoplasticity: subloading surface model, 1st edn. Springer, Berlin. https://doi.org/10.1007/978-3-319-48821-9
Hashiguchi K (2019) Multiplicative hyperelastic-based plasticity for finite elastoplastic deformation/sliding: a comprehensive review. Arch Comput Methods Eng 26(3):597–637. https://doi.org/10.1007/s11831-018-9256-5
Hashiguchi K (2020) Nonlinear continuum mechanics for finite elastoplasticity: multiplicative decomposition with subloading surface model. Elsevier. https://doi.org/10.1016/C2018-0-05398-0
Hashiguchi K (2021) Subloading-friction model with limitation of tangential contact stress. In: Proceedings of MDT2021 (JSME)
Hashiguchi K (2023) Foundations of elastoplasticity: subloading surface model, 2nd edn. Springer, Berlin. https://doi.org/10.1007/978-3-030-93138-4
Hashiguchi K, Chen ZP (1998) Elastoplastic constitutive equation of soils with the subloading surface and the rotational hardening. Int J Numer Anal Methods Geomech 22(3):197–227. https://doi.org/10.1002/(SICI)1096-9853(199803)22:3%3C197::AID-NAG914%3E3.0.CO;2-T
Hashiguchi K, Mase T, Yamakawa Y (2022) Elaborated subloading surface model for accurate description of cyclic mobility in granular materials. Acta Geotech 17:699–719. https://doi.org/10.1007/s11440-021-01203-y
Hashiguchi K, Ozaki S (2008) Constitutive equation for friction with transition from static to kinetic friction and recovery of static friction. Int J Plasticity 24(11):2102–2124. https://doi.org/10.1016/j.ijplas.2008.03.004
Hashiguchi K, Ozaki S, Okayasu T (2005) Unconventional friction theory based on the subloading surface concept. Int J Solids Struct 42(5–6):1705–1727. https://doi.org/10.1016/j.ijsolstr.2004.08.006
Hashiguchi K, Saitoh K, Okayasu T, Tsutsumi S (2002) Evaluation of typical conventional and unconventional plasticity models for prediction of softening behavior of soils. Géotechnique 52(8):561–578. https://doi.org/10.1680/geot.2002.52.8.561
Hashiguchi K, Tsutsumi S (2007) Gradient plasticity with the tangential-subloading surface model and the prediction of shear-band thickness of granular materials. Int J Plasticity 23(5):767–797. https://doi.org/10.1016/j.ijplas.2006.08.005
Hashiguchi K, Ueno M (2017) Elastoplastic constitutive equation of metals under cyclic loading. Int J Eng Sci 111:86–112. https://doi.org/10.1016/j.ijengsci.2016.11.001
Hashiguchi K, Ueno M (2023) Subloading-friction model with saturation of tangential contact stress. Friction 11:1107–1120. https://doi.org/10.1007/s40544-022-0656-z
Hashiguchi K, Ueno M, Anjiki T (2023) Subloading-overstress model: unified constitutive equation for elasto-plastic and elasto-viscoplastic deformations under monotonic and cyclic loadings-Research with systematic review. Arch Comput Methods Eng 30(4):2627–2649. https://doi.org/10.1007/s11831-022-09880-y
Hashiguchi K, Ueno M, Kuwayama T, Suzuki N, Yonemura S, Yoshikawa N (2016) Constitutive equation of friction based on the subloading-surface concept. Proc R Soc A 472(2191):20160212. https://doi.org/10.1098/rspa.2016.0212
Hashiguchi K, Ueno M, Ozaki T (2012) Elastoplastic model of metals with smooth elastic–plastic transition. Acta Mech 223:985–1013. https://doi.org/10.1007/s00707-012-0615-2
Hashiguchi K, Yamakawa Y (2012) Introduction to finite strain theory for continuum elasto-plasticity. In: Wiley series in computational mechanics. John-Wiley, Chichester. https://doi.org/10.1002/9781118437711
Hashiguchi K, Yoshimaru T (1995) A generalized formulation of the concept of nonhardening region. Int J Plasticity 11(4):347–365. https://doi.org/10.1016/S0749-6419(95)00003-8
Hassan T, Taleb L, Krishna S (2008) Influence of non-proportional loading on ratcheting responses and simulations by two recent cyclic plasticity models. Int J Plasticity 24(10):1863–1889. https://doi.org/10.1016/j.ijplas.2008.04.008
Ho K, Krempl E (2002) Extension of the viscoplasticity theory based on overstress (VBO) to capture non-standard rate dependence in solids. Int J Plasticity 18(7):851–872. https://doi.org/10.1016/S0749-6419(01)00011-0
Iwan WD (1967) On a class of models for the yielding behavior of continuous and composite systems. J Appl Mech (ASME) 34(3):612–617. https://doi.org/10.1115/1.3607751
Jiang Y, Zhang J (2008) Benchmark experiments and characteristic cyclic plasticity deformation. Int J Plasticity 24(9):1481–1515. https://doi.org/10.1016/j.ijplas.2007.10.003
Kang G, Kan Q (2017) Cyclic plasticity of engineering materials: experiments and models. Wiley. https://doi.org/10.1002/9781119180838
Khan AS, Huang S (1995) Continuum theory of plasticity. John-Wiley, New York.
Khojastehpour M, Hashiguchi K (2004) Axisymmetric bifurcation analysis in soils by the tangential-subloading surface model. J Mech Phys Solids 52(10):2235–2262. https://doi.org/10.1016/j.jmps.2004.04.005
Krempl E, McMahon JJ, Yao D (1986) Viscoplasticity based on overstress with a differential growth law for the equilibrium stress. Mech Mater 5(1):35–48. https://doi.org/10.1016/0167-6636(86)90014-1
Krieg RD (1975) A practical two surface plasticity theory. J Appl Mech (ASME) 42(3):641–646. https://doi.org/10.1115/1.3423656
Lemaitre J, Chaboche JL (1990) Mechanics of solid materials. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9781139167970
Liu D, Yang H, Elkhodary KI, Tang S, Liu WK, Guo X (2022) Mechanistically informed data-driven modeling of cyclic plasticity via artificial neural networks. Comput Methods Appl Mech Eng 393:114766. https://doi.org/10.1016/j.cma.2022.114766
Lubarda VA (2001) Elastoplasticity theory. CRC Press, Boca Raton. https://doi.org/10.1201/9781420040784
Lubliner J (1990) Plasticity theory. Macmillan, New York.
Masing G (1926) Eigenspannungen und Verfestigung beim Messing. In: Proceedings of 2nd international congr. appl. Mech., Zurich, pp 332–335.
Mayama T, Sasaki K, Ishikawa H (2007) A constitutive model of cyclic viscoplasticity considering changes in subsequent viscoplastic deformation due to the evolution of dislocation structures. Int J Plasticity 23(5):915–930. https://doi.org/10.1016/j.ijplas.2006.10.003
Mróz Z (1967) On the description of anisotropic workhardening. J Mech Phys Solids 15(3):163–175. https://doi.org/10.1016/0022-5096(67)90030-0
Mróz Z, Stupkiewicz S (1994) An anisotropic friction and wear model. Int J Solids Struct 31(8):1113–1131. https://doi.org/10.1016/0020-7683(94)90167-8
Murakami S (2012) Continuum damage mechanics: a continuum mechanics approach to the analysis of damage and fracture. Springer, Dordrecht. https://doi.org/10.1007/978-94-007-2666-6
Norton FH (1929) The creep of steel at high temperatures. McGraw-Hill, New York.
Oden JT, Martins JAC (1985) Models and computational methods for dynamic friction phenomena. Comput Methods Appl Mech Eng 52(1–3):527–634. https://doi.org/10.1016/0045-7825(85)90009-X
Ohno N (1982) A constitutive model of cyclic plasticity with a non-hardening strain region. J Appl Mech (ASME) 49(4):721–727. https://doi.org/10.1115/1.3162603
Ohno N, Kachi Y (1986) A constitutive model of cyclic plasticity for nonlinear hardening materials. J Appl Mech (ASME) 53(2):395–403. https://doi.org/10.1115/1.3171771
Ohno N, Nakamoto H, Morimatsu Y, Okumura D (2021) Modeling of cyclic hardening and evaluation of plastic strain range in the presence of pre-loading and ratcheting. Int J Plasticity 145:103074. https://doi.org/10.1016/j.ijplas.2021.103074
Ohno N, Wang JD (1993) Kinematic hardening rules with critical state of dynamic recovery, Part I: formulation and basic features for ratcheting behavior. Int J Plasticity 9(3):375–390. https://doi.org/10.1016/0749-6419(93)90042-O
Ohno N, Wang JD (1993) Kinematic hardening rules with critical state of dynamic recovery, Part II: application to experiments of ratcheting behavior. Int J Plasticity 9(3):391–403. https://doi.org/10.1016/0749-6419(93)90043-P
Ohno N, Yamamoto R, Okumura D (2018) Thermo-mechanical cyclic hardening behavior of 304 stainless steel at large temperature ranges: experiments and simulations. Int J Mech Sci 146–147:517–526. https://doi.org/10.1016/j.ijmecsci.2017.06.018
Okorokov V, Gorash Y, Mackenzie D, van Rijswick R (2019) New formulation of nonlinear kinematic hardening model, Part I: a Dirac delta function approach. Int J Plasticity 122:89–114. https://doi.org/10.1016/j.ijplas.2019.07.006
Ottosen NS, Ristinmaa M (2005) The mechanics of constitutive modeling. Elsevier Sci. https://doi.org/10.1016/B978-0-08-044606-6.X5000-0
Ozaki S, Matsuura T, Maegawa S (2020) Rate-, state-, and pressure-dependent friction model based on the elastoplasticity theory. Friction 8(4):768–783. https://doi.org/10.1007/s40544-019-0321-3
Perić D, Owen DRJ (1992) Computational model for 3-D contact problems with friction based on the penalty method. Int J Numer Methods Eng 35(6):1289–1309. https://doi.org/10.1002/nme.1620350609
Perzyna P (1963) The constitutive equations for rate sensitive plastic materials. Quart Appl Math 20:321–332. https://doi.org/10.1090/qam/144536
Perzyna P (1966) Fundamental problems in viscoplasticity. Adv Appl Mech 9:243–377. https://doi.org/10.1016/S0065-2156(08)70009-7
Prager W (1961) Linearization in visco-plasticity. Österreich Ing-Archiv 15:152–157.
Saleeb AF, Arnold SM (2004) Specific hardening function definition and characterization of a multimechanism generalized potential-based viscoelastoplasticity model. Int J Plasticity 20(12):2111–2142. https://doi.org/10.1016/j.ijplas.2004.04.002
Seguchi Y, Shindo A, Tomita Y, Sunohara M (1974) Sliding rule of friction in plastic forming of metal. In: proc. int. conf. comput. methods nonlinear mech., Univ. Texas at Austin, pp 683–692.
Shoda K, Arai K, Nakamura S, Okada H (2023) Application of redefined J-integral range ΔJ for ultra-low cycle fatigue problems with large magnitude of elastic–plastic deformation. Theor Appl Fract Mech 126:103938. https://doi.org/10.1016/j.tafmec.2023.103938
Simo JC (1998) Numerical analysis and simulation of plasticity. In: Ciarlet PG, Lions JL (eds) Handbook of numerical analysis, vol 6. Numerical methods for solids (Part 3), pp 183–499, Elsevier, Amsterdam. https://doi.org/10.1016/S1570-8659(98)80009-4
Simo JC, Hughes TJR (1998) Computational inelasticity. Springer, New York. https://doi.org/10.1007/b98904
Stupkiewicz S, Mróz Z (1999) A model of third body abrasive friction and wear in hot metal forming. Wear 231(1):124–138. https://doi.org/10.1016/S0043-1648(99)00124-6
Suzuki N, Hiwatashi S, Uenishi A, Kuwayama T, Kuriyama Y, Lemoine X, Teodosiu C (2005) Advanced constitutive model for spring back prediction of high strength steel sheet. J Jpn Soc Tech Plasticity 46(534):636–640.
Tateishi M, Hashiguchi K (2019) Accurate prediction of spring-back phenomenon by subloading surface model. In: VIII int. conf. comput. methods for coupled problem, Barcelona.
Toluei R, Kharazi M (2023) Implementation of subloading surface model for hyperelastoplasticity with nonlinear kinematic/isotropic hardening based on reference and intermediate configurations. Appl Math Model 121:751–779. https://doi.org/10.1016/j.apm.2023.05.026
Wang X, Yuan R, Cui K (2023) Modified unified critical state model for soils considering over-consolidation and cyclic loading behaviours. Sci Rep 13:3024. https://doi.org/10.1038/s41598-022-26624-x
Wriggers P (2003) Computational contact mechanics. John-Wiley, Hoboken. https://www.wiley.com/en-us/Computational+Contact+Mechanics-p-9780471496809
Wriggers P, Van Vu T, Stein E (1990) Finite element formulation of large deformation impact–contact problems with friction. Comput Struct 37(3):319–331. https://doi.org/10.1016/0045-7949(90)90324-U
Wu H-C (2004) Continuum mechanics and plasticity. Chapman & Hall/CRC, New York. https://doi.org/10.1201/9780203491997
Yamakawa Y, Hashiguchi K, Ikeda K (2010) Implicit stress-update algorithm for isotropic Cam-clay model based on the subloading surface concept at finite strains. Int J Plasticity 26(5):634–658. https://doi.org/10.1016/j.ijplas.2009.09.007
Yamakawa Y, Hashiguchi K, Sasaki T, Higuchi M, Sato K, Kawai T, Machishima T, Iguchi T (2021) Anisotropic subloading surface Cam-clay model with rotational hardening: deformation gradient-based formulation for finite strain. Int J Numer Anal Methods Geomech 45(16):2321–2370. https://doi.org/10.1002/nag.3268
Yoshida F, Amaishi T (2020) Model for description of nonlinear unloading–reloading stress–strain response with special reference to plastic-strain dependent chord modulus. Int J Plasticity 130:102708. https://doi.org/10.1016/j.ijplas.2020.102708
Yoshida F, Hamasaki H, Uemori T (2015) Modeling of anisotropic hardening of sheet metals including description of the Bauschinger effect. Int J Plasticity 75:170–188. https://doi.org/10.1016/j.ijplas.2015.02.004
Yoshida F, Uemori T (2002) A model of large-strain cyclic plasticity describing the Bauschinger effect and workhardening stagnation. Int J Plasticity 18(5–6):661–686. https://doi.org/10.1016/S0749-6419(01)00050-X
Yoshida F, Uemori T (2003) A model of large-strain cyclic plasticity and its application to springback simulation. Int J Mech Sci 45(10):1687–1702. https://doi.org/10.1016/j.ijmecsci.2003.10.013
Yoshida F, Uemori T, Fujiwara K (2002) Elastic–plastic behavior of steel sheets under in-plane cyclic tension–compression at large strain. Int J Plasticity 18(5–6):633–659. https://doi.org/10.1016/S0749-6419(01)00049-3
Zhou Y, Sheng Q, Li N, Fu X (2019) Numerical investigation of the deformation properties of rock materials subjected to cyclic compression by the finite element method. Soil Dyn Earthq Eng 126:105795. https://doi.org/10.1016/j.soildyn.2019.105795
Zhu H, Ye B, Cai Y, Zhang F (2013) An elasto-viscoplastic model for soft rock around tunnels considering overconsolidation and structure effects. Compt Geotech 50:6–16. https://doi.org/10.1016/j.compgeo.2012.12.004
Funding
No funding was received to assist with the preparation of this manuscript.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hashiguchi, K., Yamakawa, Y., Anjiki, T. et al. Comprehensive Review of Subloading Surface Model: Governing Law of Irreversible Mechanical Phenomena of Solids. Arch Computat Methods Eng 31, 1579–1609 (2024). https://doi.org/10.1007/s11831-023-10022-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11831-023-10022-1