Abstract
Various elasto-plastic models for the rate-independent deformation, various elasto-viscoplastic models for the rate-dependent deformation and their combinations have been proposed during a long time more than one or more centuries. Firstly, the history of the development of the elastoplasticiy and the elasto-viscoplasticity is reviewed comprehensively. Unfortunately, each of these models possesses their own drawbacks and limitations. The unified constitutive equation of the elasto-plastic and the elasto-viscoplastic deformations is provided by incorporating the subloading surface model into the overstress model in this article, which is capable of describing the monotonic and the cyclic loadings at the general rate ranging from the quasi-static to the impact loading. The validity of the unified model is verified by the comparison with various test data of metals under various loading conditions. Consequently, the elastoplastic constitutive equation can be disused hereinafter, while it is expressed by the cumbersome formulation including the complicated plastic modulus but limited to the description of the purely static deformation which is not induced actually.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The researches on the elastoplasticity for the quasi-static deformation behavior and the viscoplasticity for the dynamic deformation behavior have the long history in one or more centuries. In this context, the main goal of these researches would be the formulation to describe them in a unified equation for the monotonic and the cyclic loadings at the general rate of deformation, while the solids and structures in engineering practice are subjected to monotonic and the cyclic loadings at variable rate of deformation from the quasi-static to the impact loading.
Firstly, the history of the development of the elastoplastic and the elasto-viscoplastic constitutive equations will be reviewed comprehensively in the following.
The elasto-plastic and the elasto-viscoplastic deformations have been often described separately by the elastoplastic model for the quasi-static deformation and the creep model for the dynamic deformation, respectively, Norton [97], Odqvist [98], Robotnov [120], Rice [118, 119], Bodner and Partom [10], Lemaitre and Chaboche [86], Abdel-Karim and Ohno [1], Saleeb et al. [122], Betten [7], Asaro and Lubarda [5], Chaboche [17], Ohno et al. [101], de Sauza Neto et al. [25], Peirce et al. [111, 112], etc. However, it should be noticed that the creep strain rate in the creep model is induced even in any low stress level since it is formulated by the stress or the ratio of the stress to the yield stress and thus the response of the creep model is not reduced to that of the elastoplastic model in a quasi-static rate of deformation. Therefore, the deformation behavior in the intermediate rate cannot be described pertinently by them, because different responses are described by the creep and the elastoplastic constitutive equations. Consequently, the combination of the creep model and the elastoplastic model cannot be used for deformation analysis at variable rate. Besides, various empirical models, Johnson and Cook [77], Steinberg et al. [125], Zerilli and Armstrong [144], Follansbee and Kocks [34], etc. have been proposed and used to the engineering in practice but they are ad. hoc models for particular phenomena without generality. Further, the fundamentally-irrational models, Bailey [6], Garofalo [35], etc. involving the time itself in order to describe the creep behavior have been proposed, which result in the loss of the objectivity as the constitutive relation Oldroyd [104].
On the other hand, the response of the overstress model, Bingham [9], Hohenemser and Prager [70], Prager [116], Perzyna [114, 115], Duvaut and Lion [28], Krempl et al. [82], Chaboche [12, 14], Lubliner [93], Perić [113], Arnold and Saleeb [4], Simo [123], Simo and Hughes [124], Kaneko and Oyamada [78], Ho and Krempl [69], Lubarda [92], Ottosen and Ristinmaa [105], Chaboche [16, 17], Saleeb and Arnold [121], Mayama et al. [95], de Sauza Neto et al. [25], Ho [68], Chaboche et al. [19], Guo et al. [36], Chen and Feng [20], Chen, et al. [21, 22], etc. is reduced to that of the elastoplastic constitutive equation in the quasi-static rate of deformation. Therefore, the overstress model possesses the capability for the description of the deformation at the variable rate. However, the existing overstress model is incapable of describing the cyclic loading behavior under the general stress amplitude, since it adopts the conventional elastoplastic constitutive equation with the yield surface enclosing the purely-elastic domain, and it is also incapable of describing the impact loading behavior since it expresses the elastic deformation behavior leading to the infinitely high stress in the infinitely high rate of deformation.
The subloading surface model, Hashiguchi [37, 38, 40, 48, 50] is capable of describing the elastoplastic deformation under the monotonic and the cyclic loading behaviors, while it does not incorporate a purely-elastic domain so that the tangent stiffness modulus changes continuously always satisfying the continuity condition in the large, i.e. the smoothness condition, Hashiguchi [41] and the mechanical ratchetting phenomenon is described for any low stress level. The subloading surface model has been tried to describe the rate-dependent behavior by incorporating the overstress model by Hashiguchi [46, 48, 50], Hashiguchi et al. [53], Moranha et al. [94], Fincato and Tsutsumi [31, 32] and Anjiki and Hashiguchi [2]. However, the peculiar stress vs. strain curve exhibiting the softening is described by the formulations by Hashiguchi [46, 48, 50], Hashiguchi et al. [53] and Moranha et al. [94]. The formulation by Fincato and Tsutsumi [31, 32] exhibits the discontinuous tangent stiffness modulus such that the inflexion point is induced in the stress–strain curve. The formulation by Anjiki and Hashiguchi [2] is quite complex such that the similarity-center of the normal-yield and the subloading surfaces moves departing from the elastic-core and thus the quite cumbersome numerical calculation is required.
In this article, the unified constitutive equation for the elasto-plastic and the elasto-viscoplastic deformations is provided, which is capable of describing the deformation behaviors during the monotonic and the cyclic loadings at the general rate ranging from the quasi-static to the impact loading by incorporating the subloading surface model into the overstress model. Further, the isotropic stagnation phenomenon is incorporated into the model. Besides, the physical interpretations of all the formulations are given comprehensively. Then, the explicit functions included in the constitutive equation are given for metals. The validity of the present model is verified by the simulations of test data for metals under the various loadings at several strain rates including variable strain rate and the stress relaxations at fixed strains, Inoue et al. [72], Abel-Karim and Ohno [1], Saleeb and Arnold [121], Lemaitre and Chaboche [86]. Further, the test data reported as the rate-independent elastoplastic deformations at room temperature, Jiang and Zhang [74] and Chaboche et al. [18] are simulated accurately by the present model.
2 Subloading Surface Model for Elastoplastic Deformation
The complete formulation of the subloading surface model for the elastoplastic deformation modifying the past one, Hashiguchi [37, 38, 40, 48, 50] is described concisely in this section, while the subloading surface model for metals with the simplified evolution rule of the elastic-core limited to the nonhardening state and without the isotropic hardening stagnation is installed in the commercial FEM software Marc. By combining the subloading surface model and the overstress model, the subloading-overstress model will be formulated for the description of the monotonic and the cyclic loading behaviors in the general rate from the quasi-static to the impact loading in the next section.
The distinguished feature of the subloading surface model, which is not furnished in the other elastoplastic models, e.g. the superposed kinematic hardening model, Chaboche et al. [18], Ohno and Wang [102], Hassan et al. [66], etc., the multi surface model, Mróz [96], Iwan [73] and the two surface model, Dafalias and Popov [23], Krieg [83], Hashiguchi [39], Yoshida and Uemori [140], etc., is the exclusion of the purely elastic domain so that the plastic strain rate due to the variation of stress inside the yield surface can be described. Therefore, the continuity condition in the large, i.e. the smoothness condition, Hashiguchi [41, 42, 44] leading to the continuous variation of the tangent stiffness modulus tensor is fulfilled always. It is of crucial importance for the description of the cyclic loading behavior under the general stress amplitude.
2.1 Elastic and Plastic Decomposition of Strain (Rate)
The infinitesimal strain tensor \({{\varvec{\upvarepsilon}}}\) is additively decomposed into the elastic strain tensor \({{\varvec{\upvarepsilon}}}^{e}\) and the plastic strain tensor \({{\varvec{\upvarepsilon}}}^{p}\) as follows:
where \({\mathbf{x}}\) and \({\mathbf{u}}\) are the position vector and the displacement vector, respectively, of the material particle.
Let the Cauchy stress \({{\varvec{\upsigma}}}\) be given by
where the elastic modulus tensor \({\mathbf{\mathbb{E}}}\) for the Hooke’s law is given as follows:
where \(E\) and \(\nu\) are the Young’s modulus and the Poisson’s ratio, respectively. The rate form of Eq. (3) is given for the constant elastic modulus tensor, i.e. \({\mathbf{\mathbb{E}}} = {\text{const}}.\) by
2.2 Normal-Yield and Subloading Surfaces
The normal-yield surface with the isotropic and the kinematic hardening is described as
where
\(f({\hat{\varvec{\upsigma }}})\) is chosen to be the homogeneous degree-one of the variable \({\hat{\varvec{\upsigma }}}\). \(H\) is the isotropic hardening variable and \({{\varvec{\upalpha}}}\) is the back-stress (kinematic hardening variable). which evolve by the equations
where \(c_{k}\) is the material constant with the stress dimension and \(b_{k} { ( < 1)}\) is the non-dimensional material constant. Equation (9) is the slight modification of the nonlinear kinematic hardening rule of Armstrong-Frederick [3] in which \(b_{k} F\) is defined to be the material constant with the stress dimension, while it should be noticed that the translational range of the yield surface would not be independent of the size of the yield surface.
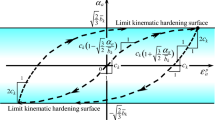
Now, let the subloading surface be incorporated, which is similar to the yield surface, renamed as the normal-yield surface, with respect to the similarity-center \({\mathbf{c}}\) and thus it is described as follows (see Fig. 1).
where \(R {(0 \le }R \le {1)}\) is the normal-yield ratio, i.e. the ratio of the size of the subloading surface to that of the normal-yield surface and
\({\overline{\varvec{\upalpha }}}\) stands for the conjugate (similar) point in the subloading surface to the point \({{\varvec{\upalpha}}}\) representing the back-stress, i.e. the kinematic hardening variable in the normal-yield surface. Here, note that the purely-elastic behavior is induced when the stress coincides with the similarity-center and thus the normal-yield ratio becomes zero \((R = 0)\). Then, let the similarity-center \({\mathbf{c}}\) be called the elastic-core. Here, the following relation holds by virtue of the similarity (see Fig. 1).
which yields
where
Besides, \({{\varvec{\upsigma}}}_{y}\) in Fig. 1 is the conjugate stress on the normal-yield surface to the current stress \({{\varvec{\upsigma}}}\) on the normal-yield surface, fulfilling \({{\varvec{\upsigma}}}{ - }{\overline{\varvec{\upalpha }}} = R({{\varvec{\upsigma}}}_{y} { - }{{\varvec{\upalpha}}})\). The time-derivative of \({\overline{\varvec{\upalpha }}}\) is described from Eq. (13) as
The subloading surface in Eq. (11) is rewritten by Eq. (15) as follows:
\(R\) is calculated by solving Eq. (18) in the elastic loading process \(\dot{\varvec\upvarepsilon}^{e} \ne {\mathbf{O}}, \dot{\varvec\upvarepsilon}^{p} = {\mathbf{O}}\) by substituting the updated values of \({{\varvec{\upsigma}}}, \, {{\varvec{\upalpha}}},\, {\mathbf{c}}\) and \(F\). Equation (18) is expressed by the quadratic equation and thus the normal-yield ratio can be expressed analytically for the Mises material as will be shown in Sect. 2.7.
The evolution rule of the normal-yield ratio \(R\) is given by
where the function \(U{(}R{)}\) of \(R\) satisfies the conditions
The material parameter \(R_{e}\) is interpreted to be the ratio of the fatigue limit stress to the yield stress \(\sigma_{y}\). Note here that the incorporation of the material parameter \(R_{e}\) does not mean the incorporation of the surface enclosing a purely-elastic domain as known from the fact: The plastic strain rate is predicted for the cyclic loading with a small stress amplitude under a high average stress by the subloading surface model with the incorporation of \(R_{e}\). Incidentally, the tangent stiffness modulus changes continuously satisfying the continuity condition in the large, i.e. the smoothness condition always in the monotonic loading process. However, the normal-yield ratio \(R\) must be calculated from Eq. (18) for the elastic loading process \((\dot {\varvec \upvarepsilon}^{p} = \varvec{0},\, \dot {\varvec \upvarepsilon}^{e} \ne \varvec{0})\). It can be expressed explicitly by Eq. (84) for metals as will be shown in Sect. 2.7.
The explicit equation satisfying Eq. (20) is given by the cotangent function
where \(u\) is the material parameter and \(\langle \, \rangle\) is the Macaulay’s bracket defined by \(\langle s\rangle = (s{ + |}s{|)/2}\), i.e. \(s < 0: \, \langle s\rangle = 0\) and \(s \ge 0: \, \langle s\rangle = s\) (\(s\): arbitrary scalar variable). Equation (21) fulfills the continuity condition in the large, i.e. the smoothness condition (Hashiguchi [42]) since the function \(U{(}R{)}\) decreases continuously from the infinite value \(U{(}R_{e} {) (} \to \infty )\). If \(u\) is fixed to be constant, Eqs. (19) with (21) can be integrated analytically as
where \(\varepsilon^{p} \equiv \int {||\dot{\varvec\upvarepsilon}^{p} ||} dt\) and \(\varepsilon_{0}^{p}\) is the initial value of \(\varepsilon^{p}\), whilst one must set \(R_{{0}} = R_{e}\) for \(R_{{0}} < R_{e}\).
2.3 Evolution Rule of Elastic-Core
The elastic-core \({\mathbf{c}}\) is not allowed to approach the normal-yield surface closely, because the purely elastic deformation is induced when the stress lies on the elastic-core but the apparent plastic deformation is induced when the stress lies on the normal-yield surface. In addition, it should be noted that a smooth elastic–plastic transition leading to the continuous variation of the tangent stiffness modulus tensor is not described violating the continuity condition in the large, i.e. the smoothness condition Hashiguchi [41], if the elastic-core lies on the normal-yield surface. On the other hand, the other plasticity models, i.e. the cylindrical superposed kinematic hardening model, Chaboche et al. [18], Ohno and Wang [102], Hassan et al. [66], etc., the multi surface model, Mróz [96], Iwan [73] and the two surface model, Dafalias and Popov [23], Krieg [83], Hashiguchi [39], Yoshida and Uemori [140], etc. violate the smoothness condition, since the purely-elastic domain contacts to the yield surface directly.
Then, it is assumed that the elastic-core surface which passes through the elastic-core is similar to the normal-yield surface with respect to the back-stress \({{\varvec{\upalpha}}}\) is smaller than the normal-yield surface. Therefore, the following inequality holds.
where \(\Re_{c}\) designates the ratio of the size of the elastic-core surface to the normal-yield surface (see Fig. 1) and \(\chi \;{( < 1)}\) is the material constant designating the maximum value of \(\Re_{c}\).
The material-time derivative of Eq. (23) at the limit state that \({\mathbf{c}}\) lies on the limit elastic-core surface \(f({\hat{\mathbf{c}}}) = \chi F(H)\) yields:
Here, noting
on account of the Euler’s homogeneous function \(f({\hat{\mathbf{c}}})\) in degree-one for the variable \({\hat{\mathbf{c}}}\), the substitution of Eq. (25) to Eq. (24) leads to
Now, assume the equation
where \(c_{e}\) is the material constant and \({{\varvec{\upsigma}}}_{\chi }\) is the conjugate stress on the limit elastic-core surfaces to the current stress \({{\varvec{\upsigma}}}\) on the subloading surface, i.e.
which is based on the relation
where \({{\varvec{\upsigma}}}_{y}\) is the conjugate stress on the normal-yield surface. Equation (27) means that the elastic-core translates so as to approach the conjugate stress \({{\varvec{\upsigma}}}_{\chi }\) in the nonhardening state: \(\mathop F\limits^{ \bullet } = 0\) and \(\mathop {{\varvec{\upalpha}}}\limits^{ \bullet } = {\mathbf{O}}\).
It follows for Eqs. (26) with (27) that
as far as the normal-yield surface satisfies the convexity condition (cf. Hashiguchi [48]), noting that \(\partial f({\hat{\mathbf{c}}})/\partial {\mathbf{c}}\) which is the outward-normal of the elastic-core surface at the current elastic-core \({\mathbf{c}}\) and \({{\varvec{\upsigma}}}_{\chi } { - }{\mathbf{c}}\) makes an obtuse angle with \(\partial f({\hat{\mathbf{c}}})/\partial {\mathbf{c}}\) when \({\mathbf{c}}\) lies on the limit elastic-core surface, while \({{\varvec{\upsigma}}}_{\chi }\) lies on the limit elastic-core surface. \({\hat{\mathbf{n}}}_{c}\) is the normalized outward-normal of the elastic-core surface (see Fig. 1), i.e.
Therefore, Eq. (27) satisfies the enclosing condition of the elastic-core so that the elastic-core can never go out from the limit elastic-core surface.
Then, the evolution rule of the elastic-core is given from Eq. (27) with Eqs. (8) and (9) by
The translation of the elastic-core would have to be influenced by the variation of the expansion/contraction (isotropic hardening) and the translation (kinematic hardening) of the normal-yield surface in general, since its movement is limited to the interior of the normal-yield surface which expands and translates with the plastic deformation. This aspect is different from the evolution rule of the kinematic hardening which causes the translation of the normal-yield surface.
2.4 Plastic Strain Rate
Adopt the associated flow rule for the subloading surface:
where
The rates of the isotropic hardening in Eq. (8) and the rate of kinematic hardening in Eq. (9) for the state in which the current stress lies on the normal-yield surface are extended to
for the state in which the current stress lies on the subloading surface.
Equation (32) with Eqs. (35) and (36) leads to
where
The material-time derivative of Eq. (11) leads to the consistency condition of the subloading surface as follows:
Here, one has
based on the homogeneous function \(f({\overline{\varvec{\upsigma }}})\) of \({\overline{\varvec{\upsigma }}}\) in degree-one by the Euler’s theorem. Then, it follows that
The substitution of Eqs. (41) into (39) leads to
The substitution of Eqs. (17) into (42) leads to
Noting the relation
it follows from Eq. (43) that
The substitutions of Eq. (33) with Eqs. (19), (35), (36) and (37) into Eq. (45) leads to
from which the plastic multiplier \(\mathop {\overline{\lambda }}\limits^{ \bullet }\) and the plastic strain rate \(\dot{\varvec\upvarepsilon}^{p}\) are given as follows:
where
The plastic modulus in Eq. (48) is reduced to \(\hat{M}^{p} = {\mathbf{\hat{n}:}}[(F^{^{\prime}} /F)f_{{H\hat{n}}} {\hat{\varvec{\upsigma }}} + {\mathbf{f}}_{{k\hat{n}}} ]\) for the conventional model in the normal-yield state by setting \(R = 1\) leading to \(U = 0\).
The strain rate is given by substituting Eqs. (5) and (47)\(_{2}\) into Eq. (2) as follows:
from which the magnitude of plastic strain rate described in terms of the strain rate, denoted by \(\mathop {\overline{{\varLambda }}}\limits^{ \bullet }\) instead of \(\mathop {\overline{\lambda}}\limits^{ \bullet }\), in the flow rule of Eq. (33) is given as follows:
The stress rate is given from Eq. (5) with Eq. (50) as follows:
The loading criterion is given as follows (Hashiguchi [43, 45, 47]):
where the judgment whether or not the stress reaches the yield surface is not required since the plastic strain rate is induced continuously as the stress approaches the normal-yield surface. Equation (52) is applicable not only to the hardening state but also to the perfectly-plastic and softening state.
2.5 Improvement of Inverse and Reloading Behavior
The unique relation \(\varepsilon^{p} - \varepsilon_{0}^{p} = f(R{ - }R_{0} )\) holds as shown in Eq. (22) under the initial condition \( \, \varepsilon_{{}}^{p} = \varepsilon_{{0}}^{p} {:}R= R_{{0}}\) in the monotonic loading process if \(U\) in Eq. (19) is the function of only the normal-yield ratio \(R\). Therefore, \(\varepsilon^{p}\) induced during a certain change of \(R\) in the monotonic loading process is identical irrespective of the difference of loading processes, e.g. the initial loading, the reloading and the inverse loading and of the proportional and non-proportional loadings. This property causes the description that the returning of the reloading stress–strain curve to the previous loading curve is unrealistically gentle. Therefore, it engenders the impertinent prediction of cyclic loading behavior, i.e. the prediction of the unrealistically large plastic strain accumulation during the cyclic loading process in the extended subloading surface model.
As the fact observed in test data, the plastic strain rate is suppressed in the loading direction in which the elastic-core exists observing from the center of the normal-yield surface, i.e. the back stress and inversely the large plastic strain rate is induced in its opposite direction leading to the Masing effect. This tendency is more remarkable when the elastic-core is closer to the normal-yield surface leading to the larger value of \(\Re_{c}\) in Eq. (23). The degree of the loading/unloading is expressed by the scalar variable \({\hat{\mathbf{n}}}_{c} {\mathbf{:\overline{n}}}\) where \({\hat{\mathbf{n}}}_{c}\) is the normalized outward-normal of the elastic-core surface as defined in Eq. (31) and \({\overline{\mathbf{n}}}\) is the normalized outward-normal of the subloading surface, i.e. the direction of the plastic strain rate in Eq. (34). The magnitude of the plastic strain rate is controlled by the material parameter \(u\) in the function \(U(R)\) in Eq. (21) for the evolution rule of the normal-yield ratio \(R\) in Eq. (19).
Then, let the material parameter \(u\) be extended to the following equation for the extended subloading surface model in which the elastic-core, i.e. the similarity-center \({\mathbf{c}}\) moves with the plastic deformation, introducing the variables \(\Re_{c}\) and \(C_{n}\).
leading to the replacement
where \(u_{c}\) is the material constant and
Then, the plastic positive proportionality factor \(\mathop {\overline{\lambda }}\limits^{ \bullet }\) is replaced to the following equation by Eq. (54), noting Eq. (19) with Eq. (21).
2.6 Cyclic Stagnation of Isotropic Hardening
As a plastic deformation induced by the mutual slips of solid particles proceeds, the isotropic hardening proceeds with the loss of the dislocation mobility caused by the piling-up of obstacles or the formation of various networks. However, when a load reversal occurs, the isotropic hardening ceases temporarily by the recovery of the dislocation mobility. This phenomenon considerably affects the cyclic loading behavior in which the reverse loading is repeated. To describe this phenomenon, the concept of the cyclic stagnation of isotropic hardening, i.e. the existence of nonhardening region was proposed by Chaboche et al. [18] (see also Chaboche [13, 14]). The concept insists that the isotropic hardening does not proceed when the plastic strain given by the time-integration of plastic strain rate lies inside a certain region, called the nonhardening region, in the plastic strain space.
Assuming that the isotropic hardening stagnates when the plastic strain \({{\varvec{\upvarepsilon}}}^{p}\) lies inside a certain region, let the following surface, called the normal-isotropic hardening surface, be introduced.
where
\(g({\tilde{\varvec{\upvarepsilon }}}^{p} {)}\) is chosen to be the homogeneous degree-one of the variable \({\tilde{\varvec{\upvarepsilon }}}^{p}\). The variables \(\tilde{K}\) and \({{\varvec{\uprho}}}\) designate the size and the center, respectively, of the normal-isotropic hardening surface, the evolution rules of which will be formulated later. Furthermore, we introduce the surface, called the sub-isotropic hardening surface, which always passes through the current plastic strain \({{\varvec{\upvarepsilon}}}^{p}\) and which has a similar shape and a same orientation to the normal-isotropic hardening surface (see Fig. 2). Here, the plastic strain \({{\varvec{\upvarepsilon}}}^{p}\) is regarded to be the internal variable as \(\mathop {{\varvec{\upalpha}}}\limits^{ \bullet } = c_{k} \dot{\varvec\upvarepsilon}^{p}\) is used in the Prager’s linear kinematic hardening rule. On the other hand, the kinematic hardening variable, i.e. back-stress \({{\varvec{\upalpha}}}\) is used instead of \({{\varvec{\upvarepsilon}}}^{p}\) by Yoshida and Uemori [140]. However, \({{\varvec{\upalpha}}}\) would not be relevant but \({{\varvec{\upvarepsilon}}}^{p}\) would be relevant as the isotropic stagnation variable, since the mechanism of the isotropic hardening would be different from that of the kinematic hardening.
The subloading-isotropic stagnation surface is expressed by the following equation.
where \(\tilde{R}{ (0} \le \tilde{R} \le 1)\) is the ratio of the size of sub-isotropic hardening surface to that of the normal-isotropic hardening surface. It plays the role as the measure for the approaching degree of the plastic strain to the normal-isotropic hardening surface. Then, \(\tilde{R}\) is referred to as the normal-isotropic hardening ratio. It is calculable from the equation \(\tilde{R} = g({\tilde{\varvec{\upvarepsilon }}}^{p} {)}/\tilde{K}\) in terms of the known values of \({{\varvec{\upvarepsilon}}}^{p}\), \({{\varvec{\uprho}}}\) and \(\tilde{K}\).
The consistency condition of the subloading isotropic hardening surface is given by
Equation (60) is reduced to the following relation which must be fulfilled when the plastic strain just lies on the normal-isotropic hardening surface.
i.e.
Then, we assume the following equations so as to fulfill Eq. (61).
where \(0 \le C \le {1}\) and \(\varsigma { (} \ge {1)}\) are the material constants and
Substituting Eqs. (62) and (63) for the evolution rules of \(\tilde{K}\) and \({{\varvec{\uprho}}}\) into Eq. (60), the rate of the normal-isotropic hardening ratio is given by
which is the monotonically-decreasing function of \(\tilde{R}\) fulfilling
Therefore, the normal-isotropic hardening ratio \(\tilde{R}\) increases when the plastic strain moves to the outward of the sub-isotropic hardening surface but it decreases such that the normal-isotropic hardening surface encloses the plastic strain when the plastic strain tends to go out from the normal-isotropic hardening surface by virtue of the inequality \(\mathop {\tilde{R}}\limits^{ \bullet } < 0\) for \(\tilde{R} > 1\) as shown in Eq. (66). Furthermore, needless to say, the judgment of whether the plastic strain reaches the normal-isotropic hardening surface is not necessary in the present formulation consistently based on the subloading concept in all aspects. In contrast, the judgment whether the plastic strain or the back-stress reaches the isotropic hardening (stagnation) surface is required and the input loading increments must be infinitesimal such that the isotropic stagnation surface encloses the plastic strain in the other models, Chaboche et al. [18], Chaboche [13,14,15], Ohno [99], Ohno and Kachi, [100], Ohno et. al. [101], Yoshida and Uemori [140, 141].
Eventually, let the evolution rule of isotropic hardening be assumed as follows:
where \(\upsilon\, { (} \ge {1)}\) is the material constant and
Employing the extended isotropic hardening rule in Eq. (67) instead of Eq. (35) into Eq. (48), the plastic modulus is modified as follows:
The function \(g({\tilde{\varvec{\varepsilon }}}^{p} {)}\) is given in the simplest form as follows:
In the subloading surface model, the stress is pulled-back to the normal-yield surface and the isotropic hardening surface translates so as to involve the plastic strain automatically, while these mechanical functions are not furnished in the other plasticity and the viscoplasticity models. Therefore, the rather large incremental steps can be input even in the Euler forward method in the numerical calculation by the subloading surface model.
2.7 Mises Metals
The material functions for metals are given in this section, while the subloading surface model has been applied to various materials other than metals, i.e. soils, Hashiguchi and Mase [51], Hashiguchi and Tsutsumi [57,58,59,−60], Hashiguchi et al. [52, 56], Bin et al. [8], Farias et al. [30], Khojastehpour and Hashiguchi [79, 80], Maranha et al. [94], Pedroso [110], Ren et al. [117], Tsutsumi and Hashiguchi [128], Xiong et al. [134], Yadav et al. [135], Yamakawa et al. [136, 137], Ye et al. [139], Yuanming et al. [142, 143], Zhang et al. [145], etc., rocks, Xiong et al. [133], Zhu et al. [146], etc., asphalt Darabi et al. [24], etc. and further the friction phenomenon [54, 55, 62, 63, 106,107,108].
The yield function for the Mises yield condition is extended to incorporate the kinematic hardening by replacing \({{\varvec{\upsigma}}}^{^{\prime}}\) to \({\hat{\varvec{\upsigma }}}^{^{\prime}}\) (()′: deviatoric part) in Eq. (6) as follows:
for which the subloading function \(f({\overline{\varvec{\upsigma }}})\) for Eq. (72) is given by
Further, the elastic-core function in Eq. (23) for Eq. (72) is given by
It follows from Eqs. (23) and (31) for Eq. (74) that
The isotropic hardening function is given by
where \( s_{r}\) and \( c_{H}\) are the material constants.
The rates of the kinematic hardening variable and the elastic-core are given by Eqs. (36) and (37) as
The plastic modulus is given by substituting Eqs. (73), (74), (78), (79) and (80) into Eq. (48) as follows:
Substituting Eq. (73) with Eq. (15) into Eq. (18), the extended subloading surface is described as follows:
i.e.
The normal-yield ratio \(R\) is derived from the quadratic Eq. (83) as follows:
3 Subloading-Overstress Model: Extension to Description of Elasto-Viscoplastic Deformation in General Rate
The subloading surface model will be extended to the subloading-overstress model which is capable of describing the monotonic and the cyclic deformations in general rate from quasi-static (elastoplastic) to the impact loading. The strain \({{\varvec{\upvarepsilon}}}\) is additively decomposed into the elastic strain \({{\varvec{\upvarepsilon}}}^{e}\) and the viscoplastic strain \({{\varvec{\upvarepsilon}}}^{vp}\) instead of Eq. (2) as follows:
3.1 Creep Model and Overstress Model for Viscoplastic Deformation
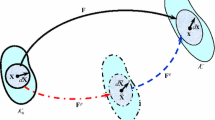
The viscoplastic models are classified into the creep model (Norton [97] and the overstress model whose rheology models are shown in Fig. 3. The creep model is regarded as the nonlinearization of the Maxwell model for the viscoelastic deformation so that the creep strain rate is induced in any low stress level. On the other hand, the overstress model, Bingham [9] is the incorporation of the slider exhibiting the yield condition into the dashpot in parallel extending the creep model such that there exists the threshold value for the generation of the viscoplastic deformation. Therefore, the viscoplastic deformation is induced by the overstress from the yield stress but it is not induced for the stress lower than the yield stress. Therefore, the response of the creep model is not reduced to that of the elastoplastic constitutive equation but that of the overstress model is reduced to the elastoplastic constitutive equation for the quasi-static deformation process. Therefore, the creep model is not acceptable, although it is used widely (e.g. Lemaitre and Chaboche [86], Abdel-Karim and Ohno [1], Betten [7], Chaboche [17], Ohno et al. [103], de Sauza Neto et al. [25]) without regard to this serious defect but the overstress model is acceptable for the description of the viscoplastic deformation. Consequently, the overstress model should be adopted for the description of the viscoplastic deformation.
3.2 Static and Limit Subloading Surfaces
The static subloading and the limit subloading surfaces (see Fig. 4) are incorporated in addition to the subloading, the normal-yield, the elastic-core and the limit elastic-core surfaces in the subloading surface model for the rate-independent elastoplastic deformation. Here, the subloading surface on which the current stress lies may become larger than the normal-yield surface in general. The normal-yield ratio \(R\) which may become larger than unity in general is calculated by the identical equation for the rate-independent elastoplastic deformation, i.e. Equation (18) in general and by Eq. (92) for metals.
The viscoplastic strain rate is induced by the overstress from the static subloading surface expressed in the following equation which is given by replacing the current stress \({{\varvec{\upsigma}}}\), the center \({\overline{\varvec{\upalpha }}}\) and the normal-yield ratio \(R\) to their conjugate points \({{\varvec{\upsigma}}}_{s}\), \({\overline{\varvec{\upalpha }}}_{s}\) and the static normal-yield ratio \(R_{s} { (} \le {1)}\), respectively, in the subloading surface in Eq. (11) for the elastoplastic deformation.
with
where \(R_{s}\) evolves by the following equation which is identical to Eq. (19) with Eq. (21) for the extended subloading surface model with the replacement of the plastic strain rate \(vp\) to the viscoplastic strain rate \(\dot{\varvec\upvarepsilon}^{vp} \).
with
\(R_{s} { (} \le 1{)}\) is called the static normal-yield ratio because the quasi-static deformation proceeds in the state \(R = R_{s}\). It can be analytically calculated by Eq. (22) with the replacement of the plastic strain rate to the viscoplastic strain rate for \(\Re_{c} C_{n} = const.\) as follows:
under the initial condition \(R_{s} = R_{s0}\) for \(\varepsilon^{vp} = \varepsilon_{0}^{vp}\), where \(\varepsilon^{vp} = \int {{||}\dot{\varvec\upvarepsilon}^{vp} {||}} dt\).
3.3 Viscoplastic Strain Rate
Now, let the flow rule of the viscoplastic strain rate be given by incorporating the crucially important variable in the subloading surface model, i.e. the normal-yield ratio \(R\) into the overstress model as follows:
where \(\varGamma\) is the positive viscoplastic multiplier given by
\(\mu_{v}\) (viscoplastic coefficient) and \(n{ (} > 1{)}\) are the material constants. The smooth elastic-viscoplastic transition is described by adopting the overstress due to \(R{ - }R_{s}\) instead of \(R{ - }1\), because \(R_{s}\) increases gradually up to \(1\) with the viscoplastic deformation, while \(R_{s}\) was fixed as \(R_{s} = 1\) in the past overstress model.
The function \(U\) for the evolution rule of the normal-yield ratio \(R\) and the positive proportionality factor (plastic multiplier) \(\mathop {\overline{\lambda }}\limits^{ \bullet }\) are modified to Eqs. (54) and (56), respectively, by incorporating the variables \(\Re_{c} { (} \equiv f{(}{\hat{\mathbf{c}}}{)/}F{)}\) and \(C_{n} \, ( \equiv {\hat{\mathbf{n}}}_{c} {\mathbf{:\overline{n}}}{)}\) in the extended subloading surface model for the rate-independent elastoplastic deformation. Analogously, for the rate-dependent deformation, the function \(U_{s}\) and the viscoplastic multiplier \(\Gamma\) be modified to Eq. (89) and
where \(\overline{u}_{c}\) is the material constant. Thus, the rising and the lowering of the stress due to the decrease and the increase of strain rate are enforced in the state \(\Re_{c} C_{n} > 0\) and \(\Re_{c} C_{n} < 0\), respectively. It leads to the description of the global Masing effect in the viscoplastic deformation process.
Further, let Eq. (93) be extended such that the infinite viscoplastic strain rate is induced for \(R \to c_{m} R_{s}\) (\(c_{m} { (} \gg {1)}\): material constant) leading to \({\varGamma} \to \infty\) in the impact loading process as follows:
The variable \(c_{m} R_{s} { (}R < c_{m} R_{s} \le c_{m} {)}\) is called the limit normal-yield ratio. Here, the surface to which the stress can reach at most is given by setting \(R = c_{m} R_{s}\) in the subloading surface in Eq. (11) is called the limit subloading surface. On the other hand, the elastic response is described unrealistically for the impact loading in the past overstress models, Perzyna [114, 115], Chaboche [14, 17], de Souza Neto et al. [25], Lemaitre and Chaboche [86], etc. The rational description of deformation in the general rate ranging from the quasi-static to the impact loading is attained by the above-mentioned subloading-overstress model in which the crucially-important variables, i.e. the normal-yield ratio \(R\), the static normal-yield ratio \(R_{s}\), \(\Re_{c}\), \(C_{n}\) and the limit normal-yield ratio \(c_{m} R_{s}\) are incorporated.
The rates of the internal variables \(H\), \({{\varvec{\upalpha}}}\) and \({\mathbf{c}}\) are given from Eqs. (35), (36) and (37) with the replacement of \(\dot{\varvec\upvarepsilon}^{p}\) to \(\dot{\varvec\upvarepsilon}^{vp}( = {\varGamma}{\overline{\mathbf{n}}})\) as follows:
The isotropic hardening stagnation can be incorporated by the identical equations formulated in Sect. 2.6 with the replacement of the plastic strain rate \(\dot{\varvec\upvarepsilon}^{p}\) to the viscoplastic strain rate \(\dot{\varvec\upvarepsilon}^{vp}\).
3.4 Strain Rate vs. Stress Rate Relation
The strain rate vs. stress rate relations are given from Eq. (85) with Eqs. (3) and (91) as follows:
which is represented in the incremental form as follows:
Then, it follows from Eqs. (99) with (92) in the quasi-static deformation that so that the stress changes along the static subloading surface given by Eq. (86). Consequently, the response of the subloading−overstress mode is reduced to that of the original subloading surface model for the rate−independent elastoplastic deformation behavior described in Sect. 2. The subloading−overstress model is no more than the generalization of the subloading surface model to the description of the elastoplastic deformation in the general strain rate. Irreversible deformations in any rate from the static to the impact loading can be described by the subloading−overstress model. Eventually, the elastoplastic constitutive equation with the plastic modulus for the rate−independent elastoplastic deformation which is derived by consistency condition of the yield condition (subloading surface for the subloading surface model) can be disused by adopting only the subloading−overstress model.
In the overstress model, we do not need to calculate the plastic modulus which possesses often a complex form as seen in Eq. (48) but instead we have only to perform the update calculation of the viscoplastic internal variables involved in the positive viscoplastic multiplier \({\varGamma}\) in Eq. (91) and \({\overline{\mathbf{n}}}\).
The stress–strain curve described by the subloading-overstress model is illustrated in Fig. 5 The smooth elastic-viscoplastic transition and the cyclic loading behavior can be described appropriately by the unified equation.
4 Verification of Subloading-Overstress Model by Simulations of Test Data
The validity of the subloading-overstress model will be verified by the comparisons with the test data of metals under various loading conditions in this section.
4.1 Material Parameters
The following 18 material constants and 5 initial values of the internal variables at most are involved in the subloading-overstress model.
Material constants:
Initial values:
The determinations of these material parameters are explained below in brief.
-
(1)
Young’s modulus \(E\) and Poisson’s ratio \(\nu\) are determined from the slope and the ratio of lateral to axial strains in the initial part of stress–strain curve.
-
(2)
\(s_{r}\), \(c_{H}\) and \(F_{0}\) for the isotropic hardening and \(c_{k}\), \(b_{k}\) and \({{\varvec{\upalpha}}}_{0}\) for the kinematic hardening are determined from the stress–strain curves in the initial and the inverse loading process.
-
(3)
\(u\), \(u_{c}\) and \(R_{e} { (} < {1)}\) for the evolution of the normal-yield ratio are determined from the stress–strain curve in the subyield state, i.e. the elastic–plastic transitional state.
-
(4)
\(c_{e}\), \(\chi\) and \({\mathbf{c}}_{{0}}\) for the elastic-core are determined from the stress–strain curves in cyclic loading.
-
(5)
\(C\), \(\varsigma\), \(\upsilon\), \(\tilde{K}_{0}\) and \({{\varvec{\uprho}}}_{0}\) for the isotropic hardening stagnation are determined from the stress–strain curves in loading–unloading process.
-
(6)
\(\mu_{v} {,} \, \overline{u}_{c} , \, n{ (} > 1{)}\) and \(c_{m} { (} \gg {1)}\) are determined by the viscoplastic deformation characteristics.
All of these material parameters can be determined only by the stress–strain curves in the uniaxial loading for initial isotropic materials. One can put \({{\varvec{\upalpha}}}_{0} = {\mathbf{c}}_{{0}} = {{\varvec{\uprho}}}_{0} = {\mathbf{O}}\) for the initial isotropy, which is assumed in all the subsequent simulations. We calculate \(\tilde{K}_{0}\) by \(\tilde{K}_{0} = ||{\tilde{\varvec{\upvarepsilon }}}_{0}^{p} ||\) leading to \(\tilde{R}_{0} = 1\) by inputting infinitesimal values of \({{\varvec{\upvarepsilon}}}_{0}^{p}\) and \({{\varvec{\uprho}}}_{0}\) in order that the isotropic hardening rule in Eq. (78) without the isotropic hardening stagnation holds in the initial loading process for all the present simulations. Besides, the three material constants \(C{ (0} \le C \le {1)}{, }\,\varsigma { (} \ge {1)}\) and \(\upsilon { (} \ge {1)}\) for the isotropic hardening stagnation can be fixed as \(C = 0.5\), \(\varsigma = 3\) and \(\upsilon = 3\) in all the simulations shown later in this section. Consequently, the number of material constants which must be determined in each test datum can be reduced to be 15 as a total.
The automatic determination function of the material parameters for the simplified version of the subloading surface model for the elastoplastic deformation of metals with the evolution rule of the elastic-core limited to the nonhardening state and without the isotropic hardening stagnation is installed in the commercial software Marc which can be used by all the Marc users. The efficient and accurate determinations of the material parameters for the simplified version can be referred to Liu et al. [91] adopting the artificial neural network.
4.2 Dynamic Loading Process Inducing Elasto-Viscoplastic Deformation
The uniaxial monotonic loading behavior at various constant strain rates at 600 °C in the test data for 21/4Cr-1Mo steel (SA 387, Gr.22) after Inoue et al. [72] is shown in Fig. 6, where the material parameters are chosen as follows:
Uniaxial loading behavior of 21/4Cr–1Mo steel (SA 387, Gr.22) under various axial strain rates at 600 °C (test data after Inoue et al. [72])
Material constants:
Initial values:
The close simulations are shown in Fig. 6, while the simulated stress for the strain rate 0.000001∕s is slightly lower than the stress in the test data.
The monotonic loading behavior at various constant strain rates at \(550^{ \circ } {\rm C}\) in the test data for Modified 9Cr-1 Mo steel after Abel-Karim and Ohno [1] is shown in Fig. 7, where the material parameters are chosen as follows:
Uniaxial loading behavior of Modified 9Cr–1Mo steel under various axial strain rates at 550 °C (test data after Abdel-Karim and Ohno [1])
Material constants:
Initial values:
The quite close simulations are also seen in Fig. 7. The accuracy of the present simulations are same levels of the simulations by the experimenters Abdel-Karim and Ohno [1] based the creep model, who have provided the test data, while the creep model is physically irrational lacking the generality, i.e. incapable of describing the rate-independent elastoplastic deformation behavior as explained in Introduction.
The stress relaxation behavior with same prior strain rate \(0.0005/{\rm s}\) but the three levels of fixed strain, i.e. \(0.139,{ 0}{\text{.400}}\) and 0.602% in the test data of TIMETAL21S at 650 °C after Saleeb and Arnold [121] is shown in Fig. 8, where the material parameters are chosen as follows:
Stress relaxation behavior with same prior strain rates but various peak stresses of TIMETAL21S at 650 °C (Test data after Saleeb and Arnold [121])
Material constants:
Initial values:
The quite close simulations are shown in Fig. 8 for the three fixed strain levels.
The deformation behavior at the variable strain rate between 0.001/s and 0.000001/s for 304 stainless steel at room temperature 20 °C in the test data after Krempl, cf. Lemaitre and Chaboche [86] is shown in Fig. 9, where the material parameters are chosen as follows:
Uniaxial loading behavior under variable axial strain rate between 0.1 and 0.001 (%/s) of 304 stainless steel at room temperature 20 °C (test data after Krempl (cf. Lemaitre and Chaboche [86]): (a) Isotropic hardening stagnation is considered, (b) Isotropic hardening stagnation is ignored
Material constants:
Initial values:
The quite close simulations are shown in Fig. 9a. The accuracies of the simulations hardly decrease by ignoring the isotropic hardening stagnation as seen in Fig. 9b.
4.3 Quasi-static Loading Process Inducing Elastoplastic Deformation Behaviors
It was verified in the previous section that the subloading-overstress model is capable of describing the elasto-viscoplastic deformations. Further, it will be verified below that the subloading-overstress model is capable of describing the elastoplastic deformations by the simulations of test data for the quasi-static rate of deformation at the room temperature.
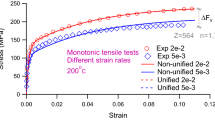
The cyclic loading behavior under the stress amplitude to both positive and negative sides can be predicted to some extent by any models, including even the conventional plasticity model Drucker [27] with the yield surface enclosing the purely elastic domain, e.g. Chaboche model, Chaboche et al. [18], Chaboche [13, 14], Ohno and Wang [102], etc. On the other hand, the prediction of the cyclic loading behavior under the stress amplitude in positive or negative one side, i.e. the pulsating loading inducing the so-called mechanical ratcheting effect requires a high ability for the description of plastic strain rate induced by the rate of stress inside the yield surface. Furthermore, it is noteworthy that we often encounter the pulsating loading phenomena in the boundary-value problems in engineering practice, e.g. railways and gears. The comparison with the test data for the 1070 steel under the cyclic loading of axial stress between 0 and \({ + 830{\text{MPa}}}\) at room temperature after Jiang and Zhang [74] is depicted in Fig. 10a, where the material parameters and the strain rate are selected as shown in the following, while the axial strain rate is chosen to be quite low, i.e. \({\dot{\varvec\upvarepsilon}}_{a} = 10^{ - 7} /s\), although the strain rate is not written in the paper of Jiang and Zhang [74].
Mechanical ratcheting during pulsating loading between 0 and \(+ 830{MPa}\) of 1070 steel at room temperature (Test data after Jiang and Zhang [74]): (a) Isotropic hardening stagnation is considered, (b) Isotropic hardening stagnation is ignored. The stress–strain curves are shown continuously up to the 10th cycle and then at the 16th, 32nd, 64th, 128th, 256th and 512th cycles for clarity
Material constants:
Initial values:
The accuracy of simulation hardly decreases by ignoring the isotropic hardening stagnation as seen in Fig. 12b.
Furthermore, examine the uniaxial cyclic loading behavior under the constant symmetric strain amplitudes to both positive and negative sides. Comparison with the test data of the 316 steel under the cyclic loading with the increasing axial strain amplitudes \(\pm 1.0, \, \pm {1}{\text{.5, }} \pm {2}{\text{.0, }} \pm {2}{\text{.5, }} \pm {3}{\text{.0\% }}\) after Chaboche et al. [18] is depicted in Fig. 11 where the material parameters and the strain rate are selected as shown in the following, while the axial strain rate is chosen to be quite low, i.e. \({\dot{\varvec\upvarepsilon}}_{a} = 10^{ - 8} / \rm s\), although the strain rate is not written in the paper of Chaboche et al. [18].
Cyclic loading behavior under increasing strain amplitude of 316 steel at room temperature (Test data after Chaboche et al. [18]): (a) Isotropic hardening stagnation is considered, (b) Isotropic hardening stagnation is ignored
Material constants:
Initial values:
The quite close simulation is shown in Fig. 11a. However, the accuracy of simulation decreases seriously by ignoring the isotropic hardening stagnation as shown in Fig. 11b, differing from the simulations of the test data shown in Figs. 9 and 10. It can be inferred from these simulation results that the influence of the isotropic hardening stagnation is induced in the loading process in which the full inverse loading is repeated many times.
The calculated results for the axial strain rates \(({\text{a}}) \, 10^{ - 10} /{\text{s}, } ({\text{b}}) \, 10^{ - 9} /{\text{s}, }\,({\text{c}}) \, 10^{ - 7} /{\text{s}}\), \(({\text{d}}) \, 10^{ - 6} /{\rm s}\) and (e)10–5/s are shown in Fig. 12. It is observed from this figures that the calculated results are identical for the strain rates slower than \(10^{ - 7} /{\rm s}\) but the stress increases with the increase of the strain rate faster than \(10^{ - 7} /{\rm s}\). In other words, the quasi-static deformation leading to the elastoplastic deformation is induced for the strain rate slower than \(10^{ - 7} /{\rm s}\). Consequently, the deformation behavior of the 316 steel at room temperature under the strain rate faster than the quite slow strain rate \(10^{ - 7} /{\rm s}\) may not be calculated accurately by the elastoplastic constitutive equation but must be calculated by the subloading-overstress model.
Variation of simulations with variation of strain rate by using values of material parameters identical to those used in Fig. 11
The accuracies of simulations of the test data in Figs. 10 and 11 by Hashiguchi et al. [64] and Hashiguchi and Ueno [61] using the rate-independent subloading surface model for the elastoplastic deformation are improved to the simulations depicted in these figures by using the subloading-overstress model.
5 Concluding Remarks and Future Works
The subloading-overstress model is provided and it is verified that the model is capable of describing not only the dynamic but also the quasi-static deformation behaviors by the comparison with various test data of metals under the monotonic and the cyclic loading processes at the various strain rates.
The elastoplastic deformation behaviors has been simulated by using the elastoplastic constitutive equation. However, it should be noticed that the elastoplastic constitutive equation holds only in the purely quasi-static deformation which does not occur actually. Therefore, an infinitely long time is required in order to perform a purely quasi-static deformation test and thus test data reported as the elastoplastic deformation behaviors should not be regarded as test data for a quasi-static deformation. In facts, the test data reported as the elastoplastic deformation behaviors can be closely simulated at the low strain rate by the subloading-overstress model as verified in Sect. 4.3. Incidentally, it should be noted that the purely quasi-static deformation is hardly induced actually in test data and engineering practice. Therefore, the subloading-overstress model should be used for the deformation analyses in any rate of deformation including the quasi-static deformation, disusing the elastoplastic constitutive equation involving the plastic modulus \(\overline{M}^{p}\) which is rather complex as shown in Eq. (81). Besides, it is revealed that the isotropic hardening stagnation can be ignored in the deformation behavior as far as the full inverse loadings are not repeated many times.
The distinguished advantages of the subloading-overstress model are summarized as follows:
-
i.
The plastic/viscoplastic strain rate can be described in any low stress level, while it cannot be described in all the other plastic/viscoplastic models because they assume the purely-elastic domain inside which the stress lies always. Incidentally, the incorporation of the subloading-overstress model would be inevitable for the analysis of fatigue phenomenon without resorting to use of the unnatural method by the two-scale damage model premised on the plasticity model assuming the purely-elastic domain, Lemaitre [84, 85], Lemaitre and Doghri [87], Lemaitre et al. [88], Lemaitre and Desmorat [89], etc. based on the law of micromechanics, Eshelby [29], in which the inclusion of the microscopic voids or cracks is incorporated in a mesoscale representative volume element.
-
ii.
The continuity condition in the large, i.e. the smoothness condition, Hashiguchi [41, 42, 44] is fulfilled always leading to the continuous variations of the tangent stiffness tensor and the isotropic hardening by virtue of the subloading concept, while it is violated leading to the discontinuous variations of the tangent stiffness modulus tensor and the isotropic hardening in all the other plasticity and the viscoplasticity models because of the incorporation of the purely-elastic domain.
-
iii.
The elastoplastic and the elasto-viscoplastic deformations under the monotonic and the cyclic loading at the general deformation rate ranging from the quasi-static to the impact loading can be described in the unified formulation. Therefore, the elastoplastic constitutive equation can be disused.
It should be emphasized that these distinguished advantages in the subloading-overstress model is provided by the incorporation of the basic variable incorporated uniquely in the subloading surface variable, i.e. the normal-yield ratio \(R\).
The following extensions of the subloading-overstress model are desirable to describe a more general deformation behavior, while the formulations and the verifications with test data will have to be performed in future works.
-
(1)
The elastoplastic deformation behavior is influenced by the temperature. However, the dependence of material functions and constants in the elastoplastic constitutive equation on the temperature would be complex so that they are specified for each temperature resulting in the piecewise-linear relation in the deformation analysis as seen in the research papers, Kou [81], Li et al. [90], Ohno et al. [103], Pandya et al. [109], Yang et al. [138], etc. and the commercial software (e.g. Marc and Abaqus). Such method for incorporation of the piecewise-linear relation is easy-going way but requires the large computational load. Therefore, it is desirable to formulate material functions and constants as functions of temperature.
-
(2)
It is desirable to perform the simulation of test data in an impact loading behavior. However, it would be difficult to obtain an accurate test data of stress–strain relation since an intense vibrational deformation is induced in test specimen at an impact loading so that it would have to be analyzed as the dynamic boundary-value problem. It will be executed in the future work.
-
(3)
The present formulation will have to be extended to the multiplicative hyperelastic-based viscoplasticity for the description of the monotonic and the cyclic loading behaviors by improving the past formulations, Hashiguchi [48,49,50], Hashiguchi and Yamakawa [65], Fincato and Tsutsumi [33] which are incapable of describing the viscoplastic deformation pertinently predicting the peculiar stress–strain curve with an inflection point even in the monotonic loading process as delineated in the introduction. Here, it should be noticed that the unconventional elastoplasticity models, i.e. the multi surface model, Mróz [96], Iwan [73] and the two surface model, Dafalias and Popov [23], Krieg [83] other than the subloading surface model cannot be extended to the hyperelastic-based plasticity model. In fact, only the conventional elastoplasticity model with the yield surface enclosing the purely-elastic domain is adopted to the formulation of the multiplicative hyperelastic-based plastic constitutive equations, Wallin et al. [131, 132], Dettmer and Reese [26], Wallin and Ristinmaa [131], Vladimirov et al. [129, 130], etc. which are capable of describing the finite elastoplastic deformation only during the monotonic loading process. Besides, it should be noted that the hypoelastic-based formulations, Truesdell [126], Truesdell and Noll [127], Hill [67], etc. are capable of describing the finite plastic deformation but they are limited to the description of the infinitesimal elastic deformation as explained in detail by Hashiguchi [48, 50] and shown by the numerical examples by Brepopols et al. [11] and Jiao and Fish [75, 76] and required the cumbersome time-integration of stress rate in numerical calculation (cf. Hughes and Winget [71], de Souza Neto et al. [25], etc.). In addition, it should be noticed that the multiplicative hyperelastic-based plastic constitutive equation is irrelevant to the hypoelastic-based plastic and viscoplastic constitutive equations but it can be derived from the infinitesimal hyperelastic-based plastic and viscoplastic constitutive equations formulated in this article (cf. Hashiguchi [48,49,50]) by the additive to the multiplicative transformation of the deformation measures.
References
Abdel-Karim M, Ohno N (2000) Kinematic hardening model suitable for ratcheting with steady-state. Int J Plasticity 16:225–240
Anjiki T, Hashiguchi K (2021) Extended overstress model and its implicit stress integration algorithm: formulations, experiments, and simulations. Int J Numer Methods Eng 24:1642–1693
Armstrong PJ, Frederick CO (1966) A mathematical representation of the multiaxial Bauschinger effect, CEGB Report RD/B/N 731 (or in Materials at High Temperature, 24:1–26 (2007))
Arnold S, Saleeb A (1994) On the thermodynamic framework of generalized coupled thermoelastic–viscoplastic-damage modeling. Int J Plasticity 10:263–278
Asaro RJ, Lubarda V (2006) Mechanics of solids and materials. Cambridge Univ. Press, Cambridge
Bayley RW (1929) Creep of steel under simple and compound stresses and the use of high initial temperature in steam powder plant. Trans World Powder Conf 3:1089
Betten J (2005) Creep mechanics, 2nd edn. Springer, New York
Bin Y, Xueqian N, Yu H, Feng Z (2018) Unified modeling of soil behaviors before/after flow liquefaction. Compt Geotech 102:125–135
Bingham EC (1922) Fluidity and plasticity. McGraw-Hill, New York
Bodner SR, Partom Y (1975) Constitutive equations for elastic viscoplastic strain hardening. J Appl Mech 42:385–389
Brepols T, Vladimirov IN, Reese S (2014) Numerical comparison of isotropic hypo- and hyperelastic-based plasticity models with application to industrial forming processes. Int J Plasticity 63:18–48
Chaboche JL (1986) Time-independent constitutive theories for cyclic plasticity. Int J Plasticity 2:149–188
Chaboche JL (1989) Constitutive equations for cyclic plasticity and cyclic viscoplasticity. Int J Plasticity 5:247–302
Chaboche JL (1989) A review of some plasticity and viscoplasticity constitutive theories. Int J Plasticity 24:1642–1693
Chaboche JL (1991) On some modifications of kinematic hardening to improve the description of ratcheting effects. Int J Plasticity 7:661–678
Chaboche J-L (1997) Thermodynamic formulation of constitutive equations and application to the viscoplasticity and viscoelasticity of metals and polymers. Int J Solids Struct 38:2239–2254
Chaboche JL (2008) A review of some plasticity and viscoplasticity constitutive theories. Int J Plasticity 24:1642–1693
Chaboche JL, Dang-Van K, Cordier G (1979) Modelization of the strain memory effect on the cyclic hardening of 316 stainless steel. In: Trans. 5th Int. Conf. SMiRT, Berlin, Division L., Paper No. L. 11/3
Chaboche J-L, Gaubert A, Kanouté P, Longuet A, Azzouz F, Mazière M (2013) Viscoplastic constitutive equations of combustion chamber materials including cyclic hardening and dynamic strain aging. Int J Plasticity 46:1–22
Chen W, Feng M (2015) A study of a cyclic viscoplasticity model based on hyperbolic sine form for the inelastic strain rate. Int J Mech Sci 101–102:155–160
Chen W, Wang F, Kitamura T, Feng M (2017) A modified unified viscoplasticity model considering time-dependent kinematic hardening for stress relaxation with effect of loading history. Int J Mech Sci 133:883–892
Chen W, Wang F, Feng M (2017) Study of a modified non-unified model for time-dependent behavior of metal materials. Mech Mater 113:69–75
Dafalias YF, Popov EP (1975) A model of nonlinearly hardening materials for complex loading. Acta Mech 23:173–192
Darabi MK, Abu Al-Rub RK, Masad EA, Huang CW, Little DA (2012) A modified viscoplastic model to predict the permanent deformation of asphaltic materials under cyclic-compression loading at high temperatures. Int J Plasticity 35:100–134
de SouzaNeto EA, Perić D, Owen DJR (2008) Computational methods for plasticity. Wiley, Chichester
Dettmer W, Reese S (2004) On the theoretical and numerical modelling of Armstrong-Frederic kinematic hardening in the finite strain regime. Compt Methods Appl Mech Eng 193:87–116
Drucker DC (1988) Conventional and unconventional plastic response and representation. Appl Mech Rev 41:151–167
Duvaut G, Lion JL (1972) Les Inequations en Mechaniqie et en Physique. Dunod, Paris
Eshelby JD (1957) The determination of the elastic field of an ellipsoidal inclusion and related problems. Proc Royal Soc Lond A 241:376–396
Farias MM, Pedroso DM, Nakai T (2009) Automatic substepping integration of the subloading tij model with stress path dependent hardening. Compt Geotech 36:537–548
Fincato R, Tsutsumi S (2020) An overstress elasto-viscoplasticity model for high/low cyclic strain rates loading conditions: Part I—formulation and computational aspects. Int J Solids Struct 207:279–294
Fincato R, Tsutsumi S (2021) Coupled elasto-viscoplastic and damage model accounting for plastic anisotropy and damage evolution dependent on loading conditions. Comput Methods Appl Mech Eng 387:114165
Fincato R, Tsutsumi S (2022) Numerical implementation of the multiplicative hyperelastic-based Extended Subloading Surface plasticity model. Comput Methods Appl Mech Eng 401:115612
Follansbee PS, Kocks UF (1988) A constitutive description of the deformation of copper based on the use of the mechanical threshold. Acta Metall 36:81–93
Garofalo F (1968) An empirical relation defining the stress dependence of minimum creep rate in metals. Trans Metall Soc AIME 227:351–355
Guo S, Kang G, Zhang J (2013) A cyclic visco-plastic constitutive model for time-dependent ratchetting of particle-reinforced metal matrix composites. Int J Plasticity 40:101–125
Hashiguchi K (1980) Constitutive equations of elastoplastic materials with elastic-plastic transition. J Appl Mech 47:266–272
Hashiguchi K (1981) Constitutive equations of elastoplastic materials with anisotropic hardening and elastic-plastic transition. J Appl Mech 48:297–301
Hashiguchi K (1988) A mathematical modification of two surface model formulation in plasticity. Int J Solids Struct 24:987–1001
Hashiguchi K (1989) Subloading surface model in unconventional plasticity. Int J Solids Struct 25:917–945
Hashiguchi K (1993) Fundamental requirements and formulation of elastoplastic constitutive equations with tangential plasticity. Int J Plasticity 9:525–549
Hashiguchi K (1993) Mechanical requirements and structures of cyclic plasticity models. Int J Plasticity 9:721–748
Hashiguchi K (1994) On the loading criterion. Int J Plasticity 8:871–878
Hashiguchi K (1997) The extended flow rule in plasticity. Int J Plasticity 13:37–58
Hashiguchi K (2000) Fundamentals in constitutive equation: continuity and smoothness conditions and loading criterion. Soils Found 40(3):155–161
Hashiguchi K (2013) General description of elastoplastic deformation/sliding phenomena of solids in high accuracy and numerical efficiency: subloading Surface Concept. Arch Compt Methods Eng 20:361–417
Hashiguchi K (2016) Exact formulation of subloading surface model: unified constitutive law for irreversible mechanical phenomena in solids. Arch Compt Methods Eng 23:417–447
Hashiguchi K (2017) Foundations of elastoplasticity: subloading surface model. Springer, New York
Hashiguchi K (2018) Multiplicative hyperelastic-based plasticity for finite elastoplastic deformation/sliding: a comprehensive review. Arch Compt Methods Eng 23:1–41
Hashiguchi K (2020) Nonlinear continuum mechanics for finite elastoplasticity: multiplicative decomposition with subloading surface model. Elsevier, Amsterdam
Hashiguchi K, Mase T (2007) Extended yield condition of soils with tensile strength and rotational hardening. Int J Plasticity 23:1939–1956
Hashiguchi K, Mase T, Yamakawa Y (2021) Elaborated subloading surface model for accurate description of cyclic mobility in granular materials. Acta Geotech 17:699–719
Hashiguchi K, Okayasu T, Saitoh K (2005) Rate-dependent inelastic constitutive equation: the extension of elastoplasticity. Int J plasticity 21:463–491
Hashiguchi K, Ozaki S (2008) Constitutive equation for friction with transition from static to kinetic friction and recovery of static friction. Int J Plasticity 24:2102–2124
Hashiguchi K, Ozaki S, Okayasu T (2005) Unconventional friction theory based on the subloading surface concept. Int J Solids Struct 42:1705–1727
Hashiguchi K, Saitoh K, Okayasu T, Tsutsumi S (2002) Evaluation of typical conventional and unconventional plasticity models for prediction of softening behavior of soils. Geotechnique 52:561–573
Hashiguchi K, Tsutsumi S (2001) Elastoplastic constitutive equation with tangential stress rate effect. Int J Plasticity 17:1941–1969
Hashiguchi K, Tsutsumi S (2003) Shear band formation analysis in soils by the subloading surface model with tangential stress rate effect. Int J Plasticity 19:1651–1677
Hashiguchi K, Tsutsumi S (2005) General non-proportional loading behavior of soils. Int J Plasticity 21:767–797
Hashiguchi K, Tsutsumi S (2007) Gradient plasticity with the tangential subloading surface model and the prediction of shear band thickness of granular materials. Int J Plasticity 22:767–797
Hashiguchi K, Ueno M (2017) Elastoplastic constitutive equation of metals under cyclic loading. Int J Eng Sci 111:86–112
Hashiguchi K, Ueno M (2022) Subloading-friction model with saturation of tangential contact stress. Friction. https://doi.org/10.1007/s40544-022-0656-z
Hashiguchi K, Ueno M, Kuwayama T, Suzuki N, Yonemura S, Yoshikawa N (2016) Constitutive equation of friction based on the subloading-surface concept. Proc R Soc Lond 472:20160212. https://doi.org/10.1098/rspa.2016.0212
Hashiguchi K, Ueno M, Ozaki T (2012) Elastoplastic model of metals with smooth elastic-plastic transition. Acta Mech 223:985–1013
Hashiguchi K, Yamakawa Y (2012) Introduction to finite strain theory for continuum elasto-plasticity. Wiley Series in Computational Mechanics, Chichester
Hassan T, Taleb L, Krishna S (2008) Influence of non-proportional loading on ratcheting responses and simulations by two recent cyclic plasticity models. Int J Plasticity 24:1863–1889
Hill R (1978) Aspects of invariance in solid mechanics. Adv Appl Mech 18:1–75
Ho K (2009) A unified constitutive law for cyclic viscoplasticity. Int J Solids Struct 46:1007–1018
Ho K, Krempl E (2002) Extension of the viscoplasticity theory based on overstress (VBO) to capture non-standard rate dependence in solids. Int J Plasticity 18:851–872
Hohenemser K, Prager W (1932) Uber die Ansatze der Mechanik isotroper Kontinua. Z A M M 12:216–226
Hughes TJR, Winget J (1980) Finite rotation effects in numerical integration of rate consistent equations arising in large-deformation analysis. Int J Numer Methods Eng 15:1862–1867
Inoue T, Ohno N, Suzuki A, Igari T (1989) Evaluation of inelastic constitutive models under plasticity-creep interaction for 21/4Cr–1Mo steel at 600 C. Nucl Eng Des 114:295–309
Iwan WD (1967) On a class of models for the yielding behavior of continuous and composite systems. J Appl Mech 34:612–617
Jiang Y, Zhang J (2008) Benchmark experiments and characteristic cyclic plasticity deformation. Int J Plasticity 24:1481–1515
Jiao Y, Fish J (2017) Is an additive decomposition of a rate of deformation and objective stress rates passé. Comput Methods Appl Mech Eng 327:196–225
Jiao Y, Fish J (2018) On the equivalence between the multiplicative hyper-elasto-plasticity and the additive hypo-elasto-plasticity based on the modified kinetic logarithmic stress rate. Compt Methods Appl Mech Eng 340:824–863
Johnson GR, Cook WH (1983) A constitutive model and data for metals subjected to large strains, high rates and high temperature. In: Proc. 7th Int. Symp. Ballistics, pp 541–547
Kaneko K, Oyamada T (2000) A viscoplastic constitutive model with effect of aging. Int J Plasticity 16:337–357
Khojastehpour M, Hashiguchi K (2004) The plane strain bifurcation analysis of soils by the tangential-subloading surface model. Int J Solids Struct 41:5541–5563
Khojastehpour M, Hashiguchi K (2004) Axisymmetric bifurcation analysis in soils by the tangential-subloading surface model. J Mech Phys Solids 52:2235–2262
Kou H, Li W, Ma J, Ma J, Shao J, Tao Y, Zhang X, Geng P, Deng Y, Li Y, Zhang X, Peng F (2018) Theoretical prediction of the temperature-dependent yield strength of solid solution strengthening Nickel-based alloys. Int J Mech Sci 140:83–92
Krempl E, McMahon JJ, Yao D (1986) Viscoplasticity based on overstress with a differential growth law for the equilibrium stress. Mech Mater 5:35–48
Krieg RD (1975) A practical two surface plasticity theory. J Appl Mech 42:641–646
Lemaitre JA (1990) Micro-mechanics of crack initiation. Int J Frac 42:87–99
Lemaitre JA (1996) A course on damage mechanics, 2nd edn. Springer, Heidelberg
Lemaitre J, Chaboche JL (1990) Mechanics of solid materials. Cambridge Univ. Press, Cambridge
Lemaitre JA, Doghri I (1994) Damage 90: a post-processor for crack initiation. Compt Methods Appl Mech Eng 115:197–232
Lemaitre J, Sermage JP, Desmorat R (1999) A two scale damage concept applied to fatigue. Int J Fract 97:67–81
Lemaitre JA, Desmorat R (2005) Engineering damage mechanics. Springer, Heidelberg
Li W, Ma J, Kou H, Shao J, Zhang X, Deng Y (2019) Modeling the effect of temperature on the yield strength of precipitation strengthening Ni-base superalloys. Int J Plasticity 116:143–158
Liu D, Yang H, Elkhodary KL, Tang S, Liu WK, Guo X (2022) Mechanistically informed data-driven modeling of cyclic plasticity via artificial neural networks. Comput Methods Appl Mech Eng 393:114766
Lubarda VA (2002) Elastoplasticity theory. CRC Press, Boca Ranton
Lubliner J (1990) Plasticity theory. Macmillan, New York
Maranha JR, Pereira C, Viera A (2016) A viscoplastic subloading soil model for rate-dependent cyclic anisotropic structured behaviour. Int J Numer Anal Methods Geomech 40:1531–1555
Mayama T, Sakai K, Ishikawa H (2007) A constitutive model of cyclic viscoplasticity considering changes in subsequent viscoplastic deformation due to the evolution of dislocation structures. Int J Plasticity 23:913–930
Mróz Z (1967) On the description of anisotropic workhardening. J Mech Phys Solids 15:163–175
Norton FH (1929) Creep of steel at high temperature. McGraw-Hill, New York
Odqvist FKG (1966) Methematical theory of creep and creep rupture. Oxford University Press, London
Ohno N (1982) A constitutive model of cyclic plasticity with a non-hardening strain region. J Appl Mech 49:721–727
Ohno N, Kachi Y (1986) A constitutive model of cyclic plasticity for nonlinearly hardening materials. J Appl Mech 53:395–403
Ohno N, Nakamoto H, Morimatsu Y, Okumura D (2021) Modeling of cyclic hardening and evaluation of plastic strain range in the presence of pre-loading and ratcheting. Int J Plasticity 145:103074
Ohno N, Wang JD (1993) Kinematic hardening rules with critical state of dynamic recovery, Part I: formulation and basic features for ratcheting behavior. Part II: application to experiments of ratcheting behavior. Int J Plasticity 9:375–403
Ohno N, Yamamoto R, Okumura D (2017) Thermo-mechanical cyclic hardening behavior of 304 stainless steel at large temperature ranges: Experiments and simulations. Int J Mech Sci 146–147:517–526
Oldroyd JG (1950) On the formulation of rheological equations of state. Proc Roy Soc Lond A200:523–541
Ottosen NS, Ristinmaa M (2005) The mechanics of constitutive modelling. Elsevier, Amsterdam
Ozaki S, Hashiguchi K (2010) Numerical analysis of stick-slip instability by a rate-dependent elastoplastic formulation for friction. Tribol Int 43:2120–2133
Ozaki S, Hikida K, Hashiguchi K (2012) Elastoplastic formulation for friction with orthotropic anisotropy and rotational hardening. Int J Solids Struct 49:648–657
Ozaki T, Yamakawa Y, Ueno M, Hashiguchi K (2022) Description of sand–metal friction behavior by subloading-friction model. Friction. https://doi.org/10.1007/s40544-021-0580-7
Pandya KS, Roth CC, Mohr D (2020) Strain rate and temperature dependent fracture of aluminum alloy 7075: experiments and neural network modeling. Int J Plasticity 135:102788
Pedroso DM (2014) The subloading isotropic plasticity as a variable modulus model. Compt Geotech 61:230–240
Peirce D, Asaro JR, Needleman A (1982) Overview 21: an analysis of nonuniform and localized deformation in ductile single crystals. Act Metall 30:1087–1119
Peirce D, Asaro JR, Needleman A (1983) Overview 32: material rate dependence and localized deformation in crystal solids. Act Metall 31:1951–1976
Perić D (1993) On a class of constitutive equations in viscoplasticity: formulation and computational issues. Int J Numer Methods Eng 36:1365–1393
Perzyna P (1963) The constitutive equations for rate sensitive plastic materials. Q Appl Math 20:321–332
Perzyna P (1966) Fundamental problems in viscoplasticity. Adv Appl Mech 9:243–377
Prager W (1961) Linearization in visco-plasticity. Ing Archiv 15:152–157
Ren F, Zhang F, Wang G, Zhao Q, Xu C (2018) Dynamic assessment of saturated reinforced-soil retaining wall. Comput Geotech 95:211–230
Rice JR (1970) On the structure of stress-strain relations for time dependent plastic deformation in metals. J Appl Mech 37:728–737
Rice JR (1971) Inelastic constitutive relations for solids: an internal variable theory and its application to metal plasticity. J Mech Phys Solids 19:433–455
Robotnov YN (1969) Creep problem in structural members. North-Holland, Amsterdam
Saleeb AF, Arnold SM (2004) Specific hardening function definition and characterization of a multimechanism generalized potential-based viscoelastoplasticity model. Int J Plasticity 20:2111–2142
Saleeb AF, Arnold SM, Castelli MG, Wilt TE, Graf W (2001) A general hereditary meltimechansm-based deformation model with application to the viscoplastic response of titanium alloys. Int J Plasticity 17:1305–1350
Simo JC (1998) Numerical analysis and simulation of plasticity. In: Ciarlet PG, Lions JL (eds) Handbook of numerical analysis, part 3 (numerical methods for solids), vol 6. Elsevier, Amsterdam
Simo JC, Hughes TJR (1998) Computational inelasticity. Springer, New York
Steinberg DJ, Cochran SG, Guinan MW (1980) A constitutive model for metals applicable at high-strain rate. J Appl Phys 51:1498–1504
Truesdell C (1955) Hypo-elasticity. J Rational Mech Anal 4:83–133
Truesdell C, Noll W (1965) The nonlinear field theories of mechanics. In: Flugge S (ed) Encyclopedia of physics, vol III/3. Springer, Berlin
Tsutsumi S, Hashiguchi K (2005) General non-proportional loading behavior of soils. Int J Plasticity 21:1941–1969
Vladimirov IN, Pietryga MP, Reese S (2008) On the modeling of nonlinear kinematic hardening at finite strains with application to springback-comparison of time integration algorithm. Int J Numer Methods Eng 75:1–28
Vladimirov IN, Pietryga MP, Reese S (2010) Anisotroipc finite elastoplasticity with nonlinear kinematic and isotropic hardening and application to shear metal forming. Int J Plasticity 26:659–687
Wallin M, Ristinmaa M (2005) Deformation gradient based kinematic hardening model. Int J Plasticity 21:2025–2050
Wallin M, Ristinmaa M, Ottesen NS (2003) Kinematic hardening in large strain plasticity. Eur J Mech A 22:341–356
Xiong Y-L, Yang Q-L, Zhang S, Ye G-L, Zheng RY, Zhang F (2018) Thermo-elastoplastic model for soft rock considering effects of structure and overconsolidation. Rock Mech Rock Eng 51:3771–3784
Xiong Y, Ye G, Zhu H, Zhang S, Zhang F (2016) Thermo-elastoplastic constitutive model for unsaturated soils. Acta Geotech 11:1287–1302
Yadav SK, Ye G, Khalid U, Fukuda M (2019) Numerical and centrifugal physical modelling on soft clay improved with floating and fixed sand compaction piles. Comput Geotech 115:103160
Yamakawa Y, Hashiguchi K, Ikeda K (2010) Implicit stress-update algorithm for isotropic Cam-clay model based on the subloading surface concept at finite strains. Int J Plasticity 26:634–658
Yamakawa Y, Hashiguchi K, Sasaki T, Higuchi M, Sato K, Kawai T, Machishima T, Iguchi T (2021) Anisotropic subloading surface Cam-clay plasticity model with rotational hardening: deformation gradient-based formulation for finite strain. Int J Numer Anal Methods Geomech 45:2321–2370
Yang H, Li H, Ma J, Wei D, Chen J, Fu MW (2020) Temperature dependent evolution of anisotropy and asymmetry of α-Ti in thermomechanical working: Characterization and modeling. Int J Plasticity 127:102650
Ye B, Ye G, Zhang F (2012) Numerical modeling of changes in anisotropy during liquefaction using a generalized constitutive model. Comput Geotech 42:62–72
Yoshida F, Uemori T (2002) A model of large-strain cyclic plasticity describing the Bauschinger effect and workhardening stagnation. Int J Plasticity 18:661–686
Yoshida F, Uemori T (2003) A model of large-strain cyclic plasticity and its application to springback simulation. Int J Mech Sci 45:1687–1702
Yuanming L, Liao M, Hu K (2016) A constitutive model of frozen saline sandy soil based on energy dissipation theory. Int J Plasticity 78:84–113
Yuanming L, Long J, Xiaoxiao C (2009) Yield criterion and elasto-plastic damage constitutive model for frozen sandy soil. Int J Plasticity 25:1177–1205
Zerilli FJ, Armstrong RW (1987) Dislocation-mechanics-based constitutive relations for material dynamics calculations. J Appl Phys 61:1816–1825
Zhang S, Leng W, Zhang F, Xiong Y (2012) A simple thermo-elastoplastic model for geomaterials. Int J Plasticity 34:93–113
Zhu H, Ye B, Cai Y, Zhang F (2013) An elasto-viscoplastic model for soft rock around tunnels considering overconsolidation and structure effects. Comp Geotech 50:6–16
Funding
No funding was received to assist with the preparation of this manuscript.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hashiguchi, K., Ueno, M. & Anjiki, T. Subloading-Overstress Model: Unified Constitutive Equation for Elasto-Plastic and Elasto-Viscoplastic Deformations Under Monotonic and Cyclic Loadings. Arch Computat Methods Eng 30, 2627–2649 (2023). https://doi.org/10.1007/s11831-022-09880-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11831-022-09880-y