Abstract
This paper presents a unified framework for continuum-molecular modeling of anisotropic elasticity, fracture and diffusion-based problems within a generalized two-dimensional peridynamic theory. A variational procedure is proposed to derive the governing equations of the model, that postulates oriented material points interacting through pair potentials from which pairwise generalized actions are computed as energy conjugates to properly defined pairwise measures of primary field variables. While mass is considered as continuous function of volume, we define constitutive laws for long-range interactions such that the overall anisotropic behavior of the material is the result of the assigned elastic, conductive and failure micro-interaction properties. The non-central force assumption in elasticity, together with the definition of specific orientation-dependent micromoduli functions respecting material symmetries, allow to obtain a fully anisotropic non-local continuum using a purely pairwise description of deformation and constitutive properties. A general and consistent micro-macro moduli correspondence principle is also established, based on the formal analogy with the classic elastic and conductivity tensors. The main concepts presented in this work can be used for further developments of anisotropic continuum-molecular formulations to include other mechanical behaviors and coupled phenomena involving different physics.
Similar content being viewed by others
1 Introduction
Continuum-molecular models in solid mechanics assume generalized distance forces as ultimate actions, and describe macroscopic behavior of bodies from a microscopic level, making use at the same time of some concepts and tools proper of mathematical field theories. The origin of this perspective lies in the classical molecular models of Nineteenth century [1, 2], developed by Cauchy, Poisson and Navier [3,4,5,6] with the aim of providing an explanation per causas of elasticity [7]. They derived the equilibrium equations of elastic bodies considered as composed of molecules [8] interacting with elastic forces linearly variable with their mutual displacements. Indeed, these molecules were regarded as simple centres of forces endowed with the property of mass, their displacement being defined by a vector field in the continuum of euclidean geometry associated with the elastic body [4, 8]. Within this mechanistic view, macroscopic constitutive relations derive from intermolecular properties, and the notion of stress is introduced basing it upon an hypothesis concerning intermolecular forces [8]. Two main features characterize such models: the assumption of central forces between pair of molecules, and the existence of a region of molecular activity beyond which these pairwise actions are not supposed to extend. As an inevitable consequence of the assumed structure theory [8], stress-strain relations have to respect internal constrains affecting the number of independent elastic constant, namely the Cauchy relations [8, 9]. Therefore, equations of motion of anisotropic bodies contain 15 independent moduli, which reduce to a single elastic constant in case of isotropic symmetry [3, 4, 8, 9]. In the development of the theory, it also became evident to its founders that Cauchy relations do not depend upon considering matter as continuous or discontinuous.
Poisson proposed later molecules as polar objects, capable of rotation and displacement [8]. This suggestion was worked out in detail later by Voigt [10, 11] who pointed out that the drawback of the classical molecular models lies in the too restrictive hypothesis of central actions depending only on the actual distance between molecules [3, 8]. According to Voigt’s model for elasticity, molecules interact in pairs via a system of actions reducible to a force and a couple [3]. He obtained that the equations of a linearized elasticity theory based on molecular assumptions, do not necessarily verify Cauchy relations, the elastic constants being 21 in the most general case. Influenced by Green’s energetic approach [8, 12], Voigt showed also that in non-dissipative processes pairwise actions can be derived from a quadratic potential which depends, in general, on the actual position and orientation of pairs of molecules. Another different model for elasticity based on corpuscular assumptions was developed by Poincaré who postulated the existence of a force function (related to a multi-body potential) depending not only on the actual position of a pair of molecules but also on the relative position of other molecules [13]. Born developed later a molecular-type model accounting for thermal and other properties of solid bodies as well as elastic properties [8]. It should be underlined that in this context the term “molecular” is strictly related to the assumption about the ultimate nature of the internal actions [14], which in this case occur at a distance. The models for elasticity here mentioned, each one with its own peculiarities, provide a description of phenomena from a perspective of a given underlying structure, making use at the same time of the powerful tools of Calculus.
After a long time, a fundamental contribution to the development of mechanical models of this kind was given by Silling [15], who proposed at the beginning of the twenty-first century a theory of solid mechanics, namely Peridynamics, based on actions at a distance with the aim of modeling discontinuities and non-linear material response adopting a set of integro-differential equations without partial derivatives in space [15]. Such theory postulates material points in a continuum interacting in pairs within a cut-off distance, the horizon, which represents in certain sense a generalization of the concept of radius of the sphere of molecular activity characterizing molecular models of the XIX century. Indeed, since the horizon is, in general, a finite measure, the model results to be non-local, while constitutive laws for long-range interactions are defined such that the macroscopic physical behavior of the material is the result of the assigned micro-interactions properties. Even if a non-linearized kinematics is assumed, pairwise forces can be derived from elastic central pair potentials depending on the actual distance between pairs of material points. Hence, as for classical molecular models based on central-forces, Cauchy relations do hold [15, 16]. In any case, the distinctive key point of Silling’s continuum-molecuar model lies in its non-local character, and in the fact that spatial derivatives do not appear in the peridynamic governing equations, with the consequence that they remain equally valid at points or surfaces of discontinuity [15]. This aspect lends itself to the description of modern problems in mechanics involving spontaneous formation of cracks [17,18,19,20,21,22,23,24,25]. It should be noted that some peridynamic fundamental concepts can also be found in other previous works on quasi-continuum models and non-local elasticity [26,27,28]. However, Silling’s work introduced a general mathematical theory including elasticity, fracture, damage as well as other mechanical behaviors.
In order to overcome constitutive restrictions such as those imposed by Cauchy relations, the original peridynamic formulation (referred to as bond-based) was extended by introducing the assumption that the interaction forces between two material points depend on the displacement of all the material points within their neighborhood (e.g. the horizon regions of the two material points) [29, 30]. These enriched models, named state-based and non-ordinary state-based, still consider the concept of distance action, requiring however the definition of point-wise defined deformation measures, namely the deformation states [29, 31,32,33]. This aspect represents an important breaking point with the original theory, since the simplicity given by the paradigm of purely pairwise formalism is lost [15]. Indeed, as in Poincaré theory for elasticity, due to the new assumption concerning the nature of the interactions, energy conserving state-based models are associated with multi-body potentials [34]. Other peridynamic models which require, directly or not, the definition of multi-body potentials are detailed in [35, 36].
A different perspective was given instead by Gerstle [37], who proposed to maintain an analytical formulation based on pair potentials, while assuming an enriched kinematics to describe isotropic elasticity by two independent material micromoduli. Actually, as already pointed out by Voigt, material points rotation (as additional kinematic descriptor) and the non-central forces assumption in a mechanism-based molecular model for elasticity, lead to resulting governing equations which do not necessarily verify Cauchy relations [4, 8]. However, the kinematic of pair interactions assumed by Gerstle et al. stems from that of an ideal Euler-Bernoulli beam model. As a consequence, the pair potential function consists of terms involving the definition of a bending micromodulus that, in general, cannot be neglected. This introduces a constitutive internal length into the model which is proper of materials homogenized as polar continua, leading to size dependent results in elasticity under general inhomogeneous deformation [38]. Diana and Casolo then proposeda polar peridynamic continuum-molecular model based on a generalized kinematic employing the definition of a non-central pair potential consisting of three independent terms, quadratic functions of equal number of pairwise deformation measures [39]. The implication is twofold. On one hand an explicit definition of a pairwise shear deformation and shear micromodulus can be obtained, and on the other, the micromodulus associated with the mutual rotation of oriented material points’ (e.g. the bending micromodulus), is independent of the other constitutive parameters and can be neglected if necessary (consistently with standard elasticity) [40]. Other polar formulations for classical elasticity have been proposed afterwards [41,42,43]. Most of them, however, still consider a kinematic of interacting material points inspired by beam models with non-vanishing bending micromoduli, these being function of the other micromoduli and/or abstract geometrical parameters.
The universal nature of integral equations used in peridynamics allows the theory to be extended also to other physical fields. This is motivated, for instance, by the need of describing transport phenomena in bodies with (possibly evolving) discontinuities, non-local diffusion in microstructured materials etc [44,45,46]. Such extensions can be obtained by adapting the integrand function expressing the ultimate action density function to the specific features of the physical phenomenon under consideration. Gerstle et al. [47] proposed a continuum-molecular (peridynamic) model for one-dimensional diffusion-type problems along with a framework which allows four coupled physical processes to be modeled simultaneously: mechanical deformation, heat transfer, electric potential distribution, and vacancy diffusion. Bobaru and Duangpanya proposed a one dimensional peridynamic heat transfer integro-differential equation using a different form of the kernel, and derived an analytical formulation for transient heat conduction by defining the peridynamic heat-flux while following a bond-based approach [44, 45, 48]. A model for transient advection-diffusion problems was instead presented by Zhao et al. [49]. Prakash and Seidel [50, 51] proposed a coupled formulation for the study of the electrical and piezoresistive response of nanocomposite materials. A peridynamic diffusion model for damage from pitting corrosion was proposed by Chen and Bobaru [52], whereas Diana and Carvelli derived a polar electro-mechanical analytical formulation accounting for damage evolution in solids [53]. Other models of this kind can be found in [54,55,56]. All the here mentioned formulations for diffusion-type problems and coupled phenomena fall in the category of bond-based models, which means in this case that the generic pairwise action between two material points depends on the actual value of their primary field variables (e.g. temperature, electric potential, concentration etc.). As stated before, models of this kind can be associated to quadratic pair potentials. As for state-based models instead, analytical formulations applied to diffusion were presented, among others, by Oterkus et al. [57, 58] and by Katiyar et al. [59].
Most of the research carried out on continuum-molecular formulations is devoted to isotropic materials, whose stiffness, conductivity and strength properties are not direction-dependent, while relatively few studies on anisotropic materials can be found in literature. In the context of elasticity and fracture, mathematical formulations of peridynamic anisotropic continua, in which Cauchy relations do not apply, were proposed later by disregarding the paradigm of purely pairwise interactions [60, 61], the available continuum bond-based models being characterized by the aforementioned restriction in the number of independent material constants [18, 62,63,64,65,66,67,68]. In particular, Ghajari et al. [63] proposed a peridynamic formulation based on continuous trigonometric functions for elasticity and fracture in orthotropic materials using an analytical approach similar to that detailed in [69]. Due to the central force assumption and the directional dependency laws adopted, two of the four elastic moduli which define orthotropic in-plane elasticity have to be preset, whereas square-symmetric materials [70] cannot be modeled. A mechanical continuum-molecular formulation based on pair potentials without restrictions in the number of material constants was proposed later by Diana et al. [40, 71, 72].
Regarding anisotropic diffusion-type models instead, theoretical studies were carried out by Seleson [46] and Mikata [73]. The latter analyzed the problem of anisotropic heat transfer focusing on the micro-conductivity function definition without making particular assumptions about the nature of the interactions. Recently, Diana and Carvelli have derived an analytical peridynamic formulation for anisotropic materials accounting for their anisotropic overall conductivity and fracture properties, together with a general procedure for the identification of the model parameters [72]. For the best of the author’s knowledge, other anisotropic models based on pair potentials with similar features have not been proposed so far.
In a computational context, pair potential based continuum-molecular models lead to mathematical formulations resulting in an easier implementation and higher computational efficiency compared to models based on multi-body potentials as state-based models [74]. Actually, their use is preferred, when possible, as the large number of literature works on bond-based type models demonstrates. Moreover a purely pairwise formalism provides an intuitive mechanism-based description of macroscopic physical properties of materials, while being at the same time closely related to the mechanics of full-discrete models. This aspect may lead to the possibility to design real lattice-like systems whose physical and mechanical effective properties may be tailoring designed by controlling those assigned to the microstructure (i.e. the pairwise interactions) [75].
This paper provides a unified theoretical and computational scheme for pair potentials based continuum-molecular modelling of anisotropic elasticity, fracture and diffusion-type problems within the framework of a revised bond-based peridynamic theory with oriented material points. As important contribution of this work, governing equations of both mechanical and diffusion-type models are derived using a unified approach based on a variational formalism. An implicit meshfree implementation strategy is also detailed together with an analytical expression of the equivalent stiffness operators. Particular attention has been given to establish a consistent micro-macro moduli correspondence between material parameters of anisotropic peridynamics and classical continuum physics. The proposed method is validated against analytical solutions and experimental data, when available. By summarizing the work that we have been doing on this topic [40, 71, 72, 76], the manucript introduces a general approach to anisotropic problems that can be used for further developments of continuum-molecular formulations to include other mechanical behaviors and coupled phenomena involving different physics. The proposed model couples the intuitive simplicity of the concept of mutual interaction in molecular models based on pair potentials (removing Cauchy relations restrictions), with the (modern) mathematical formalism of a peridynamic continuum formulation for anisotropic materials.
The paper is organized as follows: In Sect. 2 the anisotropic model for elasticity is described. The energy-based fracture model accounting for directional-dependent toughness in solids is discussed in Sect. 3, where several numerical experiments are also proposed. Finally, in Sect. 4, the analytical model for anisotropic diffusion-based problems is derived, with a focus on heat-transfer and steady-state electrical conduction.
2 Elasticity
A two-dimensional continuum body \(\Omega\), composed of oriented material points \(\mathbf {x}\), is considered.
Material points \(\mathbf {x}\) and \(\mathbf {x}'\) within a finite distance (e.g. the horizon \(\delta\) [15]), are assumed to interact with each other through non-central pairwise actions depending on pairwise constitutive parameters and pairwise deformation variables (Fig. 1). The set of all material points \(\mathbf {x}' \in \Omega\) such that \(\Vert \mathbf {x}'-\mathbf {x}\Vert \le \delta\) is denoted by \(H_{\mathbf {x}}\), which is the horizon region of \(\mathbf {x}\). The generic vector \(\varvec{\xi }=\mathbf {x}^{\prime }-\mathbf {x}\) is called bond [15] or virtual fiber. A theoretical (peridynamic) model of this kind is here referred to as (polar) continuum-molecular (CM) model.
Given the reference orthonormal basis \(\left\{ \mathbf {e}_{1}, \mathbf {e}_{2}\right\}\), the body configuration at time t is described by the displacement field \(\mathbf {u}(\mathbf {x}, t)=u_{i} \mathbf {e}_{i}\) and rotation field \({\theta }(\mathbf {x},t)\) defined over \(\Omega\). The applied body forces and couples are denoted by \(\varvec{b}(\mathbf {x},t)\) and \(c(\mathbf {x},t)\), respectively. The functions \(\rho (\mathbf {x})=\rho\) and \(\varrho (\mathbf {x})=\varrho\) denote instead the densities of mass and mass moment of inertia, and are assumed constant. Three linearized pairwise deformation measures, functions of the relative position \(\varvec{\xi }=\mathbf {x}^{\prime }-\mathbf {x}\), relative displacement \(\varvec{\eta }=\mathbf {u}( \mathbf {x'},t)-\mathbf {u}( \mathbf {x},t)=\mathbf {u}'-\mathbf {u}\) and rotations \(\theta ( \mathbf {x},t)=\theta\) and \(\theta ( \mathbf {x'},t)=\theta '\) of the generic pair of interacting points, are defined. The deformation in the direction of the material points’ joining line \(\mathbf {n}=\varvec{\xi }/\Vert \varvec{\xi }\Vert\) is the pairwise stretch s,
where \(\eta _{\mathrm {n}}={u_{\mathrm {n}}'-u_{\mathrm {n}}}\) is the component of the relative displacement vector \(\varvec{\eta }\) along the unit vector \(\mathbf {n}\). The pairwise angular or shear deformation is defined as the angle difference
where, since \(\eta _{\mathrm {t}}={u_{\mathrm {t}}'-u_{\mathrm {t}}}\) is the component of \(\varvec{\eta }\) along the unit vector \(\mathbf {t}: \,\mathbf {t}\,\bot \, \mathbf {n}\) (Fig. 1), the shear deformation can be interpreted as the difference between the linearized rotation angle of the virtual fiber \(\eta _{\mathrm {t}}/\Vert \varvec{\xi }\Vert\) and the average rotation \(\bar{\theta }\) of the interacting oriented material points \(\mathbf {x}\) and \(\mathbf {x}^{\prime }\). The third pairwise deformation variable depends instead on the relative rotation of two oriented material points according to the dimensional ratio
which can be interpreted as the average curvature of the virtual fiberFootnote 1.
Detail of the interaction between the oriented material point \(\mathbf {x}\) and the generic oriented material point \({\mathbf {x}}' \in H_{\mathbf {x}}\)
Assuming that the material is conservative, we define the elastic pairwise potential or micropotential function
such that the scalar-valued mutual actions between pairs of oriented material points can be obtained as
where \(w(\mathbf {x},\mathbf {x}^{\prime },t)=\mathrm {w}(\mathbf {x},\mathbf {x}^{\prime },t)/\Vert \varvec{\xi }\Vert\) is the pairwise elastic potential energy function per unit distance \(\Vert \varvec{\xi }\Vert\). From Eqs. 5–7 we obtain
where \(k_{\mathrm {n}}=k_{\mathrm {n}}(\mathbf {x},\mathbf {x}^{\prime })=k_{\mathrm {n}}(\psi )\), \(k_{\mathrm {t}}=k_{\mathrm {t}}(\mathbf {x},\mathbf {x}^{\prime })=k_{\mathrm {t}}(\psi )\) and \(k_{\mathrm {b}}=k_{\mathrm {b}}(\mathbf {x},\mathbf {x}^{\prime })=k_{\mathrm {b}}(\psi )\) are the micromoduli functions or pairwise constitutive parameters depending, in the general case of anisotropic materials, on the spatial orientation \(\psi ={\text {Arg}}\left( \varvec{\xi } \cdot \mathbf {e}_{1}+\imath \varvec{\xi } \cdot \mathbf {e}_{2}\right)\) of the virtual fiber. In the above, \(\Lambda =\Lambda (\Vert \varvec{\xi }\Vert )\) is instead the influence or attenuation function, that weights the nonlocal interactions within the spatial domain \({H_{\mathbf {x}}}\) with respect to \(\Vert \varvec{\xi }\Vert\) [77, 78].
At this point, it should be remarked that focusing on standard (Cauchy) solids rather than on heterogeneous materials homogenized as polar continua [79, 80], the definition of an elastic pair potential term related to mutual rotations, namely \(\mathrm {w}_{\chi }(\mathbf {x},\mathbf {x}^{\prime },t)\), is not strictly required [39].
The general form of the nonlocal elastic energy density at \(\mathbf {x}\), namely the macroelastic energy density [18], is obtained by integrating the pairwise potential \(\mathrm {w}(\mathbf {x},\mathbf {x}^{\prime },t)\) over the horizon region \(H_{\mathbf {x}}\) of radius \(\delta\)
whereas the total macroelastic energy (e.g. the elastic potential energy of the body) is given by
The Hamiltonian action integral is defined as
where the density of kinetic energy is
while the potential energy related to prescribed body forces and couples, in the first instance assumed conservative, is
By substituting Eqs. 11, 14 and 15 in Eq. 13, considering Eqs. 1–3, and imposing the stationarity of the functional \(\mathcal {H}\), we obtain
where \(\updelta\) denotes the mathematical symbol for variation [76]. Equation 16 allows deriving the field equations at \(\mathbf {x} \in \Omega, \text{whose general form reads}\)
where \({\mathbf {f}}({\mathbf {u}}',{\mathbf {u}},{\theta }',{\theta },{\mathbf {x}}',{\mathbf {x}})={\mathbf {f}}(\varvec{\eta },{\theta }',{\theta },{\mathbf {x}}',{\mathbf {x}})\) is the force density vector function given by
and \(\mathsf {m}({\mathbf {u}}',{\mathbf {u}},{\theta }',{\theta },{\mathbf {x}}',{\mathbf {x}})=\mathsf {m}(\varvec{\eta },{\theta }',{\theta },{\mathbf {x}}',{\mathbf {x}})\) is the moment density function given by
As stated previously, when considering the continuum-molecular model for equivalent Cauchy-elastic materials [81], the micro-constitutive parameter associated to the deformation measure defined in Eq. 3 is not required, and is here set equal to zero (e.g. \(k_{\mathrm {b}}=0\)). In this case, using Eqs. 8–9, the force and moment density functions can be expressed as
As a consequence, both linear and angular momentuum conservation laws in Eq. 18 can be written exclusively in terms of micro-forces, with constitutive prescriptions being then needed for \(f_{\mathrm {n}}\) and \(f_{\mathrm {t}}\) only. Eq. 21 denotes the active part of the internal action, whereas micro-moments reduce to mere constraint reactions \(\mathsf {m}_{\mathrm {t}}\) that can be determined via pairwise balance conditions. Pairwise (mutual) or active couples \(\mathsf {m}_{\mathrm {b}}\) are not present if \(k_{\mathrm {b}}=0\) is assumed. A similar feature can be found in Voigt’s molecular model [3, 11], however here it is not a consequence of a kinematic constrain imposed to rotations within \({H_{\mathbf {x}}}\), but it comes from the direct constitutive assumption \(k_{\mathrm {b}}=0\).
2.1 Discretized Equations: Elastodynamics
A meshfree discretization approach [18] is considered which requires the material domain \(\Omega\) be divided into a set of N sub-domains \(\Delta \upsilon _{p}\), each of which associated to a particle p of coordinates \(\mathrm {x_{1}}^{p}, \mathrm {x_{2}}^{p}\). Hence, a proximity search algorithm identifies particles q belonging to the p-centered horizon region \(H_{p}\) according to the one-point quadrature scheme proposed by Hu et al. [82, 83] which accounts for partial neighbor intersectionsFootnote 2. The displacements \(\mathbf {u}_{p}=u_{1}^{p} \mathbf {e}_{1}+u_{2}^{p} \mathbf {e}_{2}, \mathbf {u}_{q}=u_{1}^{q} \mathbf {e}_{1}+u_{2}^{q} \mathbf {e}_{2}\) and rotations \(\theta ^{p}, \theta ^{q}\) of the material particles p and q can be collected column-wise in vector form as
such that, for each pair of interacting particles p and \(q \in H_{p}\), we can collect column-wise \(\mathbf {v}_{p}\) and \(\mathbf {v}_{q}\) as
where \(\mathbf {R}_{p q}\) is a properly defined transformation matrix [38], and the displacements and rotations collected column-wise in vector form as
are aligned with the local reference basis \(\left\{ \hat{\mathbf {e}}_{1}, \hat{\mathbf {e}}_{2}\right\}\), where the unit vectors \(\hat{\mathbf {e}}_{1} \equiv \mathbf {n}\) and \(\hat{\mathbf {e}}_{2} \equiv \mathbf {t}\). The pairwise compatibility equation relating the pairwise deformation variables collected in the vector \({\mathbf {h}}_{pq}=\left\{ s_{pq}\;\gamma _{pq}\;\chi _{pq}\right\} ^\top\), to the interacting particles generalized displacements can be written in a compact matrix form as
where
\(\Vert \varvec{\xi }\Vert _{pq}\) being the distance between the generic particles p and q. The pairwise constitutive equation is instead
where
defines the specific elastic property of each interaction. It relates the scalar-valued mutual actions defined in Eqs. 8–10 and collected in the vector \(\mathbf{r} _{pq}\), to the pairwise deformations measures defined by Eqs. 1–3. The non-dimensional factor \(\Lambda _{pq}=\Lambda _{pq}(\Vert \varvec{\xi }\Vert _{pq} )\) controls the radial dependence of the non-local interaction between two particles, as specified in Sect. 2.
As for the balance of linear and angular momentuum of the continuum, the discrete algebraic system of governing equations in elastodynamics, and the analytical expression of the stiffness operator, can be derived from Hamilton’s variational principle referred to a closed discretized domain. The variation of the first term of Eq. 13, i.e. \(\updelta [\int _{t_{1}}^{t_{2}}\int _\Omega {\mathcal {D}}(\mathbf {x},t)\; \,\mathrm {d}\mathbf {x}\,\mathrm {d}t]\) can be written in discrete form as
where integration-by-parts is used between the first and the second steps, and
The variation of the second term of Eq. 13, i.e. \(\updelta [\int _{t_{1}}^{t_{2}}\int _\Omega \mathcal {V}(\mathbf {x},t)\; \,\mathrm {d}\mathbf {x}\,\mathrm {d}t]\), can be treated in discrete form as
where \({\mathbf {b}}_{p}=\{b_{1}^{p} \quad b_{2}^{p} \quad c^{p}\}^{T}\) is the vector of body forces and body couples applied at particle p in the global reference system of unit vectors \(\mathbf {e}_{1}, \mathbf {e}_{2}\). Finally, considering Eq. 4, the last term of Eq. 13, i.e. \(\updelta [\int _{t_{1}}^{t_{2}}\int _\Omega {\mathcal {W}}(\mathbf {x},t)\,\mathrm {d}\mathbf {x}\,\mathrm {d}t]\), can be written instead for a discretized body as
where H denotes the number of particles q within the p-centered horizon \(\delta\), while \(\alpha _{p q}\) is the partial factor for the sub-domains \(\Delta \upsilon _{q}\), related to the specific quadrature rule adopted [83]. Considering Eq. 13 together with Eqs. 30, 32 and 33, the stationary condition \(\updelta \mathcal {H}=0\) gives
where \(\mathbf {L}_{p q}=\big [ \mathbf {I}_{3} \quad \mathbf {0}_{3} \big ]^{\top }\) is a specific topology incidence matrix for non-pairwise defined matrices and vectors [76]. The assembly operator 
replaces the double sum symbol, and is introduced so that each algebraic object is added to the appropriate location in properly defined global matrices and vectors [85]. In this way, Eq. 34 can be then rewritten in compact form as
where the global mass matrix is given by
whereas the stiffness operator in global coordinate system corresponding to the whole body is defined as
and the global generalized body forces vector is
Moreover, the vector of global generalized displacements is given by
2.2 Anisotropic Elastic Pair Potentials and Material Micromoduli
Given the reference orthogonal basis \(\left\{ \mathbf {e}_{1}, \mathbf {e}_{2}\right\}\) defined in Sect. 2, the classical constitutive stress-strain relation \(\sigma _{i j}=C_{i j hk} \varepsilon _{hk}\) of a two-dimensional homogeneous linearly elastic anisotropic Cauchy continuum can be written in Voigt notation as
which in component form is given by
\(C_{ijhk}\) being the components of the elasticity tensor. Considering now a generic orthogonal basis \(\left\{ \hat{\mathbf {e}}_{1}, \hat{\mathbf {e}}_{2}\right\}\), Eq. 40 can be rewritten as
where \({\hat{\varvec{\sigma }}}=\mathbf {Q}_{\sigma }{\varvec{\sigma }}\) and \({\hat{\varvec{\varepsilon }}}=\mathbf {Q}_{\varepsilon }{\varvec{\varepsilon }}\), where
and
respectively. The angle \(\psi\) is positive if the basis rotation is anticlockwise, and the tensor \(\hat{\mathbf {C}}\) in Eq. 42 is defined as
where \(\mathbf {Q}_{\varepsilon }^{-1}=\mathbf {Q}_{\sigma }^{\top }\).
According to Eq. 45, the off-axis axial \(\hat{C}_{1111}\) and shear \(\hat{C}_{1212}\) elastic moduli can be written as circular functions of the angle \(\psi\) by
where \(C_{1111}\), \(C_{1122}\), \(C_{2222}\), \(C_{1112}\), \(C_{2212}\) and \(C_{1212}\) are the six given elastic constants defining in-plane fully anisotropic Cauchy elasticity. The mechanistic nature of the continuum-molecular model requires the definition of pairwise constitutive laws for microstructure (i.e. the virtual fibers and then the pairwise interactions) such that the overall elastic behavior of the material is the result of the assigned micro-interactions properties [76]. Besides, to assign microscopic properties on the basis of macroscopic ones, the identification of a representative cell is of the essence [76, 86]. In non-local models of this kind, the representative cell is the horizon region \(H_{\mathbf {x}}\) over the integral in Eq. 11 is defined, while the micro-macro moduli correspondence principle is based on a micro-macro energy equivalence, which allows macroscopic properties to be directly associated to microscale-defined constitutive laws [72]. Since in-plane Cauchy anisotropic linear elasticity is defined by six independent elastic moduli, it follows that \(k_{\mathrm {n}}(\psi )\) and \(k_{\mathrm {t}}(\psi )\) must be functions of at least six independent microelastic constants.
In order to preserve material symmetries, and in analogy with the classical continuum, we can assumeFootnote 3 without loss of generality that the pairwise axial and shear stiffness \(k_{\mathrm {n}}(\psi )\) and \(k_{\mathrm {t}}(\psi )\), exhibit a directional dependency as \(\hat{C}_{1111}( \psi )\) and \(\hat{C}_{1212}( \psi )\) described by Eqs. 46 and 47, respectively
where \(\mathcal {K}_{1111}\) and \(\mathcal {K}_{2222}\) are the microelastic axial moduli of virtual fibers parallel to the unit vectors \(\mathbf {e}_{1}\) and \(\mathbf {e}_{2}\), respectively, whereas \(\mathcal {K}_{1212}\) is the microelastic shear modulus corresponding to the two directions defined by the aforementioned unit vectors. Differently, \(\mathcal {K}_{1122}\), \(\mathcal {K}_{1112}\) and \(\mathcal {K}_{2212}\) are the microelastic moduli related to the axial-axial and axial-shear couplings in anisotropic Cauchy elasticity. It is worth to note that the coupling between macro shear and axial deformation is here obtained without introducing additional terms in the elastic micropotential function expressed by Eq. 4, hence without modifying the formal structure of the pairwise constitutive law characterizing the generic virtual fiber. In the following subsection, we establish analytical relations between the microelastic moduli \(\mathcal {K}_{1111}\), \(\mathcal {K}_{2222}\), \(\mathcal {K}_{1122}\), \(\mathcal {K}_{1212}\), \(\mathcal {K}_{1112}\) and \(\mathcal {K}_{2212}\), and the six elastic constants of Cauchy anisotropic two-dimensional continua, adopting a general and consistent approach that does not require the definition of specific deformation fields.
2.2.1 Micro–Macro Moduli Correspondence
Let us consider a general time-independent two-dimensional homogeneous deformation field. The strain energy density of a linear elastic fully anisotropic Cauchy continuum at a generic position \(\mathbf {x}\) is then
with \(\varepsilon _{11}\), \(\varepsilon _{22}\) and \(\varepsilon _{12}\) macro strain components (see Eq. 41) in the reference basis \(\left\{ \mathbf {e}_{1}, \mathbf {e}_{2}\right\}\).
According to Eq. 11, the corresponding quantity in the continuum-molecular model is instead given by the general integral
where, under the assumed conditions, the pairwise deformations \(s( \psi )\) and \(\gamma ( \psi )\) of the generic virtual fiber can be expressed as linear functions of the homogeneous macro strain components \(\varepsilon _{ij}\) and quadratic functions of the direction cosines of the orthonormal unit vectors \(\mathbf {n}=\mathrm {n}_{i}\mathbf {e}_{i}\) and \(\mathbf {t}=\mathrm {t}_{i}\mathbf {e}_{i}\) (as previously defined), by
which are obtained through the Cauchy-Born rule [87, 88], particularized to our caseFootnote 4 , and according to \(\varvec{\hat{\varepsilon }}=\mathbf {Q}_{\varepsilon }\varvec{\varepsilon }\), where \(\mathbf {Q}_{\varepsilon }\) is given by Eq. 44 [72, 76]. Hence, one obtains
Substituting Eq. 54 in Eq. 51, and assuming \(k_{\mathrm {n}}(\psi )\) and \(k_{\mathrm {t}}(\psi )\) by Eqs. 48, 49, and 51 gives as general solution
where \(\mathcal {N}=\mathcal {N}(\delta )\) is a scalar-valued function of the horizon \(\delta\), depending on the specific influence function considered. In case of dimensionless attenuation functions, \(\mathcal {N}\) can be expressed as
with \(\Xi \in \mathbb {R}^{+}\). In what follows, we assume without loss of generality that \(\Lambda (\Vert \varvec{\xi }\Vert )=1\), thus
Comparing Eqs. 50 and 51, and collecting the terms that multiply the same strain components \(\varepsilon _{ij}\), six independent equations expressing the classical macromoduli in terms of micromoduli are obtained
where the constant \(\mathcal {C}\) is
By solving the algebraic system given by Eqs. 58–63 for the six micromoduli, we obtain
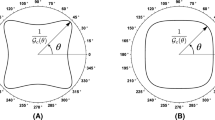
Polar plots of the micromoduli functions \(k_{\mathrm {n}}(\psi )\), \(k_{\mathrm {t}}(\psi )\) in Eqs. 48 and 49 for a representative anisotropic material are reported in Fig. 2.
Off-axis \(\hat{C}_{1111}( \psi )\), \(\hat{C}_{1212}( \psi )\) macromoduli and \(k_{\mathrm {n}}(\psi )\), \(k_{\mathrm {t}}(\psi )\) micromoduli corresponding to a Cauchy anisotopic material with \(C_{1111}=C_{2222}\), \(C_{1122}=C_{1111}/5\), \(C_{1212}=C_{1111}/3\), \(C_{1112}=C_{1111}/10\), and \(C_{2212}=C_{1111}/5\). Macromoduli and micromoduli are normalized with respect to the maximum values of \(\hat{C}_{1111}( \psi )\) and \(k_{\mathrm {n}}(\psi )\), respectively
In the case of general in-plane orthotropy with principal material exes defined by the unit vectors \(\check{\mathbf {e}}_{1}\equiv \mathbf {e}_{1}\), \(\check{\mathbf {e}}_{2}\equiv \mathbf {e}_{2}\), \(C_{1112}=C_{2212}=0\), thus \(\mathcal {K}_{1112}=\mathcal {K}_{2212}=0\). Moreover, two-dimensional materials of square symmetry or square-symmetric materials [70, 89], called also two-dimensional cubic materials or materials with two-dimensional cubic symmetry [90,91,92] (symmetry rotations \(\mathbf {R}_{3}^{\pi / 2}\)), have the further condition \(C_{1111}=C_{2222}\), hence \(\mathcal {K}_{1111}=\mathcal {K}_{2222}\). In the special case of elastic isotropy, \(C_{1111}=C_{2222}\), and \(C_{1122}=C_{1111}-2C_{1212}\). Therefore, Eqs. 65–70 provide two independent micromoduli depending on \(C_{1111}\) and \(C_{1212}\) macromoduli only, by
from which it follows that, in this case, Eqs. 65–70 lead to angle invariant pairwise axial and shear stiffness. Moreover, it can be noted that while \(k_{\mathrm {n}}\) in Eq. 71 is always positive definite (see Fig. 3), \(k_{\mathrm {t}}\) given by Eq. 72 is non-negative for \(C_{1212}\le C_{1111}/3\), thus, for Poisson’s ratios \(\nu \le 1/3\) and \(\nu \le 1/4\) in plane stress and plane strain, respectively. An important consideration is that this analytical evidence is independent of the attenuation function considered and is rather a well-known intrinsic trait of mechanistic models associated with elastic pair potentials,Footnote 5 and characterized by uniform and overall isotropic properties [14, 39, 94,95,96].
Normalized macro-moduli \(C_{1j1j}, j=1,2\) of Cauchy isotropic continuum, and corresponding micromoduli \(K_{1j1j}, j=1,2\) of the continuum-molecular model as function of the Poisson’s ratio \(\nu\) (in the studied range \(-1<\nu <1/2\)), for a given Young modulus E
Besides, this feature is proper of energy conserving full-discrete models such as periodic mass-spring lattices and architected materials featuring repetitive unit cells composed of rigid elements connected by elastic interfaces [14, 96,97,98,99], whose constitutive laws involve pairwise deformation measures, and postulate the existence of elastic mutual potentials allowing inter-molecular actions to be derived from centroidal kinematics. For further readings one may also refer to [100,101,102,103]. Equations 48 and 49 together with Eqs. 65–70 determine the axial and shear microelastic stiffness associated with each bond, thus with each orientation \(\psi\), in such a way to reproduce fully anisotropic Cauchy elasticity. Under general inhomogeneous deformations, the micropotential function \(\mathrm {w}(\mathbf {x},\mathbf {x'},t)=\mathrm {w}_{s}(\mathbf {x},\mathbf {x'},t)+\mathrm {w}_{\gamma }(\mathbf {x},\mathbf {x'},t)\) in Eq. 4, where
and
totally defines the linear elastic macroscopic behavior of an equivalent classical continuum [76], while providing a mechanism-based description of material anisotropy. In the special case of isotropic symmetry, Eqs. 71–72 hold, and Eqs. 73–74 reduce to
Moreover, it is self-apparent that in the limit case of \(C_{1111}=3C_{1212}\), the conceived elastic continuum-molecular model reduces to the well-known Silling’s non-local continuum with central actions [15].
It should be mentioned that arbitrary material rotations can be easily taken into account in the proposed model. Consider an anisotropic Cauchy solid, and \(\left\{ {\check{\mathbf {e}}_{1}}, {\check{\mathbf {e}}_{2}}\right\}\) be an orthonormal basis embedded in the material such that, initially, we have \({\check{\mathbf {e}}_{1}}\equiv {\mathbf {{e}}_{1}}\), \({\check{\mathbf {e}}_{2}}\equiv {\mathbf {{e}}_{2}}\). For arbitrary rotations of the material, Eqs. 48 and 49 modify substituting the bond angle \(\psi\) with the angle difference \(\psi -\zeta\), where \(\zeta ={\text {Arg}}\left( \check{\mathbf {e}}_{1} \cdot \mathbf {e}_{1}+\imath \check{\mathbf {e}}_{2} \cdot \mathbf {e}_{2}\right)\) is positive if denotes an anticlockwise rotations of \(\check{\mathbf {e}}_{i}\) with respect to \(\mathbf {{e}}_{i}\). Furthermore, in case of orthotropic elasticity with principal material axes in the direction of the unit vectors \(\check{\mathbf {e}}_{i}\) Eqs. 48 and 49 can be written in the equivalent reduced form
where the micromoduli given by Eqs. 65 and 66 and 69 and 70, are obtained considering macro-moduli defined in the material basis \(\left\{ {\check{\mathbf {e}}_{1}}, {\check{\mathbf {e}}_{2}}\right\}\). In any case, Eqs. 48–49 together with 65–70, can be adopted for modeling directly elastic orthotropy with macro-moduli given in the non-principal reference basis \(\left\{ {\mathbf {{e}}_{1}}, {\mathbf {{e}}_{2}}\right\}\).
Let us consider now the discretized model detailed in Sect. 2.1. The scalar-valued functions in Eqs. 48 and 49 have to be defined for given values of the angle \(\psi\) such that the directional dependent constitutive parameters are assigned in a finite number of bond directions. In case of a regular grid with spacing \(\Delta \mathrm {x}\) and given quadrature rule [83], the number of bond directions to be associated with \(k_{\mathrm {n}}(\psi )\) and \(k_{\mathrm {t}}(\psi )\), depends on the density parameter \(m=\delta /\Delta \mathrm {x}\) [104] expressing the ratio between the horizon and the grid spacing itself. Higher values of the density parameter correspond to finer angular discretizations of the the continuous circular functions in Eqs. 48 and 49. Hence, m should be chosen in such a way that the effective anisotropic elastic behavior of the material is correctly described by the discretized model [76]. Given a a homogeneous macro-deformation field defined by a deformation gradient \(\mathbf {F}\) of components \(\mathrm {F}_{ij}\) with \(i,j=1,2\) in the reference basis \(\left\{ \mathbf {e}_{1}, \mathbf {e}_{2}\right\}\), the macroelastic energy of the discretized continuum-molecular model should equal the classical continuum counterpart (i.e. its strain energy density) for any arbitrary rotation \(\zeta\) of the material [76]. As representative cases, we consider a uniaxial extension and a pure shear macro-deformation field. As Fig. 4 shows, to correctly represent the variation of the elastic energy density as function of the rigid rotation \(\zeta\) of the basis \(\left\{ \check{\mathbf {e}}_{1}, \check{\mathbf {e}}_{2}\right\}\) embedded in the material, \(m>3\) should be adopted in discretized continuum-molecular models for anisotropic elasticity. It is apparent that higher values of the density parameter lead to higher computational costs since larger is the number of non-zero elements in the elastic stiffness operator described by Eq. 37 [105]. In what follows, unless otherwise specified, \(m=5\) is used (see Fig. 4).
Normalized macroelastic energy-namely strain energy density-as function of the orientation \(\zeta\) of the material reference system and corresponding to a simple extension (first column) and pure shear (second column) homogeneous deformation fields in the case of a square-symmetric material (\(C_{1111}=C_{2222}; C_{1122}=C_{1111}/5; C_{1212}=C_{1111}/3\), first row) and a fully anisotropic material (\(C_{1111}=C_{2222}; C_{1122}=C_{1111}/5; C_{1212}=C_{1111}/3; C_{1112}=C_{1111}/10; C_{2212}=C_{1111}/5\), second row) for different values of the density paramenter m
At this point it should be noted that the analytical identification procedure (namely the micro-macro correspondence scheme) developed in this section is derived by implicitly assuming an unbounded domain, or referring to material points located in the bulk [15]. In fact, material points in \(\Omega\) that have a distance \(\breve{\mathscr {D}}<\delta\) from the nearest point on the boundary do not have a full horizon region \(H_{\mathbf {{x}}}\) [15], thus their material properties result to be slightly different from those of points in the bulk. In order to take into account this important aspect in numerical simulations, a specific surface correction algorithm is required. In this work we refer for simplicity to the volume method by Lee and Bobaru [106], particularized to our case.
2.3 Benchmark Problems
2.3.1 Crack-Tip Problem in Anisotropic Bodies
Consider the plane elastostatic problem of a horizontal semi-infinite crack under far-field loading in a homogeneous anisotropic body. The reference basis is \(\left\{ \mathbf {{e}}_{1}, \mathbf {{e}}_{2}\right\}\), with unit vector \(\mathbf {{e}}_{1}\) aligned with the axis of the crack, and a local polar coordinate system (r, \(\omega\)) is defined at the crack tip (Fig. 5). In the Lekhnitskii formalism [107], the problems of two-dimensional anisotropic elasticity are formulated in terms of two independent analytic functions of complex variables, whose determination for given boundary conditions, require the solution of the characteristic equation
in which \(S_{ijhk}\) are the components of \(\mathbf {S}=\mathbf {C}^{-1}\) with \(\mathbf {C}\) defined in Eq. 40). Due to the positive-definiteness of the elastic energy, the roots of Eq. 79 are always complex or purely imaginary and occur in conjugate pairs as \(\mu _{1}, \overline{\mu }_{1}\) and \(\mu _{2} , \overline{\mu }_{2}\) [108, 109].
Geometry and boundary conditions used for the analysis of the near-tip displacement field in anisotropic media
The displacement field in a small region surrounding the crack tip are analytically related to the mode-I and mode-II stress intensity factors by [109, 110]
where \(\mu _{1}\) and \(\mu _{2}\) are the roots of Eq. 79 [107, 109] and the scalar-valued variables \(\mathrm {p}_{i}\), \(\mathrm {q}_{i}\) for \(i = 1,2\) are given by
The ability of the CM model in describing the displacement fields surrounding a crack-tip in a fully anisotropic body is illustrated for the case of a material characterized by \(C_{1111}=C, C_{2222}=4C/5; C_{1122}=C/5; C_{1212}=C/3; C_{1112}=C/10; C_{2212}=C/6\). When examining the near-crack front region, the universal character of the asymptotic fields at the crack-tip eliminates the need to model finite geometry specimens and particular loading conditions [40]. The dominance of the asymptotic solution allows for a boundary layer analysis involving only the near-front region, to which the effects of loading and specimen geometry are transmitted by prescribing to its boundary the displacement field from this elastic solution and the associated stress intensity factors [111, 112]. This “boundary layer” analysis considerably reduces the size of the problem and allows the results to be general and applicable to finite geometry configurations characterized by their own (known) stress intensity factors [40, 111].
As representative cases, we consider far-field loadings defined by mixity mode factors \(\alpha _{K}= \tan^{-1} (K_{II}^{\infty }/K_{I}^{\infty })\) corresponding to Mode I (\(\alpha _{K}=0\)) and mode II (\(\alpha _{K}=\pi /2\)). The performed analysis setup is shown schematically in Fig. 5, where a circular shape of diameter 2a, unit thickness, and crack of length a (note that this model represents a crack whose length is infinite compared to the size of the modeled region), is subjected to displacement boundary conditions along its entire boundary corresponding to Eqs. 80 and 81. The spatial domain is discretized using a regular grid with spacing \(\Delta \mathrm {x}=a/120\), resulting in a model composed of 45344 particles. The horizon results to be \(\delta <a/25\) whereas \(m=5\), which lead to negligible non-local effects in the immediate vicinity of the crack-tip [105].
The computed displacement fields are reported in Fig. 6. Figure 7 shows that the displacements obtained by the anisotropic CM formulation are in excellent agreement with the analytical solution [109], demonstrating that the model is capable to describe correctly general inhomogeneous deformation fields in classical fully-anisotropic materials.
Displacement field near the crack-tip obtained by the CM model in the case of a fully anisotropic material (\(C_{1111}=C, C_{2222}=4C/5; C_{1122}=C/5; C_{1212}=C/3; C_{1112}=C/10; C_{2212}=C/6\)) under Mode I (\(\alpha _{K}=0\)), and Mode II (\(\alpha _{K}=\pi /2\))
Displacements \(u_{1}\) and \(u_{2}\) along different abscissae and obtained by the CM model in the case of a fully anisotropic material (\(C_{1111}=C, C_{2222}=4C/5; C_{1122}=C/5; C_{1212}=C/3; C_{1112}=C/10; C_{2212}=C/6\)) under Mode I (\(\alpha _{K}=0\)), and Mode II (\(\alpha _{K}=\pi /2\))
Besides the concept of stress is not required here since the deformation measures defined are work conjugates to actions at a distance and not to contact actions, the stress fieldFootnote 6 can be obtained from pairwise forces by particularizing to our case the original stress definition by Saint Venant and Cauchy [4, 8] given in the context of classical molecular theory of elasticity. Considering for simplicity a discrete lattice of particles, let define an arbitrary plane \(\Pi\) of unit normal \(\varvec{\mathsf {n}}^{*}\), passing through the centroid of particle p and dividing the family region \(H_{p}\) into two pieces denoted as \(H_{p}^{+}\) and \(H_{p}^{-}\), respectively. The intersection between the plane \(\Pi\) and the sub-domain \(\Delta \upsilon _{p}\) is denoted by \(A_{p}\). The force per unit area which one part exerts on the other through \(A_{p}\) can be expressed as
where \(N_{+}\) and \(N_{-}\) are the number of particles in \(H_{p}^{+}\) and \(H_{p}^{-}\), respectively. The summation involves only the set of bonds passing through (or ending at) the cross section \(A_{p}=\Delta \mathrm{x} h\) from the positive \(H_{p}^{+}\) side (one may refer to [40] for further details). The normal and tangential components of the traction vector \({\varvec{t}}(\mathbf {x}_{p},\varvec{\mathsf {n}}^{*})\) defined above are the normal and shear stress given by
where \(\varvec{\mathsf {t}}^{*}\) denotes the unit vector perpendicular to \(\varvec{\mathsf {n}}^{*}\). As illustrative example, Eq. 83 is applied to compute the \(\sigma _{22}\) stress field in the near-tip zone with assigned mixity factor \(\alpha _{K}=0\). Figure 8 shows that numerical results are consistent with the analytical solution by Sih et al. [109].
At this point it should be mentioned that, in general, the CM model (for equivalent Cauchy materials) solution converges to the classical elasticity solution as the horizon size reduces (keeping the density factor m constant) [113]. Moreover, for a given elastic problem and in the limit of \(\delta\) going to zero, it can be demonstrated that the rotation field \(\theta (\mathbf {{x}})\) is related to the macrorotation of classical elasticity such that
where \(\epsilon _{ijk}\) is the alternating symbol, while \(\mathsf {R}_{12}(\mathbf {{x}})\) and \(\mathsf {R}_{21}(\mathbf {{x}})\) are the non-zero components of the (infinitesimal) rotation tensor \(\varvec{\mathsf {R}}=\mathrm {skew}[\varvec{\nabla }\mathbf {{u}}(\mathbf {{x}})]\).
\(\sigma _{22}\) stress along the positive abscissa \(\mathrm {x_{2}}/a=0\) and detail of the \(\sigma _{22}\) field near the crack-tip obtained by Eq. 83 in the case of a fully anisotropic material (\(C_{1111}=C, C_{2222}=4C/5; C_{1122}=C/5; C_{1212}=C/3; C_{1112}=C/10; C_{2212}=C/6\)) under Mode I
Regarding the displacement map computed for the elastic problem under consideration, it is noted a fast convergence of the non-local solution to the classical (local) solution. In any case, numerical predictions result to be consistent with the exact solution by Sih et al. even in the case of coarser discretizations, as shown in Fig. 9.
Detail of the vertical displacement along the crack upper edge obtained by the CM model in the case of a fully anisotropic material (\(C_{1111}=C, C_{2222}=4C/5; C_{1122}=C/5; C_{1212}=C/3; C_{1112}=C/10; C_{2212}=C/6\)) under Mode I (\(\alpha _{k}=0\)). Grid spacings \(\Delta \mathrm {x}=a/60\) and \(\Delta \mathrm {x}=a/30\) correspond to discrete models composed of 11304 and 2828 particles, respectively
2.3.2 Elastic Behavior of Architected Meterials
The CM mechanical formulation is applied to model the effective elastic behavior of periodic mechanical metamaterials homogenized as anisotropic Cauchy continua. In particular, we consider here the two-dimensional tetrachiral blocky system by Bacigalupo and Gambarotta [76, 98] as illustrative case. This architected material is made up of square blocks of side a inclined by the chirality angle \(\beta (0 \le \beta <\pi / 4)\), and connected by elastic interfaces of length b and thickness \(\breve{\mu }\), as shown in Fig. 10. Assuming for simplicity interface made of homogeneous isotropic elastic material with Young modulus E and Poisson’s ratio \(\nu\), and plane stress-conditions, the following relations hold [76]
where \(\mathsf {K}_{\mathsf {n}}\) and \(\mathsf {K}_{\mathsf {t}}\) are the normal and tangential overall stiffness of the interface, respectively.
In the case of symmetric macro-fields, the continualization scheme outlined in in [98] leads to the effective fourth order elasticity tensor of the square symmetry group [70] (symmetry rotations \(\mathbf {R}_{3}^{\pi / 2}\)), whose components in the reference basis \(\left\{ \mathbf {e}_{1}, \mathbf {e}_{2}\right\}\) are given by
Periodic square of the tetrachiral block-lattice material [98] made of rigid units connected by elastic interfaces
which depend on the chirality angle \(\beta\) as well as on the constitutive parameters characterizing the interfaces. In fact, the overall anisotropic behavior of the here considered mechanical metamaterial (which is defined by the effective macromoduli \(C_{ijhk}\) in Eqs. 87–90) arises from geometric-topological features and specific material properties of its elastic constituents [76].
The accuracy of the CM model is assessed by considering frequency analyses and comparing homogeneous CM solutions to heterogeneous finite element solutions of a microstructured geometry. The geometry studied consists of an array of 25\(\times\)25 tetrachiral periodic square blocks with a=20mm and chirality angle \(\beta =\tan ^{-1}(1/2)\). In this case, since \(b=(1-\tan \beta )a\) [98], the interface length is equal to half side of the square block. The distance between the centroids of two neighboring blocks is denoted by \(\ell =a/ \cos \beta\). Isotropic material with Young modulus \(E=10\)MPa and Poisson’s ratio \(\nu \approx 1/2\) is considered for the interfaces. Uniform density \(\rho _{c}=1000\) Kg/\(\mathrm {m}^{3}\) are assumed instead for both rigid blocks and interfaces. The sample was chosen to be large enough in relation to the periodic cells to reduce overall size effects. In the FE microstructured model, rigid-body constraints are applied to the square blocks of the tetrachiral system, while the interfaces of (vanishing) thickness \(\breve{\mu }=a/500\), are meshed using eight-node quadratic elastic elements, resulting in a global model composed of 380311 nodes and 115962 finite elements[76]. Regarding instead the CM computational framework, by omitting the applied external load vector \({\mathbf {p}}\) in Eq. 35, and assuming simple harmonic motion \({\mathbf {v}}=\breve{\mathbf {v}}\exp (\imath \breve{\omega } t)\), the eigenvalue problem is obtained
where the eigenvalues \(\breve{\omega }\) are the circular natural frequencies of the system. The lowest five eigenvectors \(\breve{\mathbf {v}}\) (modal shapes) of the square lamina with homogenized elastic and inertial properties are produced by assembling the global stiffness and mass matrices \(\mathbf {K}\) and \(\mathbf {M}\) of the discretized CM model as detailed in Sect. 2.1. Hence, the modal shapes and natural frequencies of the heterogeneous microstructured square lamina obtained from finite element analysis are compared to those from homogeneous continuum-molecular simulations. The conceived anisotropic model for equivalent Cauchy materials predicts modal shapes and natural frequencies that are in excellent agreement with finite element solutions (see Figs. 11 and 12). The \(\delta\)-convergence analysis [114] (i.e. horizon reduction keeping m fixed) shows that the CM natural frequencies seem not to be affected by the grid spacing \(\Delta \mathrm {x}\) adopted (see Fig. 11). In fact, reducing the horizon size by eight times (while keeping \(m=5\) constant) results in minimal changes in the continuum-molecular numerical solution. However, it is noted that increasing the density parameter m (keeping \(\delta =5/4a\approx \ell\) fixed), a slight reduction in the difference between the CM heterogeneous finite elements solution is observed. In this case, a m-convergence procedure [114] allows the meshfree numerical solution to converge to the continuum-molecular non-local solution corresponding to \(\delta =\ell\) [76].
Tetrachiral block lattice with homogeneous isotropic elastic interfaces (\(\nu \approx 1/2\)): Natural frequencies obtained with the microstructured finite element model (black triangles) and the anisotropic continuum-molecular model for different discretization parameters
Tetrachiral block lattice with homogeneous isotropic elastic interfaces (\(\nu \approx 1/2\)): Eigenmodes obtained with the microstructured finite element model (first row) and the anisotropic continuum-molecular model adopting \(\delta =5/4a\) and \(m=5\) (second row) [76]
3 Fracture
Within the conceived CM frawework, brittle fracture is modeled by a general energy-based failure criterion characterized by the definition of orientation dependent critical values \(\mathrm {w}_{c}(\mathbf {x},\mathbf {x}^{\prime },\zeta )=\mathrm {w}_{c}(\psi ,\zeta )\) of the bond total stored energy density defined in Eq. 4.
An energy-based failure criterion was firstly introduced by Foster et al. [115] for isotropic materials in the theoretical framework of state-based peridynamics. Such approach was then adapted to pair potentials based continuum-molecular models with non-central interactions by Diana and Ballarini [40] for modeling fracture in orthotropic elastic materials with theoretically uniform resistance to fracture [116]. Orientation dependent fracture energy within a mechanism-based energetic failure criterion accounting for different degrees of anisotropy has been introduced instead in [72], and the resulting model successfully applied to the study of crack propagation in cortical bone tissues. In this context, the need for considering failure criteria accounting for both axial and shear pairwise deformations firstly relies on crack front which is in general locally associated to a mixed-mode deformation in anisotropic materials [40]. Therefore, a failure criterion based on critical elongation alone is not, in general, recommended for use with non-central elastic pair potentials, since it does not take into account the shear/angular deformation of the virtual fiber. This aspect may lead to reduced accuracy in kinking angle predictions or incorrect energy dissipation during crack extension [40]. Conversely, in isotropic brittle materials at atmospheric pressure the crack front is locally associated with a mode I deformation, and critical deformation based criteria generally lead to well simulated failure conditions and realistic crack paths even in the case of overall mode II loading [36, 41, 117,118,119,120]. Nevertheless, based on our experience, an energy-based failure criterion guarantees a more accurate estimation of the peak load in presence of non-central pairwise interactions [72]. A fundamental advantage of using energy-based failure criteria for materials with direction-dependent properties is that they allow for decoupling anisotropic elasticity and material fracture resistance, with evident simplification of the micro parameters identification procedure [72].
The energy-based criterion adopted considers the instantaneous bond failure when the scalar-valued micropotential energy function \(\mathrm {w}(\mathbf {x},\mathbf {x}^{\prime },t)\) attains its critical value \(\mathrm {w}_{c}(\psi ,\zeta )\).
As previously declared (see Sect. 2), the rotational material micromodulus is not defined when modeling Cauchy-elastic materials, thus \(\mathrm w_{\chi }(\mathbf {x},\mathbf {x}^{\prime },t)=0\) in our case. Assuming that the material resistance to fracture is orientation dependent, the critical value of the bond stored energy density is not direction-invariant, and rather depends on the virtual fiber angle \(\psi\). For a given orientation of the material denoted by the angle \(\zeta\) as defined in Sect. 2.2.1, the critical value \(\mathrm w_{c}(\psi )\) is obtained analytically by equating the fracture energy \(\mathrm {G}_{c}(\zeta )=\mathcal {G} (\zeta )\) to the total work required to break all the bonds per unit of fracture surface, when assumed normal to the unit vector \(\mathbf {{e}_{1}}\) (see Fig. 13).
Schematics for computing the equivalent fracture energy of the material associated to a fracture plane orthogonal to the horizontal and corresponding to a given orientation \(\zeta\) of the material reference system
Hence, we have
Considering that experimental measures of the fracture energy in materials of orthotropic symmetry (symmetry rotations \(\mathbf {R}_{3}^{\pi }\)) is, in general, given for two orthogonal orientation of the principal material basis \(\left\{ \check{\mathbf {e}}_{1}, \check{\mathbf {e}}_{2}\right\}\), namely \(\zeta =0\) and \(\zeta =\pi /2\) (with \(\mathcal {G}_{\zeta =0}> \mathcal {G}_{\zeta =\pi /2}\)), \(\mathrm w_{c}(\psi , \zeta )\) may be written as function the bond orientation angle by a general two parameter law defined as [72]
where \(n=2 N\), with \(N \in \mathbb {N}^{+}\), while \(\mathrm w_{c1}\) and \(\mathrm w_{c2}\) are the maximum and minimum values of the critical micropotential energy, namely the critical pairwise stored energy density of virtual fibers aligned with the unit vectors \(\check{\mathbf {e}_{1}}\) and \(\check{\mathbf {e}_{2}}\), respectively. By substituting Eq. 93 in Eq. 92 and considering \(\zeta =0\) and \(\zeta =\pi /2\), we get
Adopting \(n=2\), a system of two equations in the two unknown \(\mathrm w_{c1}\) and \(\mathrm w_{c2}\) is derived solving the integrals in Eqs. 94 and 95
which results in
If instead, \(n=4\) is adopted in Eqs. 93, 94 and 95 lead to the following relations
whereas with \(n=8\) we obtain
In the case of fracture energy independent of \(\zeta\), \(\mathcal {G}_{\zeta =0}=\mathcal {G}_{\zeta =\pi /2}=\mathcal {G}\), \(\lambda =1\), and Eqs. 97–99 (same for any exponent n) reduce to the well known [40, 115]
with \(\mathrm w_{c} (\psi , \zeta )=\mathrm w_{c}\) representing in this case a constant angle-independent function. Critical parameters \(\mathrm w_{c1}\) and \(\mathrm w_{c2}\) cannot be less than zero otherwise bond rupture generates energy, thus, a restriction exists on the maximum value of the ratio \(\lambda =\mathcal {G}_{\zeta =0}/\mathcal {G}_{\zeta =\pi /2}\) that can be considered for a given exponent n. For instance, assuming n=2 and n=8 in Eq. 93, we get \(\mathcal {G}_{\zeta =0}<2\mathcal {G}_{\zeta =\pi /2}\) and \(\mathcal {G}_{\zeta =0}<3.65\mathcal {G}_{\zeta =\pi /2}\), respectively, whereas n=32 leads to \(\lambda <7.14\). Hence, n can be used to model materials with varying levels of fracture resistance anisotropy, as Eqn. 93 with the corresponding values of the parameters \(\mathrm w_{c1}\) and \(\mathrm w_{c2}\), can handle \(\lambda\) values up to 2 and 3.65, respectively. As n is increased for a given anisotropy ratio \(\lambda\), the transition between the two extreme values \(\mathrm w_{c1}\) and \(\mathrm w_{c2}\) of \(\mathrm {w}_{c}(\psi ,\zeta )\) becomes increasingly less smooth (Fig. 14), and then larger values of the density parameter m may be required for an accurate angular discretization of the continuous trigonometric function in Eq. 93 [72]. Conversely, larger values of \(\lambda\) for a given exponent n result in a progressive increase of the effective anisotropy of the critical micropotential function \(\mathrm w_{c} (\psi , \zeta )\) (Fig. 15). In any case, \(\mathrm w_{c1}\) and \(\mathrm w_{c2}\) are calculated to match, for any n, the given experimental fracture energy values of the material, namely \(\mathcal {G}_{\zeta =0}\) and \(\mathcal {G}_{\zeta =\pi /2}\) (Figs. 16 and 17). However, since the integrals in Eqs. 94 and 95 are referred to (two) specific orientations \(\zeta\) of the principal material axes (or conversely, referred to specific crack surface orientation for \(\zeta =0\)), the effective fracture energy of the material model takes intermediate values for \(\pi /2>\zeta >0\) which depends indirectly on the critical micropotential function adopted, as shown in Figs. 16 and 17. A similar conceptual idea can be found in phase-field models of brittle fracture, in which direction-dependent crack propagation in solids can be modeled in a variational framework by considering anisotropic fracture energy functions satisfying given symmetry conditions [121, 122]. However, differently from the phenomenological phase-field approach, in our case fracture is described as a mechanism-based process, since cracks nucleate and grow when a number of bond failures coalescence into a surface and propagate [115]. It should be noted that other direction dependent critical micropotential energy laws \(\mathrm {w_{c}}(\psi ,\zeta )\) can be assumed, depending on the specific behavior of the material to be modeled, and on the experimental data at disposal. When considering fracture resistance properties invariant to \(\mathbf {R}_{3}^{\pi / 2}\) rotations of the material reference system, Eq. 93 may be replaced by
Continuous function \(\mathrm w_{c} (\psi , \zeta )\) for a given material inclined at \(\zeta =0\), with \(\lambda ={\mathcal {G}}_{\zeta =0}/{\mathcal {G}}_{\zeta =\pi /2}=1.8\) and corresponding to different values of the exponent n in Eq. 93
Continuous function \(\mathrm w_{c} (\psi , \zeta )\) for a given material inclined at \(\zeta =0\), with exponent \(n=8\) in Eq. 93 and corresponding to different values of \(\lambda ={\mathcal {G}}_{\zeta =0}/{\mathcal {G}}_{\zeta =\pi /2}\)
Normalized reciprocal values of the resulting fracture energy as function of the anisotropy angle \(\zeta\), and corresponding to different values of the exponent n in Eq. 93 with \(\lambda =\mathcal {G}_{\zeta =0}/\mathcal {G}_{\zeta =\pi /2}=1.8\)
Normalized reciprocal values of the resulting fracture energy as function of the anisotropy angle \(\zeta\), and corresponding to different values of the ratio \(\lambda\) in Eq. 93 with \(n=8\)
where, in this case, the extremum values \(\mathrm w_{c1}\) and \(\mathrm w_{c2}\) of the critical micropotential function are referred to bond directions that differ of \(\Delta \psi =\pi /4\), whereas the fracture energies from Eq. 92 are denoted by \(\mathcal {G}_{\zeta =0}=\mathcal {G}_{\zeta =\pi/2}\) and \(\mathcal {G}_{\zeta =\pi /4}\) (with \(\mathcal {G}_{\zeta =0} < \mathcal {G}_{\zeta =\pi /4}\)). As for Eq. 93, higher values of the exponent n correspond to higher degrees of anisotropy of the overall fracture resistance of the material which is possible to modelFootnote 7. Adopting \(n=4\), the system of two equations in the two unknown \(\mathrm w_{c1}\) and \(\mathrm w_{c2}\) is given by
which leads to
where Eqs. 103 allow to model anisotropy ratios up to \(\lambda =\mathcal {G}_{\zeta =\pi /4}/\mathcal {G}_{\zeta =0}\approx 1.2\). A typical effective reciprocal fracture energy angular-dependency (resulting from Eq. 101), is shown in Fig. 18. As previously declared, an important aspect of the energy-based failure criterion here illustrated, is that the directional dependent elastic and failure parameters of each interaction are theoretically independent of each other. In fact, when equating the total work per unit of fracture surface and material fracture energy, the integrand function in Eq. 92 is not given in terms of microelastic moduli or micromoduli functions \(k_{\mathrm {n}}(\psi )\) and \(k_{\mathrm {t}}(\psi )\), resulting in a simplification of the fracture model critical parameters calculation with respect to deformation-based failure criteria.
The status of each virtual fiber is specified by a history-dependent pairwise scalar valued function \(\upmu (\mathbf {{x}},\mathbf {{x}}',t)\) [18]
Normalized reciprocal values of the resulting fracture energy as function of the anisotropy angle \(\zeta\), with exponent \(n=16\) in Eq. 101 and corresponding to \(\lambda =5/4\)
where \(\mathrm {w}(\mathbf {{x}},\mathbf {{x}}',t)=\mathrm {w}(\psi ,t)\). Hence, a local damage scalar variable can be defined at each position \(\mathbf {{x}}\) and time t
where \(d(\mathbf {{x}},t)\) is the point-wise local damage variable associated to the energy-based failure criterion.
It is worth noting that circular functions in Eqs. 93 and 101 can also be adopted for modeling elastic direction dependency in orthotropic materials, with exponent n modulated to handle different degrees of material anisotropy, while conserving positive-definiteness of the axial and shear elastic micromoduli.
3.1 Numerical Experiments
In this subsection four numerical fracture experiments are described, assuming an increasing level of complexity of the constitutive and failure models adopted. Results obtained are compared with theoretical and experimental predictions, when available. In the first two benchmark problems proposed, we show the general capabilities of the CM approach in modeling spontaneous crack nucleation, crack propagation and curving in brittle materials assuming for the purposes of the discussion isotropic elastic and failure properties.
Then, the model is applied to predict crack kinking in elastic anisotropic bodies with orientation independent resistance to fracture, and subjected to different loading conditions. Finally, the proposed formulation is adopted to model fracture in anisotropic media considering both directional dependent elastic and failure properties of the material.
Numerical simulations are performed using an implicit non-linear quasi-static scheme in displacement control with adaptive step refinement [72, 125]. Moreover, to avoid fracture in compressive zones a further condition of positiveness of the pairwise deformation s is considered to determine the current status of each interaction. Hence, according to [40], the degradation function in Eq. 104 applies only to those interactions for which s is not negative. This is in a certain sense similar to the tension-compression split of the stored energy functional usually considered in phase field models of fracture [126, 127].
3.1.1 Crack Nucleation, Kinking and Curving
The first example is a model problem introduced in Bourdin et al. [129] to highlight the ability of the variational approach to fracture [130] to recover initiation phenomena and complex crack patterns in solids. The problem has been revised in [123] and proposed by a number of authors as a paradigmatic example to illustrate the potentiality of computational frameworks based on the aforementioned theoretical scheme [127, 131]. A two-dimensional square, brittle and elastic matrix with edge-length a is bonded to a rigid circular fiber inclusion of diameter a/3, as shown in Fig. 19. The fiber remains fixed, while a uniform displacement field \(u_{2}\) is imposed on the upper side of the square; the remaining sides are traction free, as specified in [123]. The elastic matrix is characterized by Young modulus \(E=4000\)MPa and Poisson’s ratio \(\nu =0.2\). The assumed fracture energy of the material is instead \(\mathcal {G}=0.01\)N/mm, whereas \(a=30\)mm is adopted for computational convenience [127]. The square domain is partitioned into 57600 particles, the grid spacing adopted being \(\Delta \mathrm {x}=a/240\). Fracture is not allowed at constrained borders. This forbids the development of fractures exactly at the boundary of the inclusion, and may well interpret the confining effects offered in a real experimental set-up by fractional contact or gluing of the supports [131]. An incremental applied vertical displacement \(\Delta u_{2}=\Delta u^{*}=10^{-4}\)mm is considered at each pseudo-time step of the simulation, with maximum applied displacement at the end of the numerical experiment \(u^{*}=\tilde{u}=0.02\)mm. Results obtained show that the matrix remains purely elastic until a crack of finite length appears near the top of the inclusion (Fig. 20. The crack curves almost instantaneously and symmetrically around the circular inclusion, the onset of the cracking process being brutal because the crack appears at a theoretically non-singular point [123]. The crack then continues to propagate horizontally until complete failure of the specimen. The crack trajectory obtained is practically identical to those obtained by Bourdin et al., as shown in Figs. 19 and 20. It is interesting to note that, consistently with results reported in [123, 131] the crack appear at a small distance of the order of the length-scale parameter of the fracture model (the horizon \(\delta\) in our case and the regularization length in the computational framework of the variational approach to fracture [131]). In any case, contrary to the classical variational approach to fracture, and consistently to the real physics of brittle materials, the conceived fracture model is non symmetric under tension and compression (see Sect. 3.1).
In the second example, a notched plate with hole is examined and compared to the experimental crack path obtained by Ambati et al. [124], and with numerical results obtained by a phase-field (PF) model [128]. This is a well-known numerical experiment widely used in literature to validate computational models for mixed-mode fracture. The layout of the problem is shown in Fig. 21 where all the dimensions are expressed in terms of the length \(a=5\)mm, with out of plane thickness \(h=3a\). Assuming plane stress conditions, the isotropic material parameters adopted are the following: Young Modulus \(E=5980\)MPa, Poisson’s ratio \(\nu =0.221\), and fracture energy \(\mathcal {G}=2.28\)N/mm. The rectangular domain is discretized using a regular grid spacing \(\Delta \mathrm {x}=a/10\), which leads, after removing particles from holes, to a model composed of 29345 particles.
Layout and final crack path (yellow line) of the two-dimensional traction experiment reported in [123]
Elastic matrix with inclusion: Normalized vertical displacement fields evidencing the evolution of the cracking process in four subsequent steps (\(S.1:u^{*}=0.9920 \tilde{u}\); \(S.2:u^{*}=0.9926\tilde{u}\); \(S.1:u^{*}=0.9927\tilde{u}\); \(S.1:u^{*}=0.9929\tilde{u}\))
Notched plate with hole: geometry and boundary conditions (left); envelope of the experimental crack paths [124], and final crack path obtained by the CM model (right)
Zero displacement boundary conditions \(u_{1}=u_{2}=0\), are imposed to all particles in the boundary of the lower pin, whereas the vertical displacements of all particles in the boundary of upper pin are kinematically constrained to have the same vertical displacement \(u_{2}=u^{*}\) [128]. At each pseudo-time step of the simulation an initial incremental applied vertical displacement \(\Delta u_{2}=\Delta u^{*}=10^{-3}\)mm is considered, which may be progressively reduced by the adaptive-pseudo time step refinement algorithm to reach numerical convergence. The maximum applied displacement at the end of the simulation is \(u^{*}=\tilde{u}=1.2\)mm. As shown in Fig. 22, a main crack develops from the notch. The crack then curves and reach the large off-centered hole. Later, a secondary straight crack appears from the hole to the vertical right edge. Results obtained agree very well with experimental data reported in Fig. 21, where the envelope of the experimental crack paths found for the four tested samples by Ambati et al. [124] is marked by the gray area. Moreover, it is noted from Fig. 23 that load-displacements curves corresponding to different CM density parameter \(m=\delta /\Delta \mathrm {x}\) are consistent with results by Kakouris & Triantafyllou [128] obtained using a phase-field model with the same displacement step increment, boundary conditions and material properties.
Notched plate with hole: Damage d evolution in four subsequent steps of the numerical experiment (\(S.1:u^{*}=0.326\mathrm {mm}\); \(S.2:u^{*}=0.329\mathrm {mm}\); \(S.3:u^{*}=0.702\mathrm {mm}\); \(S.4:u^{*}=1.201\mathrm {mm}\))
Notched plate with hole: Load-displacement curves obtained by the CM model using different density parameters \(m=\delta /\Delta \mathrm {x}\). The gray dashed line denotes the result obtained using a phase-field (PF) approach [128]
In the third set of numerical experiments the problem of crack kinking in anisotropic elastic bodies is examined. The layout of the problem is the same as in Fig. 5, and used for validating the anisotropic elastic model in Sect. 2.3.1. By increasing the magnitude of the prescribed far-field displacements given by Eqs. 80 and 81 so that the failure/fracture criterion is satisfied, the “pre-existing” crack of Fig. 5) extends in a direction dictated by the angle \(\beta _{K}\) (Fig. 24). Given a mode mixity ratios \(\alpha _{K}= \tan^{-1} (K_{II}^{\infty }/K_{I}^{\infty })\), the crack extension direction depends on the elastic anisotropy of the material and may be influenced also by potential anisotropy and spatially random distribution of its surface energy [40]. For the purposes of this discussion, and in order to guarantee consistency among the results compared and corresponding to different materials, illustrative examples assume always anisotropic elasticity, with homogeneous and (directionally) uniform resistance to fracture. This is similar to the approach used in [108, 116].
The simulations are performed considering a square-symmetric material and a fully anisotropic material subjected to several mode mixity ratios \(\alpha _{K}\) ranging from \(0^{\circ }\) to \(90^{\circ }\). The orthotropic material of square-symmetry is a silicon crystal of orientation \(\langle 100\rangle\), whose two-dimensional plane stress elastic tensor reads [132]
Crack kinking in anisotropic materials: Layout of the problem, horizontal displacement field (normalized with respect to the maximum displacement \(\tilde{u}_{1}\)), and kinked crack obtained considering the orthotropic material of square symmetry under pure mode II (\(\alpha _{K}=90^{\circ }\))
and whose resistance to fracture is assumed uniform within the surface plane considered [132].
The fully anisotropic material instead is characterized by same ratio among elasticities as that considered in Sect. 2.3.1 (assuming \(C=100\) GPa). Specifically, the elastic tensor in this case is
The magnitude of the K-field displacements applied at the circumferential boundary of the near tip-region is progressively increased until a small extension of the main crack appears. Such crack extension should be on one hand small enough not to alter significantly the K-field overall conditions transmitted by the boundary layer during crack propagation, and on the other should be sufficiently large to allow for its direction measurement. Taking into account these considerations, a square of edge a/2 and centered at the crack-tip is taken as a reference for kinking angle \(\beta _{K}\) measurement. The computed kinking angles are also compared with theoretical predictions by maximum-hoop stress intensity factor criterion (HSIF-criterion) [108, 133], according to which, the crack will extend along a path whose tangent forms an angle perpendicular to the maximum circumferential (hoop) stress. Actually, this fracture criterion relies on the definition of two stress intensity factors; the so-called “hoop” \(K_{\omega \omega }\) (HSIF) and “shear” \(K_{r \omega }\)(SSIF) stress intensity factors, respectively (cfr. Sect. 2.3.1 and Fig. 5) [108, 134]. The first involves the circumferential stress and the latter the shear stress, HSIF and SSIF being (for anisotropic materials) more convenient quantities than the commonly used Modes I and II stress intensity factors, since they uncouple the Modes I and II on planes at suitable angles relative to the main crack [108, 135]. Kinking angles corresponding to HSIF-criterion can be determined analytically as function of the apparent stress intensity factors (\(K_{I}^{\infty }\), \(K_{I I}^{\infty }\)), and material parameters, as specified in [40, 108]. Results obtained are reported in Figs. 25, 26 and 27. It is noted that CM crack extension directions are consistent with HSIF \(\beta _{K}\) angle predictions. Another consideration is that, for the specific materials considered in this section, the maximum energy release rate criterion (G-criterion) [116, 136] leads to similar predicted kinking angles. Moreover, it is noted that larger values of the density parameter \(m=\delta /\Delta \mathrm {x}\) in numerical simulations do not lead to considerable differences in terms of crack extension directions computed by the CM model (Figs. 25, 26 and 27).
Crack kinking in anisotropic materials: Crack extension directions obtained considering the orthotropic material of square symmetry under mode I and mixed mode loading (\(\alpha _{K}=70^{\circ }\)). Filled triangles denote the theoretical predictions by HSIF-criterion
Crack kinking in anisotropic materials: Crack extension directions obtained considering the fully anisotropic material under different mixity factors \(\alpha _{K}\). Filled triangles denote the theoretical predictions by HSIF-criterion
Crack kinking in anisotropic materials: Kinking angles \(\beta _{K}\) obtained considering the orthotropic material of square symmetry (left) and the fully anisotropic material (right) subjected to general Mixed-mode loading. A comparison with analytical predictions by HSIF criterion is also proposed
3.1.2 Anisotropic Fracture in Cortical Bone
In this section, the CM formulation is adopted to model fracture in cortical bone tissues. Bone is a complex hierarchical composite which has natural mechanisms to resist fracture [137]. Actually, the simultaneous activation of toughening mechanisms by collagen fibres, lamellar structure of collagen fibres and osteon (Haversian canals) at various length scales provides enduring strength and toughness (Fig. 28).
Layout of the compact tension test on cortical bone specimens considered for numerical experiments (unit thickness h is assumed)
As a result, the material exhibits specific anisotropic properties which limit the possibility of formation of fracture planes normal to the anatomical axis of bone which defines the so called longitudinal direction [137].
Numerical analyses are performed to simulate experimental crack paths obtained by Behiri and Bonfield [138, 139], which highlight the orientation dependence of the fracture properties of bovine cortical bone tissues. The authors used the compact tension (CT) test to produce stable fracture propagation in fluid-saturated specimens at various orientations \(\zeta\) of the material, whose principal directions are those parallel and perpendicular to the osteons (Fig. 28).
Since cortical bone is, in general, stronger in the longitudinal direction, the load conditions used in CT tests result in final crack paths almost parallel to the osteons [63, 72, 139].
Orthotropic elastic moduli of bovine bone were obtained by Van-Buskirk et al. adopting a pulse transmission ultrasound method [140]. Assuming the principal orthonormal basis of unit vectors \(\check{\mathbf {e}_{1}}\) and \(\check{\mathbf {e}_{2}}\) directed along the longitudinal \(\check{\varvec{l}}\), and transverse radial \(\check{\varvec{r}}\) directions (Fig. 28), respectively, the two-dimensional elastic tensor in compact form is
The orientation of the principal material reference system with respect to the reference basis is denoted, as usual, by the anisotropy angle \(\zeta\) (Fig. 28). Regarding fracture properties, energy-release rates \(\mathcal {G}_{\zeta =0}\) and \(\mathcal {G}_{\zeta =\pi /2}\) as defined in Sect. 3 are calculated, consistently with the elastic moduli adopted, by [72, 116]
where \(S_{iiii}, \; i=1,2\) are the conventional compliance moduli and \(\mu _{1}, \overline{\mu }_{1}\) or \(\mu _{2}, \overline{\mu }_{2}\) are the conjugate pairs root of Eqn. 79 with \(S_{1112}\)=\(S_{2212}=0\). According to Fig. 13, the critical stress intensity factors \(K_{c\check{l}}\) and \(K_{c\check{r}}\) in Eq. 109 refer to longitudinally (\(\zeta =0\)) and transversely (\(\zeta =\pi /2\)) oriented bovine cortical tissues, respectively. The values \(K_{c\check{l}}=6.5 \mathrm{MPa\cdot m}^{1/2}\) and \(K_{c\check{r}}=4.0 \mathrm{MPa \cdot m}^{1/2}\) adopted in this study are those measured experimentally by Behiri and Bonfield using grooved CT specimens of bovine bone [138, 139]. Same values can be also found in [63]. In fact, elastic and failure properties of this specific material, homogenized as a Cauchy orthotropic material, have been considered in other previous studies for validation of anisotropic models for fracture based on pair-potentials [63, 64]. However, differently from [63, 64], the model here considered does not suffer of restrictions affecting the number of independent micromoduli which define the effective in-plane elastic orthotropy of the material [72]. This allows to set all the four elastic macro-moduli given by the experimental study by Van-Buskirk et al. [140] without introducing approximations imposed by the presence of internal constrains. Moreover, the anisotropic fracture model adopted in this work is based on the definition of a energy-based failure criterion, with the advantage of decoupling elasticity from failure properties of the material in the analytical identification of the model parameters. Compact tension tests on cortical bone specimens at different orientations \(\zeta\), as performed by Behiri and Bonfield [138], have been simulated in displacement control and quasi-static conditions [125] using the conceived anisotropic CM formulation. The microelastic moduli are calculated using Eqs. 65–70, the micromoduli functions being defined by Eqs. 77 and 78. Considering the peculiarities of this material, critical micropotential energy function was determined using Es. 93 along with Eq. 99 [72]. The results, obtained adopting an almost uniform grid spacing \(\Delta \mathrm {x}=0.3\)mm and \(m=5\) resulting in a model of 12312 particles, are shown in Figs. 29, 30, and 31 along with experimental final crack paths corresponding to angles of anisotropy \(\zeta =0\), \(\zeta =\pi /4\), \(\zeta =\pi /3\) and \(\zeta =\pi /2\). The crack paths predicted using the CM model are in very good agreement with experimental data [138]. As can be seen from Fig. 29, experiments show quite complex fracture patterns especially in case of \(\zeta =\pi /4\) and \(\zeta =\pi /2\). The continuum-molecular model is able to describe the progressive reduction of the average inclination angle of the fracture surface in cortical bone specimens inclined at \(\pi /4\), as well as the initial deflection that the crack profile undergoes before propagating straight along the strongest direction in case of \(\zeta =\pi /2\). It is noted that even with coarser meshes, crack profiles correlate well with experimental data [72]. In case of \(\zeta =0\), experimental and numerical data show an almost collinear extension of the pre-existing main crack of the CT specimen. The theoretical peak load P can be then calculated by [63, 141]
where h is the thickness, \(\breve{a}\) is a geometrical parameter depicted in Fig. 28, whereas \(Y=6.554\) is a non-dimensional constant depending on the geometry of the specimen [141]. The peak load \(P=98\mathrm {N}\) is determined from Eq. 110 for \(K_{c\check{r}}=4.0 \mathrm {MPa} \cdot \mathrm {m}^{1 / 2}\) and thickness \(h=1\) mm. This theoretical prediction, calculated analytically on the basis of explicitly given experimental data [141], is in very good agreement with the peak load value \(P_\mathrm{CM}=96\) N obtained by the CM model (Fig. 32).
4 Diffusion-Based Problems: Heat Transfer and Electrical Conduction
Let us consider the two-dimensional continuum solid body \(\Omega\) described in Sect. 2, focusing here on its thermal conductive properties. Material points \(\mathbf {x}\) and \(\mathbf {x}'\) within a finite distance \(\delta\), are postulated to interact with each other through pairwise exchanges of heat energy, function of pairwise conductivity properties and pairwise thermal parameters. The homogeneous body configuration is now described by the temperature field \(\mathcal {T}(\mathbf {x}, t)\) defined over \(\Omega\). The rate of introduction of heat energy per unit volume is denoted by \({\omega _{\mathcal {T}}}(\mathbf {x},t)\). The constant parameter \(c_{\mathcal {T}}\) denotes instead the specific heat capacity of the material. The thermal diffusion model is based on the definition of a pairwise scalar thermal parameter defined by
that can be considered as the equivalent of a pairwise deformation measure in elasticity, and is function of the bond temperature gradient \(\varvec{g}(\mathbf {x},\mathbf {x}^{\prime },t)=g(\mathbf {x},\mathbf {x}^{\prime },t)\mathbf {n}\), with \(\mathbf {n}\) as defined in Sect. 2. We define a specific pair potential function for heat transfer
such that the thermal response function or pairwise thermal action (having dimensions of a heat current per unit volume squared) can be derived as
where \(\eta _{\mathcal {T}}=(\mathcal {T}'-\mathcal {T})\), while \(\Lambda =\Lambda (\Vert \varvec{\xi }\Vert )\) is the attenuation function defined in Sect. 2. In Eqs. 112 and 113, \(k_{\mathcal {T}}=k_{\mathcal {T}}(\mathbf {x},\mathbf {x}^{\prime })\) is the pairwise conductivity (assumed not to depend on temperature for simplicity), namely microconductivity of the heat transfer model, having the dimensions of a thermal conductivity per unit volume. As for the microelastic functions in elasticity, the microconductivity function in the general case of non-isotropic materials depends on the spatial orientation \(\psi ={\text {Arg}}\left( \varvec{\xi } \cdot \mathbf {e}_{1}+\imath \varvec{\xi } \cdot \mathbf {e}_{2}\right)\) of the pairwise interaction considered, such that \(k_{\mathcal {T}}(\mathbf {x},\mathbf {x}^{\prime })=k_{\mathcal {T}}(\psi )\).
The pairwise micro-heat flux density (vector) can be then defined according to Fourier’s law, particularized to our case, as
The thermal macro-potential density function is obtained by integrating the pair potential \(\mathrm {w}_{\mathcal {T}}\) over the horizon region \(H_{\mathbf {x}}\) of radius \(\delta\)
The integral \(\mathcal {I}\) can be defined [142,143,144]
If we let \(\updelta \mathcal {I}=0\) in Eq. 116, while assuming \({\dot{\mathcal {T}}}\) as invariant [142, 145, 146], after some manipulations, the field equation for time-dependent heat transfer at \(\mathbf {x}\) can be obtainedFootnote 8
where \(f_{\mathcal {T}}(\mathcal {T}, \mathcal {T}',\mathbf {x}, \mathbf {x'})\) is given by Eq. 113. Equation 117 represents the conservation of energy law for a continuum-molecular model based on pair potentials. Steady-state conditions are obtained setting the right term of Eq. 117 equal to zero.
For the steady-state electrical conduction problem we can consider the same formal structure of the heat-transfer problem, replacing Eq. 111 by
where \(\phi\) denotes the electric potential while t represents here the pseudo-time step in equivalent quasi-static conditions. The pairwise bond electric field is then \(\varvec{e}(\mathbf {x},\mathbf {x}^{\prime },t)=e(\mathbf {x},\mathbf {x}^{\prime },t)\mathbf {n}\). The electrical micropotential is instead defined as
where \(k_{e}\) is the microconductivity having the dimension of an electric conductivity per unit volume. The electrical pairwise interaction between pairs or material points has the dimensions of an electric current per unit volume squared, and can be derived in a manner analogous to that of the pairwise thermal interaction. The first derivative of the micropotential function in Eq. 119 gives
The balance equation at \(\mathbf {x}\) is
where \(\omega _{e}\) is the net current per unit volume at \(\mathbf {x}\). The current density and the heat flux can be derived as non-primary quantities using the approach described in [44, 53].
4.1 Discretized Equations: Transient and Steady-State Problems
Using a meshfree discretization procedure, the domain \(\Omega\) is divided, as usual, into N sub-domains \(\Delta \upsilon _{p}\) associated to particles p. Particles q belonging to the p-centered horizon region \(H_{p}\) are then selected as described in the previous sections. Considering the heat-transfer problem, the primary scalar field variables of the material particles p and q are denoted by \(\mathrm{z}_{p}={\mathcal {T}}_{p}\) and \(\mathrm{z}_{q}={\mathcal {T}}_{q}\), respectively. If the particle \(q \in H_{p}\), the primary field variables can be collected column-wise in vector form as
The pairwise compatibility equation relating the pairwise thermal parameter to the interacting particles temperatures can be written in compact form as
where
The scalar pairwise constitutive equation of the discretized system is instead
where \(k^{pq}_{\mathcal {T}}\) is the microconductivity characterizing the specific interaction between particles p and q. The algebraic system of governing equations of the transient heat transfer problem and the equivalent stiffness operator can be derived invoking \(\updelta \mathcal {I}=0\) subject to the condition specified above (see [142, 146]), and referred to a discretized system. Hence, for the third term of Eq. 116, we obtain
where the variation is taken keeping the quantity \({\dot{\mathcal {T}}}_{p}\) fixed [142, 145, 148]. The variation of the second term of Eq. 116 can be treated in discrete form as
where \({\omega _{\mathcal {T}}}_{p}\) represents the heat source term at particle p. Finally, for the macro-potential term in Eq. 116 we can write
where \(\mathrm {D}^{pq}_{\mathcal {T}}=\Lambda _{pq}k^{pq}_{\mathcal {T}}\), while H, and \(\alpha _{p q}\) have been defined in Sect. 2.1. Therefore, making use also of Eqs. 122–124, we obtain
where \(\mathbf {L}_{p q}^{\mathcal {T}}=\big [ \mathbf {I}_{1} \quad \mathbf {0}_{1} \big ]^{\top }\) is a specific topology incidence vector for point-wise defined vectors and scalars. As detailed in Sect. 2, the subscripts p and q are associated with different degrees of freedom of the system, thus the assembling symbol in Eq. 129 denotes that the algebraic objects have to be assembled properly through superposition.
After global assembling, Eq. 129 can be rewritten in compact form as
where \(\mathbf {M}_{\mathcal {T}}\) is given by
whereas the equivalent stiffness operator corresponding to the whole body is given by
and the global heat source vector is
Moreover, the global primary field vector is given by
In steady-state problems, Eq. 130 reduces to \(\mathbf {K}_{\mathcal {T}}{\mathbf {z}}={\mathbf {p}_{\mathcal {T}}}\). The steady-state discretized equations can be applied directly to steady-state electrical conduction, provided that the primary field in this case is represented by the electric potential. Eq 122 is then replaced by
Moreover, due to the convention used for the direction of the electric field, Eq. 124 should be multiplied by minus one.
4.2 Micro–Macro Conductivities
In the classical theory of homogeneous anisotropic materials, the thermal (electrical) conductivity is direction-dependent and the heat-flux (electric current density vector) is not necessarily parallel to the temperature gradient (electric field).
Given the usual reference orthonormal basis \(\left\{ \mathbf {e}_{1}, \mathbf {e}_{2}\right\}\), the classical constitutive equation (Fourier’s law) relating the heat flux \(\varvec{q}\) and the thermal potential (temperature) gradient \(\varvec{\nabla } \mathcal {T}(\mathbf {x}, t)=\varvec{\varsigma }\) reads
hence as
Considering a generic basis \(\left\{ \hat{\mathbf {e}}_{1}, \hat{\mathbf {e}}_{2}\right\}\) rotated by an angle \(\psi\) with respect to the reference basis, Eq. 137 can be rewritten as
where \(\varvec{\hat{{q}}}=\mathbf {Q}^{\top }_{\mathcal {T}}\varvec{q}\) and \(\varvec{\hat{{\varsigma }}}=\mathbf {Q}^{\top }_{\mathcal {T}}\varvec{\varsigma }\), with
The thermal conductivity tensor \(\hat{\mathbf {D}}_{\mathcal {T}}\) in Eq. 138 is defined as
According to Eqs. 138–140, the off-axis conductivity \(\hat{K}_{\mathcal {T}_{11}}\) can be written as function of \(\psi\), in terms of the three conductivities \(K_{\mathcal {T}_{11}}\), \(K_{\mathcal {T}_{12}}\) and \(K_{\mathcal {T}_{22}}\) by
As in Sect. 2.2, to preserve material symmetries, we can assume here that the microconductivity characterizing each interaction of the proposed continuum-molecular model exhibits a directional dependency as \(\hat{K}_{\mathcal {T}_{11}}(\psi )\) described by Eqs. 141
where \({\mathcal {K}}_{\mathcal {T}_{11}}\) and \({\mathcal {K}}_{\mathcal {T}_{22}}\) are the micro-conductivities of bonds aligned with the unit vectors \(\mathbf {e}_{1}\) and \(\mathbf {e}_{2}\), respectively, whereas, \({\mathcal {K}}_{\mathcal {T}_{12}}\) is the microcondictivity related to the non-symmetric conductive properties in anisotropic materials. Thus, three independent microcothermal moduli are defined for reproducing the overall conductive behavior of a two-dimensional anisotropic solid. The relation between the microthermal moduli, \({\mathcal {K}}_{\mathcal {T}_{11}}\), \({\mathcal {K}}_{\mathcal {T}_{22}}\), \({\mathcal {K}}_{\mathcal {T}_{12}}\) (For electrical conduction, the three micro-conductivity parameters or microelectrical moduli are denoted by \({\mathcal {K}}_{e_{11}}\), \({\mathcal {K}}_{e_{22}}\), \({\mathcal {K}}_{e_{12}}\)) and the classical macro-conductivities of anisotropic continua is obtained following a general approach consistent with that detailed in Sect. 4.2.
Consider a general time-independent two-dimensional homogeneous thermal gradient of components \(\varsigma _{1}\), \(\varsigma _{2}\). Under these conditions, \(g(\psi )=\hat{\varsigma }_{1}(\psi )\), thus the pairwise thermal measure \(g(\psi )\) of a fiber inclined at \(\psi\), is related to the homogeneous potential-gradient components \(\varsigma _{i}\) according to \(\varvec{\hat{{\varsigma }}}=\mathbf {Q}^{\top }_{\mathcal {T}}\varvec{\varsigma }\). Hence, we have
where, consistently with Eq. 53, \(g(\psi )={\varsigma }_{n}(\psi )\). Substituting Eq. 143 in Eq. 115, and assuming \(k_{\mathcal {T}}(\psi )\) by Eqs. 142, Eq. 115 gives
whose general solution is
where h denotes, as usual, the out of plane thickness and \(\mathcal {N}_{\mathcal {T}}\) is a scalar-valued function of the horizon \(\delta\), related to the specific influence function \(\Lambda\) considered. In case of dimensionless influence functions, \(\mathcal {N}_{\mathcal {T}}\) can be expressed as
where \(\Xi _{\mathcal {T}}\in \mathbb {R}^{+}\). In the following, as for the mechanical model, we assume without loss of generality that \(\Lambda (\Vert \varvec{\xi }\Vert )=1\), thus
The thermal macro-potential function \(\mathcal {W}_{\mathcal {T}}\) has the dimensions of a rate of entransy per unit volume, which is related to the specific heat transfer ability of the material [149].
The corresponding quantity in classical continuum physics can be computed by
Comparing Eqs. 148 and 145, and collecting the terms multiplying the same temperature gradient components \(\varsigma _{i}\), three independent equations expressing the macro-conductivities in terms of micro-conductivities are obtained
where the constant \(\mathcal {C}_{\mathcal {T}}\) is
By solving the algebraic system given by Eqs. 149–151 we obtain
In the special case of isotropy, we have \(K_{\mathcal {T}_{12}}=0\) and \(K_{\mathcal {T}_{11}}=K_{\mathcal {T}_{22}}=K_{\mathcal {T}}\). Hence \(\mathcal {K}_{\mathcal {T}_{12}}=0\) and \(\mathcal {K}_{\mathcal {T}_{11}}=\mathcal {K}_{\mathcal {T}_{22}}=\mathcal {K}_{\mathcal {T}}\), where
which is consistent with results for isotropic materials reported in [44, 53] and obtained using different approaches and procedures.
Given the principal material reference defined by the orthonormal basis \(\left\{ {\check{\mathbf {e}}_{1}}, {\check{\mathbf {e}}_{2}}\right\}\), inclined at \(\zeta\) with respect to the reference basis, Eq. 142 takes the equivalent form
where
\(\check{K}_{\mathcal {T}_{11}}\) and \(\check{K}_{\mathcal {T}_{22}}\) being the eigenvalues of the thermal conductivity tensor \(\mathbf {D}_{\mathcal {T}}\), that according to the Jacobi rotation method, are given by
The angle of anisotropy \(\zeta\) denoting the orientation of the principal material axes is instead
Adopting Eqs. 157–162, the effective material behavior is defined by the two microconductivities \(\mathcal {K}_{\mathcal {T}_{ii}},\, i=1,2\), and the anisotropy angle \(\zeta\). As for elasticity, the continuum-molecular model provides a mechanism-based description of direction-dependent conductive properties of materials, as the overall anisotropy is the result of pairwise properties assigned at a lower scale.
In the eventuality of negative values of the micro-conductivity moduli resulting from Eqs. 158–159, the equivalent stiffness operator may result non-positive definite. This may introduce material instability, especially in presence of non-linearities. At this point it should be reminded that Eq. 157 results from the assumption of trigonometric dependency of \(k_{\mathcal {T}}(\psi)\) on \(\psi\) (for a given anisotropy angle) as that of \(\hat{K}_{\mathcal {T}_{11}}(\psi)\). However, other different circular functions describing the direction-dependent microconductivity can be assumed, provided that the material symmetries are respected. For instance, a more general description of \(k_{\mathcal {T}}(\psi ,\zeta )\) as function of the bond spatial orientation can be obtained adopting a trigonometric law similar to that of Eq. 93
where \(n=2N\), with \(N \in \mathbb {N}^{+}\) (Eq. 157 is got assuming \(n=2\) in Eq. 163). Larger values of the exponent n are associated with higher order anisotropic microconductivity functions \(k_{\mathcal {T}}(\psi ,\zeta )\), whose moduli \(\mathcal {K}_{\mathcal {T}_{11}}\) and \(\mathcal {K}_{\mathcal {T}_{22}}\) have to be calculated, as usual, to reproduce the effective conductive properties of a material. This reflects itself in the possibility to model materials with different levels of effective anisotropy, as Eq. 163 leads to non-negative micro-conductivities for \(\check{K}_{\mathcal {T}_{11}}/\check{K}_{\mathcal {T}_{22}}\le n+1\). As an example, assuming n=4 we obtain
whereas \(n=12\) gives
Therefore, adopting Eqs. 164–165 and 166–167 together with Eq. 163, the model is able to handle overall anisotropy ratios \(\check{K}_{\mathcal {T}_{11}}/\check{K}_{\mathcal {T}_{22}}\) up to 5 and 13, respectively, while avoiding negative parameters [72]. Different exponents n with their corresponding positive-definite micro-conductivities lead, in principle, to same results since \(k_{e1}\) and \(k_{e2}\) are, in any case, derived analytically to match the effective anisotropy of the material. However, given an anisotropy ratio \(\check{K}_{\mathcal {T}_{11}}/\check{K}_{\mathcal {T}_{22}}\), incremental values of n result in microconductivity functions \(k_{\mathcal {T}}(\psi ,\zeta )\) characterized by a progressively faster transition between its extremum values. For this reason, when considering discrete lattices of particles instead of material points in a continuum, the exponent n should not be too large with respect to \(\check{K}_{\mathcal {T}_{11}}/\check{K}_{\mathcal {T}_{22}}\), in such a way to ensure an accurate angular discretization of the microconductivity function for a given density parameter \(m=\delta / \Delta \mathrm {x}\) and arbitrary grid orientations (see Sect. 2.2.1). Another consideration is that when \(n=2\) in Eq. 163, the function \(k_{\mathcal {T}}(\psi ,\zeta )\) takes the form of that proposed in [18, 63] for elasticity models based on pairwise central-forces. Moreover, the directional-dependent function obtained using eight-order spherical harmonic expansions proposed in [63] for two parameters orthotropic elasticity, can be obtained from the proposed two parameters anisotropic function by setting \(n=12\) in Eq. 163.
As stated before, the equations derived in this subsection apply directly to electrical conduction and can be extended to other diffusion-based problems. Consistently with previous sections, in what follows the density parameter is \(m=5\), whereas the volume method is adopted as surface correction algorithm.
4.3 Benchmark Problems
In order to demonstrate the effectiveness and accuracy of the CM model for diffusion-based problems in anisotropic materials, two illustrative numerical examples are considered in this section. The first example consists of a Dirichlet problem on a circular anisotropic two-dimensional domain, whereas the second set of numerical experiments deals with damage sensing and crack-length determination via potential drop technique in bone tissues.
Compact tension test on bovine cortical bone tissues: Damage and crack path evolution in four subsequent steps and obtained setting \(\zeta =\pi /4\) (\(S.1:\Delta u^{*}=0.151\mathrm {mm}\); \(S.2:u^{*}=0.183\mathrm {mm}\); \(S.3:\Delta u^{*}=0.248\mathrm {mm}\); \(S.4:\Delta u^{*}=0.355\mathrm {mm}\)). The experimental crack profile from [138] is denoted by filled triangles
Compact tension test on bovine cortical bone tissues: Damage paths obtained by CM model in the case of \(\zeta =0\) and \(\zeta =\pi /2\)
Compact tension test on bovine cortical bone tissues: Force-displacement curve obtained by CM model in the case of \(\zeta =0\). The violet dashed line denotes the theoretical peak-load
4.3.1 Heat Transfer in an Anisotropic Unit Disc
Given the usual reference basis \(\left\{ \mathbf {e}_{1}, \mathbf {e}_{2}\right\}\), let us consider an anisotropic medium with thermal conductivity tensor defined by [150, 151]
According to Eq. 162, the principal material reference system defined by \(\left\{ \check{\mathbf {e}}_{1}, \check{\mathbf {e}}_{2}\right\}\) is inclined at \(\zeta =\pi /8\) with respect to the reference basis (Fig. 33). The Dirichlet problem is solved in a circular plane domain \(\Omega =\left\{ (\mathrm {x_{1}}, \mathrm {x_{2}}): \mathrm {x_{1}}^{2}+\mathrm {x_{2}}^{2}<1\right\}\) of unit radius a. The following temperature distribution can be shown to satisfy the corresponding governing heat conduction equation [150]
which leads to inhomogeneous temperature gradient field defined over the spatial circular domain \(\Omega\). Adopting a regular grid spacing \(\Delta \mathrm {x}=a/100\), the circular domain is discretized into 31428 particles. Micro-macro conductivities correspondence is established by Eq. 163, where \(n=34\) is adopted, the effective anisotropy ratio being \(\check{K}_{\mathcal {T}_{11}}/\check{K}_{\mathcal {T}_{22}}\approx 33.96\). Eq. 169 is used to impose the boundary conditions to a circumferential boundary layer of thickness \(\delta =m\Delta \mathrm {x}=a/20\). Results provided for temperature \(\mathcal {T}\) distribution are reported in Figs. 34 and 35, where numerical solution is compared with exact analytical solution from Eq. 169. As for stress in elasticity, pairwise constitutive equations in continuum-molecular formulations for heat transfer do not involve a point-wise defined heat flux. However, considering for simplicity a discrete lattice of particles, it can be computed as postprocessing quantity by
where \({H^{\mathcal {T} +}}\) denotes the number of particles q within the p-particle’s horizon that have higher temperature with respect to particle p [48, 53].
Steady-state heat transfer in an anisotropic unit disc: Geometry of the domain and boundary conditions considered
Steady-state heat transfer in an anisotropic unit disc: Temperature distribution obtained by CM model. Plotted results are normalized with respect to the maximum temperature \(\tilde{\mathcal {T}}=0.73\)K
Steady-state heat transfer in an anisotropic unit disc: Temperature \(\mathcal {T}\) along three different abscissae
In classical continuum physics, the heat flux vector is instead given by Eq. 136, which considering Eqs. 168–169 gives
where
The heat flux magnitude \(\Vert \varvec{q}\Vert\) computed by CM model using Eq. 170 within the circular domain under consideration is reported in Fig. 36. Exact solution obtained from Eqs. 171 and 172 is compared with numerical predictions in Fig. 37, which demonstrates the consistency between Eqs. 136 and 170.
Steady-state heat transfer in an anisotropic unit disc: Heat flux magnitude distribution obtained by CM model. Plotted results are normalized with respect to the maximum value \(\Vert \tilde{\varvec{q}}\Vert =8.11\) \(\mathrm {W/m^{2}}\)
Steady-state heat transfer in an anisotropic unit disc: Detail of the heat flux magnitude \(\Vert \varvec{q}\Vert\) along two different abscissae
4.3.2 Damage Sensing in Conductive Tissues
The internal structure of bone affects not only its mechanical properties but also its effective conductive behavior [72, 152]. Reddy and Saha [153] evaluated the electrical conductivity of compact (cortical) bone in three orthogonal directions parallel to the principal directions (e.g. longitudinal, radial, and circumferential) of a long bone, indicating the overall anisotropic character of this material.
The electrical properties were found to be substantially dependent on bone moisture content and signal frequency applied to the test specimen, but essentially frequency independent below 10 kHz [153]. According to Reddy and Saha, in fluid-saturated (wet) compact bovine bone at low-frequency or DC conditions, the effective resistivity in the radial direction is roughly three times that in the longitudinal direction [153], which is consistent with Chakkalakal et al. results [152]. In particular, as reported in [153], electrical resistivity in the radial direction is \(\rho _{\check{r}}\)=540 \(\Omega\)m, whereas in longitudinal direction \(\rho _{\check{l}}\)=170 \(\Omega\)m, with \(\rho _{\check{r}}/\rho _{\check{l}}\approx 3.2\). Such electrical resistivity anisotropy is expected, compact bone material being characterized by higher porosity in the longitudinal direction due to the presence of Haversian canals [153].
Considering the principal orthonormal basis of unit vectors \(\check{\mathbf {e}_{1}}\) and \(\check{\mathbf {e}_{2}}\) directed along the longitudinal \(\check{\varvec{l}}\) and transverse radial \(\check{\varvec{r}}\) directions (Fig. 38), the two-dimensional conductivity tensor is then given by
The angle of anisotropy is instead denoted by \(\zeta\) (Fig. 38). We revisit here the numerical experiment in Sect. 3.1.2 by coupling the CM mechanical and electrical conduction models in the hypothesis of small deformations, [53] to study the effect of evolving discontinuities in cortical bone tissues effective conductive behavior. Potential drop crack length determination technique [154, 155] is used to correlate electrical output data to mechanical damage parameters.
The electromechanical setup under consideration is detailed in Fig. 38, which shows the arrangement of direct electrical current input leads and potential probe output leads. Dimensions of the specimens, mechanical boundary conditions, elastic and fracture parameters of the material as well as discretization parameters of the model are the same considered in Sect. 3.1.2.
The electrical microconductivity function \(k_{e}(\psi , \zeta )\) is determined using Eqs. 163, 164 and 165. The set of discretized equations of the quasi-static coupled electro-mechanical problem under consideration are obtained by superposition of Eqs. 35 and 130 neglecting inertial and time dependent terms. In particular, the coupled stiffness operator characterizing each pairwise interaction is given by
where, according to Eqs. 37 and 132
while \(\breve{\mathbf {L}}_{m}\) and \(\breve{\mathbf {L}}_{e}\) are specific topology incidence matrices for coupled problems [72]. As can be seen from Eq. 174, the pairwise scalar valued function \(\upmu\) defined in Sect. 3 affects also the conductivity of the bond, and when \(\upmu =0\) it is no longer able to conduct electric current. Results of the non-linear electromechanical problem for different values of the angle of anisotropy \(\zeta\) are reported in Figs. 39 and 40. As can be observed from Fig. 40, the average slope of the \(\Delta \phi /\Delta \phi _{0}\) curves depend on the angle of anisotropy \(\zeta\), on the crack angle and crack pseudo-velocity. The latter effect can be excluded by reporting \(\Delta \phi /\Delta \phi _{0}\) as function of the crack length \(b_{k}\) (see Fig. 38) measured during the simulation. In this way, by detecting the average slopes of the \(\Delta \phi /\Delta \phi _{0}\)-\(b_{k}/a\) relationships (Fig. 41), it would be possible to get a direct determination of the actual crack length \(b_{k}\) from the value of \(\Delta \phi\) registered by potential probe output leads.
Damage sensing in conductive tissues: Layout of the electromechanical problem considered and arrangement of current input leads and potential probe leads for potential drop crack length determination
Damage sensing in conductive tissues: Electric potential maps corresponding to four subsequent steps of the simulation and obtained considering \(\zeta =0\) (\(S.0:\Delta u^{*}=0\mathrm {mm}\), \(\breve{o}=1\); \(S.1:\Delta u^{*}=0.169\mathrm {mm}\), \(\breve{o}=1.03\); \(S.2:\Delta u^{*}=0.211\mathrm {mm}\), , \(\breve{o}=1.10\); \(S.3:\Delta u^{*}=0.348\mathrm {mm}\), \(\breve{o}=1.16\)). Results are normalized with respect to the of the maximum value of the electric potential in the uncracked specimen (S.0)
Damage sensing in conductive tissues: Potential drop and force-displacement (F-\(\Delta u^{*}\)) relationship corresponding to the anisotropy angles \(\zeta =0\), \(\zeta =\pi /4\), \(\zeta =\pi /3\) and \(\zeta =\pi /2\)
Damage sensing in conductive tissues: \(\Delta \phi /\Delta \phi _{0}\) vs. normalized crack length \(b_{k}/a\) for direct determination of the actual crack length from the value of \(\Delta \phi\) registered by potential probe output leads (Electric potential differences for different angles \(\zeta\) are normalized with respect to the respective initial values)
5 Coupled Phenomena and Further Developments
For thermo-mechanical problems, the scalar-valued pairwise force function \(f_{\mathrm {n}}(\mathbf {x},\mathbf {x}^{\prime },t)\) defined in Eq. 8 can be modified including the temperature effect as
where \(\alpha _{\mathcal {T}}=\alpha _{\mathcal {T}}(\mathbf {x},\mathbf {x}^{\prime })\) is the linear thermal expansion coefficient along the direction \(\psi\) of the bond between \(\mathbf {x}\) and \(\mathbf {x}'\), whereas \(\bar{\mathcal {T}}\) is the average temperature change of the virtual fiber itself [58, 156]. Field equations are then modified accordingly to include the thermoelastic constitutive relation and the contribution from deformational heating and cooling, as detailed by Oterkus et. al [58].
A piezoresistive behavior could be modeled instead considering the electrical microconductivity \(k_{e}(\psi , \zeta )\) as function of an elastic deformation measure [50, 53]. In this case, the actual length of the fiber may be required in the definition of the pairwise electric field \(\varvec{e}\) as well as in Eq. 118 [50, 53].
Regarding elasticity, the definition of the third pairwise deformation parameter in Eq. 3, allows the model to be extended to microstructured materials homogenized as polar continua, for which a micro-macro correspondence involving bending moduli is also rerquired. In that case, it would be
which leads to elastic size effect proper of two-dimensional discrete heterogeneous materials, the resulting constitutive internal length being, in principle, independent of the size of the horizon. In fact, these non-local effects are not due to the integral nature of balance Eqs. 17 and 18, and then do not vanish when the horizon \(\delta\) goes to zero. This fundamental feature characterizing the conceived continuum-molecular framework would also give the possibility to model Cosserat anisotropic materials and to include chiral effects even associated to overall isotropic elastic properties. Besides, since piezoelectricity may be related to chiral asymmetry [157], this aspect would permit to estabilish a mechanism-based description of such complex phenomenon.
Consider here for simplicity the theoretical case of an orthotropic material within the context of couple stress-elasticity [80]. Assuming unit vectors of the reference basis aligned with the principal material axes, the constitutive behavior of the (centrosymmetric) couple-stress continuum is governed by Eq. 40 and
relating the couple-stress vector \(\mathbf {{m}}\) and the curvature vector \(\varvec{\upchi }\). The components of the tensor \(\mathbf {E}\) are \(E_{3i3i}, \; i=1,2\). Considering the micro-macro correspondence procedure particularized to this case, and the micromodulus function \(k_{\mathrm {b}}(\psi )\) given by
where \(\mathcal {K}_{3131}^{\mathrm {b}}\ge \mathcal {K}_{3232}^{\mathrm {b}}\), in case of \(n=2\) in Eq. 179 we obtain
where \(\mathcal {K}_{3131}^{\mathrm {b}}=\mathcal {K}_{3232}^{\mathrm {b}}\) if the material is isotropic or square symmetric (\(E_{3131}=E_{3232}\)).
6 Conclusions
In this paper we have proposed a unified scheme based on pair-potentials for continuum-molecular modeling of anisotropic elasticity, fracture and diffusion-type problems within the framework of a revised peridynamic theory with oriented material points. The governing equations of the model for both elasticity and diffusion-based problems have been derived using a variational formalism. The obtained elasticity equations are not affected by internal restrictions involving the number of independent material constants. An implicit implementation strategy based on a meshfree approach has been also detailed together with analytical expressions of the equivalent stiffness operators. Particular attention has been given to establish a general micro-macro moduli correspondence between the continuum-molecular and classical continuum physics material parameters, in such a way that the micromoduli and their corresponding angular functions reproduce the overall anisotropy of the material. This theoretical scheme couples the intuitive simplicity of a purely pairwise description of (generalized) deformation and constitutive laws (removing Cauchy relations restrictions in elasticity), with the mathematical formalism of a continuum formulation for anisotropic materials. Moreover, the presence of oriented material points in the mechanical formulation allows to establish a natural relation with polar continua, as well as with real lattice-like and full-discrete systems. The accuracy of the method has been assessed by several numerical experiments, whose results have been compared with both analytical solutions and experimental data.
Further studies are needed to extend the conceived anisotropic continuum-molecular model with oriented material points including multi-body potentials and other physical behaviors/physical problems such as piezoelectricity, Cosserat elasticity, cohesive fracture, plastic deformations, advection-diffusion and wave propagation.
Notes
Considering for the generic virtual fiber \(\hat{\mathbf {n}}\equiv \hat{\mathbf {e}}_{1}\), and \(\hat{\mathbf {t}}\equiv \hat{\mathbf {e}}_{2}\).
The considerations made in this section are general and can be extended to other cases. For Instance, Eq. 101 can be generalized further as \(\mathrm w_{c}(\psi , \zeta )= \mathrm w_{c2} + (\mathrm w_{c1}-\mathrm w_{c2}) \mathrm {cos}^{\textit{n}} [\mathcal {A}(\psi -\zeta )]\) with \(\mathcal {A} \in \mathbb {N}^{+}\) frequency parameter which allows to model different angular-dependent behaviors [122].
References
Navier CLMH (1827) Mémoire sur les lois de l’équilibre et du mouvement des corps solides élastiques. Mémoire Acad R Sci 6:375–384
Cauchy AL (1822) Sur l’équilibre et le mouvement d’un système de points matèriels sollicités par des forces d’attraction ou de répulsion. Exerc Math 3:188–213
Capecchi D, Ruta G, Trovalusci P (2010) From classical to Voigt’s molecular models in elasticity. Arch History Exact Sci 64(5):525–559
Capecchi D, Ruta G (2015) The theory of elasticity in the 19th century. Springer, New York
Cauchy A (1850) Mémoire sur les systèmes isotropes de points matériels. Mémoires Acad Sci 22:351–386
Poisson SD (1831) Mémoire sur les équations générales de l’équilibre et le du mouvement des corps solides élastiques et des fluides. J l’École Polytech 13(20):1–174
Capecchi D, Ruta G, Trovalusci P (2011) Voigt and Poincaré’s mechanistic-energetic approaches to linear elasticity and suggestions for multiscale modelling. Arch Appl Mech 81(11):1573–1584
Love AEH (1944) A treatise on the mathematical theory of elasticity. Dover, New York
Stakgold I (1950) The Cauchy relations in a molecular theory of elasticity. Q Appl Math 8(2):169–186
Voigt W (1887) Theoretische studien über die elasticitätsverhältnisse der krystalle. Abh Ges Wiss Gott 34:3–51
Voigt W (1910) Lehrbuch der Kristallphysik. B. G Teubner, Leipzig
Green G (1839) On the reflection and refraction of light at the common surface of two non-crystallized media. In: Mathematical papers, ed. Norman Macleod Ferrers, pp 245–269
Poincaré H (1892) Leçons sur la théorie de l’élasticité. G. Carré, Paris
Casolo S (2021) A linear-elastic heuristic-molecular modelling for plane isotropic micropolar and auxetic materials. Int J Solids Struct 224:111042
Silling SA (2000) Reformulation of elasticity theory for discontinuities and long-range forces. J Mech Phys Solids 48(1):175–209
Trageser J, Seleson P (2020) Peridynamics: a tale of two Poisson’s ratios. J Peridyn Nonlocal Model 2:278–288
Madenci E, Oterkus E (2014) Peridynamic theory and its applications. Springer, New York
Silling SA, Askari E (2005) A meshfree method based on the peridynamic model of solid mechanics. Comput Struct 83(17–18):1526–1535
Macek RW, Silling SA (2007) Peridynamics via finite element analysis. Finite Elem Anal Des 43(15):1169–1178
Hu W, Ha YD, Bobaru F, Silling SA (2012) The formulation and computation of the nonlocal j-integral in bond-based peridynamics. Int J Fract 176(2):195–206
Agwai A, Guven I, Madenci E (2011) Predicting crack propagation with peridynamics: a comparative study. Int J Fract 171(1):65–78
Bobaru F, Zhang G (2015) Why do cracks branch? a peridynamic investigation of dynamic brittle fracture. Int J Fract 196(1–2):59–98
Silling SA, Weckner O, Askari E, Bobaru F (2010) Crack nucleation in a peridynamic solid. Int J Fract 162(1–2):219–227
Ha YD, Bobaru F (2010) Studies of dynamic crack propagation and crack branching with peridynamics. Int J Fract 162(1–2):229–244
Ha YD, Bobaru F (2011) Characteristics of dynamic brittle fracture captured with peridynamics. Eng Fract Mech 78(6):1156–1168
Gao H, Klein P (1998) Numerical simulation of crack growth in an isotropic solid with randomized internal cohesive bonds. J Mech Phys Solids 46(2):187–218
Kunin IA (1984) On foundations of the theory of elastic media with microstructure. Int J Eng Sci 22(8):969–978
Kröner E (1967) Elasticity theory of materials with long range cohesive forces. Int J Solids Struct 3(5):731–742
Silling SA, Epton M, Weckner O, Xu J, Askari E (2007) Peridynamic states and constitutive modeling. J Elast 88(2):151–184
Warren TL, Silling SA, Askari A, Weckner O, Epton MA, Xu J (2009) A non-ordinary state-based peridynamic method to model solid material deformation and fracture. Int J Solids Struct 46(5):1186–1195
Silling SA, Lehoucq RB (2010) Peridynamic theory of solid mechanics. Adv Appl Mech 44:73–168
Silling SA (2010) Linearized theory of peridynamic states. J Elast 99(1):85–111
Sarego G, Le QV, Bobaru F, Zaccariotto M, Galvanetto U (2016) Linearized state-based peridynamics for 2-d problems. Int J Numer Methods Eng 108(10):1174–1197
Seleson P, Parks ML, Gunzburger M (2014) Peridynamic state-based models and the embedded-atom model. Commun Comput Phys 15(1):179–205
Javili A, McBride AT, Steinmann P (2019) Continuum-kinematics-inspired peridynamics. Mechanical problems. J Mech Phys Solids 131:125–146
Wang Y, Zhou X, Wang Y, Shou Y (2018) A 3-d conjugated bond-pair-based peridynamic formulation for initiation and propagation of cracks in brittle solids. Int J Solids Struct 134:89–115
Gerstle W, Sau N, Silling S (2007) Peridynamic modeling of concrete structures. Nucl Eng Des 237(12):1250–1258
Diana V (2019) Discrete physically-based models in solid mechanics. Ph.D. Dissertation, Politecnico di Milano, Milano
Diana V, Casolo S (2019) A bond-based micropolar peridynamic model with shear deformability: elasticity, failure properties and initial yield domains. Int J Solids Struct 160:201–231
Diana V, Ballarini R (2020) Crack kinking in isotropic and orthotropic micropolar peridynamic solids. Int J Solids Struct 196–197:76–98
Yu H, Chen X, Sun Y (2020) A generalized bond-based peridynamic model for quasi-brittle materials enriched with bond tension-rotation-shear coupling effects. Comput Methods Appl Mech Eng 372:113405
Zheng G, Shen G, Xia Y, Hu P (2020) A bond-based peridynamic model considering effects of particle rotation and shear influence coefficient. Comput Methods Appl Mech Eng 121(1):93–109
Yan X, Guo L, Li W (2021) Improved timoshenko beam-based micropolar peridynamic method incorporating particle geometry. Eng Fract Mech 254:107909
Bobaru F, Duangpanya M (2010) The peridynamic formulation for transient heat conduction. Int J Heat Mass Transf 53(19):4047–4059
Chen Z, Bobaru F (2015) Selecting the kernel in a peridynamic formulation: a study for transient heat diffusion. Comput Phys Commun 197:51–60
Seleson P, Gunzburger M, Parks ML (2013) Interface problems in nonlocal diffusion and sharp transitions between local and nonlocal domains. Comput Methods Appl Mech Eng 266:185–204
Gerstle W, Silling S, Read D, Tewary V, Lehoucq R (2008) Peridynamic simulation of electromigration. Tech Sci Press 8(2):75–92
Bobaru F, Duangpanya M (2012) A peridynamic formulation for transient heat conduction in bodies with evolving discontinuities. J Comput Phys 231(7):2764–2785
Zhao J, Chen Z, Mehrmashhadi J, Bobaru F (2018) Construction of a peridynamic model for transient advection-diffusion problems. Int J Heat Mass Transf 126:1253–1266
Prakash N, Seidel GD (2016) Electromechanical peridynamics modeling of piezoresistive response of carbon nanotube nanocomposites. Comput Mater Sci 113:154–170
Prakash N, Seidel GD (2017) Computational electromechanical peridynamics modeling of strain and damage sensing in nanocomposite bonded explosive materials (NCBX). Eng Fract Mech 177:180–202
Chen Z, Bobaru F (2015) Peridynamic modeling of pitting corrosion damage. J Mech Phys Solids 78:352–381
Diana V, Carvelli V (2020) An electromechanical micropolar peridynamic model. Comput Methods Appl Mech Eng 365:112998
Bazazzadeh S, Morandini M, Zaccariotto M, Galvanetto U (2021) Simulation of chemo-thermo-mechanical problems in cement-based materials with peridynamics. Meccanica 56(9):2357–2379
Li W, Guo L (2020) A mechanical-diffusive peridynamics coupling model for meso-scale simulation of chloride penetration in concrete under loadings. Construct Build Mater 241:118021
Chen W, Gu X, Zhang Q, Xia X (2021) A refined thermo-mechanical fully coupled peridynamics with application to concrete cracking. Eng Fract Mech 242:107463
Oterkus S, Madenci E, Agwai A (2014) Peridynamic thermal diffusion. J Comput Phys 265:71–96
Oterkus S, Madenci E, Agwai A (2014) Fully coupled peridynamic thermomechanics. J Mech Phys Solids 64:1–23
Katiyar A, Foster JT, Ouchi H, Sharma MM (2014) A peridynamic formulation of pressure driven convective fluid transport in porous media. J Comput Phys 261:209–229
Zhang H, Qiao P (2019) A state-based peridynamic model for quantitative elastic and fracture analysis of orthotropic materials. Eng Fract Mech 206:147–171
Hattori G, Trevelyan J, Coombs WM (2018) A non-ordinary state-based peridynamics framework for anisotropic materials. Comput Methods Appl Mech Eng 339:416–442
Xu J, Askari A, Weckner O, Silling S (2008) Peridynamic analysis of impact damage in composite laminates. J Aerosp Eng 21(3):187–194
Ghajari M, Iannucci L, Curtis P (2014) A peridynamic material model for the analysis of dynamic crack propagation in orthotropic media. Comput Methods Appl Mech Eng 276:431–452
Ren B, Wu CT, Seleson P, Zeng D, Lyu D (2018) A peridynamic failure analysis of fiber-reinforced composite laminates using finite element discontinuous Galerkin approximations. Int J Fract 214:49–68
Hu W, Ha YD, Bobaru F (2012) Peridynamic model for dynamic fracture in unidirectional fiber-reinforced composites. Comput Methods Appl Mech Eng 217–220:247–261
Zhou W, Liu D, Liu N (2017) Analyzing dynamic fracture process in fiber-reinforced composite materials with a peridynamic model. Eng Fract Mech 178:60–76
Oterkus E, Madenci E (2012) Peridynamic analysis of fiber-reinforced composite materials. J Mech Mater Struct 7(1):45–84
Seleson P, Trageser J (2019) Anisotropic two-dimensional, plane strain, and plane stress models in classical linear elasticity and bond-based peridynamics. arXiv
Thiagarajan G, Misra A (2004) Fracture simulation for anisotropic materials using a virtual internal bond model. Int J Solids Struct 41(11):2919–2938
He Q-C, Zheng Q-S (1996) On the symmetries of 2d elastic and hyperelastic tensors. J Elast 43(3):203–225
Diana V, Casolo S (2019) A full orthotropic micropolar peridynamic formulation for linearly elastic solids. Int J Mech Sci 160:140–155
Diana V, Carvelli V (2021) A continuum-molecular model for anisotropic electrically conductive materials. Int J Mech Sci 211:106759
Mikata Y (2020) Peridynamics for heat conduction. J Heat Transf 142(8):5
Boys B, Dodwell TJ, Hobbs M, Girolami M (2021) Peripy: a high performance OpenCL peridynamics package. Comput Methods Appl Mech Eng 386:114085
Bacigalupo A, Gambarotta L (2021) Identification of non-local continua for lattice-like materials. Int J Eng Sci 159:103430
Diana A, Bacigalupo A, Lepidi M, Gambarotta L (2022) Anisotropic peridynamics for homogenized microstructured materials. Comput Methods Appl Mech Eng 114704:392
Eringen AC (1966) A unified theory of thermomechanical materials. Int J Eng Sci 4(2):179–202
Seleson P, Parks ML (2011) On the role of the influence function in the peridynamic theory. Int J Multisc Comput Eng 9(6):689–706
Cosserat E, Cosserat F (1909) Théorie des corps déformables. A. Herrmann et Fils, Paris
Toupin RA (1962) Elastic materials with couple-stresses. Arch Ration Mech Anal 11(1):385–414
Holzapfel GA (2000) Nonlinear solid mechanics: a continuum approach for engineering. Wiley, Chichester
Hu W, Ha YD, Bobaru F (2010) Numerical integration in peridynamics. Tech. Rep., University of Nebraska-Lincoln, Department of Mechanical & Materials Engineering
Seleson P (2014) Improved one-point quadrature algorithms for two-dimensional peridynamic models based on analytical calculations. Comput Methods Appl Mech Eng 282:184–217
Trask N, You H, Yu Y, Parks ML (2019) An asymptotically compatible meshfree quadrature rule for nonlocal problems with applications to peridynamics. Comput Methods Appl Mech Eng 343:151–165
Hughes TJ (2000) The finite element method: linear static and dynamic finite element analysis. Dover Publications, New York
DiCarlo A, Podio-Guidugli P (2021) From point particles to body points. Math Eng 4(1):1–29
Ericksen JL (1984) The Cauchy and born hypotheses for crystals. In: Gurtin ME (ed) Phase transformations and material instabilities in solids. Academic Press, New York, pp 61–77
Ericksen JL (2008) On the Cauchy-Born rule. Math Mech Solids 13(3–4):199–220
Trageser J, Seleson P (2022) A new proof that the number of linear elastic symmetries in two dimensions is four. J Elast 5:1–19
Lakes R (1996) Cellular solid structures with unbounded thermal expansion. J Mater Sci Lett 15(6):475–477
Taylor M, Francesconi L, Gerendás M, Shanian A, Carson C, Bertoldi K (2014) Low porosity metallic periodic structures with negative Poisson’s ratio. Adv Mater 26(15):2365–2370
Wojciechowski KW, Alderson A, Grima JN, Scarpa F (2020) Auxetics and other systems with “negative’’ characteristics. Phys Status Solidi B 257(10):2000496
Chen H, Lin E, Liu Y (2014) A novel volume-compensated particle method for 2d elasticity and plasticity analysis. Int J Solids Struct 51(9):1819–1833
Hrennikoff A (1941) Solution of problems of elasticity by the framework method. ASME J Appl Mech 12:169–175
Zhao S-F, Zhao G-F (2012) Implementation of a high order lattice spring model for elasticity. Int J Solids Struct 49(18):2568–2581
Ostoja-Starzewski M (2002) Lattice models in micromechanics. Appl Mech Rev 55(1):35–59
Griffiths DV, Mustoe GGW (2001) Modelling of elastic continua using a grillage of structural elements based on discrete element concepts. Int J Numer Methods Eng 50(7):1759–1775
Bacigalupo A, Gambarotta L (2020) Chiral two-dimensional periodic blocky materials with elastic interfaces: auxetic and acoustic properties. Extreme Mech Lett 39:100769
Liu XN, Huang GL, Hu GK (2012) Chiral effect in plane isotropic micropolar elasticity and its application to chiral lattices. J Mech Phys Solids 60(11):1907–1921
Zhennan Z, Xiurun G (2006) Micromechanical modelling of elastic continuum with virtual multi-dimensional internal bonds. Int J Numer Methods Eng 65(1):135–146
Bacigalupo A, Gambarotta L (2017) Dispersive wave propagation in two-dimensional rigid periodic blocky materials with elastic interfaces. J Mech Phys Solids 102:165–186
Kochmann DM, Drugan WJ (2012) Analytical stability conditions for elastic composite materials with a non-positive-definite phase. Proc R Soc A 468(2144):2230–2254
Drugan WJ (2007) Elastic composite materials having a negative stiffness phase can be stable. Phys Rev Lett 98:055502
Bobaru F (2011) Peridynamics and multiscale modeling. Int J Multisc Comput Eng 28:13–15
Ballarini R, Diana V, Biolzi L, Casolo S (2018) Bond-based peridynamic modelling of singular and nonsingular crack-tip fields. Meccanica 53(14):3495–3515
Le QV, Bobaru F (2017) Surface corrections for peridynamic models in elasticity and fracture. Comput Mech 61(4):499–518
Lekhnitskii SG (1963) Theory of elasticity of an anisotropic body. Holden-Day Inc, San Francisco
Azhdari A, Nemat-Nasser S (1996) Hoop stress intensity factor and crack-kinking in anisotropic brittle solids. Int J Solids Struct 33(14):2023–2037
Sih GC, Paris PC, Irwin GR (1965) On cracks in rectilinearly anisotropic bodies. Int J Fract Mech 1(3):189–203
Chiang CR (1991) Kinked cracks in an anisotropic material. Eng Fract Mech 39(5):927–930
Dontsova E, Ballarini R (2017) Atomistic modeling of the fracture toughness of silicon and silicon-silicon interfaces. Int J Fract 207(1):99–122
Paris PC (2014) A brief history of the crack tip stress intensity factor and its application. Meccanica 49(4):759–764
Silling SA, Lehoucq RB (2008) Convergence of peridynamics to classical elasticity theory. J Elast 93(1):13–37
Bobaru F, Foster JT, Geubelle PH, Silling SA (2015) Handbook of peridynamic modeling. Advances in applied mathematics. CRC Press, Boca Raton
Foster J, Silling S, Chen W (2011) An energy based failure criterion for use with peridynamic states. Int J Multisc Comput Eng 9(6):675–687
Azhdari A, Nemat-Nasser S (1996) Energy-release rate and crack kinking in anisotropic brittle solids. J Mech Phys Solids 44(6):929–951
Panchadhara R, Gordon PA (2016) Application of peridynamic stress intensity factors to dynamic fracture initiation and propagation. Int J Fract 201(1):81–96
Jiang C, Zhao G-F, Khalili N (2017) On crack propagation in brittle material using the distinct lattice spring model. Int J Solids Struct 118–119:41–57
Zheng G, Shen G, Xia Y, Hu P (2020) A bond-based peridynamic model considering effects of particle rotation and shear influence coefficient. Int J Numer Methods Eng 121(1):93–109
Bie YH, Liu ZM, Yang H, Cui XY (2020) Abaqus implementation of dual peridynamics for brittle fracture. Comput Methods Appl Mech Eng 372:113398
Mandal TK, Nguyen VP, Wu J-Y (2020) A length scale insensitive anisotropic phase field fracture model for hyperelastic composites. Int J Mech Sci 188:105941
Rezaei S, Mianroodi JR, Brepols T, Reese S (2021) Direction-dependent fracture in solids: atomistically calibrated phase-field and cohesive zone model. J Mech Phys Solids 147:104253
Bourdin B, Francfort GA, Marigo J (2008) The variational approach to fracture. J Elast 91:5–148
Ambati M, Gerasimov T, De Lorenzis L (2015) A review on phase-field models of brittle fracture and a new fast hybrid formulation. Comput Mech 55:383–405
Ni T, Zaccariotto M, Zhu Q-Z, Galvanetto U (2019) Static solution of crack propagation problems in peridynamics. Comput Methods Appl Mech Eng 346:126–151
Miehe C, Welschinger F, Hofacker M (2010) Thermodynamically consistent phase-field models of fracture: variational principles and multi-field fe implementations. Int J Numer Methods Eng 83(10):1273–1311
Amor H, Marigo J-J, Maurini C (2009) Regularized formulation of the variational brittle fracture with unilateral contact: numerical experiments. J Mech Phys Solids 57(8):1209–1229
Kakouris EG, Triantafyllou SP (2017) Phase-field material point method for brittle fracture. Int J Numer Methods Eng 112(12):1750–1776
Bourdin B, Francfort GA, Marigo J-J (2000) Numerical experiments in revisited brittle fracture. J Mech Phys Solids 48(4):797–826
Francfort GA, Marigo J-J (1998) Revisiting brittle fracture as an energy minimization problem. J Mech Phys Solids 46(8):1319–1342
Freddi F, Royer-Carfagni G (2010) Regularized variational theories of fracture: a unified approach. J Mech Phys Solids 58(8):1154–1174
Paggi M, Corrado M, Reinoso J (2018) Fracture of solar-grade anisotropic polycrystalline silicon: a combined phase field-cohesive zone model approach. Comput Methods Appl Mech Eng 330:123–148
Erdogan F, Sih GC (1963) On the crack extension in plates under plane loading and transverse shear. J Basic Eng 85(4):519–525
Gao H, Chiu C-H (1992) Slightly curved or kinked cracks in anisotropic elastic solids. Int J Solids Struct 29(8):947–972
Obata M, Nemat-Nasser S, Goto Y (1989) Branched cracks in anisotropic elastic solids 56(4):858–864
Wu CH (1978) Maximum-energy-release-rate criterion applied to a tension-compression specimen with crack. J Elast 8(3):235–257
Koester AJK, Ritchie R (2008) The true toughness of human cortical bone measured with realistically short cracks. Nat Mater 7:672–677
Bonfield W, Behiri JC (1989) Fracture toughness of natural composites with reference to cortical bone. Compos Mater Ser 6:615–635
Behiri JC, Bonfield W (1989) Orientation dependence of the fracture mechanics of cortical bone. J Biomech 22(8):863–872
Van-Buskirk WC, Owin SC, Ward RN (1981) Ultrasonic measurement of orthotropic elastic constants of bovine femoral bone. J Biomech Eng 103:67–72
Behiri JC, Bonfield W (1984) Fracture mechanics of bone-the effects of density, specimen thickness and crack velocity on longitudinal fracture. J Biomech 17(1):25–34
Emery AF, Carson WW (1971) An evaluation of the use of the finite-element method in the computation of temperature. J Heat Transf 93(2):136–145
Schechter RS (1967) The variational method in engineering. McGraw-Hill Inc, New York
Zienkiewicz OC, Cheung YK (1965) Finite elements in the solution of field problems. Engineer 220(5722):507–510
Rosen P (1954) Use of restricted variational principles for the solution of differential equations. J Appl Phys 25(3):336–338
Rosen P (1953) On variational principles for irreversible processes. J Chem Phys 21(7):1220–1221
Bathe K-J (1996) Finite element procedures. Prentice Hall, Englewood Cliffs NJ
Logan DL (2016) A first course in the finite element method. Cengage Learning, Boston
Guo Z-Y, Zhu H-Y, Liang X-G (2007) Entransy: a physical quantity describing heat transfer ability. Int J Heat Mass Transf 50(13):2545–2556
Mera NS, Elliott L, Ingham DB, Lesnic D (2001) A comparison of boundary element method formulations for steady state anisotropic heat conduction problems. Eng Anal Bound Elements 25(2):115–128
Wang H, Quin Q-H, Kang YL (2005) A new meshless method for steady-state heat conduction problems in anisotropic and inhomogeneous media. Archiv Appl Mech 74:563–579
Chakkalakal DA, Johnson MW, Harper RA, Katz JL (1980) Dielectric properties of fluid-saturated bone. IEEE Trans Biomed Eng BME 27(2):95–100
Reddy GN, Saha S (1984) Electrical and dielectric properties of wet bone as a function of frequency. IEEE Trans Biomed Eng BME 31(3):296–303
Tong J (2001) Notes on direct current potential drop calibration for crack growth in compact tension specimens. J Test Eval 29(4):402–406
Tarnowski K, Nikbin K, Dean D, Davies D (2018) A unified potential drop calibration function for common crack growth specimens. Exp Mech 58:1003–1013
Bazazzadeh S, Mossaiby F, Shojaei A (2020) An adaptive thermo-mechanical peridynamic model for fracture analysis in ceramics. Eng Fract Mech 223:106708
Lakes R (2001) Elastic and viscoelastic behavior of chiral materials. Int J Mech Sci 43(7):1579–1589
Acknowledgements
This paper is dedicated to the author’s son Matias Giacomo.
Funding
Open access funding provided by Università degli Studi di Genova within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest:
The author declares that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Diana, V. Anisotropic Continuum-Molecular Models: A Unified Framework Based on Pair Potentials for Elasticity, Fracture and Diffusion-Type Problems. Arch Computat Methods Eng 30, 1305–1344 (2023). https://doi.org/10.1007/s11831-022-09846-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11831-022-09846-0