Abstract
For a compact set \(K \subset {\mathbb {C}}^n\), let \(A \subset C(K)\) be a function algebra containing the polynomials \({\mathbb {C}}[z_1,\cdots ,z_n ]\). Assuming that a certain regularity condition holds for A, we prove a commutant-lifting theorem for A-isometries that contains the known results for isometric subnormal tuples in its different variants as special cases, e.g., Mlak (Studia Math. 43(3): 219–233, 1972) and Athavale (J. Oper. Theory 23(2): 339–350, 1990; Rocky Mt. J. Math. 48(1): 2018; Complex Anal. Oper. Theory 2(3): 417–428, 2008; New York J. Math. 25: 934–948, 2019). In the context of Hilbert-A-modules, our result implies the existence of an extension map  for hypo-Shilov-modules
for hypo-Shilov-modules  \((i=1,2)\). By standard arguments, we obtain an identification
\((i=1,2)\). By standard arguments, we obtain an identification  where
where  is the minimal \(C(\partial _A)\)-extension of
is the minimal \(C(\partial _A)\)-extension of  \((i=1,2)\), provided that
\((i=1,2)\), provided that  is projective and
is projective and  is pure. Using embedding techniques, we show that these results apply in particular to the domain algebra \(A=A(D)=C({\overline{D}})\cap {\mathcal {O}}(D)\) over a product domain \(D = D_1 \times \cdots \times D_k \subset {\mathbb {C}}^n\) where each factor \(D_i\) is either a smoothly bounded, strictly pseudoconvex domain or a bounded symmetric and circled domain in some \({\mathbb {C}}^{d_i}\) (\(1\le i \le k\)). This extends known results from the ball and polydisc-case, Guo (Studia Math. 135(1): 1–12, 1999) and Chen and Guo (J. Oper. Theory 43: 69–81, 2000).
is pure. Using embedding techniques, we show that these results apply in particular to the domain algebra \(A=A(D)=C({\overline{D}})\cap {\mathcal {O}}(D)\) over a product domain \(D = D_1 \times \cdots \times D_k \subset {\mathbb {C}}^n\) where each factor \(D_i\) is either a smoothly bounded, strictly pseudoconvex domain or a bounded symmetric and circled domain in some \({\mathbb {C}}^{d_i}\) (\(1\le i \le k\)). This extends known results from the ball and polydisc-case, Guo (Studia Math. 135(1): 1–12, 1999) and Chen and Guo (J. Oper. Theory 43: 69–81, 2000).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 A-Isometries
Let  be a separable complex Hilbert space. A spherical isometry is a commuting tuple
be a separable complex Hilbert space. A spherical isometry is a commuting tuple  of bounded linear operators on
of bounded linear operators on  that satisfies the condition
that satisfies the condition  . Athavale proved in [3] that spherical isometries are subnormal with normal spectrum \(\sigma _n(T)\) conained in \(\partial {\mathbb {B}}_n\), a fact which provides them with a natural \(A({\mathbb {B}}_n)\)-functional calculus, where \(A({\mathbb {B}}_n) = \{ f\in C({\overline{{\mathbb {B}}}}_n): f |{\mathbb {B}}_n \text { is holomorphic} \}\) denotes the ball algebra. Replacing \(A({\mathbb {B}}_n)\) with a general function algebra \(A \subset C(K)\) on a compact set \(K\subset {\mathbb {C}}^n\) and \(\partial {\mathbb {B}}_n\) with its Shilov-boundary \(\partial _A\), one arrives at the notion of A-isometry as introduced by Eschmeier in [16] (see below for a precise definition). It is this general setting in which we will formulate most of our results. We use the same notations as in [14] and [17]. A reader familiar with one of these works may readily proceed with Sect. 2.
. Athavale proved in [3] that spherical isometries are subnormal with normal spectrum \(\sigma _n(T)\) conained in \(\partial {\mathbb {B}}_n\), a fact which provides them with a natural \(A({\mathbb {B}}_n)\)-functional calculus, where \(A({\mathbb {B}}_n) = \{ f\in C({\overline{{\mathbb {B}}}}_n): f |{\mathbb {B}}_n \text { is holomorphic} \}\) denotes the ball algebra. Replacing \(A({\mathbb {B}}_n)\) with a general function algebra \(A \subset C(K)\) on a compact set \(K\subset {\mathbb {C}}^n\) and \(\partial {\mathbb {B}}_n\) with its Shilov-boundary \(\partial _A\), one arrives at the notion of A-isometry as introduced by Eschmeier in [16] (see below for a precise definition). It is this general setting in which we will formulate most of our results. We use the same notations as in [14] and [17]. A reader familiar with one of these works may readily proceed with Sect. 2.
1.1 Subnormal tuples
A tuple  is called subnormal, if there is a commuting tuple of normal operators
is called subnormal, if there is a commuting tuple of normal operators  on a Hilbert space
on a Hilbert space  such that
such that  is invariant for the components of U and
is invariant for the components of U and  . We suppose in the following that U is minimal in the sense that the only reducing subspace for U containing
. We suppose in the following that U is minimal in the sense that the only reducing subspace for U containing  is
is  . The normal spectrum of T is defined as \(\sigma _n(T) = \sigma (U)\), where \(\sigma (U)\) denotes the Taylor spectrum of U. This is independent of the special choice of U. By a result of Putinar, the spectral inclusion \(\sigma _n(T) \subset \sigma (T)\) holds. Spectral theory for normal tuples asserts the existence of a so-called scalar spectral measure, i. e., a finite positive Borel measure \(\mu \) on \(\sigma (U)\) with the property that there exists an isomorphism of von Neumann algebras
. The normal spectrum of T is defined as \(\sigma _n(T) = \sigma (U)\), where \(\sigma (U)\) denotes the Taylor spectrum of U. This is independent of the special choice of U. By a result of Putinar, the spectral inclusion \(\sigma _n(T) \subset \sigma (T)\) holds. Spectral theory for normal tuples asserts the existence of a so-called scalar spectral measure, i. e., a finite positive Borel measure \(\mu \) on \(\sigma (U)\) with the property that there exists an isomorphism of von Neumann algebras

called the \(L^\infty \)-functional calculus of U. (Note that such a measure \(\mu \) is unique up to mutual absolute continuity.) One then defines the restriction algebra

which is a \(w^*\)-closed subalgebra of \(L^\infty (\mu )\) containing the polynomials \({\mathbb {C}}[z]\) in n complex vairables \(z=(z_1, \cdots , z_n)\). By [10, Proposition 1.1], the induced \(w^*\)-continuous algebra homomorphism

is isometric again. It satisfies the following uniqueness property:
where the symbol f(T) on the right-hand side is meant in the sense of Taylor’s holomorphic functional calculus (see, e.g., [18], Chapter 2). To see this, recall that the \(L^\infty \)-calculus \(\Psi _U\) satisfies a spectral mapping theorem of the form \(\sigma (\Psi _U(f_1), \cdots , \Psi _U(f_k)) = F(\sigma (U))\) for every k-tuple \(F=(f_1, \cdots , f_k) \in C(K)^k\) with \(k \in {\mathbb {N}}\) (see, e. g., [29], Section 0.3 and the references therein). A well-known uniqueness result for Taylor’s functional calculus (cp. Theorem 5.2.4 in [18]) then guarantees that \(\Psi _U(f) = f(U)\) for every \(f\in {\mathcal {O}}(W)\) if \(W \subset {\mathbb {C}}^n\) is any open set containing \(\sigma (U)\). If we even assume that \(W \supset \sigma (T)\), we can apply Lemma 2.5.8 in [18] to the inclusion map  as intertwiner of T and U to deduce that
as intertwiner of T and U to deduce that  for \(f\in {\mathcal {O}}(W)\). Hence the asserted uniqueness (1.1) follows.
for \(f\in {\mathcal {O}}(W)\). Hence the asserted uniqueness (1.1) follows.
1.2 A-subnormal tuples, A-isometries
Fix a compact set \(K\subset {\mathbb {C}}^n\) and let C(K) denote the algebra of all continuous complex-valued functions equipped with the supremum norm. For a closed subalgebra \(A\subset C(K)\), we write \(\partial _A\) for the Shilov boundary of A, i.e. the smallest closed subset of K such that \(\Vert f\Vert _{\infty , K} = \Vert f\Vert _{\infty , \partial _A}\). Following Eschmeier, [16], we define:
Definition 1.1
Suppose that \(A\subset C(K)\) is a closed subalgebra containing \({\mathbb {C}}[z]\). A subnormal tuple \(T\in B(H)^n\) is said to be A-subnormal, if \(\sigma _n(T) \subset K\) and  . If, in addition, \(\sigma _n(T) \subset \partial _A\), then T is said to be an A-isometry. An A-isometry consisting of normal operators is called A-unitary.
. If, in addition, \(\sigma _n(T) \subset \partial _A\), then T is said to be an A-isometry. An A-isometry consisting of normal operators is called A-unitary.
Natural choices for A to consider are algebras of disc-algebra type, that is,
where \(D \subset {\mathbb {C}}^n\) is a suitably chosen bounded open set. As pointed out above, setting \(A = A({\mathbb {B}}_n)\) yields exactly the class of spherical isometries, whereas \(A({\mathbb {D}}^n)\)-isometries (\({\mathbb {D}}\subset {\mathbb {C}}\) stands for the open unit disc) are precisely commuting tuples whose components are isometric operators on  .
.
Let now  be an A-subnormal tuple for \(A\subset C(K)\) as in the definition, and fix a scalar spectral measure \(\mu \) of its minimal normal extension. Via trivial extension, we may regard \(\mu \) as an element of \(M^+(K)\), the set of all finite regular Borel measures on K. Since
be an A-subnormal tuple for \(A\subset C(K)\) as in the definition, and fix a scalar spectral measure \(\mu \) of its minimal normal extension. Via trivial extension, we may regard \(\mu \) as an element of \(M^+(K)\), the set of all finite regular Borel measures on K. Since  is \(w^*\)-closed and assumed to contain A, the restriction of \(\gamma _T\) to the algebra
is \(w^*\)-closed and assumed to contain A, the restriction of \(\gamma _T\) to the algebra
is well defined. By the properties of \(\gamma _T\) stated above, it therefore induces an isometric and \(w^*\)-continuous isomorphism onto its image \({\mathcal {T}}_a(T)=\gamma _T(H^\infty _A(\mu ))\) (the set of all so-called analytic T-Toeplitz operators). To keep the notation simple, we denote the induced map again by \(\gamma _T\), and call it the canonical \(H^\infty \)-functional calculus of T:

1.3 A-unitary dilations
Let again  be A-subnormal with minimal normal extension
be A-subnormal with minimal normal extension  . As a \(*\)-homomorphism, the map
. As a \(*\)-homomorphism, the map  is completely contractive, and hence so is
is completely contractive, and hence so is  , if A is regarded as an operator subspace of C(K). Since both embeddings \(A\subset C(K)\) and \(A\subset C(\partial _A)\) induce the same operator space structure on A (see [27, Theorem 3.9]), a theorem of Arveson (see, e.g., [27, Corollary 7.7]) asserts that there exists an A-unitary tuple
, if A is regarded as an operator subspace of C(K). Since both embeddings \(A\subset C(K)\) and \(A\subset C(\partial _A)\) induce the same operator space structure on A (see [27, Theorem 3.9]), a theorem of Arveson (see, e.g., [27, Corollary 7.7]) asserts that there exists an A-unitary tuple  on a Hilbert space
on a Hilbert space  such that
such that

We call such a tuple an A-unitary dilation of T. When restricted to the smallest closed subspace that contains  and reduces V, it is said to be a minimal A-unitary dilation.
and reduces V, it is said to be a minimal A-unitary dilation.
2 Regularity
If  is an A-subnormal tuple, then one can use its canonical functional calculus \(\gamma _T\) to carry over approximation properties of the underlying function algebra A to the algebra \({\mathcal {T}}_a(T)\) of analytic Toeplitz operators. As it turns out, of particular interest are approximation properties of A that are related to the so-called abstract inner function problem. In its classical form, the inner function problem asks if there are non-constant bounded analytic functions \(\theta : {\mathbb {B}}_n\rightarrow {\mathbb {C}}\) on the unit ball \({\mathbb {B}}_n\) such that their radial limit \({{\tilde{\theta }}} :\partial {\mathbb {B}}_n \rightarrow {\mathbb {C}}\) satisfies \(|{{\tilde{\theta }}}|= 1\) \(\sigma \)-a.e. (so-called inner functions). Here, \(\sigma \) denotes the normalized surface measure on \(\partial {\mathbb {B}}_n\). In his celebrated work [1], Aleksandrov succeded to solve the inner function problem for what he called “regular triples” \((A,K,\mu )\) (cf. Corollary 29 therein and Proposition 2.6 below for a suitable formulation in our context). The triple \((A({\mathbb {B}}_n), {\overline{{\mathbb {B}}}}_n, \sigma )\) models the classical context. The precise definition of regularity reads as follows:
is an A-subnormal tuple, then one can use its canonical functional calculus \(\gamma _T\) to carry over approximation properties of the underlying function algebra A to the algebra \({\mathcal {T}}_a(T)\) of analytic Toeplitz operators. As it turns out, of particular interest are approximation properties of A that are related to the so-called abstract inner function problem. In its classical form, the inner function problem asks if there are non-constant bounded analytic functions \(\theta : {\mathbb {B}}_n\rightarrow {\mathbb {C}}\) on the unit ball \({\mathbb {B}}_n\) such that their radial limit \({{\tilde{\theta }}} :\partial {\mathbb {B}}_n \rightarrow {\mathbb {C}}\) satisfies \(|{{\tilde{\theta }}}|= 1\) \(\sigma \)-a.e. (so-called inner functions). Here, \(\sigma \) denotes the normalized surface measure on \(\partial {\mathbb {B}}_n\). In his celebrated work [1], Aleksandrov succeded to solve the inner function problem for what he called “regular triples” \((A,K,\mu )\) (cf. Corollary 29 therein and Proposition 2.6 below for a suitable formulation in our context). The triple \((A({\mathbb {B}}_n), {\overline{{\mathbb {B}}}}_n, \sigma )\) models the classical context. The precise definition of regularity reads as follows:
Definition 2.1
Let \(K \subset {\mathbb {C}}^n\) compact and \(A\subset C(K)\) a closed subalgebra.
-
(a)
For \(\mu \in M^+(K)\), the triple \((A,K,\mu )\) is called regular (in the sense of Aleksandrov [1]), if for every \(\varphi \in C(K)\) with \(\varphi >0\), there is a sequence \((f_k)\) in A satisfying \(|f_k|<\varphi \) (on K) for all \(k \in {\mathbb {N}}\) and \(\lim _{k\rightarrow \infty }|f_k| = \varphi \) (\(\mu \)-a.e. on K).
-
(b)
We call the algebra \(A\subset C(K)\) itself regular, if \((A,K,\mu )\) is regular for every measure \(\mu \in M^+(K)\) with \(\text {supp}(\mu ) \subset \partial _A\).
Note that the condition on the support of \(\mu \) in part (b) of the preceding definition results from the fact that the stated inclusion necessarily holds for regular triples. A concrete source of regular triples is the following embedding criterion due to Aleksandrov:
Theorem 2.2
(Aleksandrov [2, Theorem 3]) Let \(A \subset C(K)\) be a function algebra on a compact set K. Suppose that, for some \(m\in {\mathbb {N}}\), there exists an injective map \(F \in A^m\) such that \(F(\partial _A) \subset \partial {\mathbb {B}}_m\). Then, \(A\subset C(K)\) is regular.
Using this criterion, one can show that the algebra A(D) is regular for various kinds of open sets \(D \subset {\mathbb {C}}^n\), among them bounded symmetric and circled domains, and relatively compact, strictly pseudoconvex open subsets of \({\mathbb {C}}^n\), or even of a Stein submanifold of \({\mathbb {C}}^n\) (cp. [1, 2] and [11, Corollary 2.1.3 (e)]). By constructing a suitable embedding, we show the following result for product domains:
Theorem 2.3
Let \(k\in {\mathbb {N}}\) and \(D_i \subset {\mathbb {C}}^{d_i}\) be open sets with \(d_i \in {\mathbb {N}}\) for \(1 \le i \le k\), each of which is either a strictly pseudoconvex domain with \(C^2\) boundary or a bounded symmetric and circled domain. Then the algebra \(A(D_1 \times \cdots \times D_k)\subset C({\overline{D}}_1 \times \cdots \times {\overline{D}}_k)\) is regular.
We first recall some basic facts about bounded symmetric domains: By definition, a bounded domain \(D \subset {\mathbb {C}}^d\) is symmetric if, for each \(z\in D\), there exists a biholomorphic map \(s_z:D \rightarrow D\) possessing z as isolated fixed point such that \(s_z \circ s_z = \text {id}_D\). We assume that D is circled at the origin, i. e., \(0 \in D\) and \(zD \subset D\) for \(z \in {\mathbb {C}}\) with \(|z|=1\). Every set of this type is convex [24, Corollary 4.6] and the Shilov boundary of A(D) consists precisely of those points in \({\overline{D}}\) with maximal Euclidean distance from the origin in \({\mathbb {C}}^d\) [24, Theorem 6.5]. Since every finite product of bounded symmetric and circled domains is again of this type, we only have to consider one such factor in Theorem 2.3. To keep the notations in the proof simple, we restrict ourselves to the case
where \(D_1\) and \(D_2\) are strictly pseudoconvex sets and \(D_3\) is the circled and bounded symmetric factor. This is no restriction, since the result is well-known for \(k=1\) (see the references given above), whereas the cases \(k=2\) and \(k > 3\) can be handled by straight-forward modifications of our construction described below. In the following, we write \(S_D = \partial _{A(D)}\).
To start with, let us fix real numbers \(r_1,r_2,r_3>0\) such that
We first calculate the Shilov boundary of D. From the existence of peaking functions for every boundary point of a strictly pseudoconvex domain (see Range [28, Corollary VI.1.14]), it follows that \(S_{D_i} = \partial D_i\) for the strictly pseudoconvex factors \(i=1,2\).
Lemma 2.4
\(S_D = \partial {D_1} \times \partial D_2 \times S_{D_3}.\)
Proof
Fix an arbitrary \(z=(z_1,z_2,z_3) \in D_1 \times D_2 \times D_3\). Since \(f(\cdot , z_2, z_3) \in A(D_1)\), there is a \(w_1 \in \partial D_1\) such that \(|f(z_1,z_2,z_3)| \le |f(w_1,z_2,z_3)|\). Repeating the argument twice, we obtain \(w_2 \in \partial D_2\) and \(w_3 \in S_{D_3}\) such that \(|f(z_1,z_2,z_3)| \le |f(w_1,w_2,w_3)|\). This shows that \(\partial {D_1} \times \partial D_2 \times S_{D_3}\) is a boundary for A(D). Now fix \(w=(w_1,w_2,w_3)\) in the latter product set. To finish the proof, it suffices to observe that \(h(z_1,z_2,z_3) = h_1(z_1)\cdot h_2(z_2)\cdot h_3(z_3)\) is a peaking function for w, if \(h_i \in A(D_i)\) is a peaking functions for \(w_i\) \((i=1,2,3)\). For the strictly pseudoconvex factors, such functions exist by the reference given above. For \(D_3\), we may take the restriction of a peaking function for \(w_3\) in \(A(r_3 \cdot {\mathbb {B}}_{d_3})\). \(\square \)
The key ingredient in the proof of Theorem 2.3, is an embedding theorem of Løw [25, Theorem 3]. Reduced to what we need, this theorem says the following: Given a strictly pseudoconvex domain \(D\subset {\mathbb {C}}^n\) with \(C^2\)-boundary and a strictly positive continuous function \(\phi : \partial D \rightarrow (0,\infty )\), there exists a mapping \(g \in A(D)^l\) for some natural number l such that \(|g(z)|= \phi (z)\) for every \(z\in \partial D\).
Proof of Theorem 2.3
Since, by assumption, \({\overline{D}}_i \subset r_i \cdot {\mathbb {B}}_{d_i}\) for \(i=1,2\), the functions \(\phi _i(z) = (r^2_i - |z|^2)^{\frac{1}{2}}\) (\(z \in \partial D_i,\ i=1,2\)) are strictly positive if \(|\cdot |\) denotes the Euclidean norm on \({\mathbb {C}}^{d_i}\). By the cited theorem of Løw, we find \(g_i \in A(D_i)^{l_i}\) \((i=1,2)\) with \(|g_i(z)| = \phi _i(z)\) \((z \in \partial D_i)\). Then we set \(r = \sqrt{r_1^2 + r_2^2+ r_3^2}\) and define
to obtain an injective mapping \(F \in A(D)^m\) with \(m = d_1+d_2+d_3+l_1+l_2\) which, for \(z = (z_1,z_2,z_3) \in \partial D_1 \times \partial D_2 \times r_3 \cdot \partial {\mathbb {B}}_{d_3}\), satisfies
Together with Lemma 2.4 and the fact that \(S_{D_3} \subset r_3\cdot \partial {\mathbb {B}}_{d_3}\), this yields the inclusion \(F(S_D) \subset \partial {\mathbb {B}}_m\). The desired regularity now follows as an application of Aleksandrov’s embedding criterion stated as Theorem 2.2 above. \(\square \)
Remark 2.5
Let \(F \in A(D)^m\), and let \(|\cdot |\) denote the Euclidean norm and \(\langle \cdot ,\cdot \rangle \) the Euclidean scalar-product on \({\mathbb {C}}^m\). By considering scalar-valued functions of the form \(\langle F(\cdot ), F(w)\rangle \) with suitably chosen \(w \in {\overline{D}}\), one can show that |F| takes its maximum value on the Shilov boundary \(S_D\), and that F must be constant if |F| takes its maximum at some point inside D. In view if this, we can – for further reference – state some additional properties of the map F constructed in the proof of Theorem 2.3, namely \(F({\overline{D}}) \subset {\overline{{\mathbb {B}}}}_{m}\) and \(F(D) \subset {\mathbb {B}}_{m}\). Moreover, we remark that the map \(F: {\overline{D}} \rightarrow F({\overline{D}})\) is a homeomorphism, as it is a continuous bijection from a compact space onto a Hausdorff space.
As for the scope of Theorem 2.3, we should remark that every bounded open set \(D \subset {\mathbb {C}}\) with \(C^2\) boundary is strictly pseudoconvex, cp. the remark at the end of Section 1.5 in [22]. So, in particular \(A(D)\subset C({\overline{D}})\), is regular for polydomains \(D=D_1\times \cdots \times D_k\) with \(C^2\)-bounded domains \(D_i \subset {\mathbb {C}}\) \((i=1,\cdots , k)\).
Now, let \((A, K, \mu )\) be a regular triple. In analogy with the classical case we define a \(\mu \)-inner function to be an element of the set
Our study of A-isometries in the following sections relies on a density result for such abstract inner functions taken from [14]. It is a slight variation of Aleksandrov’s corresponding result [1, Corollary 29]. In its original form, it says that, given the regularity of \((A,K,\mu )\), the \(w^*\)-closure of the set \(I_\mu \) in \(L^\infty (\mu )\) contains the set \(\{ [f]_\mu : f \in A,\ |f| \le 1 \text { everywhere on } K\}\) supposed that \(\mu \) is a continuous measure. Continuity means in this context that every one-point set has \(\mu \)-measure zero. The key point here is that the following result holds without any continuity assumption on \(\mu \).
Proposition 2.6
(see [14, Proposition 2.4 and Corollary 2.5]) If \((A, K, \mu )\) is a regular triple and \(A \supset {\mathbb {C}}[z]\). Then we have
where \({\overline{LH}}^{w^*}\) denotes the \(w^*\)-closed linear hull.
Note that, in the context of the preceding proposition, the first of these density relations implies the second one: The \(w^*\)-closed linear hull on the right is easily seen to be a \(w^*\)-closed subalgebra of \(L^\infty (\mu )\) that is closed under complex conjugation. Since it contains the restrictions of all polynomials (by the first density relation), it actually must be all of \(L^\infty (\mu )\).
It has turned out (cp. [14, 17, 19]) that this kind of density is exactly what is needed for operator-theoretic applications. So we define:
Definition 2.7
Let \(K \subset {\mathbb {C}}^n\) compact, \(A\subset C(K)\) a closed subalgebra.
-
(a)
Given a measure \(\mu \in M^+(K)\), the triple \((A,K,\mu )\) will be called \(w^*\)-regular, if \(H^\infty _A(\mu ) = {\overline{LH}}^{w^*}(I_\mu )\), and \(L^\infty (\mu ) = {\overline{LH}}^{w^*}(\{ {\overline{\theta }} \eta : \theta , \eta \in I_\mu \})\) hold.
-
(b)
We simply call the algbera A itself \(w^*\)-regular, if the triple \((A, K, \mu )\) is \(w^*\)-regular for every measure \(\mu \in M^+(K)\) with \(supp (\mu ) \subset \partial _A\).
-
(c)
If \(A \supset {\mathbb {C}}[z]\), then an A-isometry is called \(w^*\)-regular, if the triple \((A,K,\mu )\) is \(w^*\)-regular, where \(\mu \in M^+(\partial _A)\) denotes the scalar-valued spectral measure of a minimal normal extension of T.
Theorem 2.3 provides natural examples of \(w^*\)-regular function algebras. Further examples are the so called unit-modulus algebras introduced by Guo and Chen in [9, Definition 2.4].
3 Commutant Lifting for A-Isometries
The aim of this section is to prove the following commutant-lifting theorem that applies by the preceding section in particular to all algebras of the form \(A(D_1\times \cdots \times D_n)\) where each of the factors \(D_i\) is either a bounded strictly pseudoconvex domain with \(C^2\)-boundary, or a bounded sysmmetric and circled domain.
Theorem 3.1
Let \(K\subset {\mathbb {C}}^n\) be a compact set and \(A\subset C(K)\) a closed, \(w^*\)-regular subalgebra that contains \({\mathbb {C}}[z]\). Suppose that  is an A-subnormal tuple with minimal A-unitary dilation
is an A-subnormal tuple with minimal A-unitary dilation  and that
and that  is an A-isometry with minimal normal extension
is an A-isometry with minimal normal extension  . Then every operator
. Then every operator  satisfying
satisfying
possesses a unique extension to an operator  with the property that
with the property that
This extension satisfies \(\Vert {\widehat{X}}\Vert = \Vert X\Vert \). If X has dense range, then so has \({\widehat{X}}\). If \(U_1\) is even an A-unitary extension of \(T_1\) and, in addition, X is isometric, then so is \({\widehat{X}}\).
The above theorem contains several known intertwining results for subnormal isometric tuples as special cases (note that all but the last one require \(T_1\) to be an A-isometry):
-
A result of Guo (see [21, Lemma 3.6]) from the context of normal Hilbert modules. Actually our proof is inspired by Guo’s idea. But his hypotheses are rather special: Roughly speaking, both tuples are assumed to be spherical isometries, and the spectral measures of their minimal normal extensions are assumed to be absolutely continuous with respect to the surface measure of the sphere.
-
An intertwining result for spherical isometries by Athavale (Proposition 8 in [3]). More generally, the analogous result for so called \(\partial D\)-isometries introduced by Athavale in [4], where \(D\subset {\mathbb {C}}^n\) is a relatively compact strictly pseudoconvex domain: Our Theorem 3.1 implies Athavale’s Theorem 3.2.
We carry out the details for the convenience of the reader: First of all, note that A(D) is \(w^*\)-regular according to the remark preceding Theorem 2.3. Now, if we choose a domain \(\Omega \supset {\overline{D}}\) in such a way that \({\mathcal {O}}(\Omega )|{\overline{D}}\) is dense in A(D) (called HKL-superdomain in [4], see Remark 2.1 therein; for the existence, cp. [11, Corollary 2.1.3 (b)] and the references therein), then every \(\partial D\)-isometry with \(\sigma (T) \subset \Omega \) is actually an A(D)-isometry: To see this, note that
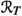 contains \({\mathcal {O}}(\Omega )\), since \(\gamma _T\) extends the \({\mathcal {O}}(\Omega )\)-functional calculus for T as observed in (1.1), Sect. 1, and hence
contains \({\mathcal {O}}(\Omega )\), since \(\gamma _T\) extends the \({\mathcal {O}}(\Omega )\)-functional calculus for T as observed in (1.1), Sect. 1, and hence 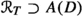 for density reasons. In Athavales result, two \(\partial D\)-isometries
for density reasons. In Athavales result, two \(\partial D\)-isometries 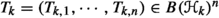 \((k=1,2)\) are assumed to satisfy the inclusion \(\sigma (T_1) \cup \sigma (T_2) \subset \Omega \) and an intertwining relation of the form $$\begin{aligned} X T_{1,i} = T_{2,i} X \qquad (i=1,\cdots , n). \end{aligned}$$
\((k=1,2)\) are assumed to satisfy the inclusion \(\sigma (T_1) \cup \sigma (T_2) \subset \Omega \) and an intertwining relation of the form $$\begin{aligned} X T_{1,i} = T_{2,i} X \qquad (i=1,\cdots , n). \end{aligned}$$To apply our theorem, it remains to check that \(X\gamma _{T_1}(f) = \gamma _{T_2}(f)X\) for every \(f \in A(D)\) hold in this case. But the assumed intertwining relation for the components immediately implies that \(X f(T_1) = f(T_2) X\) for \(f \in {\mathcal {O}}(\Omega )\), where \(f(T_k)\) is built using the holomorphic functional calculus. Again, the uniqueness of the canonical \(H^\infty \)-calculi of \(T_1\) and \(T_2\) then implies that \(X \gamma _{T_1}(f) = \gamma _{T_2}(f)X\) for all \(f \in {\mathcal {O}}(\Omega )\). So by the density of \({\mathcal {O}}(\Omega )|{\overline{D}}\) in A(D), the hypothesis of Theorem 3.1 is indeed satisfied.
-
An intertwining result for so-called \(S_\Omega \)-isometries [6, Theorem 2.1]. We sketch the main arguments: For a relatively compact, convex set \(\Omega \subset {\mathbb {C}}^n\) with \(0 \in \Omega \), it follows from the Oka-Weil theorem and radial approximation that \({\mathbb {C}}[z]\) is dense in \(A(\Omega )\). So in this case, the condition
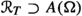 is always fulfilled. This shows in particular that \(S_\Omega \)-isometries (where \(\Omega \) is a Cartan domain of type I, II, III, or IV) as defined by Athavale in [6] are A-isometries with \(A=A(\Omega )\), which is known to be regular for bounded symmetric and circled domains. Again, for uniqueness reasons of the involved functional calculi, a componentwise intertwining relation implies the one assumed in our theorem. For another class of convex domains, where the domain algebra is regular, cp. [5] (see Proposition 2.5 therein for the regularity, and Proposition 4.6 for the corresponding commutant-lifting result). The sets considered there are special complex ellipsoids.
is always fulfilled. This shows in particular that \(S_\Omega \)-isometries (where \(\Omega \) is a Cartan domain of type I, II, III, or IV) as defined by Athavale in [6] are A-isometries with \(A=A(\Omega )\), which is known to be regular for bounded symmetric and circled domains. Again, for uniqueness reasons of the involved functional calculi, a componentwise intertwining relation implies the one assumed in our theorem. For another class of convex domains, where the domain algebra is regular, cp. [5] (see Proposition 2.5 therein for the regularity, and Proposition 4.6 for the corresponding commutant-lifting result). The sets considered there are special complex ellipsoids. -
Réolon’s analogous result for K-isometries (cp. Proposition 3.5.18 in [29]) which are by definition A-isometries with \(A= \overline{{\mathbb {C}}[z]}\subset C(K)\), where \(K \subset {\mathbb {C}}^n\) compact and A is assumed to be regular in our sense. This class contains in particular finite commuting tuples of isometries, which were first treated by Mlak [26, Proposition 5.2].
We should further remark that all but the first cited result rely on a lemma of Mlak on spectral dilations [26, Lemma 4.1]. In contrast, we give an alternative and elementary proof by writing down an explicit formula for \({\widehat{X}}\), based on an idea of Guo [21, Lemma 3.6].
For the proof of Theorem 3.1, we need an operator-theoretic version of the measure-theoretic density assumption from Definition 2.7. To formulate it appropriately, let us fix the following notation: Given two measures \(\mu , \nu \in M^+(\partial _A)\) with \(\mu \ll \nu \), let
denote the canonical map defined by \([f]_\nu \mapsto [f]_\mu \) for every bounded measurable function \(f: \partial _A \rightarrow {\mathbb {C}}\). Clearly, every \(r^\nu _\mu \) is a \(w^*\)-continuous and contractive *-homomorphism.
Given an A-unitary tuple  with scalar-valued spectral measure \(\mu \ll \nu \), we denote by \(\Psi ^\nu _U\) the composition
with scalar-valued spectral measure \(\mu \ll \nu \), we denote by \(\Psi ^\nu _U\) the composition

As a consequence of Proposition 2.6, we have:
Lemma 3.2
Let \((A, K, \nu )\) be a \(w^*\)-regular triple and  an A-unitary tuple with scalar-valued spectral measure \(\mu \in M^+(\partial _A)\) satisfying \(\mu \ll \nu \). Then, for every subspace
an A-unitary tuple with scalar-valued spectral measure \(\mu \in M^+(\partial _A)\) satisfying \(\mu \ll \nu \). Then, for every subspace  , the set
, the set

is the smallest closed subspace of  that contains
that contains  and reduces U. (Here, \({\overline{LH}}\) stands for the norm-closed linear hull in
and reduces U. (Here, \({\overline{LH}}\) stands for the norm-closed linear hull in  .)
.)
Proof
We first show that  reduces U. Towards this, let \(\theta _0, \eta _0 \in I_\nu \). Obviously, \(\Psi _U^\nu ({\overline{\theta }}_0\eta _0)\) maps the set
reduces U. Towards this, let \(\theta _0, \eta _0 \in I_\nu \). Obviously, \(\Psi _U^\nu ({\overline{\theta }}_0\eta _0)\) maps the set

into itself. By linearity and continuity, we may pass to \({\overline{LH}}\), so

Since invariant subspaces are preserved under \(w^*\)-limits, the \(w^*\)-regularity assumption (cf. Definition 2.7) allows us to conclude that  for every \(f \in L^\infty (\nu )\). By taking f to be \(z_i\) and \({\overline{z}}_i\) (\(i=1,\cdots ,n\)), we see that
for every \(f \in L^\infty (\nu )\). By taking f to be \(z_i\) and \({\overline{z}}_i\) (\(i=1,\cdots ,n\)), we see that  is actually reducing for U. Standard arguments based on the theorems of Stone-Weierstraß and Lusin yield the stated minimality. \(\square \)
is actually reducing for U. Standard arguments based on the theorems of Stone-Weierstraß and Lusin yield the stated minimality. \(\square \)
Besides the above density result, an essential ingredient of the proof is the simple observation that, for every \(\theta \in I_\nu \), the operator \(\Psi _U^\nu (\theta )\) is isometric, since it evidently satisfies  . (Actually, it is even unitary as \({\overline{\theta }}\) is the inverse of \(\theta \) in \(L^\infty (\nu )\), but isometry will suffice for our purposes.)
. (Actually, it is even unitary as \({\overline{\theta }}\) is the inverse of \(\theta \) in \(L^\infty (\nu )\), but isometry will suffice for our purposes.)
Proof of Theorem 3.1
For \(k = 1,2\), let \(\mu _k\in M^+(K)\) denote the trivial extensions of scalar spectral measures of \(U_k\) to elements in \(M^+(K)\). The proof will actually work if we replace the hypothesis on A to be a \(w^*\)-regular function algebra with the following weaker but more technical one: There exists a measure \(\nu \in M^+(\partial _A)\) such that \((A,K,\nu )\) is \(w^*\)-regular and \(\mu _1, \mu _2 \ll \nu \). Let us fix such a measure \(\nu \) for the rest of the proof. (Under the original hypothesis of the theorem, \(\nu = \mu _1+\mu _2\) evidently has the desired properties.) Throughout the proof, we use the abbreviations  and
and  for \(k=1,2\).
for \(k=1,2\).
We first define \({\widehat{X}}\) on a dense subset of  (cf. Lemma 3.2) in the obvious way, namely
(cf. Lemma 3.2) in the obvious way, namely
where \(F\subset {\mathbb {N}}\) denotes a finite set and  are arbitrary elements for \(i\in F\). To see that this is well defined, we estimate the norm of the right-hand side. If we define \(\pi = \prod _{i\in F} \theta _{i}\), then \(\pi \in I_\nu \), and so the operator \(\Psi _{U_2}^\nu (\pi )\) is isometric. This yields
are arbitrary elements for \(i\in F\). To see that this is well defined, we estimate the norm of the right-hand side. If we define \(\pi = \prod _{i\in F} \theta _{i}\), then \(\pi \in I_\nu \), and so the operator \(\Psi _{U_2}^\nu (\pi )\) is isometric. This yields
From the very definition of \(\pi \), the functions \(\pi {\overline{\theta }}_{i}\) belong to \(I_\nu \) for every choice of \(i\in F\). Since, in addition, X maps into  , and \(U_2\) is an A-unitary extension of \(T_2\), we may replace \(\Psi ^\nu _{U_2}\) with \(\gamma _{T_2}^\nu \). Then we use the intertwining relation
, and \(U_2\) is an A-unitary extension of \(T_2\), we may replace \(\Psi ^\nu _{U_2}\) with \(\gamma _{T_2}^\nu \). Then we use the intertwining relation  \((f\in A)\) from the hypothesis. We restate this as
\((f\in A)\) from the hypothesis. We restate this as

to see that it extends by \(w^*\)-WOT-continuity to

These considerations allow us to continue expression (3.2) as follows
where we again used the isometry of \(\Psi _{U_1}^\nu (\pi )\) in the last step. First of all, this shows that \({\widehat{X}}\) is indeed well defined (and then, by construction, linear) on the space  of all finite linear combinations of vectors of the form \(\Psi ^\nu _{U_1}({\overline{\theta }}_{i} \eta _{i})h_{i}\) with
of all finite linear combinations of vectors of the form \(\Psi ^\nu _{U_1}({\overline{\theta }}_{i} \eta _{i})h_{i}\) with  . Moreover, the estimate derived in (3.2)–(3.3) briefly says that
. Moreover, the estimate derived in (3.2)–(3.3) briefly says that

In particular, \({\widehat{X}}\) maps Cauchy-sequences in  to Cauchy-sequences in
to Cauchy-sequences in  and thus can be continuously extended to a linear map on the closure
and thus can be continuously extended to a linear map on the closure  , which coincides with
, which coincides with  by Lemma 3.2. This map has obviuously norm less than \(\Vert X\Vert \), and a look at the assumed density (Definition 2.7 (b)) and the defining formula (3.1) for \({\widehat{X}}\) shows that it actually has the desired intertwining property.
by Lemma 3.2. This map has obviuously norm less than \(\Vert X\Vert \), and a look at the assumed density (Definition 2.7 (b)) and the defining formula (3.1) for \({\widehat{X}}\) shows that it actually has the desired intertwining property.
In view of Lemma 3.2 and (3.1), \({\widehat{X}}\) has dense range if so has X. Moreover, if \(U_1\) is even an A-unitary extension of \(T_1\), then we may drop the operator  in the considerations preceding estimate (3.3). Thus, if X is isometric, then equality holds in (3.3) and (3.4) with \(\Vert X\Vert =1\).
in the considerations preceding estimate (3.3). Thus, if X is isometric, then equality holds in (3.3) and (3.4) with \(\Vert X\Vert =1\).
To finish the proof, note that an operator \({\widehat{X}}\) satisfying the intertwining relation from the statement of the theorem necessarily fulfills \({\widehat{X}}\Psi ^\nu _{U_1}(f) = \Psi ^\nu _{U_1}(f) {\widehat{X}}\), because \(C(\partial _A)\) is \(w^*\)-dense in \(L^\infty (\nu )\). Consequently, it satisfies (3.1), and therefore coincides with the extension constructed above. \(\square \)
When specialized to one A-isometry, Theorem 3.1 reads as follows:
Corollary 3.3
Let  be a \(w^*\)-regular A-isometry with minimal normal extension
be a \(w^*\)-regular A-isometry with minimal normal extension  . Then, every element \(X\in {\mathcal {T}}_a(T)'\) possesses a unique extension to an element \({\widehat{X}}\in (U)'\).
. Then, every element \(X\in {\mathcal {T}}_a(T)'\) possesses a unique extension to an element \({\widehat{X}}\in (U)'\).
Combining Theorem 3.1 and Lemma 1 from [3]), we can draw another standard conclusion in this context (cp. Athavale [3, Proposition 9]):
Corollary 3.4
If two \(w^*\)-regular A-isometries are quasi-similar, then their minimal unitary extensions are unitarily equivalent.
4 Lifting of Module Homomorphisms
Let \(A\subset C(K)\) be function algebra, i. e., a closed subalgebra of C(K) that separates the points of K. Recall that a Hilbert-A-module is a Hilbert space  together with a continuous bilinear map
together with a continuous bilinear map

turning  into an A-module in the algebraical sense. Given \(f \in A\), we write \(M_f\) (or
into an A-module in the algebraical sense. Given \(f \in A\), we write \(M_f\) (or  , if we want to emphasize the underlying space) for the continuos linear multiplication operator
, if we want to emphasize the underlying space) for the continuos linear multiplication operator  with \(f\in A\). The continuous linear map
with \(f\in A\). The continuous linear map  will be referred to as the underlying representation of
will be referred to as the underlying representation of  . The Hilbert module
. The Hilbert module  is called contractive, if so is
is called contractive, if so is  .
.
Definition 4.1
Let \(A\subset C(\partial _A)\) be a function algebra. A Hilbert-A-module  is called a hypo-Shilov-module, if there exists a Hilbert-\(C(\partial _A)\)-module
is called a hypo-Shilov-module, if there exists a Hilbert-\(C(\partial _A)\)-module  such that
such that  is an A-submodule. In this case,
is an A-submodule. In this case,  is called a \(C(\partial _A)\)-extension of
is called a \(C(\partial _A)\)-extension of  . If
. If  is contractive,
is contractive,  is called a Shilov module over A.
is called a Shilov module over A.
Given this definition, the following further notations are natural: The extension  of a (hypo-)Shilov-module is called minimal, if
of a (hypo-)Shilov-module is called minimal, if  is dense in
is dense in  . A hypo-Shilov-module is called reductive, if it is a \(C(\partial _A)\)-submodule of
. A hypo-Shilov-module is called reductive, if it is a \(C(\partial _A)\)-submodule of  , and pure, if no non-zero subspace of it is reductive.
, and pure, if no non-zero subspace of it is reductive.
The key observation for applying Theorem 3.1 in the context of Hilbert modules is the following simple lemma which says that A-isometries and Shilov-A-modules are essentially the same.
Lemma 4.2
Let \(A \subset C(K)\) be a closed subalgebra containing \({\mathbb {C}}[z]\).
-
(a)
If
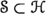 is a Shilov-A-module with minimal contractive \(C(\partial _A)\)-extension
is a Shilov-A-module with minimal contractive \(C(\partial _A)\)-extension 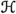 , then
, then 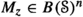 is an A-isometry with minimal normal extension
is an A-isometry with minimal normal extension 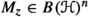 .
. -
(b)
Conversely, if
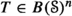 is an A-isometry with minimal normal extension
is an A-isometry with minimal normal extension 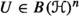 , then, introducing the multiplications
, then, introducing the multiplications 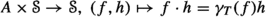 on
on 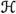 and
and 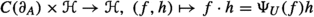 on
on 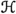 turns
turns 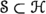 into a Shilov module over A with minimal \(C(\partial _A)\)-extension
into a Shilov module over A with minimal \(C(\partial _A)\)-extension 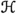 .
.
Proof
Since, in part (a), the representation  is assumed to be contractive, it is a \(*\)-homomorphism (see [15, Theorem 1.12]) and thus gives rise to a normal tuple
is assumed to be contractive, it is a \(*\)-homomorphism (see [15, Theorem 1.12]) and thus gives rise to a normal tuple  with Taylor spectrum \(\sigma (M_z) \subset \partial _A\). Since
with Taylor spectrum \(\sigma (M_z) \subset \partial _A\). Since  is an A-submodule of
is an A-submodule of  , we have the inclusion
, we have the inclusion

This implies at first that  is subnormal with normal extension
is subnormal with normal extension  . Since, by assumption,
. Since, by assumption,  is dense in
is dense in  , it follows that U is a minimal normal extension of T. By a Stone-Weiertraß argument, the identity
, it follows that U is a minimal normal extension of T. By a Stone-Weiertraß argument, the identity  , where \(\Psi _U\) is the canonical \(L^\infty \)-calculus of U (see Sect. 1) holds for all \(f \in C(\partial _A)\). Hence the inclusion (4.1) from above actually says that
, where \(\Psi _U\) is the canonical \(L^\infty \)-calculus of U (see Sect. 1) holds for all \(f \in C(\partial _A)\). Hence the inclusion (4.1) from above actually says that  as required in the definition of an A-isometry. This observation completes the proof of part (a). Part (b) is obvious. \(\square \)
as required in the definition of an A-isometry. This observation completes the proof of part (a). Part (b) is obvious. \(\square \)
By an A-module homomorphism  between two Hilbert-A-modules we mean a bounded linear map that respects the module multiplication in the sense that \(X(f \cdot h) = f\cdot Xh\) whenever \(f \in A\) and
between two Hilbert-A-modules we mean a bounded linear map that respects the module multiplication in the sense that \(X(f \cdot h) = f\cdot Xh\) whenever \(f \in A\) and  . We write
. We write  to denote the set of all A-module homomorphisms from
to denote the set of all A-module homomorphisms from  to
to  .
.
Let now two Shilov modules  with minimal \(C(\partial _A)\)-extensions
with minimal \(C(\partial _A)\)-extensions  be given. Using the identifications from the preceding proof, namely
be given. Using the identifications from the preceding proof, namely  \((f\in A)\) and
\((f\in A)\) and  \((f \in C(\partial _A))\), the following identities are evident:
\((f \in C(\partial _A))\), the following identities are evident:

As a last ingredient for the extension theorem we aim for (Theorem 4.4), we need the following well-known fact:
Theorem 4.3
(cp. [15, Theorem 1.9]) Let  be a Hilbert-C(K)-module. Then
be a Hilbert-C(K)-module. Then  is similar to a contractive C(K)-module
is similar to a contractive C(K)-module  , i. e., there exists an invertible C(K)-module map (a similarity map)
, i. e., there exists an invertible C(K)-module map (a similarity map)  .
.
Now we are ready to prove the main result of this section. In the case \(A=A({\mathbb {B}}_n)\), this appears as Lemma 3.6 in [21] (where it is stated for Shilov-modules only, and under an additional continuity assumption). For a unit modulus algebra A, the corresponding result appears as Proposition 2.5 in [9]. Our theorem contains both as special cases.
Theorem 4.4
Let  be hypo-Shilov modules over A with \(C(\partial _A)\)-extensions
be hypo-Shilov modules over A with \(C(\partial _A)\)-extensions  \((k =1, 2)\). Suppose that \(A\supset {\mathbb {C}}[z]\) is \(w^*\)-regular. Then there exists a map
\((k =1, 2)\). Suppose that \(A\supset {\mathbb {C}}[z]\) is \(w^*\)-regular. Then there exists a map

If  is minimal, then \(\varepsilon \) is unique.
is minimal, then \(\varepsilon \) is unique.
Proof
The proof is divided into three steps.
Step I: Reduction to the minimal case. To prove the existence of \(\varepsilon \), we may assume that  are minimal \(C(\partial _A)\)-extensions of
are minimal \(C(\partial _A)\)-extensions of  \((k=1,2)\). To see this, let
\((k=1,2)\). To see this, let  are arbitrary \(C(\partial _A)\)-extensions of
are arbitrary \(C(\partial _A)\)-extensions of  , and set
, and set  , which is minimal. Then
, which is minimal. Then  is a reducing submodule of
is a reducing submodule of  , whence the projection
, whence the projection  is a \(C(\partial _A)\)-module homomorphism, as is the inclusion map
is a \(C(\partial _A)\)-module homomorphism, as is the inclusion map  (for trivial reasons). Assuming the existence-assertion of the theorem to hold for the minimal extensions
(for trivial reasons). Assuming the existence-assertion of the theorem to hold for the minimal extensions  , we may set
, we may set

to obtain an extension mapping  in the general case. To finish the first step, we have to justify that replacing
in the general case. To finish the first step, we have to justify that replacing  with
with  does not impose any restriction on the uniqueness assertion either: But if
does not impose any restriction on the uniqueness assertion either: But if  is assumed to be minimal (as it is in the uniqueness part), then every
is assumed to be minimal (as it is in the uniqueness part), then every  satisfies
satisfies  and thus has range in
and thus has range in  , and may actually considered an element of
, and may actually considered an element of  . So in what follows, we may and shall assume
. So in what follows, we may and shall assume  to be a minimal extension of
to be a minimal extension of  \((k=1,2)\).
\((k=1,2)\).
Step II: Reduction to the Shilov-case. According to Theorem 4.3, we find invertible Hilbert-\(C(\partial _A)\)-module maps

onto contractive Hilbert-\(C(\partial _A)\)-modules. Since restrictions  are also invertible A-module maps, the vertical maps in the following diagram
are also invertible A-module maps, the vertical maps in the following diagram

which are defined as “conjugations”

are bijections. Assuming the theorem to hold for Shilov-modules and their minimal extensions, there is an extension map \(\varepsilon _S\) from  to
to  as stated in the theorem, which we take as the lower horizontal map of the diagram. We define the upper horizontal map so to make the diagram commutative. To state it explicitly,
as stated in the theorem, which we take as the lower horizontal map of the diagram. We define the upper horizontal map so to make the diagram commutative. To state it explicitly,

The stated extension property  for
for  is obvious. Moreover, using the diagram, it is easy to see that \(\varepsilon \) is unique with the stated extension property if and only if so is \(\varepsilon _S\) with the corresponding property.
is obvious. Moreover, using the diagram, it is easy to see that \(\varepsilon \) is unique with the stated extension property if and only if so is \(\varepsilon _S\) with the corresponding property.
Step III: The Shilov-case with minimal extensions. So we may finally assume that  are Shilov-modules with minimal \(C(\partial _A)\)-extensions
are Shilov-modules with minimal \(C(\partial _A)\)-extensions  for \(k=1,2\). By Lemma 4.2 (a) and the subsequent remarks on A-module homomorphisms, the statement of the theorem is nothing but a reformulation of Theorem 3.1. Thus, the proof is complete. \(\square \)
for \(k=1,2\). By Lemma 4.2 (a) and the subsequent remarks on A-module homomorphisms, the statement of the theorem is nothing but a reformulation of Theorem 3.1. Thus, the proof is complete. \(\square \)
The existence of a lifting map of the above type implies by standard arguments the existence of an “Hom-isomorphism theorem” for hypo-Shilov-modules and their complements (cp. [21] and [9]). To give an appropriate formulation (see Theorem 6.1 below), we need the concept of projectivity, which is introduced and studied for A(D)-modules over product domains in the next section.
5 Projectivity and Injectivity Over Product Domains
Let  denote the category of Hilbert-A-modules. An object
denote the category of Hilbert-A-modules. An object  is called projective, if for every pair of objects
is called projective, if for every pair of objects  together with A-module maps
together with A-module maps  and
and  with \(X^1_2\) onto, there exists an A-module map
with \(X^1_2\) onto, there exists an A-module map  such that the following diagram is commutative
such that the following diagram is commutative

A module  is called injective, if for every pair
is called injective, if for every pair  with A-module maps
with A-module maps  and
and  such that \(Y_1^2\) is injective with closed range, there exists an A-module map
such that \(Y_1^2\) is injective with closed range, there exists an A-module map  such that \(Y_1 = Y_2 \circ Y_1^2\).
such that \(Y_1 = Y_2 \circ Y_1^2\).
We refer to [7] for the homological background. Proposition 2.1.5 therein relates the characterization of injective and projective objects to the vanishing of cohomology groups  defined as follows: Two short exact sequences
defined as follows: Two short exact sequences

in the category  are called equivalent if there exists a morphism
are called equivalent if there exists a morphism  making the diagram
making the diagram

commutative. The first cohomology group is then defined by

The zero element of  is the split extension
is the split extension

where  and
and  denote the canonical inclusion and projection, respectively. In terms of \(Ext \)-groups, an element
denote the canonical inclusion and projection, respectively. In terms of \(Ext \)-groups, an element  is projective, if and only if
is projective, if and only if  for every
for every  , and injective, if and only if
, and injective, if and only if  for every
for every  .
.
It was shown by Carlson and Clark [8] for \(D={\mathbb {D}}^n\), by Guo [21] for \(D= {\mathbb {B}}_n\) (under an additional continuity assumption on the underlying modules related to the surface measure on \(\partial {\mathbb {B}}_n\)) and by Eschmeier and the author [13] in full generality for every strictly pseudoconvex bounded open set and every bounded symmetric domain \(D \subset {\mathbb {C}}^n\) that  and
and  , whenever
, whenever  is a Hilbert-\(C(S_D)\)-module. The main result of this section says that this remains true in the product setting we studied in Sect. 2:
is a Hilbert-\(C(S_D)\)-module. The main result of this section says that this remains true in the product setting we studied in Sect. 2:
Theorem 5.1
Let \(k\in {\mathbb {N}}\) and \(D_i \subset {\mathbb {C}}^{d_i}\) be bounded open sets with \(d_i \in {\mathbb {N}}\) for \(1 \le i \le k\), each of which is either a strictly pseudoconvex domain with \(C^5\) boundary or a bounded symmetric and circled domain, and let \(D=D_1 \times \cdots \times D_k\) be the product domain. If  is a Hilbert-\(C(S_D)\)-module, then we have
is a Hilbert-\(C(S_D)\)-module, then we have

for every Hilbert-A(D)-module  .
.
To prove this, we basically use an emedding argument similar to the one used to deduce the bounded symmetric case from the strictly pseudoconvex one in [13] (see the remarks preceding Corollary 3.2 therein). While the embedding used in the latter case was the trivial one (namely, the inclusion of a bounded symmetric and circled domain into its envelopping ball), the construction of a suitable embedding is the non-trivial part in the product setting under consideration.
In preparation of the main construction we show the following auxiliary lemma:
Lemma 5.2
Let \(D_1 \subset {\mathbb {C}}^m\) and \(D_2 \subset {\mathbb {C}}^k\) be bounded open sets and assume that \(D_2\) is convex. Then, the mapping
is an isometric isomorphism. Here, \(A(D_2, A(D_1))\subset C({\overline{D}}_2, A(D_1))\) is the closed subspace consisting of those functions that are analytic on \(D_2\), viewed as functions with values in the Banach space \(A(D_1)\).
Proof
It is elementary to check that S, viewed as a map \(A(D_1\times D_2) \rightarrow C({\overline{D}}_2, A(D_1))\) is a well-defined isometry. To see that it actually maps into \(A(D_2, A(D_1))\), we have to make sure that \(Sf|D_2\) is analytic as a function with values in \(A(D_1)\). Since \(A(D_1)\) isometrically embeds as a subspace into \(H^\infty (D_1)\) (by restriction), it suffices to check the holomorphy of \(Sf|D_2\), viewed as a map \(D_2 \rightarrow H^\infty (D_1)\). But this follows from [12, Lemma 5.4], which settles the corresponding identification \(H^\infty (D_1 \times D_2) \cong H^\infty (D_2, H^\infty (D_1))\). So the map S from the statement of the theorem is actually a well-defined isometry. To conclude the proof, it suffices to check that S is surjective. Towards this, let \(f \in A(D_2, A(D_1))\) be given. Applying a suitable translation, we may assume that \(D_2\) contains the origin. Using the uniform continuity of f, one shows that, for \(r \uparrow 1\) \((0<r<1)\), the functions \(f_r\) defined by \(f_r(z) = f(rz)\) which are holomorphic on the open set \(D_r = (1/r)\cdot D_2 \supset {\overline{D}}_2\) converge to f uniformly on \({\overline{D}}_2\). Thus we can choose a sequence \((r_n)\) in such a way that the functions
In view of the well known identification \({\mathcal {O}}(D_{r_n}) {\widehat{\otimes }} A(D_1) \cong {\mathcal {O}}(D_{r_n}, A(D_1))\) (see, e. g., [30]), where the latter space carries the topology of uniform convergence on compact subsets, we can choose, for each \(n\ge 1\), a natural number \(k_n\) and functions \(\varphi ^n_i \in {\mathcal {O}}(D_{r_n})\) and \(h^n_i \in A(D_1)\) \((1\le i \le k_n)\) such that
where \((\varphi ^n_i \otimes h^n_i) \in {\mathcal {O}}(D_{r_n}, A(D_1))\) denotes the function acting as \((\varphi ^n_i \otimes h^n_i)(z) = \varphi ^n_i(z) \cdot h^n_i\) for \(z \in D_{r_n})\). In a final approximation step, we make use of the (polynomial) convexity of \({\overline{D}}_2\) and use the Oka-Weil theorem to find polynomials \((p^n_i)_{1 \le i \le k_n}\) in \({\mathbb {C}}[z]\) such that
for each fixed \(n \ge 1\). By construction, we have
To finish the proof, it suffices to observe that the functions \(g^n_i\) defined by \(g^n_i(z_1, z_2) = p_i^n(z_1)\cdot h_i^n(z_2) \ (z_1 \in {\overline{D}}_1, z_2 \in {\overline{D}}_2)\) obviously belong to \(A(D_1 \times D_2)\) and are mapped to \(p^n_i \otimes h^n_i\) via S. This shows that S has dense range and thus is surjective, as desired. \(\square \)
The previous lemma helps us to handle the symmetric factor in the following embedding theorem. The strictly pseudoconvex parts will be handled by combining the embedding theorems of Fornaess [20, Theorem 9] and Løw [25] with a result of Jacóbczak [23, Theorem 1] on the existence of extension operators.
Proposition 5.3
Let \(D=D_1 \times \cdots \times D_k\subset {\mathbb {C}}^n\) be a product domain as in the statement of Theorem 5.1. Then there exist constants \(N \in {\mathbb {N}},\ r >0\) and a mapping \(F\in A(D)^N\) such that, with \(B = r \cdot {\mathbb {B}}_N\), the following assertions hold:
-
(a)
\(F:{\overline{D}} \rightarrow F({\overline{D}})\subset {\mathbb {C}}^N\) is a homeomorphism.
-
(b)
\(F(D) \subset B\) and \(F(S_D) \subset \partial B\).
-
(c)
The composition operator \(C_F:A(B) \rightarrow A(D)\), \(f \mapsto f\circ F\), has dense range.
Proof
As in the proof of Theorem 2.3, we may restrict ourselves to the case
where \(D_1\) and \(D_2\) are strictly pseudoconvex factors and \(D_3\) is a bounded symmetric and circled open set. The proof is divided into three steps:
Step I: Reduction to the case of convex domains. All of the following assertions hold for \(i=1,2\): Since \({\overline{D}}_i\) is a Stein compactum and hence holomorphically convex, we may apply Fornaess’ embedding theorem [20, Theorem 9] (in the special case \(X={\mathbb {C}}^{d_i}\)), to obtain holomorphic maps \(\psi _i: {\mathbb {C}}^{d_i} \rightarrow {\mathbb {C}}^{m_i}\) and strictly convex bounded domains \(C_i \subset {\mathbb {C}}^{m_i}\) with \(C^5\)-boundary such that
-
\(\psi _i\) is biholomorphic onto a closed subvariety \(M'_i = \psi ({\mathbb {C}}^{d_i})\subset {\mathbb {C}}^{m_i}\),
-
\(\psi _i(D_i) \subset C_i\) and \(\psi _i({\mathbb {C}}^{d_i}\setminus {\overline{D}}_i) \subset {\mathbb {C}}^{m_i} \setminus \overline{C_i}\) (and consequentlyFootnote 1\(\psi _i(\partial D_i) \subset \partial C_i\)), and
-
\(M'_i\) intersects \(\partial C\) transversally.
If we set \(M_i =\psi _i(D_i)\) and note that \(M_i = M'_i\cap C_i\) (with transversal intersection at \(\partial C_i\)), then these sets fulfill exactly the hypotheses of [23, Theorem 1] (cp. also the Remark preceding Section 4 therein). We write \(\psi = (\psi _1, \psi _2): {\overline{D}}_1 \times {\overline{D}}_2 \rightarrow {\overline{M}}_1\times {\overline{M}}_2\) and consider the following commuting diagram

where
-
the vertical maps are given by the identification established in the previous lemma,
-
the map \(1\otimes R_M\) acts by pointwise restriction to \(M ={\overline{M}}_1 \times {\overline{M}}_2\), i. e., \((1\otimes R_Mf)(z) = f(z)|M\) for \(z \in {\overline{D}}_3\) and \(f \in A(D_2, A(C_1 \times C_2))\),
-
the mapping \(1\otimes C_{\psi }\) acts by pointwise application of the composition operator \(C_{\psi }: A(M_1\times M_2) \rightarrow A(D_1\times D_2), \ f \mapsto f \circ \psi \),
-
the upper horizontal map R (which we think of as a restriction map) is by definition the composition operator with the map \((\psi , id): {\overline{D}}_1 \times {\overline{D}}_2 \times {\overline{D}}_3 \rightarrow {\overline{C}}_1 \times {\overline{C}}_2 \times {\overline{D}}_3\).
It is elementary to check that the diagram commutes. We claim that R is surjective, which lifts our problem to a product of convex sets (in the upper left corner). Since \(1\otimes C_{\psi }\) is obviously a topological isomorphism (with inverse \(1\otimes C_{\psi ^{-1}}\)), the difficulty lies in checking that \(1\otimes R_M\) is surjective. By a result of Jacóbczak [23, Theorem 1] (and the remark at the end of Section 3 therein), there is a continuous linear extension operator
Defining \(1\otimes E : A(D_3, A(M_1\times M_2)) \rightarrow A(D_3, A(C_1\times C_2))\) by the pointwise action of E on \(A(D_3, A(M_1\times M_2))\)-functions, we obtain a bounded linear right inverse for \(1\otimes R_M\), and the claimed surjectivity follows.
Step II: Embedding a product of convex domains into a ball. Towards an application of Løw’s embedding theorem to the sets \(C_i\) as in the proof of Theorem 2.3 on p. 4, Let us choose \(r_i>0\) such that \({\overline{C}}_i \subset r_i \cdot {\mathbb {B}}_{m_i}\) (\(i=1,2\)) and \(D_3 \subset r_3\cdot {\mathbb {B}}_{d_3}\) with \(S_{D_3} = {\overline{D}}_3 \cap r_3 \cdot \partial {\mathbb {B}}_{d_3}\). Then, exactly as in the cited proof, the application of Løw’s theorem yields a map
with \(g_i \in A(C_i)^{l^i}\) for suitable \(l_i\in {\mathbb {N}}\), such that with \(r = \sqrt{r_1^2+r_2^2+r_3^2}\) and \(B = r\cdot {\mathbb {B}}_N\) with \(N= m_1+m_2+ d_3+l_1+l_2\) the following assertions hold (consider Remark 2.5):
-
\(G: {\overline{C}}_1 \times {\overline{C}}_2 \times {\overline{D}}_3 \rightarrow G({\overline{C}}_1 \times {\overline{C}}_2 \times {\overline{D}}_3)\) is a homeomorphism,
-
\(G(S_{C_1 \times C_2 \times D_3}) \subset \partial B\),
-
\(G(C_1\times C_2 \times D_3) \subset B\).
To argue as in the referenced proof, note that the sets \(C_i\) are strictly pseudoconvex (as they are strictly convex, cp. p. 529 of [20]), so \(S_{C_1\times C_2\times D_3} = \partial C_1 \times \partial C_2 \times ({\overline{D}}_3 \cap r_3\cdot \partial {\mathbb {B}}_{d_3})\). To finally obtain a map \(F\in A(D)^N\) as in the statement of the theorem, we set

Properties (a) and (b) from the assertion of the theorem are valid by construction, so it remains to check that (c) holds.
Step III: The range of \(C_F:A(B) \rightarrow A(D)\), \(f \mapsto f\circ F\) is dense. By construction, \(C_F\) is the composition
where \(C_G(f) = f\circ G\) and R is the upper horizontal map from (5.1). To complete the proof, it suffices to check that \(C_G: A(B) \rightarrow A(C_1\times C_2 \times D_3)\) has dense range. Assuming that, for a moment, it follows immediately that \(\overline{C_F(A(B))} \supset R(\overline{C_G(A(B))}) = R(A(C_1\times C_2 \times D_3)) = A(D)\), since R is surjective as we have seen in Step I.
So let us finally aim for the density of \(C_G\). After a suitable translation, we may of course assume that the set \(C_1\times C_2 \times D_3 \subset {\mathbb {C}}^m\) contains the origin. Using radial approximation and the fact that the set \({\overline{C}}_1 \times {\overline{C}}_2 \times {\overline{D}}_3\) is polynomially convex, it suffices to check that the range of \(C_G\) contains the polynomials in \(z=(z_1, \cdots , z_m)\). Since \(C_G\) is a unital algebra homomorphism, it suffices to check that the range of \(C_G\) contains the (restrictions) of the coordinate projections \(\pi _1, \cdots , \pi _m: {\mathbb {C}}^m \rightarrow {\mathbb {C}}\), i. e., \(\pi _i(z) = z_i\). But, by construction (see (5.2) above), G acts as the identity on the first m components,
so if we denote the coordinate functions on \({\mathbb {C}}^N\) with \(\pi _j^N: {\mathbb {C}}^N \rightarrow {\mathbb {C}}\), then we clearly have \(\pi ^N_j|{\overline{B}} \in A(B)\) and
This observation finishes the proof. \(\square \)
Proof of Theorem 5.1
Let a short exact sequence  in the category
in the category  be given, where
be given, where  extends to a \(C(S_D)\)-module. For the first statement, we have to show that there is an A(D)-module map
extends to a \(C(S_D)\)-module. For the first statement, we have to show that there is an A(D)-module map  making the diagram
making the diagram

commutative in  . Towards this, let \(F: {\overline{D}} \rightarrow {\overline{B}}\) be the embedding constructed in Proposition 5.3. Note that
. Towards this, let \(F: {\overline{D}} \rightarrow {\overline{B}}\) be the embedding constructed in Proposition 5.3. Note that  and
and  can be viewed as A(B)-modules when we introduce the module multipliation
can be viewed as A(B)-modules when we introduce the module multipliation

analogously for  . Since \(F(S_D) \subset \partial B\), this module structure extends to a \(C(S_D)\)-module structure for
. Since \(F(S_D) \subset \partial B\), this module structure extends to a \(C(S_D)\)-module structure for  . As the \(Ext ^1\)-group is known to vanish in the ball case by [13, Theorem 3.1], there is an A(B)-module homomorphism X making the above diagram commuting in the category of A(B)-modules. But since the image of the composition operator \(C_F: A(B) \rightarrow A(D),\ f \mapsto f \circ F\), has dense range, the map
. As the \(Ext ^1\)-group is known to vanish in the ball case by [13, Theorem 3.1], there is an A(B)-module homomorphism X making the above diagram commuting in the category of A(B)-modules. But since the image of the composition operator \(C_F: A(B) \rightarrow A(D),\ f \mapsto f \circ F\), has dense range, the map  actually turns out to be an A(D)-module homomorphism by the continuity of the (original) module multiplication. This proves that \([E] = 0\) and thus
actually turns out to be an A(D)-module homomorphism by the continuity of the (original) module multiplication. This proves that \([E] = 0\) and thus  , as we claimed. The second half of the assertion follows analogously. \(\square \)
, as we claimed. The second half of the assertion follows analogously. \(\square \)
As a direct consequence, by [7, Proposition 2.1.5], we have:
Corollary 5.4
Let \(k\in {\mathbb {N}}\) and \(D_i \subset {\mathbb {C}}^{d_i}\) be bounded open sets with \(d_i \in {\mathbb {N}}\) for \(1 \le i \le k\), each of which is either a strictly pseudoconvex domain with \(C^5\) boundary or a bounded symmetric and circled domain, and let \(D=D_1 \times \cdots \times D_k\). Then every Hilbert-\(C(S_D)\)-module  is projective and injective in the category
is projective and injective in the category  .
.
6 A Hom-Isomorphism Theorem
Let  be a Hilbert-A-module and
be a Hilbert-A-module and  a closed A-submodule, that is, a closed subspace satisfying
a closed A-submodule, that is, a closed subspace satisfying  for \(f \in A\). If we write
for \(f \in A\). If we write  for the orthogonal projections with ranges
for the orthogonal projections with ranges  and
and  , respectively, then the identity
, respectively, then the identity

valid for arbitrary \(f,g\in A\) shows that  carries a natural A-module structure, where the module multiplication is given by
carries a natural A-module structure, where the module multiplication is given by

Furthermore, the space  can be equipped with an A-module structure by setting
can be equipped with an A-module structure by setting 
 .
.
Theorem 6.1
Let \(A \subset C(\partial _A)\) be a \(w^*\)-regular function algebra containing the polynomials \({\mathbb {C}}[z]\), and let  be hypo-Shilov modules over A with minimal \(C(\partial _A)\)-extensions
be hypo-Shilov modules over A with minimal \(C(\partial _A)\)-extensions  . If
. If  is projective and
is projective and  is pure, then the map
is pure, then the map

is an isomorphism of A-modules, where  denotes the extension map from Theorem 4.4.
denotes the extension map from Theorem 4.4.
Proof
For the convenience of the reader, we repeat the known argument from the proof of [21, Theorem 3.7]. The map \(\beta \) from the statement of the theorem is defined in such a way that the following diagram commutes:

Only the bijectivity of \(\beta \) requires an argument. To see that \(\beta \) is injective, suppose that \(\beta (X) = 0\) for some  . It follows immediately that
. It follows immediately that  is a reducing submodule. Since
is a reducing submodule. Since  is assumed to be pure, we conclude that \(\varepsilon (X)=0\) and thus \(X=0\), as desired.
is assumed to be pure, we conclude that \(\varepsilon (X)=0\) and thus \(X=0\), as desired.
For the surjectivity, let an arbitrary  be given. By the assumed projectvity of
be given. By the assumed projectvity of  , we may choose an A-module homomorphism
, we may choose an A-module homomorphism  such that
such that  . Setting
. Setting  , it follows that \(\varepsilon (X) = X'\) from uniqueness, and so
, it follows that \(\varepsilon (X) = X'\) from uniqueness, and so  . \(\square \)
. \(\square \)
The limiting factor for an application of the preceding theorem is the projectivity of  . In view of the fact that every \(C(S_D)\)-extension of a Hilbert-A(D)-module is projective for \(D\subset {\mathbb {C}}^n\) if D is either (i) a bounded strictly pseudoconvex set or (ii) a circled bounded symmetric domain (see [13, Theorem 3.1]) or (iii) a product of finitely many such domains (Theorem 5.1), the above result allows us to extend Guo [21, Theorem 3.7] and Chen and Guo [9, Theorem 3.5] to these kinds of sets. In particular, the restriction to Shilov-modules and the additional continuity assumption made in [21] to handle the ball case are not necessary.
. In view of the fact that every \(C(S_D)\)-extension of a Hilbert-A(D)-module is projective for \(D\subset {\mathbb {C}}^n\) if D is either (i) a bounded strictly pseudoconvex set or (ii) a circled bounded symmetric domain (see [13, Theorem 3.1]) or (iii) a product of finitely many such domains (Theorem 5.1), the above result allows us to extend Guo [21, Theorem 3.7] and Chen and Guo [9, Theorem 3.5] to these kinds of sets. In particular, the restriction to Shilov-modules and the additional continuity assumption made in [21] to handle the ball case are not necessary.
Corollary 6.2
Let \(k\in {\mathbb {N}}\) and \(D_i \subset {\mathbb {C}}^{d_i}\) be bounded open sets with \(d_i \in {\mathbb {N}}\) for \(1 \le i \le k\), each of which is either a strictly pseudoconvex domain with \(C^5\) boundary or a bounded symmetric and circled domain, and let \(A=A(D)\) with \(D=D_1 \times \cdots \times D_k\). Assume that  are hypo-Shilov modules with minimal \(C(S_D)\)-extensions
are hypo-Shilov modules with minimal \(C(S_D)\)-extensions  \((i=1,2)\) and that
\((i=1,2)\) and that  is pure. Then we have an isomorphism
is pure. Then we have an isomorphism  as stated in the above theorem.
as stated in the above theorem.
Data Availability
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
Notes
For a strictly pseudoconvex bounded open set \(D\subset {\mathbb {C}}^n\), one can show that \(\partial D = \partial {\overline{D}}\): While “\(\supset \)” trivially holds for all open sets, the reverse inclusion follows as an application of the maximum principle for a strictly plurisubharmonic defining function. From the two inclusions stated in the original version of Fornaess’ theorem we can therefore deduce that \(\psi _i(\partial D_i) \subset \psi _i({\overline{D}}_i) \subset {\overline{C}}_i\) and \(\psi _i(\partial D_i) = \psi _i(\partial {\overline{D}}_i) \subset \psi _i\big (\overline{{\mathbb {C}}^{d_i}\setminus {\overline{D}}_i}\big ) \subset \overline{{\mathbb {C}}^{m_i} \setminus \overline{C_i}}\). Together, these two inclusions yield \(\psi _i(\partial D_i) \subset \partial {\overline{C}}_i = \partial C_i\), as asserted above.
References
Aleksandrov, A.B.: Inner funtions on compact spaces. Functional Analysis and Its Applications 18, 87–98 (1984). https://doi.org/10.1007/BF01077819
Aleksandrov, A.B.: Inner funtions: results, methods, problems. Proceedings of the International Congress of Mathematcs (Berkeley, 1986) 1, 699–707 (1987)
Athavale, A.: On the intertwining of joint isometries. Journal of Operator Theory 23(2), 339–350 (1990)
Athavale, A.: On the intertwining of \(\partial {\cal{D}}\)-isometries. Complex Analysis and Operator Theory 2(3), 417–428 (2008). https://doi.org/10.1007/s11785-007-0040-z
Athavale, A.: Multivariable isometries related to certain convex domains. Rocky Mountain Journal of Mathematics 48(1) (2018). https://doi.org/10.1216/rmj-2018-48-1-19
Athavale, A.: A note on Cartan isometries. New York J. Math. 25, 934–948 (2019)
Carlson, J.F., Clark, D.N.: Cohomology and extensions of Hilbert modules. Journal of Functional Analysis 128(2), 278–306 (1995). https://doi.org/10.1006/jfan.1995.1032
Carlson, Jon F., Clark, D.N.: Projectivity and extensions of Hilbert modules over \(A({\mathbb{D}}^N)\). Michigan Mathematical Journal 44(2) (1997). https://doi.org/10.1307/mmj/1029005711
Chen, X., Guo, K.: Cohomology and extensions of hypo-S̆ilov modules over unit modulus algebras. Journal of Operator Theory 43 (2000). https://www.theta.ro/jot/archive/2000-043-001/2000-043-001-004.pdf
Conway, J.B.: Towards a functional calculus for subnormal tuples: The minimal normal extension. Transactions of the American Mathematical Society 326(2), 543–567 (1991). https://doi.org/10.1090/s0002-9947-1991-1005077-x
Didas, M.: Dual algebras generated by von Neumann n-tuples over strictly, volume 425. Institute of Mathematicspseudoconvex sets. Polish Academy of Sciences (2004). https://doi.org/10.4064/dm425-0-1
Didas, M., Eschmeier, J.: Subnormal tuples on strictly pseudoconvex and bounded symmetric domains. Acta Sci. Math. (Szeged) 71(3–4), 691–731 (2005)
Didas, M., Eschmeier, J.: Unitary extensions of Hilbert \(a(d)\)-modules split. Journal of Functional Analysis 238(2), 565–577 (2006). https://doi.org/10.1016/j.jfa.2006.02.002
Didas, M., Eschmeier, J.: Inner functions and spherical isometries. Proceedings of the AMS 139(8), 2877–2889 (2011). https://doi.org/10.1090/S0002-9939-2011-11034-7
Douglas, R.G., Paulsen, V.I.: Hilbert modules over function algebras, volume 217 of Pitman Res. Notes Math. Ser., vol. 217. Longman, Harlow (1989)
Eschmeier, J.: On the reflexivity of multivariable isometries. Proceedings of the AMS 134, 1783–1789 (2006). https://doi.org/10.1090/S0002-9939-05-08139-6
Eschmeier, J., Everard, K.: Toeplitz projections and essential commutants. Journal of Functional Analysis 269(4), 1115–1135 (2015). https://doi.org/10.1016/j.jfa.2015.03.017
Eschmeier, J., Putinar, M.: Spectral Decompositions and Analytic Sheaves, volume 10 of LMS Monographs, New Series. Clarendon Press, Oxford (1996)
Everard, K.: A Toeplitz projection for multivariable isometries. PhD thesis, Saarland University (2013). https://doi.org/10.22028/D291-26548
Fornaess, J.E.: Embedding strictly pseudoconvex domains in convex domains. American Journal of Mathematics 98(2), 529 (1976). https://doi.org/10.2307/2373900
Guo, K.: Normal Hilbert modules over the ball algebra \(A(B)\). Studia Mathematica 135(1), 1–12 (1999). https://doi.org/10.4064/sm-135-1-1-12
Henkin, Gennadi, Leiterer, Jürgen.: Theory of Functions on Complex Manifolds. Birkhäuser, Basel (1983). https://doi.org/10.1007/978-3-0348-6537-1
Jakóbczak, P.: Extension and decomposition operators in products of strictly pseudoconvex sets. Annales Polonici Mathematici 44(2), 219–237 (1984). https://doi.org/10.4064/ap-44-2-219-237
Loos, O.: Bounded symmetric domains and Jordan pairs. Lecture Notes. University of California at Irvine (1977). http://agt2.cie.uma.es/~loos/jordan/archive/irvine/irvine.pdf
Low, E.: Embeddings and proper holomorphic maps of strictly pseudoconvex domains into polydiscs and balls. Mathematische Zeitschrift 190, 401–410 (1985). https://doi.org/10.1007/BF01215140
Mlak, W.: Intertwining operators. Studia Mathematica 43(3), 219–233 (1972). https://doi.org/10.4064/sm-43-3-219-233
Paulsen, V.I.: Completely Bounded Maps and Operator Algebras. Number 78 in Cambridge Studies in Advanced Mathematics. Cambridge University Press (2002). https://doi.org/10.1017/CBO9780511546631
Range, R.M.: Holomorphic Functions and Integral Representations in Several Complex Variables. Springer, New York (1986). https://doi.org/10.1007/978-1-4757-1918-5
Réolon, E.: Zur Spektraltheorie vertauschender Operatortupel – Fredholmtheorie und subnormale Operatortupel. PhD thesis, Saarland University (2004)
Treves, F.: Topological Vector Spaces, Distributions and Kernels. Academic Press, New York, London (1967)
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Mihai Putinar.
Dedicated to the memory of Jörg Eschmeier, in deep gratitude for his guidance and inspiration.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is part of the topical collection “Multivariable Operator Theory. The Jörg Eschmeier Memorial” edited by Raul Curto, Michael Hartz, Mihai Putinar and Ernst Albrecht.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Didas, M. A-Isometries and Hilbert-A-Modules Over Product Domains. Complex Anal. Oper. Theory 16, 71 (2022). https://doi.org/10.1007/s11785-022-01243-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11785-022-01243-6



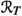 contains
contains 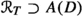 for density reasons. In Athavales result, two
for density reasons. In Athavales result, two 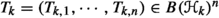
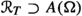 is always fulfilled. This shows in particular that
is always fulfilled. This shows in particular that 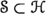 is a Shilov-A-module with minimal contractive
is a Shilov-A-module with minimal contractive  , then
, then  is an A-isometry with minimal normal extension
is an A-isometry with minimal normal extension 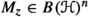 .
.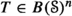 is an A-isometry with minimal normal extension
is an A-isometry with minimal normal extension 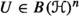 , then, introducing the multiplications
, then, introducing the multiplications 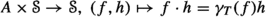 on
on 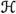 and
and 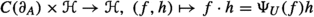 on
on  turns
turns  into a Shilov module over A with minimal
into a Shilov module over A with minimal  .
.