Abstract
The existence of solutions for the Dirichlet problem associated with bounded perturbations of positively-(p, q)-homogeneous Hamiltonian systems is considered both in nonresonant and resonant situations. To deal with the resonant case, the existence of a couple of lower and upper solutions is assumed. Both the well-ordered and the non-well-ordered cases are analysed. The proof is based on phase-plane analysis and topological degree theory.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let \(H:{\mathbb {R}}^2\rightarrow {\mathbb {R}}\) be a continuously differentiable positively-(p, q)-homogeneous positive-definite function. By this we mean that, for some \(p>1\) and \(q>1\) with \((1/p)+(1/q)=1\),
for every \(\lambda >0\) and \((x,y)\ne (0,0)\). We are interested in Dirichlet problems of the type
where the functions \(\phi ,\psi :[a,b]\times {\mathbb {R}}^2\rightarrow {\mathbb {R}}\) are continuous and bounded.
The autonomous system
is isochronous (see [25]). More precisely, (0, 0) is a global center, and all solutions are periodic of the same period, which we denote by \(\tau \). Moreover, if \(y_0>0\), for all solutions (x, y) starting with \((x(0),y(0))=(0,y_0)\) there is a first time \(\tau _+>0\) for which \(x(\tau _+)=0\), while \(x(t)>0\) for every \(t\in \,]0,\tau _+[\) , and this time \(\tau _+\) is independent of \(y_0>0\). Symmetrically, if \(y_0<0\), there is a first time \(\tau _->0\) for which \(x(\tau _-)=0\), while \(x(t)<0\) for every \(t\in \,]0,\tau _-[\) . Clearly enough, \(\tau _++\tau _-=\tau \).
First of all, let us state the following nonresonance result.
Theorem 1
Assume that there is an integer \(n\ge 0\) such that one of the following alternatives hold
Then, problem (2) has a solution.
Its proof relies on the so called shooting method, following the ideas presented in [10] (see also [3, 23]), and will be given in Section 3.
As a possible example we may consider the function
for some positive constants \(\delta ,\gamma ,\mu ,\nu \) (we use the standard notation where \(f^+=\max \{f,0\}\), \(f^-=\max \{-f,0\}\)). If we choose \(\delta =\gamma =1\) and \(\phi \equiv 0\), our problem is then equivalent to
with \(h(t,x,v)=-\psi (t,x,|v|^{p-2}v)\). In this case, \(\tau _+=\pi _p\mu ^{-1/p}\) and \(\tau _-=\pi _p\nu ^{-1/p}\), cf. [18], where
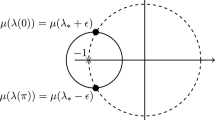
If \(p=2\), the differential equation in (6) models an asymmetric oscillator, with \(\tau _+=\pi /\sqrt{\mu }\), \(\tau _-=\pi /\sqrt{\nu }\), and it is well known that some care on the choice of \(\mu ,\nu \) must be taken to avoid resonance phenomena; when h is bounded, the existence of a solution depends on the position of \((\mu ,\nu )\) with respect to the Fučík spectrum, cf. [10]. In Fig. 1, the assumption of Theorem 1 can be visualized, when \(b-a=\pi _p\), taking the values \((\mu ^{-1/p},\nu ^{-1/p})\) in the white regions.
A different way of avoiding resonance would be the assumption of the existence of a well-ordered couple of lower/upper solutions \(\alpha \le \beta \), together with some Nagumo-type conditions. This method goes back to the pioneering papers [20,21,22]. Some more care is needed in the non-well-ordered case \(\alpha \not \le \beta \), see [1, 8, 9, 16, 17]. We refer to the book [7] for an extensive exposition on the theory of lower and upper solutions for scalar second order differential equations.
The concept of lower and upper solution has been recently extended to planar systems in [15] for the periodic problem (see also [12]), and in [14] for Sturm–Liouville type problems, including the Dirichlet problem. We recall in Section 4 the main definitions in this case.
Here is our result for problem (2), in the well-ordered case.
Theorem 2
Assume H to be a continuously differentiable positively-(p, q)-homogeneous positive-definite function, for some \(p>1\) and \(q>1\) with \((1/p)+(1/q)=1\). Let \(\phi ,\psi \) be uniformly bounded continuous functions, and let \((\alpha ,\beta )\) be a well-ordered pair of lower/upper solutions of problem (2). Then, there exists a solution (x, y) of (2) such that \(\alpha \le x\le \beta \).
The proof will be given in Section 5. We will first need some properties of positively-(p, q)-homogeneous Hamiltonian systems, which we provide in Section 2. Then, the main issue will be the construction of some guiding curves in the phase plane so to enter the framework of [14, Theorem 11].
In the sequel, we denote by \(C^{j,\ell }_{loc}\) the space of \(C^j\)-smooth real functions whose jth derivative is locally \(\ell \)-Hölder continuous, with \(\ell >0\). Moreover, defining the function
we introduce the following order relation: for any continuous function \(x:[a,b]\rightarrow {\mathbb {R}}\), we write
if and only if
We will write either \(u\gg v\) or \(v\ll u\) when \(u-v \gg 0\).
Concerning the non-well-ordered case, we recall that the existence of a pair of lower/upper solutions does not guarantee the existence of a solution, since resonance phenomena can occur with respect to the higher part of the spectrum. However, at least for scalar second-order equations, it is well known that resonance can be handled with respect to the first eigenvalue, cf. [7]. This observation leads us to assume, in the non-well-ordered case, that
Here is our result, in the non-well-ordered case.
Theorem 3
Let \(\ell >0\) and assume H to be a \(C^{1,\ell }_{loc}\)-smooth positively-(p, q)-homogeneous positive-definite function, for some \(p>1\) and \(q>1\) with \((1/p)+(1/q)=1\). Let \(\phi ,\psi \) be uniformly bounded \(C^{0,\ell }_{loc}\)-smooth functions, and let \((\alpha ,\beta )\) be a non-well-ordered pair of lower/upper solutions of (2). Assume moreover that
Then, if (8) holds, there exists a solution (x, y) of (2) such that \(\alpha \not \ll x\) and \(x\not \ll \beta \).
The above theorem generalizes [14, Theorem 19]. Its proof is provided in Section 6 by the use of topological degree techniques, which require the above regularity assumptions. It would be interesting to know whether the result still holds when the functions \(\phi ,\psi \) are only assumed to be continuous. Notice that assumption (9) is surely verified for problems like (6), where \(\frac{\partial H}{\partial y}(x,y)= |y|^{q-2}y\).
In the final section of the paper, we extend the previous results to systems in \({\mathbb {R}}^{2N}\) which can be considered as weakly coupled planar systems of the above type. The different planar systems involved could have either well-ordered or non-well-ordered lower and upper solutions. We are able to deal with this mixed type of situations, still obtaining an existence result, thus carrying out the investigation opened in [14]. However, for the non-well-ordered case, we need to ask the lower/upper solutions to be strict, a concept we will introduce in Section 7.
2 Elementary properties of positively-(p, q)-homogeneous Hamiltonian systems
For the autonomous system (3) the origin (0, 0) is an isochronous center, all solutions having minimal period \(\tau >0\). We denote by \(S(t)=(S_1(t),S_2(t))\) the periodic solution such that \(S_1(0)=0\) and \(S_2(0)>0\), with \(H(S_1(t),S_2(t))=1\) for every t. Then, the periodic solutions of system (3) having energy \(H(x,y)=E\) can be written as
for some \(\sigma \in {\mathbb {R}}\). We will use the notations
For any function \(u=(x,y):[a,b]\rightarrow {\mathbb {R}}^2\setminus \{(0,0)\}\), we can introduce the generalized polar coordinates
where \(r(t)\ge 0\). If \(u(t)=(0,0)\), we set \(r(t)=0\), while \(\theta (t)\) is not defined. Let
For every \(D>0\), one has that
Condition (1) can be rewritten as
for every \(\lambda >0\) and \((x,y)\ne (0,0)\). Then,
We can write the generalized Euler formula
We can rewrite (12) and (13) as
for every \(\mu >0\). We will need the following property.
Lemma 4
For every \(L>0\), we have that
Proof
We first prove that there are \(c_0>0\) and \(y_0\ge 1\) such that
From (14), we have both
Hence, we can find \(\delta _0>0\) and \(c_0>0\) such that
If we set
then, for every \(x\in [-L,L]\) we get, using (16) and (17),
So, for any \(x\in [-L, L]\) and \(\mu >1\), from (16) we obtain
The conclusion follows. \(\square \)
3 Proof of Theorem 1
To prove Theorem 1, let us first assume the validity of the alternative (4).
Introducing generalized polar coordinates (11), we can compute (cf. [25, Section 2])
Since the functions \(\phi ,\psi :[a,b]\times {\mathbb {R}}^2\rightarrow {\mathbb {R}}\) are bounded, there is a constant K for which
Setting \(\omega =\min \{\frac{1}{p},\frac{1}{q}\}\) and using (10), we have
when \(r(t) > 1\). As a consequence of (20), all the solutions of
are globally defined. Since we are assuming (4), choosing \(\delta >0\) sufficiently small, we have
Correspondingly, we can fix \(\overline{R}>1\) such that
From (19), a solution of (21) satisfying \(r(t)\ge \overline{R}\) for every \(t\in [a,b]\) is such that
for every \(t\in [a,b]\). Hence, recalling assumption (4), from (22) we get
Finally, from (20) and Gronwall lemma, we can find \(R_1>R_0>\overline{R}\) with the following property: if a solution of (21) satisfies \(r(t_0)=R_0\) for some \(t_0\in [a,b]\), then
Let us set
For any \(\sigma \in J:=[y_0^-,y_0^+]\), we consider the Cauchy problem
We recall that all the solutions of (25) are defined in the interval [a, b]. Then, by [6, Corollary 2.3], there exists a closed connected set
whose projection on J coincides with J.
So, we can find some \((y_0^-,(x^-,y^-))\in {\mathcal {K}}\) and \((y_0^+,(x^+,y^+))\in {\mathcal {K}}\). The solutions \((x^\pm ,y^\pm )\) satisfy (23) and
Indeed, denoting by \((r^\pm ,\theta ^\pm )\) the modified polar coordinates of \((x^\pm ,y^\pm )\), we have \(r^\pm (a)=R_0\) and so (24) holds. Then, if we consider the initial data \(y^+(a)=y_0^+\), [resp. \(y^-(a)=y_0^-\)], we can choose \(\theta ^+(a)=0\) [resp. \(\theta ^-(a)=\tau _+\)].
From (23), we get
so that
Hence, defining the continuous function \({\mathcal {Z}}: {\mathcal {K}} \rightarrow {\mathbb {R}}\) as \({\mathcal {Z}} (\sigma , (x,y))=x(b)\), from (26) we easily deduce that
By continuity, \({\mathcal {Z}}({\mathcal {K}})\) is an interval and we find the existence of \((\overline{\sigma },(\overline{x},\overline{y}))\in {\mathcal {K}}\) satisfying \({\mathcal {Z}}(\overline{\sigma },(\overline{x},\overline{y}))=0\). Hence, \((\overline{x},\overline{y})\) is the solution we were looking for.
The proof is thus completed if (4) holds. If (5) holds, the proof is similar: we need to replace (22) by
and (23) by
Finally, we get
which gives (26), permitting us to conclude as above.
The proof of Theorem 1 is now completed. \(\square \)
Remarks. Other types of boundary conditions can be considered, leading to similar results. The case of a Neumann-type problem, with boundary conditions \(y(a)=0=y(b)\), is nothing but the previous Dirichlet-type problem by a simple switch in the variables  . The mixed problem
. The mixed problem
can be considered, as well. Going back to the solution \(S=(S_1,S_2)\) of the unperturbed system (3), we can find the positive values \(\tau _1,\tau _2,\tau _3,\tau _4\) such that
leading to the following.
Theorem 5
Assume that there is an integer \(n\ge 0\) such that one of the following alternatives hold
Then, problem (27) has a solution.
Similarly, we can consider the boundary conditions \(y(a)=0=x(b)\), as well, thus obtaining the corresponding existence result. Finally, Carathéodory conditions on \(\phi \) and \(\psi \) could be assumed. We avoid entering into details, for briefness.
4 The definition of lower and upper solutions
Let us consider the boundary value problem
where \(f,g:[a,b]\times {\mathbb {R}}^2\rightarrow {\mathbb {R}}\) are continuous functions, and recall the definitions introduced in [14].
Definition 6
A continuously differentiable function \(\alpha :[a,b]\rightarrow {\mathbb {R}}\) is said to be a lower solution for problem (28) if there exists a continuously differentiable function \(y_\alpha :[a,b]\rightarrow {\mathbb {R}}\) such that, for every \(t\in [a,b]\),
and
Definition 7
A continuously differentiable function \(\beta :[a,b]\rightarrow {\mathbb {R}}\) is said to be an upper solution for problem (28) if there exists a continuously differentiable function \(y_\beta :[a,b]\rightarrow {\mathbb {R}}\) such that, for every \(t\in [a,b]\),
and
We say that \((\alpha ,\beta )\) is a well-ordered pair of lower/upper solutions of problem (28), if \(\alpha \) and \(\beta \) are respectively a lower and an upper solution for problem (28) and they satisfy
On the other hand, if the above inequality does not hold, we say that the pair \((\alpha ,\beta )\) is non-well-ordered.
5 Proof of Theorem 2
Define
and set \(m_\alpha =\min \alpha \) and \(M_\beta =\max \beta \). To apply [14, Theorem 11], we need to construct some guiding curves \(\gamma ^\pm _{1,2}:[m_\alpha ,M_\beta ]\rightarrow {\mathbb {R}}\) such that, for every \(t\in [a,b]\) and \(x\in [\alpha (t),\beta (t)]\),
This can be obtained as an immediate consequence of the next two lemmas.
Lemma 8
For any \(L>0\) and \(y_0>0\) we can define two continuously differentiable functions \(\gamma ^+_1,\gamma ^+_2:[-{L}, {L}]\rightarrow {\mathbb {R}}\) satisfying
and such that (29) and (30) hold for every \(t\in [a,b]\) and \(x\in [-L,L]\).
Proof
Since both \(\phi \) and \(\psi \) are bounded, let us consider \(K>0\) as in (18). From Lemma 4 we can find \(y_1\ge y_0\) such that
Since H is \(C^1\), we can find a positive constant \(c_1\) such that
Now, since \(2-q<1\), we can find \(M>1\) sufficiently large so to have
We define \(\gamma ^+_{1,2}:[-{L}, {L}]\rightarrow {\mathbb {R}}\) as
Notice that \(\gamma ^+_{1,2}(x)\ge y_1\ge y_0\), for every \(x\in [-L,L]\). If we show that, for \(i=1,2\),
then, since from (36) and (33) the denominator in (37) is positive, we get both
and
for every \(t\in [a,b]\) and \(x\in [-L,L]\) and the lemma will be proved. Hence, we need to prove the validity of (37).
Using equality (15) and the estimate (34), we have that
Moreover, using equality (16) and recalling (33), we have that
Since, using (36), for all \(x\in [-L,L]\) we have \(\frac{1}{M} \gamma ^+_i(x)\in [y_1,y_1+2L]\), \(i=1,2\), then we get
Hence, recalling (33) and (36), we have
where the last estimate is given by (35). We have thus proved (37), and so the proof of the lemma is completed. \(\square \)
Lemma 9
For any \(L>0\) and \(y_0>0\) we can define two continuously differentiable functions \(\gamma ^-_1,\gamma ^-_2:[-{L}, {L}]\rightarrow {\mathbb {R}}\) satisfying
and such that (31) and (32) hold for every \(t\in [a,b]\) and \(x\in [-L,L]\).
The proof of this lemma is analogous to the previous one, so we omit it, for briefness.
Let us now conclude the proof of Theorem 2. Choosing
we can apply Lemmas 8 and 9 to get the existence of the needed curves \(\gamma _i^\pm \). Moreover, for every \(t\in [a,b]\),
This is an immediate consequence of Lemma 4, choosing a larger value of \(y_0\), if necessary. Then, [14, Theorem 11] applies, thus completing the proof of Theorem 2.
6 Proof of Theorem 3
As a first step, we need the following two lemmas, where the ordering relation defined in Introduction is used.
Lemma 10
([14, Lemma 17]). Given a continuous function \(\varphi :[a,b]\rightarrow {\mathbb {R}}\), the sets
are open in \(C^1_0([a,b])= \{x\in C^{1}([a,b]) \,:\, x(a)=0=x(b)\}\).
Lemma 11
([14, Lemma 18]). Given a continuously differentiable function \(\varphi :[a,b]\rightarrow {\mathbb {R}}\), we have that
We now use the notation introduced in Section 2, and set \({\widetilde{S}}_1(t)=S_1(t+\tau _+)\).
Lemma 12
Given a continuously differentiable function \(\varphi :[0,\tau ^+]\rightarrow {\mathbb {R}}\), we have that
Similarly, given a continuously differentiable function \(\varphi :[0,\tau ^-]\rightarrow {\mathbb {R}}\), we have that
Proof
To prove the former statement, we apply Lemma 11 with \([a,b]=[0,\tau ^+]\), recalling that \(S_1\gg 0\). To prove the latter statement, we apply the same lemma with \([a,b]=[0,\tau ^-]\), recalling that \({\widetilde{S}}_1 \ll 0\). \(\square \)
Let us introduce a \(C^\infty \)-smooth cut-off function \(\chi :{\mathbb {R}}\rightarrow [0,1]\) such that
and, for every \(d\ge 1\), consider the modified problem
where
with
Notice that (2) and (41) coincide in the set \([-d\overline{S},d\overline{S}]\times [-d^{\frac{p}{q}}\overline{S},d^{\frac{p}{q}} \overline{S}]\). In particular, if a solution \(u=(x,y)\) of (41) is such that \({\mathcal {N}}_p(u)<d\), then u is necessarily a solution of (2).
Lemma 13
There exists \(D>1\) with the following property: if \(u=(x,y)\) is any solution of (41), with \(d\in [D,+\infty ]\), satisfying  and
and  , then \({\mathcal {N}}_p(u) < D\).
, then \({\mathcal {N}}_p(u) < D\).
Proof
Assume by contradiction that there exist a diverging sequence \((d_n)_n\) and some solutions \(u_n=(x_n,y_n)\) of (41), with \(d=d_n\), such that  ,
,  and \({\mathcal {N}}_p(u_n) >n\). We introduce the functions
and \({\mathcal {N}}_p(u_n) >n\). We introduce the functions
In particular, \({\mathcal {N}}_p(v_n,w_n)=1\). Notice that, from (11) and (10), we have
By (12) and (13), we see that \((v_n,w_n)\) solves
where
Then, by (42), since \((v_n,w_n)\) solves (43), it is bounded in \(C^1\times C^1\). By a standard compactness argument, a subsequence converges to some \((\overline{v},\overline{w})\) in \(C^1\times C^1\), and
Hence, we have either \((\overline{v}(t),\overline{w}(t))=S(t)\), or \((\overline{v}(t),\overline{w}(t))=S(t+\tau _+)\). More precisely, using (8), the first case is possible if and only if \(b-a=\tau _+\), the second one if and only if \(b-a=\tau _-\). In the first case, since \(v_n\) \(C^1\)-converges to \(S_1\gg 0\), we have that \(v_n \gg \frac{1}{2} S_1\) when n is sufficiently large, so that, recalling Lemma 12, we get the contradiction
In the second case, since \(v_n\) \(C^1\)-converges to \({\widetilde{S}}_1= S_1(\,\cdot \,+\tau _+)\ll 0\), we have that \(v_n \ll \frac{1}{2} {\widetilde{S}}_1\) when n is sufficiently large, thus providing the contradiction
The proof is thus completed. \(\square \)
We now fix \(D>1\) as in Lemma 13, assuming also
From Lemma 13, if \(u=(x,y)\) is any solution of (41) with \(d\ge D\), satisfying both  and
and  , then u is a solution of (2), too.
, then u is a solution of (2), too.
Lemma 14
The functions \(\alpha \) and \(\beta \) are a lower and an upper solution of (41), respectively, provided that d is chosen large enough.
Proof
From Lemma 4 and the boundedness of \(\phi \), we deduce the existence of a constant \({\widetilde{K}}>0\) such that, for every \(d\ge 1\), we have both \({\widetilde{\phi }}_d(t,\alpha (t),y)\ge -{\widetilde{K}}\) when \(y>0\), and \({\widetilde{\phi }}_d(t,\alpha (t),y)\le {\widetilde{K}}\) when \(y<0\), for every \(t\in [a,b]\). Moreover, using again Lemma 4, we can take d large enough so that, if \(y>d^{p/q}\overline{S}\) then
and if \(y<-d^{p/q}\overline{S}\) then
On the other hand, if \(y\in [-d^{p/q}\overline{S},d^{p/q}\overline{S}]\), then \((\alpha (t),y)\) belongs to the region where the problem has not been modified and the desired estimates hold.
The inequality for \(y_\alpha '(t)\) still holds since, for every \(t\in [a,b]\), also the point \((\alpha (t),y_\alpha (t))\) belongs to the region where the problem has not been modified. \(\square \)
Our aim now is to construct a lower solution \({\widehat{\alpha }}\) and an upper solution \({\widehat{\beta }}\) such that \({\widehat{\alpha }}\ll \beta \) and \(\alpha \ll {\widehat{\beta }}\). To do so, let us consider, for every \(d>1\), the slowed autonomous system
It is isochronous, all solutions being periodic with minimal period \(\tau \frac{d}{d-1}>\tau \).
Lemma 15
For every \(\xi >0\), the problem
has a unique solution \((x_\xi ,y_\xi )\). Moreover, \(x_\xi (t)>\xi \) for every \(t\in \,]a,b[\). Similarly, the problem
has a unique solution \((x_{-\xi },y_{-\xi })\), satisfying \(x_{-\xi }(t)<-\xi \) for every \(t\in \,]a,b[\).
Proof
If we parametrize the solutions (x, y) with the energy \(E=\frac{d-1}{d}H(x,y)\), we see that they cross the line \({\mathcal {L}}=\{(x,y)\in {\mathbb {R}}^2:x=\xi \}\) if and only if E is greater than a well determined value \({\overline{E}}_\xi >0\), and assumption (9) ensures that there are exactly two crossing points \((\xi , {\bar{y}}_\xi ^+)\) and \((\xi , {\bar{y}}_\xi ^-)\), with \({\bar{y}}_\xi ^+>{\bar{y}}_\xi ^-\). Since \(b-a\le \tau _-<\tau _-d/(d-1)\), the solution (x, y) we are looking for cannot follow the path to the left of \({\mathcal {L}}\), hence, if it exists, it has to be \(x_\xi (t)>\xi \) for every \(t\in \,]a,b[\,\).
Let us denote by \(T_\xi (E)\) the time needed to go from \((\xi , y_\xi ^+)\) to \((\xi , y_\xi ^-)\). We have thus defined a function \(T_\xi :\,]{\overline{E}}_\xi ,+\infty [\,\rightarrow {\mathbb {R}}\) which is continuous, positive and strictly increasing. Surely \(T_\xi (E)<b-a\) if E is in a small right neighbourhood of \({\overline{E}}_\xi \). Hence, since \(\lim _{E\rightarrow +\infty }T_\xi (E)=\tau _+d/(d-1)>b-a\), there is a unique value \(E_\xi >{\overline{E}}_\xi \) for which \(T_\xi (E_\xi )=b-a\), and this value of the energy determines the solution we are looking for.
We have thus proved the first part of the lemma; the proof of the second part is similar.\(\square \)
We are now ready to define the lower and upper solutions \({\widehat{\alpha }}\) and \({\widehat{\beta }}\).
Lemma 16
Taking \(d>D\) and \(\xi >2d\overline{S}\), the functions \({\widehat{\alpha }}=x_{-\xi }\) and \({\widehat{\beta }}=x_\xi \) are a lower and an upper solution of (41), respectively. Moreover,
Proof
Let us show that \({\widehat{\beta }}=x_\xi \) is an upper solution, with associated function \(y_{{\widehat{\beta }}}=y_\xi \). Recalling that \({\widetilde{\phi }}_d(t,x,y)\) and \({\widetilde{\psi }}_d(t,x,y)\) vanish when \(x\notin [-2d{\overline{S}},2d{\overline{S}}]\), since \(\xi >2d\overline{S}\), using assumption (9), we have
Moreover,
since equality holds. Finally, \(x_\xi (a)\ge 0\) and \(x_\xi (b)\ge 0\), thus proving that \(x_\xi \) is an upper solution. Analogously one proves that \(x_{-\xi }\) is a lower solution.
Now, since from (44) we have \(\xi>2d\overline{S} > \max \{\Vert \alpha \Vert _\infty \,,\Vert \beta \Vert _\infty \}\), one has
thus ending the proof of the lemma. \(\square \)
Let us now fix \(d>D\) sufficiently large to ensure the validity of Lemma 14. We thus have three well-ordered pairs of lower/upper solutions of (41):
Let \({\bar{a}}=\min {\widehat{\alpha }}\) and \({\bar{b}}=\max {\widehat{\beta }}\). By Lemma 4, we can find \(\overline{M}>0\) such that, if \(t\in [a,b]\) and \(x\in [{\bar{a}},{\bar{b}}]\), then
We now need to introduce the guiding curves.
Lemma 17
There are four continuously differentiable functions \(\gamma _i^\pm :[{\bar{a}},{\bar{b}}]\rightarrow {\mathbb {R}}\), with \(i=1,2\), satisfying
and such that
for every \(t\in [a,b]\) and \(x\in [{\bar{a}},{\bar{b}}]\).
Proof
It follows the lines of the proofs of Lemmas 8 and 9. \(\square \)
Let us now introduce our functional setting for the problem (41).
Set \({\mathcal {I}}=[a,b]\), denote by \(C^{0,\ell }({\mathcal {I}})\) the space of \(\ell \)-Hölder continuous functions and by \(C^{1,\ell }({\mathcal {I}})\) the space of functions having derivative belonging to \(C^{0,\ell }({\mathcal {I}})\). Moreover, define
We consider the linear operator
and the Nemitskii operator
Problem (41) is then the same as
with
Lemma 18
The operator L is invertible with continuous inverse, and problem (41) is equivalent to \(u=L^{-1}N_d u\). Moreover, the operator
is completely continuous.
Proof
It is rather standard, using the fact that \(C^{1,\ell }({\mathcal {I}})\) is compactly imbedded in \(C^1({\mathcal {I}})\). \(\square \)
Let us define the sets
with the notation
where
These sets are open in \(X=C_0^{1}({\mathcal {I}}) \times C^{1}({\mathcal {I}})\), by Lemma 10.
We say that an open set \(\Omega \subset X\) is admissible if \(L^{-1}N_d\) has no fixed points on \(\partial \Omega \) and the set of fixed points of \(L^{-1}N_d\) in \(\Omega \) is bounded, i.e., it is contained in some open ball \(B_\rho \,\). In this case, we can define
where \(d_{LS}\) denotes the Leray–Schauder degree. By excision, this definition does not depend on the choice of \(\rho \).
Our aim is to prove that, if there are no solutions of (41) on \(\partial {\mathcal {V}}_j\), then \({\mathcal {V}}_j\) is admissible and
This fact will be proved in Lemma 22.
In the following we denote by \((\varphi ,\eta )\) any of the three pairs
We need to truncate the functions \({\widehat{f}}_d\) and \({\widehat{g}}_d\) so to modify system (41). Define, for any \(\mu \le \nu \),
Fix \(\overline{Y}>0\) such that
for every \(x\in [{\bar{a}},{\bar{b}}]\). Let
and consider the problem
which is equivalent to \(Lu=N_{\varphi ,\eta }u\), with the appropriate Nemitskii operator. Notice that the functions \(f_{\varphi ,\eta }\) and \(g_{\varphi ,\eta }\) are bounded. Moreover, if (x, y) is a solution of (51) satisfying \(\varphi \le x \le \eta \) and \(-\overline{Y}< y < \overline{Y}\), then it is a solution of (41), too.
Lemma 19
Each \((\varphi ,\eta )\) is a well-ordered pair of lower/upper solutions for (51).
Proof
Assume for instance that \((\varphi ,\eta )=(\alpha ,{\widehat{\beta }})\). Then, if \(y\in [-\overline{Y},\overline{Y}]\),
while
Since \(-\overline{Y}<y_\alpha (t)<\overline{Y}\) for every \(t\in [a,b]\) from the choice (48), the inequality for \(y_\alpha '(t)\) still holds, since \((\alpha (t),y_\alpha (t))\) belongs to the region where the problem has not been modified. All the other cases can be treated similarly. \(\square \)
Lemma 20
Every solution \(u=(x,y)\) of (51) satisfies \(\varphi \le x\le \eta \).
Proof
Let us define the following regions
As in [12] and [14], one can verify that, if \(u=(x,y)\) is a solution of
then, for any \(t_0\in [a,b]\),
Moreover, for any \(t_0\in [a,b]\), if
then there exists \(\delta >0\) such that
Similarly, if, for any \(t_0\in [a,b]\),
then there exists \(\delta >0\) such that
Indeed, by contradiction, let \(u=(x,y)\) be a solution of (51) such that \(x(t_0)<\varphi (t_0)\), for some \(t_0\in [a,b]\). Since \(x(a)=0\ge \varphi (a)\) and \(x(b)=0\le \varphi (b)\), then \(t_0\in \,]a,b[\) and by the above considerations it cannot be that \((t_0,u(t_0))\in A_{NW}\cup A_{SW}\). Hence, \(y(t_0)=y_\varphi (t_0)\), and there exists \(\delta >0\) such that \((t,u(t))\in A_{NW}\) for \(t\in \,]t_0-\delta , t_0[\) , which leads to a contradiction. The case \(x(t_0)>\eta (t_0)\) leads to a similar contradiction, as well. \(\square \)
Lemma 21
Every solution \(u=(x,y)\) of (51) satisfies
Proof
We introduce the functions \(G^\pm _i(t)=y(t)-\gamma ^\pm _i(x(t))\), with \(i=1,2\). We first show that \(y(a)<\gamma ^+(x(a))\) and \(y(b)<\gamma ^+(x(b))\).
Let us prove that we cannot have \(y(a)\ge \gamma ^+_1(x(a))\). At first, assume that \(y(t)\ge \gamma ^+_1(x(t))\) for every \(t\in [a,b]\). Then, from (48) we get \(y(t)\ge \overline{M}\) for every \(t\in [a,b]\), so that (46) gives \(x(b)>0\), a contradiction. So, there exists \(t_0\in [a,b[\,\) such that \(G^+_1(t_0)=0\) and \(G^+_1(t)<0\) in a right neighborhood of \(t_0\). We can compute, recalling (47),
getting again a contradiction. Hence, \(y(a)<\gamma ^+_1(x(a))\le \gamma ^+(x(a))\), recalling (49).
Similarly one shows that \(y(b)<\gamma ^+_2(x(b))\le \gamma ^+(x(b))\), going backwards in time.
We now prove that \(y(t)<\gamma ^+(x(t))\) for every \(t\in [a,b]\). Assume by contradiction that there is \(t_0\in \,]a,b[\) such that \(y(t_0)\ge \gamma ^+(x(t_0))\). We distinguish two possibilities. First, if \(x(t_0)\ge 0\), then the solution remains above \(\gamma _1^+\) for all \(t\in \,]t_0,b]\); hence, \(y(t)>{\overline{M}}\) and \(x'(t)>0\) for all \(t\in \,]t_0,b]\), leading to \(x(b)>0\), which is impossible. Second, if \(x(t_0)<0\), then there must exist a \(t_1\in [a,t_0[\) such that \(y(t_1)\le {\overline{M}}\). But then the solution remains below \(\gamma _2^+\) for all \(t\in [t_1,b]\), in contradiction with the assumption.
Similarly, one proves that \(y(t)>\gamma ^-(x(t))\) for every \(t\in [a,b]\). \(\square \)
Lemma 22
If there are no solutions of (41) on \(\partial {\mathcal {V}}_j\), then \({\mathcal {V}}_j\) is admissible and
Proof
For any sufficiently large \(\rho >0\), denoting by \(B_\rho \) the open ball in X with radius \(\rho \), centered at the origin, we claim that
Indeed, let us show that there is a \(\rho >0\) such that, for every \(\lambda \in [0,1]\), every solution of \(Lu=\lambda N_{\varphi ,\eta }u\) satisfies \(\Vert u\Vert _{C^1}<\rho \). By contradiction, if this is not true, there exist a sequence \((\lambda _n)_n\) in [0, 1] and some solutions \(u_n=(x_n,y_n)\) of \(Lu_n=\lambda _n N_{\varphi ,\eta }u_n\) such that \(\Vert u_n\Vert _{C^1}\rightarrow \infty \). Let \(v_n=x_n/\Vert u_n\Vert _{C^1}\) and \(w_n=y_n/\Vert u_n\Vert _{C^1}\). By a standard argument it can be seen that, for a subsequence, \(\lambda _n\rightarrow {\bar{\lambda }}\in [0,1]\), while \((v_n,w_n)\rightarrow ({\bar{v}},{\bar{w}})\) in X. Moreover, \({\bar{v}}'={\bar{w}}\), \({\bar{w}}'={\bar{\lambda }}{\bar{v}}\), so that \({\bar{v}}''={\bar{\lambda }}{\bar{v}}\), and since \({\bar{v}}(a)=0={\bar{v}}(b)\), this implies \({\bar{v}}\equiv 0\), hence also \({\bar{w}}\equiv 0\), a contradiction. By homotopy invariance, the degree is then equal to 1.
Fix \(\rho >0\) as above. Since there are no solutions of (41) on \(\partial {\mathcal {V}}(\varphi ,\eta )\), we also have that there are no solutions of (51) on \(\partial {\mathcal {V}}(\varphi ,\eta )\). Hence, \({\mathcal {V}}(\varphi ,\eta )\) is admissible and, by excision,
Now, since \(N_{\varphi ,\eta }=N_d\) on \({\mathcal {V}}(\varphi ,\eta )\), the result follows. \(\square \)
Lemma 23
There are no solutions of (41) on \(\partial {\mathcal {V}}_1\).
Proof
We recall that in Lemma 16 we provided the definition of the functions \({\widehat{\alpha }}=x_{-\xi }\) and \({\widehat{\beta }}=x_\xi \) with the choice \(\xi > 2d\overline{S}\). Let \(u=(x,y)\) be a solution belonging to the closure of \({\mathcal {V}}_1\). Then \({\widehat{\alpha }}(t)\le x(t)\le {\widehat{\beta }}(t)\), for every \(t\in {\mathcal {I}}\). Assume by contradiction that \(x\not \ll {\widehat{\beta }}\). Since \(x(a)=0<\xi ={\widehat{\beta }}(a)\) and \(x(b)=0<\xi ={\widehat{\beta }}(b)\), there must be a \(t_0\in \,]a,b[\) such that
Hence, as \(\xi > 2d\overline{S}\), both (x(t), y(t)) and \((x_\xi (t),y_\xi (t))\) solve the autonomous system (45) in a neighborhood of \(t_0\). Since
and
being \(x'(t_0)=x_\xi '(t_0)\) and \(x(t_0)=x_\xi (t_0)\), by assumption (9) it has to be that \(y(t_0)=y_\xi (t_0)\). Since autonomous planar Hamiltonian systems have the uniqueness property for Cauchy problems when the initial value is not an equilibrium (cf. [19, Theorem 1]), then the two solutions (x(t), y(t)) and \((x_\xi (t),y_\xi (t))\) coincide, as long as they remain in \([\xi ,+\infty [\,\times {\mathbb {R}}\), leading to a contradiction. Hence, \(x\ll {\widehat{\beta }}\). Similarly, one proves that \({\widehat{\alpha }}\ll x\). So, there are no solutions of (41) on \(\partial {\mathcal {V}}_1\). \(\square \)
Now, if there is a solution \(u=(x,y)\) of (41) on \(\partial {\mathcal {V}}_2\), then \(x\le \beta \) and \(x\not \ll \beta \). Since \(\alpha \not \le \beta \), there is a \(t_0\) such that \(x(t_0)\le \beta (t_0)<\alpha (t_0)\), implying that \(\alpha \not \ll x\). So, u is the solution of (28) we are looking for.
A similar argument shows that if \(u=(x,y)\) is a solution of (41) on \(\partial {\mathcal {V}}_3\), then u is the solution of (28) we are looking for.
Finally, if there are no solutions of (41) on \(\partial {\mathcal {V}}_2\cup \partial {\mathcal {V}}_3\), then
Then, there is a solution of (41) in \({\mathcal {V}}_1\setminus \overline{{\mathcal {V}}_2\cup {\mathcal {V}}_3}\), and this is the solution of (28) we are looking for.
The proof of Theorem 3 is thus completed.
7 Higher dimensional systems
Let us now introduce a higher dimensional version of problem (2). We will write \(x=(x_1,\dots ,x_N)\in {\mathbb {R}}^N\), \(y=(y_1,\dots ,y_N)\in {\mathbb {R}}^N\), and assume that the continuously differentiable function \(H:{\mathbb {R}}^{2N}\rightarrow {\mathbb {R}}\) is of the type
Moreover, for every \(n\in \{1,\dots ,N\}\), we assume that there exist \(p_n>1\) and \(q_n>1\), with \((1/p_n)+(1/q_n)=1\), such that
for every \(\lambda >0\) and \((u,v)\ne (0,0)\). We consider the problem
where the functions \(\phi ,\psi :[a,b]\times {\mathbb {R}}^{2N}\rightarrow {\mathbb {R}}^N\) are continuous and bounded. Equivalently, writing \(\phi =(\phi _1,\dots , \phi _N)\) and \(\psi =(\psi _1,\dots , \psi _N)\),
For \(\xi ,\upsilon \in {\mathbb {R}}^N\) we write \(\xi \preceq \upsilon \) (or \(\upsilon \succeq \xi \)) if
and in this case we define
We now adapt the definition of lower/upper solutions given in [14, Definition 31] to the higher dimensional problem
where \(f,g:[a,b]\times {\mathbb {R}}^{2N}\rightarrow {\mathbb {R}}^N\) are continuous functions. As usual, we write \(f=(f_1,\dots ,f_N)\) and \(g=(g_1,\dots , g_N)\). Similarly for the vector-valued functions considered below.
Definition 24
Given two \(C^1\)-functions \(\alpha ,\beta :[a,b]\rightarrow {\mathbb {R}}^N\), we say that \((\alpha ,\beta )\) is a well-ordered pair of lower/upper solutions of problem (54) if
and there exist two \(C^1\)-functions \(y^\alpha ,y^\beta :[a,b]\rightarrow {\mathbb {R}}^N\) such that, for every \(t\in [a,b]\), \(x,y\in {\mathbb {R}}^N\) with \(x\in {\langle \!\langle }\alpha (t) \,,\, \beta (t) {\rangle \!\rangle }\), and \(n\in \{1,\dots ,N\}\), one has
and
Here is our result in the well-ordered case.
Theorem 25
Assume H to be as in (52), with components \(H_n\) being positively-\((p_n,q_n)\)-homogeneous positive-definite continuously differentiable functions, for some \(p_n>1\) and \(q_n>1\) with \((1/p_n)+(1/q_n)=1\). Let \(\phi ,\psi \) be uniformly bounded continuous functions, and let \((\alpha ,\beta )\) be a well-ordered pair of lower/upper solutions of problem (53). Then, there exists a solution (x, y) of (53) such that \(\alpha (t)\preceq x(t) \preceq \beta (t)\), for every \(t\in [a,b]\).
Proof
One proceeds like in the proof of [14, Theorem 32]. The main difference here is that the functions \(\phi \) and \(\psi \) depend on all variables x and y. However, setting
the fact that \(\phi \) and \(\psi \) are bounded permits to recover, for every \(n=1,\dots ,N\), the required guiding curves \(\gamma _{1,n}^\pm ,\gamma _{2,n}^\pm :[m_\alpha ,M_\beta ]\rightarrow {\mathbb {R}}\), with \(i=1,2\), and the result follows. \(\square \)
For the non-well-ordered case, we need to introduce the notion of strict lower and upper solutions. To this aim we will follow the ideas developed in [11], and distinguish the components which are well ordered from the others.
The couple \(({\mathcal {J}},{\mathcal {K}})\) is a partition of \(\{1,\dots ,N\}\) if and only if \({\mathcal {J}} \cap {\mathcal {K}} = \varnothing \) and \({\mathcal {J}} \cup {\mathcal {K}} = \{1,\dots ,N\}\). We denote by \(\#{\mathcal {J}}\) and \(\#{\mathcal {K}}\) the cardinality of the sets \({\mathcal {J}}\) and \({\mathcal {K}}\). For a given partition \((\mathcal J,{\mathcal {K}})\), a vector
can be decomposed as \(x=(x_{{\mathcal {J}}}, x_{{\mathcal {K}}})\) where \(x_{{\mathcal {J}}}=(x_j)_{j\in {\mathcal {J}}}\in {\mathbb {R}}^{\#{\mathcal {J}}}\) and \(x_{{\mathcal {K}}}=(x_k)_{k\in {\mathcal {K}}}\in {\mathbb {R}}^{\#{\mathcal {K}}}\). Similarly, we can decompose every function \({\mathcal {F}}: {\mathcal {D}} \rightarrow {\mathbb {R}}^N\) as \({\mathcal {F}}(x)=\big ({\mathcal {F}}_{{\mathcal {J}}}(x),\mathcal F_{{\mathcal {K}}}(x)\big )\) with \({\mathcal {F}}_{{\mathcal {J}}}: {\mathcal {D}} \rightarrow {\mathbb {R}}^{\#{\mathcal {J}}}\) and \({\mathcal {F}}_{{\mathcal {K}}}: {\mathcal {D}} \rightarrow {\mathbb {R}}^{\#{\mathcal {K}}}\), for any domain \({\mathcal {D}}\). Moreover, for \(\xi ,\upsilon \in {\mathbb {R}}^N\) we write
Definition 26
Let \(\alpha ,\beta :[a,b]\rightarrow {\mathbb {R}}^N\) be two \(C^1\)-functions. We will say that \((\alpha ,\beta )\) is a pair of lower/upper solutions of (54) related to the partition \((\mathcal J,{\mathcal {K}})\) of \(\{1,\dots ,N\}\) if the following conditions hold:
-
1.
\(\alpha _j \le \beta _j\), for any \(j\in {\mathcal {J}}\,;\)
-
2.
\(\alpha _k \not \le \beta _k\), for any \(k\in {\mathcal {K}}\,;\)
-
3.
\(\alpha (a)\preceq 0 \preceq \beta (a)\) and \(\alpha (b)\preceq 0 \preceq \beta (b)\,;\)
-
4.
there are two \(C^1\)-functions \(y^\alpha ,y^\beta :[a,b]\rightarrow {\mathbb {R}}^N\) such that (55), (56), (57), and (58) hold for every \(t\in [a,b]\), \(x,y\in {\mathbb {R}}^N\) with \(x\in {\langle \!\langle }\alpha (t) \,,\, \beta (t) {\rangle \!\rangle }_{{\mathcal {J}}}\), and \(n\in \{1,\dots ,N\}.\)
In the following definition, we will use the relation \(\gg \) introduced in (7).
Definition 27
Let \((\alpha ,\beta )\) be a pair of lower/upper solutions of (54) related to the partition \(({\mathcal {J}}, {\mathcal {K}})\). We will say that this pair of lower/upper solutions is strict with respect to the jth component, with \(j\in {\mathcal {J}}\), if \(\alpha _j \ll \beta _j\) and, for every solution (x, y) of (54),
We will say that this pair of lower/upper solutions is strict with respect to the kth component, with \(k\in {\mathcal {K}}\) if, for every solution (x, y) of (54),
To prove the existence of a solution of (53), once a pair of lower/upper solutions \((\alpha ,\beta )\) is given, we need to ask the strictness property with respect to the non-well-ordered components \(\alpha _k,\beta _k\). Moreover, we will need to ask more regularity on the functions \(\phi \) and \(\psi \): we will ask them to be locally \(\ell \)-Hölder continuous for a certain \(\ell >0\). Here is our result.
Theorem 28
Let \(\ell >0\) and assume \(H:{\mathbb {R}}^{2N}\rightarrow {\mathbb {R}}\) to be as in (52), with components \(H_n\) being \(C^{1,\ell }_{loc}\)-smooth positively-\((p_n,q_n)\)-homogeneous positive-definite functions, for some \(p_n>1\) and \(q_n>1\) with \((1/p_n)+(1/q_n)=1\). Let \((\alpha ,\beta )\) be a pair of lower/upper solutions of (53) related to the partition \((\mathcal J,{\mathcal {K}})\) of \(\{1,\dots ,N\}\) which is strict with respect to the kth component, for every \(k\in {\mathcal {K}}\). Moreover, assume that for every \(k\in {\mathcal {K}}\),
Let \(\phi ,\psi \) be uniformly bounded \(C^{0,\ell }_{loc}\)-smooth functions. If
then (53) has a solution (x, y) with the following properties:
- (J):
-
for any \(j\in {\mathcal {J}}\), \(\alpha _j(t)\le x_j(t)\le \beta _j(t)\), for every \(t \in [a,b]\,;\)
- (K):
-
for any \(k\in {\mathcal {K}}\), there exist \(t_k^1,t_k^2\in \,]a,b[\,\) such that \(x_k(t_k^1)<\alpha _k(t_k^1)\) and \(x_k(t_k^2)>\beta _k(t_k^2)\).
Proof
The case \({\mathcal {K}}=\varnothing \) has been already treated in Theorem 25. To simplify the exposition, we assume both \({\mathcal {J}}\ne \varnothing \) and \(\mathcal K\ne \varnothing \), and that \({\mathcal {J}} = \{1,\dots ,M\}\) and \({\mathcal {K}}=\{M+1,\dots N\}\) for a certain \(M\in \{1,\dots ,N-1\}\). The proof can be easily adapted to the case \(\mathcal J=\varnothing \).
As in Section 2, for every \(n\in \{1,\dots ,N\}\), let \(S_n(t)=(S_{1,n}(t),S_{2,n}(t))\) be the periodic solution of the planar autonomous system
such that \(S_{1,n}(0)=0\) and \(S_{2,n}(0)>0\), with \(H_n(S_{1,n}(t),S_{2,n}(t))=1\) for every t. We set
and
For each \(n\in \{1,\dots ,N\}\), we will mainly follow the procedure developed in Section 5 if \(n\in {\mathcal {J}}\), and the one in Section 6 if \(n\in {\mathcal {K}}\), so that the couple of variables \((x_n,y_n)\) will overshadow the remaining ones, which will essentially act as parameters. We first need to modify problem (53) both in the k-variables, following the lines of the proof of Theorem 3, and in the j-variables, to apply a topological degree argument, as in the proof of [11, Theorem 10].
Let us rewrite (53) as
We introduce the functions
where \(\zeta \) was defined in (50), and
Then we set
Concerning the non-well-ordered components, we need to consider a positive parameter d, which will be fixed later, following the construction of problem (41) in Section 6. We set
with
where \(\overline{S}\) is defined in (60) and the cut-off function \(\chi \) in (40). We thus are led to the modified problem
We will now provide, working separately on every component, an indexed family of well-ordered pairs of lower/upper solutions of the modified problem (61), which will be strict in every component.
Let us first operate on a component \(j\in \{1,\dots ,M\}\). We can argue as in Lemmas 8 and 9 so to find some guiding curves \(\gamma ^\pm _{1,j}\) and \(\gamma ^\pm _{2,j}\). To be more precise, for an illustrative purpose, the curve \(\gamma ^+_{1,j}\) will satisfy the analogue of (29), i.e.,
for every \(t\in [a,b]\), every \(x\in {\mathbb {R}}^n\) with \(\alpha _j(t)\le x_j \le \beta _j(t)\) and every \(y\in {\mathbb {R}}^N\) with \(y_j= \gamma ^+_{1,j}(x_j)\).
Then, we can follow the reasoning in [14, Theorem 11, Claim 3] and prove that all the solutions (x, y) of (61) satisfy
and
for every \(t\in [a,b]\). We then define the functions
and conclude that
- (S1):
-
for every \(j\in {\mathcal {J}}\), the functions \(\check{\alpha }_j\) and \(\check{\beta }_j\) satisfy
$$\begin{aligned} \check{\alpha }_j\ll \check{\beta }_j\,, \quad \check{\alpha }_j(a)<0< \check{\beta }_j(a)\,, \quad \check{\alpha }_j(b)<0< \check{\beta }_j(b)\,. \end{aligned}$$Moreover, the conditions (55), (56), (57) and (58) hold with \(n=j\), replacing \(\alpha _j,\beta _j,f_j,g_j\) by \(\check{\alpha }_j,\check{\beta }_j,\widehat{f}_j,{\widehat{g}}_j\,\), setting \(y^{\check{\alpha }}_j=y^\alpha _j\) and \(y^{\check{\beta }}_j=y^\beta _j\). Finally, every solution (x, y) of (61) satisfies \(\check{\alpha }_j\ll x_j\ll \check{\beta }_j\) and (63).
Let us now focus our attention on a component \(k\in {\mathcal {K}}\). Arguing as in Lemma 13 we can prove that
- (S2):
-
there exists \(D>1\) with the following property: if \(u=(x,y)\) is a solution of (61), with \(d\ge D\), such that
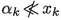 and
and 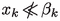 , then \({\mathcal {N}}_{p_k}(u_k) < D\).
, then \({\mathcal {N}}_{p_k}(u_k) < D\).
We can surely take the same constant D for every \(k\in {\mathcal {K}}\). Now, as in Lemma 14, enlarging D if necessary we can prove that
- (S3):
-
for every \(k\in {\mathcal {K}}\) and \(d\ge D\), the functions \(\alpha _k\) and \(\beta _k\) still satisfy conditions (55), (56), (57) and (58), replacing \(f_k,g_k\) by \(\widehat{f}_{k,d},{\widehat{g}}_{k,d}\), respectively.
Then, Lemma 16 suggests us how to continue the proof once we have fixed \(d>D\) sufficiently large:
- (S4):
-
for every \(k\in {\mathcal {K}}\), there are two couples of functions \(({\widehat{\alpha }}_k, y^{{\widehat{\alpha }}}_k)\) and \(({\widehat{\beta }}_k, y^{{\widehat{\beta }}}_k)\) such that \(\widehat{\alpha }_k\ll {\widehat{\beta }}_k\), \({\widehat{\alpha }}_k \ll \beta _k\), and \(\alpha _k \ll {\widehat{\beta }}_k\) satisfying the conditions (55), (56), (57) and (58), replacing in all formulas \(\alpha _k\), \(y^\alpha _k\), \(\beta _k\), \(y^\beta _k\), \(f_k\), \(g_k\) by \({\widehat{\alpha }}_k\), \(y^{{\widehat{\alpha }}}_k\), \({\widehat{\beta }}_k\), \(y^{{\widehat{\beta }}}_k\), \({\widehat{f}}_{k,d}\), \({\widehat{g}}_{k,d}\,\), respectively.
Now a further step is needed. We are going to prove that
- (S5):
-
for every \(k\in {\mathcal {K}}\), if (x, y) is a solution of (61) such that \({\widehat{\alpha }}_k\le x_k\), then \({\widehat{\alpha }}_k\ll x_k\). Analogously, if (x, y) is a solution of (61) such that \(x_k\le {\widehat{\beta }}_k\), then \(x_k\ll {\widehat{\beta }}_k\).
We prove the second assertion, the proof of the first one being similar. Following the proof of Lemma 23, assume by contradiction that there is a solution (x, y) of (61) such that \(x_k\le {\widehat{\beta }}_k\) but  . Since \(x_k(a)=0<{\widehat{\beta }}_k(a)\) and \(x_k(b)=0<{\widehat{\beta }}_k(b)\), there exists \(t_0\in \,]a,b[\,\) such that \(x_k(t_0)={\widehat{\beta }}_k(t_0)\) and \(x_k'(t_0)={\widehat{\beta }}_k'(t_0)\). Using assumption (59), since
. Since \(x_k(a)=0<{\widehat{\beta }}_k(a)\) and \(x_k(b)=0<{\widehat{\beta }}_k(b)\), there exists \(t_0\in \,]a,b[\,\) such that \(x_k(t_0)={\widehat{\beta }}_k(t_0)\) and \(x_k'(t_0)={\widehat{\beta }}_k'(t_0)\). Using assumption (59), since
we get \(y^{{\widehat{\beta }}}_k(t_0)=y_k(t_0)\). Recalling that \({\widetilde{\phi }}_{k,d}=0\) and \({\widetilde{\psi }}_{k,d}=0\) in a neighborhood of \(\{({\widehat{\beta }}_k, y^{{\widehat{\beta }}}_k)(t)\,:\, t\in [a,b]\}\), arguing as in the proof of Lemma 23, we conclude that \(({\widehat{\beta }}_k, y^{{\widehat{\beta }}}_k)\) and \((x_k,y_k)\) coincide on [a, b], leading to a contradiction with the fact that \(x_k(a)=x_k(b)=0\). Hence, (S5) is proved.
For every multi-index \(\mu =(\mu _{M+1},\dots ,\mu _N)\in \{1,2,3\}^{N-M}\), we define the couple of functions \((\varphi ^\mu ,\eta ^\mu )\) by components: for every \(j\in {\mathcal {J}}\), we set
and, for every \(k\in {\mathcal {K}}\),
From (S1), (S3), (S4) and (S5), we can verify that, for every \(\mu \in \{1,2,3\}^{N-M}\), the couple \((\varphi ^\mu ,\eta ^\mu )\) is a well-ordered pair of lower/upper solutions of problem (61) which is strict with respect to all its components. Let
As in Lemmas 8, 9 and 17, we can construct some guiding curves \(\gamma ^\pm _{1,n}\), \(\gamma ^\pm _{2,n}\), for every \(n\in \{1,\dots ,N\}\). Then, for every couple \((\varphi ^\mu ,\eta ^\mu )\in \Xi \), we can modify system (61), only in the components \(k\in \mathcal K\), exactly as we did to define problem (51), and obtain the new problem
With the same procedure we can show that every couple \((\varphi ^\mu ,\eta ^\mu )\) is a well-ordered pair of lower/upper solutions for the new problem, too. Moreover, as in Lemmas 20 and 21, we can show that each solution of (64) satisfies, for every \(t\in [a,b]\),
and, for every \(n\in \{1,\dots ,N\}\),
We need now to introduce the functional setting. We denote by \({\widehat{f}}_d\) and \({\widehat{g}}_d\) the functions
which describe system (61). Recalling the notations introduced in Section 6, we consider the linear operator
and the Nemitskii operator
Then, the analogue of Lemma 18 holds and \(u=(x,y)\) is a solution of (61) if and only if it solves
with
For every \((\varphi ^\mu ,\eta ^\mu )\in \Xi \), we introduce the set
where
Notice that \({\mathcal {V}}^\mu \) is open in X.
Fix any \((\varphi ^\mu ,\eta ^\mu )\in \Xi \). From (S1) and (S5), we see that there are no solutions of (61) on \(\partial {\mathcal {V}}^\mu \). Then, arguing as in the proof of Lemma 22, the set \({\mathcal {V}}^\mu \) is admissible and
Then, we can follow the procedure in [11, Section 3.1] and define, for every multi-index \(\mu =(\mu _{M+1},\dots ,\mu _N)\in \{1,2,3,4\}^{N-M}\), the open set
where the conditions \(({\mathcal {A}}_j^0)\), \(({\mathcal {A}}_k^{\mu _k})\), and \(({\mathcal {A}}_n^\gamma )\) read as
- \(({\mathcal {A}}^0_j)\):
-
\(\check{\alpha }_j \ll x_j \ll \check{\beta }_j\,;\)
- \(({\mathcal {A}}^1_k)\):
-
\({\widehat{\alpha }}_k \ll x_k \ll {\widehat{\beta }}_k\,;\)
- \(({\mathcal {A}}^2_k)\):
-
\({\widehat{\alpha }}_k \ll x_k\ll \beta _k\,;\)
- \(({\mathcal {A}}^3_k)\):
-
\(\alpha _k \ll x_k \ll {\widehat{\beta }}_k\,;\)
- \(({\mathcal {A}}^4_k)\):
-
\({\widehat{\alpha }}_k \ll x_k \ll {\widehat{\beta }}_k\), and there are \(t_k^1,t_k^2\in \,]a,b[\) such that \(x_k(t_k^1)<\alpha _k(t_k^1)\) and \(x_k(t_k^2)>\beta _k(t_k^2)\,;\)
- \(({\mathcal {A}}^\gamma _n)\):
-
\(\gamma ^-_n(x_n(t))<y_n(t)<\gamma ^+_n(x_n(t))\), for every \(t\in [a,b]\) .
Notice that
Moreover, for any \(\mu \in \{1,2,3,4\}^{N-M}\) and \(\kappa \in \{M+1,\dots ,N\}\), using the notation
the arguments in [14, Proposition 23] show that
giving easily, passing to the complementary, \(\Omega ^\mu _{\kappa ,1}\setminus \overline{ \Omega ^\mu _{\kappa ,4}} = \Omega ^\mu _{\kappa ,2} \cup \Omega ^\mu _{\kappa ,3}\) and consequently
Arguing as in [11, Propositions 15–18], we can prove that \(\deg \big (I-L^{-1}N_d,\Omega ^\mu \big )\) is well defined for every \(\mu \in \{1,2,3,4\}^{N-M}\), and it is equal to \((-1)^m\), where m is the number of times the number 4 appears in the multi-index \(\mu \). In particular, we have that
So, there exists a solution (x, y) of (61) belonging to \(\Omega ^{(4,4,\dots ,4,4)}\). This solution satisfies \(({\mathcal {A}}_k^4)\), for every \(k\in {\mathcal {K}}\), hence  and
and  , for every \(k\in {\mathcal {K}}\). Then, from (S2) we conclude that \({\mathcal {N}}_{p_k}(u_k)<D\), so that (x, y) is indeed a solution of the original problem (53), since the differential equation defining the two problems coincide in the set \(\{u\in {\mathbb {R}}^{2N} \,:\, {\mathcal {N}}_{p_k}(u_k)<D\}\). Moreover, from (62), we have \(\alpha _{{\mathcal {J}}}(t) \preceq x_{\mathcal J}(t) \preceq \beta _{{\mathcal {J}}}(t)\) for every \(t\in [a,b]\). The proof is thus completed. \(\square \)
, for every \(k\in {\mathcal {K}}\). Then, from (S2) we conclude that \({\mathcal {N}}_{p_k}(u_k)<D\), so that (x, y) is indeed a solution of the original problem (53), since the differential equation defining the two problems coincide in the set \(\{u\in {\mathbb {R}}^{2N} \,:\, {\mathcal {N}}_{p_k}(u_k)<D\}\). Moreover, from (62), we have \(\alpha _{{\mathcal {J}}}(t) \preceq x_{\mathcal J}(t) \preceq \beta _{{\mathcal {J}}}(t)\) for every \(t\in [a,b]\). The proof is thus completed. \(\square \)
As an example of application, consider the Dirichlet problem
where \(p>1\), \(\mu _n>0\) and \(\nu _n>0\). In this case, if \(\alpha :[0,\pi _p]\rightarrow {\mathbb {R}}^N\) is a lower solution, then taking \(y^\alpha _n=|\alpha _n'|^{p-2}\alpha _n'\), for every \(n=1,\dots ,N\), conditions (55) are always satisfied, while (57) reads as
for every \(x\in {\mathbb {R}}^N\) and \(y\in {\mathbb {R}}^N\). Similarly for an upper solution.
As an immediate consequence of Theorem 28, we have the following.
Corollary 29
Let \(\ell >0\) and \(h_n\) be a uniformly bounded \(C^{0,\ell }\)-smooth function, for every n. Assume that \((\alpha ,\beta )\) is a pair of lower/upper solutions of (65) related to the partition \(({\mathcal {J}},{\mathcal {K}})\) of \(\{1,\dots ,N\}\), which is strict with respect to the kth component, for every \(k\in {\mathcal {K}}\). If \(\max \{\mu _k\,, \nu _k \,:\, k\in {\mathcal {K}}\} \le 1\), then problem (65) has a solution x with the following properties:
- (J):
-
for any \(j\in {\mathcal {J}}\), \(\alpha _j(t)\le x_j(t)\le \beta _j(t)\), for every \(t \in [0,\pi _p]\,;\)
- (K):
-
for any \(k\in {\mathcal {K}}\), there exist \(t_k^1,t_k^2\in \,]0,\pi _p[\,\) such that \(x_k(t_k^1)<\alpha _k(t_k^1)\) and \(x_k(t_k^2)>\beta _k(t_k^2)\).
The above result should be compared with [5, Theorem 2.4] (see also [2] and the references therein) where some monotonicity assumptions on the nonlinearities were assumed.
Notice that, since we are dealing with second order differential equations, the strictness property asked in the statement can be verified by a standard argument, e.g., simply verifying that a strict inequality holds in (66).
As an illustrative example, we suggest the system
where \(s_n\in \{-1,+1\}\) and \(\Vert {\widetilde{h}}_n\Vert _\infty <1\) for every n. Moreover, for those components having \(s_n=-1\), we ask that \(\mu _n \le 1\) and \(\nu _n\le 1\).
In this example, the pair of lower/upper solutions can be defined by components as follows. The set \({\mathcal {J}}\) is made of those n for which \(s_n=+1\), while the set \({\mathcal {K}}\) consists of those n with \(s_n=-1\). If \(n\in {\mathcal {J}}\), we simply need to choose some sufficiently large constants \(\beta _n=-\alpha _n>0\). If \(n\in {\mathcal {K}}\), we can argue as in [14, Proposition 26], where the case \(p=2\) is treated, to find \(\alpha _n\) and \(\beta _n\) such that \(\alpha _n \not \le \beta _n\).
Remark 30
A generalization of Theorem 28 can be obtained removing the strictness assumption on one of the components \(\kappa \in {\mathcal {K}}\). Indeed, the above proof can be easily adapted following the ideas in the proof of [11, Theorem 19]. In such a situation, the conclusion (K) of the statement must be slightly changed concerning the estimates on the \(\kappa \)th component: the solution will be such that

References
Amann, H., Ambrosetti, A., Mancini, G.: Elliptic equations with noninvertible Fredholm linear part and bounded nonlinearities. Math. Z. 158, 179–194 (1978)
Bernfeld, S.R., Lakshmikantham, V.: An introduction to nonlinear boundary value problems. Academic Press, New York (1974)
Boscaggin, A., Garrione, M.: Resonant Sturm-Liouville Boundary Value Problems for Differential Systems in the Plane. J. Anal. Appl. 35, 41–59 (2016)
Capietto, A., Dambrosio, W.: Multiplicity results for some two-point superlinear asymmetric boundary value problem. Nonlinear Anal. 38, 869–896 (1999)
Cheng, X., Lü, H.: Multiplicity of positive solutions for a \((p_1, p_2)\)-Laplacian system and its applications. Nonlinear Anal. Real World Appl. 13, 2375–2390 (2012)
Dalbono, F., Zanolin, F.: Multiplicity results for asymptotically linear equations, using the rotation number approach. Mediterr. J. Math. 4, 127–149 (2007)
De Coster, C., Habets, P.: Two-point boundary value problems. Lower and upper solutions. Elsevier, Amsterdam (2006)
De Coster, C., Henrard, M.: Existence and localization of solution for elliptic problem in presence of lower and upper solutions without any order. J. Diff. Equ. 145, 420–452 (1998)
De Coster, C., Omari, P.: Unstable periodic solutions of a parabolic problem in the presence of non-well-ordered lower and upper solutions. J. Funct. Anal. 175, 52–88 (2000)
Fonda, A., Garrione, M.: Generalized Sturm-Liouville boundary conditions for first order differential systems in the plane. Topol. Methods Nonlinear Anal. 42, 293–325 (2013)
Fonda, A., Klun, G., Sfecci, A.: Periodic solutions of second order differential equations in Hilbert spaces. Mediterr. J. Math. 18(223), 26 (2021)
Fonda, A., Klun, G., Sfecci, A.: Well-ordered and non-well-ordered lower and upper solutions for periodic planar systems. Adv. Nonlinear Stud. 21, 397–419 (2021)
Fonda, A., Klun, G., Sfecci, A.: Non-well-ordered lower and upper solutions for semilinear systems of PDEs, Commun. Contemp. Math., online first. https://doi.org/10.1142/S021919972150080
Fonda, A., Sfecci, A., Toader, R.: Two-point boundary value problems for planar systems: a lower and upper solutions approach. J. Diff. Equ. 308, 507–544 (2022)
Fonda, A., Toader, R.: A dynamical approach to lower and upper solutions for planar systems. Discrete Contin. Dynam. Systems 41, 3683–3708 (2021)
Gossez, J.-P., Omari, P.: Non-ordered lower and upper solutions in semilinear elliptic problems. Comm. Partial Diff. Equ. 19, 1163–1184 (1994)
Habets, P., Omari, P.: Existence and localization of solutions of second order elliptic problems using lower and upper solutions in the reversed order. Topol. Methods Nonlinear Anal. 8, 25–56 (1996)
Lindqvist, P.: Some remarkable sine and cosine functions. Ricerche Mat. 44, 269–290 (1995)
Rebelo, C.: A note on uniqueness of Cauchy problems associated to planar Hamiltonian systems. Portugal. Math. 57, 415–419 (2000)
Nagumo, M.: Über die Differentialgleichung \(y^{\prime \prime }=f(t, y, y^{\prime })\). Proc. Phys-Math. Soc. Japan 19, 861–866 (1937)
Picard, E.: Sur l’application des méthodes d’approximations successives à l’étude de certaines équations différentielles ordinaires. J. Math. Pures Appl. 9, 217–271 (1893)
Scorza Dragoni, G.: Il problema dei valori ai limiti studiato in grande per le equazioni differenziali del secondo ordine. Math. Ann. 105, 133–143 (1931)
Sfecci, A.: Double resonance in Sturm-Liouville planar boundary value problems. Topol. Methods Nonlinear Anal. 55, 655–680 (2020)
Yang, X.: The method of lower and upper solutions for systems of boundary value problems. Appl. Math. Comput. 144, 169–172 (2003)
Yang, X.: Existence of periodic solutions of a class of planar systems. Z. Anal. Anwend. 25, 237–248 (2006)
Funding
Open access funding provided by Università degli Studi di Trieste within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The authors of this paper have been partially supported by the GNAMPA–INdAM research project “MeToDiVar: Metodi Topologici, Dinamici e Variazionali per equazioni differenziali”.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fonda, A., Klun, G., Obersnel, F. et al. On the Dirichlet problem associated with bounded perturbations of positively-(p, q)- homogeneous Hamiltonian systems. J. Fixed Point Theory Appl. 24, 66 (2022). https://doi.org/10.1007/s11784-022-00980-7
Accepted:
Published:
DOI: https://doi.org/10.1007/s11784-022-00980-7
Keywords
- Hamiltonian systems
- Dirichlet boundary value problems
- lower and upper solutions
- degree theory
- shooting method





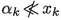 and
and 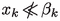 , then
, then