1 Introduction

The linear canonical transform (LCT) is a three-parameter transform

$$\begin{aligned} {\left( L_{a, b, d} f\right) (t)= \frac{1}{\sqrt{2i \pi b}} \int _{-\infty }^{\infty } e^{\frac{i}{2b}[a x^{2}+ d t^{2}- 2 x t]} f(x) dx,} \end{aligned}$$
(1)

where a, b, d are fixed real constants and \(b\ne 0\). While the case \(b = 0\), cf. [7, 11, 13] can be also considered with a four-parameter transform, it is not of interest in this work as it is nothing but a chirp multiplication. Integration (1) converges for \(L^{p}({\mathbb {R}})\)-functions, \(p\ge 1\). For simplicity, we replace \(L_{a, b, d}\) by L and use the subscripts only when it is necessary. The LCT turns out to be the fractional Fourier transform (FrFT) when \(a=d=\cos \alpha \) and \(b=\sin \alpha ;\) to the Fourier transform when \(a=d=0, b=1\); and to the Fresnel transform when \(a=1, b\in {\mathbb {R}}, b\ne 0, d=0\), see [16, 26, 30, 31] for more details. For this reason, the LCT has become a basic tool in signal and image processing, cf., e.g., [7].

For the derivations of sampling theorems of Shannon type in the LCT domain, the space of band-limited signals in the LCT and FrFT domains is precisely investigated in [8, 14, 28, 30]. Sampling theorem of Shannon type has been derived extensively, see, e.g., [1, 3, 5, 6, 10, 11, 15, 19, 23, 24, 29], using different approaches. The associated truncation, amplitude, and jitter errors are analytically considered in [2, 3, 9, 22, 25].

The space of band-limited signals in the LCT domain is defined as follows. Let \(\Omega >0\) be fixed. A signal f is said to be band-limited with band width \(\Omega \) if \(f\in L^{2}({\mathbb {R}})\) and \((Lf)(t)=0, |t|>\Omega .\) This space is denoted by \(\mathbf {B}^{2}_{\Omega }.\) Thus, \(f\in \mathbf {B}^{2}_{\Omega }\) if and only if there is a band-limited signal in the classical sense with band width \(\Omega /b, \phi ,\) for which \(f(t)= e^{i(\frac{a}{2b})t^{2}} \phi (t)\). The derivative sampling theorem for \(f\in \mathbf {B}^{2}_{\Omega }\) is given in [11], see also [12], by

$$\begin{aligned} { f(t)}&:={\sum _{n\in {\mathbb {Z}}} e^{-i\left( \frac{a}{2b}\right) \left( t^{2}-(n h)^{2}\right) } \left\{ \left( 1+ \frac{i a}{b} n h (t-n h)\right) f(n h)\right. }\nonumber \\&{ \bigg . +(t-n h)f^{\prime }(n h)\bigg \} \, \mathrm {sinc\,}^{2}\left( h^{-1} t -n\right) ,} \end{aligned}$$
(2)

where \(h\in \left( 0, \frac{2\pi b}{\Omega }\right] \) is fixed and

$$\begin{aligned} {\mathrm {sinc\,}(t):=\left\{ \begin{array}{ll} \displaystyle \frac{\sin \left( \pi t\right) }{\pi t}, &{} \quad t\ne 0,\\ 1, &{}\quad t= 0. \end{array}\right. } \end{aligned}$$
(3)

The convergence of (2) is absolute on \({\mathbb {C}}\) and uniform on compact subsets of \({\mathbb {C}}\). See also [21, 27] for derivative sampling theorem in the FrFT domain.

The rate of convergence of (2) is slow, unless f decays fast. Our purpose in this work is to incorporate (2) with a Gaussian regularization kernel that hastens the reconstruction rate. In addition, we do not necessarily assume the reconstructed signals to be band-limited and/or to have a finite energy, i.e., square integrable. The regularized sampling theorem is derived in the next section. Section 3 is devoted to investigating the associated amplitude error, which results from using approximate samples in the reconstruction procedure. In Sect. 4, we carry out several numerical experiments.

2 Regularized Gaussian Sampling of Derivative Representation

For fixed \(x\in {\mathbb {R}}, \, N\in {\mathbb {N}}\), define the integer-type interval

$$\begin{aligned} {\mathbb {Z}}_{N}(x):=\left\{ n\in {\mathbb {Z}}: \left| n- \left\lfloor x + 1/2 \right\rfloor \right| \le N\right\} , \end{aligned}$$
(4)

where \(\lfloor \cdot \rfloor \) is the floor function, see Fig. 1.

Fig. 1
figure 1

\( {\mathbb {Z}}_{5}\left( \frac{1}{4}\right) =\{-5,-4,\cdots ,0,1,\cdots ,5\}\)

Full size image

Let \(h \in \left( 0,\frac{2\pi b}{\Omega }\right) \), \(\alpha := \left( 2\pi - \frac{ h \Omega }{b} \right) /2\), \( a, b\in {\mathbb {R}}, b>0, N\in {\mathbb {N}}\) be also fixed. As we have indicated in the previous section, the reconstruction (convergence) rate of (2) is slow, unless f(t) decays fast. We incorporate (2) with the Gaussian function \(G(t)=e^{-t^2},\, t\in {\mathbb {C}},\) which decays fast as \( |t|\rightarrow \infty .\) Indeed, define the regularized Gaussian sampling of derivative representation operator for \(f:{\mathbb {C}}\rightarrow {\mathbb {C}}\) to be

$$\begin{aligned} \nonumber { \left( \mathcal {H}_{h,N} f\right) (t)}&:= { \sum _{n\in {\mathbb {Z}}_{N}(t)} \left\{ \left( 1+ \frac{i an h}{b}(t-nh) + \frac{2\alpha }{N h^{2}} \right. \right. }\\ \nonumber&{ \times \, (t-nh)^{2}\biggr ) f(n h)+(t-n h)f^{\prime }(n h)\biggr \}}\\ \nonumber&{\times \, e^{- i \left( \frac{a}{2b}\right) \left( t^{2}-h^2 n^2\right) } \,\mathrm {sinc\,}^{2} (h^{-1} t-n) } \\&{ \times \, e^{-\frac{\alpha }{N}\left( \frac{t}{h}-n\right) ^2}.} \end{aligned}$$
(5)

For defining (5), no conditions are imposed on f, neither integrability nor analyticity. In the following, we estimate \(|f(t)- \left( \mathcal {H}_{h,N} f\right) (t)|\) for analytic functions with a prescribed growth. Let \(\varphi : [0,\infty )\rightarrow [0,\infty )\) be non-decreasing and \(E_{\Omega /b}(\varphi )\) denote the space of all entire functions f for which

$$\begin{aligned} |f(t)|\le \varphi (|x|) \,e^{\frac{a}{b} x y}\, e^{\frac{\Omega }{b} |y|},\quad t= x + i y\in {\mathbb {C}}. \end{aligned}$$
(6)

The major result of this section is the following theorem, which gives an estimate of the error associated with (5).

Theorem 1

Let \(f\in E_{\Omega /b}(\varphi ), t=x+iy\in {\mathbb {C}},\, x,y \in {\mathbb {R}},\, |y|< N \). Hence,

$$\begin{aligned} \nonumber |f(t)- \left( \mathcal {H}_{h,N} f\right) (t)| \le \,&\frac{2\, e^{-\alpha N}}{\sqrt{\pi \alpha N}} \,e^{\frac{a}{b} x y}\, |\sin ^{2} (h^{-1} \pi t)| \\ \nonumber&\times \, \varphi \left( |x|+h(N+1)\right) \\&\times \,\lambda _N \left( h^{-1} y\right) , \end{aligned}$$
(7)

where

$$\begin{aligned} \lambda _N (t) := 2 \cosh (2\alpha t)+ \mathcal {O}(N^{-1/2})\quad (N\rightarrow \infty ), \end{aligned}$$
(8)

locally uniformly on \({\mathbb {R}}\).

Proof

We may assume that \(\Omega /b < 2 \pi , \, h = 1,\) and \(y \ge 0\), cf. [4]. Let \(N_{0}:=N+1/2,\, m_{0}:=\lfloor x + 1/2\rfloor \), and \(\mathcal {C}_{N}\) be the positively oriented rectangle (more precisely the boundary of the rectangle) whose vertices are \( (\pm N_{0}+ m_{0}, y \pm N )\), see Fig. 2.

Fig. 2
figure 2

The rectangle \(\mathcal {C}_{4}\) for \(t= \frac{3}{2}+ i\)

Full size image

For \(t=x + i y\in {\mathbb {C}},\, |y|<N\), consider the function

$$\begin{aligned} { \mathcal {K}_{t}(\zeta ):= \frac{\sin ^{2}\left( \pi t\right) }{2\pi i }\times \,\frac{ e^{ -i \left( \frac{a}{2b}\right) (t^2-\zeta ^{2})-\frac{\alpha }{N}\left( t-\zeta \right) ^2} \, f(\zeta ) }{(\zeta -t)\sin ^{2}\left( \pi \zeta \right) }.} \end{aligned}$$
(9)

The residue theorem implies, \(t\notin {\mathbb {Z}},\)

$$\begin{aligned} \oint _{\mathcal {C}_{N}} \mathcal {K}_{t}(\zeta ) d\zeta= & {} 2\pi i \mathrm {Res} (\mathcal {K}_t; t) \nonumber \\&+ \, 2\pi i \sum _{n=-N+m_{0}}^{N+m_{0}} \mathrm {Res} (\mathcal {K}_t; n). \end{aligned}$$
(10)

Obviously,

$$\begin{aligned} { \mathrm {Res} (\mathcal {K}_{t}; t)}= & {} {\lim _{\zeta \rightarrow t} (\zeta - t) \mathcal {K}_{t}(\zeta )= \frac{f(t)}{2\pi i },} \end{aligned}$$
(11)
$$\begin{aligned} \nonumber { \mathrm {Res} (\mathcal {K}_{t}; n)}= & {} { \lim _{\zeta \rightarrow n}\frac{d}{d\zeta } \left\{ (\zeta - n)^{2} \mathcal {K}_{t}(\zeta )\right\} }\\ \nonumber= & {} { \frac{ \sin ^{2}\left( \pi t\right) }{2\pi i } \lim _{\zeta \rightarrow n} \frac{d}{d\zeta } \left\{ \frac{ e^{-i \left( \frac{a}{2b}\right) (t^2-\zeta ^{2})-\frac{\alpha }{N}\left( t-\zeta \right) ^2}}{(\zeta -t)} \right. } \\ \nonumber&\left. \times \,f(\zeta ) \,\left( \frac{\zeta -n}{\sin \left( \frac{\Omega }{b}\zeta \right) }\right) ^{2}\right\} \\ \nonumber= & {} \frac{ - 1}{2\pi i } \left\{ \left( 1+ \frac{i an }{b} (t-n) + \frac{2\alpha }{N } (t-n)^{2}\right) f(n)\right. \\ \nonumber&+\,(t-n )f^{\prime }(n)\biggr \} \times \,\,\mathrm {sinc\,}^{2}( \pi t-n)\, \\&\times \, e^{ -i \left( \frac{a}{2b}\right) \left( t^2-n^{2}\right) -\frac{\alpha }{N}\left( t-n\right) ^2}. \end{aligned}$$
(12)

Combining (11), (12), and (10) yields

$$\begin{aligned} \oint _{\mathcal {C}_{N}} \mathcal {K}_{t}(\zeta ) d\zeta = f(t)- \mathcal {H} _{1,N}[f](t). \end{aligned}$$
(13)

In the case \(t = n \in {\mathbb {Z}}\), we have

$$\begin{aligned} f (n) = \mathcal {H}_{1, N}[f](n). \end{aligned}$$

Now, we estimate the integration

$$\begin{aligned} \oint _{\mathcal {C}_{N}} \mathcal {K}_{t}(\zeta ) d\zeta= & {} \frac{\sin ^{2}\left( \pi t\right) }{2\pi i }\sum _{k=1}^{4} I_{k}, \end{aligned}$$
(14)
$$\begin{aligned} I_{k}:= & {} \int _{c_{k}}\frac{ e^{ -i \left( \frac{a}{2b}\right) (t^2-\zeta ^{2})-\frac{\alpha }{N}\left( t-\zeta \right) ^2}}{(\zeta -t)\sin ^{2}\left( \pi \zeta \right) } \, f(\zeta ) \, d\zeta , \end{aligned}$$
(15)

and \(c_{1}, c_{2}, c_{3},\) and \(c_{4}\) are the line segments \(\overline{AB},\) \( \overline{BC},\) \(\overline{CD},\) and \(\overline{DA}\), respectively, cf. Fig. 2. Let us estimate these four integrals. For \(I_1\), let \(\zeta =N_{0}+m_{0}+i \eta \in c_1\). Then,

$$\begin{aligned} I_{1}= & {} i \int _{-N+y}^{N+y} \left[ \frac{ e^{ -i \left( \frac{a}{2b}\right) (t^2-( N_{1}+ i \eta )^{2})- \frac{\alpha }{N}\left( t- N_{1}- i \eta \right) ^2} }{( N_{1}+ i \eta - t) \sin ^{2} \pi ( N_{1}+ i \eta )}\right. \nonumber \\&\quad \times \, f( N_{1}+ i \eta )\biggr ]d \eta , \quad N_1=N_{0}+m_{0}. \end{aligned}$$
(16)

To estimate \(I_1\), we estimate the integrand over \(c_1\). Inequality (6) implies

$$\begin{aligned} |f(N_1 +i \eta )| \le \varphi \left( |x|+N+1\right) \,e^{\frac{a}{b} N_1 \eta } \,e^{\frac{\Omega }{b} |\eta |}. \end{aligned}$$
(17)

We also have

$$\begin{aligned} \left| e^{-i\left( \frac{a}{2b}\right) t^2}\right|= & {} e^{\frac{a}{b} xy}, \end{aligned}$$
(18)
$$\begin{aligned} \left| e^{i\left( \frac{a}{2b}\right) (N_1+i\eta )^2}\right|= & {} e^{-\frac{a}{b} N_1 \eta }, \end{aligned}$$
(19)
$$\begin{aligned} \left| e^{-\frac{\alpha }{N} (t-N_1-i\eta )^2}\right|= & {} e^{-\frac{\alpha }{N}(x- N_1)^2} e^{\frac{\alpha }{N}(y- \eta )^2}. \end{aligned}$$
(20)

Using (17)–(20), we obtain

$$\begin{aligned} \nonumber \left| I_{1} \right|\le & {} \varphi (|x|+N+1) e^{\frac{a}{b} xy} e^{-\frac{\alpha }{N}(x- N_1)^2} \\&\times \, \int _{-N+y}^{N+y} \frac{e^{\frac{\Omega }{b}|\eta |} e^{ \frac{\alpha }{N}(y-\eta )^2}}{| N_{1}+ i t- t|\, |\sin ^{2} \pi ( N_{1}+ i \eta )|} d\eta . \end{aligned}$$
(21)

Since

$$\begin{aligned} \left| \sin \pi \left( n+\frac{1}{2}+i v\right) \right| =\cosh (\pi v),\, n\in {\mathbb {Z}}, \, v\in {\mathbb {R}}, \end{aligned}$$

then

$$\begin{aligned} \left| \sin \pi \left( N_1 +i \eta \right) \right| = \cosh \left( \pi \eta \right) \ge \frac{e^{\pi | \eta |}}{2}. \end{aligned}$$
(22)

Using the fact \(t-1<\lfloor t\rfloor \le t, \, t\in {\mathbb {R}}\) implies

$$\begin{aligned} | N_{1} +i \eta -t| \ge N. \end{aligned}$$
(23)

Substituting from (22) and (23) in (21) yields

$$\begin{aligned} \nonumber \left| I_{1} \right|\le & {} \frac{4 \varphi (|x|+N+1)\, e^{\frac{a}{b} xy}\, e^{-\alpha N} }{N } \\ \nonumber&\times \, \int _{-N+y}^{N+y} e^{-\left( 2\pi -\frac{\Omega }{b}\right) |\eta |+ \frac{\alpha }{N}(y-\eta )^2} d\eta \\ \nonumber= & {} \frac{ 4 \varphi (|x|+N+1) e^{\frac{a}{b} xy} e^{- \alpha N}}{N} \\&\times \,\int _{-N}^{N} e^{-2\alpha |u+y|+ \frac{\alpha }{N} u^2} du. \end{aligned}$$
(24)

Using the estimate obtained by Schmeisser and Stenger for the last integral, cf. [20, p. 205], \(I_1\) is estimated via

$$\begin{aligned} | I_{1}| < \frac{8 \varphi (|x|+N+1) \,e^{\frac{a}{b} xy} \,e^{- \alpha N}\, e^{\alpha y^2 /N} }{\alpha N \left( 1- (y/N)^2 \right) }. \end{aligned}$$
(25)

In a similar manner, we estimate \(I_{3}\) to have

$$\begin{aligned} | I_{3}| < \frac{8 \varphi (|x|+N+1)\, e^{\frac{a}{b} xy} \,e^{- \alpha N}\, e^{\alpha y^2 /N} }{\alpha N \left( 1- (y/N)^2 \right) }. \end{aligned}$$
(26)

Let \(\zeta =\xi +i (y+N)\in c_2\), i.e., \(N_{2}\le \xi \le N_{1}\) where \( N_{2}=- N_{0}+m_{0} \). Then, \(I_{2}\) turns out to

$$\begin{aligned} \nonumber I_{2}= & {} - \int _{N_{2}}^{N_{1}} \left[ \frac{e^{ -i \left( \frac{a}{2b}\right) (t^2-(\xi +i (y+N))^{2})-\frac{\alpha }{N}\left( x-\xi - i N\right) ^2}}{(\xi -x + i N) \sin ^{2} \pi (\xi + i (y+ N))}\right. \\&\qquad \times \, f(\xi +i (y+N)) \biggr ] d \xi . \end{aligned}$$
(27)

Inequality (6) leads to

$$\begin{aligned} |f(\xi +i (y+N))| \le \varphi \left( |x|+N+1\right) \,e^{\frac{a}{b} (y+N)\xi }\, e^{\frac{\Omega }{b} |y+N|}.\nonumber \\ \end{aligned}$$
(28)

Moreover, we have

$$\begin{aligned} \left| e^{i\left( \frac{a}{2b}\right) (\xi +i(y+N))^2}\right|= & {} e^{-\frac{a}{b} (y+N)\xi }, \end{aligned}$$
(29)
$$\begin{aligned} \left| e^{-\frac{\alpha }{N} (x-\xi -i N)^2}\right|= & {} e^{-\frac{\alpha }{N}(x-\xi )^2} e^{\alpha N}. \end{aligned}$$
(30)

Hence,

$$\begin{aligned} \nonumber |I_{2}|\le & {} \varphi (|x|+N+1)\, e^{\frac{a}{b} xy}\, e^{\alpha N} \, e^{\frac{\Omega }{b} |y+N|} \\&\times \,\int _{N_{2}}^{N_{1}} \frac{e^{-\frac{\alpha }{N}(x-\xi )^2}}{(\xi -x + i N) \sin ^{2} \pi (\xi + i (y+ N))} d \xi .\nonumber \\ \end{aligned}$$
(31)

The inequalities

$$\begin{aligned} \nonumber \left| \sin \pi \left( \xi +i (y+N)\right) \right|\ge & {} \sinh \pi \left( y+N\right) \\= & {} \frac{e^{\pi | y+N|}}{2}\left( 1-e^{-2\pi | y+N|}\right) , \end{aligned}$$
(32)

and

$$\begin{aligned} |\xi -x+i N| \ge N, \end{aligned}$$
(33)

imply

$$\begin{aligned} \nonumber | I_{2}|\le & {} \frac{4 \varphi (|x|+N+1)\, e^{\frac{a}{b} xy}\, e^{\alpha N} e^{-\left( 2\pi -\frac{\Omega }{b}\right) |y+ N|} }{N \left( 1-e^{-2\pi |y+ N|}\right) ^{2}} \\ \nonumber&\times \,\int _{N_{2}}^{N_{1}} e^{-\frac{\alpha }{N} (x-\xi )^2} d\xi \\ \nonumber\le & {} \frac{4 \varphi (|x|+N+1)\, e^{\frac{a}{b} xy}\, e^{-2\alpha y} e^{- \alpha N} }{\sqrt{N \alpha } \left( 1-e^{-2\pi |y+ N|}\right) ^{2}} \\ \nonumber&\times \, \int _{-\infty }^{\infty } e^{- u^2} du \\= & {} \frac{4 \pi \varphi (|x|+N+1) e^{\frac{a}{b} x y} e^{-2\alpha y} e^{- \alpha N} }{\sqrt{N \alpha \pi } \left( 1-e^{-2\pi |y+ N|}\right) ^{2}}. \end{aligned}$$
(34)

Likewise,

$$\begin{aligned} | I_{4}|\le & {} \frac{4 \pi \varphi (|x|+N+1) e^{\frac{a}{b} x y} e^{2\alpha y} e^{- \alpha N} }{\sqrt{N \alpha \pi } \left( 1-e^{-2\pi |y- N|}\right) ^{2}}. \end{aligned}$$
(35)

Combining (25), (26), (34), and (35) yields

$$\begin{aligned} \nonumber \left| \oint _{\mathcal {C}_{N}} \mathcal {K}_{t}(\zeta ) d\zeta \right|\le & {} \frac{2 \,e^{-\alpha N}}{\sqrt{\pi \alpha N}} \, e^{\frac{a}{b} x y}\, |\sin ^{2} ( \pi t)|\\&\times \, \varphi \left( |x|+(N+1)\right) \lambda _N \left( y\right) , \end{aligned}$$
(36)

where

$$\begin{aligned} \nonumber \lambda _N (t):= & {} \frac{4 e^{\alpha t^2 /N}}{\sqrt{\pi \alpha N}[1-(t/N)^2] }+\frac{e^{2\alpha t}}{\left( 1-e^{-2\pi (N-t)}\right) ^{2}} \\&+\frac{e^{-2\alpha t}}{\left( 1-e^{-2\pi (N+t)}\right) ^{2}}. \end{aligned}$$
(37)

The proof is completed as \(\lambda _N (\cdot )\) has the asymptotic (8) locally uniformly on \({\mathbb {R}}\).

Remark 1

The following special cases can be directly deduced from Theorem 1:

(i):

Let f be entire, and there be \(M, \kappa \ge 0\) such that

(38)

For \(h \in \left( 0, \pi \left( \frac{\Omega }{b} + 2\kappa \right) \right) ,\) and \(| y| < N\), estimate (7) becomes

(39)

The proof is based on the fact that we can take \(\varphi (x)=M e^{\kappa x}\).

(ii):

If \(f\in \mathbf {B}_{\Omega }^{\infty }\) (in the LCT domain), i.e.,

$$\begin{aligned} |f(x+iy)|\le \Vert f\Vert _{\infty } \,e^{\frac{a}{b} x y}\, e^{\frac{\Omega }{b} |y|}, \end{aligned}$$
(40)

then Theorem 1 implies

(41)
(iii):

If \(f \in \mathbf {B}_{\Omega }^{2}\), then we have, cf. [18, p. 319], \(\Vert f\Vert _{\infty }\le \sqrt{\Omega /\pi b} \, \Vert f\Vert _2\) and consequently

(42)

3 Amplitude error

The amplitude error associated with (5) arises if the exact samples f(nh), \(f^{\prime }(n h)\) are replaced by approximate closer ones \(\widetilde{f}(n h)\), \(\widetilde{f^{\prime }}(n h)\). Let \(\varepsilon _{n}:=f\left( n h\right) -\widetilde{f}\left( n h\right) \), \(\varepsilon ^{\prime }_{n}:=f^{\prime }\left( n h\right) -\widetilde{f^{\prime }}\left( n h\right) \) be uniformly bounded, i.e., there exists a sufficiently small \(\varepsilon > 0\), such that \( |\varepsilon _{n}|, |\varepsilon ^{\prime }_{n}|<\varepsilon \). The amplitude error is defined for \( t\in {\mathbb {R}}\) in this case to be

(43)

Theorem 2

Let \(f \in \mathbf {B}_{\Omega }^{\infty }\). Assume that \( |\varepsilon _{n}|, |\varepsilon ^{\prime }_{n}|<\varepsilon \). Then, we have for \(t\in {\mathbb {R}}\)

(44)

Proof

Let \(f \in \mathbf {B}_{\Omega }^{\infty }\) and \(t\in {\mathbb {R}}\). Using triangle inequality,

(45)

Since \(|\sin (t)|, |\mathrm {sinc\,}(t)|\le 1, \, e^{t}> 0,\, t\in {\mathbb {R}}\),

(46)

Simplifying (46), we obtain

(47)

Let \(\lfloor h^{-1} t + 1/2\rfloor -n = l\). Then,

(48)

Using the inequality, cf. [17],

$$\begin{aligned} {\int _{x}^{\infty } e^{-u^2} du \le \frac{2\,e^{-x^2}}{x+\sqrt{x^2 +4/\pi }},\quad x>0,} \end{aligned}$$
(49)

we obtain

$$\begin{aligned} { \sum _{n\in {\mathbb {Z}}_{N}(t)} e^{-\frac{\alpha }{N}\left( \frac{t}{h}-n\right) ^2} \le 2 e^{-\frac{\alpha }{ 4N}}\left( 1+\sqrt{\frac{N\pi }{\alpha }}\right) .} \end{aligned}$$
(50)

Likewise, letting \(\lfloor h^{-1} t + 1/2\rfloor -n = l\), then

(51)

Estimate (50) implies

(52)

Simple calculations and using inequality (49) yield

(53)

Hence,

(54)

The proof is accomplished by combining (50), (54), and (47). \(\square \)

4 Numerical experiments

This section includes two examples illustrating the above method. In the first example, we compare the results obtained by Gaussian regularization of derivative sampling in the LCT domain, which is investigated in this paper, with the derivative sampling theorem in the LCT domain \(f^D_N(t)\). Here, \(f^D_N(t)\) is the truncated reconstruction formula of (2), i.e.,

(55)

The other example is devoted to the comparison between the absolute error \(\left| f (t)- \left( \mathcal {H}_{h,N} \widetilde{f}\right) (t) \right| \) and its associated bound. Let \(\mathcal {B} (\mathcal {H}_{h,N}; t)\) and \(\mathcal {A} (\varepsilon , \mathcal {H}_{h,N}; t)\) be the error bounds of (41) and (44), respectively. For \(t\in {\mathbb {R}}\), \(N \in \mathbb {Z^{+}}\), we have

(56)

Since \( \left( \mathcal {H}_{h,N} f\right) (t)\) duplicates f(t) at the points kh for \(k\in {\mathbb {Z}}\), it looks reasonable to study the absolute errors at the intermediate points \(x_{k}:=\left( k-\frac{1}{2}\right) h\).

Example 1

Consider the \(B^{2}_{\pi /2}\)-function

$$\begin{aligned} f(t)=\frac{e^{ -i \frac{t^{2}}{2}} \cos \left( \frac{\pi t}{\sqrt{2}}\right) }{\pi ^{2}( 2 t^{2}-1)}, \end{aligned}$$
(57)

where \(a=b=1/\sqrt{2},\; h=\sqrt{2},\) and \(\Omega =\pi /2\). Table 1 and Figs. 3–4 exhibit comparisons between the approximations of f using \(f_{N}^{D}(\cdot )\) and \(\left( \mathcal {H}_{h,N} f \right) (\cdot )\). In Fig. 3 we restrict ourselves to the case when \(N=2, t\in (-4,4)\) is real, while in Fig. 4 we illustrate the case when \(|t|<2, t\in {\mathbb {C}}, N=10\). It is noted from Table 1 that while the obtained error estimates are topping the absolute (exact) error, they are pretty close to the exact error. Moreover, the regularized Gaussian sampling of derivative representation is giving a more accurate reconstruction of signals than the derivative sampling theorem. Furthermore, as N increases, the gap between the exact error \(|f(\cdot )-\left( \mathcal {H}_{h,N} f\right) (\cdot )|\) and its bound narrows noticeably.

Table 1 Comparison between \(f_{N}^{D}(\cdot )\) and \( \left( \mathcal {H}_{h,N} f\right) (\cdot )\) of Example 1 where \(h=\sqrt{2}\) and \(a=b=1/\sqrt{2}\)
Full size table
Fig. 3
figure 3

Illustrations associated with Example 1. Here \(t\in [-4,4]\). The green continuous lines in (a) and (b) are real parts of f(t), while the red dashed lines in (a) and (b) are real parts of \( f_{2}^{D}(t)\) and \(\left( \mathcal {H}_{\sqrt{2},2} f\right) (t)\), respectively. The green continuous lines in (c) and (d) are imaginary parts of f(t), while the red dashed lines in (c) and (d) are imaginary parts of \(f_{2}^{D}(t)\) and \(\left( \mathcal {H}_{\sqrt{2},2} f\right) (t)\), respectively

Full size image
Fig. 4
figure 4

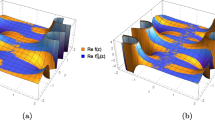
Approximations of (57) illustrated throughout the complex domain. Here, \(|t|<2\). The orange surfaces in (a) and (b) are real parts of f(t), while the blue surfaces in (a) and (b) are real parts of \(f_{10}^{D}(t) \) and \(\left( \mathcal {H}_{\sqrt{2}, 10} f\right) (t)\), respectively. The orange surfaces in (c) and (d) are imaginary parts of f(t), while the blue surfaces in (c) and (d) are imaginary parts of \(f_{10}^{D}(t) \) and \(\left( \mathcal {H}_{\sqrt{2}, 10} f\right) (t)\), respectively

Full size image

Example 2

Consider the \(B^{\infty }_{\pi }\)-function

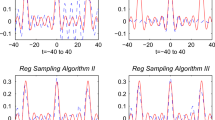
$$\begin{aligned} f(t)=e^{-i \frac{t^{2}}{2\sqrt{3}}} \sin \left( \frac{2 \pi t}{\sqrt{3}} \right) . \end{aligned}$$
(58)

Here, \(a=1/2,\, b=\sqrt{3}/2,\, \Omega =\pi \). Tables 2, 3, and 4 demonstrate the absolute error \(\left| f (\cdot )- \left( \mathcal {H}_{h,N} \widetilde{f}\right) (\cdot ) \right| \) and its associated bound \(\mathcal {B}(\mathcal {H}_{h,N};\cdot )+\mathcal {A}(\varepsilon ,\mathcal {H}_{h,N};\cdot )\), where \(\varepsilon = 10^{-7}, N=5, 10\), and \(h =1, 1/2, 1/4\), respectively. We notice from Tables 2, 3, and 4 that, as predicted by the theory, the number of correct digits increases when N doubles. Moreover, the precision increases when N is fixed but h decreases, as expected in the over sampling case. Furthermore, the error bounds are quite realistic; that is, they do not overestimate the absolute error very much. Graphs of the real and imaginary parts of f(t) and \(\left( \mathcal {H}_{\frac{1}{2},10}\tilde{f}\right) (t)\) on the interval \([-4, 4]\) are exhibited in Fig. 5. It is noted from Fig. 5 that \(\left( \mathcal {H}_{\frac{1}{2},10}\widetilde{f}\right) (t)\) denoted by dashed line overlaps f(t) exactly, denoted by continuous line.

Table 2 Exact error \(\left| f (x_{k})- \left( \mathcal {H}_{h,N} \widetilde{f}\right) (x_{k}) \right| \) and its associated bound \(\mathcal {B}(\mathcal {H}_{h,N};x_k)+\mathcal {A}(\varepsilon ,\mathcal {H}_{h,N};x_k) \) of Example 2 where \(\varepsilon = 10^{-7}\), \(N =5, 10, \) and \(h=1\)
Full size table
Table 3 Exact error \(\left| f (x_{k})- \left( \mathcal {H}_{h,N} \widetilde{f}\right) (x_{k}) \right| \) and its associated bound \(\mathcal {B}(\mathcal {H}_{h,N};x_k)+\mathcal {A}(\varepsilon ,\mathcal {H}_{h,N};x_k) \) of Example 2 where \(\varepsilon = 10^{-7}\), \(N =5, 10, \) and \( h=\frac{1}{2}\)
Full size table
Table 4 Exact error \(\left| f (x_{k})- \left( \mathcal {H}_{h,N} \widetilde{f}\right) (x_{k}) \right| \) and its associated bound \(\mathcal {B}(\mathcal {H}_{h,N};x_k)+\mathcal {A}(\varepsilon ,\mathcal {H}_{h,N};x_k) \) of Example 2 where \(\varepsilon = 10^{-7}\), \(N =5, 10, \) and \( h=\frac{1}{4}\)
Full size table
Fig. 5
figure 5

Illustrations associated with Example 2 where \(t\in [-4,4]\). (a) The blue continuous line is a real part of f(t), while the red dashed line is a real part of \(\left( \mathcal {H}_{\frac{1}{2},10}\widetilde{f}\right) (t)\). (b) The blue continuous line is an imaginary part of f(t) and the red dashed line is an imaginary part of \(\left( \mathcal {H}_{\frac{1}{2},10}\widetilde{f}\right) (t)\)

Full size image

5 Conclusion

This paper regularizes the derivative sampling theorem for signals in the LCT domain through incorporating the reconstruction sampling representation with a carefully scaled Gaussian regularization kernel. The new sampling operator is applicable for band-limited and non-band-limited signals provided that analyticity and growth conditions are determined. The truncation and amplitude errors are precisely estimated. Numerical simulations have verified the efficiency of the proposed sampling theorem.