Hyperspectral imaging is emerging as one of the most popular non-destructive approaches for assessing food quality, and safety [1, 2]. Hyperspectral imaging performs digital imaging from spatial information augmented with spectral information based on spectroscopy. Exceeding the predictive performance of digital RGB imaging and human visual examination [3], spectral and spatial information captured in hyperspectral images allows for highly accurate sensory and chemical attribute prediction. This technology has enabled applications such as predicting the soluble solid content of kiwifruit [4] and classifying brands of Cheddar cheeses [5].

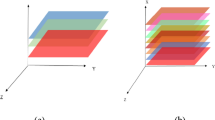
Hyperspectral images capture hundreds of contiguous narrow wavelengths, typically only a few nanometers wide, compared with the 5-50 broad bands captured by multispectral sensors. The captured images consider the spatial context of the samples, which is not possible with single point sampling of spectroscopy [6]. Figure 1 illustrates the differences between these modalities.

Using multivariate analysis, important information can be extracted from the observed reflectance images to predict attributes of the target sample [7]. Multivariate analysis establishes statistical or mathematical relationships between samples and their chemical attributes [8]. Predicting continuous measurements is a regression problem (e.g., total soluble solids of fruits [9]), whereas assigning a discrete class to each observation is a classification problem (e.g., identifying the geographical origin [2]). Most hyperspectral imaging studies in food science typically regress a target variable or classify a sample [10] based on the rich spatial and spectral information delivered by hyperspectral sensors.

Fig. 1
figure 1

Comparison of RGB channel digital imaging (left) to hyperspectral imaging (middle) and spectroscopy (right). Hyperspectral images capture hundreds of wavelength channels across the electromagnetic spectrum

Full size image

High dimensionality is the main challenge when analyzing hyperspectral data. Many applications of hyperspectral sensors require low-cost real-time (online) decision-making, such as sensors for unmanned aerial vehicles (UAVs) [11], assessment of food safety on processing lines [12], and guided surgery [13]. The high cost and low acquisition speed of hyperspectral sensors render these applications infeasible. High dimensionality also leads to models that overfit redundant features or noise [14], a phenomenon known as the Hughes phenomenon [15]. Dimensionality reduction is a way to address all three of these issues.

Two methods exist for dimensionality reduction: projection-based methods and wavelength (feature) selection. Projection-based methods require capturing all the wavelengths, whereas wavelength selection reduces the required wavelengths. Based on the selected wavelengths, multispectral sensors can be designed that are cheaper, faster, and more robust than the original hyperspectral sensors [3]. Wavelength selection is essential for rapid and robust models [7, 16]. However, there is no consensus regarding which wavelength selection techniques provide the best predictive performance, as the results vary among studies [1, 6, 7, 17,18,19,20].

Previous reviews on hyperspectral imaging have comprehensively assessed the applications of hyperspectral imaging and spectroscopy in individual disciplines. For food science applications, reviews have surveyed applications in muscle foods [3, 12, 20, 21], seafood [22, 23], fruits [6, 9, 24], or plant foods and vegetation [19, 25]. Other reviews have also investigated methods for making sense of hyperspectral image data, such as data mining [10], machine learning techniques [26], and deep learning [8]. Previous reviews have only discussed a small set of feature selection methods and have not covered all commonly used methods [2, 10, 12, 19, 20, 24, 25, 27,28,29]. Our review comprehensively surveys wavelength selection techniques across all applications of hyperspectral imaging that apply wavelength selection to provide a detailed answer to the best and most common wavelength selection methods.

Hyperspectral imaging is unique compared with other spectroscopic techniques because the images produced include the spatial context of each pixel. Spatial features are an element of hyperspectral image analysis that is often disregarded in studies. Data fusion refers to how different feature modalities are combined. Selecting the best data fusion method is vital for maximizing the benefits of including spatial information. Although models based on spectral information are often sufficient for high classification or prediction accuracy, including spatial data has been shown to further increase the predictive performance [26, 30]. Previously published reviews discussed the importance of considering both spectral and spatial features to improve the reliability and prediction accuracy of models  [22]. However, a review has yet to explore the best practices for considering both the spectral and spatial features. Our study comprehensively reviews spectral and spatial feature selection techniques in hyperspectral imaging across disciplines to inform the use of spatial features in future investigations.

This review provides a complementary guide to discipline-specific reviews by making the following contributions:

  • A comprehensive review of the best and most common wavelength selection techniques for hyperspectral imaging applications.

  • A comprehensive review of previous studies incorporating spatial features from optimal wavelengths.

  • An overview of the typical sample sizes and targeted wavelength ranges of hyperspectral imaging studies using wavelength selection.

Methods

Systematic reviews are essential to quantify the usefulness of techniques and practices across all studies in a research area. This systematic review followed the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) framework developed by David Moher [31] to survey hyperspectral imaging research that applied wavelength selection techniques to reduce dimensionality and the subset of studies that investigated spatial features. PRISMA reviews consist of four steps: identification, screening, eligibility, and inclusion criteria. This section describes the methodology followed in each step.

Research questions and conceptual framework

This study examined research related to wavelength selection for hyperspectral images by following the PRISMA framework on publications retrieved from the Scopus database. The first stage of research questions focuses on three areas: application area, study design, and methods (i.e., feature selection and learning). We also included an extended second stage of questions for the subset of studies that extracted spatial features. This study answers the following research questions:

Standard hyperspectral study design (Section 2.2)

RQ 1:

How many samples are acquired in hyperspectral imaging studies?

RQ 2:

What wavelength ranges are most common for hyperspectral image analysis?

Feature selection and learning (Section 2.3)

RQ 3:

What are the most common wavelength selection algorithms?

RQ 4:

Which wavelength selection algorithms provide the best predictive performance?

RQ 5:

Which learning algorithms are most common after wavelength selection?

Spatial features (Section 2.4)

RQ 6:

What are the most common spatial features, and what parameters are used to extract these features?

RQ 7:

How are spectral and spatial features combined for learning models?

RQ 8:

How do studies select representative images to extract spatial features?

RQ 9:

Does combining spectral and spatial features improve the predictive performance, and which type of feature performs best individually?

Selection criteria and search strategy

The Scopus database was the primary source of publications. Scopus provides a wide selection of studies with more coverage than other academic databases such as Web of Science [32]. Scopus integrates more sources, particularly conference proceedings, and is still manually curated, unlike Google Scholar.Footnote 1 Our search included abstracts because not all publications mentioned wavelength selection within the title or keywords. We searched the titles, keywords, and abstracts of publications in the Scopus database using the following search string:

(( “hyperspectral imaging” OR“spectroscopic imaging” OR “chemical imaging” OR “imaging spectroscopy” ) AND( “wavelength” OR “waveband” OR “wave band” OR “wave length” ) AND ( “selection” OR “selected” ))

While the search string included multiple synonyms for hyperspectral imaging and wavelength selection, this does not have the effect of excluding studies missing “wavelength selection”, meaning that the search results may include unwanted studies. Studies were manually included and excluded based on the criteria listed in Table 1. The analysis was limited to a subset of hyperspectral imaging studies with wavelength selection to reduce the dimensionality. We did not exclude studies based on language (e.g., English, Chinese, and French) or year of publication. We only excluded studies based on publication type (e.g., conference or peer-reviewed journal) if the publication lacked a full methodology (e.g., published abstracts).

Table 1 Selection criteria for the review process
Full size table

Study selection process

The initial search stage of the literature review returned 1063 studies. The articles were retrieved on the 14th of October 2021. Our review was then updated with 166 more recent studies on the 13th of December 2022, resulting in a total of 1229 studies. The selection criteria defined in Table 1 were applied to reduce the total number of studies. Figure 2 shows a flowchart of the study’s selection process. Duplicate studies (n = 2) and conference announcements (n = 2) were excluded resulting in 1,225 records screened. Next, we set aside 17 reviews before screening the full-text results, leaving 1208 publications. Reviews were excluded because they did not provide empirical results comparing wavelength selection methods or follow a methodology to analyze the images.

Fig. 2
figure 2

Study selection process flow chart. This details the database search, the screening process and the number of studies included for two parts of the review

Full size image

The selection criteria addressed hyperspectral imaging, wavelength selection, and empirical results. This study defined hyperspectral imaging as acquiring images with a hyperspectral sensor capturing at least 90 wavelengths. Hyperspectral imaging is commonly defined in the literature as 100 wavelengths or more. We applied leniency to include studies that initially captured over 100 wavelengths but removed noisy bands during their analysis, reducing the total number of wavelengths to between 90 and 100.

The second criterion is wavelength selection, which is defined as algorithm-based feature selection to select a subset of optimal wavelengths without limiting the size (such as restricting the search to a single band or pair of bands). These distinctions excluded studies that could perform a brute-force search of all wavelength combinations to select wavelengths. We excluded non-algorithmic and expert knowledge-based wavelength selection methods, such as manually selected band ratios. However, we included methods in which humans needed to manually interpret charts to select wavelengths (e.g., principal component plots or derivative curves).

The final criterion was empirical results: each study required a transparent methodology incorporating selected wavelengths with machine learning or other statistical methods for hyperspectral image analysis. Each study was required to provide clear experimental results. This criterion excluded studies proposing novel hyperspectral systems or sensors without experimentation and studies with very few details available to answer our research questions.

We screened the full texts of 1208 publications selected to establish which studies met our inclusion criteria (Table 1). As the lack of details in the abstract was not an exclusion criterion, all the studies required full-text screening. In this stage, 395 studies were eliminated. Of the eliminated studies, 156 did not apply an appropriate wavelength selection technique, while 100 did not investigate hyperspectral images. Finally, 14 studies were inaccessible to the researchers and associates. We contacted the original authors of 13 studies through ResearchGate.Footnote 2 Fourteen of the 16 originally inaccessible did not respond in time for this publication. The first stage of this review included 799 studies. A complete list of these publications is available in the Supplementary Material of this manuscript.

The second stage of this review included 62 English studies that extracted spatial features from hyperspectral images to answer the spatial feature research questions defined in Section 1.1. The entire study population (n = 799) and the subset that utilized spatial features (n = 71) were the two groups of studies investigated.

Encoding of the studies

A single reviewer manually checked whether each study met our inclusion criteria and recorded all relevant information in a Google form.Footnote 3 The reviewer then completed multiple passes, checking one attribute at a time across all the studies to check the information collected, and our inclusion criteria were applied consistently. Google Translate was sufficient to extract information from non-English studies during the first stage of the review. The second stage was limited to studies written in English to avoid misrepresentation of information due to incorrect translations. The data collection process was manual, as some studies were not readable using automation tools.

The language, year of publication, and broad application area (e.g., meat science or medical imaging) of each study were collected for demographic and application area analyses. The wavelength range and sample size were collected from each study to answer the hyperspectral study design research questions. The effective wavelength ranges were collected after the authors discarded noisy bands (if applicable) of all hyperspectral systems investigated. The sample size was recorded as the number of unique objects imaged in the study after the outlying samples were excluded (if applicable).

The collected publications contained over 200 wavelength selection techniques and learning algorithms. From each study, we collected a comma-separated list of the techniques for wavelength selection and machine learning and an ordered list of the best wavelength selection methods based on their performance. Performance was defined as the accuracy of predicting the class or continuous measurement of interest. The performance of the sets of optimal wavelengths was determined based on the prediction set (testing set) accuracy of the best learning model for this subset. When there was a tie, the validation set followed by the calibration set accuracy acted as the tiebreaker. The methods were ranked based on their performance on the prediction set when one method clearly outperformed a subset of the others. If no method decisively outperformed the others, or if there was no comparison between multiple methods, we recorded the best method as inconclusive. Many studies have applied only a single wavelength selection method. In this case, the best method was recorded as only one.

The results were tabulated with Python scripts, ranking which wavelength selection methods performed better based on the number of comparisons with other methods. We only included wavelength selection techniques applied in seven or more studies, and binned all others into the Other category. For example, if one study applied genetic algorithms (GA), successive projections algorithm (SPA), and regression coefficients (RC) to select an optimal subset, and they were ranked as such, we recorded three comparisons: GA outperformed SPA, GA outperformed RC, and SPA outperformed RC.

We tabulated the number of studies that utilized each learning algorithm using Python scripts based on the collected comma-separated lists. Many studies have tested multiple variants of the same family of algorithms, such as random forests and decision trees. For more valuable insights, we counted the number of studies as a measure of popularity rather than the number of occurrences of each algorithm, meaning a study comparing two versions of support vector machines counted as a single observation.

We recorded details from a subset of studies that extracted spatial features for the final research questions related to spatial features using a separate Google form. We recorded a list of the extracted spatial features, the parameters of these feature extractors, the performance of spectral features compared to spatial features, the performance of data fusion compared to individual models, how representative feature images were selected to extract spatial features, and how spectral-spatial features were fused. We recorded whether the data fusion models outperformed the individual models as yes, no, or inconclusive. The best individual set of features was recorded as spectral features, spatial features, not compared individually, or inconclusive. Both were determined based on the accuracy on the prediction set of the best model.

All studies required details regarding wavelength selection techniques to meet our inclusion criteria. Not all the other attributes collected were compulsory. For each research question, we ignored studies in which the related attributes of interest were not stated or unclear. Only studies investigating spatial features were gathered to answer the spatial feature research questions. Since the information gathered is essential for the reproducibility of each study, missing data could indicate lower publication quality.

A spreadsheet stored the information collected by this review and generated simple statistics (e.g., counts). Python scripts extracted other information required to answer questions (e.g., comparisons of methods and the wavelength range graph) and were used to generate tables and figures. The Python libraries required were PandasFootnote 4 for reading the data,Footnote 5 and MatplotlibFootnote 6 for creating figures.

Biases in this study

This review may introduce bias by including several studies from prevalent authors or research groups. Some research groups may follow the same methodology for multiple hyperspectral imaging applications. This imbalance may skew the conclusions on which wavelength selection, learning algorithms, camera models, and other attributes of interest are the most popular for hyperspectral imaging applications.

No methods explored the causes of heterogeneity among the study results because each study acquired different datasets, and no control groups were available. No method assessed the risk of bias due to missing results, the robustness of results, or the certainty of the body of evidence for an outcome. There is a significant imbalance in the occurrence of many wavelength selection techniques. Some wavelength selection techniques have been utilized in a small set of studies (e.g., LASSO [33]), and others have been consistently applied across hundreds of studies (i.e., SPA [34], and CARS [35]). We limited the analysis to methods applied in more than five studies to reduce the impact of less common techniques.

Results

The initial search returned 1229 publications. After applying the selection criteria, 799 publications were selected as relevant and analyzed, as described in the following subsections. Although all 799 studies informed the conclusions of this review, not all were cited here. The complete list of included and excluded studies with the reason for their exclusion is available in the Supplementary Material.

Demographic characteristics of research studies

Fig. 3
figure 3

Number of studies included in this review between 2000 and 2022. The number of studies increases over time. There has been a decline in recent years due to the COVID-19 pandemic limiting research

Full size image

The reviewed studies included 734 journal articles and 65 conference papers based on the classification provided by Scopus. Of the total 799 studies, the publication language included 646 studies in English, 149 in Chinese, and four published in other languages (German, Spanish, French, and Persian). An analysis of publications per year showed an increase in hyperspectral imaging studies with wavelength selection (Figure 3). This increase is likely due to the increased accessibility of affordable hyperspectral sensors. The COVID-19 pandemic may have restricted access to research laboratories, causing a slight decline in research outputs since 2020.

Standard hyperspectral study design

Sample sizes

The first aspect of designing a hyperspectral imaging study examined in this review is the number of samples required (RQ 1). It is essential to ensure that each study has an adequate number of samples for training the models and a representative set of unseen samples for validation. To compare the sample sizes across the population of hyperspectral imaging studies included in this review, we must define a single sample. The number of images cannot represent the sample sizes because some may contain multiple samples (e.g., multiple maize kernels or grains of rice). The number of subjects purchased or retrieved may not be reliable since researchers can obtain measurements from multiple subsamples (e.g., measuring the tenderness of broiler breast fillets [36]). Therefore, we determined the number of samples as the number of individual samples of interest with the corresponding reference values or classes.

The box and whisker plot shown in Fig. 4 summarizes this data on a logarithmic scale due to the skew in observations; the median number of samples was 180, with the middle 50% between 105 and 300 samples. The mean was 424.04 samples, and the maximum and minimum were 19,000 and 1, respectively, indicating a clear skew in the data due to outliers. Some studies had as few samples as a single image, such as studies using the Indian pines dataset [37, 38] for land use classification. Studies with thousands of samples typically investigated low-cost, easy-to-image subjects, such as oats, maize kernels, or other types of seeds [39,40,41,42,43,44]. The study with the second highest number of samples (15,000) collected multiple years of data to detect diseases affecting grape cultivars [43].

Fig. 4
figure 4

Number of samples (log scale) encountered in hyperspectral studies that applied wavelength selection. The median number of samples was 180, with the middle 50% between 105 and 300 samples. The log scale was required for the outliers, which included one study using a single image and another using 19,000 samples

Full size image

Some studies acquired images of the same subjects across multiple timestamps to see how damage symptoms developed over time [45] or to compare before and after treatment [46, 47]. Sampling like this increases the number of observations and sample variation. However, this is possible only when there is no destructive analysis to retrieve the ground-truth reference values from a sample. In these studies, we counted the number of imaged samples rather than the number of unique samples. The chemical analysis of samples is often destructive. Depending on the amount of material required for this analysis, measuring multiple attributes of each sample may not always be possible [48,49,50].

For classification, a single sample could be subdivided into regions with multiple classes, such as those for detecting white stripping on chicken fillets [51], where multiple affected areas were visible from a single sample. Another example is where multiple defective and unaffected regions are visible in the same image. Researchers studying the spectral response of damage to fruit samples typically defined multiple regions of interest for the damaged and unaffected areas [52, 53]. In conclusion, most studies captured between 105 and 300 samples, but the differences in methodologies between study types made recording the sample sizes difficult.

Wavelength ranges

The second aspect of the study design investigated in this review is how to select a suitable wavelength range to capture hyperspectral images (RQ 2). Figure 5 shows the wavelength ranges studied in the 681 studies that clearly indicated their sensor range. Based on the sensors available on the market, the three most common ranges were visible/near-infrared (VIS/NIR: 400–1000 nm), near-infrared (NIR: 900–1700 nm), and shortwave infrared (SWIR: 900–2500 nm). The specific range of interest depends on the application. For example, predicting the attributes of samples correlated with moisture is more suitable in an infrared range where water absorbs more light, but where pigments are correlated with the target attribute, a sensor focusing on visible light is more appropriate.

Most studies focused on one of these ranges, and only 50 investigated multiple ranges. When researchers combine multiple sensors (to examine the spectral features over a more extensive wavelength range), the authors extracted the mean spectra from each sensor and concatenated the vectors to form a single contiguous spectral vector that represented the sample. The researchers then fitted a model to the selected wavelengths from the combined spectra. No study in this review extracted extended pixel-wise spectra by combining data from multiple sensors because they could not find corresponding pixels between sensors.

Fig. 5
figure 5

Histogram of the number of studies investigating each wavelength range

Full size image

Figure 5 shows a spike around 900–1000 nm in the wavelength range of interest due to the overlap between VIS/NIR and other sensors. The VIS/NIR range was the most common due to the accessibility of these sensors [54], and the lower cost of the detector coatings for this wavelength range [7]. There is no significant difference in the choice of sensors based on the sample type between these different ranges. The proportion number of studies looking at the SWIR and VIS/NIR is approximately the same for meat products as for fruit and vegetable-related studies, as shown by the lines on the plot.

Feature selection and machine learning

Wavelength selection

Previous reviews of wavelength selection techniques have divided the field into three categories based on how the methods find optimal features [29]. These categories are filter, embedded, and wrapper methods. Filter methods apply a threshold to a feature importance score to select the best wavelengths. Examples of filter methods include regression coefficients and variable importance in projection (VIP). Embedded methods integrate learning and feature selection, such as LASSO regression [33] and decision trees. Wrapper methods are the most popular category, and they operate by iteratively updating the wavelength subsets and fitting models to evaluate the performance. Wrapper methods include successive projection algorithms (SPA) [34] and genetic algorithms [55]. We also propose a fourth category of techniques, manual selection methods, in which an algorithm provides an output that is interpretable by experts to select the key wavelengths. Principal component analysis loading plots are an example of this type of method. Researchers typically determine points at the peaks/troughs of a plot as the important wavelengths.

We extend this categorization to two other categories of wavelength selection methods: concatenated and interval-based methods. Concatenated methods string multiple selection algorithms together to select important features from previously selected subsets, and interval-based methods select an informative interval of wavelengths, often of a manually determined width. Concatenated methods can combine the advantages of multiple algorithms, such as UVE and SPA. UVE has problems with multicollinearity, and SPA may select uninformative variables. UVE-SPA first removes uninformative wavelengths and SPA removes variables with the least multicollinearity [16]. In Table 2, we have categorized the most popular wavelength selection techniques into these categories and cited recent English studies that employed each technique (RQ 3).

Table 2 An overview of wavelength selection techniques ranked by popularity
Full size table

Tables 3 provide an exhaustive comparison of wavelength selection techniques applied in the area against each other (RQ 4). These tables present the number of studies in which the selected method (rows) outperformed the comparison method (columns). Where the table reads “Only one”, it counts the number of studies where the comparison method was the only wavelength selection method. The “Inconclusive” row presents the number of studies that applied the wavelength selection technique, where the ranking of each method was unclear. Finally, the “Not compared” row provides the number of studies using the method that did not compare it to the other methods. From these tables, we find that there is a clear set of common methods: successive projections algorithm (SPA) [34], competitive adaptive reweighted sampling (CARS) [35], regression coefficients (RC) [60], and principal component analysis (PCA) loadings. Among these techniques, CARS was most often the best method. CARS performed better than SPA in 50 of 76 comparisons, where one was better than the other.

Researchers in 122 studies manually examined the peaks and troughs in the PCA loadings plot to select the key wavelengths. 79 studies applied this as the only wavelength selection technique, compared with 59 studies that compared it with other methods. PCA loadings outperformed SPA in four out of 14 comparisons, CARS in one out of 6 comparisons, and regression coefficients in three out of seven comparisons, where one method was better. PCA loadings are among the worst-performing techniques despite being among the most popular methods.

The most common and consistent methods found in this review were the CARS and SPA methods. The concatenated methods and variable importance in projection (VIP) are the only comparison methods in which the CARS algorithm did not perform well. Concatenated and interval-based methods, UVE and CARS outperformed SPA, whereas SPA performed well in all other comparisons. Regression Coefficients were the sole wavelength selection method used in 89 studies, and in 57 studies where researchers compared it to others, it did not perform well. The performance of regression coefficients is demonstrated by comparisons with genetic algorithms (best in two out of seven comparisons), CARS (best in five out of 16 comparisons), and SPA (best in 11 out of 30 comparisons). Regression coefficients, as with PCA loadings, is a simple feature selection method, making it more popular than novel methods that are not available in standard libraries for different programming languages or built into commercial software.

For the two concatenated methods utilized in more than five studies, there were very few comparisons with the other techniques. Studies that included these methods often compared them to other concatenated methods [129, 130]. CARS-SPA and UVE-SPA performed well but were only applied in 20 and 15 studies, respectively. CARS-SPA had the highest performance, outperforming SPA in ten out of 15 comparisons and an equal performance against CARS (better in eight out of 16 comparisons). UVE-SPA similarly performed well but underperformed other concatenated approaches, such as CARS-SPA (best in two out of five comparisons). UVE-SPA was outperformed by CARS and UVE individually (best in two out of nine and one out of seven comparisons, respectively).

The most common interval-based approaches encountered are interval-partial least squares (iPLS) [89], interval-VISSA (iVISSA) [103], Synergy interval partial least squares (siPLS) [123], and interval random frog (iRF) [105] were often compared to each other. These methods divide the full spectrum into equidistant partitions and fit regression models to the intervals [91]. There were not enough comparisons of these methods to conclude which interval-based method was the best, and their performance against single-feature methods was generally poor.

Many studies have proposed a novel wavelength selection method and compared it to a small set of the most common approaches while claiming superior performance. Comparisons with a broader range of techniques over multiple datasets are required to benchmark their performance. Since five or fewer studies applied each of these methods, we grouped them methods into the “other” column of Table 3. To the best of our knowledge, no standardized benchmark datasets are available for wavelength selection.

Other popular methods for wavelength selection include genetic algorithms [55], random frog [70], uninformative variable elimination [67], and variable importance in projection [60]. Genetic algorithms performed well, but it is not easy to compare to this algorithm because many hyperparameters must be manually set.

Machine learning methods

The final step in model creation is to fit the model to the selected wavelengths. Here, we list the most common machine learning and statistical models applied to the selected wavelengths (RQ 5). Partial least squares (PLS) is the most common learning algorithm for analyzing hyperspectral data after wavelength selection. A total of 470 studies chose a variant of PLS. The most common variants are partial least squares regression (PLSR) for regression and partial least squares discriminant analysis (PLS-DA) for classification. Previous reviews have reported the high utilization of PLSR and PLS-DA [131]. Instead of directly operating on the variables, PLS extracts a set of latent variables with the best predictive performance [21]. Seventy-four studies applied a more straightforward multiple linear regression (MLR) that fits a simple linear equation to the observed data. MLR struggles with high multicollinearity between wavelengths [132], which makes prior wavelength selection important. The advantage of MLR is the interpretability of the results, whereas the meaning of the latent variables or principle components is unclear. The second most common algorithm was support vector machines (SVM) [133] in 333 studies, the most common variants of which were least squares support vector machines (LS-SVM) and support vector regression (SVR).

Table 3 Comparative performance of wavelength selection algorithms
Full size table

Various studies applied variants of artificial neural network (ANN) architectures, such as backpropagation neural networks (BPNN) [134], extreme learning machines (ELM) [135], stacked autoencoders (SAE), and convolutional neural networks (CNN) [136]. These machine learning approaches apply a series of processing layers to extract higher-level features and are often referred to as deep learning approaches. Non-linear methods such as ANNs and SVMs are valuable for modelling complex relationships between dependent and independent variables. These non-linear approaches have a higher computational complexity [10]. Only a few studies have applied deep learning to hyperspectral imaging for food applications because of the time and cost requirements for gathering large datasets with corresponding reference (ground-truth) measurements [8]. Few studies (n = 20) have combined convolutional neural networks with wavelength selection despite their popularity in computer vision outside hyperspectral imaging, but these techniques have become more common since 2022 [57, 137,138,139]. Due to the challenges of big data and small sample sizes, CNN approaches typically apply one-dimensional filters to the spectral response rather than two- or three-dimensional filters to the hyperspectral image. Table 4 displays the counts for each learning algorithm found by this study.

Table 4 Machine learning models with wavelength selection sorted by popularity
Full size table

Decision trees were found in 67 studies, including variants such as random forests and classification and regression trees (CART). K-nearest neighbors (KNN) is a simple method for classifying samples based on their distance from other labelled samples. Because of the number of neighborhood comparisons required, KNN becomes more computationally expensive with larger datasets. Projection methods such as linear discriminant analysis (LDA) and principal component analysis (PCA) distinguish classes within data by projecting the remaining wavelengths onto new axes to maximize variance and class separability. Principal component regression (PCR) is applied instead of PCA for regression analysis. Fifty-three studies utilized LDA compared with 26 studies that chose PCA instead. Of the 799 studies surveyed, 77 compared learning algorithms that did not fit these categories.

Spatial features

Spatial descriptors (image texture descriptors) provide information about the spatial arrangement of pixels, whereas spectral information describes how light interacts with samples. As discussed earlier, many reviews acknowledged that including spatial features as independent modelling variables helps to improve the predictive performance of models [22]. Spatial information includes statistical features that summarize the distribution of intensities, such as statistical moments, and higher-order spatial descriptors (statistics) describe the distribution of groups of pixels, such as pairs for grey-level co-occurrence matrices. Spatial features may also include local neighborhood operations, such as local binary patterns (LBP) [140], or shape features describing the shape of the regions of interest. This section describes the different techniques for extracting spatial features from hyperspectral images (RQ 6), approaches to select feature images (RQ 8), the predictive performance of models incorporating spatial features (RQ 9), and how studies combine spatial features with spectral features (RQ 7).

Table 5 Comparison between the 71 studies included in this review sorted chronologically, using spatial features with hyperspectral imaging and wavelength selection
Full size table

Spatial features descriptors

A total of 71 out of the 799 studies selected for review included spatial features and wavelength selection for hyperspectral image analysis. Table 5 provides a breakdown of these studies, answering RQ 6. The most popular spatial features were the grey-level co-occurrence matrices (GLCM) texture descriptors found in 41 out of 71 studies. GLCM descriptors (also known as Haralick features) describe the two-dimensional feature image by creating a matrix of the probability of joint occurrences of pixel grey level values at a given angle (\(\theta\)) and distance (d) [202].

Haralick et al. [202, 203] described 14 features to summarize GLCM matrices into texture descriptors. Studies such as Clausi [204] and Soh and Tsatsoulis [205] further extended this set of features. The five most common features encountered were: contrast/inertia moment (n = 38), energy/uniformity/angular second moment (n = 38), correlation (n = 36), homogeneity/inverse difference moment (n = 35), and entropy (n = 19). Four studies investigated features beyond this set of five core features [171, 178, 184, 194], but two did not provide sufficient information on the extracted features. One of the earliest studies combining spatial features with wavelength selection [194] extracted 22 GLCM features, including multiple methods for selecting the feature image. However, these studies did not examine the effectiveness of each feature.

The main parameters of the GLCM are the angle and distance used to measure pixel correlation. Typically, studies chose four angles 0°, 45°, 90°, and 135° describing the relationships diagonally, vertically, and horizontally to create GLCM matrices. Different angles and distances create different matrices. Eleven studies averaged the descriptors over the four orientations to produce a rotation-invariant descriptor. Many studies did not state whether they averaged over multiple angles (n = 16), did not average over angles (n = 8), or only employed a single angle (n = 5). For the distance parameter, the typical approach is to create matrices based on a one-pixel distance. Few studies have examined a broader range of distances, such as one to ten pixels [201] or one to five pixels [164, 190]. Because we can fix the distance between the samples and sensors in controlled environments, a single distance should be sufficient. Future studies should be conducted using multiple distances to determine the best effect.

The second most popular spatial feature extraction method was the grey-level gradient co-occurrence matrix (GLGCM) [206] (n = 11). Similar to GLCM, GLGCM captures second-order statistics about the spatial image content by describing the grey-level gradients of the images. The GLGCM matrix represents the relative frequency of occurrence between a pixel with a given grey value and gradient. The data fusion model outperformed the single modality models for all studies extracting GLGCM features that compared fusion models to individual models (n = 10). GLGCM has a much larger set of features than GLCM, describing the dominance and distribution of gradients and the entropy, average, standard deviation, asymmetry, and nonuniformity of both the pixel gradients and grey level. The popularity of GLCM and GLGCM was consistent with previous reviews [1, 14].

Another spatial feature extraction approach is local binary patterns (LBP) [169, 175, 182] where each pixel was compared to its horizontal, vertical, and diagonal neighbors to give an eight-digit binary code [140]. Each position in the binary code describes whether the neighboring pixel value is larger (1) or smaller (0) than the target pixel. There were mixed results from the LBP features for hyperspectral images. One study extracted LBP features from RGB images to classify freezer-burnt salmon with no data fusion and found that the spectral-based model performed better for discriminating classes [175]. Another study found that GLGCM and GLCM significantly outperformed LBP without data fusion [169].

GLCM, GLGCM, and LBP provide second-order statistics based on the relationships between pixel pairs [207]. SSome studies have extracted first-order statistics, such as histogram descriptors, based on the histogram of intensities in the feature image. Histogram statistics summarize the grey value distribution of the image without considering the spatial interactions between pixels. The most common features extracted from these grey-level histograms are mean, uniformity, entropy, standard deviation, and third-moment (skewness) [186, 195, 208], as well as kurtosis, energy, smoothness, contrast, consistency, and roughness [141, 149, 154, 178, 180]. One study applied feature selection to the precomputed spatial features and found that the selection algorithm did not select histogram-based features for beef tenderness forecasting [182]. Other studies found that histogram statistics improved the model accuracy more than GLCM features [178] or shape descriptors [186]. The GLCM features significantly outperformed histogram statistics in another study [51].

Five studies investigated Gabor filters for extracting spatial features from hyperspectral images [146, 165, 170, 182, 191]. Gabor filters, which are linear filters used for texture analysis, apply convolutions with kernels generated by combining the Gaussian and sinusoidal terms. The results are often averaged over multiple angles to obtain rotationally invariant descriptors [146, 165].

Prior to 2020, only one study extracted spatial features with a convolutional neural network (CNN) [153]. This CNN architecture utilized two branches: one extracted spectral features with a one-dimensional CNN and the second extracted spatial features with a two-dimensional CNN. The model concatenated the extracted feature vectors for classification into a single feature vector. Feature importance was evaluated using the weights learned by the CNN in the first layer to select the optimal wavelengths. Since then, more advanced two-dimensional CNN architectures have been used to utilize the spatial information within images [84, 143]. One study applied the YOLOv3 algorithm [209], a popular object detection algorithm, to detect defects on apples [139].

The final common spatial feature extraction approaches accounted for were morphological/shape features. These approaches described the contour of the region of interest encompassing the sample with shape features. Shape features require only the ROI mask of the sample. The typical features extracted were the area, perimeter, major- and minor-axis lengths, and eccentricity. The studies that extracted shape features had good results for discriminating the varieties of seeds [197] and black beans [181] because of the correlation between shape and variety. The accuracy of the models trained on spectral features in both cases outperformed spatial features, and the data fusion model further improved the results. Other studies have applied edge detection algorithms to detect cracks and morphological features to detect scattered egg yolk [142].

Other less frequently used spatial features extracted include grey-level run-length matrix analysis [183], wide line detectors [146, 191], and wavelet-based transformations, such as Discrete Wavelet Transform (DWT) [96, 192], and Discrete cosine transformation [172].

Selecting feature images

Each feature extraction approach requires an image to form the basis of spatial feature descriptors. The most common methods extract features from the principal component (PC) score images of a full hyperspectral image or pre-selected wavelengths. Selecting the optimal wavelengths before extracting spatial features is less computationally intensive. Preselecting optimal wavelengths assumes that wavelengths with important spectral information also carry important spatial information. Selecting the optimal wavelengths before extracting the spatial features was employed in 48 studies. Another approach is to extract spatial features from each wavelength within the hyperspectral images and then apply feature selection to reduce the features to a set of optimal features from a reduced number of bands (post-selected). Two studies directly selected bands with important spatial features by extracting them from all wavelengths [146, 188]. Other studies have applied feature selection to select informative features from a selected or full feature set [144, 165, 173, 191].

Twenty-five studies selected PC score images as feature images. Although extracting texture descriptors across the entire spectrum is possible, this increases the computational complexity, making it infeasible in real-time systems. A single study utilised spatial features from all available wavelengths without feature selection [177], and five studies created either RGB images from the hyperspectral sensor or captured RGB images from a secondary camera [84, 142, 166, 175, 201]. The selected feature images are listed in the feature image column of Table 5.

Data fusion

There are three levels of data fusion for combining features from different feature spaces [210]. Pixel-level fusion integrates multiple modalities as co-registered inputs into a single feature extraction model, feature-level fusion combines features after extracting characteristic features, and decision-level fusion combines multiple model outputs after fitting models to the extracted features. Almost all studies that considered spatial features combined spectral and spatial features with feature-level fusion, with some CNN-based models integrating spectral-spatial information at the pixel level [84, 139]. They first extracted features from the images to combine spectral and spatial features before fitting the models to the fused feature vector. It is possible to apply decision-level fusion by training independent models on the spectral and spatial features and then using a meta-model to the decisions of the separate models. Models trained after feature-level fusion can incorporate interactions between individual features, which decision-level fusion models cannot. Feature-level fusion avoids the computational burden of high-dimensional feature extraction in pixel-level fusion.

Pixel-level fusion is feasible when data from two hyperspectral sensors with different wavelength ranges are fused. All the studies that merged data from multiple sensors extracted the mean spectra from each sensor’s ROI and combined them into a single spectrum for modelling, which would also be considered feature-level fusion. However, regions of interest could be registered together to combine multiple wavelength ranges for each pixel.

Mean normalization is often applied to features of different modalities (spectral and various types of spatial descriptors) to overcome problems caused by disparities between features [154, 165, 171, 180, 183, 185, 189]. Normalization rescales each feature in the training set (calibration) by its mean and standard deviation, giving all features a comparable magnitude.

Performance

Thirty-seven studies that included spatial features within their feature sets found that the predictive performance of models trained on spectral features alone outperformed those trained solely on spatial features (Table 5). Only five studies discovered that spatial characteristics were more helpful for predicting attributes than spectral features, and 29 studies failed to compare the two approaches in a way that allowed us to determine which model was the most effective. However, the selected model also affected the results. The performance metric that we used was the accuracy of the best model. When combining spectral and spatial features, we found that most studies (n = 40) performed better by combining spectral and spatial features than by using spatial or spectral features individually. The individual model outperformed the data fusion model in six studies. Finally, 25 studies did not compare the individual models to the spectral-spatial fusion models.

In these outlying studies, spatial features tended to be more appropriate for the problem because they corresponded to clearly visible texture indicators. For example, pork marbling can be detected using a wide-line detector to predict intramuscular fat [146]. Other studies related to pork meat assessment found that Gabor and GLGCM features outperformed spectral features for prediction of the total volatile base nitrogen content (TVB-N) [165] and freshness prediction [187], respectively. For the classification of tea varieties [167] and prediction of the water content of tea leaves [196], the GLCM features outperformed the spectral features. These studies showed that spatial features could be more valuable than spectral features of hyperspectral images in predicting the attributes of interest.

Studies have likely found worse performance from data fusion models because they did not include spatial features correlated with the prediction variable. One study observed a significant drop in performance between the calibration set and the prediction set for classifying maize seed quality, possibly indicating that the model was overfitting to the data [154]. Overfitting occurs when the model identifies trends in the calibration set that are less prevalent in the prediction dataset. Another study reported a similar predictive performance between spectral and data fusion models for predicting the tenderness of salmon [190]. GLCM features did not help predict chilling injury classes of green jujubes [162]. In these studies, the spatial features may have been inappropriate for the particular problem, or the wavelengths selected based on the spectral data may have been unsuitable.

Discussion

This review systematically surveyed studies that applied wavelength selection to hyperspectral imaging and found that food quality and safety accounted for most of the applications. Popular subjects included pork, apples, maize kernels, wheat, and potatoes, and common attributes of interest included moisture content, variety, and adulteration.

Standard hyperspectral study design

Surveying the number of samples in each study showed that hyperspectral imaging studies utilized significantly fewer samples than other machine learning applications in computer vision. The main reason for this is the cost and time required to acquire sample images. Due to the lower accessibility of sensors, it is not possible to use crowd-source training data such as popular RGB image datasets [211]. Condensing each sample to a single mean reflectance spectrum reduces spatial dimensionality at the cost of losing potentially useful spatial information. While deep learning has become the most popular approach for many computer vision tasks, typical datasets for deep learning, such as object detection or image classification datasets, often have millions of annotated RGB images. With more cost-effective hyperspectral sensors, researchers can create larger hyperspectral imaging datasets and apply deep learning models that reduce the feature set to find reliable trends with fewer observations.

This review also concludes that VIS/NIR range sensors are the most common for hyperspectral imaging applications with wavelength selection. VIS/NIR sensors are cheaper and provide adequate information for most studies. Future studies should consult prior works to determine which wavelength range suits their application.

Feature selection and machine learning

Wavelength selection

Given the current state of the literature, determining which feature selection technique yields the best wavelengths remains highly application dependent. Many confounding factors affected the accuracy of the models. Studies that have evaluated multiple wavelength selection methods and multiple classifiers may have one wavelength selection technique that performs best with one classifier and another performing best with a different classifier. Each study may differ in the implementation of each algorithm, experimental conditions, and datasets. The specific implementation may differ for methods with multiple hyperparameters, such as genetic algorithms, which require a fixed population size, genetic operator probability, number of generations, and a fitness function.

Many studies have proposed novel methods to select features but have not comprehensively compared the most common wavelength selection methods. We suggest that future studies compare the most common related methods to provide a more accurate benchmark for new feature selection methods on a particular dataset. The best-performing and most popular methods are the SPA, CARS, and genetic algorithm methods.

This review does not consider the number of wavelengths selected by each method. UVE often uses hundreds of wavelengths with high multicollinearity. Creating multispectral models for real-time analysis of hundreds of influential bands is not feasible. We also did not consider the differences between the interval-based and individual-feature approaches. Creating a multispectral model from a small subset of features may benefit from informative intervals instead of informative narrow wavelengths because some spectral features are visible over several adjacent wavelengths.

Machine learning

Our review concluded that there are fewer regression or classification methods than wavelength selection techniques. The most common methods are based on Support Vector Machines (SVM) or Partial Least Squares (PLS). We did not compare the effectiveness of these machine learning algorithms. This review attempts to gauge their popularity in literature. Partial least squares, decision trees, and multiple linear regression methods are explainable approaches compared to neural network approaches but are limited in extracting features. Wavelength selection for hyperspectral imaging studies follows the process of first extracting features from sample images, applying feature selection, and applying a regression or classification algorithm. This process limits the search space of models and contradicts the integrated approach of deep learning, where a model learns to extract meaningful features and applies regression or classification. This review found no algorithm combining feature extraction, selection, and regression (or classification) steps. The only similar example we found was the two-branch CNN approach by Liu et al., which extracted spectral and spatial features independently [153].

Spatial features

Our review found that GLCM and GLGCM were the most common methods for extracting spatial features. These handcrafted features require high levels of domain knowledge and may only be beneficial for certain problems. GLCM and GLGCM improved the accuracy of the learning algorithms in studies that incorporated them. Features learned by deep learning methods have dominated image classification of RGB images over the last decade [212]. Learning spatial features is complicated when considering the high number of channels in hyperspectral imaging (extensive fea- ture space), small sample sizes, and simultaneous challenge of selecting important wavelengths to enable online (real-time) applications.

The number of spatial features available exacerbates the high dimensionality of wavelength selection. GLCM alone has 14 standard texture descriptors per angle, distance, and wavelength. The feature space can quickly grow to extremely high dimensions with many combinations. Many studies have limited the feature image set to the selected wavelengths. Experimenting with enough features almost guarantees that at least one will correlate with the reference attributes in the training set, but this trend may not apply to the validation data.

Very few studies have selected important spatial features independent of the spectral features. Huang et al. [188] showed that the spatial features can be plotted over the entire wavelength range to form a continuous curve, similar to the standard approach to mean reflectance. Other types of features also share a high correlation between adjacent wavelengths. Many studies have extracted spatial features from the Principal Component score images and spectral features using wavelength selection. However, generating a PC score image requires a complete set of wavelength bands. All wavelengths would be needed to extract spatial features making wavelength reduction redundant and creating a lower-cost multispectral system impossible. The most common approach is to pre-select wavelengths based on the spectral features.

Most studies have revealed that spectral features are superior to spatial descriptors for the classification or prediction of attributes. Models incorporating both spectral and spatial data had higher predictive performance than individual features alone.

The two main limitations of studies investigating spatial features are that they assume that wavelengths with the most meaningful spectral information also have the most meaningful spatial information. In most cases, the set of available spatial features is limited to a set selected by the authors. More work is needed to create flexible feature selection techniques and test them on larger sets of spatial features.

Limitations

Due to the restrictions of our inclusion criteria used in this review, such as only including studies with wavelength selection, some aspects of the studies investigated in this review may not represent all hyperspectral imaging research. We did not compare spatial feature extraction methods for hyperspectral imaging rather than wavelength selection.

Studies may also have been missing from this review. They were either unavailable on Scopus, or the search string did not retrieve them. We mitigated this as much as possible by searching titles, keywords, and abstracts for multiple synonyms of “wavelength” and “selection”. However, we found some relevant studies that did not mention these keywords in their abstracts. Searching for an acronym for each wavelength selection technique is not feasible.

Conclusion

This review included 799 hyperspectral imaging studies from Scopus from the 1229 studies collected. This review excluded studies that did not investigate hyperspectral imaging and wavelength selection or did not provide a transparent methodology and experimentation results. We analyzed these studies to understand the methods for feature selection, machine learning, and spectral-spatial feature fusion.

Regarding the design of wavelength selection studies, this review found that hyper- spectral image analysis studies tended to have only a small number of samples, with the studies included in this review having a median sample size of 180. We investigated the wavelength ranges for studies that applied wavelength selection and found three commonly investigated regions of the electromagnetic spectrum: namely, 400–1000 nm, 900–1700 nm, and 900–2500 nm.

Many studies have applied an extensive range of wavelength selection algorithms. Although the comparative performance of the wavelength selection techniques is not an objective of most studies in hyperspectral imaging, we recommend that future work should apply a range of different techniques rather than just a single technique. We recommend the popular SPA, CARS, and genetic algorithms wavelength selection methods as benchmarks for future wavelength selection studies. Concatenated methods, such as CARS-SPA and UVE-CARS tend to provide features that lead to more accurate models. However, the number of studies that applied each of these techniques is not high enough to conclude whether they are better than other techniques. Any newly introduced wavelength selection method should be compared to a wide range of best-performing methods because there is no clear best selection method for all applications. The most common learning algorithms were partial least squares, support vector machines, and artificial neural networks. These wavelength selection and modelling steps were not integrated into the same solution because combining feature reduction with feature extraction and learning remains challenging.

This review found that spectral features were more informative than spatial features in most studies employing spatial features, whereas combining both feature types increased predictive performance. Spectral and spatial features are typically extracted independently and fused using feature-level fusion. The most common method is to select wavelengths with important spectral information and extract spatial features from each selected wavelength. GLCM features were the most common texture descriptor combined with wavelength selection and were applied in more than half of the studies that considered spatial features.

There is a need for more flexible feature selection and extraction methods, further investigation of spatial features, and publicly available large-scale hyperspectral image datasets. Flexibility can arise from flexible intervals of wavelengths or more flexible methods for extracting informative spatial features independent of spectral features.