Passivation Threshold for the Oxidation of Liquid Silicon and Thermodynamic Non-equilibrium in the Gas Phase

Abstract

The present study focuses on a specific step of the metallurgical path of purification to provide solar-grade silicon: the removal of boron through the injection of H₂O(g)-H₂(g)-Ar(g) (cold gas process). A progressive increase of the oxidant H₂O(g) concentration at injection increases the speed of the process until a silica layer appears at the surface of the liquid silicon to be purified. It then stops the purification. During the process, silica aerosols may form in the gas boundary layer. This modifies the flows of oxidants and the gas concentrations at the liquid silicon surface. Using a monodimensional model, this article shows that a hypothesis of thermodynamic equilibrium of silica aerosols with the gas phase in the boundary layer has to be dropped in order to explain the appearance of a silica passivating layer. The passivation threshold is defined as the limit concentration of the oxidant at the injection below which there is no silica on the liquid silicon surface and beyond which silica particles appear on the liquid silicon surface. Three experiments of estimation of the passivation threshold with the injection of water vapor are used to confirm an empirical criterion for the prediction of the appearance of the silica layer. Two other sets of experiments with the injection of Ar-O₂ are also being studied where the kinetics of the formation of silica aerosols seems to be slower than when water vapor is used. An optimization of the speed of boron removal under the assumption of a maximal concentration of water vapor before the appearance of a passivating silica layer would require an increase of the liquid silicon surface temperature from the fusion temperature of silicon.

Appendices

Appendix A: Simplified 1D isothermal model

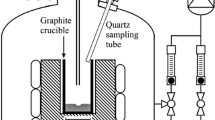
We consider a boundary layer of thickness δ, where the only reactive species out of the boundary layer are H₂O(g) ($P_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{0}$ at injection) and H₂(g) ($P_{{{\text{H}}_{{\text{2}}} }}^{0}$ at injection). Remember that the convection is not considered, and the model included only reactive and diffusive phenomena. At the reactive surface z = 0, there is liquid silicon. The structure of this layer is given in Figure 2, which means there is liquid silicon at the surface.

Hypotheses:

• Thermodynamic equilibrium everywhere

• Net flow of oxygen and hydrogen atoms at the surface equal to zero

• Sufficient dilution for the use of the Fick’s law

For this part, let’s define the effective pressures that will be used to express the flow of oxygen and silicon atoms in a more simple way.

$$ \begin{aligned} P_{{{\text{Si}}}}^{{{\text{eff}}}} \, = \, & \Psi _{{{\text{Si}}}} P_{{{\text{Si}}}} \, + \,\Psi _{{{\text{SiO}}}} P_{{{\text{SiO}}({\text{g}})}} \\ & + \,\Psi _{{{\text{SiO}}_{{\text{2}}} }} P_{{{\text{SiO}}_{{\text{2}}} ({\text{g}})}} \\ P_{{{\text{O}}_{{\text{2}}} }}^{{{\text{eff}}}} \, = & \,\frac{1}{2}\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} P_{{{\text{H}}_{{\text{2}}} {\text{O}}}} + \frac{1}{2}\Psi _{{{\text{SiO}}}} P_{{{\text{SiO}}({\text{g}})}} \\ & + \,\Psi _{{{\text{SiO}}_{{\text{2}}} }} P_{{{\text{SiO}}_{{\text{2}}} ({\text{g}})}} \\ P_{{{\text{H}}_{{\text{2}}} }}^{{{\text{eff}}}} & \, = \,\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} \,P_{{{\text{H}}_{{\text{2}}} {\text{O}}}} \, + \,\Psi _{{{\text{H}}_{{\text{2}}} }} P_{{{\text{H}}_{{\text{2}}} }} \\ \end{aligned} $$

(A1)

These effective pressures are defined by rearranging the partial pressures and adimensionalized diffusivities $\Psi$ in such a way that the flow of atoms of Si, H and O can be found straightfowardly. The flows of atoms of Si, H and O can later be found by deriving these effective pressures via Fickian-type diffusive fluxes.

First, let’s write Fick’s law for a diluted gas at uniform pressure to express the diffusive fluxes at the surface of arbitrary gas species X:

$$ \begin{aligned} J_{{\text{X}}}^{{{\text{mol}}}} = & - D_{\text{X}} c\frac{{\partial x_{\text{X}} }}{{\partial z}} \\ = & - \frac{{D_{\text{X}} }}{{RT}}\frac{{\partial P_{\text{X}} }}{{\partial z}} \\ \end{aligned} $$

(A2)

Remember that the adimensionalized diffusivity for gas species X is written $\Psi _{{\text{X}}} = \frac{{D_{{\text{X}}} }}{{D_{{{\text{O}}_{{\text{2}}} }} }}$. Thus, using Eq. [A1] and Fick’s law for a diluted gas: $- \frac{{2D_{{{\text{O}}_{{\text{2}}} }} }}{{RT}}\frac{{\partial P_{{{\text{O}}_{{\text{2}}} }}^{{{\text{eff}}}} }}{{\partial z}}$ gives the flow of oxygen atoms:

$$ - \,\frac{{2D_{{{\text{O}}_{{\text{2}}} }} }}{{RT}}\frac{{\partial P_{{{\text{O}}_{{\text{2}}} }}^{{{\text{eff}}}} }}{{\partial z}}\, = \, - \,D_{{{\text{H}}_{{\text{2}}} {\text{O}}}} \frac{{\partial P_{{{\text{H}}_{{\text{2}}} {\text{O}}}} }}{{\partial z}}\, - \,D_{{{\text{SiO}}}} \frac{{\partial P_{{{\text{SiO}}}} }}{{\partial z}}\, - \,2D_{{{\text{SiO}}_{{\text{2}}} }} \frac{{\partial P_{{{\text{SiO}}_{{\text{2}}} }} }}{{\partial z}}\, = \,J_{{{\text{H}}_{{\text{2}}} {\text{O}}}} \, + \,J_{{{\text{SiO}}}} \, + \,2J_{{{\text{SiO}}_{{\text{2}}} }} \, = \,J_{{\text{O}}} {\text{ }} $$

(A3)

Similarly, $- \frac{{2D_{{{\text{H}}_{{\text{2}}} }} }}{{RT}}\frac{{\partial P_{{{\text{H}}_{{\text{2}}} }}^{{{\text{eff}}}} }}{{\partial z}}$ gives the flow of hydrogen atoms and $- \frac{{D_{{{\text{Si}}}} }}{{RT}}\frac{{\partial P_{{{\text{Si}}}}^{{{\text{eff}}}} }}{{\partial z}}$ the flow of silicon atoms. We used expressions similar to Ratto et al.[15] and Vadon et al.[4] Hence, $P_{{{\text{O}}_{{\text{2}}} }}^{{{\text{eff}}}}$ and $P_{{{\text{H}}_{{\text{2}}} }}^{{{\text{eff}}}}$ are used to follow flows of atoms (with a multiplicator of two) to simplify expressions further in the model.

A reasoning on an elementary layer of thickness dz shows that $\frac{{\partial ^{2} \left( {P_{{{\text{O}}_{{\text{2}}} }}^{{{\text{eff}}}} - P_{{{\text{Si}}}}^{{{\text{eff}}}} } \right)}}{{\partial z^{2} }} = 0$ because one atom of silicon for every two atoms of oxygen goes from the gas phase to the silica phase, using Fick’s law:

$$ \begin{aligned} P_{{{\text{O}}_{{\text{2}}} }}^{{{\text{eff}}}} - P_{{Si}}^{{eff}} = \, & Az + B \\ P_{{{\text{H}}_{{\text{2}}} }}^{{{\text{eff}}}} = \, & {\text{constant}} \\ \end{aligned} $$

(A4)

The net flow of oxygen atoms at the surface is equal to zero by the hypothesis, and hence by Fick’s law, at the surface:

$$ {\frac{{\partial P_{{{\text{O}}_{{\text{2}}} }}^{{{\text{eff}}}} }}{{\partial z}} = 0} $$

(A5)

The flow of silicon atoms at the surface is given by Fick’s law for diluted gases; then, using Eqs. [A5] and [A4]:

$$ {J_{{{\text{Si}}}} \, = \, - \,\frac{{D_{{{\text{O}}_{{\text{2}}} }} }}{{RT}}\frac{{\partial P_{{{\text{Si}}}}^{{{\text{eff}}}} }}{{\partial z}}\, = \,\frac{{D_{{{\text{O}}_{{\text{2}}} }} }}{{RT}}A} $$

(A6)

Thus, by looking at the conditions at the surface (z = 0) and at the top of the boundary layer ($z =\delta$), the molar flow of silicon per m² J_Si can be written using Eq. [A4]:

$$ \begin{array}{ll} {J_{{{\text{Si}}}} \, = \,\frac{{D_{{{\text{O}}_{{\text{2}}} }} }}{{RT}}\,\frac{{\Psi _{{{\text{Si}}}} \,P_{{{\text{Si}}}}^{{{\text{sat}}}} \, + \,\frac{1}{2}\,\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} \,P_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{0} \, + \,\frac{1}{2}\,\Psi _{{{\text{SiO}}}} \,P_{{{\text{SiO}}}}^{{{\text{surf}}}} \, - \,\frac{1}{2}\,\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} \,P_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{{{\text{surf}}}} }}{\delta }} \hfill \\ \end{array} $$

(A7)

Then, using thermodynamic data from JANAF,[7] we can neglect $\Psi _{{{\text{Si}}}} \,P_{{{\text{Si}}}}^{{{\text{sat}}}}$ and $\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} \,P_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{{{\text{surf}}}}$ compared with $P_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{0}$ for $P_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{0}$ more than a 100 Pa like in the studied cases.

$$ {J_{{{\text{Si}}}} \, \approx \,\frac{{D_{{{\text{O}}_{{\text{2}}} }} }}{{RT}}\frac{{\frac{1}{2}\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} \,P_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{0} \, + \,\frac{1}{2}\Psi _{{{\text{SiO}}}} \,P_{{{\text{SiO}}}}^{{{\text{surf}}}} }}{\delta }} $$

(A8)

Let’s remark that from Vadon et al.,[8] there is a similar equation for non-isothermal cases, which neglects the effect of Soret thermodiffusion:

$$ {J_{{{\text{Si}}}} \, \approx \,\frac{{\frac{1}{2}\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} \,p_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{0} \, + \,\frac{1}{2}\Psi _{{{\text{SiO}}}} \,p_{{{\text{SiO}}}}^{{{\text{surf}}}} }}{{R\int_{0}^{\delta } {\frac{{T(z^{\prime})}}{{D_{{{\text{O}}_{{\text{2}}} }} (z^{\prime})}}} dz^{\prime}}}} $$

(A9)

SiO₂(g) is a minority species (${P_{{{\text{SiO}}_{{\text{2}}} }} \, \ll \,P_{{{\text{SiO}}}} }$) at thermodynamic equilibrium. The gradient of ${P_{{{\text{SiO}}_{{\text{2}}} }} }$ does not play any role in the heterogeneous sublayer at thermodynamic equilibrium because its concentration is fixed by the reaction ${{\text{SiO}}_{2}{\text{(g)}} \leftrightarrows {\text{SiO}}_{2}{\text{(s/l)}}}$.

$$ {\frac{{\partial P_{{{\text{SiO}}_{{\text{2}}} }} }}{{\partial z}} = 0} $$

(A10)

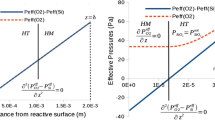
By using the conditions at the intersection of the lower homogeneous sublayer (zero flow of oxygen atoms) and the heterogeneous sublayer like in Figure 2, we can thus find an analytical expression of the partial pressure of SiO(g) at the surface in Eq. [1]. In the lower homogeneous sublayer, the zero net flow of oxygen atoms at the surface and the absence of silica particles give the conservation of oxygen atoms:

$$ {\frac{{\partial P_{{{\text{O}}_{{\text{2}}} }}^{{{\text{eff}}}} }}{{\partial z}} = 0} $$

(A11)

In the heterogeneous sublayer we have (using ${K_{{{\text{nucl}}}} }$ the equilibrium constant of the reaction ${{\text{SiO(g)}} + {\text{H}}_{{\text{2}}} {\text{O(g)}} \leftrightarrows {\text{SiO}}_{2}{\text{(s/l)}} + {\text{H}}_{{\text{2}}}{\text{(g)}}}$):

$$ p_\mathrm{{SiO}}=K_\mathrm{{nucl}}^{-1}p_\mathrm{{H_2}}/p_\mathrm{{H_2O}}$$

(A12)

Therefore, at at the limit between the homogeneous sublayer and the heterogeneous sublayer (the superscript “inf” is used for a variable located at this limit):

$$ {p_{{{\text{SiO}}}}^{{{\text{inf}}}} \, = \,K_{{{\text{nucl}}}}^{{ - 1}} \,p_{{{\text{H}}_{{\text{2}}} }}^{{{\text{inf}}}} /p_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{{{\text{inf}}}} } $$

(A13)

With a derivation of the expression of ${\begin{array}{ll} {P_{{{\text{O}}_{{\text{2}}} }}^{{{\text{eff}}}} } \hfill \\ \end{array} }$ in $z=z_{inf}$ at the intersection between the homogeneous sublayer and the heterogeneous sublayer, using Eqs. [A1], [A12], [A10] and [A11]:

$$ {0\, = \,\frac{{\partial p_{{{\text{H}}_{{\text{2}}} {\text{O}}}} }}{{\partial z}}\left( {\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} \, - \,\Psi _{{{\text{SiO}}}} \,K_{{{\text{nucl}}}}^{{ - 1}} \,p_{{{\text{H}}_{{\text{2}}} }} /p_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{2} } \right)\, + \,\frac{{\partial p_{{{\text{H}}_{{\text{2}}} }} }}{{\partial z}}\,\Psi _{{{\text{SiO}}}} \,K_{{{\text{nucl}}}}^{{ - 1}} /p_{{{\text{H}}_{{\text{2}}} {\text{O}}}} } $$

(A14)

Then, with a simplification using the conservation of hydrogen atoms (Eqs. [A1] and [A4]):

$$ \begin{aligned} 0 & = \;\frac{{\partial p_{{{\text{H}}_{{\text{2}}} {\text{O}}}} }}{{\partial z}}\left( {\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} \;p_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{2} \; - \;\frac{{\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} \Psi _{{{\text{SiO}}}} }}{{\Psi _{{{\text{H}}_{{\text{2}}} }} }}K_{{{\text{nucl}}}}^{{ - 1}} \;p_{{{\text{H}}_{{\text{2}}} {\text{O}}}} \; - \;\Psi _{{{\text{SiO}}}} \;K_{{{\text{nucl}}}}^{{ - 1}} \;(p_{{{\text{H}}_{{\text{2}}} }}^{{{\text{eff}},{\text{0}}}} \; - \;\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} p_{{{\text{H}}_{{\text{2}}} {\text{O}}}} )/\Psi _{{{\text{H}}_{{\text{2}}} }} } \right) \\ 0 & = \;\frac{{\partial p_{{{\text{H}}_{{\text{2}}} {\text{O}}}} }}{{\partial z}}\left( {\Psi _{{{\text{H}}_{{\text{2}}} }} \;\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} \;p_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{2} \; - \;\Psi _{{{\text{SiO}}}} \;K_{{{\text{nucl}}}}^{{ - 1}} \;p_{{{\text{H}}_{{\text{2}}} }}^{{{\text{eff}},{\text{0}}}} } \right) \\ \end{aligned} $$

(A15)

which, given the fact that the gradient of H₂O is non-zero everywhere, using Eq. [A13] for ${p_{{{\text{SiO}}}}^{{{\text{inf}}}} }$, gives the expression:

$$ \begin{aligned} p_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{{{\text{inf}}}} & = \left( {\frac{{p_{{{\text{H}}_{{\text{2}}} }}^{{{\text{eff}},{\text{0}}}} \Psi _{{{\text{SiO}}}} }}{{K_{{{\text{nucl}}}} \Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} \Psi _{{{\text{H}}_{{\text{2}}} }} }}} \right)^{{1/2}} \\ p_{{{\text{SiO}}}}^{{{\text{inf}}}} & = \left( {\frac{{p_{{{\text{H}}_{{\text{2}}} }}^{{{\text{eff}},{\text{0}}}} \Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} }}{{K_{{{\text{nucl}}}} \Psi _{{{\text{SiO}}}} \Psi _{{{\text{H}}_{{\text{2}}} }} }}} \right)^{{1/2}} \\ & = \frac{{\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} }}{{\Psi _{{{\text{SiO}}}} }}p_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{{{\text{inf}}}} \\ \end{aligned} $$

(A16)

Then, using the conservation of oxygen atoms in the lower homogeneous sublayer (Eq. [A1] combined with the integration of [A11] between $z=0$ and $z=z_{inf}$) and with the thermodynamic equilibrium, since in the presence of Si(l), $p_\mathrm{{H_2O}}^\mathrm{{surf}} \ll p_\mathrm{{SiO}}^\mathrm{{surf}}$ and everywhere $p_\mathrm{{SiO_2}} \ll p_\mathrm{{SiO}}$:

$$ {\Psi _{{{\text{SiO}}}} p_{{{\text{SiO}}}}^{{{\text{surf}}}} \, = \,\Psi _{{SiO}} \,p_{{{\text{SiO}}}}^{{{\text{inf}}}} \, + \,\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} \,p_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{{{\text{inf}}}} } $$

(A17)

hence:

$$ {p_{{{\text{SiO}}}}^{{{\text{surf}}}} \, = \,2\left( {\frac{{p_{{{\text{H}}_{{\text{2}}} }}^{{{\text{eff}},{\text{0}}}} \,\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} }}{{K_{{{\text{nucl}}}} \,\Psi _{{{\text{SiO}}}} \,\Psi _{{{\text{H}}_{{\text{2}}} }} }}} \right)^{{1/2}} } $$

(A18)

All other data can be reconstructed from known conditions at the surface and above the layer, including the thickness of the lower homogeneous sublayer, which is always non-zero.

Appendix B: Configuration of the boundary layer at the passivation threshold, isothermal case with zero oxygen atoms net flow

First, let’s remark that:

$$ {p_{{{\text{SiO}}}} \, = \,K_{{{\text{nucl}}}}^{{ - 1}} \frac{{p_{{{\text{H}}_{{\text{2}}} }} }}{{p_{{{\text{H}}_{{\text{2}}} {\text{O}}}} }}\, < \,K_{{{\text{nucl}}}}^{{ - 1}} \frac{{p_{{{\text{H}}_{{\text{2}}} }}^{{{\text{eff}},{\text{0}}}} }}{{\Psi _{{{\text{H}}_{{\text{2}}} }} \,p_{{{\text{H}}_{{\text{2}}} {\text{O}}}} }}} $$

(B1)

Now, let’s consider the equation of net zero oxygen atom flux at the surface, deriving Eq. [A1], the difference from the previous case of non-passivation being that this time Eq. [A12] of the thermodynamic equilibrium of the silica aerosols is also valid all the way down to z = 0:

$$ {\begin{aligned} {0 = - \,\frac{{D_{{{\text{O}}_{{\text{2}}} }} }}{{RT}}\frac{{\partial p_{{{\text{H}}_{{\text{2}}} {\text{O}}}} }}{{\partial z}}\left( {\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} - \Psi _{{{\text{SiO}}}} K_{{{\text{nucl}}}}^{{ - 1}} \frac{{p_{{{\text{H}}_{{\text{2}}} }}^{{{\text{eff}},{\text{0}}}} }}{{\Psi _{{{\text{H}}_{{\text{2}}} }} p_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{2} }}} \right)} \hfill \\ {= - \,\frac{{D_{{{\text{O}}_{{\text{2}}} }} }}{{RT}}\frac{{\partial p_{{{\text{H}}_{{\text{2}}} {\text{O}}}} }}{{\partial z}}\left( {\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} - \Psi _{{{\text{SiO}}}} \frac{{p_{{{\text{SiO}}}} }}{{p_{{{\text{H}}_{{\text{2}}} {\text{O}}}} }}\frac{{p_{{{\text{H}}_{{\text{2}}} }}^{{{\text{eff}},{\text{0}}}} }}{{\Psi _{{{\text{H}}_{{\text{2}}} }} p_{{{\text{H}}_{{\text{2}}} }} }}} \right)} \hfill \\ \end{aligned} } $$

(B2)

Since in the presence of Si(l) ${p_{{{\text{SiO}}}} /p_{{{\text{H}}_{{\text{2}}} {\text{O}}}} \gg 1}$ and ${\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} }$,${\Psi _{{{\text{SiO}}}} }$ and ${\Psi _{{{\text{H}}_{{\text{2}}} }} }$ are of the same order, from Eq. [B1], we deduce ($P_\mathrm{{H_2}}^\mathrm{{eff}}$ non-infinitesimal because ${P_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{0} }$ non-infinitesimal):

$$ {\left( {\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} \, - \,\Psi _{{{\text{SiO}}}} \frac{{p_{{{\text{SiO}}}} }}{{p_{{{\text{H}}_{{\text{2}}} {\text{O}}}} }}\frac{{p_{{{\text{H}}_{{\text{2}}} }}^{{{\text{eff}},{\text{0}}}} }}{{\Psi _{{{\text{H}}_{{\text{2}}} }} p_{{{\text{H2}}}} }}} \right)\, \simeq \, - \,\Psi _{{SiO}} \frac{{p_{{{\text{SiO}}}} }}{{p_{{{\text{H}}_{{\text{2}}} {\text{O}}}} }}\frac{{p_{{{\text{H}}_{{\text{2}}} }}^{{{\text{eff}},{\text{0}}}} }}{{\Psi _{{{\text{H}}_{{\text{2}}} }} p_{{{\text{H}}_{{\text{2}}} }} }}\, \ne \,0} $$

(B3)

Hence, ${\frac{{\partial p_{{{\text{H}}_{{\text{2}}} {\text{O}}}} }}{{\partial z}}\,(z = 0) = 0}$ and the flow is zero for all species at the surface. Using the relationship, [A4] we deduce that the concentrations are all uniform, equal to the concentrations at the surface. This is an absurdity because experimentally we have a passivation while ${p_{{{\text{SiO}}}}^{0} = 0}$ at injection. Therefore, we need to drop the hypothesis of the thermodynamic equilibrium of the silica aerosols with the gas phase at the passivation threshold in the isothermal case with zero oxygen atom net flow.

Appendix C: Configuration of the boundary layer at the passivation threshold, non-isothermal case with zero oxygen atom net flow

We suppose we have a case of injection of cold gases ($\frac{\partial T}{\partial z}<0$ ). We suppose that the ratio of diffusivities does not vary with temperature, which is realistic at these high temperatures (Vadon et al.[8]). This time, we rewrite Eqs. [A14] and [A15] at the surface:

$$\begin{aligned} \begin{array}{ll} 0&=\frac{\partial p_\mathrm{{H_2O}}}{\partial z} \left( \Psi _\mathrm{{H_2O}}- \frac{\Psi _\mathrm{{SiO}}K_\mathrm{{nucl}}^{-1}p_\mathrm{{H_2}}^\mathrm{{eff,0}}}{\Psi _\mathrm{{H_2}}p_\mathrm{{H_2O}}^2} \right) +\Psi _\mathrm{{SiO}} \frac{\partial K_\mathrm{{nucl}}^{-1}}{\partial T} \frac{\partial T}{\partial z} \frac{p_\mathrm{{H_2}}}{p_\mathrm{{H_2O}}} \end{array} \end{aligned}$$

(C1)

Using Eq. [B1] and remarking again that in the presence of Si(l) $p_\mathrm{{SiO}}/p_\mathrm{{H_2O}} \gg 1$ and $\Psi _\mathrm{{H_2O}}$,$\Psi _\mathrm{{SiO}}$ and $\Psi _\mathrm{{H_2}}$ are of the same order:

$$\begin{aligned} \frac{\partial p_\mathrm{{H_2O}}}{\partial z} \approx \frac{\partial K_\mathrm{{nucl}}^{-1}}{\partial T} \frac{\partial T}{\partial z} \frac{p_\mathrm{{H_2O}}}{p_\mathrm{{SiO}}} \frac{p_\mathrm{{H2}}\Psi _\mathrm{{H_2}}}{p_\mathrm{{H_2}}^\mathrm{{eff,0}}} \end{aligned}$$

(C2)

Let’s now express the gradient of SiO at the surface, starting from the zero flux of oxygen at the surface.

$$\begin{aligned} 0=\Psi _\mathrm{{SiO}}\frac{\partial p_\mathrm{{SiO}}}{\partial z} + \Psi _\mathrm{{H_2O}}\frac{\partial p_\mathrm{{H_2O}}}{\partial z} \end{aligned}$$

(C3)

and then using Eq. [C2]:

$$\begin{aligned} \frac{\partial p_\mathrm{{SiO}}}{\partial z} = -\frac{\Psi _\mathrm{{H_2O}}}{\Psi _\mathrm{{SiO}}} \frac{\partial K_\mathrm{{nucl}}^{-1}}{\partial T} \frac{\partial T}{\partial z} \frac{p_\mathrm{{H_2O}}}{p_\mathrm{{SiO}}} \frac{p_\mathrm{{H_2}}\Psi _\mathrm{{H_2}}}{p_\mathrm{{H_2}}^\mathrm{{eff,0}}} \end{aligned}$$

(C4)

Since $\frac{\partial K_\mathrm{{nucl}}^{-1}}{\partial T}>0$ and $\frac{\partial T}{\partial z}<0$, this means there must be $\frac{\partial p_\mathrm{{SiO}}}{\partial z}>0$ to be at the passivation threshold and thus an influx of silicon atoms in the form of SiO(g), which is absurd. Therefore, we need to drop the hypothesis of the thermodynamic equilibrium of the silica aerosols with the gas phase at the passivation threshold in the non-isothermal case with zero oxygen atom net flow.

We neglect the thermodiffusion effect in this demonstration, which is all the more understandable since the molecular mass of Ar (0.040 kg/mol) is near the molecular mass of SiO(g).

Appendix D: Configuration of the boundary layer at the passivation threshold, isothermal case with non-zero oxygen atom net flow

If we have a net density of flow of oxygen atoms J from the surface, we rewrite Eq. [A15] for the flow of oxygen atoms at the surface:

$$\begin{aligned} \begin{array}{ll} J_O &{}= -\frac{D_\mathrm{{O_2}}}{RT} \frac{\partial p_\mathrm{{H_2O}}}{\partial z} \left( \Psi _\mathrm{{H_2O}}-\Psi _\mathrm{{SiO}}K_\mathrm{{nucl}}^{-1} \frac{p_\mathrm{{H_2}}^\mathrm{{eff,0}}}{\Psi _\mathrm{{H_2}}p_\mathrm{{H_2O}}^2} \right) \\ &{}=-\frac{D_\mathrm{{O_2}}}{RT} \frac{\partial p_\mathrm{{H_2O}}}{\partial z} \left( \Psi _\mathrm{{H_2O}}-\Psi _\mathrm{{SiO}} \frac{p_\mathrm{{SiO}}}{p_\mathrm{{H_2O}}} \frac{p_\mathrm{{H_2}}^\mathrm{{eff,0}}}{\Psi _\mathrm{{H2}}p_\mathrm{{H_2}}} \right) \end{array} \end{aligned}$$

(D1)

Reasoning similarly as previously, neglecting the concentration of H₂O(g) at the surface to take into account the presence of Si(l):

$$\begin{aligned} \begin{array}{ll} J_O&\approx \frac{D_\mathrm{{O_2}}}{RT} \frac{\partial p_\mathrm{{H_2O}}}{\partial z} \left( \Psi _\mathrm{{SiO}} \frac{p_\mathrm{{SiO}}}{p_\mathrm{{H_2O}}} \frac{p_\mathrm{{H_2}}^\mathrm{{eff,0}}}{\Psi _\mathrm{{H_2}}p_\mathrm{{H_2}}} \right) =-\frac{D_\mathrm{{O_2}}}{RT}\Psi _\mathrm{{SiO}} \frac{\partial p_\mathrm{{SiO}}}{\partial z} =J_\mathrm{{Si}} \end{array} \end{aligned}$$

(D2)

Thus, at the passivation threshold, the oxygen must be supplied in the form of SiO(g) at the surface in the absorption/adsorption zones. This is absurd. Therefore, we need to drop the hypothesis of the thermodynamic equilibrium of the silica aerosols with the gas phase at the passivation threshold in the non-isothermal case with a positive oxygen atoms net flow towards the liquid.