Liszt’s Étude S.136 no.1: audio data analysis of two different piano recordings

Abstract

In this paper, we review the main signal processing tools of Music Information Retrieval (MIR) from audio data, and we apply them to two recordings (by Leslie Howard and Thomas Rajna) of Franz Liszt’s Étude S.136 no.1, with the aim of uncovering the macro-formal structure and comparing the interpretative styles of the two performers. In particular, after a thorough spectrogram analysis, we perform a segmentation based on the degree of novelty, in the sense of spectral dissimilarity, calculated frame-by-frame via the cosine distance. We then compare the metrical, temporal and timbrical features of the two executions by MIR tools. Via this method, we are able to identify in a data-driven way the different moments of the piece according to their melodic and harmonic content, and to find out that Rajna’s execution is faster and less various, in terms of intensity and timbre, than Howard’s one. This enquiry represents a case study able to show the potentialities of MIR from audio data in supporting traditional music score analyses and in providing objective information for statistically founded musical execution analyses.

1 Introduction

The digitization process in which we are immersed is affecting many fields of human activity, from business to personal relationships. This new digital age has led to the introduction of radically new technologies for communicating and storing information, making available vast and ever-expanding sources of data in digital format. Musicology, too, has recently been invested in this revolution, thanks to the great expansion of specific computational tools and data sources. In fact, the modern ease of data transmission has given rise to the possibility of performing, by means of ad hoc computational routines, a statistical analysis of a piece of music based on a symbolic digital representation, or on one or more recorded executions of it. This process gradually led to the emergence of a new discipline, called computational musicology Meredith (2016).

Although supported for centuries by paper sources, musicology has always been the subject of very fruitful application of mathematical concepts, such as algebraic topology, set theory and number theory Fauvel et al. (2006), long before the advent of modern computers. This occurred because a piece of music can be represented as a set of sequences, understood as ordered collections, of musical parameters over a number of time points. Considering the symbolic digital representation of a music sheet, in fact, all the elements of music (Martineau 2008), like harmony, melody, rhythm etc., could be simply serialized and analyzed by the tools of (discrete) time series analysis (Priestley 1981). This type of investigation remains strongly linked to traditional musical score analysis, although today it can be performed with digital tools.

On the other hand, since any recorded music object is essentially a discrete collection of signals sampled over time, their analysis requires the discovery of music information from the recovered signals in absence of a direct mapping to the original music score. The analysis of audio content Lerch (2012) requires tools from signal processing (Little 2019) to perform Music Information Retrieval (MIR), which may complement both score analysis and direct listening.

Throughout history, music data types include: sheet music data, i.e., graphical representations of music via symbols; symbolic data, referring to musical notation in a digital format, like MIDI (Musical Instrument Digital Interface) or MusicXML (eXtensible Markup Language) format; audio data, encoding the acoustic waves produced by a physical execution, typically in MP3 (MPEG-1 Audio Layer III) or WAV (WAVeform audiofile) format. Symbolic music data contain the relevant information for music-theoretical analysis, as opposed to audio data, containing the musical recordings.

While most of research on classical music data is focused on analyzing a huge number of audio traces pertaining to different epochs Nakamura and Kaneko (2019), composers Georges and Nguyen (2019), or pieces Weiss et al. (2019), in this paper we focus on how to employ standard MIR tools to perform the analysis of a single piece from audio data, and to compare objectively two different recordings of it. In fact, MIR may uncover from audio recordings hidden similarities and unexpected patterns, which may be missed by a music score analyst. For this reason, our aim is to present a case study able to show how the data-driven extraction of musical features can complement traditional score analyses, or catch the difference between two different executions of a simple piece. Our article’s style is intentionally divulgative, with the declared scope to interest unfamiliar readers to this topic.

For this purpose, we have chosen to exploit Franz Liszt’s Étude S.136 no.1 because of its clear recognizability, as the first study (in C major) of a collection of piano studies. We have chosen the first version of it, instead of the more popular definitive version, Transcendental Étude S.139 no.1, because S.139 no.1 is much more virtuoso in nature, and this could obscure the underlying harmonic and melodic patterns, for instance. We consider two recordings of Franz Liszt’s Étude S.136 no.1, one by Leslie Howard (1994), and the other by Thomas Rajna (1979), because they are two of the most renowned experts of Liszt’s piano performance, with a contrastive execution style.

The paper proceeds as follows. In Sect. 2, we present the different tasks of MIR with respect to symbolic and audio music data analysis. In Sect. 3, we review the MIR statistical techniques used to estimate the spectrogram, to perform a segmentation based on spectral features, to retrieve harmonic patterns by estimating the chromagram, to recover temporal and metrical structures, and to analyze timbrical features from audio data. Our review moves from the MIR toolbox in Matlab (Lartillot et al. 2008), which is a complete collection of tools in this respect. In particular, we describe in Sects. 3.1, 3.2, and 3.3 the spectral analysis tools needed to recover frequency and intensity patterns over time by a WAV/MP3 trace, we explain how to automatically segment it in Sect. 3.4 according to its spectral content over time, we present in Sect. 3.5 the harmonic-melodic analysis over time based on the estimated chromagram, and we show how to derive temporal, metrical and timbrical parameters in Sect. 3.6. In Sect. 4, we employ the described tools to the two recordings of Franz Liszt’s Étude S.136 no.1, with the aim to perform a systematic macro-formal data-driven analysis, and to compare Howard’s recording with the same Étude recording by Thomas Rajna, to identify the different interpretative styles. Finally, Sect. 5 provides some concluding remarks.

2 MIR between symbolic and audio data

In Li et al. (2014), it is argued that MIR systems were created to provide music recommendations tailored to a person’s tastes and needs, and therefore should be based on four main musical characteristics: genre, emotion, style, and similarity. This has opened up significant computational challenges: how to translate these qualitative characteristics into numerical terms? Furthermore, how to infer from symbolic data (such as MIDI files) or audio data (such as actual recordings encoded in WAV/MP3 format) such characteristics?

In principle, these features can be inferred from both symbolic and audio data, and the statistical methods used may overlap to some extent. While symbolic data preserve a direct correspondence with the original musical score, audio data bring relevant information not only about the musical text, but also about the musical performance. This requires first of all a thorough estimation of spectral characteristics, which represent the physical qualities of the recorded sound, instead of its abstract symbolic representation, and has paved the way to analyze musical performance via audio data analysis, beyond the musical score Lerch et al. (2021). In fact, the specific recording is one empirical realization of a musical text, that may also substantially differ from other recordings and from the theoretical realization represented by the music score. This twofold nature of MIR analyses may also depend on the type of performed task: for instance, extracting tempo, intensity, and timbre mainly refers to performance analysis, while retrieving key and chords mainly refers to score analysis.

MIR tasks can be grossly divided in three different categories:

• 1. Retrieval of spectral features over time frames: time-frequency spectrum, based on Short-Time Fourier Transform (STFT), amplitude spectrum, envelope spectrum, spectral statistics.

• 2. Retrieval of functional musical features, like beats, tempo, rhythm, key, timbre and chromagram (i.e. the harmonic characterization in terms of the 12 pitch classes at each retrieved beat).

• 3. More difficult tasks like recommender system, genre classification, musical source separation, audio tagging, segmentation, and automatic music transcription.

These tasks are mostly already included in the MIR packages of modern statistical/mathematical software, which typically work on MP3 or WAV data, indifferently. In particular, the MIR toolbox performs most of these tasks in Matlab, where the built-in Audio toolbox and Signal Processing toolbox already performed many of them (with less graphical features). Similarly, in Python the package LIBROSA is a complete suite for music analysis in digital format. An overview of MIR toolboxes can be found in Moffat et al. (2015), where one can realize that, beyond Matlab and Phyton, relevant feature extraction tools are written in C++ and Javascript, among others.

The difficult tasks mentioned above are usually referred to as high-level descriptors Ras and Wieczorkowska (2010). Retrieving high-level descriptors requires a massive use of statistical methodologies, like classification, clustering, dimension reduction, text mining, neural networks. However, as widely explained in Müller (2015), high-level descriptors are subject to the prior estimation of the functional musical features described above, usually labelled as middle-level descriptors, that in turn rely on the correct estimation of spectral features (the so called low-level descriptors).

Specific music signal processing tools have been developed for these purposes Müller et al. (2011). For example, recovering hidden harmonic patterns requires first to provide a characterization of the piece in terms of the 12 pitch classes, and then to recover simultaneously onsets throughout the track. This means that, in advance, one needs to estimate from the WAV/MP3 trace the onsets, i.e. the time points at which musical events are occurring. Similarly, the detection of segment boundaries (which can be seen as event location) requires first to estimate relevant music parameters, like intensity, pitch or duration, across the recovered onsets, and then to label recovered segments, whose degree of mutual similarity is estimated.

Exhaustive reviews on the retrieval of high-level descriptors include Kim et al. (2010); Yang et al. (2018) for emotion recognition, Humphrey and Bello (2015); Pauwels et al. (2019) for automatic chord estimation, Benetos et al. (2018) for automatic music transcription, Cano et al. (2018) for musical source separation, Tzanetakis and Cook (2002) for musical genre classification, Theodorou et al. (2014) for automatic audio segmentation. Those tasks rely on crucial middle-level descriptor tasks such as beat tracking, tempo estimation, and chroma retrieval. Foundational algorithms for their solution can be found in Ellis (2007) and Ellis and Graham (2007), respectively. In Sect. 3, we report the up-to-date techniques to retrieve the middle-level and low-level descriptors relevant to the real signal analysis of Sect. 4, following the Matlab MIR toolbox explained in Lartillot et al. (2008).

3 MIR and spectral analysis

The aim of this work is to practically show how to exploit the insights of Music Information Retrieval (MIR) from audio data. Our guide in this journey will be the Matlab MIR toolbox (Lartillot et al. 2008), which provides a detailed explanation of many signal processing tools able to retrieve music information from audio data. In particular, the MIR toolbox in Matlab can estimate and plot spectral features, retrieve functional music parameters, and propose a spectrum-based segmentation of any input WAV/MP3 trace. In this section, following Priestley (1981), we briefly review the foundations of such signal processing tools, in order to prepare the ground for our subsequent case study.

3.1 Spectrum definition

With the aim to get a mathematically founded understanding of a music piece, we consider the input WAV/MP3 trace as a sequence of signals $x_t$, $t=1,\ldots ,T$, discrete-time and real-valued, where T is the total number of samples. The observed signal $x_t$ can be seen as a single empirical realization of the underlying stochastic process $X_t$, usually re-centered in order to be zero-mean (i.e., $\textrm{E}(X_t)=0$) across the samples. Audio traces contain a high number of samples (typically, 44,100 per second), each one bringing a value between $-1$ and 1.

In order to introduce the notion of spectrum, it is worth recalling the definition of elementary wave in the real field, which is defined as any function f(t), $t \in \mathbb {R}$, such that:

$$\begin{aligned} f(t)=r\cos {(\omega t-\phi )}=r \cos {\omega (t-\xi )}, \end{aligned}$$

(1)

where $\omega \in [-\pi ,\pi ]$ is the angular frequency (or fundamental frequency) in radians, $f=\omega /2\pi$, with $f\in [-\frac{1}{2},\frac{1}{2}]$, is the normalized frequency, that represents the number of cycles per time unit, $p=1/f$ is the period, i.e. the time necessary to complete a whole cycle, r is the wave amplitude, $\phi$ is the phase in radians, $\xi =\phi /\omega$ is the phase shift in time units. The frequencies $2\omega ,3\omega , \ldots$ are the partial harmonics. We refer to Fig. 1 to display all the listed features.

The sequence of values $x_t$, $t=1,\ldots ,T$, is the time domain representation of the recorded signal. From those values, it is convenient to derive the Fourier transform $d^{x}(\omega )$ of $x_t$, defined at each frequency $\omega \in [-\pi ,\pi ]$ as $d^{x}(\omega )=\frac{1}{\sqrt{2\pi }}\sum _{t=1}^T x_t \exp \{-2\pi i \omega \}$. The Fourier transform $d^{x}(\omega )$ allows to provide the frequency domain representation of the recorded signal. The corresponding stochastic quantity is $d^{X}(\omega )=\frac{1}{\sqrt{2\pi }}\sum _{t=1}^T X_t \exp \{-2\pi i \omega \}$.

Fig. 1

Elementary wave with fundamental frequency $\omega =\frac{2\pi }{100}$ radians and $f=\frac{1}{100}$ cycles, period $p=100$ time units, amplitude $r=10$, phase $\phi =\frac{\pi }{4}$ radians and $\xi =12.5$ time units

Even if the stochastic process $X_t$ is not periodic, it is possible to measure the contribution of each frequency $\omega$ to the total power of $X_t$ (i.e., its variance $\textrm{E}(X_t^2)$), as $h(\omega )=\lim _{T\rightarrow \infty } \mathbb {E}\left( \frac{\vert d^{X}(\omega ) \vert ^2}{2T}\right)$, where $\vert x \vert$ denotes the modulus of the complex number $x=a+bi$, defined as $\vert x \vert =\sqrt{a^2+b^2}$. The limit $h(\omega )$ is defined as the power spectral density (or spectrum) of $X_t$ at frequency $\omega$, and a sufficient condition for its existence is the absolute integrability of $X_t$, i.e. $\int _{D_X} \vert X_t \vert \textrm{d}t < \infty$, with $D_X=[-1,1]$. The spectrum of $X_t$ represents the contribution of frequency $\omega$ to the total power of the process $X_t$. Parseval’s theorem (see Percival and Walden (1993)) ensures that the integral of all spectra across the frequency range equals the total power of the process: $\int _{-\pi }^{\pi } h(\omega ) \textrm{d}\omega =\textrm{E}(X_t^2)$. More, the spectrum of real-valued discrete-time stochastic processes is periodic over the frequency range $[0,\pi ]$ (also see Priestley (1981)).

Once recalled that a frequency of 1 Hertz ($\textrm{Hz}$) is equal to $2\pi$ radians per second (rad/s), such that 1 rad/s equals 0.1591549 Hz, we can note that the spectrum may actually be estimated at frequencies expressed in Hertz. It is possible to establish an approximate correspondence between the twelve notes of the chromatic scale at each register (as identified by the 12 equal temperament, 12TET) and their Hertz values, that may also be expressed as wave time periods. This correspondence may be imprecise for several reasons: there might be different tuning systems (other than 12TET) or intonations (other than A4=440 $\textrm{Hz}$), there can be intonation inaccuracies (which are still understood as a certain pitch by the listener), and there are simply many frequencies that do not match a particular pitch of any discrete system (including 12TET). For this reason, as explained in Sect. 3.5, the Matlab MIR toolbox allocates recorded pitches to specific notes of the chromatic scale with a certain tolerance around the expected Hertz value.

3.2 Spectrum estimation

Even if the spectrum $h(\omega )$ is defined on a continuous frequency range, because $X_t$ is not periodic, it is actually estimated on a discrete set of frequencies: the Fourier frequencies, defined as $\omega _h=2\pi f_h$, $f_h=h/T$, $h=0,1,\ldots ,[T/2]$ ([.] denotes the integer part). The discrete Fourier transform $d(\omega )^{x}$ is actually computed via the Fast Fourier Transform (FFT), that presents many possible variants (Takahashi 2019). Denoting by ${\widehat{h}}(\omega _h)$ the estimated spectrum at frequencies $\omega _h$, $h=0,1,\ldots ,[T/2]$, we note that it naturally holds ${\widehat{h}}(-\omega _h)={\widehat{h}}(\omega _h)$, as for real-valued discrete-time stochastic processes the spectrum $h(\omega )$ is periodic over $[0,\pi ]$.

The most immediate estimator of the spectrum at each frequency $\omega _h=2\pi f_h$, with $f_h \in [0,\frac{1}{2}]$, would be the natural periodogram $I(\omega _h)$, defined as $I(\omega _h)=d^{x}(\omega _h)d^{x}(\omega _h)^{*}$, where $d^{x}(\omega _h)^{*}$ denotes the complex conjugate of $d^{x}(\omega _h)$. However, $I(\omega _h)$ is not a consistent estimator of $h(\omega _h)$, which means that the estimation error of $I(\omega _h)$ does not disappear as $T \rightarrow \infty$ (see Priestley (1981), Chap. 6). In order to get a consistent estimate of $h(\omega _h)$, a possible way is to calculate the smoothed periodogram, which can be defined as the spectral density estimator ${\widehat{h}}(\omega _h)=\sum _{k=-[T/2]}^{[T/2]}I(\omega _h)W(\omega _h-\omega _k)$, where the function $W(\theta )$, with $\theta =\omega _h-\omega _k$ and $\theta \in [-\pi ,\pi ]$, is the spectral window (see Brillinger (2001), Chap. 5). $W(\theta )$ is a function of $\theta$, such that $W(\theta )=W(-\theta )$ and $\arg \max _{\theta } W(\theta )=0$. There are many different kinds of spectral windows, as shown in Priestley (1981), paragraph 6.2.3. The spectral window choice impacts on the bias and the variance of ${\widehat{h}}(\omega _h)$.

The estimated spectra, or power spectral densities, are nonnegative quantities by definition. If the signal is discrete-time and real-valued, the spectrum is real as well, and the complex modulus $\vert {\widehat{h}}(\omega _h)\vert$, that is the amplitude spectrum, actually coincides with ${\widehat{h}}(\omega _h)$. The estimated root mean square energy RMS, displaying the average amount of energy across frequencies, is defined as $RMS=\sqrt{\frac{1}{[T/2]}\sum _{h=0}^{[T/2]}\vert {\widehat{h}}(\omega _h)\vert ^2}$.

The definition of spectral density $h(\omega )$ implicitly presupposes that the recurrence structure behind the stochastic process is constant over time (see Stoica and Moses (2005)). The intensity and the direction of time recurrences can be measured by the auto-covariance function $C(s)=\mathbb {E}\left( \frac{1}{T}\sum _{t=s+1}^T X_t X_{t-s}\right)$ and the autocorrelation function $R(s)=\frac{C(s)}{C(0)}$ or order s, with $s=0,1,\ldots$ It naturally holds that $R(s)\in [-1,1]$ for any s, with $R(0)=1$. R(s) expresses the expected correlation intensity between the signal $X_t$ and the signal $X_{t-s}$ (s steps behind). C(s) and R(s) are symmetric functions, i.e., $C(-s)=C(s)$ and $R(-s)=R(s)$. If the recurrence structure of the stochastic process $X_t$ is constant over time, it means that C(s) and R(s) are constant for $t=1,\ldots ,T$, and that the zero-mean process $X_t$ is covariance stationary. C(s) and R(s), $s=0,1,\ldots$, can be estimated as ${\widehat{C}}(s)=\frac{1}{T-\vert s \vert }\sum _{t=s}^T X_t X_{t-s}$ and ${\widehat{R}}(s)=\frac{{\widehat{C}}(s)}{{\widehat{C}}(0)}$, respectively.

3.3 Spectrogram

A music piece is typically characterized by a continuous change in the recurrence structure, such that the assumption of covariance stationarity is pretty unrealistic. For this reason, the observed signal can only assumed to be locally stationary. In order to provide spectral estimates, the signal is thus divided in many partially overlapping frames. On each of these small intervals, the stationarity assumption is assumed to hold, and the spectrum is consequently estimated. The discrete Fourier transform is estimated over each frame by the Short-Time Fast Fourier Transform (STFT). The sequence of estimated spectra over the partially overlapping frames is the spectrogram, that provides a time-frequency representation of the observed signal (Sejdić et al. 2009).

The spectral window choice varies across available functions in software packages (see Gharaibeh (2021) for a recent comparison of spectral windows). The function mirspectrum in the MIR toolbox uses the Hanning window by default. Spectral statistics like spectral centroid, entropy, and flux (i.e., spectral change) over time frames may also be estimated via the functions mircentroid, mirentropy and mirflux, respectively. The function mirenvelope extracts instead the spectral envelope, which is the spectral strength over time frames, as follows (see MIRtoolbox 1.8.1 User’s Manual, pp. 30–36 for more details):

• (1) Full-wave rectification of $X_t$, that corresponds to the reflection of the negative wave lobes of $X_t$ to the positive field (absolute value function).

• (2) Application of Infinite Impulse Response (IIR) filter to the output of (1).

• (3) Downsampling, by dividing the sampling rate by 16.

Any spectral plot may appear different according to the frequency scale used, visible in the x-axis. Frequencies may be expressed in Hertz, but also in alternative ways, like in Mel or Bark scales, that provide a sequence of frequency bands, according to human ear perception. More, frequencies can be expressed in Cents too, assuming that one octave equals 1200 Cents. Concerning the y-axis, spectral values may be reported in the original or in the decibel (dB) scale, or normalized by the maximum value across frequencies.

3.4 Segmentation

Music data mining is described in Hand (2002) as follows:

In music data mining one seeks to “detect”, “discover”, “extract” or “induce” melodic or harmonic (sequential) patterns in given sets of composed or improvised works.

In more detail, a sequential pattern is therein defined as a set of music segments sharing a significant degree of resemblance, meaning similarity over a certain threshold, according to some measure. For the purpose of MIR-based segmentation, which is a boundary identification procedure according to some macro-formal criterion, it is therefore crucial to properly define the appropriate notion of similarity. Such choice may help traditional, score-based segmentations, due to the capability of the machine to identify hidden similarities over time.

Let us denote the spectrogram as ${\widehat{h}}_{\tau }(\omega _h)$, $h=1,\ldots ,[T/2]$, $\tau =1,\ldots ,\mathcal {T}$. The spectral vector at frame $\tau$ is denoted by $\widehat{\textbf{h}}_{\tau }$. The most common similarity measure between two estimations of the spectrum at different frames is the cosine distance, that is defined as $s^{\cos }(\widehat{\textbf{h}}_{\tau '},\widehat{\textbf{h}}_{\tau ''})=1-\frac{\vert \langle \widehat{\textbf{h}}_{\tau '},\widehat{\textbf{h}}_{\tau ''}\rangle \vert }{\Vert \widehat{\textbf{h}}_{\tau '}\Vert \Vert \widehat{\textbf{h}}_{\tau ''}\Vert }$, where $\tau ',\tau ''=1,\ldots ,\mathcal {T}$, and $\frac{\vert \langle \widehat{\textbf{h}}_{\tau '},\widehat{\textbf{h}}_{\tau ''}\rangle \vert }{\Vert \widehat{\textbf{h}}_{\tau '}\Vert \Vert \widehat{\textbf{h}}_{\tau ''}\Vert }$ is the cosine of the angle between the two spectral vectors at $\tau '$ and $\tau ''$. The similarity matrix of the framed spectrum, obtained via the function mirsimatrix, collects the pairwise similarity measures for each pair of frames. The function mirnovelty estimates instead the degree of novelty of the spectrum at each frame compared to the previous one, via the multi-granular approach (see Lartillot et al. (2013)), that performs the task by comparing the spectrum of each new frame with the spectra estimated over a homogenous segment of previous frames, thus detecting the piece macro-formal markers and their degree of importance. In this case, the similarity measure used is typically the function $s^{\exp }(\widehat{\textbf{h}}_{\tau '},\widehat{\textbf{h}}_{\tau ''})=\exp \left\{ -\frac{\vert \langle \widehat{\textbf{h}}_{\tau '},\widehat{\textbf{h}}_{\tau ''}\rangle \vert }{\Vert \widehat{\textbf{h}}_{\tau '}\Vert \Vert \widehat{\textbf{h}}_{\tau ''}\Vert }\right\}$, further normalized between 0 and 1. This is the method called by default by the function mirsegment, that automatically segments any WAV/MP3 trace, typically pre-framed in 50ms long half-overlapping portions.

It is worth defining in a formal way spectral flux and novelty, explaining their conceptual differences. The spectral flux at time frame $\tau$ is defined as $\frac{1}{[T/2]}\Vert \widehat{\textbf{h}}_{\tau }-\widehat{\textbf{h}}_{\tau -1} \Vert _2$ where $\Vert \cdot \Vert _2$ is the Euclidean norm. It is a descriptive measure which calculates spectral variations across consecutive time frames. The novelty is instead a quantity estimated in a more complex way. According to Lartillot et al. (2013), first, the exponential similarity $s^{\exp }(\widehat{\textbf{h}}_{\tau '},\widehat{\textbf{h}}_{\tau '-1})$ is calculated between consecutive frames at each $\tau$, until $s^{\exp }(\widehat{\textbf{h}}_{\tau '},\widehat{\textbf{h}}_{\tau '-1})$ decreases and is lower than ${\bar{s}}^{\exp }(\widehat{\textbf{h}}_{\tau '},\widehat{\textbf{h}}_{\tau '-1})-2\sigma (s^{\exp }(\widehat{\textbf{h}}_{\tau '},\widehat{\textbf{h}}_{\tau '-1}))$, where ${\bar{s}}^{\exp }(\widehat{\textbf{h}}_{\tau '},\widehat{\textbf{h}}_{\tau '-1})$ and $\sigma (s^{\exp }(\widehat{\textbf{h}}_{\tau '},\widehat{\textbf{h}}_{\tau '-1}))$ are the mean and the standard deviation of the exponential similarity measure over the current segment. When this condition is no longer satisfied, the current segment ends and a new one starts in $\tau$. At each time frame $\tau$, the recorded similarity measure is then ${s}^{\exp }(\widehat{\textbf{h}}_{\tau },\widehat{\textbf{h}}_{\tau ^{-}})$, where $\tau ^{-}$ is the previous segment boundary detected as just described. In the end, this similarity measure will be normalized to stand between 0 and 1, and will be adaptive, as it measures the resemblance with reference to homogenous segments in the piece structure. Note that, in principle, both flux and novelty can be estimated with objects other than spectrograms, like autocorrelation functions or chromagrams (see Sect. 3.5).

3.5 Chromagram

Once the WAV/MP3 trace has been segmented determining segment boundaries by novelty peak detection (see Sect. 3.4), we may perform a melodic-harmonic analysis of each segment by the function mirchromagram, which produces the chromagram, also known as Harmonic Pitch Class Profile, of each segment Ellis and Graham (2007). The chromagram is the redistribution, normalized to the maximum value, of the spectrum over the twelve notes of the chromatic scale across all the registers. In this way, we may both acquire melodic information (i.e., the most relevant notes for each segment) and harmonic information (i.e., the most relevant chords behind each segment). This results in a relative frequency histogram over the twelve pitch classes, where each pitch class interval is centered on a specific note frequency (in Hertz) of the twelve, and the pitch class intervals are equally wide and non-overlapping. The chromagram of a piece allows to relate the segmentation based on spectral dissimilarity to the harmonic content, thus providing a solid ground for the macro-formal analysis of any recorded music signal, even in absence of its music score.

3.6 Rhythm, tempo and timbre

When dealing with pulsation, rhythmical and temporal structures in music, the relevant concept coming into play is recurrence. In fact, it is reasonable to estimate the occurrences of the main musical events, the pulsation pace, the tempo and the metrical structure by retrieving the recurrences in the estimated spectra or spectral envelope. For any given WAV/MP3 music trace, the identification of beats (also called onsets), i.e. the time points at which musical events are occurring, can be performed by the function mirevents, that determines the most relevant peaks in the overall intensity to disentangle two consecutive events across time frames, by deriving the peaks in the estimated spectral envelope over time frames, as returned by mirenvelope.

The function mirtempo returns an estimate of the piece tempo, by calculating the autocorrelation function of the output of mirevents, and identifying the autocorrelation peak, representing the most relevant time recurrence. The options Change and Metre of mirtempo can display how tempo and rhythmical pulse evolve over time frames. The former option is based on applying the just described technique to each time frame individually, while the latter explores all the possible metrical pulses coherent with the estimated tempo and then determines the most relevant ones (see Lartillot and Grandjean (2019) for more details). Their results are plotted in beats per minute (BPM) over time.

Finally, the function mirroughness estimates the degree of dissonance between successive spectral peaks, i.e., the contrast between consecutive estimated spectra (see MIRtoolbox 1.8.1 User’s Manual, pp. 140–142 for more details). These tools are particularly important when comparing different executions of the same piece.

4 MIR-based analysis of Étude S.136 no.1

In this section, we apply the MIR statistical tools explained in Sect. 3 to the WAV recording of Franz Liszt’s Étude S.136 no.1 by Leslie Howard, drawn by his piano album “The Young Liszt” (Hyperion, 1994), and the MP3 recording of Thomas Rajna, drawn by his album “Douze Etudes op.1 and Etudes d’execution transcendante” (CRD Records, 1979). Our aim is to uncover the piece macro-formal structure from the recorded traces and to perform a comparative analysis by using the MIR tools uncovering intensity, metrical and timbrical structures, which are particularly important when comparing different performances of the same piece, as they represent the different interpretative styles of the performers. We adopt as reference musical text the work “Franz Liszt. Neue Ausgabe sämtlicher Werke”, which is the second complete authentic edition of the music of Franz Liszt, published jointly by Edition Musica Budapest and the Bärenreiter-Verlag Kassel from 1970 to 1985.

4.1 Spectral analysis

We first load the WAV trace of Howard’s and the MP3 trace of Rajna’s recording by the function miraudio, that automatically sums the two audio channels of each trace in a single mono channel. In Fig. 2, we can note that Howard’s version (left panel) is 74.2 s long, with silence frames at the beginning and at the end. The wave peaks exactly correspond to the frames with extreme intensity: for instance, the large oscillations of the interval [55–60  s] correspond to the cadence in forte of bars 29–30 with chords at both hands, while the smallest intensity region around 25  s corresponds instead to bar 14. Both fragments are reported in Fig. 3. On the contrary, Rajna’s version (right panel), 59 s long, does not present so relevant differences between the different moments of the piece, even if the same waveform shape is clearly recognizable.

In Fig. 4, we report the spectrogram of the recording by Leslie Howard, obtained via the function mirspectrum. That plot contains in white the spectral bands over time frames, like a radiography of the music trace. Looking at the spectrogram, we can immediately perceive the frequency evolution over time, thus identifying repetitions, ascending/descending patterns and sudden shifts. We have reported specific excerpts of the Étude during the exposition, but we always refer for an overview to the "Appendix", where the whole macro-formal and harmonic analysis is reported, and to the music score with comments attached as a Supplement.

Fig. 2

Étude S.136 no.1: miraudio output, featuring the waveforms of Howard’s (left panel) and Rajna’s (right panel) execution

Fig. 3

Étude S.136 no.1: bars 14–15 and bars 29–30

A close look at Fig. 4, containing the spectrogram of the trace of Howard’s execution, allows to recognize several patterns. First, the spectral bands in the regions [4–7 s] and [8–11 s] are very similar. This occurs because those intervals represent bars 1–2 and 3–4, that contain two repetitions of the same element, reported in Fig. 5. That motif, repeated twice, is the key element of the first musical phrase (bars 1–4). More, we can see that across the regions [38–41 s] and [42–45 s] the spectral bands look very similar to the regions [4–7 s] and [8–11 s]. This cannot surprise, because they represent bars 20–23, where the first phrase is repeated. Also, regions [12–15 s] and [16–19 s] roughly present the same spectral bands, as they contain the same element, reported in Fig. 5 and repeated in bars 5–6 and 7–8, that constitute together the second phrase. Another repetition lies in the Coda, bars 31–35, where an arpeggio structure is recurring five times, as it can be inferred at the right end of the plotted spectrogram, across the region [60–70 s].

Across the region [19–24 s], we observe a sharp and continuous increase of the frequency range, resembling the continuous ascent of bars 9–10, that contain two-octave scales in C major on both hands, one third apart (Fig. 6). Another continuous ascent is clearly visible across the region [44–52 s], representing bars 24–27, reported in Fig. 7. The region [25–38 s] is instead more heterogenous, even if two descending patterns, roughly located across intervals [25–30 s] and [31–36 s], are clearly visible. The first one corresponds to bars 11–13, reported in Fig. 8, the second one corresponds to bars 15(Q4)-17, reported in Fig. 9.

Fig. 4

Étude S.136 no.1 (Howard’s version): mirspectrum output with Frame option and frequency range $[27.5 \textrm{Hz}, 4000 \textrm{Hz}]$, frame length 50ms and overlapping proportion 0.5, and mirspectrum output with Bark option, featuring spectral values in the Bark scale

Fig. 5

Étude S.136 no.1: bars 1–2 and bars 5–6

Fig. 6

Étude S.136 no.1: bars 9–10

Fig. 7

Étude S.136 no.1: bars 24–27

Fig. 8

Étude S.136 no.1: bars 11–13

Fig. 9

Étude S.136 no.1: bars 16–17

The plotted spectral shape also allows to spot the sudden upward shift of bar 28, clearly visible in the region [52–55 s] (see Fig. 10). Across the interval [55–60 s], corresponding to bars 29–30, we then notice a very wide frequency range, resembling the cadence in forte with chords on both hands reported in Fig. 3.

Fig. 10

Étude S.136 no.1: bars 27–28

As previously explained, the spectrogram is mostly similar when comparing different recordings of the same piece, as it essentially represents the frequencies over time, that strictly depend on the given music score. On the contrary, the spectral envelope, featuring intensity over time, may present much more variety.

Figure 11 shows the spectral envelope of Howard’s (left panel) and Rajna’s (right panel) recording. In Howard’s version, the envelope peak clearly stands in the region [55–60 s], corresponding to the cadence of bars 29–30. The envelope profile of regions [4–7 s] and [8–11 s] is very similar, as they both contain the motif reported in Fig. 5 (bars 1–2). For the same reason, regions [38–41 s] and [42–45 s] present a similar envelope profile, even if the estimated envelope is higher, thus showing that the second repetition is played louder by the pianist.

Then, the interval [18–27 s] presents a continuous descent. It roughly corresponds to bars 9–14, which are played increasingly piano, starting from the forte of bar 10 (see Fig. 6). That descent is followed by a sudden rebound around 30 s, corresponding to bar 15 (see Fig. 3). A stable intensity region ([30–38 s]), corresponding to bars 16–19, is then followed by a strong upturn, corresponding to bar 20, where the first phrase is repeated. The sudden power drop around 52 s corresponds to bar 28, due to the high register shift, repeating the right hand pattern of bar 27 one octave above (see Fig. 10). As already highlighted, the cadence in C major ([55–60 s]) presents the most outstanding envelope values. Finally, the plot interestingly shows that in the Coda ([60–70 s]) the first four arpeggios are played with increasing intensity, while the last one shows a power decrease, just before the last C2 closing the piece.

In Rajna’s version, the intensity differences appear much less relevant than in Howard’s one. However, we can note that, in the final part, the pattern concerning the consecutive arpeggios is still the same. In addition, the peaks at 32 s and 35 s represent the starts of the two repetitions of the motif in Fig. 5, at bars 20 and 22. The peak at 40 s represents the end of the ascent of Fig. 7 (bar 27). The main cadence, around 45 s, is instead not as prominent as before. The local peak around 15 s represents the end of the ascent of Fig. 3, at bar 11(Q1). The plot also shows that the first part of Rajna’s execution does not present a remarkable variety of colors compared to Howard’s. This is confirmed by the spectral flux of both recordings (Fig. 12), where we can see that Howard’s recording (left panel) presents a much more pronounced variation than Rajna’s recording (right panel).

The described intensity differences between the two recordings would be very difficult to detect in real time even by an experienced human listener, due to their volatile nature and to the possible presence of external noise. Only repeated listening in a quiet environment could guarantee to pick up some of these differences, which would still remain questionable without a systematic spectral analysis of quantitative nature such as that presented.

Fig. 11

Étude S.136 no.1: mirenvelope output with the default Filter option, featuring the envelope spectrum of Howard’s (left panel) and Rajna’s (right panel) execution

Fig. 12

Étude S.136 no.1: mirflux output, featuring the spectral flux of Howard’s (left panel) and Rajna’s (right panel) execution

4.2 Tempo, rhythm and timbre

Figure 13 shows the onset curve derived from the function mirevents applied to the two different recordings. We can see that the event curve of Howard’s version (left panel) presents a much more pronounced trend than Rajna’s version (right panel), reflecting the envelope curve (Fig. 11).

The estimated tempo is 118.2959 beats per minute (BPM) for Howard’s and 154.5757 BPM for Rajna’s execution, which is much faster, while the tabulated tempo in the music score is 132 BPM. We can note in Fig. 14 that both pianists tend to increase the execution tempo, although starting from different levels. The climax is reached around 55 s (cadence area) by Howard, while Rajna reaches the climax around 30 s (bar 20, repetition of the first phrase) and at the end (the Coda region).

Fig. 13

Étude S.136 no.1: mirevents output featuring the event curve of Howard’s (left panel) and Rajna’s (right panel) execution

Fig. 14

Étude S.136 no.1: mirtempo with Change option output featuring the estimated tempo of Howard’s (left panel) and Rajna’s (right panel) execution

Figure 15 reports the temporal evolution of the metrical centroid for the two music traces, that is a proxy of the rhythmical activity across time. Its value (in BPM) is high when fast figures, like semiquavers, are prevailing, while it is low when slow figures, like half notes, are prevailing. For this reason, it cannot surprise that a low is attained in correspondence of the main cadence of bars 29–30 (see Fig. 3), characterized by long chords at both hands. We can note that the metrical centroid of Rajna’s execution is systematically higher than Howard’s one.

Fig. 15

Étude S.136 no.1: mirtempo with Metre option output featuring the rhythmical pace of Howard’s (left panel) and Rajna’s (right panel) execution

Figure 16 displays the degree of dissonance over time for both executions. We can see that Howard’s one presents a much higher degree of dissonance than Rajna’s, particularly at the repetition of the first phrase (bar 20) and the main cadence (bars 28–29, see Fig. 3). Although the music score is the same, in fact, the intensity is much more variable in Howard’s execution, thus leading to a roughness peak in correspondence of the main cadence, characterized by long chords with a descending chromatic scale in the bass.

Fig. 16

Étude S.136 no.1: mirroughness output featuring the roughness of Howard’s (left panel) and Rajna’s (right panel) execution

Just as changes in intensity can be difficult even for an expert listener to perceive, changes in tempo can be even more so, as establishing a comparison from a live recording is very difficult. The same goes for timbrical contrasts over time. A MIR-based analysis such as the one exposed provides a validation tool for human perceptions of subtle variations in tempo or timbre when comparing different live performances.

4.3 Macro-formal analysis

The function mirsimatrix provides a way to weigh the inherent difference between different moments in a piece of music. In particular, mirsimatrix performs a pairwise comparison, frequency by frequency, of the estimated spectra across a high number of time frames. In Fig. 17, we observe that for Howard’s recording a high degree of similarity, signalled by intense yellow, is found out between frames at intervals [4–12 s], [38–45 s], [55–70 s], corresponding to bars 1–4 (first phrase), 20–23 (first phrase repetition), main cadence and Coda region (bars 29–36). It cannot surprise that these regions are all characterized by a clear and stable presence of C major chord. According to this criterion, the other frames do not show any relevant mutual similarity.

For Rajna’s recording, the similarity matrix is very similar to Howard’s. This may be expected, as the similarity matrix mainly depends on the played frequencies, which are given by the music score.

Fig. 17

Étude S.136 no.1: mirsimilarity of framed spectra for Howard’s (left panel) and Rajna’s (right panel) recording. This picture provides a summary of the mutual similarities between different time frames, based on the frequency-by-frequency comparison of their estimated spectra. The intense yellow is the highest intensity in the color legend, followed by ocher, dark blue and light blue. Color legend is reported below

Fig. 18

Étude S.136 no.1: mirnovelty output of Howard’s (left panel) and Rajna’s (right panel) execution. The picture displays the novelty over time, i.e., the degree of novelty measured as explained in Sect. 3.4. It helps to distinguish the most relevant musical events over time

The function mirnovelty is able to identify the occurrences of major musical events across the two recordings of Étude S.136 no.1, as Fig. 18 shows. We can note that, even if the novelty peaks may differ for the two executions, due to the different interpretation, the relevant peaks, exceeding 0.3, identify the fundamental moments of the piece in a similar way. This highlights the important role of MIR in identifying the most relevant macro-formal markers of a piece, which may prevent a human analyst to separate homogenous segments or merge dissimilar segments. The values of the novelty measure across time, in fact, allow to distinguish the most relevant changes from other minor changes in the underlying spectrum. In this case, the two executions of the same piece provide an implicit validation of identified macro-formal markers.

Figure 18 provides a clear idea of the macro-formal structure of the piece. In the left panel (Howard’s execution), we can observe that the novelty peaks exceeding 0.3 are located at:

• 4 s, i.e., the beginning of the first phrase (bar 1, Fig. 5);

• 12 s, i.e., the beginning of the second phrase (bar 5, Fig. 5);

• 20 s and 22 s, i.e., bars 9 and 11 (Figs. 6 and 8), at the development start;

• 35 s, i.e., the median cadence in C major (bar 18);

• 52 s, i.e., the sudden upward shift of bar 28 (Fig. 10),

• 55 s, i.e., the main cadence in C major (bar 29, Fig. 3);

• 65 s, i.e., the fourth arpeggio in the Coda region (bar 34);

• 70 s, i.e., the recording end.

In the right panel (Rajna’s execution), we can find almost the same markers in a compressed time frame, because Rajna’s execution is faster than Howard’s (see Figs. 14 and 15). The novelty peaks exceeding 0.3 are located at:

• 6 s, i.e., the beginning of the second phrase (bar 5, Fig. 5);

• 13 s, i.e., bar 9 (Fig. 6), where the development starts;

• 21 s and 25 s, i.e. bars 14 and 16;

• 40 s, i.e., the sudden upward shift of bar 28 (Fig. 10),

• 43 s, i.e., the main cadence in C major (bar 29, Fig. 3);

• 48 s, i.e., the Coda beginning (bar 31);

• 52 s, i.e., the fourth arpeggio in the Coda region (bar 34).

Commenting the outcomes of Fig. 18, we notice that there are strong similarities and some differences. On one hand, the second phrase (bar 5), the development (bar 9), the main cadence (bars 29–30) and the fourth arpeggio in the Coda region (bar 34) are commonly highlighted. It is relevant that these points are characterized in the score by the presence of forte or crescendo. On the other hand, the novelty peaks at bar 1 and at the recording end are highlighted in Howard’s recording because of the silence frames which start and close it, differently from Rajna’s. The other main differences between the two novelty profiles regard the development: Rajna emphasizes more bars 14 and 16, while Howard emphasizes more bars 11 and 18. These are subtle stylistic differences between the two interpretations.

All in all, while reading novelty profiles, score and performance analysis mix up together, thus allowing to identify the most relevant macro-formal markers of the piece as well as differences in performance between the two interpreters.

4.4 Harmonic analysis

In MIR toolbox, the fundamental tool to perform harmonic analysis is the chromagram. Figure 19 reports the chromagram estimated on the two traces segmented by the function mirsegment, as explained in Sect. 3.4. This leads to a MIR-based systematic harmonic analysis of the whole piece. Considering Howard’s recording (left panel), we observe:

• Across the interval [4–11 s], corresponding to the bar interval 1–4, we observe a clear prevalence of the pitches in the C7 chord;

• Across the interval [12–24 s], corresponding to bars 5–10, we note the superposition of pitches from C major and G major chords (C-G-D);

• Across the interval [25–38 s], corresponding to bars 11–19, the harmony is first changing every measure within the C major tune, before reverting to C in measure 16, and re-affirming C major by a cadence in bars 18–19;

• Across the interval [38–42 s], bars 20–21, we observe a very similar pitch distribution compared to the region [4–8 s], because here the same phrase is repeated;

• Across the interval [42–52 s], bars 22–27, we find a long region characterized by a three-octave chromatic scale in the bass, C2–C5, where the pitches of C major and F major chords show a prevalence;

• Across the interval [52–55 s], bar 28, the four pitches E-A-G-F, played by the right hand, are prevalent;

• Across the interval [55–60 s], bars 29–30, the pitches of G major are prevalent, as we are in the main cadence area;

• Across the interval [60–70 s], bars 31–36, the pitches of C major (C, E and G) are clearly prevalent, as we are in the Coda area.

Concerning Rajna’s recording (right panel), the described patterns are essentially the same, although we note that Rajna’s chromagram is quite less clear and more noisy. In particular, Rajna’s chromagram often presents $C\sharp$, F and $G\sharp$ highlighted when C, E, and G are, differently from Howard’s. This inconvenient typically occurs whenever the instrument tuning is sharper than the expected tuning (with C4=261.63 $\textrm{Hz}$ and A4=440 $\textrm{Hz}$). This fact is clearly perceivable while listening. Therefore, instrument tuning accuracy is another information which MIR harmonic analysis is able to uncover.

Fig. 19

Étude S.136 no.1: output of mirchromogram applied to Howard’s (left panel) and Rajna’s (right panel) recordings, segmented by the function mirsegment as explained in Sect. 3.4. This picture shows a different chromagram into each retrieved segment, and allows to get a clear idea of the harmonic dynamics across time. The intense yellow is the highest intensity in the color legend, followed by ocher, dark blue and light blue. Color legend is reported below

Based on this information, we can eventually resort to traditional means to perform the detailed score-based analysis of the piece, relying on the novelty measures provided in Fig. 18, and the chromagram of the segmented traces reported in Fig. 19. In this case, the MIR functions performing harmonic-formal analysis constitute a data-driven starting point for a traditional score analysis, with the relevant plus to be an automatic guide to identify macro-formal structure and underlying harmonies. The full analysis, reported in the "Appendix", can also be appreciated by looking at the music score with comments attached as a Supplement.

5 Concluding remarks

In this work, we have reviewed the main statistical tools that are used in Matlab MIR toolbox to retrieve the functional parameters of a music composition, and we have presented a case study about Liszt’s Étude S.136 no.1, which has been analyzed by means of a comparison between two live recordings: a WAV trace by Leslie Howard (1994) and an MP3 trace by Thomas Rajna (1979). The piece macro-formal and harmonic structure has been uncovered, and the intensity, tempo and timbre of the two executions have been systematically compared. At the end of this journey, we provide a summary of the main results in the case study, and a discussion regarding the main advantages and limitations of the described tools.

Concerning the main results of our case study (Sect. 4), we have discovered that Rajna’s execution of Liszt’s Étude S.136 no.1 is faster and less various, in terms of intensity and timbre, than Howard’s one. This means that Howard’s playing style emphasizes contrasts much more than Rajna’s. Spectrograms, novelty measures and chromagrams over time frames have provided a macro-formal and harmonic analysis of the piece, which has become the starting point for a subsequent traditional analysis.

All in all, it emerges that MIR-based analysis of a simple piano solo piece from audio data can complement and support traditional score analysis as far as pitch, macro-formal and harmonic analyses are concerned, while it can provide a reliable set of tools for comparative performance analysis regarding tempo, timbre, and intensity, with a degree of detail that is very difficult even for trained human listeners to achieve. In this respect, MIR toolbox is like a huge extension of human memory and elaboration capability, which relevantly enlarges the natural perception of a human listener. This results in a superior ability of the machine to objectively compare different executions.

Beyond the presented case study, we can illustrate the general usefulness of the described MIR tools for formal and harmonic analysis via the following example. Suppose that a new musical archive is discovered, with several unedited manuscripts. In that case, the problem to attribute discovered music to a precise style rises up. Therefore, while preparing a critical edition, recording live executions of discovered pieces may already allow to uncover important facts on the underlying style.

Suppose for instance that the discovered pieces are thought to be sonatas belonging to the Viennese style. In that case, we expect to observe a specific tripartite form and typical chord sequences based on the tonic-dominant relationship. Should segmentation and chromagram say anything different, the belonging of those sonatas to the Viennese style could be questioned.

Another relevant argument that shows the general usefulness of those MIR tools regards the pieces which belong to a transition phase between two different styles. In this respect, a pregnant example regards for instance the famous Liebestraum n.3 by Liszt, where tonal harmony coexists with a triad circle called Weitzmann region, so that Cohn (2012) refers to this practice as “double syntax”. In such a case, MIR-based chromagram over the segmented trace can provide a useful tool to compare theoretical expectations with empirical recordings, to verify if the identified co-existence of two harmonic grammars is consistent to the outcome of a MIR analysis, which could be enlarged to a corpus of coeval works by the same author.

Anyway, the engine of automatic MIR is spectral analysis. The spectrum is a powerful tool: it allows for a clear understanding of two fundamental parameters like frequency and intensity, on the base of which more complex tasks may be performed. One of those is segmentation, that provides the division of the music piece in mutually exclusive sections, on the base of the spectral evolution. The machine is also able to provide an importance ranking of proposed segments, and to retrieve timbrical differences over time.

These tasks are particularly informative when applied to sound-based music like electro-acoustic music, for which there is nothing similar to a music score and a sound ordering is hard to identify. In that case, a thorough spectral analysis is unavoidable to explore the musical structure, while segmentation allows to identify the different moments of a piece according to some founded criterion, unlike human perception Emmerson and Landy (2016). Beyond that, synthesized timbres are typical materials in this music, so that roughness measure becomes crucial to identify homogenous or dissimilar segments over time.

In the end, we should mention that automatising complex tasks like harmonic analysis may lead to possible issues, as it happens when complex techniques requiring specific knowledge are popularized (see for instance the effects of the surge in popularity of ChatGPT). At the same time, a judicious use of MIR tools can really open new avenues in the music analysis field. For instance, the retrieval of hidden motifs and their occurrences over time Weiss and Bello (2011) is a relevant and very refined task, that may potentially uncover the roots of the composition style of a specific period or author. Comparing recovered harmonic, dynamic, rhythmical, or timbrical patterns to existing codified musical grammars, in order to test for the overlapping degree, is now a concrete path, that could open up unforeseen possibilities in the understanding of our immense musical heritage.

Appendix

In this section, we report the harmonic-formal analysis of Liszt’s Étude S.136 no.1, and we show the correspondence with the outcomes of Section 4, particularly in Figs. 18 and 19. All reported elements are also highlighted in the music score with comments attached as a Supplement.

• Exposition starts at bar 1. Bars 1–4 (Fig. 5), which constitute Phrase 1, are characterized by a stable presence of C major.

• Phrase 2 (Fig. 5) is constituted by bars 5–8, featuring the alternation of C major and G major.

• Development starts at bar 9. Bars 9 and 10 (Fig. 6) constitute Phrase $D_1$, and contain an ascending pattern in octaves on both hands, one third apart, along C major diatonic scale.

• Phrase $D_2$ is constituted by bars 11–14(Q1) (Fig. 8), Phrase $D_3$ by bars 14(Q2)-15(Q3) (Fig. 3). They contain a descending thirds progression built over the bass C–A–F–D–B, which ends in a G7 major segment.

• Phrase $D_4$ goes from bar 15(Q4) to bar 17 (Fig. 9). It contains the same descending progression of bars 11–15, at double speed, characterized by a pattern of descending thirds in the bass interjected by leading notes one semitone below (from the last quaver of bar 15, we can find in the bass the sequence B–C–G$\sharp$–A–E–F–C$\sharp$–D–B).

• The median cadence, a cadenza composta in C major, lies in bars 18–19.

• Reprise starts at bar 20. Bars 20–23 contain the repetition of Phrase 1.

• Bars 24–29(Q1) constitute a new Development (see Fig. 7).

• Bars 22–27 contain a long chromatic progression, where a three-octave chromatic scale from C2 to C5 is featured in the bass. Bar 28 contains a sudden upturn shift of the motif E–A–G–F by one octave at the right hand (see Fig. 10).

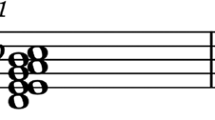
• The main cadence, a cadenza composta in C major preceded by a chromatic descent in the bass (C–B$\flat$–A–A$\flat$–G), occupies bars 29–30 (Fig. 3).

• Coda region occupies bars 31–36, subdivided in three sub-regions: $C_1$ (bars 31–32, with two C major—G major arpeggios, ending in G5), $C_2$ (bars 33–35, with three C major arpeggios, ending in C6), $C_3$ (bar 36, the final C2, gradually disappearing).