Introduction

Both climate change (Hattermann et al. 2013) and the effect of anthropopressure enforce the use of hydrological methods to assess the scale of threats and to predict their occurrence that have been neglected so far. Hydrological methods attempt to describe extreme phenomena. Increasing attention is paid to their definition in a time-variant system, i.e., focusing not only on extreme values but also on the time course of these phenomena, which is related to the determination of the shape of a flood wave.

The knowledge of the theoretical shape of a flood wave and the possibility of its definition using its basic parameters is very much needed and desired in a number of design tasks in the field of water management, hydraulic engineering (Mioduszewski 2014), water and sewage management, spatial management (Zevenbergen et al. 2011) as well as forest management. In contrast to the commonly used design flows, the hypothetical waves expand the range of usable data, e.g., by the volume of a flood wave with a given exceedance probability and the variation of the flow rate for the rising and falling limbs. Therefore, the design can take into account the flow in the form of a hydrograph with a given exceedance probability (Ciepielowski 1987, 2001).

The hypothetical hydrograph is understood as such theoretical hydrograph that demonstrates representative flood wave form, which may occur under specific conditions at a selected location, for a given maximum (design) value (Gądek and Środula 2014). It is being increasingly utilized in the widely understood flood risk assessment (Apel et al. 2006; Vrijling et al. 1998; Zeleňáková et al. 2017) and in the estimation of loss of lives and property (Ernst et al. 2010; Jonkman and Vrijling 2008).

These hydrographs are presented in an analytical form, using a variety of functions, or in a synthetic form, which uses two-dimensional statistical analysis (De Michele et al. 2005; Serinaldi and Grimaldi 2011). In some countries, analytical hydrographs are called parametric flow hydrographs. Their main advantage is that they can be determined at any cross section of the river, with the influence of climate change on their course taken into consideration (O’Connor et al. 2014; Bayliss 1999; Mills et al. 2014). In order to describe the course of the parametric design hydrograph, it is necessary to use the appropriate mathematical function. The most common one is the gamma distribution function, which was proposed by Nash in 1957 (Nash 1957).

The function gamma describes the rising limb very well with large flow heights (above 50% of the maximum flow Qmax), but in the lower part of the recession (falling) limb, large discrepancies occur. For this reason, in Ireland, the exponential function known as the UPO-ERR-Gamma (unit-peak-at-origin gamma curve coupled with an exponential replacement recession curve) has been introduced for the recession limb (O’Connor et al. 2014).

It is more reasonable to use homogeneous functions instead of spline functions for the needs of analytic hydrographs. The attempt to use the Hayashi distribution (Hayashi et al. 1986; Aziz et al. 2006), the negative binomial distribution, the inverse Gaussian distribution and the gamma distribution with algebraic replacement recession curve was considered unconvincing (O’Connor et al. 2014). The authors of this manuscript also verified the applicability of the three-parameter Pearson Type III distribution function with two shape parameters (Gądek et al. 2017b). Although the proposed method yielded positive results, it could not be recommended due to the very large number of solutions for the parameters tp, m and n (where m and n represent the shape parameters). The function describing a hydrograph must not only be adapted to the time course of flow variations but also yield the unique solution. Such rigorous assumption allows to determine the parametric design hydrograph in any section of the river, which has only been possible so far using hydrological models (Ozga-Zielińska et al. 2002; Wałęga 2013; Pietrusiewicz et al. 2014), being a rather cumbersome process and not always yielding unambiguous results, mainly due to the lack of procedures to determine the course of a hyetograph or a possibility to assess the moisture conditions in the catchment.

In the design hydrology, parametric hydrographs may be determined in any cross section of the river. This is in line with the expectations regarding this type of solutions and the idea originating in the 1930s associated with the isochrones theory developed by Dubelir, Boldakov and Čerkašin. This theory is based on the genetic flood wave equation which is given by:

$$Q_{t} = \mathop \int \limits_{\tau = 0}^{\tau = t} h_{t - \tau } b_{\tau } v_{\tau } {\text{d}}\tau$$
(1)

where Qt is the outflow rate from the catchment at time t, ht−τ the thickness of water layer discharged by the catchment in the time unit t − τ, bτ the average width of the partial runoff area, vτ the runoff velocity, t the time of discharge from the catchment, and τ the time needed for water to reach the cross section.

This method was used until the mid-1960s and resulted in the creation of hydrographs presented in the form of a triangle or trapezium. Its advantage was the ability to determine the hydrograph in a selected cross section, which was not possible later as a result of the use of the so-called hypothetical hydrographs determined by the Reitz and Kreps method (Reitz and Kreps 1945), the Warsaw University of Technology method (Gądek et al. 2017b), the Hydroprojekt method (Gądek and Środula 2014) or the Krakow method (Gądek and Tokarczyk 2015).

The modified Pearson Type III distribution function, consistent with the nonparametric hydrograph with one shape parameter m, is given by (Gądek et al. 2017b):

$$q_{t} = \left( {1 + \frac{t}{{t_{p} }}} \right)^{m} \,\exp \left( { - m \frac{t}{{t_{p} }} } \right) 100\%$$
(2)

and with two shape parameters:

$$q_{t} = \left( {1 + \frac{t}{{t_{\text{p}} }}} \right)^{m} \exp \left\{ { \frac{m}{n} \left[ {1 - \left( { 1 + \frac{t}{{t_{\text{p}} }}} \right)^{n} } \right]} \right\} 100\%$$
(3)

where qt is the percentage of peak flow at time t [%], tp the time to peak [h], t the time from the beginning of rising limb [h], and m, n the shape parameters [−].

Similar solutions with one shape parameter were presented in the USA (McEnroe 1992) and in Ireland under the name UPO gamma (unit-peak-at-origin gamma) (O’Connor et al. 2014).

The authors of this research paper propose to use the Pearson Type IV distribution with one shape parameter and two shape parameters for the description of the analytical hydrograph. This distribution was tested for the analytical description of hydrographs in the 1960s, which was then considered to be less accurate than the Pearson Type III distribution with two shape parameters (Strupczewski 1964; Strupczewski et al. 2013). Currently, this distribution is practically disused. The authors modified the Pearson Type IV distribution functions proposed by Strupczewski to match the analytical hydrograph to the nonparametric hydrograph determined by the Archer’s method. The objective of this paper is to prove that the modified Pearson Type IV distribution functions are well suited for describing a parametric hydrograph based on three parameters: hydrograph widths at 50% and 75% of peak flow (W50 and W75) and the skewness coefficient s. Innovative research has been carried out for two water regions of Poland: the upper Vistula River and the middle Oder River. Thirty gauged cross sections were included in the calculations for each of these regions. To determine the parameters W50, W75 and s, nonparametric hydrographs were developed in each of these cross sections. The developed method ought to have a universal character; it should enable determining parametric hydrographs in any cross section of any river. In order to prove the universality of the proposed distribution functions, a large number of catchments with diverse hydrological regime were adopted for the calculations.

Materials and methods

Study area

The research studies were carried out based on the recorded hydrographs in 60 measurement cross sections, located in the upper Vistula River and the middle the Oder River water regions (Fig. 1). The selected catchments represented the areas of various types of hydrograph formation. The selection was made so that they represented different types of geographic areas: mountain, highland as well as lowland catchments. Eight unimodal hydrographs with the highest flow values Qmax selected from the period 1960–2014 were adopted. Table 1 illustrates the gauged stations systematized from 1 to 30 for the Vistula River, and from 31 to 60 for the Oder River. Some gauged stations are located downstream of the water reservoirs, but the distances from the reservoirs are so large that no influence of the reservoirs on the hydrographs in gauged stations could have been assumed.

Fig. 1
figure 1

Location of water gauge in: a the middle Oder River water region and b the upper Vistula River water region (see Table 1)

Full size image
Table 1 Water gauges in the hydrologic order for the Oder River and Vistula River water region
Full size table

Methods

Parametric flow hydrographs can be determined in any cross section of the river regardless of the size of the catchment. It is made possible thanks to the Archer’s method of determining nonparametric hydrograph (i.e., the median of recorded hydrographs). The nonparametric hydrograph determined by the Archer’s method is used only to determine the value of hydrograph width at 50% (W50) and 75% (W75) of peak flow and the skewness coefficient s (Archer et al. 2000). The Archer’s method uses W50 and W75 similarly to the Snyder method (1938) where with similar parameters characterizing the Synthetic Unit Hydrograph (Snyder 1938; Challa 1997).

According to this method, the nonparametric hydrograph has an independent rising limb and an independent recession limb (Fig. 2). The flows are presented as percentages of peak flow. The horizontal axis indicates the duration of percent flow exceeding the given value. The time for the rising limb of the hydrograph is expressed in negative values, and for the recession limb in positive values. At the time t = 0 there is a maximum percentage of peak value q = 100%. The time t of the individual percent flows is the median of the durations of percent flow of the recorded hydrographs, separately for the rising limb and separately for the recession limb (O’Connor et al. 2014; Gądek et al. 2017a). Such a nonparametric hydrograph is determined based on the recorded hydrographs. The applied methods of analytical hydrographs determination based on nonparametric hydrographs assume various numbers of unimodal flow hydrographs. The Warsaw University of Technology method uses six unimodal flow hydrographs (Gądek et al. 2016), the Hydroprojekt method—one (Gądek and Środula 2014), and the Krakow method—eight (Gądek and Tokarczyk 2015; Gądek et al. 2016). The authors applied the maximum number of hydrographs from used methods, i.e., eight unimodal flow hydrographs.

Fig. 2
figure 2

Exemplary nonparametric hydrograph according to Archer

Full size image

In 1964, Strupczewski proposed to use the Pearson Type III distribution function with one shape parameter m and with two shape parameters m and n as well as Type IV with one shape parameter to describe the parametric hydrographs (Strupczewski 1964; Ciepielowski 1987, 2001). The solutions proposed by Strupczewski concerned the methods based on the traditional presentation of nonparametric and parametric hydrographs. The authors of this manuscript adapted the function notation to the description consistent with the properties of the nonparametric hydrograph (median of the hydrographs), developed using the Archer’s method. A parametric hydrograph is created from the parameters W50, W75 and s determined of the nonparametric hydrograph developed using the Archer’s method (see Fig. 3).

Fig. 3
figure 3

Exemplary parametric design hydrograph

Full size image

The parametric hydrograph is developed on the basis of the Archer’s nonparametric hydrograph. For analytical description, two versions: the first with one shape parameter and the second with two shape parameters, of the Strupczewski Pearson Type IV distribution function were adopted. The first function is defined as follows

$$q_{t} = \left( {1 + \frac{{t_{\text{p}} }}{t}} \right)^{m} \,\exp \left( { - m \frac{{t_{\text{p}} }}{t} } \right) 100\% .$$
(4)

The second function is given by:

$$q_{t} = \left( {1 + \frac{{t_{\text{p}} }}{t}} \right)^{m} \exp \left\{ { \frac{m}{n} \left[ {1 - \left( { 1 + \frac{{t_{\text{p}} }}{t}} \right)^{n} } \right]} \right\} 100\%$$
(5)

The authors modified Eqs. (4) and (5):

$$q_{t} = \left( { \frac{{t_{\text{p}} }}{{t + t_{\text{p}} }}} \right)^{m} \exp \left[ {m\left( {1 - \frac{{t_{\text{p}} }}{{t + t_{\text{p}} }}} \right)} \right] 100\% \quad {\text{for}}\,t > - t_{\text{p}}$$
(6)
$$q_{t} = \left( { \frac{{t_{\text{p}} }}{{t + t_{\text{p}} }}} \right)^{m} \exp \left[ {\frac{m}{n}\left( {1 - \frac{{t_{\text{p}} }}{{t + t_{\text{p}} }}} \right)^{n} } \right] 100\% \quad {\text{for}}\,t > - t_{\text{p}}$$
(7)

The optimization of the shape parameters and the time to peak tp in all formulas was carried out based on the values W50 and W75 of the Archer hydrograph and the skewness coefficient s, determined for the hydrograph width W50 (see Fig. 2). It was also assumed that the shape parameters were positive values to enable application of empirical formulas. The descriptors and the skewness coefficient s were calculated based on the median of hydrographs for 30-year data sequences for both catchments.

The smallest deviation of the values calculated from the given values of hydrograph width at 50% and 75% of peak flow was adopted as the selection criterion (the objective function) in accordance with the following dependence:

$$S = \left( {W75 - \hat{a}} \right)^{2} + \left( {b - \hat{b}} \right)^{2} + \left( {c - \hat{c}} \right)^{2} = \hbox{min}$$
(8)

where W75 is the hydrograph width at 75% of peak flow determined by the nonparametric hydrograph [h], \(\hat{a}\) the hydrograph width at 75% of peak flow W75 calculated from one of the formulas (6) and (7) [h], b the duration of the percent flow exceeding 50% for the rising limb of the nonparametric hydrograph, b = s·W50 [h], \(\hat{b}\) the duration of the percent flow exceeding 50% calculated from one of the formulas (6) and (7) [h], c the duration of the percent flow exceeding 50%, for the recession limb of the nonparametric hydrograph [h], and \(\hat{c}\) the duration of the percent flow exceeding 50% calculated from one of the formulas (6) and (7) [h].

Results

The calculations consisted of:

  1. 1.

    Determination of Archer’s nonparametric hydrographs for 60 water gauges.

  2. 2.

    Determination of parameters based on the Archer’s nonparametric hydrographs: hydrograph width at 50% of peak flow (W50), hydrograph width at 75% of peak flow (W75) and skewness coefficient s.

  3. 3.

    Definition of hydrograph shape parameters (m and n) and the rising time tp for each water gauge cross section according to the selection criterion (Eq. 8).

  4. 4.

    Determination of the Pearson Type IV parametric hydrographs with one and two shape parameters for the calculated parameters: m, n and tp.

  5. 5.

    Determination of the W50, W75 and s parameters of the Pearson Type IV parametric hydrographs.

Specific steps of calculation were adopted for the calculated shape parameters m and n (0.01) and for the time of rising limb tp (1 h).

The analytical hydrographs calculated using the Pearson Type IV function with one and two shape parameters exhibit similarity.

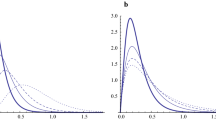
Figure 4 shows the values of W50, W75 and s of selected Archer’s hydrographs calculated using the Pearson Type IV distribution function with one and two shape parameters. Table 2 shows the hydrograph parameters for all 60 water gauges.

Fig. 4
figure 4

Parametric hydrographs calculated using the Pearson Type IV distribution with one shape parameter (Pearson 1) and two shape parameters (Pearson 2), and nonparametric hydrographs determined by the Archer’s method for the following cross sections: a Odra–Cigacice (2), b Nysa Kłodzka–Kłodzko (5), c Kaczawa–Piątnica (22), d Bóbr–Kamienna Góra (25), e Wisła–Sandomierz (32), f Lubieńka–Lubień (43), g Koprzywianka–Koprzywnica (55), h San–Radomyśl (58)

Full size image
Table 2 Values of parameters W50, W75 and s of the Archer’s nonparametric hydrographs and the Pearson Type IV parametric hydrographs with one shape parameter (Pearson 1) and two shape parameters (Pearson 2)
Full size table

Figure 4 confirms that parametric hydrographs (Pearson 1 and Pearson 2) deviate from nonparametric hydrographs determined by the Archer’s method. Much better fit occurs in the upper parts of the hydrographs (above W50). The fit in the lower parts is much worse which can be expected because of the assumption that the hydrographs are adjusted based on the W50 and W75 parameter values.

Analysis and discussion

Several types of quality measures for matching nonparametric and parametric hydrographs were adopted for the analysis. Relative error (RE) and mean relative error (MRE) are criteria recommended in Technical Research Report Volume III Hydrograph Analysis (O’Connor et al. 2014) to assess the compliance of the parametric and nonparametric hydrographs (Fig. 5).

Fig. 5
figure 5

Relative errors of hydrograph width Wp: a for p = 50%; b for p = 75%

Full size image

Relative error of hydrograph width was calculated from the following formula:

$${\text{RE}}_{\text{p}} = \frac{{\left| {W_{\text{p}} - \widehat{{W_{\text{p}} }}} \right|}}{{W_{\text{p}} }}$$
(9)

where REp is the relative error of hydrograph width Wp, p = 50%, p = 75% [−], Wp the hydrograph width at p = 50%, p = 75% determined from nonparametric design hydrograph [h], and \(\widehat{{W_{\text{p}} }}\) the hydrograph width at p = 50%, p = 75% determined from parametric hydrograph for specific formulas which were used (gamma and Strupczewski) [h].

To analyze the calculated values of relative errors of hydrograph width Wp, the following quality assessment measures for W50 and W75 were adopted (Table 3).

Table 3 Quality measures for relative errors of hydrograph width Wp
Full size table

More stringent criteria were adopted for the W50 due to the objective function used in the optimization process. The best possible adjustment of the parametric hydrograph to nonparametric for this value was the main assumption of the objective function.

With the adopted criteria, the match quality of the W50 value of the parametric hydrograph to nonparametric is very good (see Fig. 6a), while for the W75 value is good (see Fig. 6b), which confirms the correctness of the objective function adopted in the study (Fig. 7).

Fig. 6
figure 6

Quality measures for relative errors of hydrograph width Wp: ap = 50%; b = 75%

Full size image
Fig. 7
figure 7

Mean relative errors for the p percent flow: ap = 50%; bp = 75%

Full size image

Mean relative error (Elshorbagy et al. 2000) was calculated for the p percent flow, p = 75% and p = 50%, using the following definition:

$${\text{MRE}}_{\text{p}} = \frac{1}{N}_{\text{p}} \mathop \sum \limits_{i = 1}^{{N_{\text{p}} }} {\text{RE}}_{i}$$
(10)

where \({\text{MRE}}_{\text{p}}\) is the mean relative error for the p percent flow p = 75% and p = 50%, Np the number of percent flows exceeding p percent flow, 6 for p = 75% and 11 for p = 50%, REi the relative error of percent flows, p1 = 98, p2 = 95, p3 = 90, p4 = 85, p5 = 80, p6 = 75,…, p11 = 50 (see Fig. 3) [−], and i the percent flow number.

To analyze the calculated values of mean relative errors for the p percent flow, the following quality assessment measures for W50 and W75 were adopted (Table 4).

Table 4 Quality measures for mean relative errors for the p percent flow
Full size table

Figure 8 shows that the mean relative error criterion for the p percent flow for evaluating the fit of the parametric hydrograph to nonparametric one is weak. The visual evaluation of the hydrographs shown in Fig. 4 suggests much smaller matching errors.

Fig. 8
figure 8

Quality measures for mean relative errors for the p percent flow: ap = 50%; bp = 75%

Full size image

The REp and MREp measures do not answer unambiguously as to whether the functions used should be recommended for the Vistula or the Oder water regions, or not. A similar observation was reported by Chai and Draxler (2014).

Therefore, two other measures were assumed to assess the similarity of the parametric and nonparametric hydrographs: the volume of hydrograph, V, and the center of gravity time coordinate, rp.

The volume of hydrograph was determined above the p percent flow, p = 50% and p = 75%, using the following definition (see Fig. 9):

$$V_{\text{p}} = \mathop \sum \limits_{i = 1}^{{N_{\text{p}} }} V_{{{\text{p}},i }}$$
(11)

where Vp is the volume of hydrograph above the p percent flow, p = 50%, p = 75%, Np the number of percent flows exceeding p percent flow: 6 for p = 75% and 11 for p = 50%, and Vp,i the partial volume of the hydrograph between successive p percent flows.

Fig. 9
figure 9

Sketch for determining partial volume of hydrograph (trapezoidal area) and the center of gravity time coordinate used in Eqs. 11 and 12

Full size image

The center of gravity time coordinate was determined for the hydrograph part above the p percent flow, p = 50% and p = 75% (see Fig. 9).

$$r_{\text{p}} = \frac{{\mathop \sum \nolimits_{i}^{{N_{\text{p}} }} V_{{{\text{p}},i }} l_{i} }}{{\mathop \sum \nolimits_{i}^{{N_{\text{p}} }} V_{{{\text{p}},i }} }}$$
(12)

where rp is the time coordinate of the center of gravity of the hydrograph above the p percent flow, p = 50% and p = 75% [h], Np the number of percent flows exceeding p percent flow, 6 for p = 75% and 11 for p = 50%, Vp,i the partial volume of the hydrograph between successive p percent flow [h], li the time coordinate of the gravity center ri of the partial volume [h], and ri the gravity center of the partial volume.

The analysis involved the assessment of the conformity between the centers of gravity of the parametric hydrographs relative to the flow axis for the percentage of peak p = 75% and higher, and for the percentage of peak p = 50% and higher (Fig. 10). The position of the center of gravity indicates the proportion between the rising limb volume and the recession limb volume of the hydrograph. The slope coefficient of the trend line represents the relationship between the position of the center of gravity of the parametric hydrograph rp and the nonparametric hydrograph rar. Slope coefficient values below 1 indicate that the center of gravity of the nonparametric hydrograph rar is located further away from the q axis than the center of gravity of the parametric hydrograph rp. Figure 10 shows that the position of the centers of gravity of both hydrographs is better in case of distribution with two shape parameters m and n than with one parameter.

Fig. 10
figure 10

Relationships between centers of gravity for parametric hydrographs determined by the Person Type IV (rp) and the centers of gravity for Archer’s nonparametric hydrographs (rar)

Full size image

The analysis of the volume of the parametric hydrographs Vp compared to the nonparametric Var, for the percentage of peak p = 75% and higher, and for the percentage of peak p = 50% and higher (Fig. 11), shows a better fit above W50. This analysis confirms that the fit of parametric hydrographs to nonparametric ones above W75 is weak and the volume of parametric hydrographs is about 30% larger than that of the nonparametric ones.

Fig. 11
figure 11

Relationships between volumes of parametric flow hydrographs determined by the Person Type IV (Vp) and Archer’s nonparametric hydrographs (Var)

Full size image

The proposed criteria (13) and (14) offer a possibility to evaluate the determined parametric hydrograph when compared to the input (nonparametric) hydrograph. In addition, an analysis of the absolute deviation Ss of the values of the calculated hydrograph width at 50% (W50) and 75% (W75) of peak flow, depending on the skewness coefficient s, was carried out.

$$S_{s} = \sqrt {\left( {a - \hat{a}} \right)^{2} + \left( {b - \hat{b}} \right)^{2} }$$
(13)

where a is the duration of the percentage of peak flow p = 50% or p = 75%, or higher, for the rising limb of the nonparametric hydrograph, a = s W50 or a = s W75 [h], \(\hat{a}\) the duration of the percentage of peak flow p = 50% or p = 75%, or higher, calculated from one of the formulas (8) and (9) for the rising limb [h], b the duration of the percentage of peak flow p = 50% or p = 75%, or higher, for the recession limb of the nonparametric hydrograph [h], and \(\hat{b}\) the duration of the percentage of peak flow p = 50% or p = 75%, or higher, calculated from one of the formulas (8) and (9) for the recession limb [h].

Figures 12 and 13 demonstrate the relationship between the absolute deviation Ss and the skewness coefficient s for the hydrograph widths W50 and W75, respectively. This analysis is used to determine the possibility of using Pearson Type IV distribution in both considered water regions. The skewness coefficient of the hydrograph characterizes the proportion of the rising limb of the hydrograph to the recession limb. The smaller the value of the skewness coefficient s, the larger the share of the recession limb. The analysis shows that for hydrographs with values of the coefficient s about 0.2 and above 0.5, the compliance of parametric hydrographs above W50 described with the Pearson Type IV distribution with one shape parameter m with nonparametric hydrographs is smaller (see Fig. 12a). In the case of two shape parameters m and n (see Fig. 12b) fit differences of hydrographs are already visible for the value of the skewness coefficient s > 0.3. For hydrographs above W75, both for one and for two shape parameters, the fit for values of s < 0.4 is less than for values s > 0.4 (see Fig. 13). In the whole range of variation the skewness coefficient of the hydrograph s for the W75 fitting of the both hydrographs is much worse than for the W50.

Fig. 12
figure 12

Absolute error values Ss versus values of skewness coefficient s for the Pearson distribution function Type IV: a one shape parameter m; b two shape parameters m and n for W50

Full size image
Fig. 13
figure 13

Absolute error values Ss versus values of skewness coefficient s for the Pearson distribution function Type IV: a one shape parameter m; b two shape parameters m and n for W75

Full size image

Summary and conclusions

The gamma distribution function, i.e., Pearson Type III distribution function with one shape parameter, is the most often used function for parametric hydrographs description in the relevant literature. Authors of such publications (for example, O’Connor et al. 2014) indicate the imprecise fit of the recession limb of parametric hydrograph to the nonparametric one. One of the proposed solutions is to use a spline function consisting of two different functions describing independently two parts. The upward part of the recession limb to the inflection point, which is located between the parameters W75 and W50, is described by the gamma function. The recession limb below the inflection point is described by the exponential function. In Ireland, this spline function is known as UPO gamma (unit-peak-at-origin gamma) (O’Connor et al. 2014). The research conducted for the Ireland area showed that this solution is not universal. This prompted the authors of this manuscript to find one function that would allow us to describe both the rising and recession limbs of a nonparametric hydrograph in any water gauge.

The Pearson Type IV distribution function proposed by Strupczewski concerned the description of a nonparametric flow hydrograph obtained as a medium hydrograph from unimodal recorded hydrographs. Strupczewski claimed that this distribution function is recommended to use only when the duration of the recession limb of the hydrograph is six times longer than the rising limb duration.

Current trends in hydrology recommend the use of the Archer’s method for the nonparametric hydrographs description. This hydrograph represents the median durations of a given percent flow independently for rising and falling limbs. It is used to determine the value of the hydrograph width at 50% (W50) and 75% (W75) of peak flow and the skewness coefficient s (Archer et al. 2000). The parameters are used to determine the shape of a parametric hydrograph from W50 to peak flow. The Archer’s method allows to use the Pearson Type IV distribution function under conditions other than those considered by Strupczewski.

In this paper, the authors modified the formulas for the Pearson Type IV distribution with one and two shape parameters proposed by Strupczewski.

The analyses were conducted for the two water regions: the upper Vistula River and the middle Oder River. For each of these regions, 30 catchments were selected, for which multiannual flow records were available. In these areas, large floods occurred. The flood hydrographs were highly variable, with variable ratio of the rising/recession limb duration.

The REp and MREp measures do not answer unambiguously as to whether the functions used should be recommended for the Vistula or the Oder water regions, or not. That is why the three independent methods were used to verify the obtained results: How the absolute error changed in relation to the skewness coefficient of the hydrograph (Figs. 12, 13); what relationships are between the calculated and the input hydrographs related to the changes in the position of the centers of gravity (Fig. 10) and the volume of the hydrographs (Fig. 11). The results of relative and average relative error analysis do not allow unambiguous application or rejection of the Pearson Type IV distribution function to describe the parametric hydrograph. The remaining three analyses confirmed that both Pearson Type IV distribution functions could be used to describe the parametric hydrograph. They confirm a good fit for the recession limb of the hydrograph. In the upper part of the parametric hydrograph above the 75% percent flow (W75), a relatively weak fit is observed, but it does not affect either the values of the volume in this part or the position of the center of gravity of the hydrograph. The applied measures of the volume and the position of the center of gravity of the hydrograph are more objective than the relative error (RE) and mean relative error (MRE) recommended in Technical Research Report Volume III Hydrograph Analysis (O’Connor et al. 2014). When using the Pearson Type IV distribution it is difficult to state clearly what effect the skewness coefficient s has on the function’s fit for the given input parameters (W50 and W75) (Figs. 12, 13).

As a result of additional tests performed, it was observed that there exist many potential pairs of shape parameters m and n for Pearson Type IV distribution function satisfying the objective function criterion (Eq. 8). This is a major inconvenience because the shape parameters are to be determined for ungauged cross sections, based on the physical catchment descriptors. Thus, the development of empirical formulas using the physical catchment descriptors to determine the parameters W50, W75 and s is impossible. Therefore, the Pearson Type IV distribution with a single shape parameter to describe the parametric hydrograph well enough is recommended.