Effect of varying normal stress on stability and dynamic motion of a spring-slider system with rate- and state-dependent friction

Abstract

Incorporating rate and state friction laws, stability of linearly stable (i.e., with stiffness greater than the critical value) spring-slider systems subjected to triggering perturbations was analyzed under variable normal stress condition, and comparison was made between our results and that of fixed normal stress cases revealed in previous studies. For systems associated with the slip law, the critical magnitude of rate steps for triggering unstable slips are found to have a similar pattern to the fixed normal stress case, and the critical velocity steps scale with a/(b − a) when k = k_cr for both cases. The rate-step boundaries for the variable normal stress cases are revealed to be lower than the fixed normal stress case by 7 %–16 % for a relatively large α = 0.56 with (b − a)/a ranging from 0.25 to 1, indicating easier triggering under the variable normal stress condition with rate steps. The difference between fixed and variable normal stress cases decreases when the α value is smaller. In the same slip-law-type systems, critical displacements to trigger instability are revealed to be little affected by the variable normal stress condition. When k ≥ k_cr(V_*), a spring-slider system with the slowness law is much more stable than with the slip law, suggesting that the slowness law fits experimental data better when a single state variable is adopted. In stick-slip motions, the variable normal stress case has larger stress drops than the constant normal stress case. The variable normal stress has little effect on the range of slip velocity in systems associated with the slowness law, whereas systems associated with the slip law have a slowest slip velocity immensely smaller than the fixed normal stress case, by ~10 orders of magnitude.

1 Introduction

Laboratory-derived rate and state friction laws and related analyses have provided important discovery in the mechanism of sliding stability (Ruina 1983; Rice and Ruina 1983; Gu et al. 1984; Dieterich and Kilgore 1992; Gu and Wong 1994) and that of seismic slip nucleation on fault surfaces (Tse and Rice 1986; Dieterich 1992). While friction coefficient is found to depend mainly on sliding rate and ‘state’ (the latter describes the evolution effect between steady-state values of friction) by early experiments (Dieterich 1978, 1979; Ruina 1983), subsequent experiments also reveal dependencies on changes in normal stress (Linker and Dieterich 1992), temperature (Chester 1994), and even in shear stress (Nagata et al. 2012; Fan et al. 2014).

Occurrence of seismic slips on a fault plane depends on the fault constitutive relation and interaction with the elastic surrounding under steady tectonic loading or a loading rate pulse as driven by an earthquake in the vicinity, and each of the above-mentioned effects in the constitutive relation has an influence in the whole process. There is no doubt that exploring these effects is important in gaining insight into the mechanism of earthquake processes, but large-scale numerical modeling incorporating all these effects is quite time-consuming, and it is probably not easy to summarize the results. On the other hand, these effects can be isolated in numerical models for purposes of understanding their influences separately, and such analyses can be readily done in a single spring-slider system which reflects the friction constitutive relation and interaction with the elastic surrounding. As tectonic loading to active faults is generally inclined to orientation of fault planes, normal stress acting on fault surfaces is varying during the loading and slip processes.

In a single spring-slider system, the temperature effect has been found to have an indirect influence on the stability through shear heating (Blanpied et al. 1998), whereas normal stress influences the stability directly through the geometric relation between fault and the driving force orientations (Dieterich and Linker 1992; He et al. 1998). In researches of earthquake nucleation based on rate and state friction, it is found that variable normal stress on a planar fault surface imposed by remote stressing increases the nucleation time of a seismic fault slip (He 2000; Fang et al. 2011). Limit cycles of stick-slip motions of a spring-slider system have been found to have larger static stress drops under variable normal stress originated from a principal stress inclined to the fault plane, as compared to the fixed normal stress case (He 1999).

With the background mentioned above, this work focuses on the influence of varying normal stress to both sliding stability and dynamic motion of a spring-slider system with the driving force inclined to the fault surface, compared with results for the fixed normal stress case. Our analyses are based on a numerical procedure developed in previous works, which compares the dynamic motions associated respectively with the slip law and the slowness law (He and Ma 1997; He 1999). In the succeeding sections, we begin with review and discussion on the result of linear stability analyses in previous studies (Dieterich and Linker 1992; He et al. 1998) and then focus on the following problems that have not been touched yet: (a) non-linear stability in a single degree of freedom system under varying normal stress in response to rate step and displacement step perturbations as compared to the fixed normal stress case and (b) difference between the two laws in non-linear stability and dynamic motions. In this way, we hope to see a more complete picture of the dynamics of a spring-slider system when the normal stress is varying, thereby better understanding the behavior of constitutive laws in an analogous seismogenic system under variable normal stress condition.

2 Constitutive laws with variable normal stress

2.1 Constitutive laws

There are two types of rate and state friction law that have been most commonly used in previous analyses. When normal stress is constant, one of the friction laws uses a state variable that evolves only with slip, whereas the state variable in the other also evolves with time of truly stationary contact. Following Beeler et al. (1994), here the former is referred to as “slip law” and the latter as “slowness law”. The laws have different features in two major aspects: a previous study has revealed that the slowness law fits better to observations on strength change during hold-slide tests than the slip law does (Beeler et al. 1994). Direct observation of frictional contact (Dieterich and Kilgore 1994, 1996) also found that contact area increases with time of stationary contact, which the slip law fails to describe. In another study (Perrin et al. 1995) on existence of self-healing pulse during earthquake fault slip as proposed by Heaton (1990), it was found that steady pulse solution exists with the slowness law but does not exist when the slip law is adopted. On the other hand, the responses of the slip law to upward and downward steps are symmetric, whereas that of the slowness law is not. The symmetric feature of the slip law is believed to fit better the transient sliding behavior after a step change of slip rate (Kato and Tullis 2001; Bayart et al. 2006; Ampuero and Rubin 2008); thus the slip law reproduces well the responses to changes from a steady state. The advantages of each of the evolution laws can be combined in a composite rate and state friction law as Kato and Tullis (2001, 2003) proposed and demonstrated in their studies, though the formulation is more complicated than the commonly used ones. Despite the difference between the two evolution laws and other differences especially in evolution patterns of the state variable during stick-slip motions (He et al. 2003), the two evolution laws have many features in common. At a steady state under a given sliding rate, the friction coefficient is the same for both the slip and slowness laws. In a single spring-slider system, the two laws also have common criteria of stability under small perturbations for both constant normal stress (Ruina 1983) and varying normal stress cases (Dieterich and Linker 1992).

In the slip law, shear stress τ is related to normal stress σ, slip velocity V, and state variable Θ as follows (Linker and Dieterich 1992):

$$\mathit{\tau }={\mathit{\mu }}_{\ast }\mathit{\sigma }+a\mathit{\sigma }ln\frac{V}{V_{\ast }}+\mathit{\sigma }\mathrm{\Theta },$$

(1a)

where μ_* is steady-state value of friction coefficient at a reference velocity V_*, and a is a parameter to describe the amplitude of direct rate effect.

The evolution of the state variable is governed by the following differential equation:

$$\frac{\text{d}\mathrm{\Theta }}{\text{d}t}=-{\frac{1}{D}}_{\text{c}}\left(\mathrm{\Theta }+bln\frac{V}{V_{\ast }}\right)\frac{\text{d}\mathit{\delta }}{\text{d}t}-\frac{\mathit{\alpha }}{\mathit{\sigma }}\frac{\text{d}\mathit{\sigma }}{\text{d}t},$$

(1b)

where b is a parameter representing the amplitude of evolution effect on shear stress, and δ is slip distance with V = dδ/dt. The first term on the right side of (1b) is a description of state evolution under constant normal stress, and it is evident that the evolution is a exponential decay from a previous state if V is held constant, and D_c is the characteristic slip distance in the evolution. The second term of the above equation describes the effect of normal stress on state variable, and increase of normal stress reduces the state value, with parameter α representing the degree of the normal stress effect on the state variable. For the constant normal stress case, this term equals to 0. It is evident that Θ does not evolve during stationary contact, i.e., V = dδ/dt = 0, this is why it has been referred to as slip law (evolves only when slip occurs). The effect of normal stress can be illustrated by imposing a step change of normal stress and then observing the response. According to (1a) and (1b), it is evident that a jump from σ_* to σ_* +∆σ causes an instantaneous changes in Θ and friction stress as follows (He and Ma 1997):

$$\mathrm{\Delta }\mathrm{\Theta }=-\mathit{\alpha }ln\left(1+\mathrm{\Delta }\mathit{\sigma }/{\mathit{\sigma }}_{\ast }\right),$$

(2)

$$\mathrm{\Delta }\mathit{\tau }={\mathit{\mu }}^{\text{ss}}\mathrm{\Delta }\mathit{\sigma }-\mathit{\alpha }ln\left(1+\mathrm{\Delta }\mathit{\sigma }/{\mathit{\sigma }}_{\ast }\right),$$

(3)

with μ^ss = μ_* − (b − a)ln(V/V_*). During the subsequent evolution, dσ/dt = 0, and it is evident from (1a) and (1b) that Θ and τ evolve exponentially to –b ln(V/V_*) and μ^ss(σ_* + ∆σ), respectively.

The slowness law with variable normal stress is described by the following equations (Linker and Dieterich 1992):

$$\mathit{\tau }={\mathit{\mu }}_{\ast }\mathit{\sigma }+a\mathit{\sigma }\text{ln(}V/V_{\ast })+b\mathit{\sigma }ln(\mathit{\theta }/{\mathit{\theta }}_{\ast }),$$

(4a)

$$\frac{\text{d}\mathit{\theta }}{\text{d}t}=\left(1-\frac{\mathit{\theta }V}{D_{\text{c}}}\right)-\frac{\mathit{\alpha }\mathit{\theta }}{b\mathit{\sigma }}\frac{\text{d}\mathit{\sigma }}{\text{d}t}.$$

(4b)

The second equation characterizes the evolution of the state variable θ, and it is clear that the state variable can increase with time even when the slip velocity is 0. At a steady state under slip rate V, θ = D_c/V, i.e., the state variable increases with the inverse of velocity, a measure of slowness. Again, the second term describes the effect of normal stress on state variable, and increase of normal stress reduces the state value.

It should be noted that Θ in (1a) can be replaced by ln(θ/θ_*) and (1b) can be described equivalently by the state variable θ in a different form.

2.2 Spring-slider system driven by inclined principal stress and its linear stability

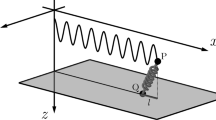
Consider a single degree of freedom spring-slider system shown in Fig. 1. It is seen that shear stress and normal stress on the slipping surface are related by

$$\mathit{\sigma }={\mathit{\sigma }}_3+\mathit{\tau }cot\mathit{\phi }.$$

(5)

Fig. 1

A single degree of freedom spring-slider system. V₀ and V are velocities of load point and the slider in the slipping direction, respectively. The system is driven by a horizontal principal stress, with the minimum principal stress σ₃ held constant. In this case, normal stress σ and shear stress τ on the slipping surface are linearly coupled

We discuss the case when the minimum principal stress σ₃ is constant. Under this condition, shear stress and normal stress are linearly coupled.

The equation of motion is

$$m\frac{{\text{d}}^2\mathit{\delta }}{\text{d}{t}^2}=k({\mathit{\delta }}_0-\mathit{\delta })-\mathit{\tau },$$

(6)

where m is mass of the slider per unit area and k the equivalent stiffness in the slipping direction. δ₀ is the load point displacement induced by shear stress in the slipping direction. To simplify the parameters in (6), m/k can be replaced with (T/2π)², where T is the period of free oscillation (Rice and Tse 1986). For quasi-static motion, the left side of the equation can be put to 0. Similar to the constant normal stress case, this system is unstable around a certain steady state with any amount of perturbation when the stiffness k is lower than a critical value k_cr (Dieterich and Linker 1992):

$$k_{\text{cr}}=\frac{\left(b-a\right){\mathit{\sigma }}^{\text{ss}}}{D_{\text{c}}\left[1-cot\mathit{\phi }\left({\mathit{\mu }}^{\text{ss}}-\mathit{\alpha }\right)\right]},$$

(7)

where μ^ss and σ^ss are the steady-state coefficients of friction and normal stress, respectively, with μ^ss = μ _*  − (b − a)ln(V/V_*).

With further derivation, k_cr can be expressed by an explicit function of slip velocity V (He et al. 1998) as follows:

$$k_{\text{cr}}(V)=\frac{(b-a){\mathit{\sigma }}_{\ast }(1-{\mathit{\mu }}_{\ast }cot\mathit{\phi })}{D_{\text{c}}(1-{\mathit{\mu }}^{\text{ss}}cot\mathit{\phi })[1-({\mathit{\mu }}^{\text{ss}}-\mathit{\alpha })cot\mathit{\phi }]},$$

(8)

with μ^ss = μ_* − (b − a) ln(V/V_*). For velocity weakening (i.e., b − a > 0), k_cr is a decreasing function of V, as plotted in Fig. 2 with different values of fault angle φ. Every single curve divides the k-V plane into two regions. For stiffness and velocity values in the upper region, the system is linearly stable, i.e., stable under small perturbation around the steady state. In the region below the curve, the system is always unstable. For a given spring stiffness, the system can either be stable or unstable depending on the value of load point velocity. It is obvious that increasing velocity may stabilize the system, and vice versa.

Fig. 2

Linear stability boundaries under condition of variable normal stress when α = 0.56, a = 0.0145, b/a = 2, and μ_* = 0.76. Numbers are the angles between driving direction and the normal of slipping surface

There is another stability boundary: the system is unstable (Dieterich and Linker 1992) whenever

$$\mathit{\phi }<{tan}^{-1}{\mathit{\mu }}^{\text{ss}}.$$

(9)

When this condition is satisfied, the system will be unstable when stress decreases but the slider will lock up during loading. Also from this boundary, it is true that high load point velocity can improve the stability of the system.

By numerical simulation with the slip law, He et al. (1998) have shown that transition between stable sliding and stick slip occurs due to a jump in load point velocity that is sufficient to cross the stability boundary shown in Fig. 2. In the previous study, φ  = 60° was used in the model. The transition is not sensitive to velocity change in this case, because the curve is very flat. The boundaries become steeper with smaller values of φ, as shown in Fig. 2. This means that for fault angle that is less favorable for slip (as the case of San Andreas fault in central California), such transitions are more sensitive to the variation of load point velocity.

2.3 Responses to rate steps of a rigid body driven by inclined principal stress

To understand the effect of varying normal stress on the sliding behavior of an inclined fault, here we compare the responses to rate steps of an inclined rigid slider with that of a slider under constant normal stress. For the slip law, the responses in the constant and variable normal stress cases are basically similar (Fig. 3a, b), but the variable normal stress (Fig. 3a) tends to slow down the evolution to the new steady state as compared to the constant normal stress case (Fig. 3b). This trend is more prominent in the downward rate steps. Moreover, the direct effect of the rate steps also makes asymmetric responses in the upward and downward steps, leading to higher direct stress changes with the downward steps. Similarly, the effect of variable normal stress on the evolution of shear stress associated with the slowness law does not change much the evolution style except for some minor differences (Fig. 4a, b). Similar to the slip law, the effect of variable normal stress leads to slowing down evolution to the new steady state (Fig. 4a). The effect of variable normal stress also makes the indistinguishable response curves (Fig. 4b) for downward steps of 2–4 orders of magnitude seen in the constant normal stress case become separate (Fig. 4a).

Fig. 3

Plots of normalized stress as a function of normalized slip representing responses to upward rate steps (solid lines) and downward rate steps (dashed lines) of rigid sliders associated with the slip law. The variable normal stress cases (a) have slower evolution to the new steady state than in the constant normal stress cases (b), and the effect of normal stress makes the upward and downward rate steps asymmetric. Calculations were performed with a = 0.0145, b/a = 2, μ_* = 0.76, and α = 0.56. Numbers are new rate to reference rate ratio, and τ_ss is the future steady-state value

Fig. 4

Plots of normalized stress as a function of normalized slip representing responses to upward rate steps (solid lines) and downward rate steps (dashed lines) of rigid sliders associated with the slowness law. Similar to the slip law, the variable normal stress cases a have slower evolution to the new steady state than in the constant normal stress cases (b). The indistinguishable response curves for downward steps of 2–4 orders of magnitude seen in the constant normal stress case b become separate in the variable normal stress cases (a). Calculations were performed with a = 0.0145, b/a = 2, μ_* = 0.76, and α = 0.56. Numbers are new rate to reference rate ratio, and τ_ss is the future steady-state value

3 Non-linear stability analyses

In this section, we analyze the stability when the system is linearly stable, i.e., k > k_cr(V). We first analyze the stability of the system associated with the slip law, and make comparison with analytical results for constant normal stress case (Gu et al. 1984). Two types of perturbation are considered below: velocity steps and displacement steps imposed at the load point.

3.1 Stability under velocity step perturbations with the slip law

This analysis is to determine the amplitudes of velocity perturbation that is critical for triggering instability for given stiffness values. The step rate perturbations were made at the load point from the steady state at the reference velocity V₀ = V_* with a sudden step change to V₀ = cV_*, where c is the ratio between the current and previous rates. A procedure with numerical integration was used to find the critical values of load point velocity steps (for details see He and Ma 1997). Instability was determined by observing the slip velocity to see if the velocity accelerates to dynamical inertial motion by checking if VT/(2πD_c) is high enough to reach a predetermined norm, where T is the period of free oscillation of the system (He et al. 1997). Reducing to constant normal stress case, the procedure was checked using an analytical result by Gu et al. (1984). Though the numerical procedure tends to underestimate the critical velocity by 1 %–2 % when k > k_cr (the k = k_cr case has an error level less than 0.4 %), the results systematically agree with the analytic result.

First stability boundary is calculated for k = k_cr(V_*) with different b/a values, as shown in Fig. 5. The broken line corresponds a function

$$V_0/V_{\ast }=1+1/\mathit{\lambda },\mathit{\lambda }=(b-a)/a,$$

(10)

Fig. 5

Critical values of load point velocity for triggering instabilities with the slip law when k = k_cr(V_*). Broken line is an analytical result for σ = const. by Gu et al. (1984). Values for the variable normal stress cases are smaller in comparison with the constant normal stress one. The slopes are coefficients to be multiplied with a/(b − a) in the linear relation between V₀/V_* and a/(b − a). The constant normal stress case has a slope of unity. Parameters are set as in Table 1

which is analytically derived for fixed normal stress case by Gu et al. (1984). The numerical calculation was conducted for α = 0.56 and α = 0.25, with other parameters shown in Table 1. Similar to the fixed normal stress case, the critical rate steps in the variable normal stress case scale with a/(b − a) when k = k_cr with a form of V₀/V _*  = 1 + ζa/(b − a), where ζ is a coefficient smaller than unity. The boundaries for varying normal stress cases are below the boundary for fixed normal stress, and a smaller value of α corresponds to a higher boundary. For a relatively large α = 0.56, the rate-step boundary in the variable normal stress case is lower than the fixed normal stress case by 7 %–16 % when (b − a)/a ranges from 0.25 to 1. Another result is given for b/a = e ≈ 2.71828 with different stiffness values, shown in Fig. 6. Analytical result is also available for this case when σ = const (Gu et al. 1984):

$$V_0/V_{\ast }=\left(1/\mathit{\lambda }\right)exp(\mathit{\kappa }/\mathit{\lambda }),\mathit{\lambda }=\mathbf{e}-1,$$

(11)

Table 1 Parameters used in the calculations for non-linear stability analysis

Fig. 6

Stability boundary for perturbations in load point velocity with b/a = e ≈ 2.71828 and other parameters shown in Table 1. When α = 0.56, the result for variable normal stress is smaller than the constant normal stress case by ~12 %, while another result for α = 0.25 is very close to the constant normal stress result (solid line) by Gu et al. (1984)

where κ = kD_c/aσ. While the numerical result for α = 0.56 is below the boundary for the fixed normal stress case, but the result for α = 0.25 is very close to the fixed normal stress case. For α = 0.56, the critical values of velocity is smaller than the values for the fixed normal stress case by ~12 %. These results indicate that systems with varying normal stress is systematically less stable than the fixed normal stress case when the system is imposed to step-like velocity perturbations.

3.2 Stability of systems with the slip law under displacement step perturbation

We consider the system stability under step-like displacement perturbation imposed at the load point. The system is assumed sliding in steady state, then imposed to a step of load point displacement with stationary load point velocity, as has been analyzed for fixed normal stress case by Gu et al. (1984).

This problem is a little different from the analyses above because imposing a step change in load point displacement causes instantaneous changes in shear stress and state variable. For a time marching integration procedure, such instantaneous changes should be dealt as initial conditions.

When a step increment in load point displacement ∆δ₀ is imposed, shear stress will change instantaneously by δτ = k∆δ₀. According to (5), normal stress changes simultaneously by ∆σ = k∆δ₀ cotφ.

By integrating (1b) at t = 0 during the instantaneous change in normal stress, we obtain the instantaneous change in state:

$$\begin{array}{cc}\hfill \mathrm{\Delta }\mathrm{\Theta }& =-\mathit{\alpha }ln(\mathit{\sigma }/{\mathit{\sigma }}_{\ast })\hfill \\ \hfill & =-\mathit{\alpha }ln(1+\mathrm{\Delta }\mathit{\sigma }/{\mathit{\sigma }}_{\ast }).\hfill \\ \hfill \end{array}$$

To determine the slip velocity immediately after the instantaneous change, we need a general relation between shear stress, state and slip velocity. It is evident from (1a) and (5) that any state away from the reference state at V = V_* has a general relation as follows:

$$\frac{\mathit{\tau }-{\mathit{\tau }}_{\ast }}{a{\mathit{\sigma }}_{\ast }}=\frac{ln\left(V/V_{\ast }\right)+\mathrm{\Theta }/a}{1-cot\mathit{\phi }\left[{\mathit{\mu }}_{\ast }+aln\left(V/V_{\ast }\right)+\mathrm{\Theta }\right]}.$$

(12)

At the moment immediately after the instantaneous change, τ − τ* = ∆τ = k∆δ₀ and Θ = ∆Θ = −αln(1 + Δσ/σ_*). By rearranging the above equation, the ultimate slip velocity after the instantaneous change can be calculated explicitly by

$$V=V_{\ast }exp\left\{\frac{\left[1-cot\mathit{\phi }({\mathit{\mu }}_{\ast }+\mathrm{\Delta }\mathrm{\Theta })\mathrm{\Delta }\mathit{\tau }/(a{\mathit{\sigma }}_{\ast })-\mathrm{\Delta }\mathrm{\Theta }/a\right]}{1+\mathrm{\Delta }\mathit{\tau }cot\mathit{\phi }/{\mathit{\sigma }}_{\ast }}\right\}.$$

(13)

With these instantaneous changes derived, the initial values for further numerical procedure are straightforward. For comparison, we also show the analytical result for the case with σ = const., which has been derived by Gu et al. (1984) for any stiffness k ≥ k_cr, as follows:

$$\mathrm{\Delta }{\mathit{\delta }}_0=D_{\text{c}}/\mathit{\lambda }.$$

(14)

Figure 7 shows the numerical result when k/k_cr(V_*) = 1, with parameters shown in Table 1. Numerical analysis for σ = const. is also conducted for checking the numerical procedure. As seen in Fig. 7, the results for different situations are very close to one another. Results with other stiffness values show maximum difference of a few percents as compared with (14), the boundary for fixed normal stress case.

Fig. 7

Stability boundary for perturbations in load point displacement with the slip law, with b/a = 2, k = k_cr(V_*), and other parameters set as in Table 1. Broken line is the result for constant normal stress by Gu et al. (1984). All cases show no significant difference from one another

It should be noticed that the stability is poor around the steady state when imposed to a displacement step because the displacement step increase for triggering an instability is D_c/λ, a very small value. The reason for this is that a small amount of displacement causes a considerable instantaneous change in slip velocity. With parameters given in Table 1 and according to (13), when α = 0.56 and k = k_cr(V_*), the ultimate slip velocity V after the instantaneous change in responding to load point displacement change of D_c/λ is 2.697 V _* .

3.3 Non-linear stability of systems associated with the slowness law

Ranjith and Rice (1999) have conducted analyses on the fixed normal stress case. The result says that when k > k_cr, slip is always stable. In this sub-section, we conduct numerical integration to examine the problem for variable normal stress case. Concretely, we examine the quasi-static motion under various amounts of load point velocity jump, and see whether slip velocity is always bounded when k > k_cr(V_*). In quasi-static motion, equation of motion reduces to

$$\mathit{\tau }=k({\mathit{\delta }}_0-\mathit{\delta }).$$

(15)

Solving (4a), (4b), (5), and (15) by numerical integration with a time marching procedure (He and Ma1997), quasi-static solutions can be obtained so far as the slip velocity is bounded.

Existence of such quasi-static solutions was confirmed by our numerical procedure for a broad range of load point velocity steps. Figure 8 shows two examples with jump of V₀ from V_* to 2 V_* and to 200 V_*, respectively. The former shows a slowly decaying oscillation, whereas the other (for V₀ = 200 V_*) shows a remarkable difference in amplitude between the first and the subsequent oscillations.

Fig. 8

Two examples of quasi-static solution for a system associated with the slowness law after perturbations are imposed to the load point velocity, with k = k_cr(V_*), b/a = 2, α = 0.56, and other parameters set as in Table 1. The existence of such solutions is confirmed for a broad range of large perturbations when k ≥ k_cr(V_*). Broken line is the steady-state line

These results mean that the slip velocity can be bounded under considerable amplitude of perturbations. Theoretically, a numerical procedure cannot prove vigorously that this is always true for any amount of velocity perturbation, but these results can be regarded as evidences if we assume hypothetically that velocity is always bounded in quasi-static motion when k > k_cr(V_*).

As displacement disturbances imposed at the load point lead to instantaneous changes in sliding velocity (similar to the slip law case), such disturbances do not destabilize the system as well because any change in sliding velocity does not destabilize the system when k > k_cr(V_*).

3.4 Features of Stick-slip Motions

The first analysis on complete stick-slip motions that incorporate inertia was conducted by Rice and Tse (1986) with the slip law and under constant normal stress condition. The same analysis with the slip law under variable normal stress condition was documented by He and Ma (1997) and subsequent works (He et al. 1998; He 1999). With k = 0.8k_cr(V_*) < k_cr(V_*), here we show an example in stress-velocity phase plane plots (Fig. 9) for comparison with the fixed normal stress case (with b/a = 2, a = 0.0145, α = 0.56, μ_* = 0.76, T = 5 s, φ = 60°, and V_*/D_c = 1.1710⁻⁸/s). Unstable slips are initiated by a step change in V₀ from V_* to 2 V_*, and the subsequent motions are limit cycles (periodic stick-slips). It is evident that the variable normal stress case has larger stress drop than the constant normal stress case, and the stress-velocity phase plot exhibits a long tail in the deceleration phase. The slowest velocity for the variable normal stress case is lower than the constant normal stress case by 10 orders of magnitude. While the trajectory of the fixed normal stress case during the deceleration phase mostly follows a constant state line, that of the variable normal stress intersects with the constant state lines (numbered dot lines), indicating that the state variable increases with decreasing normal stress in the deceleration phase, governed by the evolution law (1b).

Fig. 9

Phase plane plots of stick-slip motion with the slip law when k = 0.8k_cr(V_*), b/a = 2, V₀ = 2 V_*, α = 0.56, and other parameters set as in Table 1. Numbers are values of state variable at the constant state lines (dot lines). In the deceleration phase, the variable normal stress case has a long tail and greater stress drop in comparison with the constant normal stress case. See text for details

Similar complete stick-slip motions with the slowness law under variable normal stress have preliminarily been documented by He (1999). By replacing (1a) and (1b), respectively, with (4a) and (4b), the same procedure employed in analyses with the slip law can be used for analyses with the slowness law. Also, constant normal stress case can be easily reduced from the variable normal stress case. The calculation starts from steady-state sliding at the reference velocity V_*, so the initial value of θ is θ_* = D_c/V_*. With the same parameters as set in the slip law cases shown in Fig. 9, results for the slowness law are shown in Fig. 10, making comparison between fixed and varying normal stress cases. Unlike the stick-slip motions with the slip law, the range of velocity variation for both cases are similar. Moreover, there is a segment where the stress is roughly constant, corresponding to an important recovery process after the instability where the major proportion of state value reduced during the acceleration phase regains. From (4a), it is evident that logarithms of velocity and state are linearly related in this segment, and the state variable is approximately proportional to V^−a/b. When b/a = 2, as in the two cases here, θ increases with V^−1/2 as V decreases. Compared to results with the slip law, stress drops in these results are smaller, and the effect of varying normal stress is much less pronounced.

Fig. 10

Phase plane plots of stick-slip motions with the slowness law when k = 0.8k_cr(V_*), b/a = 2, V₀ = 2 V_*, α = 0.56, and other parameters set as in Table 1. In the deceleration phase, both cases have a segment where shear stress is roughly constant. See text for details

Figure 11 shows the stress-slip trajectory of the stick-slip motions corresponding to Fig. 10. Different to the slip law (Rice and Tse 1986; He and Ma 1997), an evident feature of these curves is that the stress drops in the acceleration and deceleration phases are strongly asymmetrical. This is easily understood when the effect of a velocity jump is considered in a rigid system for a σ = Const case. It is evident from (4b) that the evolution of state variable θ is an exponential decay as follows:

$$\mathit{\theta }=D_{\text{c}}/V+\left(D_{\text{c}}/V_{\ast }-D_{\text{c}}/V\right){\text{e}}^{-\mathit{\delta }/D_{\text{c}}},$$

(16)

with θ = D_c/V_* at t = 0, and δ = 0.

Fig. 11

Plots of stress versus slip of the examples shown in Fig. 10. Stress drops in acceleration and deceleration are strongly unsymmetrical. The “shear fracture” energy is larger in comparison with the slip law

However, the stress variation corresponding to the evolution of θ is more complicated than a simple exponential function as follows:

$$\mathit{\tau }=-b\mathit{\sigma }ln(V/V_{\ast })+b\mathit{\sigma }ln[1+(V/V_{\ast }-1){\text{e}}^{-\mathit{\delta }/D_{\text{c}}}].$$

(17a)

When the velocity step is small, this relation can be approximated by an exponential function through employing an approximation ln(1 + x) ≈ x (|x| ≪ 1) twice as follows:

$$\mathit{\tau }\approx -b\mathit{\sigma }ln(V/V_{\ast })+b\mathit{\sigma }ln(V/V_{\ast }){\text{e}}^{-\mathit{\delta }/D_{\text{c}}},\left|(V-V_{\ast })/V_{\ast }\right|\ll 1.$$

(17b)

This approximate relation is identical to the result with the slip law (Gu et al. 1984).

For large steps of velocity, (17b) is no longer valid. The full function (17a) is a decay that is much slower than the exponential function (17b), see evolution patterns of shear stress in Fig. 4. For example, if V jumps from V_* to 200 V_*, drop of stress to 1/e of the total stress reduction requires a slip of ~3.5D_c, a much longer distance than otherwise in the exponential decay (where slip distance of D_c is required). Due to this sluggish property, stress in the acceleration phase decreases slowly, hence the excess energy is relatively smaller than what would be if the slip law applies. In the deceleration phase, stress drop has to be smaller than the dynamic drop to balance with the small excess energy.

3.5 Loading rate dependence of stress drops

For the slip law, it has been found that dynamic stress drop scales with ln(V₀) and (a − b)σ when σ = Const. (Cao and Aki 1986; Gu and Wong 1991). The full stress drops (static stress drop) have a similar scaling law with a steeper slope 2(a − b)σ instead of (a − b)σ. For the variable normal stress case shown in Fig. 1, these relations can be corrected by replacing a − b with (a − b)/(1 − μ_*cotφ) for velocity step changes from V_* to V₀ (He and Ma 1997).

We also conducted some calculations with the slowness law and found that the stress drops similarly scale with ln(V₀) and (a − b)σ_*. Analysis on the fixed normal stress case indicates that the stress drop also depends on stiffness, thus the static stress drop scales with (a − b)σ ln(V₀)f(k) (He et al. 2003), where f(k) is a function of stiffness. Though the relation between stress drop and ln(V₀) for the variable normal stress case is more complicated as seen in our results, it is evident from Figs. 9 and 10 that the stress drop has a higher sensitivity to ln(V₀) than in the fixed normal stress case, thus it should scale with ln(V₀) by a slope steeper than (a − b)σf(k).

4 Discussion and conclusion

For systems associated with slip law and when k > k_cr(V) under variable normal stress (i.e., stable under small perturbations), boundaries for triggered instability in such systems are quite similar to the constant normal stress case. While smaller critical velocity step perturbations are revealed for the variable normal stress case as compared to the fixed normal stress case, the boundaries of stability in response to displacement perturbations are approximately identical for fixed and variable normal stress cases. On the other hand, for systems associated with the slowness law and under fixed normal stress, slip is always stable when k ≥ k_cr as shown by Ranjith and Rice (1999). By mathematical analysis, this ‘stable’ situation only means the existence of quasi-static solution for any amounts of perturbations, and the absence of high-velocity inertial slip is not guaranteed here. As shown in Fig. 8, a quasi-static solution for variable normal stress case after a very large perturbation (V₀ stepped from V_* to 200 V_*) shows a much higher slip velocity than expected for real quasi-static motion, and this implies the necessity of incorporating inertia. Figure 12 shows the corresponding full solution (inertia included) compared with the quasi-static one shown in Fig. 8. The full solution and the quasi-static counterpart deviate from each other at a certain point in the acceleration phase and merge again in the deceleration phase on the constant stress segment. The maximum slip velocity in full solution is lower than the quasi-static solution by one order of magnitude. The significant inertia-controlled motion indicates the occurrence of triggered instability. In other words, when k ≥ k_cr(V_*), the slip can also be unstable if the system is imposed to a perturbation of sufficient amplitude, despite the fact that the slip velocity is mathematically bounded and thus mathematically defined as ‘stable’.

Fig. 12

Comparison between the full and quasi-static solutions with the slowness law when k = k_cr(V_*), α = 0.56, b/a = 2, V₀ = 200 V_*, and other parameters set as in Table 1

Nevertheless, the existence of quasi-static solution with the slowness law for large perturbations implies that, when k ≥ k_cr(V_*), a system associated with the slowness law is much more stable than systems associated with the slip law. As an example of a system with the slowness law, when k = k_cr(V_*), b/a = e ≈ 2.71828, α = 0.56 and other parameters shown in Fig. 6, numerically obtained critical perturbation in V₀ is ~11.8 V_*, which is a much higher value than the result with the slip law (Fig. 6). Likewise, when k = 1.5 k_cr(V_*), the critical perturbation amount of V₀ is ~2361 V_*, suggesting that the system is very stable.

Though the slip law is commonly considered to be more suitable to fit stable sliding data than the slowness law, it seems not to be suitable to fit oscillatory slips when the system stiffness is around the critical value. From oscillatory slips observed in experiments on plagioclase gouge under hydrothermal conditions (He et al. 2013), the persisting oscillations when the load point velocity was stepped by tenfold changes back and forth were fitted to the slowness law but failed to be fitted to the slip law when a single state variable was adopted, because a system associated with the slip law is prone to inertial slips under such large perturbations(Fig. 5).

As for the effect of variable normal stress on stick-slip motions, two points are worth mentioning here: (1) The static stress drop of spring-slider systems increases significantly due to the effect of variable normal stress. The effect is more pronounced for systems associated with the slip law, and the static stress drop scales with ~2ln(V₀) (a − b)σ_*/[1 − μ_*cot(φ)] instead of ~2ln(V₀) (a − b)σ for the fixed normal stress case. (2) While the variable normal stress has little effect on the range of slip velocity in systems associated with the slowness law, systems associated with the slip law have a slowest slip velocity immensely smaller than the fixed normal stress case, roughly by 10 orders of magnitude.

Finally, it should be noted that the mechanical behavior exhibited by the spring-slider system cannot be regarded as an example of more realistic systems such as a planar fault in the earth crust, though some of the properties are similar in the two categories, as seen in similar slip-weakening behavior in both the spring-slider system and in coseismic slip simulation on a planar fault (Bizzarri and Cocco 2003). Thus, the mechanical behavior shown in this study through analyses on a simple system serves to help understand the intrinsic property of the rate and state friction laws rather than to know mechanical processes of more realistic systems.