Inertial Halpern-type method for solving split feasibility and fixed point problems via dynamical stepsize in real Banach spaces

Abstract

In this paper, we introduce a modified Halpern inertial method for approximating solutions of split feasibility problem and fixed point problem of Bregman strongly nonexpansive mappings in the framework of p-uniformly convex and uniformly smooth real Banach spaces. We establish a strong convergence result for the sequence generated by our iterative scheme under some mild conditions without the computation of the operator norm. We state some consequences and present some examples to show the efficiency and implementation of our proposed method. The result discussed in this paper extends and generalizes many recent results in this direction. Our result extends and complements some related results in literature.

1 Introduction

Let $X_1$ and $X_2$ be p-uniformly convex and uniformly smooth real Banach spaces, C and Q are nonempty, closed and convex subsets of $X_1$ and $X_2$ respectively. The Split Feasibility Problem (SFP) is to find

$$\begin{aligned} x \in C ~\text {such that}~y=Fx \in Q, \end{aligned}$$

(1.1)

where $F: X_1 \rightarrow X_2$ is a bounded linear operator. We denote by $\Omega := C \cap F^{-1}(Q)$ the solution set of SFP, then we have that $\Omega$ is a closed and convex.

One of the most attractive problem in optimization is the SFP due to its numerous applications to real life problems such as signal processing, image reconstruction and medical care, (see [9, 10, 20]). Many interesting optimization problems such as equilibrium, variational inequality, variational inclusion and convex minimization problems have been defined in terms of SFP, (see [1, 5, 14, 20,21,22]). Many well known iterative algorithms have been proposed to solve the SFP (see [3, 4, 6, 17, 20]). In 1994, Censor and Elving [10] used the idea of multi-distance to obtain iterative methods for solving SFP. Their iterative methods, as well as others later, involve matrix inverses at each iteration. Bryne [8] introduced a projection method known as the CQ algorithm for approximating the SFP that does not involve matrix inverses, but assumed that the metric projections onto C and Q are easily calculated. However in most cases, it is impossible or needs too much work to compute the metric projections. Therefore if such appears, the efficiency of the projection-type methods including the CQ algorithm will be affected. In 2004, Yang [31] introduced a relaxed CQ for solving the SFP, where he employed two half spaces $C_k$ and $Q_k$ to replace C and Q respectively, at the kth iteration and the metric projections onto $C_k$ and $Q_k$ are easily computed. Recently Lopez et al. [15] introduced a self-adaptive step size to improve the CQ and the relaxed CQ iterative methods. It was noted that all these aforementioned iterative methods only use the current point to get the next iteration, which does not use the previous iteration $x^{k-1}, x^{k-2}, \ldots ,$ and affect the flexibility. It is known that using some information of previous iterates will increase the flexibility of the algorithm. The study of SFP has been extended to the framework of 2-uniformly convex and uniformly smooth real Banach spaces. For instance, Ma et al. [17] proposed a shrinking iterative method for SFP and fixed point problem of quasi-$\phi$-nonexpansive mappings in Banach spaces. They proved a strong convergence result without imposing any compactness conditions and display a numerical example to show the behavior of their result.

In 2007, Schopfer [25] introduced the following algorithm: $x_1 \in X_1$ and

$$\begin{aligned} x_{n+1}=\Pi _{C}J_{X_{1}^{*}}\big [J_{X_{1}}(x_n)-\gamma _nF^*J_{X_2}(Fx_n-P_{Q}(Fx_n))\big ],~n \ge 1, \end{aligned}$$

(1.2)

where $\Pi _C$ denotes the Bregman projection and J is the duality mapping. It is clear that (1.2) contains the CQ algorithm as a special case. In addition, Schopfer [25] obtained a weak convergence result for solving SFP provided the duality mapping J is weak-to-weak continuous and $\gamma _n \in \bigg (0, \big (\frac{q}{C_q\Vert F\Vert ^{q}}\big )^{\frac{1}{q-1}}\bigg )$, where $\frac{1}{p}+ \frac{1}{q}=1$ and $C_q$ is the uniform smoothness coefficient of X. Readers should consult [3, 4, 6, 10, 20, 22, 24, 31] for more results on SFP and its generalization.

In optimization theory, one of the best ways to fasten up the rate of convergence of iterative method is to combine the iterative method with an inertial term. This term which is represented in its originality as $\theta _n(x_n-x_{n-1})$ is a remarkable tool for improving the performance of iterative methods and it is known to have some nice convergence properties. Polyak [23] was the first to proposed the inertial extrapolation method for solving convex minimization problem. The inertial method is a two-step iterative method, using the first two iterations to define the next iteration. Nestrov [19] proposed a modified method to improve the convergence rate as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} v_n=x_n + \theta _n (x_n-x_{n-1}),\\ x_{n+1}=v_n-\lambda _n \nabla f(v_n),~n \ge 1, \end{array}\right. } \end{aligned}$$

(1.3)

where $\theta _n \in [0,1)$ is an extrapolation factor, and $\{\lambda _n\}$ is a positive sequence. Inspired by the inertial extrapolation method, many authors have proposed different inertial iterative methods to solve a number of optimization problems, see [1, 2, 4, 23, 24, 28]. It is worth mentioning that most results involving inertial extrapolation method in Banach spaces requires the modification or relaxation of the inertial term (most especially when Halpern method is employed, see (1.4) below) due to the geometry of the space and convexity problem. To retain its originality (i.e. $\theta _n(x_n-x_{n-1}))$ in the aforementioned space, the shrinking or Hybrid iterative methods need to be employed. For instance, Godwin et al. [14] introduced the following inertial Halpern method for solving common solution of split minimization and fixed point problems with finite family of Bregman relatively nonexpansive mappings in the framework of p-uniformly convex and uniformly smooth Banach spaces. Given iterates $x_{n-1}, x_n,$ compute $\{x_n\}$ as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} w_n=J_{X^{*}}^{q}\big [J_{X}^{p}(x_n) + \theta _n(J_{X}^{p}(x_{n-1})-J_{X}^{p}(x_n))\big ],\\ y_n=J_{X^{*}}^{q}\bigg [\sum \limits _{i=0}^{N}\beta _{i,n}(J_{X}^{p}(w_n)-\tau _{i,n}T_i^{*}J_{X_i}^{p}(I^{X_i}-prox_{\lambda ^{i}}^{f_i})T_i(w_n))\bigg ]\\ z_n=J_{X^{*}}^{q}\bigg [\phi _{n,0}J_{X}^{p}(y_n) + \sum \limits _{j=1}^{m}\phi _{n,j}J_{X}^{p}(S_jy_n)\bigg ]\\ x_{n+1}= J_{X^{*}}^{q}\big (\alpha _{n} J_{X}^{p}(u) + (1-\alpha _{n})J_{X}^{p}(z_n)\big ), \end{array}\right. } \end{aligned}$$

(1.4)

where

$$\begin{aligned} \tau _{i,n} \in \left( \epsilon , \left( \frac{q\Vert T_i(w_n)-(prox_{\lambda _n^{i}}^{f_i})T_i(w_n)\Vert ^{p}}{C_q\Vert T_i^{*}J_{X_i}^{p}(I^{X_i}-prox_{\lambda _n^{i}}^{f_i})T_i(w_n)\Vert ^{q}}-\epsilon \right) ^{\frac{1}{q-1}}\right) , \end{aligned}$$

$\forall ~n \in \Omega ,$ where the index set $\Omega :=\{n \in {\mathbb {N}}: T_i(w_n)-(prox_{\lambda _n^{i}}^{f_i}T_i(w_n)\ne 0)\}$, otherwise, $\tau _{i,n}=\tau _i$ is any nonnegative real number for each $i=0,1, \ldots , N.$ (Readers should consult [14] for definition of terms used in (1.4)). Also see [1, 2, 22] for results on modified inertial methods in Banach spaces.

Very recently, Shehu et al. [24] introduced the following self adaptive projection method with an inertial technique for split feasibility problems in Banach spaces: set $x_0, x_1 \in C,$ define a sequence $\{x_n\}$ by the following manner:

$$\begin{aligned} {\left\{ \begin{array}{ll} w_n=J_{E_1}^{q}\bigg [J_{X_1}^{p}(x_n) + \alpha _{n}(J_{X_1}^{p}(x_n)-J_{X_1}^{p}(x_{n-1}))\bigg ]\\ y_n=\Pi _{C}J_{X_1}^{q}\bigg [J_{X_1}^{p}(w_n)-\rho _n\frac{f^{p-1}(w_n)}{\Vert \nabla f(w_n)\Vert ^{p}}\nabla f(w_n)\bigg ]\\ C_n=\{u \in X_1: \Delta _p(y_n,u)\le \Delta _p(w_n, u)\}\\ Q_n=\{u \in X_1: \langle x_n-u, J_{X_1}^{p}(x_0)-J_{X_1}^{p}(x_n)\rangle \ge 0\}\\ x_{n+1}=\Pi _{C_n \cap Q_n}(x_0), \end{array}\right. } \end{aligned}$$

(1.5)

for all $n \ge 0$ where $f(w_n):=\frac{1}{p}\Vert (I-P_Q)Aw_n\Vert ^{p}$, $\{\rho _n\} \subset (0, \infty ),$ and $\liminf \limits _{n \rightarrow \infty }\rho _n(p-C_q\frac{\rho _n^{q-1}}{q})> 0.$ In (1.5), $X_i, i=1,2$ is a p-uniformly convex real Banach space which is also uniformly smooth, C and Q are nonempty, closed and convex subsets of $X_1$ and $X_2.$

It cab be seen from (1.4) where the Halpern method is employed that the inertial term is being modified. Also, in (1.5), the inertial term retain its originality as defined by Polyak [23] due to the nature of the algorithm.

Question Can we approximate solution of SFP and fixed point problem in p-uniformly Banach spaces which are also uniformly smooth with an inertial-Halpern method without modifying the inertial term, (see [2])?

In this article, we give an affirmative answer to the above question. We also state our contributions in this article as follows:

Remark 1.1

• (i) We consider SFP in p-uniformly convex and uniformly smooth Banach space which generalizes the results of [17].

• (ii) The step size $\rho _n$ employed in our main result is generated at each iteration by some computation. Thus our algorithm is easily implemented without prior knowledge of operator norm.

• (iii) The inertial term employed in our main result retain its originality as defined by Polyak [23]. It is worth-mentioning that the results on inertial Halpern method in Banach spaces requires the modification or relaxation of the inertial term (see [2, 14, 22]) due to the geometry of the spaces (convexity to be precise). Thus, in our result, we proved a strong convergence result without modifying the inertial term.

• (iv) Our algorithm does not require at each step of the iteration process, the computation of subsets of $C_n,~ Q_n$ and $D_n$ (or $C_{n+1})$ as in the case in [24] and the computation of the projection of the initial point onto their intersection, which leads to a high computational cost of iteration processes. The removal of all these restrictions makes our work applicable to more real world problems.

• (v) The inertial technique employed in our article is easily implemented since the value of $\Vert J_{E}^{p}(x_n)-J_{E}^{p}(x_{n-1})\Vert$ is a prior known before choosing $\theta _n$.

Motivated by the works of [20, 22, 24] and other related results in literature, we proposed a modified Halpern inertial method for approximating solution of split feasibility problem of Bregman strongly nonexpansive mappings in p-uniformly Banach spaces which are also uniformly smooth. We establish a strong convergence result for solving the solution of the aforementioned problems. It is worth-mentioning that the iterative algorithm employed in this article is designed in such a way that it does not require the computation of operator norm. The result discussed in this article extends and complements many related results in the literature.

2 Preliminaries

We state some known and useful results which will be needed in the proof of our main theorem. In the sequel, we denote strong and weak convergence by "$\rightarrow$" and "$\rightharpoonup$", respectively.

Let X be a re al Banach space with norm $\Vert .\Vert$ and $X^*$ be the dual space of E. Let $K(X):=\{x \in X:\Vert x\Vert =1\}$ denote the unit sphere of X. The modulus of convexity is the function $\delta _X:(0,2]\rightarrow [0,1]$ defined by

$$\begin{aligned} \delta _X(\epsilon )=\inf \big \{1-\frac{\Vert x+y\Vert }{2}: x, y \in K(X),~\Vert x-y\Vert \ge \epsilon \big \}. \end{aligned}$$

The space X is said to be uniformly convex, if $\delta _X(\epsilon )> 0$ for all $\epsilon \in (0,2]$. Let $p > 1$, then X is said to be p-uniformly convex (or to have a modulus of convexity of power type p) if there exists $c_p > 0$ such that $\delta _X(\epsilon ) \ge c_p\epsilon ^{p}$ for all $\epsilon \in (0,2]$. Note that every p-uniformly convex space is uniformly convex. The modulus of smoothness of X is the function $\rho _X: {\mathbb {R}}^{+}:=[0, \infty )\rightarrow {\mathbb {R}}^{+}$ defined by

$$\begin{aligned} \rho _X(\tau )=\sup \big \{\frac{\Vert x+\tau y +\Vert x-\tau y\Vert }{2}-1: x, y \in K(X)\big \}. \end{aligned}$$

The space X is said to be uniformly smooth, if $\frac{\rho _X(\tau )}{\tau }\rightarrow 0$ as $\tau \rightarrow 0$. Let $q > 1$, then a Banach space X is said to be q-uniformly smooth if there exists $\kappa _q >0$ such that $\rho _X(\tau ) \le \kappa _q \tau ^{q}$ for all $\tau > 0$. Moreover, a Banach space X is p-uniformly convex if and only if $X^*$ is q-uniformly smooth, where p and q satisfy $\frac{1}{p}+ \frac{1}{q}= 1$, (see [12]).

Let $p > 1$ be a real number, the generalized duality mapping $J_{X}^{p}:X \rightarrow 2^{X^*}$ is defined by

$$\begin{aligned} J_{X}^{p}(x)=\{{\bar{x}}\in X^*: \langle x, {\bar{x}}\rangle =\Vert x\Vert ^p, \Vert {\bar{x}}\Vert =\Vert x\Vert ^{p-1}\}, \end{aligned}$$

where $\langle \cdot ,\cdot \rangle$ denotes the duality pairing between elements of X and $X^*$. In particular, $J_{X}^p=J_{X}^2$ is called the normalized duality mapping.

If X is p-uniformly convex and uniformly smooth, then $X^*$ is q-uniformly smooth and uniformly convex. In this case, the generalized duality mapping $J_{X}^{p}$ is one-to-one, single-valued and satisfies $J_{X}^p=(J_{X^*}^{q})^{-1}$, where $J_{X^*}^{q}$ is the generalized duality mapping of $X^*$. Furthermore, if X is uniformly smooth then the duality mapping $J_{X}^{p}$ is norm-to-norm uniformly continuous on bounded subsets of X, (see [13] for more details).

Let $f: X \rightarrow (-\infty , + \infty ]$ be a proper, lower semicontinuous and convex function, then the Frenchel conjugate of f denoted as $f^*: X^* \rightarrow (-\infty ,+ \infty ]$ is define as

$$\begin{aligned} f^*(x^*)=\sup \{\langle x^*, x\rangle -f(x): x \in X\},~x^*\in X^*. \end{aligned}$$

Let the domain of f be denoted as $(dom f)=\{x \in X: f(x)< +\infty \}$, hence for any $x \in int(dom f)$ and $y \in X$, we define the right-hand derivative of f at x in the direction y by

$$\begin{aligned} f^{0}(x, y)=\lim _{t \rightarrow 0^+}\frac{f(x+ty)-f(x)}{t}. \end{aligned}$$

Definition 1.2

[7] Let $f:X \rightarrow (-\infty ,+ \infty ]$ be a convex and G${\hat{a}}$teaux differentiable function. The function $\Delta _f: X \times X \rightarrow [0, + \infty )$ defined by

$$\begin{aligned} \Delta _f(x, y):=f(y)-f(x)- \langle \nabla f(x), y-x\rangle \end{aligned}$$

is called the Bregman distance with respect of f.

It is well-known that Bregman distance $\Delta _f$ does not satisfy the properties of a metric because $\Delta _f$ fail to satisfy the symmetric and triangular inequality property. Moreover, it is well known that the duality mapping $J_{X}^{p}$ is the sub-differential of the functional $f_p(.)= \frac{1}{p}\Vert .\Vert ^{p}$ for $p > 1$, see [11]. Then, the Bregman distance $\Delta _p$ is defined with respect to $f_p$ as follows:

$$\begin{aligned} \Delta _p(x,y)&= \frac{1}{p}\Vert y\Vert ^p-\frac{1}{p}\Vert x\Vert ^p-\langle J_{X}^{p}x, y-x \rangle \nonumber \\&=\frac{1}{q}\Vert x\Vert ^p-\langle J_{X}^{p}x, y \rangle + \frac{1}{p}\Vert y\Vert ^p\nonumber \\&=\frac{1}{q}\big (\Vert x\Vert ^p-\frac{1}{q}\Vert y\Vert ^p\big )-\langle J_{X}^{p}x-J_{X}^{p}y, y \rangle . \end{aligned}$$

(2.1)

The Bregman distance is not symmetric therefore is not a symmetric but it possess the following important properties:

$$\begin{aligned} \Delta _p(x,y)=\Delta _p(x,z) + \Delta _p(z,y)+ \langle z-y, J_{X}^{p}x-J_{X}^{p}y\rangle ,~\forall ~x,y, z \in X, \end{aligned}$$

(2.2)

and

$$\begin{aligned} \Delta _p(x,y) + \Delta _p(y,x)=\langle x-y, J_{X}^{p}-J_{X}^{p}\rangle ,~\forall ~x, y \in X. \end{aligned}$$

(2.3)

Let Fix(T) denotes the set of fixed points of a mapping T from C into itself. That is $Fix(T)=\{x \in C: Tx=x\}$. A point $p \in C$ is said to be an asymptotic fixed point of T, if C contains a sequence $\{x_n\}_{n=1}^{\infty }$ which converges weakly to p and $\lim \limits _{n\rightarrow \infty }\Vert x_n-Tx_n\Vert =0$. We denote by ${\hat{F}}ix(T),$ the set of asymptotic fixed points of T. Moreso, a mapping $T:C \rightarrow int(dom f)$ is said to be

• (i) Bregman relatively nonexpansive, if

  $$\begin{aligned} {{\hat{F}}ix(T)}=Fix(T)~\text {and}~\Delta _p(p, Tx) \le \Delta _p(p,x),~\forall ~x \in C,~p \in Fix(T). \end{aligned}$$

• (ii)   Bregman quasi-nonexpansive, if

  $$\begin{aligned} Fix(T) \ne \emptyset ~ \text {and}~ \Delta _p(p, Tx) \le \Delta _p(p, x),~\forall ~x \in C,~p \in Fix(T). \end{aligned}$$

• (iii) Bregman firmly nonexpansive mapping (BFNE) if

  $$\begin{aligned} \langle J_{p}^{X}(Tx)-J_{p}^{X}(Ty), Tx-Ty\rangle \le \langle J_{p}^{X}(x)-J_{p}^{X}(y), Tx-Ty\rangle ,~\forall ~x, y \in C, \end{aligned}$$

• (iv) Bregman strongly nonexpansive mapping (BSNE) [27] with ${{\hat{F}}ix(T)}\ne \emptyset$ if

  $$\begin{aligned} \Delta _{p}(y, Tx) \le \Delta _p(y,x),~\forall ~y \in {\hat{F}}ix(T) \end{aligned}$$

  and for any bounded sequence $\{x_n\}_{n \ge 1} \subset C$,

  $$\begin{aligned} \lim _{n \rightarrow \infty }(\Delta _p(y, x_n)-\Delta _p(y, Tx_n))=0 \end{aligned}$$

  implies

  $$\begin{aligned} \lim _{n \rightarrow \infty }\Delta _p(Tx_n, x_n)=0. \end{aligned}$$

Recall that a metric projection $P_C$ from X onto C satisfies the following property:

$$\begin{aligned} \Vert x-P_Cx\Vert \le \inf _{y \in C}\Vert x-y\Vert ,~\forall ~x \in X. \end{aligned}$$

It is well known that $P_Cx$ is the unique minimizer of the norm distance. Moreover, $P_Cx$ is characterized by the following properties:

$$\begin{aligned} \langle J_{X}^{p}(x-P_Cx), y-P_C x\rangle \le 0,~\forall ~y \in C. \end{aligned}$$

(2.4)

The Bregman projection from X onto C denoted by $\Pi _{C}$ also satisfies the property

$$\begin{aligned} \Delta _p(x, \Pi _C(x))=\inf _{y \in C}\Delta _p(x, y),~\forall ~x \in X. \end{aligned}$$

(2.5)

Also, if C is a nonempty, closed and convex subset of a p-uniformly convex and uniformly smooth Banach space X and $x \in X$. Then the following assertions holds:

• (i) $z=\Pi _{C}x$ if and only if

  $$\begin{aligned} \langle J_{X}^{p}(x)-J_{X}^{p}(z),~ y-z\rangle \le 0,~\forall ~y \in C; \end{aligned}$$

  (2.6)
• (ii)
  $$\begin{aligned} \Delta _p(\Pi _{C}x, y)+ \Delta _p(x, \Pi _Cx)\le \Delta _p(x,y),~\forall ~y \in C. \end{aligned}$$

  (2.7)

When considering the p-uniformly convex space, the Bregman distance and the metric distance have the following relation, (see [24]).

$$\begin{aligned} \pi _p\Vert x-y\Vert ^p \le \Delta _p(x,y) \le \langle x-y, J_{X}^{p}(x)-J_{X}^{p}(y)\rangle , \end{aligned}$$

(2.8)

where $\pi _p > 0$ is some fixed number. If $\frac{1}{p}+\frac{1}{q}=1$, by Young’s inequality, we have

$$\begin{aligned} \langle J^{p}_{X}(x),y\rangle \le \nonumber \Vert J^{p}_{X}(x)\Vert \Vert y\Vert\le & {} \frac{1}{q}\Vert J^{p}_{X}(x)\Vert ^{q}+\frac{1}{p}\Vert y\Vert ^{p}\\= & {} \frac{1}{q}(\Vert x\Vert ^{p-1})^{q}+\frac{1}{p}\Vert y\Vert ^{p}\nonumber \\= & {} \frac{1}{q}\Vert x\Vert ^{p}+\frac{1}{p}\Vert y\Vert ^{p}. \end{aligned}$$

(2.9)

Lemma 1.3

[11] Let X be a Banach space and $x, y \in X$. If X is q-uniformly smooth, then there exists $C_q > 0$ such that

$$\begin{aligned} \Vert x-y\Vert ^q \le \Vert x\Vert ^q - q\langle J_{q}^{X}(x),y \rangle + C_{q}\Vert y\Vert ^q. \end{aligned}$$

Lemma 1.4

[26] Let X be a real p-uniformly convex and uniformly smooth Banach space. Let $V_p: X^* \times X \rightarrow [0, +\infty )$ be defined by

$$\begin{aligned} V_p(x^*, x) = \frac{1}{q}\Vert x^*\Vert ^q- \langle x^*,x\rangle + \frac{1}{p}\Vert x\Vert ^p,~ \forall ~x \in X, x^* \in X. \end{aligned}$$

Then the following assertions hold:

• (i) $V_p$ is nonnegative and convex in the first variable.

• (ii) $\Delta _p(J_{q}^{X^*}(x^*), x)= V_p(x^*, x),~ \forall ~x \in X, ~x^* \in X$.

• (iii) $V_p(x^*, x) + \langle y^*,J_{q}^{X^*}(x^*)-x\rangle \le V_p(x^*+y^*,x), \forall ~x \in X,~x^*, y^* \in X$.

Lemma 1.5

[12] Let X be a real p-uniformly convex and uniformly smooth Banach space. Suppose that $\{x_n\}$ and $\{y_n\}$ are bounded sequences in X. Then  $\lim \limits _{n\rightarrow \infty } \Delta _p(x_n, y_n)=0$ implies  $\lim \limits _{n\rightarrow \infty }\Vert x_n-y_n\Vert =0$.

Lemma 1.6

[30] Assume $\{a_n\}$ is a sequence of nonnegative real sequence such that

$$\begin{aligned} a_{n+1} \le (1- \sigma _n)a_n + \sigma _n\delta _n, ~ n>0, \end{aligned}$$

where $\{\sigma _n\}$ is a sequence in (0, 1) and $\{\delta _n\}$ is a real sequence such that

• (i)  $\sum \limits _{n=1}^{\infty } \sigma _n = \infty ,$

• (ii)  $\limsup \limits _{n\rightarrow \infty }\delta _n \le 0$ or $\sum \limits _{n=1}^{\infty }|\sigma _n \delta _n| < \infty .$ Then $\lim \limits _{n\rightarrow \infty } a_n = 0.$

Lemma 1.7

[18] Let $\Gamma _n$ be a sequence of real numbers that does not decrease at infinity, in the sense that there exists a subsequence $\{\Gamma _{n_j}\}_j\ge 0$ of $\{\Gamma _{n_j}\}$ which satisfies $\Gamma _{n_j}\le \Gamma _{n_j+1}$ for all $j\ge 0$. Also consider a sequence of integers $\{\tau (n)\}_n\ge n_0$ defined by

$$\begin{aligned} \tau (u)=\max \{k\le n | \Gamma _{n_k}\le \Gamma _{n_k+1}\}. \end{aligned}$$

Then $\{\tau (n)\}_n\ge n_0$ is a nondecreasing sequence satisfying $\lim \limits _{n\infty }\tau (n)=\infty$.

If it holds that $\Gamma _\tau (n)\le \Gamma _{\tau (n)+1}$

3 Main result

Theorem 1.8

Let $X_1$ and $X_2$ be p-uniformly convex and uniformly smooth real Banach spaces and $F:X_1 \rightarrow X_2$ be a bounded linear operator with its adjoint $F^*: X_2^{*} \rightarrow X_1^{*}$. Let C and Q be nonempty, closed and convex subsets of $X_1$ and $X_2$ respectively, and $f:X_2 \rightarrow {\mathbb {R}}$ be a non-negative lower semi-continous convex function. Suppose $S: X_1 \rightarrow X_1$ is a Bregman strongly nonexpansive mapping with $\Gamma :=\Omega \cap Fix(S)$ is nonempty. Let $\{\lambda _n\}$ be a positive sequence in $(0, \dfrac{p\pi _p}{2^{p-1}})$, where $\pi _p$ is defined in (2.8), $\lambda _n=\circ (\alpha _n), \{\alpha _{n}\}, \{\beta _n\}$, $\{\gamma _n\}$ are sequences in (0, 1) and $\alpha _{n}+\beta _n+ \gamma _n=1$ such that $\lim \limits _{n\rightarrow \infty }\alpha _n=0$ and $\sum \limits _{n=1}^{\infty }\alpha _{n}=\infty , \beta _n \in (a,b) \subset (0,1)$ and $\gamma _n\in (c,d) \subset (0,1)$ for all $n \ge 1$. For fixed ${v}, x_0, x_1 \in X_1,$ choose $\theta _n$ such that $0\le \theta _n \le {\bar{\theta }}_n,$ then define a sequence $\{x_n\}$ by the following manner:

$$\begin{aligned} {\left\{ \begin{array}{ll} u_n=J_{X_{1}^{*}}^{q}\bigg [J_{X_1}^{p}(x_n)+ \theta _n (J_{X_1}^{p}(x_n)-J_{X_1}^{p}(x_{n-1}))\bigg ]\\ y_n=\Pi _{C}J_{X_{1}^{*}}^{q}\bigg [J_{X_1}^{p}(u_n)-\rho _n\dfrac{f^{p-1}(u_n)}{\Vert \nabla f(u_n)\Vert ^{p}}\nabla f(u_n)\bigg ]\\ x_{n+1}=\Pi _{C}J_{X_{1}^{*}}^{q}\bigg [\alpha _{n} J_{X_1}^{p}(v) + \beta _n J_{X_1}^{p}(y_n) + \gamma _n J_{X_1}^{p}(Sy_n)\bigg ],~n\ge 1, \end{array}\right. } \end{aligned}$$

(3.1)

where

$$\begin{aligned} {\bar{\theta }}_{n}= \left\{ \begin{array}{ll} \min \{\theta , \dfrac{\lambda _n}{\Vert J^{p}_{X_1}(x_n)-J^{p}_{X_1}(x_{n-1})\Vert }\}, \quad if \ \ x_n\ne x_{n-1},\\ {}\\ \theta , \quad otherwise, \end{array} \right. \end{aligned}$$

(3.2)

$f(u_n):=\frac{1}{p}\Vert (I-P_Q)Fu_n\Vert ^{p}, {\nabla f(u_n):=F^*J_{X_2}^{p}(I-P_Q)Fu_n},~ \{\rho _n\}\subset (0, \infty )$ and $\liminf \limits _{n \rightarrow \infty }\rho _n(p-C_q\frac{\rho _{n}^{q-1}}{q})>0,$ where $C_q$ is the uniform smoothness coefficient of $X_1$. Then $\{x_n\}$ converges strongly to $x^*=\Pi _{\Gamma }v$.

Proof

Let $z \in \Gamma$ and $b_n=J_{X_{1}^{*}}^{q}[J_{X_1}^{p}(u_n)-\rho _n \frac{f^{p-1}(u_n)}{\Vert \nabla f(u_n)\Vert ^{p}}\ f(u_n)]$ for all $n \ge 1$. We obtain from Lemma 2.2 that

$$\begin{aligned} \Vert b_n\Vert _{X_1^{*}}^{q}&=\Vert J_{X_1}^{p}(u_n)-\rho _n\frac{f^{p-1}(u_n)}{\Vert \nabla f(u_n)\Vert ^{p}}\nabla f(u_n)\Vert ^{q}_{X_{1}^{*}}\nonumber \\&\le \Vert u_n\Vert ^{p}-q\rho _n\frac{f^{p-1}(u_n)}{\Vert \nabla f(u_n)\Vert ^{p}}\langle u_n, \nabla f(u_n)\rangle \nonumber \\ {}&\quad + C_q\rho _n^{q}\frac{f^{(p-1)q}(u_n)}{\Vert \nabla f(u_n)\Vert ^{pq}}\Vert \nabla f(u_n)\Vert ^{q}\nonumber \\&=\Vert u_n\Vert ^{p}-q\rho _n\frac{f^{p-1}(u_n)}{\Vert \nabla f(u_n)\Vert ^{p}}\langle u_n, \nabla f(u_n)\rangle +C_q\rho _n^{q}\frac{f^{p}(u_n)}{\Vert \nabla f(u_n)\Vert ^{p}}. \end{aligned}$$

(3.3)

By applying (2.7) and (3.3), we get

$$\begin{aligned} \Delta _p(y_n, z)&\le \Delta _p(J_{X_1}^{p}(b_n), z)\nonumber \\&=\frac{\Vert z\Vert ^{p}}{p} + \frac{\Vert J_{X_1}^{p}(b_n)\Vert ^{p}}{q}-\langle z, b_n\rangle \nonumber \\&=\frac{\Vert z\Vert ^{p}}{p}+ \frac{1}{q}\Vert b_n\Vert ^{(q-1)p}-\langle z, b_n\rangle \nonumber \\&=\frac{\Vert z\Vert ^{p}}{p} + \frac{1}{q}\Vert b_n\Vert ^{(q-1)\frac{q}{q-1}}-\langle z, b_n\rangle \nonumber \\&=\frac{\Vert z\Vert ^{p}}{p} +\frac{1}{q}\Vert b_n\Vert ^{q}-\langle z, J_{X_1}^{p}(u_n)\rangle +\rho _n \frac{f^{p-1}(u_n)}{\Vert \nabla f(u_n)\Vert ^{p}}\langle z, \nabla f(u_n)\rangle \nonumber \\&\le \frac{\Vert z\Vert ^{p}}{p}+ \frac{1}{q}\big (\Vert u_n\Vert ^{p}-q\rho _n\frac{f^{p-1}(u_n)}{\Vert \nabla f(u_n)\Vert ^{p}}\langle u_n, \nabla f(u_n)\rangle +C_q\rho _n^{q}\frac{f^{p}(u_n)}{\Vert \nabla f(u_n)\Vert ^{p}}\big )\nonumber \\ {}&\quad -\langle z, J_{X_1}^{p}(u_n)\rangle +\rho _n \frac{f^{p-1}(u_n)}{\Vert \nabla f(u_n)\Vert ^{p}}\langle z, \nabla f(u_n)\rangle \nonumber \\&=\frac{\Vert z\Vert ^{p}}{p} + \frac{\Vert u_n\Vert ^{p}}{q}-\langle z, J_{X_1}^{p}(u_n)\rangle +\frac{C_q\rho _n^{q}}{q}\frac{f^{p}(u_n)}{\Vert \nabla f(u_n)\Vert ^{p}} \nonumber \\&\quad + \rho _n \frac{f^{p-1}(u_n)}{\Vert \nabla f(u_n)\Vert ^{p}}\langle z-u_n, \nabla f(u_n)\rangle \nonumber \\&=\Delta _p(u_n,z) +\frac{C_q\rho _n^{q}}{q}\frac{f^{p}(u_n)}{\Vert \nabla f(u_n)\Vert ^{p}} + \rho _n \frac{f^{p-1}(u_n)}{\Vert \nabla f(u_n)\Vert ^{p}}\langle z-u_n, \nabla f(u_n)\rangle . \end{aligned}$$

(3.4)

But from (2.4) and that $Fz \in Q$

$$\begin{aligned} \langle \nabla f(u_n), z-u_n\rangle&=\langle F^* J_{X_2}^{p}(I-P_Q)Fu_n, z-u_n\rangle \nonumber \\&=\langle J_{X_2}^{p}(I-P_Q)Fu_n, Fz-Fu_n\rangle \nonumber \\&=\langle J_{X_2}^{p}(I-P_Q)Fu_n, P_QFu_n-Fu_n\rangle \nonumber \\&\quad + \langle J_{X_2}^{p}(I-P_Q)Fu_n, Fz-P_QFu_n\rangle \nonumber \\&\le -\Vert (I-P_Q)Fu_n\Vert ^{p}\nonumber \\&=-p f(u_n). \end{aligned}$$

(3.5)

On substituting (3.5) into (3.4), it yields

$$\begin{aligned} \Delta _p(y_n,z)&\le \Delta _p(u_n,z) + \big (\frac{C_q\rho _n^{q}}{q}-\rho _np\big )\frac{f^{p}(u_n)}{\Vert \nabla f(u_n)\Vert ^{p}}. \end{aligned}$$

(3.6)

Hence, we conclude that

$$\begin{aligned} \Delta _p(y_n,z) \le \Delta _p(u_n, z). \end{aligned}$$

(3.7)

Now, using (2.8), (2.9) and (3.1), we have

$$\begin{aligned} \langle J_{X_1}^{p}u_n-J_{X_1}^{p}x_n, u_n-z\rangle&\le \Vert J_{X_1}^{p}u_n-J_{X_1}^{p}x_n\Vert ~\Vert u_n-z\Vert \nonumber \\&=\theta _{n}\Vert J_{X_1}^{p}x_n-J_{X_1}^{p}x_{n-1}\Vert ~\Vert u_n-z\Vert \nonumber \\&\le \theta _{n}\Vert J_{X_1}^{p}x_n-J_{X_1}^{p}x_{n-1}\Vert \bigg [\frac{1}{p}\Vert u_n-z\Vert ^{p}+ \frac{1}{q}\bigg ]\nonumber \\&\le \theta _{n}\Vert J_{X_1}^{p}x_n-J_{X_1}^{p}x_{n-1}\Vert \bigg [2^{p-1}(\Vert x_n-u_n\Vert ^{p}+ \Vert x_n-z\Vert ^{p})\bigg ]\nonumber \\&\quad + \frac{\theta _n}{q}\Vert J_{X_1}^{p}x_n-J_{X_1}^{p}x_{n-1}\Vert \nonumber \\&\le \frac{2^{p-1}\lambda _n}{p \pi _p}\bigg (\Delta _p(x_n,u_n) + \Delta _p(x_n,z)\bigg ) + \frac{\lambda _n}{q}. \end{aligned}$$

(3.8)

Also using (2.3), we get

$$\begin{aligned} \Delta _p(u_n,z) =\Delta _p(x_n,z)-\Delta _p(x_n,u_n) + \langle J_{X_1}^{p}u_n-J_{X_1}^{p}x_n, u_n-z\rangle . \end{aligned}$$

(3.9)

On substituting (3.8) into (3.9), we have

$$\begin{aligned} \Delta _p(u_n,z)&=\Delta _p(x_n,z) -\Delta _p(x_n, u_n) + \frac{2^{p-1}\lambda _n}{p \pi _p}\bigg (\Delta _p(x_n, u_n) + \Delta _p(x_n,z)\bigg ) + \frac{\lambda _n}{q}\nonumber \\&\le \bigg (1 + \frac{2^{p-1}\lambda _n}{p \pi _p}\bigg )\Delta _p(x_n,z) -\bigg (1-\frac{2^{p-1}\lambda _n}{p \pi _p}\bigg )\Delta _p(x_n,u_n) + \frac{\lambda _n}{q}. \end{aligned}$$

(3.10)

From (3.1), (3.8) and (3.10), we obtain

$$\begin{aligned} \Delta _p(x_{n+1},z)&\le \Delta _p\big (J_{X_1}^{q}[\alpha _{n} J_{X_1}^{p}(v)+ \beta _nJ_{X_1}^{p}(y_n)+ \gamma _n J_{X_1}^{p}(Sy_n)], z\big )\nonumber \\&\le \alpha _{n}\Delta _p(v,z) + \beta _n\Delta _p(y_n,z) + \gamma _n \Delta _p(Sy_n,z)\nonumber \\&\le \alpha _n \Delta _p(v,z) +\beta _n \Delta _p(y_n,z) + \gamma _n (y_n,z)\nonumber \\&=\alpha _n \Delta _p(v,z) + (1-\alpha _{n})\Delta _p(y_n,z)\nonumber \\&=\alpha _n \Delta _p(v,z) + (1-\alpha _{n})\Delta _p(u_n,z). \end{aligned}$$

(3.11)

From the assumption that $\lim \limits _{n \rightarrow \infty } \frac{\lambda _n}{\alpha _n}=0$, taking $\phi \in (0, \frac{p \pi _p}{2^{p-1}})$. Then there exists $N \in {\mathbb {N}}$ such that $\lambda _n < \alpha _n$ for all $n \ge {\mathbb {N}}$.

Hence

$$\begin{aligned} {\frac{\lambda _n 2^{p-1}}{p \pi _p}< \alpha _n \phi < \frac{2^{p-1}}{p \pi _p}\alpha _n,~\forall ~n \in {\mathbb {N}}}. \end{aligned}$$

For some constant $M > 0,$ it follows from (3.10) that

$$\begin{aligned} \Delta _p(u_n,z) \le (1 + \alpha _n \phi )\Delta _p(x_n,z) -(1-\alpha _{n}\phi )\Delta _p(x_n,u_n) + \alpha _{n}M. \end{aligned}$$

(3.12)

By substituting (3.12) into (3.11), we get

$$\begin{aligned} \Delta _p(x_{n+1}, z)&\le \alpha _n \Delta _p(v,z) + (1-\alpha _n)\big [(1+\alpha _n\phi )\Delta _p(x_n,z) + \alpha _n M \big ]\nonumber \\&\le (1-\alpha _{n}(1-\phi ))\Delta _p(x_n,z) + \alpha _n \Delta _p(v,z) + \alpha _n M\nonumber \\&=(1-\alpha _{n}(1-\phi ))\Delta _p(x_n,z) + \alpha _n(1-\phi )\frac{\Delta _p(v,z)+M}{1-\phi }\nonumber \\&\le \max \{\Delta _p(x_n,z), \frac{\Delta _p(v,z)+M}{1-\phi }\}\nonumber \\&\vdots \nonumber \\&\le \max \{\Delta _p(x_1,z), \frac{\Delta _p(v,z)+M}{1-\phi }\}, ~\forall ~n \ge 1. \end{aligned}$$

This implies that $\{\Delta _p(x_n,z)\}$ is bounded. Consequently, $\{\Delta _p(u_n,z)\}$ and $\{\Delta _p(y_n,z)\}$ are bounded. By applying Lemma 2.4, we obtain that $\{x_n\},~ \{u_n\}$ and $\{y_n\}$ are bounded.

From (3.1), (3.6) and (3.12), we obtain

$$\begin{aligned} \Delta _p(x_{n+1}, z)&\le \alpha _n \Delta _p(v,z) + (1-\alpha )\Delta _p(y_n,z)\nonumber \\&\le \alpha _n \Delta _p(v,z) + (1-\alpha _{n})\Delta _p(u_n,z) + (1-\alpha _{n})\big (\frac{C_q\rho _n^{q}}{q}-\rho _np\big )\frac{f^{p}(u_n)}{\Vert \nabla f(u_n)\Vert ^{p}}\nonumber \\&\le \alpha _{n}\Delta _p(v,z)+ (1-\alpha _{n}\phi )\Delta _p(x_n,z)-(1-\alpha _{n}\phi )\Delta _p(x_n,u_n) + \alpha _{n}M\nonumber \\ {}&-(1-\alpha _{n})\big (\frac{C_q\rho _n^{q}}{q}-\rho _np\big )\frac{f^{p}(u_n)}{\Vert \nabla f(u_n)\Vert ^{p}}. \end{aligned}$$

(3.13)

Case 1: Suppose that there exists $n_0 \in {\mathbb {N}}$ such that $\{\Delta _p(x_n,z)\}$ is non-increasing for all $n \ge n_0$. Then $\{\Delta _p(x_n,z)\}$ converges and

$$\begin{aligned} \Delta _p(x_{n+1},z)-\Delta _p(x_n,z) \rightarrow 0,~n \rightarrow \infty . \end{aligned}$$

(3.14)

From (3.13), we get

$$\begin{aligned}&(1-\alpha _{n}\phi )\Delta _p(x_n,u_n)-(1-\alpha _{n})\big (\frac{C_q\rho _n^{q}}{q}-\rho _np\big )\frac{f^{p}(u_n)}{\Vert \nabla f(u_n)\Vert ^{p}} \nonumber \\&\quad \le (1-\alpha _n \phi )\Delta _p(x_n,z)-\Delta _p(x_{n+1},z)\nonumber \\ {}&\quad + \alpha _{n} M. \end{aligned}$$

(3.15)

Hence,

$$\begin{aligned} \lim _{n \rightarrow \infty }\Delta _p(x_n,u_n)=0=\lim _{n \rightarrow \infty }\rho _n(p-\frac{C_q\rho _n^{q-1}}{q})\frac{f^{p}(u_n)}{\Vert \nabla f(u_n)\Vert ^{p}}. \end{aligned}$$

(3.16)

Since $\liminf \limits _{n \rightarrow \infty }\rho _n(p-\frac{C_q\rho _n^{q-1}}{q})> 0,$ we obtain that

$$\begin{aligned} \lim _{n \rightarrow \infty }\frac{f^{p}(u_n)}{\Vert \nabla f(u_n)\Vert ^{p}}=0, \end{aligned}$$

(3.17)

and hence

$$\begin{aligned} \lim _{n \rightarrow \infty }\frac{f(u_n)}{\Vert \nabla f(u_n)\Vert }=0. \end{aligned}$$

(3.18)

Since $\{\nabla f(u_n)\}$ is bounded, we obtain from (3.18) that

$$\begin{aligned} 0&\le f(u_n) =\Vert \nabla f(u_n)\Vert \frac{f(u_n)}{\Vert \nabla f(u_n)\Vert }\nonumber \\&\le N_1 \frac{f(u_n)}{\Vert \nabla f(u_n)\Vert }\rightarrow 0,~n \rightarrow \infty , \text {for some}~N_1 > 0. \end{aligned}$$

Hence,

$$\begin{aligned} \lim _{n \rightarrow \infty } f(u_n)=0, \end{aligned}$$

(3.19)

and thus

$$\begin{aligned} \lim _{n \rightarrow \infty }\Vert Fu_n-P_QFu_n\Vert =0. \end{aligned}$$

(3.20)

By applying Lemma 2.4 in (3.16), we obtain

$$\begin{aligned} \lim _{n \rightarrow \infty }\Vert x_n-u_n\Vert =0. \end{aligned}$$

(3.21)

From the definition of $b_n$, we obtain that

$$\begin{aligned} \lim _{n \rightarrow \infty }\Vert J_{X_1}^{p}(b_n)-J_{X_1}^{p}(u_n)\Vert&= \lim _{n \rightarrow \infty }\rho _n \frac{f^{p-1}(u_n)}{\Vert \nabla f(u_n)\Vert ^{p}}\Vert \nabla f(u_n)\Vert \nonumber \\&=\lim _{n \rightarrow \infty }\rho _n \frac{f^{p-1}(u_n)}{\Vert \nabla f(u_n)\Vert ^{p-1}} \rightarrow 0. \end{aligned}$$

(3.22)

Since $J_{X_{1}^{*}}^{q}$ is norm-to-norm uniformly continuous subsets on $X_{1}^{*},$ then

$$\begin{aligned} \lim _{n \rightarrow \infty }\Vert b_n-u_n\Vert =0, \end{aligned}$$

(3.23)

and in view of (2.8), we get

$$\begin{aligned} \lim _{n \rightarrow \infty }\Delta _p(b_n, u_n)=0. \end{aligned}$$

(3.24)

By applying (3.20), we have

$$\begin{aligned} \Vert F^{*}J_{X_2}^{p}(I-P_Q)Fu_n\Vert \le \Vert F\Vert ~\Vert (I-P_Q)Fu_n\Vert \rightarrow 0,~n \rightarrow ~\infty . \end{aligned}$$

(3.25)

Let $h_n=J_{X_{1}^{*}}^{p}\big [\frac{\beta _n}{1-\alpha _{n}}J_{X_1}^{p}(y_n) + \frac{\gamma _n}{1-\alpha _{n}}J_{X_1}^{p}(Sy_n)\big ]$, then

$$\begin{aligned} \Delta _p(h_n, z)&=\Delta _p(J_{X_{1}^{*}}^{p}[\frac{\beta _n}{1-\alpha _n}J_{X_1}^{p}(y_n) + \frac{\gamma _n}{1-\alpha _{n}}(Sy_n)],z)\nonumber \\&\le \frac{\beta _n}{1-\alpha _{n}}\Delta _p(y_n,z) + \frac{\gamma _n}{1-\alpha _{n}}\Delta _p(Sy_n,z)\nonumber \\&\le \frac{\beta _n}{1-\alpha _{n}}\Delta _p(y_n,z) + \frac{\gamma _n}{1-\alpha _{n}}\Delta _p(y_n,z)\nonumber \\&=\Delta _p(y_n,z). \end{aligned}$$

Hence from (3.12), we have

$$\begin{aligned} 0&\le \Delta _p(y_n,z)-\Delta _p(h_n,z)\nonumber \\&=\Delta _p(y_n,z)-\Delta _p(x_{n+1},z) + \Delta _p(x_{n+1},z)-\Delta _p(h_n,z)\nonumber \\&=\Delta _p(u_n,z)-\Delta _p(x_{n+1},z) + \alpha _{n}\Delta _p(v,z) + (1-\alpha _{n})\Delta _p(h_n,z)-\Delta _p(h_n,z)\nonumber \\&\le (1+\alpha _{n}\phi )\Delta _p(x_n,z)-\Delta _p(x_{n+1},z) + \alpha _n M + \alpha _{n}\Delta _p(v,z) -\alpha _{n}\Delta _p(h_n,z) \nonumber \\&=\Delta _p(x_n,z)-\Delta _p(x_{n+1},z) +\alpha _{n}(\Delta _p(v,z)+ \phi \Delta _p(x_n,z)-\Delta _p(h_n,z)+M)\nonumber \\&\rightarrow 0,~n \rightarrow \infty . \end{aligned}$$

(3.26)

Also

$$\begin{aligned} \Delta _p(h_n,z)&\le \frac{\beta _n}{1-\alpha _{n}}\Delta _p(y_n,z) + \frac{\gamma _n}{1-\alpha _{n}}\Delta _p(Sy_n,z)\nonumber \\&=(1-\frac{\gamma _n}{\alpha _{n}})\Delta _p(y_n,z) + \frac{\gamma _n}{1-\alpha _{n}}\Delta _p(Sy_n,z)\\&\le \Delta _p(y_n,z) + \frac{\gamma _n}{1-\alpha _{n}}\Delta _p\big ((Sy_n,z) -\Delta _p(y_n,z)\big )\nonumber . \end{aligned}$$

(3.27)

Thus,

$$\begin{aligned} \Delta _p(y_n,z) -\Delta _p(Sy_n,z)&\le \frac{\gamma _n}{1-\alpha _n}\big (\Delta _p(y_n,z)-\Delta _p(Sy_n,z)\big )\nonumber \\&\le \Delta _p(y_n,z)-\Delta _p(h_n,z)\rightarrow 0,~n \rightarrow \infty . \end{aligned}$$

(3.28)

Hence, we conclude that

$$\begin{aligned} \lim _{n \rightarrow \infty }\Delta _p(y_n, Sy_n)=0, \end{aligned}$$

(3.29)

which implies from Lemma 2.4 that

$$\begin{aligned} \lim _{n \rightarrow \infty }\Vert y_n-Sy_n\Vert =0. \end{aligned}$$

(3.30)

Using (2.7), we get

$$\begin{aligned} \Delta _p(y_n,u_n)&\le \Delta _p(b_n,u_n)-\Delta _p(y_n,b_n)\nonumber \\&\le \Delta _p(b_n,u_n) \rightarrow 0,~n \rightarrow \infty . \end{aligned}$$

(3.31)

In view of Lemma 2.4, we obtain that

$$\begin{aligned} \lim _{n \rightarrow \infty }\Vert y_n-u_n\Vert =0. \end{aligned}$$

(3.32)

Let $k_n:=J_{X_{1}^{*}}^{q}\big [\alpha _{n}J_{X_1}^{p}(v) + \beta _n J_{X_1}^{p}(y_n) + \gamma _n J_{X_1}^{p}(Sy_n)\big ]$, then from (3.1), (3.29) and Lemma 2.4, we obtain

$$\begin{aligned} \Delta _p(k_n, y_n)&=\Delta _p(J_{X_{1}^{*}}^{q}\big [\alpha _{n}J_{X_1}^{p}(v) + \beta _n J_{X_1}^{p}(y_n) + \gamma _n J_{X_1}^{p}(Sy_n)\big ],y_n)\nonumber \\&\le \Delta _p(v,y_n) + \beta _n \Delta _p(y_n,y_n) +\gamma _n\Delta _p(Sy_n,y_n) \rightarrow 0,~n \rightarrow \infty . \end{aligned}$$

(3.33)

Hence,

$$\begin{aligned} \lim _{n \rightarrow \infty }\Vert k_n-y_n\Vert =0. \end{aligned}$$

(3.34)

By applying (2.7), (3.33) and Lemma 2.4, we get

$$\begin{aligned} \Delta _p(x_{n+1}, y_n)&\le \Delta _p(k_n,y_n)-\Delta _p(x_{n+1}, k_n)\nonumber \\&\le \Delta _p(k_n,y_n) \rightarrow 0,~n \rightarrow \infty , \end{aligned}$$

(3.35)

and hence,

$$\begin{aligned} \lim _{n \rightarrow \infty }\Vert x_{n+1}-y_n\Vert =0. \end{aligned}$$

(3.36)

From (3.21)and (3.32), we obtain

$$\begin{aligned} \lim _{n \rightarrow \infty }\Vert y_n-x_n\Vert =0. \end{aligned}$$

(3.37)

By applying (3.34) and (3.37), we have

$$\begin{aligned} \lim _{n \rightarrow \infty }\Vert k_n-x_n\Vert =0. \end{aligned}$$

(3.38)

Consequently, using (3.36) and (3.37), we get

$$\begin{aligned} \lim _{n \rightarrow \infty }\Vert x_{n+1}-x_n\Vert =0. \end{aligned}$$

(3.39)

Since $\{x_n\}$ is bounded, there exists a subsequence $\{x_{n_j}\}$ of $\{x_n\}$ which converges weakly to $z \in C$. Using (3.21) and (3.37), there exist susbsequences $\{u_{n_j}\}$ of $\{u_n\}$ and $\{y_{n_j}\}$ of $\{y_n\}$ which converge weakly to z. Using (3.30), it follows that $z \in Fix(S)$ as $Fix(S)={{\hat{Fix}}(S)}$. Next, we show that $Fz \in Q$. Now from (2.4), we obtain

$$\begin{aligned} \Vert (I-P_Q)Fz\Vert ^{p}&=\langle J_{X_2}^{p}(Fz-P_{Q}Fz), Fz-P_{Q}Fz\rangle \\&=\langle J_{X_2}^{p}(Fz-P_QFz), Fz-Fu_{n_j}\rangle \nonumber \\ {}&\quad + \langle J_{X_2}^{p}(Fz-P_QFz), Fu_{n_j}-P_{Q}Fu_{n_j}\rangle \nonumber \\ {}&\quad + \langle J_{X_2}^{p}(Fz-P_{Q}Fz), P_{Q}Fu_{n_j}-P_{Q}Fz\rangle \nonumber \\&\le \langle J_{X_2}^{p}(Fz-P_{Q}Fz), Fz-Fu_{n_j}\rangle \nonumber \\ {}&\quad + \langle J_{X_2}^{p}(Fz-P_{Q}Fz), Fu_{n_j}-P_{Q}Fu_{n_j}\rangle . \end{aligned}$$

By the continuity of F and (3.32), we obtain that $Fu_{n_j}\rightharpoonup Fz$ as $j \rightarrow \infty$. Hence, if we let $j \rightarrow \infty$, we get

$$\begin{aligned} \Vert Fz-P_{Q}Fz\Vert =0. \end{aligned}$$

Therefore, $Fz=P_{Q}Fz,$ which implies that $Fz \in Q$. Hence, we conclude that $z \in Fix(S) \cap \Omega =\Gamma .$ Since $x^*=\Pi _{\Gamma }v,$ then applying Lemma 2.3 (ii), (iii) and (3.12), we have

$$\begin{aligned}&\Delta _p(x_{n+1},x^*) \le \Delta _p(J_{X_{1}^{*}}^{q}(\alpha _{n}J_{X_1}^{p}(v) + \beta _n J_{X_1}^{p}(y_n) + \gamma _n J_{X_1}^{p}(Sy_n)),x^*)\nonumber \\&=V_p(\alpha _{n}J_{X_1}^{p}(v) + \beta _n J_{X_1}^{p}(y_n) + \gamma _n J_{X_1}^{p}(Sy_n), x^*)\nonumber \\&\le V_p(\alpha _{n} J_{X_1}^{p}(v) + \beta _n J_{X_1}^{p}(y_n)+ \gamma _n J_{X_1}^{p}(Sy_n), x^*-\alpha _{n}(J_{X_1}^{p}(v)-J_{X_1}^{p}(x^*))\nonumber \\ {}&\quad -\langle -\alpha _{n} J_{X_1}^{p}(v)-J_{X_1}^{p}(x^*)), J_{X_{1}^{*}}^{q}\big [\alpha _{n}J_{X_1}^{p}(x^*) + \beta _n J_{X_1}^{p}(y_n) + \gamma _nJ_{X_1}^{p}(Sy_n)\big ]-x^*\rangle \nonumber \\&=V_p(\alpha _{n}J_{X_1}^{p}(x^* + \beta _nJ_{X_1}^{P}(y_n) + \gamma _n J_{X_1}^{p}(Sy_n)) + \alpha _{n}\langle J_{X_1}^{p}(v)-J_{X_1}^{p}(x^*), k_n-x^*\rangle \nonumber \\&\le \alpha _{n}\Delta _p(x^*,x^*) + \beta _n\Delta _p(y_n,x^*) + \gamma _n\Delta _p(Sy_n,x^*) + \alpha _{n}\langle J_{X_1}^{p}(v)-J_{X_1}^{p}(x^*), k_n-x^*\rangle \nonumber \\&\le (1-\alpha _n)\Delta _p(y_n,x^*)+ \alpha _{n}\langle J_{X_1}^{p}(v)-J_{X_1}^{p}(x^*), k_n-x^*\rangle \nonumber \\&\le (1-\alpha _n(1-\phi ))\Delta _p(x_n,x^*) + \alpha _n(1-\phi )\big [(1-\phi )^{-1}(\langle J_{X_1}^{p}(v)-J_{X_1}^{p}(x^*), k_n-x^*\rangle ) + \frac{\lambda _n}{\alpha _n}]. \end{aligned}$$

(3.40)

Next, since $x_{n_j}\rightharpoonup x^*\in \Gamma$, then for any $x^*=\Pi _{\Gamma }u$ we get from (2.6) that

$$\begin{aligned} \limsup _{n\rightarrow \infty }\langle J_{X_1}^{p}(v)-J_{X_1}^{p}(x^*), x_n-x^*\rangle&=\lim _{j \rightarrow \infty }\langle J_{X_1}^{p}(v)-J_{X_1}^{p}(x^*), x_{n_j}-x^*\rangle \nonumber \\&=\langle J_{X_1}^{p}(v)-J_{X-1}^{p}(x^*), z-x^*\rangle \nonumber \\&\le 0. \end{aligned}$$

Hence, from (3.38), we get

$$\begin{aligned} {\limsup _{n\rightarrow \infty }\langle J_{X_1}^{p}(u)-J_{X_1}^{p}(x^*), k_n-x^*\rangle }&=\langle J_{X_1}^{p}(u)-J_{X_1}^{p}(x^*), x_{n}-x^*\rangle \nonumber \\&\le 0. \end{aligned}$$

(3.41)

Therefore, on substituting (3.41) into (3.40) and applying Lemma 2.5, we obtain that $\Delta _p(x_n,x^*) \rightarrow 0$ as $n \rightarrow \infty$. By (2.7), we know that $\tau _p\Vert x_n-x^*\Vert \le \Delta _p(x_n,x^*) \rightarrow 0.$ Hence $\{x_n\}$ converges strongly to $x^*=\Pi _{\Gamma }v$.

Case 2: Suppose that there exists a subsequence $\{\eta _j\}$ of $\{\eta \}$ such that $\Delta _p(x_{n_j},x^*) < \Delta _p(x_{n_{j+1}},x^*)$ for all $j \in {\mathbb {N}}$. Then by Lemma 2.6, there exists a nondecreasing sequence $\{m_k\} \subseteq {\mathbb {N}}$ such that $m_{k} \rightarrow \infty ,$ and

$$\begin{aligned} \Delta _p(x_{m_k}, x^*) \le \Delta _p(x_{m_{k+1}},x^*)~\text {and}~\Delta _p(x_k, x^*) \le \Delta _p(x_{k+1},x^*). \end{aligned}$$

Following the same process as in Case 1, we obtain that

$$\begin{aligned} {\left\{ \begin{array}{ll} \lim \limits _{k \rightarrow \infty }\Vert u_{n_k}-x_{n_k}\Vert =0,\\ \lim \limits _{k \rightarrow \infty }\Vert y_{n_k}-u_{n_k}\Vert =0,\\ \lim \limits _{k \rightarrow \infty }\Vert x_{n_{k+1}}-x_{n_k}\Vert =0,\\ {\limsup \limits _{k\rightarrow \infty }\langle J_{X_1}^{p}(v)-J_{X_1}^{p}(x^*), k_{n_k}-x^*\rangle \le 0.} \end{array}\right. } \end{aligned}$$

Again from (3.40), we have

$$\begin{aligned}&\Delta _p(x_{m_{k+1}},x^*) \le (1-\alpha _{m_k}(1-\phi ))\Delta _p(x_{m_k},x^*) \\&\quad + \alpha _{m_k}(1-\phi )\big [(1-\phi )^{-1}(\langle J_{X_1}^{p}(v)-J_{X_1}^{p}(x^*), k_{m_k}-x^*\rangle + \frac{\lambda _{m_k}}{\alpha _{m_k}})\big ], \end{aligned}$$

that is,

$$\begin{aligned} (1-\phi )\Delta _p(x_{m_k},x^*)&\le (1-\phi )\alpha _{m_k}\Delta _p(x_{m_k},x^*)-\Delta _p(x_{m_{k+1}},x^*)\nonumber \\ {}&\quad + \alpha _{m_k}(1-\phi )\bigg [(1-\phi )^{-1}(\langle J_{X_1}^{p}(v)-J_{X_1}^{p}(x^*), k_{m_k}-x^*\rangle + \frac{\lambda _{m_k}}{\alpha _{m_k}})\bigg ], \end{aligned}$$

which implies that

$$\begin{aligned} \Delta _p(x_{m_k},x^*)&\le \alpha _{m_k}\bigg [(1-\phi )^{-1}(\langle J_{X_1}^{p}(v)-J_{X_1}^{p}(x^*), k_{m_k}-x^*\rangle + \frac{\lambda _{m_k}}{\alpha _{m_k}})\bigg ]. \end{aligned}$$

Therefore, $\Delta _p(x_{m_k},x^*)=0$ and since

$$\begin{aligned} \Delta _p(x_k,x^*)\le \Delta _p(x_{k+1},x^*)~\forall ~k \in {\mathbb {N}}, \end{aligned}$$

we conclude that $x_{k}\rightarrow x^*, k \rightarrow \infty .$ $\square$

Corollary 1.9

Let $X_1$ and $X_2$ be p-uniformly convex and uniformly smooth Banach spaces and $F:X_1 \rightarrow X_2$ be a bounded linear operator with its adjoint $F^*: X_2^{*} \rightarrow X_1^{*}$. Let C and Q be nonempty, closed and convex subsets of $X_1$ and $X_2$ respectively, and $f:X_1 \rightarrow {\mathbb {R}}$ be a non-negative lower semi-continous convex function. Suppose $\Omega \ne \emptyset$ and let $\{\lambda _n\}$ be a positive sequence in $(0, \frac{p\pi _p}{2^{p-1}})$, where $\pi _p$ is defined in (2.8), $\lambda _n=\circ (\alpha _n), \{\alpha _{n}\}, \{\beta _n\}$, $\{\gamma _n\}$ are sequences in (0, 1) and $\alpha _{n}+\beta _n+ \gamma _n=1$ such that $\lim \limits _{n\rightarrow \infty }\alpha _n=0$ and $\sum \limits _{n=1}^{\infty }\alpha _{n}=\infty , \beta _n \in (a,b) \subset (0,1)$ and $\gamma _n\in (c,d) \subset (0,1)$ for all $n \ge 1$. For fixed ${v}, x_0, x_1 \in X_1,$ choose $\theta _n$ such that $0\le \theta _n \le \overline{\theta _n},$ then define a sequence $\{x_n\}$ by the following manner:

$$\begin{aligned} {\left\{ \begin{array}{ll} u_n=J_{X_{1}^{*}}^{q}\bigg [J_{X_1}^{p}(x_n)+ \theta _n (J_{X_1}^{p}(x_n)-J_{X_1}^{p}(x_{n-1}))\bigg ]\\ y_n=\Pi _{C}J_{X_{1}^{*}}^{q}\bigg [J_{X_1}^{p}(u_n)-\rho _n\frac{f^{p-1}(u_n)}{\Vert \nabla f(u_n)\Vert ^{p}}\nabla f(u_n)\bigg ]\\ x_{n+1}=\Pi _{C}J_{X_{1}^{*}}^{q}\bigg [\alpha _{n} J_{X_1}^{p}(v) + (1-\alpha _n)J_{X_1}^{p}(y_n)\bigg ],~n\ge 1, \end{array}\right. } \end{aligned}$$

(3.42)

where

$$\begin{aligned} {\bar{\theta }}_{n}= \left\{ \begin{array}{ll} \min \{\theta , \frac{\lambda _n}{\Vert J^{p}_{X_1}(x_n)-J^{p}_{X_1}(x_{n-1})\Vert }\}, \quad if \ \ x_n\ne x_{n-1},\\ {}\\ \theta , \quad otherwise, \end{array} \right. \end{aligned}$$

(3.43)

$f(u_n):=\frac{1}{p}\Vert (I-P_Q)Fu_n\Vert ^{p}, \{\rho _n\}\subset (0, \infty )$ and $\liminf \limits _{n \rightarrow \infty }\rho _n(p-C_q\frac{\rho _{n}^{q-1}}{q})>0,$ where $C_q$ is the uniform smoothness coefficient of $X_1$. Then $\{x_n\}$ converges strongly to $x^*=\Pi _{\Omega }v$.

4 Numerical example

Example 4.1

Let $X_1=X_2=L_2([0,1])$ with the inner product given as

$\langle f,g\rangle =\int _{0}^{1}f(t)g(t)dt.$

Let

$C:=\{x \in L_2([0,1]): \langle x,a\rangle \ge b\},$

where $a=2t^2$ and $b=0.$ Then

$P_{C}x=x + \frac{b-\langle a,x\rangle }{\Vert a\Vert ^2}a$.

Also, let

$Q:=\{x \in L_2([0,1]): \langle x,c\rangle = d\},$

where $c=\frac{t}{3},~d=-1.$ Then

$\Pi _{Q}(x)=P_{Q}(x)=x + \max \big \{0, \frac{d-\langle c,x\rangle }{\Vert c\Vert ^2}c\big \}.$

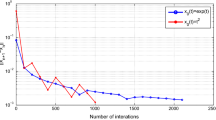
Let $F:L_2([0,1]) \rightarrow L_([0,1])$ be defined by $Fx(t)=\frac{x(t)}{2}$ with adjoint $F^{*}x(t)=\frac{x(t)}{2}$. Then F is a bounded linear operator. We set $Sx(t)=P_C(x(t))$. Hence by taking $\alpha _n=\frac{1}{n+1},~\beta _n=\frac{n}{2n+5}, \gamma _n=1-\alpha _{n}-\beta _n,~\theta _{n}=2$ and $\rho _n=10^{-7},~\forall ~n \ge 1.$ We choose the stopping criterion as in Example 4.1, we make a comparison of Algorithm 3.1 with one in which the direction of the momentum $x_n-x_{n-1}$ is altered. The report of this experiment is reported in Fig. 2 for different initial values of $x_0$ and $x_1.$

• Case i $x_0=t$ and $x_1=2t+1;$

• Case ii $x_0=\frac{5t^2}{2}-2t$ and $x_1=\exp (2t);$

• Case iii $x_0=2t$ and $x_1=\log (2t);$

• Case iv $x_0=t^{\frac{3}{4}}+3$ and $x_1=t^2+2t+1.$

Fig. 1

Example 4.1, Top left: Case (i); Top right: Case (ii); Bottom left: Case (iii); Bottom right: Case (iv)

Example 4.2

We give a numerical example in $({\mathbb {R}}^{3}, \Vert .\Vert _2)$ of the problem considered in Theorem 3.1.

Let

$C:=\{x=(x_1,x_2,x_3) \in {\mathbb {R}}^3: \langle a,x\rangle = b\},$

where $a=(3, 5, 7)$ and $b=2,$ then

$\Pi _{C}(x)=P_{C}(x)=\max \left\{ 0,\frac{ b- \langle a,x\rangle }{\Vert a\Vert ^{2}_{2}}\right\} a +x.$

Also, let

$Q:=\{x=(x_1, x_2, x_3)\in {\mathbb {R}}^3: \langle a,x\rangle \ge b\},$

where $a=(2,-1,5)$ and $b=1,$ then

$P_{Q}(x)=\frac{b-\langle a, x\rangle }{\Vert a\Vert _{2}^{2}}a +x.$

In addition, let $S=P_{C}$ and

$$\begin{aligned} F= \begin{pmatrix} 5&{}-5&{}-7\\ -4&{}2&{}-4\\ -7&{}-4&{}5 \end{pmatrix} \end{aligned}$$

Hence, by taking $\alpha _n=\frac{1}{n+1},~\beta _n=\frac{n}{2n+5}, \gamma _n=1-\alpha _{n}-\beta _n$, $\rho _{n}=0.1~$ and $\theta _{n}=1~\forall ~n \ge 1.$ By choosing $\Vert x_{n+1}-x_n\Vert =10^{-4}$ as the stopping criterion, we make a comparison of Algorithm 3.1 with one in which the direction of the momentum $x_n-x_{n-1}$ is altered. The report of this experiment is reported in Fig. 2 for different initial values of $x_0$ and $x_1.$

• Case i $x_0=[3,0,0]'$ and $x_1=[2,3,2]';$

• Case ii $x_0=[1,1,1]'$ and $x_1=[2,1,2]';$

• Case iii $x_0=[2,2,2]'$ and $x_1=[1,0,2]';$

• Case iv $x_0=[5,5,3]'$ and $x_1=[4,4,4]'$

Fig. 2

Example 4.2, Top left: Case (i); Top right: Case (ii); Bottom left: Case (iii); Bottom right: Case (iv)

Remark 4.3

Our proposed method has connections with some recent methods in literature. For instance, the inertial factor $\theta _{n}$ in our iterative algorithm has similar property with the recent papers of Shehu et al. [24] where the inertial factor is bounded. In these articles, In this article, several choices of $\{\theta _{n}\}$ are considered in numerical implementations and the authors showed that their proposed methods are efficient and implementable.

5 Conclusion

It is well known that the inertial extrapolation method plays a crucial role in the convergence rate of iterative methods in optimization problems. In our article, we proposed an inertial extrapolation method (without modification) together with an Halpern method to approximate solution of split feasibility problem and fixed point problem of Bregman strongly nonexpansive mappings in p-uniformly convex and uniformly smooth real Banach spaces. Some numerical examples were presented to illustrate the performance of our method.

In our future research, we would like to extend this concept to nonlinear spaces due to its numerous applications to real-life problems.