Block preconditioners for linear systems in interior point methods for convex constrained optimization

Abstract

In this paper, we address the preconditioned iterative solution of the saddle-point linear systems arising from the (regularized) Interior Point method applied to linear and quadratic convex programming problems, typically of large scale. Starting from the well-studied Constraint Preconditioner, we review a number of inexact variants with the aim to reduce the computational cost of the preconditioner application within the Krylov subspace solver of choice. In all cases we illustrate a spectral analysis showing the conditions under which a good clustering of the eigenvalues of the preconditioned matrix can be obtained, which foreshadows (at least in case PCG/MINRES Krylov solvers are used), a fast convergence of the iterative method. Results on a set of large size optimization problems confirm that the Inexact variants of the Constraint Preconditioner can yield efficient solution methods.

1 Introduction

In this paper, we consider linear and convex quadratic programming (LP and QP) problems of the following form:

$$\begin{aligned} \min _{x} \ \big ( c^Tx + \frac{1}{2}x^T Q x \big ), \ \ \text {s.t.} \ Ax = b, \ x \ge 0, \end{aligned}$$

(1.1)

where $c,x \in {\mathbb {R}}^n$, $b \in {\mathbb {R}}^m$, $A \in {\mathbb {R}}^{m\times n}$. For quadratic programming problems we assume that $Q \succeq 0 \in {\mathbb {R}}^{n \times n}$, while for linear programming we have $Q=0$. The problem (1.1) is often referred to as the primal form of the quadratic programming problem; the dual form of the problem is given by

$$\begin{aligned} \text {max}_{x,y,z} \ \big (b^Ty - \frac{1}{2}x^T Q x\big ), \ \ \text {s.t.}\ -Qx + A^Ty + z = c,\ z\ge 0, \end{aligned}$$

(1.2)

where $z \in {\mathbb {R}}^n$, $y \in {\mathbb {R}}^m$. Problems of linear or quadratic programming form are fundamental problems in optimization, and arise in a wide range of scientific applications.

A variety of optimization methods exist for solving the problem (1.1). Two popular and successful approaches are interior point methods (IPMs) and proximal methods of multipliers (PMMs). Within an IPM, a Lagrangian is constructed involving the objective function and the equality constraints of (1.1), to which a logarithmic barrier function is then added in place of the inequality constraints. Hence, a logarithmic barrier sub-problem is solved at each iteration of the algorithm (see [36] for a survey on IPMs). The key feature of a PMM is that, at each iteration, one seeks the minimum of the problem (1.1) as stated, but one adds to the objective function a penalty term involving the norm of the difference between x and the previously computed estimate. Then, an augmented Lagrangian method is applied to approximately solve each such sub-problem (see [55, 63] for a review of proximal point methods, and [16, 41, 61, 62] for a review of augmented Lagrangian methods).

Upon applying either naive IPM or IP-PMM, the vast majority of the computational effort arises from the solution of the resulting linear systems of equations at each IP–PMM iteration. These linear equations can be tackled in the form of an augmented system, or the reduced normal equations: we focus much of our attention on the augmented system, as unless Q has some convenient structure it is highly undesirable to form the normal equations or apply the resulting matrix within a solver. Within the linear algebra community, direct methods are popular for solving such systems due to their generalizability, however if the matrix system becomes sufficiently large the storage and/or operation costs can rapidly become excessive, depending on the computer architecture used. The application of iterative methods, for instance those based around Krylov subspace methods such as the Conjugate Gradient method (CG) [42] or MINRES [54], is an attractive alternative, but if one cannot construct suitable preconditioners which can be applied within such solvers then convergence can be prohibitively slow, and indeed it is possible that convergence is not achieved at all. The development of powerful preconditioners is therefore crucial.

A range of general preconditioners have been proposed for augmented systems arising from optimization problems, see [14, 17, 24, 29, 53, 66] for instance. However, as is the case within the field of preconditioning in general, these are typically sensitive to changes in structure of the matrices involved, and can have substantial memory requirements. Preconditioners have also been successfully devised for specific classes of programming problems solved using similar optimization methods: applications include those arising from multicommodity network flow problems [22], stochastic programming problems [21], formulations within which the constraint matrix has primal block-angular structure [23], and PDE-constrained optimization problems [56, 57], or various applications [26]. However, such preconditioners exploit particular structures arising from specific applications; unless there exists such a structure which hints as to the appropriate way to develop a solver, the design of bespoke preconditioners remains a challenge. We finally remark that also selection of a proper stopping criterion for the inner linear solver is crucial to devise an efficient outer–inner iteration (see [74] for a recent study).

The block structure of the linear system we will address is the well-known saddle-point system:

$$\begin{aligned} \begin{bmatrix} G &{} \quad A^T \\ A &{}\quad 0 \end{bmatrix} \begin{bmatrix} u_{1} \\ u_{2} \end{bmatrix} = \begin{bmatrix} d_{1} \\ d_{2} \end{bmatrix} \end{aligned}$$

(1.3)

where G is an ${\mathbb {R}}^{n \times n}$ SPD matrix, while $A \in {\mathbb {R}}^{m \times n }$ rectangular matrix with full row rank, as usually $m < n$. The exact constraint preconditioner (CP) is defined as

$$\begin{aligned} M = \begin{bmatrix} D &{}\quad A^T \\ A &{}\quad 0 \end{bmatrix}. \end{aligned}$$

(1.4)

Application of $M^{-1}$ to a vector, required at each iteration of a Krylov solver, rests on the efficient computation of the square-root free Cholesky factorization of the negative Schur complement of D in M,

$$\begin{aligned} A D^{-1} A^T = L D_0 L^T, \end{aligned}$$

(1.5)

which allows for the following factorization:

$$\begin{aligned} M = \left[ \begin{array}{cc} I &{} 0 \\ A D^{-1} &{} I \end{array} \right] \left[ \begin{array}{cc} D &{} 0 \\ 0 &{} -LD_0L^T \end{array} \right] \left[ \begin{array}{cc} I &{} D^{-1} A^T \\ 0 &{} I \end{array} \right] . \end{aligned}$$

(1.6)

The aim of this paper is to review the block preconditioners proposed mainly for solving system (1.3) with focus on the approximate construction (or factorization) of the Schur complement matrix, a key issue for the development of efficient iterative solver.

This paper is structured as follows. In Sect. 2 we describe the structure of a linear system to be solved at each IP iteration in the case of Quadratic (Linear) and Non Linear problems. In Sect. 3 we recall the main properties of the exact constraint preconditioner (see e.g. [44]), whereas in Sects. 4, 5 and 6 we describe three variants of this approach, to make the cost of the preconditioner application affordable also when addressing large size problems. Namely, in Sect. 4 we describe the Inexact Constraint Preconditioner obtained by sparsifying matrix A [12, 13], in Sect. 5 we approximate directly the Schur complement matrix $A D^{-1} A^T$ by neglecting small terms in $D^{-1}$ as proposed in [11]; in Sect. 6 we review an approach which considers application of the exact CP at selected IP iterations while simply updating it (by a BFGS-like formula) in the subsequent iterations [8]. Some numerical results are shown in Sect. 7 and, finally, in Sect. 8 we give some concluding remarks.

Notation: Given an arbitrary square (or rectangular) matrix A, then $\lambda _{\max }(A)$ and $\lambda _{\min }(A)$ (or $\sigma _{\max }(A)$ and $\sigma _{\min }(A)$) denote the largest and smallest eigenvalues (or singular values) of the matrix A, respectively. In all the following sections we will indicate with the symbol H the coefficient matrix, with M the preconditioner in its “direct” form (i.e. $M \approx H$) and with P the inverse preconditioner (satisfying $P \approx H^{-1}$).

2 Linear algebra in interior point methods

Interior point methods for linear, quadratic and nonlinear optimization differ obviously in many details but they rely on the same linear algebra kernel. We discuss briefly two cases of quadratic and nonlinear programming, following the presentation in [14].

2.1 Quadratic programming

Consider the convex quadratic programming problem

$$\begin{aligned} \text{ min }&c^T x + \frac{1}{2} x^T Q x&\\ \text{ s.t. }&A x = b,&\\&\; \; \; x \ge 0,&\end{aligned}$$

where $Q \in {\mathbb {R}}^{n \times n}$ is positive semidefinite matrix, $A \in {\mathbb {R}}^{m \times n}$ is the full rank matrix of linear constraints and vectors x, c and b have appropriate dimensions. The usual transformation in interior point methods consists in replacing inequality constraints with the logarithmic barriers to get

$$\begin{aligned} \begin{array}{rc} \text{ min } &{} c^T x + \dfrac{1}{2} x^T Q x - \mu \sum \limits _{j=1}^{n} \, \ln x_j \\ \text{ s.t. } &{} A x \ = b, \\ \end{array} \end{aligned}$$

where $\mu \ge 0$ is a barrier parameter. The Lagrangian associated with this problem has the form:

$$\begin{aligned} L(x,y,\mu )= c^T x + \dfrac{1}{2} x^T Q x - y^T(A x - b) - \mu \sum \limits _{j=1}^{n} \, \ln x_j \end{aligned}$$

and the conditions for a stationary point write

$$\begin{aligned} \begin{array}{rcrcl} \nabla _x L(x,y,\mu ) &{}=&{} c - A^T y - \mu X^{-1} e + Q x &{}=&{} 0 \\ \nabla _y L(x,y,\mu ) &{}=&{} A x - b &{}=&{} 0, \end{array} \end{aligned}$$

where $X^{-1} = {{\,\mathrm{diag}\,}}\{ x_1^{-1}, x_2^{-1}, \ldots , x_n^{-1} \}.$ Having denoted

$$\begin{aligned} s= \mu X^{-1} e, \qquad \text{ i.e. } \qquad XS e= \mu e, \end{aligned}$$

where $S = {{\,\mathrm{diag}\,}}\{ s_1, s_2, \ldots , s_n \}$ and $e = (1, 1, \ldots , 1)^T$, the first order optimality conditions (for the barrier problem) are:

$$\begin{aligned} A x= & {} b, \nonumber \\ A^{T} y+ s -Q x= & {} c, \nonumber \\ XS e= & {} \mu e \nonumber \\ (x,s)\ge & {} 0. \end{aligned}$$

(2.1)

Interior point algorithm for quadratic programming [72] applies Newton method to solve this system of nonlinear equations and gradually reduces the barrier parameter $\mu$ to guarantee the convergence to the optimal solution of the original problem. The Newton direction is obtained by solving the system of linear equations:

$$\begin{aligned} \left[ \begin{array}{rcc} A &{} 0 &{} 0 \\ -Q &{} A^{T} &{} I \\ S &{} 0 &{} X \end{array} \right] \left[ \begin{array}{c} \Delta x \\ \Delta y \\ \Delta s \end{array} \right] = \left[ \begin{array}{c} \xi _{p} \\ \xi _{d} \\ \xi _{\mu } \end{array} \right] , \end{aligned}$$

(2.2)

where

$$\begin{aligned} \xi _{p}= & {} b-A x, \\ \xi _{d}= & {} c-A^{T} y- s + Q x, \\ \xi _{\mu }= & {} \mu e - X S e. \end{aligned}$$

By elimination of

$$\begin{aligned} \Delta s = X^{-1}(\xi _{\mu } - S \Delta x) = - X^{-1} S \Delta x + X^{-1} \xi _{\mu }, \end{aligned}$$

from the second equation we get the symmetric indefinite augmented system of linear equations

$$\begin{aligned} \left[ \begin{array}{cc} -Q - \Theta _1^{-1} &{} A^T \\ \quad A \quad &{} 0 \end{array} \right] \left[ \begin{array}{c} \Delta x \\ \Delta y \end{array} \right] = \left[ \begin{array}{c} \xi _{d} - X^{-1} \xi _{\mu } \\ \xi _{p} \end{array} \right] . \end{aligned}$$

(2.3)

where $\Theta _1 = X S^{-1}$ is a diagonal scaling matrix. By eliminating $\Delta x$ from the first equation we can reduce (2.3) further to the form of normal equations

$$\begin{aligned} H_{NE} \equiv (A (Q + \Theta _1^{-1})^{-1} A^{T}) \Delta y \; = \; \mathbf{b}_{QP}. \end{aligned}$$

For a generic large and sparse matrix Q it is generally inefficient to form explicitly the normal equation matrix $H_{NE}$ so that this kind of problems are usually tackled in their augmented form (2.3).

2.2 Special cases. linear programming, separable problems

Simplified versions of (2.3) are obtained for linear programming by simply setting $Q \equiv 0$, thus obtaining

$$\begin{aligned} \left[ \begin{array}{cc} - \Theta _1^{-1} &{} A^T \\ \quad A \quad &{} 0 \end{array} \right] \left[ \begin{array}{c} \Delta x \\ \Delta y \end{array} \right] = \left[ \begin{array}{c} \xi _{d} - X^{-1} \xi _{\mu } \\ \xi _{p} \end{array} \right] . \end{aligned}$$

(2.4)

This problem is usually solved by resorting to the normal equation system which now reads

$$\begin{aligned} H_{NE} \equiv (A \Theta _1 A^{T}) \Delta y \; = \; \mathbf{b}_{LP}. \end{aligned}$$

Differently from the quadratic case, the normal equation matrix can be explicitly formed. As $H_{NE}$ is symmetric positive definite, the system $H_{NE} \Delta y = \mathbf{b}_{LP}$ can be solved by the Preconditioned Conjugate Gradient (PCG) iterative method. However, as it is observed by many authors, the condition number of $H_{NE}$ grows rapidly as the Interior Point method approaches the solution to the optimization problem, and finding suitable preconditioners for this problem is currently under research. This topic will be discussed in Sect. 5.

Separable problems are characterized by the fact that Q is a diagonal matrix and hence easily invertible. As in the linear case, $H_{NE}$ can be formed allowing to address the normal equation system.

2.3 Nonlinear programming

Consider the convex nonlinear optimization problem

$$\begin{aligned} \text{ min }&f(x)&\\ \text{ s.t. }&g(x)&\le 0, \end{aligned}$$

where $x \in {\mathbb {R}}^{n}$, and $f: {\mathbb {R}}^n \mapsto {\mathbb {R}}$ and $g: {\mathbb {R}}^n \mapsto {\mathbb {R}}^m$ are convex, twice differentiable. Having replaced inequality constraints with an equality $g(x) + z = 0$, where $z \in {\mathbb {R}}^m$ is a nonnegative slack variable, we can formulate the associated barrier problem

$$\begin{aligned} \text{ min }&f(x) - \mu \sum \limits _{i=1}^m \ln z_i&\\ \text{ s.t. }&g(x) + z = 0. \end{aligned}$$

and write the Lagrangian for it

$$\begin{aligned} L(x,y,z,\mu ) = f(x) + y^T (g(x) + z) - \mu \sum \limits _{i=1}^m \ln z_i. \end{aligned}$$

The conditions for a stationary point write

$$\begin{aligned} \begin{array}{rcrcl} \nabla _x L(x,y,z,\mu ) &{} = &{} \nabla f(x) + \nabla g(x)^T y &{} = &{} 0 \\ \nabla _y L(x,y,z,\mu ) &{} = &{} g(x) + z &{} = &{} 0 \\ \nabla _z L(x,y,z,\mu ) &{} = &{} y - \mu Z^{-1} e &{} = &{} 0, \end{array} \end{aligned}$$

where $Z^{-1} = {{\,\mathrm{diag}\,}}\{ z_1^{-1}, z_2^{-1}, \cdots ,z_m^{-1} \}$. The first order optimality conditions (for the barrier problem) have thus the following form

$$\begin{aligned} \begin{array}{c} \nabla f(x) + \nabla g(x)^T y = 0, \\ g(x) + z = 0, \\ YZ e = \mu e \\ (y,z) \ge 0, \end{array} \end{aligned}$$

(2.5)

where $Y = {{\,\mathrm{diag}\,}}\{ y_1, y_2, \cdots ,y_m \}$. Interior point algorithm for nonlinear programming [72] applies Newton method to solve this system of equations and gradually reduces the barrier parameter $\mu$ to guarantee the convergence to the optimal solution of the original problem. The Newton direction is obtained by solving the system of linear equations:

$$\begin{aligned} \left[ \begin{array}{ccl} Q(x,y) &{} A(x)^T &{} 0 \\ A(x) &{} 0 &{} I \\ 0 &{} Z &{} Y \end{array} \right] \! \left[ \begin{array}{l} \Delta x \\ \Delta y \\ \Delta z \end{array} \right] = \left[ \begin{array}{c} - \nabla f(x) - A(x)^T y \\ - g(x) - z \\ \mu e - Y Z e, \end{array} \right] , \end{aligned}$$

(2.6)

where

$$\begin{aligned} \begin{array}{rclcl} A(x) &{} = &{} \nabla g(x) &{} \in &{} {\mathbb {R}}^{m \times n} \\ Q(x,y) &{} = &{} \nabla ^2 f(x) \! + \! \sum \limits _{i=1}^m \! y_i \nabla ^2 g_i(x) &{} \in &{} {\mathbb {R}}^{n \times n}. \end{array} \end{aligned}$$

Using the third equation we eliminate

$$\begin{aligned} \Delta z = \mu Y^{-1} e - Z e - Z Y^{-1} \Delta y, \end{aligned}$$

from the second equation and get

$$\begin{aligned} \left[ \begin{array}{cc} -Q(x,y) &{} A(x)^T \\ A(x) &{} \! Z Y^{-1} \end{array} \right] \left[ \begin{array}{c} \Delta x \\ - \Delta y \end{array} \right] = \left[ \begin{array}{c} \nabla f(x) + A(x)^T y \\ - g(x) - \mu Y^{-1} e \end{array} \right] . \end{aligned}$$

(2.7)

The matrix involved in this set of linear equations is symmetric and indefinite. For convex optimization problem (when f and g are convex), the matrix Q is positive semidefinite and if f is strictly convex, Q is positive definite and the matrix in (2.7) is quasidefinite. Similarly to the case of quadratic programming by eliminating $\Delta x$ from the first equation we can reduce this system further to the form of normal equations

$$\begin{aligned} \left( A(x) Q(x,y)^{-1} \! A(x)^{T} + Z Y^{-1} \right) \Delta y = \mathbf{b}_{NLP}. \end{aligned}$$

The two systems (2.3) and (2.7) have many similarities. The main difference is that in (2.3) only the diagonal scaling matrix $\Theta _1$ changes from iteration to iteration, while in the case of nonlinear programming not only the matrix $\Theta _2 = Z^{-1} Y$ but also the matrices Q(x, y) and A(x) in (2.7) change in every iteration. Both these systems are indefinite. However, to avoid the need of using $2 \times 2$ pivots in their factorization we transform them to quasidefinite ones by the use of primal and dual regularization [1]. Our analysis in the following sections is concerned with the quadratic optimization problems, and hence A and Q are constant matrices. However, the major conclusions can be generalized to the nonlinear optimization case.

3 Exact constraint preconditioner

In this section we shall discuss the properties of the preconditioned matrices involved in (2.3). For ease of the presentation we shall focus on the quadratic programming case with linear equality constraints hence we will assume that $\Theta _2^{-1} = 0$ (we also drop the subscript in $\Theta _1$). In [14] these results are extended to the nonlinear programming case.

Due to the presence of matrix $\Theta ^{-1}$, the augmented system

$$\begin{aligned} H = \left[ \begin{array}{cc} -Q - \Theta ^{-1} &{} A^T \\ A &{} 0 \end{array} \right] . \end{aligned}$$

(3.1)

is very ill-conditioned. Indeed, some elements of $\Theta$ tend to zero while others tend to infinity as the optimal solution of the problem is approached. The performance of any iterative method critically depends on the quality of the preconditioner in this case.

Block-type preconditioners are widely used in linear systems obtained from a discretization of PDEs [10, 15, 34, 58, 73]. The preconditioners for the augmented system have also been used in the context of linear programming [33, 53] and in the context of nonlinear programming [29, 44, 47, 48, 64]. As was shown in [53], the preconditioners for indefinite augmented system offer more freedom than those for the normal equations. Moreover, the factorization of the augmented system is sometimes much easier than that of the normal equations [2] (this is the case, for example, when A contains dense columns). Hence even in the case of linear programming (in which normal equations is a viable approach) augmented system offers important advantages. For quadratic and nonlinear programming the use of the augmented system is a must and so we deal with the augmented system preconditioners in this paper. On the other hand, we realize that for some specially structured problems such as multicommodity network flows, very efficient preconditioners for the normal equations [22, 43] can also be designed.

3.1 Spectral analysis

We consider the augmented system

$$\begin{aligned} H u = d, \quad \text {with} \quad H = \left[ \begin{array}{cc} G &{} A^T \\ A &{} 0 \end{array} \right] , \quad u = \left[ \begin{array}{cc} x \\ y \end{array} \right] , d = \left[ \begin{array}{cc} b \\ c \end{array} \right] , G = Q + \Theta ^{-1}.\nonumber \\ \end{aligned}$$

(3.2)

CPs for matrix H have the following form:

$$\begin{aligned} M = \left[ \begin{array}{cc} D &{} A^T \\ A &{} 0 \end{array} \right] , \end{aligned}$$

(3.3)

where D is some symmetric approximation to G. Any preconditioner of this type can be regarded as the coefficient matrix of a Karush-Kuhn-Tucker (KKT) system associated with an optimization problem with the same constraints as the original problem, thus motivating the name of the preconditioner. We note that D should be chosen so that M is nonsingular and is “easier to factorize” than H; furthermore, it must involve $\Theta$ in order to capture the key numerical properties of H. A common choice is

$$\begin{aligned} D = {{\,\mathrm{diag}\,}}(G) ; \end{aligned}$$

(3.4)

a different approach consists in implicitly defining D by using a factorization of the form $M=U C U^T$, where U and C are specially chosen matrices [28]. Here we consider (3.4), which is SPD. The spectral properties of the preconditioned matrix $M^{-1}H$ and the application of CG with preconditioner M to the KKT linear system have been deeply investigated. For the sake of completeness, in the next theorem we summarize some theoretical results about CPs, given in e.g. [8, 14, 44, 47].

Theorem 3.1

Let $Z \in {\mathbb {R}}^{n \times (n-m)}$ be a matrix whose columns span the nullspace of A. Assume also that D is SPD. The following properties hold.

• 1. $M^{-1} H$ has an eigenvalue at 1 with multiplicity 2m.

• 2. The remaining $n-m$ eigenvalues of $M^{-1} H$ are defined by the generalized eigenvalue problem

  $$\begin{aligned} Z^T G Z w = \lambda Z^T D Z w. \end{aligned}$$

  (3.5)

• 3. The eigenvalues, $\lambda$, of (3.5) satisfy

  $$\begin{aligned} \lambda _{min} (D^{-1} G) \le \lambda \le \lambda _{max} (D^{-1} G). \end{aligned}$$

  (3.6)

• 4. If CG is applied to system (3.2) with preconditioner M and starting guess $u_0 = [\, x_0^T \; y_0^T \,]^T$ such that $A x_0 = c$, then the corresponding iterates $x_j$ are the same as the ones generated by CG applied to

  $$\begin{aligned} (Z^T G Z) x = Z^T (b - G x_0), \end{aligned}$$

  (3.7)

  with preconditioner $Z^T D Z$. Thus, the component $x^*$ of the solution $u^*$ of system (3.2) is obtained in at most $n-m$ iterations and the following inequality holds:

  $$\begin{aligned} \Vert x_j - x^* \Vert \le 2 \sqrt{\kappa } \left( \frac{\sqrt{\kappa }-1}{\sqrt{\kappa } + 1} \right) ^j \Vert x_0 - x^* \Vert , \quad j=1,\ldots ,n-m, \end{aligned}$$

  where $\kappa = \kappa ( (Z^T D Z)^{-1} Z^T G Z )$.

• 5. The directions $p_j$ and the residuals $r_j$ generated by applying CG with preconditioner M to system (3.2), with the same starting guess as in item 4, take the following form:

  $$\begin{aligned} p_j = \left[ \begin{array}{c} Z {\bar{p}}_{j,1} \\ p_{j,2} \end{array} \right] , \quad r_j = \left[ \begin{array}{c} r_{j,1} \\ 0 \end{array} \right] , \end{aligned}$$

  (3.8)

  where ${\bar{p}}_{j,1}$ and $r_{j,1}$ are the direction and the residual, respectively, at the j-th iteration of CG applied to (3.7) with preconditioner $Z^T D Z$, and

  $$\begin{aligned} p_j^T H p_i = {\bar{p}}_{j,1} ^T Z^T G Z {\bar{p}}_{i,1} . \end{aligned}$$

  (3.9)

From the previous theorem it follows that the preconditioned matrix has 2m unit eigenvalues independently of the particular choice of D; on the other hand, properties 2 and 3 show that the better D approximates G, the more the remaining $n-m$ eigenvalues of $M^{-1} H$ are clustered around 1. Furthermore, the application of CG to the KKT system (3.2) with preconditioner M is closely related to the application of CG to system (3.7) with preconditioner $Z^T D Z$. We note that property 4 does not guarantee that $y_j = y^*$ after at most $n-m$ iterations; actually, a breakdown may occur at the $(n-m+1)$-st iteration. However, this is a “lucky breakdown”, in the sense that $y^*$ can be easily obtained starting from the last computed approximation of it, as shown in [47]. More generally, since it may happen that the 2-norm of the PCG residual may not decrease as fast as the H-norm of the PCG error, a suitable scaling of the KKT system matrix can be used to prevent this situation [64]. We mention that other constraint-preconditioned Krylov solvers, such as MINRES, SYMMLQ and GMRES have been analyzed and implemented in [27].

Remark 3.2

The excellent spectral properties of the constraint-preconditioned matrix and the possibility of employing a suitable Conjugate Gradient method makes this preconditioner a natural choice for solving the IP linear systems. However, we note that the effectiveness of CPs may be hidden by the computational cost for the factorization of their Schur complements, thus reducing the efficiency of the overall IP procedure. Sects. 4, 5 and 6 will be devoted to address this issue. In particular we will focus on

• 1. Constructing an inexact-constraint preconditioner, thus allowing a sparser L-factor for the Normal Equation matrix $A D^{-1} A^T$.

• 2. Dropping small elements in $D^{-1}$, in this way producing a far sparser Schur complement matrix.

• 3. Avoiding factorization of the Schur complement matrix at each IP iteration by modifying, with a low rank matrix, the preconditioner computed at one of the previous iterations.

4 Inexact jacobian constraint preconditioner

We consider the preconditioning of the KKT system $H u = d$ by the inexact Jacobian constraint preconditioner $M_{IJ}$, where

$$\begin{aligned} H = \left[ \begin{array}{cc} G &{} A^T \\ A &{}0 \end{array} \right] \qquad \text {and} \qquad M_{IJ}= \left[ \begin{array}{cc} D &{} {\tilde{A}}^T \\ {\tilde{A}} &{}0 \end{array} \right] , \end{aligned}$$

(4.1)

Once again we will consider D as a diagonal approximation of G and ${\tilde{A}}$ a sparsification of A in order to have a sparse matrix ${\tilde{A}} D^{-1} {\tilde{A}}^T$ which is needed at each application of the preconditioner $M_{IJ}$. The eigenvalue distribution of $M_{IJ}^{-1} H$ has been investigated in [12, 13].

Following [12] we define $E = A - {\tilde{A}}, \, {{\,\mathrm{rank}\,}}(E) = p$. Here ${\tilde{\sigma }}_1$ is the smallest singular value of $\tilde{A} D^{-1/2}$. We introduce two error terms:

$$\begin{aligned} e_Q = \Vert E_Q\Vert = \Vert D^{-1/2} QD^{-1/2} - I \Vert \qquad \text {and} \qquad e_A = \dfrac{\Vert ED^{-1/2} \Vert }{\sigma _1({\tilde{A}} D^{-1/2})} \end{aligned}$$

(4.2)

which measure the errors of the approximations to the (1, 1) block and to the matrix of the constraints, respectively. The distance $|\epsilon |$ of the complex eigenvalues from one with $\epsilon = \lambda -1$, will be bounded in terms of these two quantities.

Theorem 4.1

Assume A and $\tilde{A}$ have maximum rank. If the eigenvector is of the form $(0, y)^T$ then the eigenvalues of $M_{IJ}^{-1}H$ are either one (with multiplicity at least $m-p$) or possibly complex and bounded by $|\epsilon | \le e_A$. The eigenvalues corresponding to eigenvectors of the form $(x,y)^T$ with $x \ne 0$ are

• 1. equal to one (with multiplicity at least $m-p$), or

• 2. real positive and bounded by

  $$\begin{aligned} {{ \lambda _{\min }(D^{-1/2}QD^{-1/2}) \le \lambda \le \lambda _{\max }(D^{-1/2}QD^{-1/2})}}, \ or \end{aligned}$$

• 3. complex, satisfying

  $$\begin{aligned} | \epsilon _R|\le & {} e_Q + e_A \end{aligned}$$

  (4.3)
  $$\begin{aligned} | \epsilon _I|\le & {} e_Q + e_A, \end{aligned}$$

  (4.4)

  where $\epsilon = \epsilon _R + \mathrm{i} \epsilon _I$.

The efficiency of the inexact Jacobian constraint preconditioner rely on (1) the clustering of the eigenvalues around one, stated by Theorem 4.1, and (2) by the ability to exactly (and economically) factorize ${\tilde{A}} D^{-1} {\tilde{A}}^T =: L D_0 L^T$.

5 An inexact normal equations preconditioner

Following [11] we consider the following augmented system after regularization.

$$\begin{aligned} \begin{bmatrix} -(Q + \Theta _k^{-1} + \rho _k I_n) &{} A^T\\ A &{} \delta _k I_m \end{bmatrix} \begin{bmatrix} \Delta x_k\\ \Delta y_k \end{bmatrix} = \begin{bmatrix} r_x \\ r_y \end{bmatrix}, \end{aligned}$$

(5.1)

In (5.1) two positive and decreasing sequences $\rho _k$ and $\delta _k$ have been introduced in order to obtain a regularized interior point method. In the sequel we will assume that both $\rho _k$ and $\delta _k$ are $O(\mu _k)$ i.e. go to zero as the barrier parameter.

We remind the important feature of the matrix $\Theta _k$: as the method approaches an optimal solution, the positive diagonal matrix has some entries that (numerically) grow like $\mu _k^{-1}$, while others approach zero. By observing the matrix in (5.1), we can immediately see the benefits of using regularization in IPMs. On one hand, the dual regularization parameter $\delta _k$ ensures that the system matrix in (5.1) is invertible, even if A is rank-deficient. On the other hand, the primal regularization parameter $\rho _k$ controls the worst-case conditioning of the (1, 1) block of (5.1), improving the numerical stability of the method (and hence its robustness). We refer the reader to [1, 59, 60] for a review of the benefits of regularization in the context of IPMs.

The normal equations, at a generic step k of the Interior Point method, read as follows:

$$\begin{aligned} H_{NE} \Delta y = \xi , \qquad H_{NE} = A (\Theta _k^{-1} + Q + \rho _k I_n)^{-1} A^T + \delta _k I_m , \end{aligned}$$

(5.2)

In order to employ preconditioned MINRES or CG to solve (5.1) or (5.2) respectively, we must find an approximation for the coefficient matrix in (5.2). To do so, we employ a symmetric and positive definite block-diagonal preconditioner for the saddle-point system (5.1), involving approximations for the negative of the (1,1) block, as well as the Schur complement $H_{NE}$. See [45, 51, 68] for motivation of such saddle-point preconditioners. In light of this, we approximate Q in the (1,1) block by its diagonal, i.e. $\tilde{Q} = \text {diag}(Q)$ and define the diagonal matrix ${\tilde{G}}_k$ as

$$\begin{aligned} {\tilde{G}}_k = \big (\Theta _k^{-1} + \tilde{Q} + \rho _k I_n \big )^{-1}. \end{aligned}$$

(5.3)

Then, we define the diagonal matrix $E_k$ with entries (dropping the index k in $E_k$ and ${\tilde{G}}_k$)

$$\begin{aligned} E_{ii} = {\left\{ \begin{array}{ll} 0 &{} \ \text {if} \quad G_{ii} < C_{k} \min \{\mu _k, 1\}, \\ G_{ii} &{} \ \text {otherwise,} \end{array}\right. } \end{aligned}$$

(5.4)

where $i \in \{1,\ldots ,n\}$, $C_{k}$ is a constant, and we construct the normal equations approximation $M_{NE} = L_M L_M^T$, by computing the (exact) Cholesky factorization of

$$\begin{aligned} M_{NE} = A E_k A^T + \delta _k I_m. \end{aligned}$$

(5.5)

The dropping threshold in (5.4) guarantees that a coefficient in the diagonal matrix $(\Theta ^{-1} + \tilde{Q}+ \rho _kI_n)^{-1}$ is set to zero only if it is below a constant times the barrier parameter $\mu _k$. As a consequence fewer outer products of columns of A contribute to the normal equations, and the resulting preconditioner $M_{NE}$ is expected to be more sparse than $H_{NE}$. This choice is also crucial to guarantee that the eigenvalues of the preconditioned normal equations matrix are independent of $\mu$. Before discussing the role of the constant $C_{k}$, let us first address the preconditioning of the augmented system matrix in (5.1). The matrix $M_{NE}$ acts as a preconditioner for CG applied to the normal equations. In order to construct a preconditioner for the augmented system matrix in (5.1), we employ a block-diagonal preconditioner of the form:

$$\begin{aligned} M_{AS} = \begin{bmatrix} {\tilde{G}}_k^{-1} &{} 0 \\ 0 &{} M_{NE} \end{bmatrix}, \end{aligned}$$

(5.6)

with ${\tilde{G}}_k$ and $M_{NE}$ defined in (5.3) and in (5.5), respectively. Note that MINRES requires a symmetric positive definite preconditioner and hence many other block preconditioners for (5.1) are not applicable.

As we will show in the sequel, following the developments in [60], forcing the regularization variables $\delta _k,\ \rho _k$ to decrease at the same rate as $\mu _k$ is numerically beneficial, will provide the spectrum of the preconditioned normal equations to be independent of $\mu _k$; a very desirable property for preconditioned systems arising from IPMs.

5.1 Spectral analysis. LP or separable QP cases

In this section we provide a spectral analysis of the preconditioned normal equations in the LP or separable QP case, assuming that (5.5) is used as the preconditioner. Although this is a specialized setting, we may make use of the following result in our analysis of the augmented system arising from the general QP case.

Let us define this normal equations matrix $\tilde{H}_{NE}$, using the definition of ${\tilde{G}}_k$ (5.3), as

$$\begin{aligned} \tilde{H}_{NE} = A \tilde{G}_k A^T + \delta _k I_m. \end{aligned}$$

(5.7)

The following Theorem provides lower and upper bounds on the eigenvalues of $M_{NE}^{-1} \tilde{H}_{NE}$, at an arbitrary iteration k of Algorithm IP–PMM.

Theorem 5.1

There are $m-r$ eigenvalues of $M_{NE}^{-1} \tilde{H}_{NE}$ at one, where r is the column rank of $A^T$, corresponding to linearly independent vectors belonging to the nullspace of $A^T$. The remaining eigenvalues are bounded as

$$\begin{aligned} 1 \le \lambda \le 1 + \frac{C_{k} \mu _k}{\delta _k} \sigma ^2_{\max } (A). \end{aligned}$$

Proof

The eigenvalues of $M_{NE}^{-1} \tilde{H}_{NE}$ must satisfy

$$\begin{aligned} A \tilde{G}_k A^T u + \delta _k u = \lambda A E_k A^T u + \lambda \delta _k u . \end{aligned}$$

(5.8)

Multiplying (5.8) on the left by $u^T$ and setting $z = A^T u$ yields

$$\begin{aligned} \lambda = \frac{z^T \tilde{G}_k z + \delta _k \Vert u\Vert ^2}{z^T E_k z + \delta _k \Vert u\Vert ^2} = 1 + \frac{z^T \left( \tilde{G}_k-E_k\right) z}{z^T E_k z + \delta _k \Vert u\Vert ^2} = 1 + \alpha . \end{aligned}$$

For every vector u in the nullspace of $A^T$ we have $z = 0$ and $\lambda = 1$. The fact that both $E_k$ and $\tilde{G}_k - E_k \succeq 0$ (from the definition of $E_k$) implies the lower bound. To prove the upper bound we first observe that, in view of (5.4), $\lambda _{\max } (\tilde{G}_k-E_k) \le C_{k} \mu _k$; then

$$\begin{aligned} \alpha= & {} \frac{z^T \left( \tilde{G}_k-E_k\right) z}{z^T E_k z + \delta _k \Vert u\Vert ^2} \le \frac{z^T \left( \tilde{G}_k-E_k\right) z}{\delta _k \Vert u\Vert ^2} \\= & {} \frac{z^T \left( \tilde{G}_k-E_k\right) z}{\Vert z\Vert ^2} \frac{1}{\delta _k} \frac{\Vert z\Vert ^2}{\Vert u\Vert ^2} \le \frac{C_{k} \mu _k}{\delta _k} \frac{u^T A A^T u}{\Vert u\Vert ^2} \le \frac{C_{k} \mu _k}{\delta _k} \sigma ^2_{\max } (A). \end{aligned}$$

$\square$

Remark 1

Following the discussion in the end of the previous section, we know that $\dfrac{\mu _k}{\delta _k} = O(1)$, since IP–PMM forces $\delta _k$ to decrease at the same rate as $\mu _k$. Combining this with the result of Theorem 5.1 implies that the condition number of the preconditioned normal equations is asymptotically independent of $\mu _k$.

Remark 2

In the LP case ($Q = 0$), or the separable QP case (Q diagonal), Theorem 5.1 characterizes the eigenvalues of the preconditioned matrix within the CG method.

5.1.1 BFGS-like low-rank update of the ${M_{NE}}$ preconditioner

Given a rectangular (tall) matrix $V \in {\mathbb {R}}^{m \times p}$ with maximum column rank, it is possible to define a generalized block-tuned preconditioner M satisfying the property

$$\begin{aligned} M^{-1} \tilde{H}_{NE} V = \nu V, \end{aligned}$$

so that the columns of V become eigenvectors of the preconditioned matrix corresponding to the eigenvalue $\nu$. A way to construct M (or its explicit inverse) is suggested by the BFGS-based preconditioners used e.g. in [7] for accelerating Newton linear systems or analyzed in [50] for general sequences of linear systems, that is

$$\begin{aligned} M^{-1}= & {} \nu V \Pi V^T + (I_m - V \Pi V^T \tilde{H}_{NE}) M_{NE}^{-1} (I_m - \tilde{H}_{NE} V \Pi V^T), \quad \text {with} \quad \\ \Pi= & {} (V^T \tilde{H}_{NE} V)^{-1}. \end{aligned}$$

We notice that BFGS-like updates for sequences of linear systems have also been investigated e.g. in [31, 38].

Note also that if the columns of V would be chosen as e.g. the p exact rightmost eigenvectors of $M_{NE}^{-1} \tilde{H}_{NE}$ (corresponding to the p largest eigenvalues) then all the other eigenpairs,

$$\begin{aligned} (\lambda _1, z_1), \ldots , (\lambda _{m-p}, z_{m-p}), \end{aligned}$$

of the new preconditioned matrix $M^{-1} \tilde{H}_{NE}$ would remain unchanged (nonexpansion of the spectrum of $M^{-1} \tilde{H}_{NE}$, see [39]).

Usually columns of V are chosen as the (approximate) eigenvectors of $M_{NE}^{-1} \tilde{H}_{NE}$ corresponding to the smallest eigenvalues of this matrix [6, 65]. However, this choice would not produce a significant reduction in the condition number of the preconditioned matrix as the spectral analysis of Theorem 5.1 suggests a possible clustering of smallest eigenvalues around 1. We choose instead, as the columns of V, the rightmost eigenvectors of $M_{NE}^{-1} \tilde{H}_{NE}$, approximated with low accuracy by the function eigs of MATLAB. The $\nu$ value must be selected to satisfy $\lambda _{\min }(M_{NE}^{-1}\tilde{H}_{NE}) < \nu \ll \lambda _{\max }(M_{NE}^{-1}\tilde{H}_{NE})$. We choose $\nu = 10$, to ensure that this new eigenvalue lies in the interior of the spectral interval, and the column size of V as $p = 10$. This last choice is driven by experimental evidence that in most cases there are a small number of large outliers in $M_{NE}^{-1}\tilde{H}_{NE}$. A larger value of p would (unnecessarily) increase the cost of applying the preconditioner.

Finally, by computing approximately the rightmost eigenvectors, we would expect a slight perturbation of $\lambda _1, \ldots , \lambda _{m-p}$, depending on the accuracy of this approximation. For a detailed perturbation analysis see e.g. [70].

Updating a given preconditioner and reusing it, in the framework of solution of sequences of linear systems, have been analyzed in various papers. Among the others we quote [71] in which an adaptive automated procedure is devised for determining whether to use a direct or iterative solver, whether to reinitialize or update the preconditioner, and how many updates to apply. In [69] the update involves an inexact LU factorization of a given matrix in the sequence, [46] in the context of slightly varying coefficient matrices in the sequence (which is not the case in IP optimization). More related to the Interior Point iteration are [3, 4] where the $LDL^T$ factorization of the saddle point matrix is updated at each IP iteration, and cheap approximations of the initial Schur complement matrix are provided.

5.2 Spectral analysis. QP case

In the MINRES solution of QP instances the system matrix is

$$\begin{aligned} H_{AS} = \begin{bmatrix} -F_k &{} A^T \\ A &{} \delta _k I_m \end{bmatrix}, \qquad F_k = Q + \Theta _k^{-1} + \rho _k I_n, \end{aligned}$$

while the preconditioner is

$$\begin{aligned} M_{AS} = \begin{bmatrix} {\tilde{F}}_k &{} 0 \\ 0 &{} M_{NE} \end{bmatrix}, \qquad {\tilde{F}}_k = {\tilde{Q}} + \Theta _k^{-1} + \rho _k I_n \equiv \tilde{G}_k^{-1}. \end{aligned}$$

The following Theorem will characterize the eigenvalues of $M_{AS}^{-1} H_{AS}$ in terms of the extremal eigenvalues of the preconditioned (1,1) block of (5.1), ${\tilde{F}}_k^{-1} F_k$, and of $M_{NE}^{-1} \tilde{H}_{NE}$ as described by Theorem 5.1. We will work with (symmetric positive definite) similarity transformations of these matrices defined as

$$\begin{aligned} {\hat{F}}_k = {\tilde{F}}_k^{-1/2} F_k {\tilde{F}}_k^{-1/2}, \quad \hat{M}_{NE} = M_{NE}^{-1/2} \tilde{H}_{NE} M_{NE}^{-1/2}, \end{aligned}$$

(5.9)

and set

$$\begin{aligned} \begin{array}{lcllcllcl} \alpha _{NE} &{}=&{} \lambda _{\min } ( \hat{M}_{NE}), &{} \beta _{NE} &{}=&{} \lambda _{\max } \left( \hat{M}_{NE}\right) , &{} \kappa _{NE} &{}=&{} \dfrac{\beta _{NE}}{\alpha _{NE}}, \\ \alpha _{F} &{}=&{} \lambda _{\min } \left( {\hat{F}}_k\right) , &{} \beta _{F} &{}=&{} \lambda _{\max } \left( {\hat{F}}_k\right) , &{} \kappa _{F} &{}=&{} \dfrac{\beta _{F}}{\alpha _{F}}. \end{array} \end{aligned}$$

Hence, an arbitrary element of the in the range of the Rayleigh Quotient of these matrices is represented as:

$$\begin{aligned} \begin{array}{lcllcl} \gamma _{NE}\in & {} q(\hat{M}_{NE}) = [\alpha _{NE}, \beta _{NE}], ~~&~~\gamma _{F}\in & {} q({\hat{F}}_k) = [\alpha _{F}, \beta _{F}]. \end{array} \end{aligned}$$

Similarly, an arbitrary element of $q(M_{NE})$ is denoted by

$$\begin{aligned} \begin{array}{lcllclcl} \gamma _{p}\in & {} [\lambda _{\min }(M_{NE}),\lambda _{\max } (M_{NE})]\subseteq & {} \left[ \delta _k,\dfrac{\sigma _{\max }^2(A)}{\rho _k} + \delta _k\right) . \end{array} \end{aligned}$$

Observe that $\alpha _{F} \le 1 \le \beta _{F}$ as

$$\begin{aligned} \frac{1}{n} \sum _{i=1}^n \lambda _i \left( {\tilde{F}}_k^{-1} F_k\right) = \frac{1}{n} \,\text {Tr}\left( {\tilde{F}}_k^{-1} F_k\right) = 1. \end{aligned}$$

Theorem 5.2

Let k be an arbitrary iteration of IP–PMM. Then, the eigenvalues of $M_{AS}^{-1} H_{AS}$ lie in the union of the following intervals:

$$\begin{aligned} I_- = \left[ - \beta _{F} -\sqrt{\beta _{NE}}, -\alpha _{F}\right] ; \quad I_+ = \left[ \frac{1}{1+\beta _{F}} , 1 + \sqrt{\beta _{NE}-1}\right] . \end{aligned}$$

Proof

The proof of this theorem, following an idea in [5], can be found in [11]. $\square$

Remark 5.3

It is well known that a pessimistic bound on the convergence rate of MINRES can be obtained if the sizes of $I_-$ and $I_+$ are roughly the same [40]. In our case, as usually $\beta _F \ll \beta _{NE}$, we can assume that the length of both intervals is roughly $\sqrt{\beta _{NE}}$. As a heuristic we may therefore use [30,  Theorem 4.14], which predicts the reduction of the residual in the $M_{AS}^{-1}$-norm in the case where both intervals have exactly equal length. This then implies that

$$\begin{aligned} \frac{\Vert r_k\Vert }{\Vert r_0\Vert } \le 2 \left( \frac{\kappa - 1}{\kappa +1} \right) ^{\lfloor k/2 \rfloor }, \end{aligned}$$

where

$$\begin{aligned} \kappa\approx & {} \frac{1+\beta _F}{\alpha _F} \left( 1+\sqrt{\beta _{NE}-1}\right) (\beta _F + \sqrt{\beta _{NE}}) \le 2 \kappa _F \left( \sqrt{1+\beta _{NE}}\right) (\beta _F + \sqrt{\beta _{NE}}) \\\approx & {} 2 \beta _{NE} \cdot \kappa _F \le 2 \kappa _{NE} \cdot \kappa _F. \end{aligned}$$

6 Multiple BFGS-like updates of the constraint preconditioner

In order to avoid the factorization (1.5) at a certain IP iteration k, we construct a preconditioner for the KKT system at that iteration by updating a CP computed at an iteration $i < k$. We extend to KKT systems and CPs the preconditioner updating technique for SPD matrices presented in [39], which in turn exploits ideas from [52, 67].

Let us consider, as before,

$$\begin{aligned} H = \left[ \begin{array}{cc} G &{} A^T \\ A &{} 0 \end{array} \right] , \quad M = \left[ \begin{array}{cc} D &{} A^T \\ A &{} 0 \end{array} \right] , \quad P = M^{-1} \end{aligned}$$

(6.1)

and

$$\begin{aligned} S = \begin{bmatrix} S_1 \\ S_2 \end{bmatrix} \in {\mathbb {R}}^{(n+m) \times q}, \quad q \le n-m \end{aligned}$$

(6.2)

with $S_1 \in {\mathbb {R}}^{n \times q}$ such that

$$\begin{aligned} {{\,\mathrm{rank}\,}}(S_1) =q, \quad A S_1 = 0. \end{aligned}$$

(6.3)

We first define a preconditioner for H by applying a BFGS-like rank-2q update to $M$:

$$\begin{aligned} M_{upd}= M+ H S (S^T H S)^{-1} S^TH - MS (S^T MS)^{-1} S^T M, \end{aligned}$$

(6.4)

which is well defined because $S^T MS = S_1^T D S_1$ and $S^T H S = S_1^T G S_1$. By using the Sherman-Morrison-Woodbury inversion formula, we get the inverse of $M_{upd}$:

$$\begin{aligned} P_{upd}= & {} M_{upd}^{-1} =S (S^T H S)^{-1} S^T\nonumber \\&+ (I - S (S^T H S)^{-1} S^T H ) P(I - H S (S^T H S)^{-1} S^T), \end{aligned}$$

(6.5)

which is analogous to the BFGS update discussed in [39] for SPD matrices.

It is easy to see that the previous rank-2q update allows the preconditioned matrix to have at least q eigenvalues equal to 1 by directly verifying that

$$\begin{aligned} (P_{upd}H) S = S. \end{aligned}$$

We also prove most important property of $M_{upd}$ i.e. that the rank-2q update (6.4) (or, equivalently, (6.5)) produces a CP. To this aim, define

$$\begin{aligned} {\mathscr {S}}= S L_S^{-T}, \end{aligned}$$

(6.6)

where $L_S$ is the lower triangular Cholesky factor of the matrix $S^T H S$.

Theorem 6.1

The matrix $M_{upd}$ given in (6.4) is a CP for the matrix H in (3.2).

Proof

We show that the update (6.4) involves only the (1, 1) block of $M$ and that $M_{upd}$ is nonsingular; hence the thesis holds. Let us split ${\mathscr {S}}$ into two blocks:

$$\begin{aligned} {\mathscr {S}}= \begin{bmatrix} {\mathscr {S}}_1 \\ {\mathscr {S}}_2 \end{bmatrix}, \quad {\mathscr {S}}_1 \in {\mathbb {R}}^{n \times q}, \quad {\mathscr {S}}_2\in {\mathbb {R}}^{m \times q}. \end{aligned}$$

From (6.3) it follows that $A {\mathscr {S}}_1 = 0$. Then,

$$\begin{aligned} H S S^TH = \begin{bmatrix} G {\mathscr {S}}_1 + A^T {\mathscr {S}}_2 \\ 0 \end{bmatrix} \begin{bmatrix} {\mathscr {S}}_1^T G + {\mathscr {S}}_2^T A&0 \end{bmatrix} = \begin{bmatrix} \Gamma &{} 0 \\ 0 &{} 0 \end{bmatrix}, \end{aligned}$$

where

$$\begin{aligned} \Gamma = ( G {\mathscr {S}}_1 + A^T {\mathscr {S}}_2 ) ( {\mathscr {S}}_1^T G + {\mathscr {S}}_2^T A ). \end{aligned}$$

Likewise, we have

$$\begin{aligned} MS_1 (S^T MS)^{-1} S^T M= \begin{bmatrix} \Phi &{} 0 \\ 0 &{} 0 \end{bmatrix}, \end{aligned}$$

where

$$\begin{aligned} \quad \Phi =( DS_1 + A^T S_2) (S_1^T DS_1)^{-1} (S_1^T D+ S_2^T A ). \end{aligned}$$

It follows that

$$\begin{aligned} M_{upd}= M+ H {\mathscr {S}}{\mathscr {S}}^TH - MS (S^T MS)^{-1} S^T M= \begin{bmatrix} D+ \Gamma -\Phi &{} A^T \\ A &{} 0 \end{bmatrix}. \end{aligned}$$

(6.7)

In order to prove that $M_{upd}$ is nonsingular, we consider a matrix $Z \in {\mathbb {R}}^{n \times (n-m)}$ whose columns span the nullspace of A and prove that $Z^T (D+ \Gamma -\Phi ) Z$ is SPD (see, e.g., [25]). We observe that

$$\begin{aligned} \displaystyle Z^T (D+ \Gamma -\Phi ) Z= & {} \displaystyle Z^T DZ + Z^T (G {\mathscr {S}}_1 + A^T {\mathscr {S}}_2)({\mathscr {S}}_1^T G + {\mathscr {S}}_2^T A)Z \nonumber \\&- \, \displaystyle Z^T ( DS_1 + A^T S_2) (S_1^T DS_1)^{-1} (S_1^T D+ S_2^T A ) Z \nonumber \\= & {} \displaystyle Z^T DZ + Z^T G {\mathscr {S}}_1 {\mathscr {S}}_1^T GZ - Z^T DS_1 (S_1^T DS_1)^{-1} S_1^T DZ \nonumber \\= & {} \displaystyle Z^T D_{upd} Z, \end{aligned}$$

(6.8)

where we set

$$\begin{aligned} D_{upd} = D+ G {\mathscr {S}}_1 {\mathscr {S}}_1^T G - DS_1 (S_1^T DS_1)^{-1} S_1^T D. \end{aligned}$$

(6.9)

Then, by using the Sherman-Morrison-Woodbury formula, we have

$$\begin{aligned} D_{upd}^{-1} = {\mathscr {S}}_1 {\mathscr {S}}_1^T + (I - {\mathscr {S}}_1 {\mathscr {S}}_1^T G ) D^{-1} (I - G {\mathscr {S}}_1 {\mathscr {S}}_1^T), \end{aligned}$$

(6.10)

which implies that $D_{upd}$ is SPD. This concludes the proof. $\square$

The unit eigenvalues of the preconditioned matrix $P_{upd}H$, in view of Theorem 3.1, are those of

$$\begin{aligned} (Z^T G Z) w = \lambda (Z^T (D+ \Gamma -\Phi ) Z)w, \end{aligned}$$

(6.11)

where $Z \in {\mathbb {R}}^{n \times (n-m)}$ spans the nullspace of A.

Following [8] the following results on the eigenvalue distribution of $P_{upd}H$ can be proved:

Theorem 6.2

Let $P_{upd}$ be the matrix in (6.5). Then $P_{upd} H$ has an eigenvalue at 1 with multiplicity at least $2m+q$.

The next theorem shows that the nonunit extremal eigenvalues of $D_{upd}^{-1} G$ are bounded by the extremal eigenvalues of $D^{-1} G$. Thus, by Theorem 3.1, we expect the application of $P_{upd}$ to H to yield better spectral properties than the application of $P$.

Theorem 6.3

Let $D_{upd}$ be as in (6.9), then any eigenvalue of $D_{upd}^{-1} G$ satisfies

$$\begin{aligned} \min \left\{ \lambda _{min} (D^{-1} G) , 1 \right\} \le \lambda ( D_{upd}^{-1} G ) \le \max \left\{ \lambda _{max} (D^{-1} G) , 1 \right\} . \end{aligned}$$

Proof

See [8]. $\square$

We defer a discussion on the choice of columns of matrix S in Sect. 7.3.

7 Numerical results

Extensive numerical results regarding all the proposed inexact block preconditioners can be found in [8, 11,12,13]. We will briefly report some examples in which the advantages for the proposed inexact CP variants are evident. The problems we will consider, whose characteristics are reported in Table 1, are taken from the CUTEst [37] collection or they are modifications of them.

Table 1 Characteristics of the test problems. L is the Cholesky factor of $A D^{-1} A^T$

7.1 Inexact jacobian

In the definition of preconditioner $M_{IJ}$ we used the following dropping rule to determine matrix E:

$$\begin{aligned} e_{ij} = {\left\{ \begin{array}{ll} a_{ij} &{} \text {if} \ |a_{ij}| < \mathtt{drop}\cdot \Vert A_j\Vert \ \ \textsc {and} \ \ |i-j| > \mathtt{nband} \\ 0 &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

where with $A_j$ we denote the jth column of A.

In other words, we drop an element from matrix A if it is below a prescribed tolerance and outside a fixed band. The first requirement prevents $\Vert E\Vert$ from becoming too large with consequent going away of the eigenvalues from the unity (see the bounds in Theorem 4.1). The second requirement attempts to control the fill-in of $A A^T$ and hence of its Cholesky factor L.

The following results refer to the runs on an Intel Xeon PC 2.80 GHz with 2 GB RAM of a pure FORTRAN version of the HOPDM code [35], with the g77 compiler and the -O4 option. We solved the SQP2500_2 problem using both the exact CP (with PCG as the inner solver) and with the Inexact Jacobian Constraint Preconditioner (IJCP – in combination with QMRs [32]).

The results are reported in Table 2 which shows the impressive gain in terms of CPU time provided by the inexact preconditioner. The number of inner iterations are (clearly) larger using IJCP, however the extreme sparsity of the preconditioner reduces considerably the cost of a single iteration.

Table 2 Performance of the proposed preconditioner with optimal combination of the parameters vs PCG preconditioned with exact CP for problem SQP2500_3

To show how the drop and nband values may affect the distribution of the eigenvalues of $M_{IJ}^{-1}H$, we have plotted in Fig. 1 all the eigenvalues of the preconditioned matrix on the complex plane. In the “no-drop” case (exact constraint preconditioner), the eigenvalues are all real (the ones are $4007 > 2m = 4000$, as expected). With $E \ne 0$, the number of unit eigenvalues is smaller but still remains important. Increasing the drop parameter, also $|\epsilon |$ increases, but the real part of eigenvalues still remains bounded away from zero.

Fig. 1

Distribution of the eigenvalues of $M_{IJ}^{-1} H$ in the complex plane for problem sqp2500_2 with different combinations of the parameters $\mathtt{nband, drop}$

This is also shown in Table 3, where we report the number of unit eigenvalues, the maximum distance from the unity ($|\epsilon |$, see Theorem 4.1), and the smallest real part of all the eigenvalues.

Table 3 Spectral properties of the preconditioned matrices for problem sqp2500_2

7.2 Inexact NE preconditioner

The experiments reported in this Section were conducted on a PC with a 2.2GHz Intel Core i7 processor (hexa-core), 16GB RAM The MATLAB version used was R2019a. We set the tolerance for the PCG/MINRES relative residual to $10^{-4}$ and 100 (300) the maximum number of PCG (MINRES) iterations.

7.2.1 Low-rank updates and dynamic refinement

At each IP iteration we check the number of non-zeros of the preconditioner used in the previous iteration. If this number exceeds some predefined constant (depending on the number of constraints m), we perform certain low-rank updates to the preconditioner, to ensure that its quality is improved, without having to use very much memory. In such a case, the following tasks are performed as sketched in Algorithm LRU-0. Then, at every Krylov iteration, the computation of the preconditioned residual $\hat{r} = M^{-1} r$ requires the steps outlined in Algorithm LRU-1.

In our implementation, the first step of Algorithm LRU-0 is performed using the restarted Lanczos method through the inbuilt MATLAB function eigs, requesting 1-digit accurate eigenpairs. We finally remark that a good approximation of the largest eigenvalues of the preconditioned matrix could be extracted for free [9] during the iterative solution of the correction linear system and used them to accelerate the predictor linear system by the low-rank correction. This approach, would save on the cost of computing eigenpairs but would provide acceleration in the second linear system only.

The quality of both preconditioners in (5.6) and (5.5) depends heavily on the quality of the approximation of the normal equations. If the Krylov method converged fast in the previous IP–PMM iteration (compared to the maximum allowed number of Krylov iterations), while requiring a substantial amount of memory, then the preconditioner quality is lowered (i.e. $C_{k+1} > C_{k}$). Similarly, if the Krylov method converged slowly, the preconditioner quality is increased (i.e. $C_{k} > C_{k+1}$). If the number of non-zeros of the preconditioner is more than a predefined large constant (depending on the available memory), and the preconditioner is still not good enough, we further increase the preconditioner’s quality (i.e. we decrease $C_{k}$), but at a very slow rate. This behavior is observed in practice very close to the IP convergence especially on large scale problems.

To show the efficiency of this variant we first present in Table 4 the results of the $M_{NE}$ preconditioner for the LP-NUG-20 and LP-NUG-30 problems.

Table 4 Results of the $M_{NE}$ preconditioner for LP-NUG problems

From this table we can see that the $M_{NE}$ preconditioner (plus low-rank correction) is able to keep very low the number of inner iterations in both problems. Note that the largest instance can not be solved by an exact Constraint Preconditioner. In order to clarify the benefit of the low-rank (LR) updates in Table 5 we report the results in solving these linear systems with the low-rank strategy and different accuracy/number of eigenpairs (LR($p, \texttt {tol}$) meaning that we approximate p eigenpairs with eigs with a tolerance tol). The best choice, using $p=10$ and 0.1 accuracy, improves the $M_{NE}$ preconditioner both in terms of linear iterations and total CPU time.

Table 5 CPU times and number of linear iterations for the various preconditioners at IP iteration #12 for problem LP-NUG-20

To summarize the comparison of the two approaches, we include Fig. 2. It contains the performance profiles of the two methods, over the 26 largest linear programming problems of the QAPLIB, Kennington, Mittelmann, and Netlib libraries, for which at least one of the two methods was terminated successfully. In particular, in Fig. 2a we present the performance profiles with respect to time, while in Fig. 2b we show the performance profiles with respect to the number of IPM iterations. IP–PMM with factorization is represented by the green line (consisting of triangles), while IP–PMM with PCG is represented by the blue line (consisting of stars).

As one can observe, IP–PMM with factorization was able to solve only 84.6% of these problems, due to excessive memory requirements (namely, problems LP-OSA-60, LP-PDS-100, RAIL4284, LP-NUG-30 were not solved due to insufficient memory). As expected, however, it converges in fewer iterations for most problems that are solved successfully by both methods. Moreover, IP–PMM with PCG is able to solve every problem that is successfully solved by IP–PMM with factorization. Furthermore, it manages to do so requiring significantly less time, which can be observed in Fig. 2a. Notice that we restrict the comparison to only large-scale problems, since this is the case of interest.

Fig. 2

Performance profiles for large-scale linear programming problems

Finally, with regards to convex quadratic problems, the IP–PMM method with MINRES as the inner iterative solver and $M_{AS}$ as the preconditioner was able to solve more than $99\%$ of the Maros–Mészáros test set [49], which is comprised of 127 convex quadratic programming problems. See [11] for details.

7.3 Low-rank update of an exact CP

To experimentally analyze this CP variant, we first focus on the choice of the matrix S needed for building $P_{upd}$ for the k-th KKT system in the sequence under consideration, by suggesting a number of choices:

BFGS-P. k-th iteration is obtained by setting its columns equal to the he first q H-orthonormal directions constructed during the PCG solution of IP step $k-1$. Since we have experimentally verified that the PCG directions can rapidly lose the property of being mutually $H_{k-1}$-orthogonal when $H_{k-1}$ is highly ill conditioned, we perform a selective reorthogonalization of the directions forming S, during their computation. More precisely, $p_i$ is $H_{k-1}$-reorthogonalized against $p_l$, with $l < i$, whenever needed. We now present a different choice of S, which deserves a detailed explanation.

BFGS-C. Matrix S used to build $P_{upd}$ for the KKT system at the k-th iteration is obtained by setting its columns equal to the first q H-orthonormal directions constructed during the PCG solution of the current IP step k. The suffix -C in BFGS-C refers to the fact that PCG directions from the current system are used to define S. As for BFGS-P, a selective $H_k$-reorthogonalization of the directions is performed in the first q PCG iterations.

It is easy to show [8] that in exact arithmetic the BFGS-C procedure is equivalent to PCG with preconditioner $P$. Thus, BFGS-C may appear completely useless. Nevertheless, it is useful in finite-precision arithmetic. Freezing the preconditioner $P$ computed at a certain IP iteration and using it in subsequent IP iterations yields directions which rapidly and dramatically lose orthogonality. BFGS-C appears to mitigate this behavior, improving the performance of PCG.

In order to illustrate this situation, we discuss some numerical results obtained with one of the 35 KKT systems arising in the solution, by an IP procedure, of the CVXQP3 convex QP problem, with dimensions $n = 20000$ and $m = 15000$ (see Sect. 7 for the details).

We considered PCG with the following preconditioning procedures:

• BFGS-C with $q=50$ and seed CP recomputed every 6 IP iteration;

• CP recomputed from scratch every sixth IP iteration and frozen in the subsequent five iterations (henceforth this is referred to as FIXED preconditioning procedure).

In order to make a fair comparison, we performed a selective reorthogonalization of the first 50 directions during the execution of PCG with FIXED preconditioning. We also run PCG with FIXED preconditioning without any reorthogonalization. We focus on the KKT system at the 24-th IP iteration, hence the seed preconditioner comes from the 19-th IP iteration.

Fig. 3

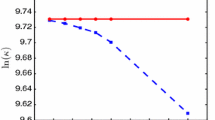
CVXQP3 test problem, KKT system at the 24-th IP iteration: normalized scalar products (7.1) for BFGS-C and FIXED (the latter with and without orthogonalization) and $l=50$.

Figure 3 shows the normalized scalar products

$$\begin{aligned} \frac{ p_j^T H p_l }{ \Vert p_j \Vert \Vert H p_l \Vert }, \quad l=50, \; j > l, \end{aligned}$$

(7.1)

for BFGS-C and both versions of the FIXED procedure. In the latter case, we observe a quick loss of orthogonality with respect to the first q directions, even when the reorthogonalization procedure is applied. Conversely, BFGS-C appears to better preserve orthogonality. As a consequence, the number of PCG iterations corresponding to BFGS-C is smaller than in the other cases (122 iterations for BFGS-C vs 176 and 196 for FIXED with and without reorthogonalization, respectively).

Applying the FIXED preconditioning approach with a selective reorthogonalization of each PCG direction with respect to the first 50 ones we achieved a worst PCG behavior than the one obtained with the BFGS-C strategy. This observation led us to consider a further preconditioning procedure.

DOUBLE. We apply q PCG iterations to the current system $H_k u = d_k$ by using a CP, say $P_{upd}^{(0)}$, built with the BFGS-P procedure, i.e., by updating a seed preconditioner $P$ with the first q normalized PCG directions obtained at the $(k-1)$-st IP iteration. Then we restart PCG from the last computed iterate $u_q$, with the following preconditioner:

$$\begin{aligned} P_{upd}= S^{C} (S^{C})^T + ( I - S^{C} (S^{C})^T H_k ) P_{upd}^{(0)} ( I - H_k S^{C} (S^{C})^T ) , \end{aligned}$$

(7.2)

where $S^C$ contains the normalized directions computed in the first q PCG iterations. As for the previous preconditioning procedures, a selective reorthogonalization is applied to the PCG directions used to build $P_{upd}^{(0)}$ and to those used for $P_{upd}$.

The sequences of KKT systems have been obtained by running the Fortran 95 PRQP code, which implements an infeasible inexact potential reduction IP method [18, 20, 25] using as the tolerances on the relative duality gap and the relative infeasibilities $10^{-6}$ and $10^{-7}$, respectively. Within PRQP, the PCG iterations have been stopped as soon as

$$\begin{aligned} \Vert r^{(j)} \Vert \le \tau , \quad \tau = \min \{\max \{\tau _1, 10^{-8}\}, 10^{-2} \Vert r^{(0)} \Vert \}, \end{aligned}$$

where $\tau _1$ depends on the duality gap value at the current IP iteration (see [19] for the details). A maximum number of 600 PCG iterations has been considered. The preconditioning procedures FIXED, BFGS-P, BFGS-C and DOUBLE have been applied with different values of s and q, while the PCG solver has been also applied with the CP recomputed from scratch for each KKT system (RECOM).

The code has been implemented in Fortran 95 and run on an Intel Core i7 CPU (2.67 GHz) with 6 GB RAM and 8 MB cache. The factorization of the Schur complement has been performed by the MA57 routine from HSL Mathematical Software Library (http://www.hsl.rl.ac.uk).

In Table 6 we report some results concerning the application of the preconditioning procedures, including the FIXED one, to CVXQP3N: the cumulative number of PCG iterations (PGC iters), the relevant CPU times (in seconds), namely: for the factorization of the Schur complement (Tf-Schur), for the application of the seed preconditioner $P$ within PCG (Ta-seed), for the preconditioner updates and the reorthogonalization steps (Tupd), and the total times (Ttot).

Table 6 Results for problem CVXQP3N (number of KKT systems in the sequence: 36)

Fig. 4

Problem CVXQP3N, KKT system at IP iteration #24: PCG convergence profile for the different updates and with $s=8$ and $q_{\max } = 50$. The seed preconditioner comes from the IP iteration #17

The factorization of the Schur complement is rather expensive, and the recomputation of the CP from scratch produces by far the largest execution time, even if it yields a much smaller number of PCG iterations than the other preconditioning procedures. Furthermore, the updating procedures generally produce a significant reduction of the number of iterations with respect to the FIXED one, and hence smaller execution times. BFGS-C and DOUBLE turn out to be the most efficient procedures.

The PCG convergence histories for the KKT systems at the 24-th IP iteration, with the updating procedures and the FIXED ones for $s=8$ and $q_{max}=50$, clearly show how each procedure compares with the others in terms of PCG iterations (see Fig. 4): the best preconditioning procedure is DOUBLE, followed by BFGS-P, BFGS-C and then FIXED. This is a general behavior, although sporadic failures have been observed with BFGS-P and DOUBLE in cases where BFGS-C and FIXED work.

8 Concluding remarks

We have presented three inexact variants of the Constraint Preconditioner for solving Convex Linear and Quadratic Programming Problems of very large size. Any of these procedures aims at reducing the complexity of the exact factorization of the CP, often prohibitive for realistic problems. We list below the pros and cons of these approaches to help driving the reader to the best choice for the problem at hand.

• Inexact Jacobian. This preconditioner is suggested when the coefficients in the matrix of constraint display variation of magnitudes and/or the matrix displays some band structure. Solvers like PCG or MINRES can not be used, and theoretical convergence estimates are problematic due to the presence of complex eigenvalues in the preconditioned matrix.

• Inexact NE preconditioner. This is a promising variant which drives the sparsity of the of the Cholesky factor of the (approximate) Schur complement matrix by means of a sequence, $\{C_k\}$. At each IP iteration k, $C_k$ is defined dynamically as a function of the fill-in and the number of iterations at previous iteration $k-1$. Krylov solvers such as PCG (Linear and Quadratic separable Problems) or MINRES (Quadratic Problems) are allowed.

• Low Rank updates of an exact CP. This method can be employed whenever the exact CP factorization is expensive but applicable. It reduces considerably the main cost of the overall algorithm, which is the factorization of the Schur complement. The PCG is allowed also for the augmented system since updated CPs are still CPs (see Theorem 3.1).