Skip to main content
SpringerLink
Log in

Feedback stabilization for a scalar conservation law with PID boundary control

  • Published:
Chinese Annals of Mathematics, Series B Aims and scope Submit manuscript

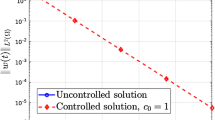
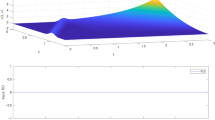
Abstract

This paper deals with a scalar conservation law in 1-D space dimension, and in particular, the focus is on the stability analysis for such an equation. The problem of feedback stabilization under proportional-integral-derivative (PID for short) boundary control is addressed. In the proportional-integral (PI for short) controller case, by spectral analysis, the authors provide a complete characterization of the set of stabilizing feedback parameters, and determine the corresponding time delay stability interval. Moreover, the stability of the equilibrium is discussed by Lyapunov function techniques, and by this approach the exponential stability when a damping term is added to the classical PI controller scheme is proved. Also, based on Pontryagin results on stability for quasipolynomials, it is shown that the closed-loop system subject to PID control is always unstable.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Åström, K. J. and Hägglund, T., PID Controllers: Theory, Design, and Tunning, Instrument Society of America, Research Triangle Park, NC, 1995.

    Google Scholar 

  2. Bastin, G. and Coron, J. M., On boundary feedback stabilization of non-uniform linear 2 × 2 hyperbolic systems over a bounded interval, Systems Control Lett., 60(11), 2011, 900–906.

    Article  MathSciNet  MATH  Google Scholar 

  3. Cooke, K. L. and Van den Driessche, P., On zeroes of some transcendental equations, Funkcial Ekvac., 29(1), 1986, 77–90.

    MathSciNet  MATH  Google Scholar 

  4. Coron, J. M., Control and nonlinearity, Mathematical Surveys and Monographs, Vol. 136, AMS, Providence, RI, 2007.

    Google Scholar 

  5. Coron, J. M., Bastin, G. and d’Andréa-Novel, B., Dissipative boundary conditions for one-dimensional nonlinear hyperbolic systems, SIAM J. Control Optim., 47(3), 2008, 1460–1498.

    Article  MathSciNet  MATH  Google Scholar 

  6. Coron, J. M., d’Andréa-Novel, B. and Bastin, G., A strict Lyapunov function for boundary control of hyperbolic systems of conservation laws, IEEE Trans. Automat. Control, 52(1), 2007, 2–11.

    Article  MathSciNet  Google Scholar 

  7. Coron, J. M. and Wang, Z. Q., Output feedback stabilization for a scalar conservation law with a nonlocal velocity, SIAM J. Math. Anal., 45(5), 2013, 2646–2665.

    Article  MathSciNet  MATH  Google Scholar 

  8. Dick, M., Gugat, M. and Leugering, G., Classical solutions and feedback stabilization for the gas flow in a sequence of pipes, Netw. Heterog. Media, 5(4), 2010, 691–709.

    Article  MathSciNet  MATH  Google Scholar 

  9. Dos Santos, V., Bastin, G., Coron, J. M. and d’Andréa-Novel, B., Boundary control with integral action for hyperbolic systems of conservation laws: Stability and experiments, Automatica J. IFAC, 44(5), 2008, 1310–1318.

    Article  MathSciNet  MATH  Google Scholar 

  10. Greenberg, J. and Li, T. T., The effect of boundary damping for the quasilinear wave equation, J. Differential Equations, 52(1), 1984, 66–75.

    Article  MathSciNet  MATH  Google Scholar 

  11. Hale, J. K. and Verduyn Lunel, S. M., Strong stabilization of neutral functional differential equations, IMA Journal of Mathematical Control and Information, 19, 2002, 5–23.

    Article  MathSciNet  MATH  Google Scholar 

  12. Li, T. T., Global classical solutions for quasilinear hyperbolic systems, Research in Applied Mathematics, Vol. 32, Masson, Paris, 1994.

  13. Lichtner, M., Spectral mapping theorem for linear hyperbolic systems, Proc. Amer. Math. Soc., 136(6), 2008, 2091–2101.

    Article  MathSciNet  MATH  Google Scholar 

  14. Pontryagin, Lev Semionovitch, On the zeros of some elementary transcendental functions, Amer. Math. Soc. Transl. (2), 1, 1955, 95–110.

  15. Prieur, C., Winkin, J. and Bastin, G., Robust boundary control of systems of conservation laws, Math. Control Signals Systems, 20(2), 2008, 173–197.

    Article  MathSciNet  MATH  Google Scholar 

  16. Renardy, M., On the linear stability of hyperbolic PDEs and viscoelastic flows, Z. Angew. Math. Phys., 45(6), 1994, 854–865.

    Article  MathSciNet  MATH  Google Scholar 

  17. Silva, G. J. and Datta, A. and Bhattacharyya, S. P., PID controllers for time-delay systems, Control Engineering, Birkhäuser, Boston, 2005.

    MATH  Google Scholar 

  18. Walton, K. and Marshall, J. E., Direct method for TDS stability analysis, Proceedings of IEEE, 134(D), 1987, 101–107.

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. UPMC University Paris 06, NUMR 7598 Laboratoire Jacques-Louis Lions, Sorbonne Universités, F-75005, Paris, France

    Jean Michel Coron

  2. Université Paris Sud, F-91405, Orsay, France

    Simona Oana Tamasoiu

Authors
  1. Jean Michel Coron
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Simona Oana Tamasoiu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jean Michel Coron.

Additional information

Dedicated to Luc Tartar with the Souvenir of His Wonderful Course at Ecole Plytechnique

This work was supported by the ERC Advanced Grant 266907 (CPDENL) of the 7th Research Framework Programme (FP7), FIRST, Initial Training Network of the European Commission (No. 238702) and PITNGA-2009-238702.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Coron, J.M., Tamasoiu, S.O. Feedback stabilization for a scalar conservation law with PID boundary control. Chin. Ann. Math. Ser. B 36, 763–776 (2015). https://doi.org/10.1007/s11401-015-0975-8

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11401-015-0975-8

Keywords

2000 MR Subject Classification

Search

Navigation