Abstract
Burullus lagoon is part of Egypt’s protected area network. The lagoon serves as a reservoir for drainage water discharged from agricultural areas, and the lake’s sediments provide a unique opportunity to record environmental behavior and reconstruct of the heavy metal contamination history. In the present study, the sediment chronology, sedimentation rates, and metal accumulation fluxes were estimated in four sediment cores using 210Pb dating models to evaluate how human activities have affected the coastal environment. Using the radioisotopes 210Pb and 137Cs, radiometric dating was carried out using gamma-ray spectrometry. At the Egypt Second Research Reactor (ETRR-2), the element concentrations were determined using the instrumented neutron activation analysis (INAA- k0 method). Our findings show that the constant rate of supply (CRS), which has been verified with the peak of artificial radionuclide 137Cs, is the best model performed for the chronology of Burullus Lagoon. The average sedimentation rate, according to 210Pb dating models, is 0.85 cm/year. The large variation in sedimentation rates, especially after the 1990s, is consistent with an increase in the anthropogenic flux of heavy metals. This may be led into a significant environmental problem such as reducing the size of the lake and degrading the quality the water in Burullus Lagoon. Enrichment factor (EF) of the studied elements displayed the following order: Cl > Ca > Na > Br > Zn > Ta > Ti > V > Cr > Sc > Mg > Mn > Fe > Hf which is higher than unity. Furthermore, the Nemerow pollution index (PI Nemerow) revealed that pollution was increasing in the direction of the drains and slightly polluted. Consequently, pollutant indices showed that urbanization and industrial development may have increased the depositional fluxes of the metals in sediments over time.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Lake sediment cores supply a useful information on anthropogenic and natural inputs, the history of sedimentation, and the sources of pollution (Lin et al. 2018; Pappa et al. 2018). Natural environmental archives can be used to manage processes, identify pertinent sources, reconstruct temporal trends in concentrations, and evaluate the pollution state of ecosystems. Sediment chronologies are essential for the interpretation of natural ecosystems, such as lake sediments, which have been used to track atmospheric contamination such as heavy metals, organic contaminants, and radioactive releases from nuclear power plants as well as to assess the past history of changes in lake water quality related to phenomena like acid rain (Appleby 2001; Palani et al. 2023). Furthermore, it plays a significant role in the investigation of physico-chemical processes (e.g., bioturbation, early diagenesis), the study of geological phenomena (e.g., floods, landslides), and the determination of marine radiomodeling variables (e.g., vertical dispersion velocity, radionuclides’ diffusion coefficient in the sediment) (Eleftheriou et al. 2018; Pappa et al. 2018, 2019). The radiochronology of sediments is largely based on the vertical profiles of radionuclides in this frame. Combining two types of fallout radionuclides man-made 137Cs \({(T}_{1/2}=30.07\) a) and natural 210Pb (\({T}_{1/2}= 22.3\) a) has shown to be a valuable method for calculating sediment/mass accumulation rates and understanding sediment geochronology in different lakes (Appleby 2001; Semertzidou et al. 2019; Imam and Salem 2023). Sediment dating with 210Pb, which has been successfully used to reconstruct a variety of environmental processes linked to climatic change, is the most popular method for determining recent chronologies (100–150 year) and aquatic ecosystem sedimentation rates (Barsanti et al. 2020). Three models of 210Pb have been developed to balance the diverse influences of human activity, geology, and sedimentary processes (Appleby and Oldfield 1992). The three models are known by the acronyms constant rate of supply (CRS), constant flux constant sedimentation (CFCS), and constant initial concentration (CIC). Based on various environmental factors, each model has a unique set of assumptions.
The CIC model assumes a uniform and monotonic decrease in 210Pbex activity with depth, which means that the CIC model predicts younger dates for more active deeper layers, which is physically impossible (Zhang et al. 2015a). In the CFCS model, 210Pbex activity decreases exponentially with dry mass accumulation when the 210Pbex flux and sedimentation rate remain constant (Appleby and Oldfield 1983). Because the CIC and CFCS models are strongly influenced by the initial 210Pb concentration, these models cannot provide reliable chronology. Conversely, the CRS model is not sensitive to these changes in the initial concentration and sedimentation rate of different layers. The sedimentation processes in each aquatic ecosystem should be taken into consideration when choosing models, as each one makes specific assumptions based on various environmental conditions (Guo et al. 2020). The different dating models were used for the same cores with the 137Cs event marker to confirm the dating estimates of the sediment records and to circumvent the discrepancy between the three models (Appleby 2008; Putyrskaya et al. 2015). According to previous (Eleftheriou et al. 2018; Pappa et al. 2018, 2019), the above models can be used to reconstruct historical pollution events associated with environmental phenomena such as strong earthquakes, volcanic eruptions, and hydrological changes, as well as industrial. The man-made radioisotope 137Cs, a well-known chronostratigraphic marker, was created in nuclear fission events and largely discharged into the environment during nuclear weapon testing in the 1950s and 1960s, particularly the 1963 fallout maximum (Kumar et al. 2014; Brandon Michael Boyd 2016). Indeed, the majority of studies on 137Cs distribution as an artificial radionuclide in the Mediterranean Sea have been attributed to global fallout from nuclear weapons tests, the Chernobyl accident, and the nuclear industry (Iridoy 2017), and furthermore, the nuclear accident at the Fukushima Daiichi (FD) nuclear disaster in Japan (2011) (Stäger et al. 2023). The FD accident, caused by the tsunami resulting from the Tohoku earthquake on 11 March 2011, involves a large release of radioisotopes into the environment (Bin Feng et al. 2022; Stäger et al. 2023). In recent sedimentary deposits, the use of 137Cs dating as a complementary technique to 210Pb dating has become increasingly important for determining age-depth models (Sarı et al. 2018; Shah et al. 2020).
Lake pollution is one of the biggest environmental problems caused by various sorts of pollutants in many parts of the world, and it poses a significant threat to the planet’s freshwater supplies (Vörösmarty et al. 2010). Sediment pollution in lakes is a result of both anthropogenic and natural processes (Li et al. 2013). These include natural processes such as soil and rock degradation, erosion, wildfires and volcanic eruptions, and anthropogenic processes such as industrial discharges, mining and refining processes, agricultural runoff, wildlife runoff, domestic wastewater, and atmospheric deposition from burning fossil fuels (Davutluoglu et al. 2011). Indeed, anthropogenic sources strongly influence heavy metal accumulation in the marine environment (Perumal et al. 2021). Due to their toxicity and insolubility, heavy metals are one of the emerging environmental contaminants that should be concerned us in aquatic environments (Kumar et al. 2019). Heavy metals in aquatic systems have multiple sources. Bedrock weathering, erosion, and leaching are natural sources; anthropogenic sources include sewage, industrial discharges, fertilizers, and agricultural activities (Kostka and Leśniak 2020, 2021). Therefore, it is important to understand how pollutants are deposited, transformed, and remobilized over time and under changing environmental conditions (such as climate change). Several techniques can be used for element analysis, including instrumented nuclear activation analysis (INNA), X-ray fluorescence (XRF), atomic absorption spectroscopy (AAS), and inductively coupled plasma mass spectrometry (ICP-MS). Activation analysis is an elemental determination method based on nuclear reactions in which stable nuclei are converted into other, usually radioactive nuclei, and the reaction products are then measured (Greenberg et al. 2011). INAA is the most commonly used method due to its small sample size, high sensitivity, selectivity, non-destructive analysis, sample matrix independence, and ability to simultaneously identify multiple elements in the same sample. A variety of indices such as the enrichment factor (EF), ecological risk factor (Er), and Nemerow pollution index (PI Nemerow) have been used to measure the ecotoxicological hazard of contaminants in the sediment cores. The enrichment factor was determined for all examined elements to discriminate between anthropogenic and natural elemental sources.
The Nile Delta’s Manzala, Burullus, Edku, and Mariut lagoons are a major source of water for thousands of Egyptians (Younis 2019). These lakes began to receive a sizable amount of drainage water from agricultural activities after the Aswan High Dam was built in 1964, in addition to seasonal overflow of saltwater. In recent decades, urbanization and industrialization have contributed to an increase in pollutants from a variety of sources, such as industry, agriculture, and waste water (Negm et al. 2019). Burullus Lagoon is among the coastal lagoons that are most at risk because of the abundance of aquatic vegetation, overfishing, an increase in fish farming, and agricultural drainage (Khalil and El-Gharabawy 2016). The main factors contributing to the rise in the concentrations of heavy metals in lake water are increased irrigation, effluent from near-shore aquaculture ponds, and untreated domestic sewage discharge (Al-Afify et al. 2023). In order to better assess and manage the entire ecosystem, it is possible to identify the processes that contribute to the degradation of wetlands as well as the sources of pollution through studies of the spatial and temporal distribution of heavy metals in the delta banks. A thorough analysis is urgently required to determine whether these levels are the result of exposure to contaminants in sediment that have accumulated in the past or inflow from nearby anthropogenic sources of pollution.
Therefore, the purpose of the investigation was to analyze sediment core samples from the Burullus lagoon to achieve the following goals: (i) determine the sediment chronology and sedimentation rates using different models of 210Pb; (ii) reconstruct historical trends and fluxes of anthropogenic metal into the lake and the influence of the catchment area; and (iii) determine pollution indices to evaluate the levels of contamination with heavy metals. We hope that the results of this research will aid in making decisions on the future structure and distribution of Burullus Lagoon.
Material and procedures
Research area
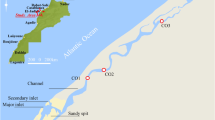
The second largest of the northern lagoons on Egypt’s Mediterranean coast, Burullus Lagoon, is a UNESCO-protected area. It has a surface area of about 410 km2 and is one of four lagoons with shallow brackish water. It is situated along the Rosetta Nile bend, in the middle of Egypt’s Mediterranean coast, between 31° 22′ and 31° 26′ North and 30° 30′ and 31° 10′ East longitudes. Boughaz El-Burullus, which is in the northeastern corner of the lagoon and has depths ranging from 0.4 to 2.00 m, is the passage that connects the lagoon to the Mediterranean. Thirty-four percent of the lagoon’s surface is made up of islands and floating vegetation. In the western region of Burullus Lagoon, there is the Brimbal Canal, which is a source of fresh water, and numerous agricultural drains that empty into the lake (Negm et al. 2019). The Burullus Lagoon has recently received drainage water from a number of drains, including drains 7, 8, 9, 11, Nasser, El-Gharbiya, and El-Burullus, totaling about 3900 Mm3/year (Shalby et al. 2020; Shetaia et al. 2022). There are many serious problems affecting the lakes in Egypt’s northern Nile Delta, including an increase in the flow of fresh water, pollution, lake degradation, rapid population growth, and erosion rates (Younis 2019).
Field sampling
In 2018, four sediment cores from the Burullus lagoon were collected, as shown in Table 1 and Fig. 1. The maps were produced using the ArcGIS program (version 10.8) (ESRI, CA, USA). Core sediments were taken by manually taking a sample inside a plastic tube that was 2 to 3 m long and 10 cm in diameter. The sediment samples were kept in a refrigerator at 4 °C until they were opened for analysis. Glass and plastic were chosen as the material types to avoid contaminating the samples with metal. Before subsamples were collected for additional analysis, the central tubes were cut lengthwise, opened with nylon string, described, and photographed in the lab. The collected sediment cores were cut into 4-cm-long slices for the analysis of radioactivity and heavy metals.
Radiometric dating models based on 210Pb
The sediment cores were analyzed using the 210Pb models to determine the mass accumulation rate (MAR, (r), g/cm year) and sediment accumulation rate (SAR, (s), cm/year). The artificial radionuclide 137Cs (T1/2 = 30.08 a) was used as an independent constraint on the sediment ages for the 2011 and 1986 events in order to validate these models. The 210Pbex was used as the main parameter in the ensuing models. It was calculated by subtracting the actual 226Ra activity from the total 210Pb activity.
Constant flux constant sedimentation
In the CFCS model, the mass accumulation rate and 210Pb flux are treated as constants (Appleby and Oldfield 1983). The slope of the regression line can be utilized to determine the mass accumulation rate because the 210Pbex logarithm against cumulative mass depth will most closely reflect a straight line (Guo et al. 2020).
Calculating the uncertainty (U) in the mass accumulation rate can be done using the equation below (Sanchez-Cabeza and Ruiz-Fernández 2012):
Additionally, by replacing the section depth (zi) for the cumulative mass depth (mi) in a linear regression analysis, it is feasible to determine the sediment accumulation rate (Bruel and Sabatier 2020).
To determine the uncertainty (U) in the mass accumulation rate, apply the equation below:
The CFCS model can be used to calculate the age (t) of the sediment at a depth (i) as follows:
The uncertainty (U) in the sediment age may be calculated using the equation below.
Constant rate of supply
The fundamental hypothesis of the CRS model is the 210Pbex flux to the sediment surface (Appleby et al. 2001). This depends on comparing the 210Pex inventory in sediment cores at various depths to the overall 210Pex inventory. According to the CRS model, the following equations can be used to compute the layer age (ti) at depth I, the MAR (r, g/cm year), the SAR (s, cm/year), and their uncertainty (U) (Sanchez-Cabeza and Ruiz-Fernández 2012; Loan et al. 2023).
where \(\rho \left(i\right)\) is a dry bulk density.
According to Binford (1990), the deeper core regions of the CRS model consistently display a too-old age mistake. The underestimating of 210Pbex, which can be the result of analytical constraints, sampling design, or both, is what leads to the too-old age error (Bruel and Sabatier 2020). Tylmann et al. (2016) recommend that 210Pbex dating based on the CRS model be corrected by reference age to prevent too-old age mistakes for deeper core sections. If x1 is the depth of one reference point (the 137Cs peak marker) with a known age t1 in the core, the mean 210Pb flux (f) above the reference point can be calculated using the following equation (Appleby 2000, 2001; Chen et al. 2019).
where ΔA represents the total inventory of 210Pbex between reference depths x1 and x2, corresponding to age t1 and t2, respectively. The following equation can be used to determine sediment age (t) between \({\text{x}}_{1}\) and \({\text{x}}_{2}\) at any depth using the estimated average flux f(Zhang et al. 2015b):
The age was determined for the layers below the depth of the time marker using the following formula (Chen et al. 2019):
where T1 is the chronostratigraphic date of the x1 depth and Ax1 is the 210Pbex inventory below the x1 depth.
Ecological assessment of heavy metals
A group of metrics known as pollution indices are used to evaluate the state of the environment and forecast how long pollution will last. The enrichment factor (EF), the Nemerow contamination index (PI Nemerow), and the environmental risk factor (Er) are a few examples of contamination indices.
Enrichment factor
One of the most popular ways to differentiate between anthropogenic and natural sources is the enrichment factor (Badawy et al. 2021). Commonly used reference elements for EF calculations are Ti, Zr, Fe, Al, and Sc (Ye et al. 2020). We chose Al as a normalizing element in this investigation for the following reasons: because (a) it is always found as a background metal in combination with other elements due to its uniform natural concentration and abundance in the Earth’s crust (Man et al. 2022); (b) it is largely generated from alumina-silicates (Wang et al. 2019). The following formula was used to compute the EF of heavy metals (Li et al. 2017):
where \({\left[{C}_{Metal}/{C}_{Al}\right]}_{Background}\) and \({\left[{C}_{Metal}/{C}_{Al}\right]}_{sample}\) are the corresponding ratios of the concentrations of the element and the normalizing element (Al) in the background (in the continental shale abundance reported by (Li and Schoonmaker 2014)) and sample, respectively. The existence of pollution is indicated by an EF value greater than 1 (Li et al. 2022), and the following formula can be used to determine the anthropogenic contribution to the metals.
Nemerow pollution index
According to Kowalska et al. (2016), PI Nemerow is employed to determine the degree of heavy metal contamination of the soil environment. The formula used to calculate it is as follows:
N stands for total heavy metals, PI stands for single pollution index, and PI max stands for maximum single pollution index for all heavy metals combined.
Ecological risk factor
The level of metal toxicity and environmental sensitivity to metal contamination are determined by the ecological risk factor. It is calculated using the equation shown below (Hakanson 1980):
where Tir is the toxic response factor of the specified metal as recommended by Hakanson (1980), and CSample and CBackground are heavy metal concentrations in the sample and background, respectively. The \({T}_{i}^{r}\) values of As, Zn, Mn, and Cr are 10, 1, 1, and 2, respectively (Karuppasamy et al. 2017; Man et al. 2022).
Analytical technique
Gamma spectrometry
A gamma-ray spectrometer was used to measure the activity concentrations of 210Pb, 226Ra, and 137Cs in the sediment samples. The high purity germanium (HPGe) detector (type GEM-50210-P) of the Physics Department of the Faculty of Women for Arts, Science, and Education at Ain Shams University in Egypt had a relative efficiency of almost 50% of the efficiency of the 3″ in 3″ NaI (Tl) crystal. By using the photopeak at 661.6 keV, the specific activity for 137Cs was estimated. By using 46.5 keV gamma line energy and after correcting for self-absorption, the specific activity for 210Pb was determined. According to Ramos-Lerate et al. (1998), the correction factor was determined by utilizing a 241Am (point source) placed over the filled and empty sediment containers. The decay products of the 226Ra (214Pb at 609, 1120 keV, and 214Bi at 295, 352 keV) were used to calculate the specific activity of 226Ra. The dry samples were placed in sealed Marinelli beakers and stored for at least 1 month before measurement to ensure radioactive equilibrium between 226Ra and 222Rn (half-life of 3.8 days) (Lin et al. 2019).
The calibration of the detector efficiency was performed by measuring the spectrum of a source emitting γ-rays of precisely known energy, using the IAEA standard sources RGU-1, RGTh-1, RGK-1 (IAEA 1987). In addition, the precision and accuracy of the analysis was estimated using the certified reference materials: IAEA-412 and IAEA-312 (soil) provided by the International Atomic Energy Agency (IAEA). The measured activity concentrations were very close to the reported values of the certified materials, with mean deviations and errors not exceeding 5%. Figure 2-a and 2-b shows a typical gamma spectrum of background and sample of core C-2 (4 cm).
The specific activity (A) (Bq/kg) is calculated as follows (Başkaya et al. 2014; Abbasi 2019):
where \({N}_{s}\) is the sample’s count rate, \({N}_{B}\) is the background’ count rate, t is the counting time (sec), \({\text{I}}_{\upgamma }\) is the gamma line’s emission probability corresponding to the radionuclide’s peak energy, \(\upvarepsilon\) is the spectrometer’s efficiency corresponding to the peak energy, and M is the sample’s weight (kg).
The most important uncertainty sources in our procedure for the determination of the activity concentration of gamma emitters in environmental samples are sample weight, geometry, detector Efficiency, counting statistics, and gamma-ray intensities. The activity concentration uncertainty (UA) is calculated by the following equation (Lépy et al. 2015; Rasul et al. 2018; Imam et al. 2024):
where \(U\left({N}_{s}\right), U\left({N}_{B}\right), U\left({I}_{\gamma }\right), U\left(\varepsilon \right), and U\left(M\right)\) are sample counting, background counting, efficiency, sample mass and gamma line energy uncertainties, respectively. The statistical uncertainty was about 8% in all the energy range.
Heavy metals determination by INAA
The neutron activation analysis laboratory at the ETRR-2 research reactor in Egypt irradiated 18 sediment core samples to identify the existence of short- and long-lived isotopes, respectively. The sample materials were placed in high-purity polyethylene capsules ranging in size from 100 to 300 mg for both short and long irradiations. Depending on the radionuclides’ half-lives to be measured, there are two different types of irradiations (i.e., irradiations lasting 30 to 60 s for radionuclides with short half-lives and 1 h for radionuclides with long half-lives). Eight elements (Mg, Al, Ca, Ti, V, Na, K, and Mn) were found in our samples after a brief irradiation in which polyethylene capsules containing one sample were transmitted into an irradiation position using a pressurized and pneumatic system. The samples were placed in two groups of aluminum cans, each with two flux monitors (F1 and F2). These cans were packed for prolonged irradiation. Each can hold 9 samples in high-purity polyethylene capsules with a flux monitor. The nuclear parameters of the elements identified through short and long irradiation (keV) are displayed in Table 2.
The emitted gamma rays were measured using n-type and p-type HPGe detectors (models GMP-100250-S and GEM-100210-P-Plus, respectively). The gamma ray spectra were analyzed by a gamma vision computer program. Using the 133Ba, 137Cs, 60Co, and 152Eu standard point sources from Isotope Products Laboratories, the detector’s energy and efficiency calibrations were carried out. Figure 3-i and ii is an example of the typical gamma-ray spectrum of sample core C-2 (4 cm) after short and long irradiation.
INAA’s relative method was used, specifically k0-standardization method (Williams and Antoine 2020). The concentration \({\rho }_{a}\) (ppm) of an element is found from the following equation (De Corte and Simonits 2003).
where “Au” denotes to the gold monitor that has been co-irradiated [197Au (n;\(\upgamma\))198Au, E \(\upgamma\) = 411.8 keV], “Np” denotes the net number of counts in the full-energy peak, W is the sample weight, w is the gold monitor weight, tm is the measurement time, saturation factor (S=\(1-exp\left(-\lambda {t}_{irr}\right), {t}_{irr}\) is irradiation time and \(\uplambda\) is the decay constant, decay factor (D = \(exp\left(-\lambda {t}_{d}\right)\)), \({\text{t}}_{\text{d}}\) is decay time, counting factor (C = \(\frac{1-exp\left(-\lambda {t}_{m}\right)}{{t}_{m}}\)) and \({\varepsilon }_{p(Comp, a)}\) is the full-energy peak detection efficiency of comparator and element, respectively, f is the thermal to epithermal neutron flux ratio, \({Q}_{0}=\frac{{I}_{0}}{{\sigma }_{0}}\) is resonance integral to 2200 m/s cross-section ratio), and \(\alpha\) is the measure for the epithermal neutron flux distribution, approximated by a \(\frac{1}{{E}^{\alpha +1}}\) dependence (with \(\alpha\) considered to be independent of neutron energy). The uncertainty in the concentration of the element (\(\sigma ({\rho }_{a}\))) was obtained by the following relation:
Quality assurance
The accuracy and precision of the radiometric analysis were estimated by measuring the 210Pb values and the 226Ra values in the certified reference materials IAEA-410 (radionuclides in bikini atoll sediment), IAEA-312 (radionuclides in soil), and IAEA-314 (radionuclides in stream sediment) that provided by the National Institute of Oceanography and Fisheries, Cairo, Egypt. The activity concentrations obtained for all verified radionuclide values were within 10% of the reported values.
Statistical analysis
Statistics were used to analyze the analytical data related to the distribution and the relationship between the parameters used in the study. The statistical analysis was carried out using Minitab statistics software and MS Excel (365). Pearson’s correlation matrix was calculated using MS Excel (365) to determine the correlation between elements for the identification of the source of heavy metals. Furthermore, principle component analysis (PCA) is a multivariate statistical technique that uses a linear distribution to minimize the variances in two principal components. It is useful for analyzing multiple variables at once and indicates which parameter in the analysis has greater statistical significance; the x component indicates variance that is more significant than the y component (Gonçalves et al. 2021).
Results and discussions
Radionuclides activity concentration, chronology, and sedimentation rates
The distribution of 210Pbtotal, 226Ra, 210Pbex, and 137Cs in the sediment cores samples is represented in Table 1S and Fig. 4. The activity concentrations of supported 226Ra were practically constant in each core with an average value of 23.37 ± 0.62 Bq/kg, 23.13 ± 0.62 Bq/kg, 18.57 ± 0.44 Bq/kg, and 22.41 ± 0.81 Bq/kg for the core samples C-1, C-2, C-3, and C-4, respectively. The 210Pbex activity concentration can be calculated by subtracting the 210Pbtotal from the supported 226Ra. The distribution of 210Pbex activity coincided with that of 210Pbtotal activity due to the relatively constant activity of 226Ra. The specific activity of 210Pbex in the core samples typically decline significantly with the cumulative mass depth (Fig. 4). In the sediment cores, the 210Pbex activity profiles can be a good tracer for the dating of marine sediments and the sedimentation rates over the past century. The vertical distributions of the 210Pbex activity profiles were quite irregular, reflecting the biological and/or physical activity of the very extensive aquaculture in the area (Guo et al. 2020). The 137Cs radioactivity was measured and varying from 0.30 ± 0.05 to 4.14 ± 0.17 Bq/kg in core C-1, 0.12 ± 0.03 to 3.10 ± 0.29 Bq/kg in core C-2, 0.15 ± 0.02 to 2.18 ± 0.16 Bq/kg in core C-3, and 0.60 ± 0.08 to 3.08 ± 0.24 Bq/kg in core C-4. Since the early 1950s, the137Cs has been a part of the environment. There have been two peaks for the 137Cs, the first occurring in 1965 as a result of nuclear weapons testing and the second in 1986 as a result of the Chernobyl accident (Appleby 2008). The majority of the sediment cores contain two distinct 137Cs peaks, which are peak markers for 137Cs from the nuclear accidents at Chernobyl and Fukushima in 1986 and 2011, respectively, except for the sediment core C-1 which had one peak. It is evident that the activity concentration of 137Cs is quite low in all sediment cores, which is most likely due to the relatively large losses from the lake by runoff, because of the high solubility of 137Cs (Chen et al. 2019). It is possible that the behavior of 137Cs in the sediments mirrored that of 210Pbex, according to the events recorded in these cores. The chronology of sediment core can be derived from the depth distribution of the 137Cs in the sediment profile based on the temporal patterns of the atmospheric fallout from the nuclear tests and accidents.
Chronologies were estimated for the cores studied using the CRS, CFCS, and 137Cs-corrected CRS (C-CRS) as shown in Fig. 3 and Table 2S. Although these models produced a variety of chronologies, the trends seen in each sediment core were consistent. Compared to other models, the 137Cs-corrected CRS model generally produced older ages. The chronologies calculated by the various models revealed a considerable discrepancy in the same core. In the upper layers of C-1, C-2, C-3, and C-4, the chronologies calculated by the CFCS and CRS models showed good agreement. The overestimated and underestimated chronologies in the CFCS model can be explained in part by the rapid urbanization of these coastal areas over the last 50 a, which undoubtedly had an impact on the distribution of 210Pbex in these sediments (Xu et al. 2017). There was agreement between the CFCS and CRS model age estimates for the upper layer of recent sediments (nearly 24 cm) of the four sediment cores, as shown Fig. 5. One of the weaknesses of the CFCS model for these samples is that the CFCS model gives a younger age for the deepest cores than the CRS model. In these samples, the activity concentration of 137Cs showed two events in the core samples, except for core C-1 which showed a single peak. In the core C-1, it is obvious that the peak of 137Cs at 16 cm represents the event of 2011, the accident of Fukushima, which agrees with the CFCS model (2011.66 ± 0.93). The ages estimated by the CRS model appear to be in good agreement with the chronology based on the 137Cs time marker in cores C-2 and C-3 as shown in Table 2S. The small amounts of 137Cs concentration have been found in all the sediment cores, which is of interest for the validation of the CRS model. The low concentration of 137Cs may be the result of the physical and biological mixing of modern sediments and the diffusion of organisms in pore water (Imam and Salem 2023). The first detected peak of 137Cs was at 32, 24, and 32 cm in cores C-2, C-3, and C-4, which were thought to be related to the Chernobyl accident (AD 1986). In the same context, there are some hypotheses that could be related to the second peak of 137Cs at 12 cm. This peak could be related to global fallout and the nuclear industry, which could be exchanged of the Black Sea with the Mediterranean region (Evangeliou et al. 2009). It may also be due to new 137Cs deposition in the study area from the Fukushima nuclear accident (AD 2011). This is consistent with the distribution of 137Cs found in the eastern Black Sea coast of Turkey (Baltas et al. 2016) and the freshwater Hazar Lake, Turkey (Bilici et al. 2019). Furthermore, the Mediterranean region is already under environmental stress due to heat waves, erratic precipitation, limited water supply, and droughts. Flash floods are therefore relatively common in the Mediterranean and represent one of the most significant natural hazards in the region (Forcing and Region 2014).
Table 2S and Fig. 6 show the estimated sedimentation rates based on the CRS and C-CRS models. There are no regular changes in sedimentation rates as a function of core depth, which may be due to variations in atmospheric deposition over time. In the core C-1, the SAR values gradually increased from 1930 to 1980, slightly decreased from 1980 to 1990, and then rapidly increased from 1990 to 2016, as shown in Fig. 6. Obviously, the sedimentation rates increased during 1920 to 2009 and decreased during 2009 to 2016, in the core C-2 (Fig. 6). This may be due to the discharge of wastewater from agricultural and industrial activities. On the contrary, there is successive increase in the sedimentation rates from 1990 to 2017 in core C-3 (Fig. 6). For core C-4, sedimentation rates decrease from 1964 to 1980 as shown in Fig. 6, which is in agreement with Xu et al. (2008). This is because sedimentation on the lower Nile coast in the lagoons via the main river distributaries (Rosetta and Damietta) decreased significantly after the construction of the Aswan High Dam.
It is clear that the sediment cores examined in our study can be divided into two periods, pre and post the High Dam (1964). Our results are compared with previous studies, and we found that the mean sedimentation rate of Burullus Lake before the High Dam (1964) was 0.25 cm a−1. This is in agreement with the previous study by Flower et al. (2009) as shown in Table 3. After 1964, the sedimentation rate of Burullus Lagoon was 0.96 cm/a, which is in agreement with Gu et al. (2011). The mean values of sedimentation rates (0.81, 0.96, 0.70, and 0.75 in sediment cores C-1, C-2, C-3, and C-4, respectively) in Burullus Lake were higher than in the other marine environments. The majority of the lagoon area has been lost since the 1980s due to the highway establishing, redevelopment for farming, and growth in urbanization (Hamza 2009), which may be the main cause of the rising sedimentation rates in this lagoon.
Vertical distribution of the heavy metals and historical variations of anthropogenic flux
Heavy metal concentration measurements were carried out on three sediment cores C-2, C-3, and C-4, collected from different locations in Burullus Lagoon. The elemental concentrations (μg/g) in the sediment cores of Burullus Lagoon are shown in Table 4. It can be seen that the concentrations of these metals vary considerably in each core. The average concentration of metals in all cores decreased in the following order: Ca > Al > Fe > Mg > Na > Ti > > Cl > K > Mn > V > Zn > Cr > Rb > Br > Nd > Sc > Th > S > Hf > As > U > Cs. There are some elements that show significant variations in their concentrations such as Mg, Cl, Ca, Ti, V, Na, Zn, Br, Hf, Cr, Mn, Fe, and Ta, while the other metals show values below the detection limit or slightly above the regional background values, according to the abundance of continental shales (Li and Schoonmaker 2014). As the results show, there are three metals with a high degree of variability: Na, Cl, and Mg near El-Boughaz and in the northern parts of the lagoon are due to the seawater intrusion (El-Amier et al. 2016; Badawy et al. 2022). Furthermore, there were high levels of sodium and magnesium near the drains, which may be due to agricultural waste (El-Amier et al. 2016). In the case of the Ca, the average concentration of this element in the sediment cores was about 7–8 times higher than the value of the shale continental abundance. This could be the result of a significant accumulation of shell fragments in the sediments of Burullus Lagoon (El-Amier et al. 2016). Figures 1S, 2S, and 3S show the vertical distributions of metals in the analyzed cores, to demonstrate historical variations in various contaminants linked with sources. In core C-2, the concentration of all elements except Na, Mn, Cl, and Br fluctuated during 2016 to 1990 and increased rapidly from the 1990s to the 1930s. Furthermore, the concentration of Rb, Zn, Th, Cr, Cs, Fe, Sc, and Ta was high in AD 2011 (Fig. 1S); this is probably due to high effluent discharged through drains. Similarly, in core C-3, the highest concentration of most elements was at AD 2017 (Fig. 2S). However, in core C-4, the element content of Rb, Zn, Th, Cr, Cs, Fe, Sc, and Ta decreased during the 1930s to 1940s (Fig. 3S) increased sharply during the 1940s to 1960s and remained slightly constant during the 1960s to AD 2011. The results showed that the average concentrations of the heavy metals were distributed among the cores in the following order: C-2 > C-4 > C-3, indicating high influence of the effluent from the drains. El-Alfy et al. (2017) mentioned that the lagoon receives over 950,000 feddans (approximately 4.1 billion cubic meters per a) of agricultural drainage water, which is approximately 74.3% of the total area of the Nile Delta. Furthermore, after the construction of Aswan High Dam, heavy metals in the Nile sediments increased dramatically (Shetaia et al. 2022). This is evidenced by the upward trend of most of the metals examined in the core samples. This indicates the increased anthropogenic impact.
The correlation analysis between the heavy metals in sediment cores samples is presented in Table 5. The strong positive correlations are indicated by a deep red color (correlations close to + 1), while the negative correlations are indicated by a deep blue color (correlations close to − 1). The matrix correlation was created with a significant level of P < 0.1 and a confidence level of 0.95%. The strong positive correlation (r ≥ 0.7) was observed between Th and Ta, Cs, Rb, Zn, Fe, Cr, Sc; Na—Mn, Br, Cl, K; Ti: V, Mg, and Al (core C-2), while Hf showed positive correlation with Ta, Cs, Rb, Zn, Fe, Cr, Sc, K, and Th; Ti: Mn, V, Cl, Al, Mg, Na, and Br (core C-3). In the same context, there is a significant correlation between Th- Ta, Hf, Cs, Rb, As, Zn, Fe, Cr, Sc, and K; Ti: V, Al, Mg and Na (core C-4). According to the results of Pearson’s correlation coefficient, the substantial positive correlation between metal pairings supported (interpreted) the vertical behavior of these metals for each core. This could be pointing to the same source due to human activities and the weathering of the nearby rocks (Kumar et al. 2019; Hossain et al. 2021). In contrast, Cl showed a negative correlation with other metals (core C-3), and the correlation between Mn and Fe, Zn, As, Br, Rb, Cs, Hf, Ta, and Th (core C-4) indicates a negative or weak correlation, suggesting a different source (El-Alfy et al. 2017). Anthropogenic activities and natural factors influence the distribution of metals in the aquatic environment (Li et al. 2017). The correlations between the investigated elements may also help in identifying the sources of pollution. The results showed that the distribution of heavy metals in sediments can be influenced by changes in human activities. According to the PCA analysis, the sources of metals were grouped into three main categories as shown in Fig. 7. Accordingly, these metals are mainly derived from the same sources of pollution as well as natural weathering (Pan et al. 2016), represented by their association with clay minerals (Khan et al. 2020). This is confirmed by the fact that elements such as Br, Cl, Na, and Mn can be indicators of seawater salinity. Elements such as K, Fe, Th, Rb, Sc, Cr, Mg, Al, and Ti can be indicators of terrigenous origin (Cuellar-Martinez et al. 2017). On the other hand, elements such as Cr, As, V, Zn, and Hf can be derived from terrestrial discharges of wastewater directly discharged from local industrial, aquacultural, and urban areas with metal contamination (Wang et al. 2015).
The concentrations of heavy metals in sediments depend on both the rate of sedimentation at the sampling location and the emission factor of the sources due to the effects of sediment dilution (Wang et al. 2015). Therefore the fluxes reflect anthropogenic contribution much more effectively than their concentrations due to wide variation of sedimentation rates (Bing et al. 2016; Li et al. 2022). The depositional fluxes (μg/cm2 a1) of Cl, Ca, Na, Br, Zn, Ta, Ti, V, Cr, Sc, Mg, Mn, Fe, Hf were estimated by multiplying the mass accumulation rate g/cm2 yr. by anthropogenic concentrations (μg/g) in each section of core (Jha et al. 2002; Ye et al. 2020; Gong et al. 2023). According to Fig. 8, the time-dependent anthropogenic fluxes showed considerable variability and were remarkably similar to the enrichment factor profile found in cores C-2, C-3, and C-4. The mean values of anthropogenic fluxes decreased in order: Ca > Fe > Mg > Na < Cl > Ti > Mn > V > Zn > Cr > Br > Sc > Hf > Ta. The results showed that the sedimentary fluxes of all anthropogenic elements in both cores C-2 and C-3 showed an increasing trend, especially since the 1990s. This could be since several drains, such as 8, 9, El Burullus, and El-Gharbiya, discharge significant amounts of wastewater into the lake along with high concentrations of pesticides and fertilizers, causing severe metal pollution. On the contrary, in core C-4, the depositional fluxes of all elements except Cl, Br and Ca showed a sharp decrease from the 1960s to 2011 AD, as shown in Fig. 6-c. This might be explained by the presence of fresh water supply from the Brimbal canal, which might cause surface sediments to be washed away, and the input of legacy metals under intense soil erosion. We can learn more about past climate change and the effects of human activity on the environment by examining the 100-a records of metals in lagoon sediments (Wang et al. 2019). In comparison with other coastal lagoons, as shown in Table 6, the As concentration in Burullus is lower than in other marine environments. In contrast, the Burullus sediment contains higher levels of Mn, V, Cr, Fe and Zn compared to the former marine environments, indicating anthropogenic activities.
The sediment quality indices
The values of heavy metal concentrations do not always represent a system’s true pollution status because this method only considers each metal’s individual severity in terms of biological effects. As a result, the same area could have different pollution states and consequently different conclusions if multiple pollution indices were calculated. In order to thoroughly assess the pollution levels of various heavy metals in the aquatic system of the Burullus Lagoon, EF, PI(Nemerow), and Er were used.
Enrichment factor
Using the enrichment factor (EF), trace element pollution over the previous 100 a was calculated (Li et al. 2022; Man et al. 2022). Table 7 and Fig. 8 show that the average EF values in the examined cores decreased in the following order: Cl > Ca > Na > Br > Zn > Ta > Ti > V > Cr > Sc > Mg > Mn > Fe > Hf. The relatively high EF (EF > 1) values point to anthropogenic pollution, which will require a lot of future attention. The enrichment factors of metals in sediment cores C-2, C-3, and C-4 dramatically increased after mid 1980s as shown in Fig. 8; this may be due to the asynchronous of economic development patterns in this lagoon during this period. This may be due to the increase in economic development patterns in this lagoon during this period which included industrial, residential, fish farm waste and agricultural waste products (Krishnan et al. 2022; Al-Afify et al. 2023), whereas the percentage of gross domestic product (GDP) during the 1980s was 8.9% which was the highest percentage of annual GDP as shown in (https://www.imf.org/external/datamapper).
Nemerow pollution index
The Burullus lagoon’s sediment quality was evaluated using the Nemerow pollution index. The PI Nemerow values of the heavy metal Zn, Ta, Ti, V, Cr, Sc, Mg, Mn, Fe, and Hf showed that the sediments of core C-2 were moderately polluted from 1937 to 1993, with values generally between 2 and 3 as shown in Fig. 9-I. In addition, PI Nemerow was between 1 and 2 in 2003, indicating light pollution, while in 2011, values were between 2 and 3, indicating heavy pollution (Fig. 9-I). In the same context, all the values of PI Nemerow were between 1 and 2, indicating that the sediments of core C-3 were severely polluted from 1944 to 2017 (Fig. 9-I). On the other hand, for core C-4, between 1938 and 1963, the values of PI Nemerow were between 2 and 3, indicating moderate pollution, while from 1995 to 2011, the values of PI Nemerow were slightly polluted, as shown in Fig. 9-I. The PI Nemerow values ranged from 1.13 to 3.11 with a mean value 2.22 for the core C-2, 1.21 to 2.03 with a mean value 1.55 for core C-3, and from 1.04 to 2.77 with mean value 1.98 for core C-4 as demonstrated in Table 7. The vertical distribution of PI Nemerow showed that the values increased in the direction of the drains and the mean values arranged the studied cores in the following order C-2 > C-4 > C-3 and were slightly polluted. According to the PI Nemerow category interpretation suggested by Kowalska et al. (2018), this may be attributed to the high content of heavy metals in cores C-2 and C-4.
Ecological risk factor
The ecological risk factor (Er), which is calculated for Co, Cr, Mn, As, and Zn, is an individual pollution indicator that assesses the possible risk posed by a single element. Except for core C-3, the calculated Er values for each heavy metals in the examined cores are in the following order: Cr > Zn > As > Mn, as shown in Table 7 and Fig. 9-II. The Er values show that there was little contamination in the sediments of cores C-2, C-3, and C-4 during the investigation period.
Conclusions and recommendations:
Discharges of agricultural, industrial, and domestic effluents from several drains have caused changes in the sedimentological regime, degradation of sediment quality, and increased sedimentation rates in Burullus Lagoon. Therefore, this study highlights the use of 210Pb dating models to establish an accurate chronological framework for recent sediments in order to understand historical climate changes and the impact of human activities on the ecology of Burullus Lagoon. Two main models (CRS and CFCS) were tested to determine these chronologies. The 210Pbex and 137Cs activity profiles were used to calculate the sedimentation rates studied. The results show that the constant rate of supply (CRS) model performed best and appears to be in good agreement with the chronology based on the 137Cs technique in the investigated cores. The age estimates from the CFCS and CRS models agreed for the recent sediments in the uppermost layer of the four cores. As a result of our analysis, possible explanations for the 137Cs peaks include the nuclear industry, global fallout, possible exchange of the Black Sea with the Mediterranean region, and the Fukushima (2011 AD) and Chernobyl (1986 AD) accidents. The mean values of sedimentation rates (0.81, 0.96, 0.70 and 0.75 in sediment cores C-1, C-2, C-3, and C-4, respectively) in the Burullus lagoon were higher than in the other marine environments. This could be due to the construction of new roads, urbanization, and agricultural reclamation, which have consumed most of the lagoon area since the 1980s, in line with the annual percentage of GDP during this period. It can also be explained by the different dynamic geophysical and/or hydrological conditions that each site has, which control the sedimentation process. This study explains how drainage water discharged into Burullus Lagoon, carrying silt loads, has historically influenced sedimentation rates.
Due to its high sensitivity and minimal sample handling requirements, NAA has been used to identify contamination standards and to detect trace impurities, whereas the INAA technique has a wide range of potential applications because it can simultaneously and non-destructively provide accurate data on a large number of elements at the nanogram level. The main disadvantage of using NAA is that the irradiated sample remains radioactive for many years after the initial analysis, requiring special handling and disposal techniques for low to intermediate level radioactive material. In the same context, the XRF method is also non-destructive, but it requires the analysis of a large amount of sample (usually more than one gram). Furthermore, the difficulty of identification of elements lighter than sodium and the difficulty of discrimination between isotopes of the same element or ions of the same element in different valence states are some of the disadvantages of the XRF method. Therefore, the k0-INAA technique has been successfully applied for a sensitive and reliable multi-element analysis for the assessment of environmental changes in sediments and the impact of anthropogenic activities during 100 a in the Burullus lagoon.
The results show that elements such as Mg, Cl, Ca, Ti, V, Na, Zn, Br, Hf, Cr, Mn, Fe, and Ta have concentrations above background in the continental shales. Core C-2 at El-Boughaz has higher concentrations of Na, Cl, and Mg than the other cores C-3 and C-4; this could be due to seawater intrusion. The mean concentration of Ca in the sediment cores was about 7–8 times higher than the continental abundance of the shale. A possible explanation for this could be a significant accumulation of shell fragments in the sediments of the Burullus lagoon. As a result of the results, it can be concluded that there are different sources in the Burullus lagoon, based on the variable vertical distribution of elements in the core samples. Strong positive correlations between most of the elements studied indicate similar sources, most likely as a result of human activity and weathering of the surrounding rocks. The information presented here is the first attempt to use sediment cores from Burullus Lagoon to estimate the fluxes of different elements in the Nile Delta. The observed increase in fluxes of anthropogenic elements in cores C-2 and C-3 since the 1990s is mainly due to run-off, overfishing, increased fish farming, and sewage discharge. These anthropogenic elements include Br, Ca, Cl, Cr, Fe, Na, Sc, Ti, Hf, V, Fe, Mg, Mn, and Zn. The input of legacy metals under severe soil erosion and the availability of fresh water from the Brimbal Canal, which may have caused washing of surface sediments, are probably responsible for the sharp decrease in fluxes of some elements in core C-4 from the 1960s to 2011 AD. The asynchronous economic development patterns in this lagoon may be the cause of the dramatic increase in metal enrichment factors in sediment cores C-2, C-3, and C-4 after the mid-1980s.
According to the results, anthropogenic activities may have an impact on Burullus Lake. Monitoring is necessary to give coastal zone managers and decision-makers the knowledge they need to take serious protective measures for this lake, which is one of Egypt’s most valuable economic resources. Pre-treatment of wastewater prior to discharge into lakes, control of additional pollutants from chemical pesticides and fertilizers used on agricultural crops, and lake water replenishment with seawater should all be included in these measures.
Data availability
The datasets and materials used during the current study are available from the corresponding author on reasonable request.
All data generated or analyzed during this study are included in this published article.
References
Abbasi A (2019) 210Pb and 137Cs based techniques for the estimation of sediment chronologies and sediment rates in the Anzali Lagoon, Caspian Sea. J Radioanal Nucl Chem 322:319–330. https://doi.org/10.1007/s10967-019-06739-8
Al-Afify ADG, Abdo MH, Othman AA, Abdel-Satar AM (2023) Water quality and microbiological assessment of burullus lake and its surrounding drains. Water Air Soil Pollut 234:1–19. https://doi.org/10.1007/s11270-023-06351-3
Ali MR, Islam MA, Hossain MF et al (2021) Depth-wise elemental contamination trend in sediment cores of the Sundarbans mangrove forest, Bangladesh. J Radioanal Nucl Chem 328:1349–1359. https://doi.org/10.1007/s10967-021-07739-3
Appleby PG (2000) Radiometrie dating of sediment records in European mountain lakes. J Limnol 59:1–14. https://doi.org/10.4081/jlimnol.2000.s1.1
Appleby PG (2001) Chronostratigraphic techniques in recent sediments. In: Last WM, Smol JP (eds) Tracking Environmental Change Using Lake Sediments. Basin Analysis Coring and Chronological Techniques. Kluwer Acad Publ Dordr 1:171–172
Appleby PG (2008) Three decades of dating recent sediments by fallout radionuclides: a review. Holocene 18:83–93. https://doi.org/10.1177/0959683607085598
Appleby PG, Oldfield F (1983) The assessment of 210Pb data from sites with varying sediment accumulation rates. Paleolimnology 29–35. https://doi.org/10.1007/978-94-009-7290-2_5
Appleby PG, Oldfield F (1992) Application of lead-210 to sedimentation studies. In: Ivanovich M, Harman RS (eds) In: Uranium-series disequilibrium: application to earth, marine and environment sciences. Clarendon Press, Oxford, pp 731–738
Appleby PG, Birks HH, Flower RJ et al (2001) Radiometrically determined dates and sedimentation rates for recent sediments in nine North African wetland lakes (the CASSARINA project). Aquat Ecol 35:347–367. https://doi.org/10.1023/A:1011938522939
Ashraf A, Saion E, Gharibshahi E et al (2018) Distribution of heavy metals in core marine sediments of Coastal East Malaysia by instrumental neutron activation analysis and inductively coupled plasma spectroscopy. Appl Radiat Isot 132:222–231. https://doi.org/10.1016/j.apradiso.2017.11.012
Badawy WM, Duliu OG, El Samman H et al (2021) A review of major and trace elements in Nile River and Western Red Sea sediments: an approach of geochemistry, pollution, and associated hazards. Appl Radiat Isot 170:109595. https://doi.org/10.1016/j.apradiso.2021.109595
Badawy W, Elsenbawy A, Dmitriev A et al (2022) Characterization of major and trace elements in coastal sediments along the Egyptian Mediterranean Sea. Mar Pollut Bull 177:113526. https://doi.org/10.1016/j.marpolbul.2022.113526
Baltas H, Kiris E, Dalgic G, Cevik U (2016) Distribution of 137Cs in the Mediterranean mussel (Mytilus galloprovincialis) in Eastern Black Sea Coast of Turkey. Mar Pollut Bull 107:402–407. https://doi.org/10.1016/j.marpolbul.2016.03.032
Barsanti M, Garcia-Tenorio R, Schirone A, et al (2020) Challenges and limitations of the 210Pb sediment dating method: results from an IAEA modelling interlaboratory comparison exercise. Quat Geochronol 59. https://doi.org/10.1016/j.quageo.2020.101093
Başkaya H, Doǧru M, Küçükönder A (2014) Determination of the 137Cs and 90Sr radioisotope activity concentrations found in digestive organs of sheep fed with different feeds. J Environ Radioact 134:61–65. https://doi.org/10.1016/j.jenvrad.2014.02.023
Benninger L, Suayah I, Stanley D (1998) Manzala lagoon, Nile delta, Egypt: modern sediment accumulation base on radioactive tracers. Env Geol 34:183–193
Bilici S, Külahcı F, Bilici A (2019) Spatial modelling of Cs-137 and Sr-90 fallout after the Fukushima nuclear power plant accident. J Radioanal Nucl Chem 322:431–454. https://doi.org/10.1007/s10967-019-06713-4
Binford M (1990) Calculation and uncertainty analysis of 210Pb dates for PIRLA project lake sediment cores. J Paleolimnol 3:253–267
Bing H, Wu Y, Zhou J et al (2016) Chemosphere Historical trends of anthropogenic metals in Eastern Tibetan Plateau as reconstructed from alpine lake sediments over the last century. Chemosphere 148:211–219. https://doi.org/10.1016/j.chemosphere.2016.01.042
Boyd BM (2016) A radiometric study of sediment accumulation and accretion in tidal marshes of Delaware and New Jersey. A dissertation submitted to the faculty of the University of Delaware in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Oceanography
Bruel R, Sabatier P (2020) Serac: A R package for ShortlivEd RAdionuclide chronology of recent sediment cores. J Environ Radioact 225:106449. https://doi.org/10.1016/j.jenvrad.2020.106449
Chen Z, Salem A, Xu Z, Zhang W (2010) Ecological implications of heavy metal concentrations in the sediments of Burullus Lagoon of Nile Delta Egypt. Estuar Coast Shelf Sci 86:491–498. https://doi.org/10.1016/j.ecss.2009.09.018
Chen X, Qiao Q, McGowan S et al (2019) Determination of geochronology and sedimentation rates of shallow lakes in the middle Yangtze reaches using 210Pb, 137Cs and spheroidal carbonaceous particles. CATENA 174:546–556. https://doi.org/10.1016/j.catena.2018.11.041
Cuellar-Martinez T, Carolina Ruiz-Fern Andez A, Sanchez-Cabeza J-A, Alonso-Rodríguez R (2017) Sedimentary record of recent climate impacts on an insular coastal lagoon in the Gulf of California. https://doi.org/10.1016/j.quascirev.2017.01.002
Davutluoglu OI, Seckin G, Ersu CB et al (2011) Heavy metal content and distribution in surface sediments of the Seyhan River, Turkey. J Environ Manage 92:2250–2259. https://doi.org/10.1016/j.jenvman.2011.04.013
De Corte F, Simonits A (2003) Recommended nuclear data for use in the k0 standardization of neutron activation analysis. At Data Nucl Data Tables 85:47–67. https://doi.org/10.1016/S0092-640X(03)00036-6
Do Nascimento Gonçalves P, Damatto SR, Leonardo L, Souza JM (2021) Natural radionuclides in soil profiles and sediment cores from Jundiaí reservoir, state of Sao Paulo. Braz J Rad Sci 9:1–18
El-Alfy MA-H, El-Azim HA, El-Amier YA (2017) Assessment of heavy metal contamination in surface water of Burullus Lagoon Egypt. J Sci Agric 1:233. https://doi.org/10.25081/jsa.2017.v1.814
El-Amier YA, El-Azim HA, El-Alfy MA (2016) Spatial assessment of water and sediment quality in burullus lake using GIS technique. J Geogr Environ Earth Sci Int 6:1–16. https://doi.org/10.9734/jgeesi/2016/23311
Eleftheriou G, Tsabaris C, Papageorgiou DK et al (2018) Radiometric dating of sediment cores from aquatic environments of north-east Mediterranean. J Radioanal Nucl Chem 316:655–671. https://doi.org/10.1007/s10967-018-5802-8
Evangeliou N, Florou H, Bokoros P, Scoullos M (2009) Temporal and spatial distribution of 137Cs in Eastern Mediterranean Sea. Horizontal and vertical dispersion in two regions. J Environ Radioact 100:626–636. https://doi.org/10.1016/j.jenvrad.2009.04.014
Feng B, Onda Y, Wakiyama Y et al (2022) Persistent impact of Fukushima decontamination on soil erosion and suspended sediment. Nat Sustain 5:879–889. https://doi.org/10.1038/s41893-022-00924-6
Forcing C, Region M (2014) Storminess and environmental change (climate forcing and responses in the Mediterranean Region), Edited by Nazzareno Diodato and Gianni, Dordrecht: Springer Netherlands. 39, 268. https://books.google.de/books?id=YY_FBAAAQBAJ&pg=PA11&lpg=PA11&dq=Storm. Accessed 2016
Glascock MD (2015) Tables for analytical methods at MURR: NAA, XRF and ICP-MS. Research Reactor Center, University of Missouri, Columbia
Gong J, Ouyang W, He M, Lin C (2023) Heavy metal deposition dynamics under improved vegetation in the middle reach of the Yangtze River. Environ Int 171:107686. https://doi.org/10.1016/j.envint.2022.107686
Greenberg RR, Bode P, De Nadai Fernandes EA (2011) Neutron activation analysis: a primary method of measurement. Spectrochim Acta - Part B at Spectrosc 66:193–241. https://doi.org/10.1016/J.SAB.2010.12.011
Gu J, Chen Z, Salem A (2011) Post-Aswan dam sedimentation rate of lagoons of the Nile Delta Egypt. Environ Earth Sci 64:1807–1813. https://doi.org/10.1007/s12665-011-0983-2
Guo J, Costa OS, Wang Y et al (2020) Accumulation rates and chronologies from depth profiles of 210Pbex and 137Cs in sediments of northern Beibu Gulf South China Sea. J Environ Radioact 213:106136. https://doi.org/10.1016/j.jenvrad.2019.106136
Hakanson L (1980) An ecological risk index for aquatic pollution control.a sedimentological approach. Water Res 14:975–1001. https://doi.org/10.1016/0043-1354(80)90143-8
Hamza W (2009) The Nile delta. In: Dumont HJ (ed) The Nile: origin, environments, limnology and human use. Springer, New York
Hossain MB, Runu UH, Sarker MM et al (2021) Vertical distribution and contamination assessment of heavy metals in sediment cores of ship breaking area of Bangladesh. Environ Geochem Health 43:4235–4249. https://doi.org/10.1007/s10653-021-00919-w
Imam N, Salem G (2023) The potential influence of drains on the recent sediment characteristics and sedimentation rates of Lake Qarun , Western Desert , Egypt. Environ Earth Sci 1–20. https://doi.org/10.1007/s12665-023-11036-5
Imam N, El-Shamy AS, Abdelaziz GS, Belal DM (2024) Influence of the industrial pollutant on water quality, radioactivity levels, and biological communities in Ismailia Canal, Nile River, Egypt. Environ Sci Pollut Res. https://doi.org/10.1007/s11356-024-32672-9
Iridoy MC (2017) Sources and distribution of artificial radionuclides in the oceans: from Fukushima to the Mediterranean Sea, Doctorat en Ciència i Tecnologia Ambientals Institut de Ciència i Tecnologia Ambientals Universitat Autònoma de Barcelona
Jha SK, Acharya RN, Reddy AVR et al (2002) Heavy metal concentration and distribution in a dated sediment core of Nainital Lake in the Himalayan region. J Environ Monit 4:131–137. https://doi.org/10.1039/b108318j
Karuppasamy MP, Qurban MA, Krishnakumar PK et al (2017) Evaluation of toxic elements As, Cd, Cr, Cu, Ni, Pb and Zn in the surficial sediments of the Red Sea (Saudi Arabia). Mar Pollut Bull 119:181–190. https://doi.org/10.1016/j.marpolbul.2017.04.019
Khalil M, El-Gharabawy S (2016) Evaluation of mobile metals in sediments of Burullus Lagoon. Egypt Mar Pollut Bull 109:655–660. https://doi.org/10.1016/j.marpolbul.2016.04.065
Khan R, Islam MS, Tareq ARM, et al (2020) Distribution, sources and ecological risk of trace elements and polycyclic aromatic hydrocarbons in sediments from a polluted urban river in central Bangladesh. Environ Nanotechnology Monit Manag 14. https://doi.org/10.1016/j.enmm.2020.100318
Kostka A, Leśniak A (2020) Spatial and geochemical aspects of heavy metal distribution in lacustrine sediments, using the example of Lake Wigry (Poland). Chemosphere 240. https://doi.org/10.1016/j.chemosphere.2019.124879
Kostka A, Leśniak A (2021) Natural and anthropogenic origin of metals in lacustrine sediments; assessment and consequences—a case study of wigry lake (Poland). Minerals 11:1–22. https://doi.org/10.3390/min11020158
Kowalska J, Mazurek R, Gąsiorek M et al (2016) Soil pollution indices conditioned by medieval metallurgical activity – A case study from Krakow (Poland). Environ Pollut 218:1023–1036. https://doi.org/10.1016/j.envpol.2016.08.053
Kowalska JB, Mazurek R, Gąsiorek M, Zaleski T (2018) Pollution indices as useful tools for the comprehensive evaluation of the degree of soil contamination–a review. Environ Geochem Health 40:2395–2420. https://doi.org/10.1007/s10653-018-0106-z
Krishnan K, Saion EB, Yap CK et al (2022) Determination of trace elements in sediments samples by using neutron activation analysis. J Exp Biol Agric Sci 10:21–31. https://doi.org/10.18006/2022.10(1).21.31
Kumar A, Rout S, Chopra MK et al (2014) Modeling of 137Cs migration in cores of marine sediments of Mumbai Harbor Bay. J Radioanal Nucl Chem 301:615–626. https://doi.org/10.1007/s10967-014-3116-z
Kumar P, Meena NK, Diwate P et al (2019) The heavy metal contamination history during ca 1839–2003 AD from Renuka Lake of Lesser Himalaya, Himachal Pradesh, India. Environ Earth Sci 78:1–14. https://doi.org/10.1007/s12665-019-8519-2
Lépy MC, Pearce A, Sima O (2015) Uncertainties in gamma-ray spectrometry. Metrologia 52:S123–S145. https://doi.org/10.1088/0026-1394/52/3/S123
Li F, Huang J, Zeng G et al (2013) Spatial risk assessment and sources identification of heavy metals in surface sediments from the Dongting Lake, Middle China. J Geochemical Explor 132:75–83. https://doi.org/10.1016/j.gexplo.2013.05.007
Li K, Liu E, Zhang E et al (2017) Historical variations of atmospheric trace metal pollution in Southwest China: Reconstruction from a 150-year lacustrine sediment record in the Erhai Lake. J Geochemical Explor 172:62–70. https://doi.org/10.1016/j.gexplo.2016.10.009
Li S, Sun W, Chen R et al (2022) A historical record of trace metal deposition in northeastern Qinghai - Tibetan Plateau for the last two centuries. Environ Sci Pollut Res 29:24716–24725
Li Y, Schoonmaker JE (2014) 9.1 - Chemical composition and mineralogy of marine sediments. In: Holland HD, Turekian KK (eds) Treatise on geochemistry, 2nd edn. Elsevier, Oxford, pp 1–32
Lin H, Liu J, Dong Y et al (2018) Absorption characteristics of compound heavy metals vanadium, chromium, and cadmium in water by emergent macrophytes and its combinations. Environ Sci Pollut Res 25:17820–17829. https://doi.org/10.1007/s11356-018-1785-9
Lin W, Yu K, Wang Y et al (2019) Radioactive level of coral reefs in the South China Sea. Mar Pollut Bull 142:43–53. https://doi.org/10.1016/j.marpolbul.2019.03.030
Loan BTT, Nhon DH, Ve ND, et al (2023) Assessment of the distribution and ecological risks of heavy metals in coastal sediments in Vietnam’s Mong Cai area. Environ Monit Assess 195. https://doi.org/10.1007/s10661-022-10779-1
Man X, Huang H, Chen F, et al (2022) Anthropogenic impacts on the temporal variation of heavy metals in Daya Bay (South China). Mar Pollut Bull 185. https://doi.org/10.1016/j.marpolbul.2022.114209
Negm AM, Bek MA, Abdel-Fattah S (2019) Egyptian coastal lakes and wetlands : Part II climate change and biodiversity. In: Abdelazim M. Negm, Mohamed Ali Bek SA-F (eds) The Handbo. Springer Nature Switzerland AG 2019, p 6221
Palani B, Vasudevan S, Ramkumar T et al (2023) Determination of sedimentation rates and life of Kodaikanal Lake, South India, using radiometric dating (210Pb and 137Cs ) techniques. Environ Earth Sci. https://doi.org/10.1007/s12665-023-10896-1
Pan LB, Ma J, Wang XL, Hou H (2016) Heavy metals in soils from a typical county in Shanxi Province, China: levels, sources and spatial distribution. Chemosphere 148:248–254. https://doi.org/10.1016/j.chemosphere.2015.12.049
Pappa FK, Tsabaris C, Patiris DL et al (2018) Historical trends and assessment of radionuclides and heavy metals in sediments near an abandoned mine, Lavrio, Greece. Environ Sci Pollut Res 25:30084–30100. https://doi.org/10.1007/s11356-018-2984-0
Pappa FK, Tsabaris C, Patiris DL et al (2019) Temporal investigation of radionuclides and heavy metals in a coastal mining area at Ierissos Gulf, Greece. Environ Sci Pollut Res 26:27457–27469. https://doi.org/10.1007/s11356-019-05921-5
Perumal K, Antony J, Muthuramalingam S (2021) Heavy metal pollutants and their spatial distribution in surface sediments from Thondi coast, Palk Bay, South India. Environ Sci Eur 33. https://doi.org/10.1186/s12302-021-00501-2
Putyrskaya V, Klemt E, Röllin S et al (2015) Dating of sediments from four Swiss prealpine lakes with 210Pb determined by gamma-spectrometry: progress and problems. J Environ Radioact 145:78–94. https://doi.org/10.1016/j.jenvrad.2015.03.028
Ramos-Lerate I, Barrera M, Ligero RA, Casas-Ruiz M (1998) A new method for gamma-efficiency calibration of voluminal samples in cylindrical geometry. J Environ Radioact 38:47–57
Rasul S, Kajal AM, Khan A (2018) Quantifying uncertainty in analytical measurements. J Bangladesh Acad Sci 41:145–163. https://doi.org/10.3329/jbas.v41i2.35494
Sanchez-Cabeza JA, Ruiz-Fernández AC (2012) 210Pb sediment radiochronology: an integrated formulation and classification of dating models. Geochim Cosmochim Acta 82:183–200. https://doi.org/10.1016/j.gca.2010.12.024
Sarı E, Çağatay MN, Acar D et al (2018) Geochronology and sources of heavy metal pollution in sediments of Istanbul Strait (Bosporus) outlet area, SW Black Sea, Turkey. Chemosphere 205:387–395. https://doi.org/10.1016/j.chemosphere.2018.04.096
Semertzidou P, Piliposian GT, Chiverrell RC, Appleby PG (2019) Long-term stability of records of fallout radionuclides in the sediments of Brotherswater, Cumbria (UK). J Paleolimnol 61:231–249. https://doi.org/10.1007/s10933-018-0055-7
Shah C, Banerji US, Chandana KR, Bhushan R (2020) 210Pb dating of recent sediments from the continental shelf of western India: factors influencing sedimentation rates. Environ Monit Assess 192. https://doi.org/10.1007/s10661-020-08415-x
Shalby A, Elshemy M, Zeidan BA (2020) Assessment of climate change impacts on water quality parameters of Lake Burullus Egypt. Environ Sci Pollut Res 27:32157–32178. https://doi.org/10.1007/s11356-019-06105-x
Shetaia SA, Abu Khatita AM, Abdelhafez NA et al (2022) Human-induced sediment degradation of Burullus lagoon, Nile Delta, Egypt: heavy metals pollution status and potential ecological risk. Mar Pollut Bull 178:113566. https://doi.org/10.1016/j.marpolbul.2022.113566
Stäger F, Zok D, Schiller AK et al (2023) Disproportionately high contributions of 60 year old weapons-137Cs explain the persistence of radioactive contamination in Bavarian Wild Boars. Environ Sci Technol 57:13601–13611. https://doi.org/10.1021/acs.est.3c03565
Tylmann W, Bonk A, Goslar T et al (2016) Calibrating 210Pb dating results with varve chronology and independent chronostratigraphic markers: problems and implications. Quat Geochronol 32:1–10. https://doi.org/10.1016/j.quageo.2015.11.004
Vörösmarty CJ, McIntyre PB, Gessner MO et al (2010) Global threats to human water security and river biodiversity. Nature 467:555–561. https://doi.org/10.1038/nature09440
Wang S, Wang Y, Zhang R et al (2015) Historical levels of heavy metals reconstructed from sedimentary record in the Hejiang River, located in a typical mining region of Southern China. Sci Total Environ 532:645–654. https://doi.org/10.1016/j.scitotenv.2015.06.035
Wang Q, Sha Z, Wang J et al (2019) Historical changes in the major and tracea elements in the sedimentary records of Lake Qinghai, Qinghai – Tibet Plateau : implications for anthropogenic activities. 3:2093–2111
Williams JA, Antoine J (2020) Evaluation of the elemental pollution status of Jamaican surface sediments using enrichment factor, geoaccumulation index, ecological risk and potential ecological risk index. Mar Pollut Bull 157:111288. https://doi.org/10.1016/j.marpolbul.2020.111288
Xu M, Dong X, Yang X et al (2017) Recent sedimentation rates of shallow lakes in the middle and lower reaches of the Yangtze River: patterns, controlling factors and implications for lake management. Water (switzerland) 9:1–18. https://doi.org/10.3390/w9080617
Xu Z, Salem A, Chen Z et al (2008) Pb-210 and Cs-137 distribution in Burullus lagoon sediments of Nile river delta, Egypt: sedimentation rate after Aswan High Dam. Front Earth Sci China 2:434–438. https://doi.org/10.1007/s11707-008-0059-0
Ye Z, Chen J, Gao L et al (2020) 210Pb dating to investigate the historical variations and identification of different sources of heavy metal pollution in sediments of the Pearl River Estuary Southern China. Mar Pollut Bull 150:110670. https://doi.org/10.1016/j.marpolbul.2019.110670
Younis AM (2019) Environmental impacts on Egyptian delta Lakes’ Biodiversity: a case study on Lake Burullus. Handb Environ Chem 72:107–128. https://doi.org/10.1007/698_2017_120
Zhang XC, Zhang GH, Garbrecht JD, Steiner JL (2015a) Dating sediment in a fast sedimentation reservoir using cesium-137 and lead-210. Soil Sci Soc Am J 79:948–956. https://doi.org/10.2136/sssaj2015.01.0021
Zhang Y, Huo S, Zan F et al (2015b) Historical records of multiple heavy metals from dated sediment cores in Lake Chenghai, China. Environ Earth Sci 74:3897–3906. https://doi.org/10.1007/s12665-014-3858-5
Acknowledgements
We would like to thank Dr. Reda E. Bendary, Researcher at National Institute of Oceanography and Fisheries, Cairo, Egypt.
Funding
Open access funding provided by The Science, Technology & Innovation Funding Authority (STDF) in cooperation with The Egyptian Knowledge Bank (EKB). This research was supported by Faculty of Women for Arts, Science and Education, Ain Shams University, and partial funding from National Network of Nuclear Science (NNS), Academy of Scientific Research and Technology (ASRT), Egypt.
Author information
Authors and Affiliations
Contributions
Conceptualization, validation, data analysis of the radioactivity concentration, numerical models, statistical analysis, writing—original draft, review and editing were performed by Alia Ghanem, Afaf Nada, Hosnia M. Abu-Zeid, and Noha Imam. Sampling and sampling preparation were examined by Said A. Shetaia and neutron activation analysis (NAA) were performed by Waiel E. Madcour.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Competing interests
The authors declare no competing interests.
Additional information
Responsible Editor: Georg Steinhauser
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original online version of this article was revised: The 4th author name is missing the middle initial. It should be Said A. Shetaia.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ghanem, A., Nada, A., Abu-Zeid, H. et al. Historical trends of heavy metals applying radio-dating and neutron activation analysis (NAA) in sediment cores, Burullus Lagoon, Egypt. Environ Sci Pollut Res (2024). https://doi.org/10.1007/s11356-024-33761-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11356-024-33761-5