Matched-filter design to improve self-interference cancellation in full-duplex communication systems

Abstract

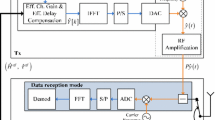
A new method for capacity and spectral efficiency increases is a full-duplex communication, where sending and receiving are done simultaneously. Hence, severe interference leaked from the transmitter to the receiver, which can disrupt the system’s operation completely. For interference reduction, the transceiver tries to estimate the interfering symbols to remove their effects. A typical method is to use the Hammerstein model. In this method, nonlinear power amplifier (PA) and multipath channel are modeled with a successive nonlinear system and a finite impulse response filter. Then, the model parameters are adjusted, and interference symbols are estimated from the transmitted symbols. In the Hammerstein method, the interference symbols are estimated directly from the transmitted symbols. But practically, the transmitted symbols first pass through the pulse-shaping filter and become a signal. Then, this signal passes through the nonlinear PA and communication channel. Finally, the received signal is filtered by the matched filter (MF) at the receiver and converted to the symbols again. In this procedure, the amplifier and the communication channel affect the transmitted signal directly and distort transmitted symbols indirectly. Therefore, in the practical situation, when we consider the transmitter’s pulse-shaping filter and the receiver’s MF, the estimated symbols with the Hammerstein method are erroneous. To solve this problem, a new MF at the receiver is proposed and adjusted according to the interfering signal. We have shown that this method is far better than the Hammerstein method.

Appendix: A computational complexity of the Hammerstein and proposed method during the training

The computational complexity of the two methods during the training calculate here. In the Hammerstein method, first in the MR, there is a $N\times ML_g$ rows and $N\times ML_g$ columns matrix multiplication into a $ML_g\times 1$ vector. So, its computational complexity is $2N\left( ML_g+1\right)$. Then, to construct the matrix ${\mathbf{{S}}^{(\mathrm{{p}})}}$ in Eq. (9), $2N\tilde{P}L_g$ real multiplication is required. $\tilde{P}$ is equal to $\tilde{P}=\frac{P+1}{2}$. Matrix multiplication ${\mathbf{{S}}^{(\mathrm{{p}})}}^\dag {\mathbf{{S}}^{(\mathrm{{p}})}}$ has $4N\left( \tilde{P}L_g\right) ^2$ real multiplications. The matrix inversion ${\left( {{\mathbf{{S}}^{(\mathrm{{p}})\dag }}{\mathbf{{S}}^{(\mathrm{{p}})}}} \right) ^{ - 1}}$ requires $4{(\tilde{P}{L_g})^3}$ real multiplications in the simple inversion method. In the same way, the matrix operations ${\left( {{\mathbf{{S}}^{(\mathrm{{p}})\dag }}{\mathbf{{S}}^{(\mathrm{{p}})}}} \right) ^{ - 1}}{\mathbf{{S}}^{(\mathrm{{p}})\dag }}$ and ${\left( {{\mathbf{{S}}^{(\mathrm{{p}})\dag }}{\mathbf{{S}}^{(\mathrm{{p}})}}} \right) ^{ - 1}}{\mathbf{{S}}^{(\mathrm{{p}})}} \times {\mathbf{{\lambda }}^{(\mathrm{{p}})}}$ require $4N{(\tilde{P}{L_g})^2}$ and $4N\tilde{P}{L_g}$ real multiplications respectively. If we assume ${N^{(\mathrm{{p}})}} = N$, the total number of real multiplications and the computational complexity associated with it in the Hammerstein method is equal to

$$\begin{aligned} {\mathcal{O}_{\mathrm{{Hammerstein}}}} = 2N\left( {M{L_g} + 1} \right) + 2N\tilde{P}{L_g}\left( {4\tilde{P}{L_g} + 3} \right) + 4{\left( {\tilde{P}{L_g}} \right) ^3}. \end{aligned}$$

(A-1)

In the proposed new method according to eq. (17), matrix multiplication by matrix, matrix inversion, inverse matrix multiplication by matrix and finally matrix to vector multiplication have $4N{(M{L_g})^2}$, $4{(M{L_g})^3}$, $4N{(M{L_g})^2}$ and $4N(M{L_g})$ real multiplications, respectively. Therefore, the total number of real multiplications and related computational complexity in the presented method is

$$\begin{aligned} {\mathcal{O}_\mathrm{{1}}} = 4N\left( {2{{\left( {M{L_g}} \right) }^2} + M{L_g}} \right) + 4{\left( {M{L_g}} \right) ^3}. \end{aligned}$$

(A-2)

If we assume that M, $L_g$ and $\tilde{P}$ have an equal order or almost similar to M and $N \gg M$, then the computational complexity of both methods is of the same order of $NM^2$. However, the number of multiplications in the Hammerstein method may be less than the proposed method.