1 Introduction

Mountains play a crucial role as a freshwater source, supporting the livelihoods of nearly two billion people globally (Schneiderbauer et al. 2021). At the same time, mountains face complex challenges from climate and socio-economic changes that threaten water supply and other essential ecosystem services (IPCC et al. 2018; Hock et al. 2019; Shah 2021). Despite their importance, mountain regions remain understudied leading to a wide range of uncertainties that challenge the design of adequate adaptation measures (Adler et al. 2023; Doblas-Reyes et al. 2023). There is an urgent need to develop suitable methods to identify robust and locally tailored adaptation measures that ensure long-term water supply for social-ecological systems under current and future conditions (Poff et al. 2016; Hasan et al. 2023).

In mountain regions, uncertainties arise from a combination of scarce data, limited understanding of the glacio-hydrological and socio-economic processes, and from the variability in climate and socio-economic projections (Berkhout et al. 2014; Hock et al. 2019). The limited understanding of glacial meltwater contribution, groundwater dynamics, and the role of wetlands hinders mathematical representations and models (Buytaert et al. 2017; Correa et al. 2020). Further limited socio-economic understanding is related, among others, to missing data on local economic development, demographic dynamics, and changes in water demand (Berkhout et al. 2014; Scott et al. 2021). Climate models, though useful globally or regionally, are yet unable to incorporate local variability realistically, strongly influencing projections of hydrological changes (Vetter et al. 2017; Kundzewicz et al. 2018). Inherent dynamics and uncertainty when projecting long-term social and economic trends limit the ability to assign probabilities to future socio-economic scenarios (Riahi et al. 2017; Kundzewicz et al. 2018). Furthermore, errors in input data and knowledge gaps can hinder the accuracy of model predictions to conditions beyond those used for model calibration.

The described uncertainties are usually quantified through methods such as uncertainty bounds, error propagation, or sensitivity analysis (Huss and Hock 2018; McMillan et al. 2018). Beyond these, more sophisticated approaches, such as interval, stochastic, and fuzzy mathematical programming address variability and ambiguity by modeling and optimizing water management systems (Wang et al. 2024). However, these methods require probability distributions which can be difficult to obtain in data-scarce regions. This lack of clear probabilities leads to deep uncertainty, a situation where decision-makers deal with unknown probabilities for key factors, making the range of future system states unclear (Lempert 2019; Marchau et al. 2019).

Most often, the design of water policies relies on historical data, e.g. precipitation or water demand patterns (Cosgrove and Loucks 2015). However, using the past to predict the future has limitations given that climate change leads to conditions not observed in the historical record (van Vuuren et al. 2012; Poff et al. 2016). Recent progress in integrative optimization methods enables identifying optimal water management strategies across multiple criteria and uncertain futures to supports decision-making (e.g. Ucler and Kocken 2023; Wang et al. 2024).

Currently, management strategies focus on engineering-based increases in water supply, followed by measures to enhance water efficiency, while explicit efforts towards reducing water demand or improving water governance and policies have often been neglected (Shah 2021; Drenkhan et al. 2022). To increase the water supply side, efforts have long been put into grey infrastructure including large reservoirs and dams (Shah 2021). Nonetheless, reservoirs often imply considerable impacts on local and downstream ecosystems, substantial investments, and social feasibility (Haeberli et al. 2016). Increasing water efficiency can potentially reduce water losses, particularly in mountain regions where water-intense flood irrigation and low investments in water infrastructure prevail (Cunha et al. 2019; Motschmann et al. 2022).

Recent studies reveal that adaptation strategies can unintentionally increase vulnerabilities and risks, known as maladaptation, due to an inappropriate project design and future uncertainties (Aggarwal et al. 2022; Adler et al. 2023). This highlights the value of robust decision-making which focuses on making informed decisions rather than improving predictions, an alternative paradigm to traditional approaches such as predictive or optimization models (Haasnoot et al. 2013; Marchau et al. 2019). Robust decision-making can be operationalized through Exploratory Modeling and Analysis (EMA) that maps diverse future scenarios without fixed probabilities and, as a result, all future (and potentially contradicting) scenarios are equally assessed (Lempert et al. 2003; Bryant and Lempert 2010). Through this approach, EMA goes beyond the “what if” question, exploring the circumstances under which a policy would succeed or fail (Kwakkel 2017; Moallemi et al. 2020). EMA has been successfully applied in the water sector, particularly for assessing urban water management or operational dam plans (cf. Kalra et al. 2015; Giuliani and Castelletti 2016). While these applications demonstrate EMA’s effectiveness in addressing water management challenges, their focus on specific and data-rich areas limits their ability to capture the complex dynamics occurring across entire catchments. Therefore, applications that show how EMA can contribute to support robust decision-making in data-scarce and complex regions are still missing.

This study aims to illustrate the potential of EMA to design robust water management strategies and define operational ranges at the catchment scale under uncertain climate and socio-economic changes in data-scarce and complex mountain environments. Through a case study in the Peruvian Andes, water management strategies are assessed to avoid potential water scarcity by 2050. Such an approach transcends conventional modeling approaches, offering significant advantages for informed decision-making processes.

2 Study Site

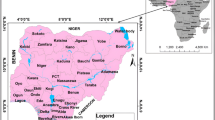
The case study is situated in the headwaters of the Vilcanota-Urubamba Basin in Cusco, Peru, specifically in the glacierized and data-scarce Pitumarca catchment (685 km2) (Fig. 1-A). The catchment elevation ranges from 3,413 to 6,315 m a.s.l. with a glacier surface of 20.6 km2 in 2016 which has decreased by about 30% in the last 40 years (INAIGEM 2018). The region is characterized by strong seasonality with most precipitation occurring from December to April and a pronounced dry season (June – August) when human and natural systems strongly rely on glacial meltwater (Buytaert et al. 2017; Drenkhan et al. 2019).

The Pitumarca catchment consists of two districts, Pitumarca and Checacupe, with 7,170 and 4,720 inhabitants, respectively (INEI 2020). The catchment covers only 59% of the Pitumarca district and 3% of the Checacupe district. The local economy considerably depends on traditional agriculture of potatoes, wheat, corn, and small-scale horticulture (INCLAM 2015). Approximately 45% (5,812 hectares) of cropland in both districts are irrigated, mostly with limited water infrastructure and inefficient practices such as flood irrigation (INCLAM 2015; INEI 2020).

Fig. 1
figure 1

Panel A Map of the study site including land cover – see Supplementary material S1 (MINAM 2015), the change in glacier surface from 1986 (see Sect. 3.1) to 2016 (INAIGEM 2018), as well as the lakes (ANA 2014) selected to be used as reservoirs (see Sect. 3.2). Panel B Schematic representation of the methods used in the study

Full size image

3 Data and Methods

In this study, we used EMA to identify the operational ranges of two widely implemented water management strategies to avoid water scarcity, while considering uncertainties from hydrological simulation and climate and socio-economic projections by 2050 (Fig. 1-B): (i) water reservoirs to increase water availability, and (ii) changes in water infrastructure efficiencies to reduce water losses.

3.1 Historical Glacio-Hydrological Simulation

Here we used the lumped and water balance model Shaman (Muñoz et al. 2021) because of its parsimonious approach and its successful application in the region (Muñoz et al. 2021). The model integrates surface and subsurface discharge, including a glacier routine that simulates the seasonal meltwater variability of tropical glaciers. The model accounts for sectorial water demand with backflows linked to water supply efficiencies (Supplementary material S2). We conducted calibration (1981–2000) and validation (2000–2016) at monthly time step, using multi-data calibration parameters and assessing runoff components (cf. Vetter et al. 2017; Muñoz et al. 2021). Glacier meltwater contribution to river discharge was compared to the regional dataset of Buytaert et al. (2017), while simulated runoff was compared to the national dataset on simulated river discharge by Llauca et al. (2021) (Supplementary material S3).

The Shaman model calculates water supply as a function of precipitation, potential evapotranspiration, and glacier discharge (Table 1). We obtained historical monthly precipitation and temperature data from the Peruvian-wide available 10 km gridded datasets PISCOp v2.1 and PISCOt v1.1, respectively (Huerta et al. 2018; Aybar et al. 2020). Potential evapotranspiration was calculated with the Penman-Monteith equation using the FAO calculator (Allen et al. 1998). Glacier discharge in Shaman is estimated through a sinusoidal function that depends on seasonal melting factors and glacier surface (Supplementary material S2). The latter was obtained by computing the Normalized Difference Snow Index (Hall and Riggs 2011) from multispectral satellite imagery of Landsat 5 (1987) and Landsat 7 (1998), and from the two Peruvian glacier inventories in 2010 and 2016 (cf. Muñoz et al. 2021).

Table 1 Datasets used for historical and future glacio-hydrological simulations
Full size table

We calculated historical domestic water demand by multiplying population data (from national censuses) with water allocation per person and day of 120 L/capita/day, an estimate that represents water needs for rural areas and considerable water losses (about 70%) in Peru (Drenkhan et al. 2019; Motschmann et al. 2022). Likewise, we calculated irrigation needs using irrigated areas (from national censuses) and the average catchment-wise crop water allocation of 18,000 m3/hectare/day that considers dominant crops such as potato, wheat, corn, and horticulture (INCLAM 2015). Catchment population and irrigated areas were a function of the district fraction inside the catchment because census data is available on a district level only. Environmental flow requirements were calculated as the equivalent of a discharge with 95% persistence (percentile 5%) at the catchment outlet assessed from 1981 to 2016 following an official methodology by the Peruvian Water Authority (R.J. N°098-2016-ANA).

The lumped Shaman model neglects spatial allocation of water, focusing instead on prioritized sectoral demands. Water is allocated first to domestic use, then to irrigation, and lastly to environmental needs.

3.2 Setting the Problem

In EMA all variables are categorized as uncertainties (X), policy levers (L), relationships (R), or metrics (M) using the XLRM framework (Lempert et al. 2003; Bankes et al. 2013). It structures variables into testable hypotheses to determine the operational range for policy options, while also accounting for uncertainties. In the case study, each input data to the hydrological model was considered as an uncertainty, namely future climate scenarios (X1_sce), future population (X2_pop), future irrigated areas (X3_irr), and backflows from domestic (X4_backd) and agricultural (X5_backi) water systems. We also defined three policy levers as changes in the efficiency from irrigation (L1_irreff) and domestic (L2_domeff) water systems, and water reservoir schemes (L3_res). Next, we defined variability ranges for uncertainties and policies (Table 2) based on diverse criteria (see following paragraphs). These uncertainties and policies then served as input data for the calibrated Shaman model, which accounts for the relationships (R) among these factors. Finally, the model output (metric M) is used for further analysis of policy performance. In the case study, this metric measures water sufficiency by counting the number of months in the dry season (May to September, 2022 to 2050) where total water supply exceeds 80% of total water demand including environmental flow requirements. The 80% considers that not all water demands can be fulfilled because of real-world limitations, as documented in local reports (INEI 2018).

We used future climate series for precipitation and temperature (X1_sce) from the Coupled Model Intercomparison Project Phase 6 (O’Neill et al. 2016), bias-correcting them with the quantile-quantile mapping method (Teutschbein and Seibert 2013; Andres et al. 2014). Glacier surface by 2050 was estimated according to Schauwecker et al. (2017) using projected changes in the freezing level heights derived from future temperature data. Future population (X2_pop) and irrigated areas (X3_irr) were calculated by applying rates of change, derived from the SSP database 2.0 (Riahi et al. 2017) and governmental projections (INEI 2019) at country scale, to historical data. X3_irr was exclusively derived from SSP scenarios due to the absence of local data from governmental reports. As backflows from the domestic and agricultural water systems (X4_backd, X5_backi) are widely uncertain (Cunha et al. 2019), an arbitrary range of 10 − 50% was set to represent the efficiency degree in the region (Drenkhan et al. 2019; Motschmann et al. 2022).

Table 2 Description of the uncertainties (X), policy levers (L), and the metric (M) used in this study
Full size table

Changes in irrigation (L1_irreff) and domestic water use (L2_domeff) efficiencies were considered in a wide range considering both, currently low efficiencies and future scenarios with high efficiencies driven by new technical development, e.g. drip irrigation (cf. INCLAM 2015; Drenkhan et al. 2019). We considered four reservoir management schemes (L3_res), ranging from no reservoirs to scenarios that combine one large reservoir with the utilization of multiple smaller lakes. All schemes uniformly released water solely during the dry season. The size of the large reservoir was set to 10 km2 representing a medium-sized lake in the region. Small lakes were selected according to their proximity to downstream areas where water demands are high (Fig. 1). Due to the lack of bathymetric data, small lake volumes were estimated using lake area and an empirical relationship between lake width and mean depth following Muñoz et al. (2020).

3.3 Operationalization and Scenario Discovery

We used the open-source Python library Exploratory Modeling and Analysis Workbench (ema-workbench) (Kwakkel 2017) to systematically run simulations and assess results. First, we integrated the calibrated Shaman model into the ema-workbench to conduct 12,000 simulations from 2022 to 2050 and calculated the water sufficiency metric. Each simulation combined uncertainties and policies from their respective ranges of variability using a Latin Hypercube sampling strategy. Second, we used the feature-scoring algorithm (Guyon 2003) to illustrate how uncertainties and policies influence the variability of the metric via a heatmap. Subsequently, we employed the Patient Rule Induction Method (PRIM) algorithm (Friedman and Fisher 1999) to explore the uncertainty and policy space and to identify combinations of factors triggering water sufficiency values exceeding or falling below a pre-defined water security threshold. This threshold was set as insufficient water supply, defined as water supply dropping below water demand levels within a specific period, where threshold = 1 (100%) means water supply > water demand every month until 2050. In the domestic water sector, utilities aim for 75 to 90% (0.75 to 0.90) of temporal water supply (Kalra et al. 2015; SUNASS 2022). For irrigation, temporal water supply varies by crops and weather conditions making it difficult to obtain a single target value (Levy et al. 2013). Regarding the environmental flow requirements, no target value is available due to data and knowledge gaps in the Andes. In this context, we applied a unique threshold of 0.8 (80%) for both human and environmental needs at the catchment scale. That means policies where metric < 0.8 are considered unsuccessful in avoiding water scarcity, while those where metric > = 0.8 are considered successful. This approach, known as stress-testing (Moallemi et al. 2020), has been commonly applied in other EMA applications.

4 Results

4.1 Future Hydroclimatic and Socio-Economic Development

The analysis of 15 future climate series reveals significant changes in precipitation, temperature, and glacier dynamics (Table 3 and Supplementary material S5), aligning with other research in the region (cf. Andres et al. 2014; Buytaert et al. 2017; Drenkhan et al. 2019). Between the historical and projected period up to 2050, an increase in total annual precipitation of up to 5% is observed under various SSP scenarios, except SSP1-1.9, which shows no significant change. Mean air temperatures are expected to rise by 1.2 °C to 1.9 °C, contributing to increased freezing level heights by up to 296 m and considerable glacier area reductions of up to 52%. Runoff simulations indicate a wide range across scenarios, with a significant increase at the annual scale under SSP1-2.6 and SSP5-8.5, and a marked decrease in dry season runoff under SSP5-8.5. Overall, glacier contribution to total annual runoff in the Pitumarca catchment is expected to decline reducing its buffering capacity during the dry season.

Table 3 Changes in hydroclimatic and socio-economic-related variables where a statistically significant change has been observed between the historical period (1981–2016) and the future climate series by end of 2050 according to climate scenarios
Full size table

Calculated environmental flow requirements range between 1.7 m3/s in July and 14.7 m3/s in February. These estimates correspond to approximately 50% of monthly discharge in all months (Supplementary material S6) and align with global estimates that vary between 20 and 50% (cf. Smakhtin et al. 2004).

Overall, 42 lakes were identified in the Pitumarca catchment which range from 0.5 to 10 hectares (total area: 0.91 km2) with an estimated total volume of 4.38 million m3 (Supplementary material S7). From these, 22 lakes (2.25 million m3) are near the high-demand lower catchment and were selected as potential reservoirs (Fig. 1).

Population dynamics show SSP scenarios projecting a decline of up to 10% in contrast with governmental projections that report an increase of up to 30% in comparison with 2016 levels. For all SSP scenarios, an expansion of irrigated areas between 5% and 35% is projected from 2017.

4.2 Scenario Discovery and Exploration

Simulations without policy implementation (Fig. 2-A and B) show that population changes have little impact on changes in water scarcity due to the low proportion (∼10%) of the domestic sector on overall water demand. However, expanding irrigated areas increases the risk of water scarcity (Fig. 2-A). In addition, climate scenarios (Fig. 2-B) potentially exert a strong influence on water scarcity levels. While optimistic scenarios such as SSP1-2.6 can prevent water scarcity, the pessimistic SSP5-8.5 scenario frequently leads to levels below the water scarcity threshold.

When considering all uncertainties and policies, out of 12,000 simulations, in 57% of these metric ≥ 0.8 showing success in avoiding water scarcity, while 43% of simulations failed (Supplementary material S8). The heatmap (Fig. 2-C) ranks all factors affecting the water sufficiency metric across the 12,000 simulations, showing policies, particularly the reservoir scheme (L3_res) and irrigation efficiency (L1_irreff), as key influencers. This suggests that rather than uncertainties specific policies play a decisive role in water scarcity in the catchment (Poff et al. 2016; Drenkhan et al. 2022). In 32% of all simulations, policies have considerably improved the metric values. However, in 15% of all cases initially above the 0.8 threshold, policies had contributed to water scarcity. This highlights the importance of identifying operational ranges to avoid unsuccessful cases (Haasnoot et al. 2013; Poff et al. 2016). Figure 2-D, based on the analysis of successful against unsuccessful cases from the PRIM algorithm, shows that while factors L1_irreff and L3_res are consistently important in both cases, other factors differ (e.g. X2_pop for unsuccessful cases, X1_sce for successful cases) (e.g. Haasnoot et al. 2013; Buytaert et al. 2017). Figure 2-D also shows the operational ranges for each of the factors with their statistical significance, confirming the key roles of L1_irreff and L3_res (Supplementary material S8).

Fig. 2
figure 2

Panel A: metric values from simulations without policy implementation plotted in terms of change in population and irrigated areas with boxplots showing their variability. Panel B: simulations without policy implementation plotted according to the climate scenarios indicating the percentage of simulations from each scenario where the metric is above (success) or below (fail) the threshold. Panel C: heatmap that shows the influence (0 to 1) of each uncertainty (X) and policy (L) on the variability of the metric. Panel D: operational ranges and statistical significance of each of the relevant factors according to successful ( > = 0.8) or unsuccessful (< 0.8) cases. Go to Table 2 for description of variables

Full size image

Building on results from the PRIM algorithm, Fig. 3 shows the successful (Fig. 3-A) and unsuccessful (Fig. 3-B) cases to avoid water scarcity. Scatter plots are a 2-dimensional representation of an 8-dimensional problem (five uncertainties and three policies) that facilitates the analysis. Overall, Fig. 3 highlights specific combination of factors that helps to avoid water scarcity. For instance, in Fig. 3-A, the combination of X1_sce with L2_domeff does not show a particular region where metrics are below or above the threshold. In contrast, X1_sce with L1_irreff or L3_res shows specific operational ranges to avoid water scarcity (L1_irreff > 0.45 and L3_res > 1).

Scatter plots also show the operational ranges to achieve metric ≥ 0.8 acknowledging overlaps between the analysis of successful and unsuccessful cases from Fig. 2-D. In Fig. 3-A, the scatter plot of L1_irreff and L3_res outlines a broad operational range, although much of this range overlaps with water scarcity regions, as shown in the corresponding scatter plot in Fig. 3-B. Therefore, for this case study, decision-makers should focus on results from Fig. 3-B where the operational range suggests two water strategies to avoid water scarcity: (i) high irrigation efficiency (> 0.63) with the large reservoir, or (ii) medium irrigation efficiency (> 0.45) with the large reservoir plus lakes as additional reservoirs.

Fig. 3
figure 3

Scatter plots depicting the influence of selected factors (policies or uncertainties) on metric values, grouped by focus on successful (Panel A) or unsuccessful (Panel B) cases in avoiding water scarcity. The red rectangle highlights operational ranges. Density functions further reveal trends of each factor. Go to Table 2 for description of variables

Full size image

5 Discussion

5.1 Identifying Water Management Strategies in a Data-Scarce Context

As for other mountain regions, the Pitumarca catchment illustrates the challenges posed by data scarcity and deep uncertainties that hinder the application of e.g. probabilistic approaches to support water management. Although the lack of hydrometeorological measurements can be increasingly compensated by satellite data, considerable errors and uncertainties persist (Vetter et al. 2017; Aybar et al. 2020). Similarly, multitemporal and locally available socio-economic data are often lacking and had to be estimated using broader-scale data points. Projections for both climatic and socio-economic conditions by 2050 exhibited variability and partially contradictory results. For instance, while the Peruvian government projects a population decrease by 2060 (INEI 2019), SSPs data projects this to occur before 2050 (Riahi et al. 2017).

Despite the deep uncertainty context, EMA leveraged the decision-making process by identifying the critical factors that influence the metric (policies L1_irreff and L3_res) and by reducing the analysis to select these factors (Bryant and Lempert 2010). While policies proved to be the most influential in the case study, uncertainties might dominate in other cases. The latter could be a signal of a need for model improvements. Alternatively, chosen policies might not perform well due to changing conditions, e.g. historically successful policies failing under changing climate conditions (Berkhout et al. 2014; Poff et al. 2016). Evaluating policies across many scenarios (e.g. 12,000 simulations) helps decision-makers to identify weaknesses and guide decision-makers to explore new, potentially, more effective policies (van Vuuren et al. 2012; Marchau et al. 2019).

EMA results highlighted that some policies can unintentionally lead to the risk of increased water scarcity which links to recent concerns about maladaptation (IPCC et al. 2018; Kundzewicz et al. 2018; Aggarwal et al. 2022). Identifying such potential failures is challenging due to the complexity of social-ecological systems. For instance, Fig. 2-A shows a three-dimensional problem where patterns are identifiable, such as the little influence of population in the metric. However, with an increasing number of dimensions (8-dimensions problem in this case study), it becomes much harder to identify these patterns. While statistical tools, e.g. principal component analysis or cluster analysis, help to understand these multidimensional problems, they do not explicitly identify the related operational ranges.

EMA tackles multidimensionality with the PRIM algorithm by searching for a combination of policies and uncertainties that best cluster cases above or below the water security threshold (Bryant and Lempert 2010; Kwakkel 2017). The degree of clustering is expressed as coverage, so a high coverage value (like 0.8 in Fig. 3-B) means more successful cases within the identified operational range, but also a higher risk of including undesired cases (Bryant and Lempert 2010). Consequently, EMA does not identify the best or optimal solution rather than a solution that works well in most scenarios (Bankes et al. 2013; Kwakkel and Pruyt 2013). While selected operational ranges might still include unsuccessful policies, EMA highlights these for further investigation, allowing researchers and decision-makers to refine strategies and identify which conditions will trigger policy failure.

5.2 EMA in Water Management: Key Considerations

5.2.1 Uncertainties

EMA can theoretically handle as many uncertainties as needed (e.g. Kalra et al. 2015; Giuliani and Castelletti 2016). However, exploring a large set of variables demands time and computing resources that must be considered (Moallemi et al. 2020), so users need to carefully select variables relevant to their objectives. While defining ranges for each uncertainty is important, EMA does not require highly accurate values (e.g. Kalra et al. 2015). These ranges can be calculated (e.g., climatic projections in this case study) or estimated through sensitivity analysis. Broad ranges are also a viable option, an advantage in data-scarce regions (Moges et al. 2021; Motschmann et al. 2022). For instance, EMA applications in Peru assessed the vulnerabilities of water plans using future precipitation ranges from − 60% to + 90% without specifying climate scenarios (Kalra et al. 2015).

5.2.2 Policy Levers

EMA focuses on testing policies across a broad spectrum of uncertainties, not designing new policies (Lempert et al. 2003; Marchau et al. 2019). Consequently, results depend on policy details. For instance, EMA might suggest high irrigation efficiencies to avoid water scarcity, but the lack of detailed information hinders policy implementation (Schneiderbauer et al. 2021). Maintaining clarity regarding the relationships between policies, uncertainties, and metrics is crucial (Lempert et al. 2003; Bankes et al. 2013). Infrastructure policies are generally easier to assess in hydrological models, while others like governance might require extra steps for operationalization. Selecting and adjusting policies for EMA demands collaboration between scholars and decision-makers, underscoring a pivotal aspect of effective water management (Cosgrove and Loucks 2015; Scott et al. 2021).

5.2.3 Metric and Threshold

The selection of the metric(s) and threshold(s) is crucial for EMA, as these determine the criteria to categorize system performance as successful or unsuccessful (Kwakkel and Pruyt 2013; Marchau et al. 2019). For instance, we focused only on water access, neglecting economic and social feasibility. As a result, EMA suggests the implementation of a large reservoir to avoid water scarcity, but its construction could be socially, environmentally, or financially challenging (Haeberli et al. 2016). By considering multiple metrics that address these concerns, potential trade-offs can be identified allowing for an informed selection of policies (Ucler and Kocken 2023).

Thresholds should be viewed as points on a gradient rather than fixed tipping points, as a marginal improvement in the system may lead to a shift from unsuccessful to successful cases (Bankes et al. 2013; Haasnoot et al. 2013). But thresholds can also help to incorporate the IPCC (2018) risk framework e.g. to identify the acceptable risk to unmet water demands. Changing the threshold can yield different outcomes, prompting users to assess and understand the implications of such changes (Kwakkel and Pruyt 2013).

5.2.4 Relationships

Choosing the hydrological model is key in evaluating water management strategies and their effectiveness (Vetter et al. 2017; Moges et al. 2021). In the case study, a lumped model was used, thus not allowing for a spatial analysis. Semi-distributed models would offer more detailed insights by considering the spatio-temporal distribution of water access and availability (Moges et al. 2021). Socio-hydrological models go further, integrating socio-economic factors to assess e.g. governance strategies (Berkhout et al. 2014; Scott et al. 2021). While the ema-workbench supports the integration with external software, Python-based models offer easier implementation but might have limitations in representing real-world complexities.

5.3 Beyond EMA: Links with Other Tools and Methods

EMA can complement and benefit from existing optimization and uncertainty reduction methods. Optimization methods (e.g. Vetter et al. 2017; Ucler and Kocken 2023; Wang et al. 2024), can identify viable strategies for specific scenarios. Then, EMA evaluates these strategies across uncertainties to identify weaknesses and operational ranges. Additionally, methods such as sensitivity analyses (e.g. Huss and Hock 2018; Moges et al. 2021) can help to find the ranges of uncertainties for exploration. Furthermore, collaborative approaches (e.g. Muccione et al. 2019), can be effective in delineating policies, metrics, and their associated thresholds through the engagement of policy-makers and stakeholders (Schneiderbauer et al. 2021; Hasan et al. 2023). This comprehensive approach allows practitioners to benefit from the diverse array of available tools in water management to identify robust solutions.

In this study, a stress-testing approach was adopted to implement EMA. However, other approaches are also available, such as the worst-case scenario discovery or the many-objective optimization (cf. Moallemi et al. 2020). Finally, the dynamic policy pathways (Haasnoot et al. 2013) can further assist policy-makers in adapting strategies based on new information, e.g. adjusting plans if precipitation patterns change.

6 Conclusions

In this study, Exploratory Modeling and Analysis (EMA) is employed to address the challenges of water management in mountain regions under uncertain future climate and socio-economic scenarios. The case study in the Peruvian Andes demonstrates the effectiveness of EMA to identify robust water management strategies that can accommodate a range of uncertain outcomes. Furthermore, EMA can support the identification of operational ranges of water policies. This allows to address deep uncertainties and avoid cases that trigger maladaptation. Although all factors assessed within EMA are important (uncertainties, policies, metrics, and relationship), metrics and their thresholds are key factors as they classify policies as successful or unsuccessful to achieve water security. EMA is suggested to complement existing methods based on probabilistic approaches. Further studies should delve into the integration of semi-distributed socio-hydrological models in EMA to assess non-infrastructural-based policies, such as changes in governance and water culture.