1 Introduction

Groundwater contamination risk analysis is a basic part of the assessment process regarding the necessity of implementing potential protective measures on a regional scale, mainly in regard to catchment areas. However, a particularly important type of analysis of the groundwater contamination risk combined with the human health risk encompasses water source evaluation. This analysis is performed to assess the need for groundwater source protection zone (GSPZ) establishment and pollution prevention measures. The World Health Organization has recommended that a drinking water safety plan and risk management system should be developed to manage groundwater resources (WHO 2017a). This is necessary to prevent possible hazards within wellhead protection areas (WHPAs).

Groundwater source risk assessment (GSRA) is performed based on analysis of the impact of land use (Huan et al. 2018; Li et al. 2018). Land use forms potentially threatening the quality of abstracted groundwater mainly include agricultural and point sources of contamination (Lima et al. 2019; Li et al. 2020). In regard to the agricultural impact, risk analysis has been conducted targeting nitrate pollution (Su et al. 2013; Teng et al. 2019; Zambito Marsala et al. 2020). In addition to qualitative methods for groundwater risk estimation (Li et al. 2015; Zhang et al. 2016; Duda et al. 2020), advanced methods such as numerical modeling of mass transport through the vadose zone and saturated aquifer have been adopted (Troldborg et al. 2009; Enzenhoefer et al. 2012; Huan et al. 2015, 2020; Locatelli et al. 2018). Enzenhoefer et al. (2015) presented a more holistic and probabilistic approach, which additionally considered, inter alia, aggregation of the impacts stemming from different contaminants and spill locations into a cumulative impact on the risk and a method considering the stochastic nature of spill event accounting when converting the aggregated impact into risk estimates. Furthermore, Rodak and Silliman (2012) proposed an advanced approach combining probabilistic risk analysis (PRA) with fault trees of contamination sources, in addition to chemical transport modeling and human health impact assessment to estimate the health effects on abstracted water users. The methods adopted in PRA of engineering system failure scenarios have been described by Ostrom and Wilhelmsen (2019) and Modarres and Kim (2020). Fuzzy fault tree analysis in risk assessment of water resource development plans was performed according to Abedzadeh et al. (2020).

Moreover, it remains a problem that most GSRA approaches usually adopt a specific concentration of the groundwater contaminant under analysis as an assessment basis (for example, nitrates), i.e., a situation that has already occurred as a result of the actual impact of pollution sources. However, these sources are usually not specified and characterized in detail. In the case of industrial facilities, overall facility characterization is lacking, which should consider not only technical aspects but also nontechnical aspects that may influence the failure probability. The approaches adopted to date typically still do not involve simultaneous estimation of the event probability and chemical compound mass emitted from a potential source of contamination (PSC).

The deficiencies identified in existing GSRA methods particularly concern the estimation of the potential total effective nitrogen load for a given crop. This total nitrogen mass is dissolved in water, and as nitrates, it moves toward the aquifer and only then is it transported to the water source. Thus, when analyzing the risk of nitrates reaching a given well at concentrations that threaten the health of users, it is important to estimate the risk directly originating from PSCs, not solely the risk, which is the observed effect of the PSC impact. Furthermore, existing GSRA approaches do not consider the annoyance attributed to the adverse effect of the PSC impact to water users.

The purpose of this article is to propose a method to bridge the indicated gaps by establishing a comprehensive and interdisciplinary approach to GSRA. Improving the GSRA quality is particularly important within the context of groundwater protection given its increasing scarcity. The proposed method accounts for both those risk factors that have been previously considered by other researchers and additional factors considered for the first time in this study. Our source-pathway-receptor approach is a semiquantitative and modular framework for a process-based GSRA.

2 Methodology

2.1 Calculation of the Degree of Risk

The method and presented example concern a situation where a well field contains a delineated GSPZ, and a risk analysis is required to determine the necessity of its legal establishment so that a groundwater protection plan can be implemented. The purpose of implementing this plan is to eliminate the possibility of degradation in the quality of abstracted groundwater resulting in discontinuation of the water supply originating from this source to users. The GSRA method adopted assumes that at the time of assessment, the well field draws uncontaminated water, and no PSCs located within the GSPZ have released any contamination yet.

In the approach adopted, the greatest of the risks identified for the individual PSCs located within the GSPZ is regarded as the risk of groundwater source contamination:

$$R=\mathrm{max}{R}_{i}$$
(1)

where:

$$R_i={LU}_i\cdot{PA}_i\cdot{AE}_i\cdot A_{AEi}$$
(2)

where R is the degree of risk to the groundwater source, Ri is the risk caused by a given PSC, i is the number of PSCs, LUi is the adverse impact of the PSC on the groundwater quality, PAi is the probability of occurrence of the unwanted event/failure, AEi is the adverse effect of aquifer contamination and AAEi is the annoyance caused by the adverse effect to water users.

In our approach, the factors determining the risk to groundwater sources include the adverse effect of any unwanted events and the annoyance due to this effect. If no such effect occurs (AE = 0) or no annoyance ensues (AAE = 0), then there is no risk to the groundwater source (R = 0). Where a certain PSC yields an adverse effect, the increase in risk is affected by (i) the increase in severity of its impact, (ii) the increase in contaminant emission potential, and (iii) the increase in annoyance.

The performed GSRA results in appropriate decisions concerning water source management. If risk occurs (R > 0), GSPZ establishment should be required to protect the water resources occurring within this zone.

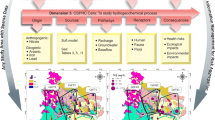
An organigram of the factors considered in GSRA and a process flowchart are shown in Figs. 1 and 2, respectively.

Fig. 1
figure 1

Organigram of the factors considered in GSRA

Full size image
Fig. 2
figure 2

Flowchart of the GSRA process

Full size image

2.2 Adverse Impact (LU)

The degree of the adverse impact of PSCs on groundwater is determined using relevant classifications (Table 1). The adverse impact of a given PSC is assumed to depend on:

  • - the chemical compound mass that may be emitted by a given source,

  • - the concentration of chemical compounds in the leachate,

  • - the toxicity of the chemicals that may be emitted,

  • - the depth of the groundwater table, and

  • - the degree of insulation of the PSC from the ground.

Table 1 Adverse impact of the land use forms acting as PSCs on groundwater
Full size table

2.3 Probability of an Unwanted Event

An unwanted event entails the worst-case emission of a contaminant into groundwater among the emissions possible for a given PSC. The probability of an unwanted event (PA) is defined in a different manner depending on the type of land use.

2.3.1 Industrial and Infrastructure Facilities and Installations

The PA is determined by assessing the technical conditions of the facility in question. The technical conditions are determined based on the age of the facility, the method of its construction, the scope and frequency of periodic checks/inspections, and the fail-safe protection measures employed. Depending on the scenario implemented, risk analysis may concern the current or projected technical conditions.

The PA is expressed on a scale from 0 to 1 (Table 2), where a value of 0 corresponds to the impossibility of an accident/failure occurring within a 25-year horizon under any scenario considered. A value of 1 corresponds to a situation where a failure/accident will occur at a 100% probability within a 25-year horizon under at least one scenario. A span of 25 years is considered because this period is adopted as a limit when delineating the GSPZ range based on the isochrone of the arrival of nonreactive contaminants stemming from the land surface at the well.

Table 2 Classification of the PA for infrastructure and industrial facilities and installations
Full size table
Table 3 Assessment criteria and ranks of factors influencing the risk of groundwater contamination
Full size table

To determine the PA for industrial and infrastructure-type PSCs, a two-stage approach is adopted (Fig. 2). Stage I consists of a qualitative assessment: if for the PSC in question, the probability of event occurrence is low (PA ≤ 0.3), in subsequent stages, it is then assumed that there is no adverse effect (AE = 0) and consequently no risk to the well field (R = 0). If the assessment result indicates that 0.3 < PA ≤ 0.5, the degree of the adverse effect of the event is then determined. In contrast, if qualitative assessment demonstrates that the probability of occurrence of an unwanted event is very high (PA > 0.5), stage II of PA determination thus follows (quantitative assessment).

  • Step I – qualitative PA assessment

It is assumed that the PA of an industrial and infrastructure facility results in possible groundwater contamination increase with deteriorating technical conditions of the facility in question. The technical conditions of an industrial or infrastructure facility are determined by the construction manner of the facility and its anti-accident protection measures (C), its operation or production technology (T) and the frequency and scope of inspections and fail-safe protection measures and procedures to be followed in the event of an incident (IM). Nontechnical factors are also considered in the assessment (Table 3), namely, the possibility of natural (N) and economic and legal (EL) random events and human errors (H). Natural events include geohazards, which are extreme weather events, landslides caused by natural factors, earthquakes, and tsunamis. Economic and legal factors include the liquidation of a company as a result of bankruptcy, a change in business profile, or a certain negligence and omission resulting from cost cutting.

Human errors include the deliberate flouting of approved procedures and norms, negligence, lack of responsibility, lack of necessary qualifications and competences among hired employees without compliance with relevant requirements, bending to pressure stemming from superiors for fear of losing employment, and pressure on subordinates to force them to act improperly or to refrain from implementing certain actions, reporting irregularities, achieving group solidarity, etc.

It is assumed that the degree of impact of individual factors determining the technical conditions of industrial and infrastructure facilities varies, which is expressed by their weights. The weights adopted for the individual factors are 5 (Cw and IMw), 4 (Tw), 3 (Nw), 2 (ELw) and 1 (Hw). Each factor can attain a value (rank) ranging from 0.1 to 1 (Table 3). We define the index of the potential impact of industrial and infrastructure sources on groundwater as:

$$I_{in}=C_r\cdot C_w+{IM}_r\cdot{IM}_w+T_r\cdot T_w+N_r\cdot N_w+{EL}_r\cdot{EL}_w+H_r\cdot H_w$$
(3)

Depending on the value of the Iin index, the PA is estimated for industrial and infrastructure facilities (Table 3).

Regarding noninert waste landfills, following the concept proposed by Zhang et al. (2016), several factors are considered that impact the risk of groundwater contamination. It is assumed that factors related to the landfill design and nature of the waste stored provide a more reliable estimate of the risk of groundwater contamination. The factors ultimately considered for assessment purposes include the type of waste (T), the method of landfill insulation from the ground (I), the method of waste covering (Cov) and the degree of compaction (Cmp).

The degree of impact of the individual factors varies, which is expressed by their weights. Weights of 5 (Iw and Covw) or 3 (Tw and Cmpw) were assumed for the individual factors. Each factor can attain a value (rank) ranging from 0.1 to 1 (Table 5). The potential impact of a noninert waste landfill on groundwater is determined by the Il index:

Table 4 Criteria to assess and rank the factors impacting the risk of groundwater contamination as a result of the potential impact of a landfill and the relationship between PA and Il
Full size table
Table 5 Classification of the unwanted event probability in fertilized areas
Full size table
$$I_I=T_r\cdot T_w+I_r\cdot I_w+{Cov}_r\cdot{Cov}_w+{Cmp}_r\cdot{Cmp}_w$$
(4)

Depending on the calculated Il index value, the probability of an unwanted event (PA) considering a landfill and a noninert waste heap is accordingly estimated (Table 4).

  • Step II – quantitative PA calculation

In regard to industrial and infrastructure PSCs, an unwanted event involves the worst-case emission of a certain contaminant into groundwater among the emissions possible for a given PSC. The probability is quantitatively estimated as:

$$PA={PA}_{BZ}\cdot PSF$$
(5)

where PABZ is the probability of failure occurrence for a given PSC (Eq. 6), and PSF is the combined probability of security failure, i.e., the failure of individual independent fail-safe protections (Eq. 7).

$${PA}_{BZ}=\max({Pa}_i\cdot\mathrm m\mathrm a\mathrm x{Pc}_j)$$
(6)

where Pai is the probability of occurrence of the accident initiating the emission of a certain contaminant from a given PSC into the environment, i is the number of initiating accidents in question, Pcj is the probability of occurrence of a certain condition triggering a given accident initiating contaminant emission (Pai), and j is the number of situations conditioning a given initiating accident.

$$PSF=\mathrm{max}{PSF}_{i}$$
(7)

where PSFi is the probability of failure of the fail-safe protection measure in question, and i is the number of protection measures. Examples of protection measures include process automation, safety automation, operator or system action, isolation or protection systems, fail-safe protection procedures, etc.

2.3.2 Fertilized Agricultural Areas

The probability of nitrate emissions into groundwater originating from diffuse pollution sources (fertilized areas) was calculated in an approximate manner. Atmospheric nitrogen deposition was disregarded, similar to certain processes resulting in nitrogen losses, such as volatilization (Søgaard et al. 2002; Huijsmans et al. 2003), surface runoff and soil erosion. It was assumed that the predicted emission of nitrates into groundwater depends on the relationship between the predicted amount of nitrogen fertilization and the ability of crops to utilize this nitrogen fertilization (FN). The predicted FN relationship was calculated as the difference between the total annual effective nitrogen load (Na) and the maximum annual nitrogen load that could be utilized by the crop species under the given agronomic conditions (Nd) according to Eq. (8):

$${F}_{N}={N}_{a}-{N}_{d}={N}_{an}+{N}_{am}+{N}_{as}-{N}_{d}$$
(8)

where Nan is the effective nitrogen load stemming from natural fertilization, kg∙ha−1∙y−1 (Eq. 9), Nam is the nitrogen load originating from mineral fertilization, kg∙ha−1∙y−1, and Nas is the effective nitrogen load contained in the soil, kg∙ha−1⋅y−1 (Eq. 10).

$$N_{an}=N_n\cdot\beta$$
(9)

where Nn is the nitrogen dose originating from manure, kg⋅ha−1∙y−1, and β is a correction coefficient that determines the effectiveness of nitrogen stemming from manure relative to nitrogen originating from mineral fertilizers (Jensen 2013).

$$N_{as}=N_s\cdot\alpha$$
(10)

where Ns is the stock of mineral nitrogen in soil, kg⋅ha−1⋅y−1, and α is a correction coefficient that determines the effectiveness of soil nitrogen relative to nitrogen stemming from mineral fertilizers (Stanford et al. 1973).

To obtain the total amount Nn applied to crops in a given GSPZ, the nitrogen loads produced by the animals reared in the region should be summed depending on the farming system. The total annual amounts of nitrogen originating from both the various fertilizer types and soil nitrogen were divided by the area of fertilized land in the GSPZ to determine the nitrogen load per unit area.

PA classification in fertilized areas based on the difference between the nitrogen fertilization level and potential utilization by crops is presented in Table 4. If FN is negative, the probability is low or very low (PA ≤ 0.3). Consequently, no adverse effect is assumed (AE = 0), which indicates no risk to the well field (R = 0).

2.4 Adverse Effect of an Unwanted Event

The maximum concentration attainable by a chemical emitted by the PSC in the aquifer situated beneath the source (cmax) is the sum of the predicted injection concentration of the chemical transported through the vadose zone into groundwater (cinj) and the concentration originally present in the aquifer due to geogenic and/or anthropogenic causes (c0). The injection concentration (cinj) is the concentration in water percolating through the vadose zone. The maximum concentration (cmax) attainable by a chemical compound in the aquifer is:

$$c_{max}\left(Q_f+Q_i\right)=c_0\cdot Q_f+c_{inj}\cdot Q_i$$
(11)

hence:

$$c_{max}=\frac{c_0\cdot Q_f+c_{inj}\cdot Q_i}{Q_f+Q_i}$$
(12)

where Qf is the groundwater flux into the aquifer and Qi is the groundwater flux through the vadose zone beneath the PSC.

The adverse effect of an unwanted event (AE) reflects the potential contamination of groundwater flowing into the well field. This effect is determined as the ratio of the predicted concentration attainable by a given chemical released by the PSC in water abstracted from the well (cw) to its permissible concentration in drinking water (ctr):

$$c_w\leq c_{tr}\rightarrow AE=0 \;\;\; (no\;adverse\;effect)$$
(13)
$$c_w>c_{tr}\rightarrow AE=1\;\;\;(adverse\;effect\;present)$$
(14)

The permissible concentration limit of a chemical compound in drinking water (ctr) corresponds to the concentration stipulated in relevant legal acts for water directed to the water supply network after disinfection.

The concentration attainable by a chemical compound emitted by a PSC in water abstracted from the well (cw) depends on the maximum concentration in groundwater beneath the PSC (cmax) and the concentration originally present in the aquifer (c0):

$${c_w}=\frac{c_{max}\cdot{\left(Q_i+Q_f\right)}+{c_0}\cdot{\left({Q_w}-{Q_i}-{Q_f}\right)}}{Q_w}$$
(15)

where Qw is the well pumping rate.

The predicted maximum concentration reached by the contaminant (cmax) was determined with an analytical method at the time upon reaching the groundwater table, considering the processes associated with mass migration. Details of the analytical method used to predict mass migration through the vadose zone can be found in the Supplementary Materials – Sect. 1.

In a given fertilized area, AE was determined if the PA was at least high (Fig. 2, Table 5). To calculate the predicted nitrate injection concentration (mg∙L−1) migrated from the topsoil through the unsaturated zone into groundwater (cNO3), the following equation was used:

$$c_{inj}=c_{{NO}_3}=\frac{F_N}{I_e}\cdot0.443$$
(16)

where FN is the predicted nitrogen load greater than the fertilization needs (kg∙ha−1∙y−1) and 0.443 is the conversion factor employed with respect to the units of the parameters occurring in this equation, considering the ratio of the equivalent weights of nitrogen and nitrates.

The nitrate injection concentration (cNO3) is equal to the nitrate concentration in the topsoil leachate due to the assumed absence of denitrification and volatilization during transport through the vadose zone.

2.5 Annoyance Related to the Adverse Effect

The annoyance related to the adverse effect to users of abstracted water (AAE) is determined on the basis of its duration. The duration of annoyance, or supply nonfunctioning (tnf), is assumed to encompass the number of days during which groundwater drawn from a well would be unfit for drinking and users would have to temporarily rely on another supply source, e.g., water tankers. The annoyance related to the adverse effect increases with the period during which the water supply is interrupted (Table 6).

The contaminant concentration upon reaching the well field (cw) can be determined analytically, considering the processes associated with mass migration in groundwater, but hydrodynamic dispersion may be disregarded. Details of the analytical method used to predict mass transport in groundwater can be found in the Supplementary Materials – Sect. 2.

3 Materials

3.1 Adopted Model

To illustrate the application of the proposed method, risk analysis of a groundwater well field was conducted considering an idealized model in which frequently occurring selected types of human pressures and typical hydrogeological conditions were assumed (Fig. 3). The phreatic aquifer is unconfined and exhibits a hydraulic conductivity k = 10 m⋅d−1, a thickness m = 7 m, and a hydraulic gradient I = 0.1%. In the vadose zone with a thickness mv = 4 m, silty and loamy sand occurs with a volumetric moisture content of Θs = 0.2 (based on Witczak et al. 2011). Precipitation is P = 0.65 m⋅y−1. Recharge was estimated via an infiltration method (Staśko et al. 2012) according to Eq. (17):

$${I}_{e}=P\cdot \omega$$
(17)

where ω is the effective infiltration coefficient of precipitation (for topsoil, ω = 0.20, and for compacted municipal waste in a landfill, ω = 0.30).

Fig. 3
figure 3

Schematic 3D cross-section of the example test site (not to scale). The PSCs are numbered in accordance with Tables 7 and S1

Full size image

Several PSCs are present within the well catchment. These are point sources, i.e., gas stations, industrial plants, landfills, and farms, namely, PSC Nos. 1 to 9, and agricultural areas fertilized with nitrogen where different crops are grown, namely, I, II and III (Table 7, Tables S1 and S2 in the Supplementary Materials – Sect. 3). In the model described, the values of the individual factors determining the probability of an unwanted event stemming from the considered PSCs are not actual values but rather figures adopted to better illustrate the issue of concern.

Table 6 Classification of the annoyance of an adverse effect to water users
Full size table

3.2 Sensitivity Analysis

To analyze the sensitivity of the adopted GSRA method to the variation in the values of the parameters considered, AE assessment was performed under three scenarios (Table 8). Adverse effect analysis concerned those PSCs for which the determined PA indicated that this analysis was necessary. It was assumed that the differences between the analyzed scenarios concerned the set of analyzed PSCs and the amount of water abstracted from the well field. The sensitivity analysis of PSC No. 8 included two suboptions: 8.1 and 8.2 (a larger amount of waste in the landfill under suboption 8.2 over suboption 8.1). It was assumed that the variation in well yield determines the degree of contaminant mass dilution in water pumped from the well and the extent of the well catchment.

Table 7 Risk attributed to a given PSC estimated based on the PA qualitative assessment method (refer to Table S1 for the PSC characteristics and assumed values of the factors determining the risk)
Full size table
Table 8 Scenarios assumed for sensitivity analysis purposes
Full size table
Table 9 Risk due to a given PSC estimated based on PA quantitative assessment (evaluation details in Table S3)
Full size table

4 Results and Discussion

Regarding industrial and infrastructure PSCs, the first GSRA stage entails a qualitative assessment of the PA (Table 7). The assessment demonstrated that for PSC No. 6, PA = 0.4, indicating the need to assess the adverse effects. In terms of those PSCs for which the qualitatively estimated probability PA > 0.5, it was necessary to proceed to the second stage of probability assessment (additional quantitative assessment). For these PSCs, possible failure initiating accidents and events that condition initiating accidents were assumed, for which, in turn, the estimated occurrence probability values were assumed, i.e., Pai and Pcj. Possible typical anti-accident protection measures were also assumed together with the estimated probability (PSFi) of their failure or ineffectiveness (Table 9). In the example described, the values of the individual probabilities are not actual values obtained from source materials but rather figures adopted to better illustrate the issue of concern.

Quantitative assessment of the PA for PSCs Nos. 2, 4, and 9 demonstrated that adequate anti-accident protection measures resulted in the absence of an adverse effect (AE = 0) and consequently the absence of risk (R = 0). Regarding the municipal landfill (8), given that it was certain that precipitation would infiltrate the landfill (Pcj = 1.0) and that it was not insulated, the probability PA = 1, which necessitated adverse effect (AE) assessment.

In terms of agricultural crops, quantitative PA assessment results are listed in Table S2. For type II and III crops, the calculated excess nitrogen loads FN were high. This occurred due to the lower nitrogen utilization capacities of these vegetables than those of other typical crops. As a result, for both crops, the quantitatively calculated PA was extremely high (PA = 0.9). Hence, it was necessary to assess the AE.

Adverse effect assessment was performed under the three scenarios adopted to analyze the sensitivity of the method (Tables 8 and 10).

Scenario A

In regard to PSC No. 6, the calculated vertical migration time of chromium through the vadose zone, considering delay due to sorption, amounts to tvCr = 26.3 years. This indicates the key role of sorption in AE risk assessment since the calculated chromium concentration in the well 25 years after possible leakage of this PSC remains lower than the permissible value in drinking water. This suggests no adverse effect and no risk to the well originating from this PSC throughout the assumed time horizon (Table 11).

In regard to PSC No. 8.1, the sulfate concentration in well water is lower than the permissible limit for drinking water. This suggests no adverse effects and no risk to the well field. This is attributed to sulfate concentration reduction during transport to the well because of leachate dilution after mixing with clean influent stream water.

Regarding crop No. II, the predicted nitrate concentration in well water does not exceed the permissible limit for drinking water, indicating no adverse effect and consequently no risk to the well field stemming from this PSC. This is attributed to the reduction in contaminant concentration due to the mixing of leachate originating from crop fertilization with the water into the aquifer.

Scenarios B and C

The results obtained under both scenarios are similar and indicate a threat to the well field originating from the landfill under options 8.1 and 8.2 and from crops II and III (Tables 10 and 11). As the landfill is not insulated from the ground, the adverse effect of its impact under both options is permanent, resulting in the need for wells to be shut in for a long time. This will create a very high annoyance to water users. Hence, AAEi = 4 was adopted. Therefore, the projected risk to the well field stemming from this PSC is Ri = 16. Similarly, regarding crops, since crops II and III are perennial crops, the adverse effect of excess nitrogen fertilization also persists for many years, requiring long-term well field closure. This situation causes a very high annoyance to water users (AAEi = 4), so Ri = 16.

Table 10 Assessment of the adverse effect of the possible events detected at the stage of PA assessment (evaluation details in Table S4)
Full size table
Table 11 Summary of the GSRA results
Full size table

Scenario B indicates that despite the unchanged amount of water flowing into the well over Scenario A, there exists an adverse effect of the PSC impact and, therefore, a risk to the well field. This is the effect of human pressure under scenario B, i.e., a higher contaminant concentration occurs in the leachate present under the larger landfill, thus affecting a larger cultivation area, and its adoption in the analysis of crop III, characterized by a lower maximum effective nitrogen load than that of crop II, was considered under scenario A.

In addition to the magnitude of the dissolved contaminant load in the leachate of these PSCs, the ratio of the amount of water pumped through the well to the amount of water flowing below these PSCs into the well plays an important role in assessing the threat to the well field. The difference between these figures is the amount of uncontaminated groundwater inflow. Under scenario A, the considerable amount of water abstracted from the well results in notable contaminant plume dilution due to the water flowing laterally into the well from the entire well catchment. As a result, the averaged contaminant concentration in the inflowing water into the well is lower than that in the inflowing water into a well experiencing less water abstraction. Under scenario C, the inflow of uncontaminated groundwater from outside the PSCs threatening the well field is low. As a result, the proportion of contaminants in the inflowing water into the well is higher, and consequently, the risk increases. Where the amount of abstracted water is small, even a small local PSC can pose a risk to the well field. Nevertheless, proper GSRA should also consider the analysis of hydrogeological conditions and distribution of the hydrodynamic field in terms of the assumed well yield, which greatly affects the extent and shape of the WHPA.

The probability of groundwater contamination as a result of overfertilization in agricultural areas may vary over time, depending on crop species changes. The total nitrogen load originating from the different types of manure obtained from various species of livestock may also vary. The types and amounts of mineral fertilizers may also differ. The probability of exceeding prescribed fertilizer dosage rates may also exhibit spatial variation depending on the crop species grown, soil category and nitrogen load originating from the different sources occurring in individual GSPZ regions. To predict the total nitrogen load as accurately as possible, analyses should be carried out of individual agricultural subareas.

The above considerations indicate that it is important to optimize the amount of water abstracted from the well or distribute the water abstraction amount between individual wells in a multiwell field under nitrogen fertilization optimization to protect well fields against a high risk resulting in their closure (Salcedo-Sanchez et al. 2013; Zdechlik and Kałuża 2019). Ghandi and Roozbahani (2020) presented how the risk to the drinking water supply can be managed under critical conditions if it is impossible to avoid these conditions.

Where a contaminant is continuously emitted into groundwater, the annoyance to water users plays a key role in the assessment of the resulting risk. The outcome of risk analysis also depends on the adverse impact of PSCs and the effect of unwanted events. Comparable results of regional groundwater risk analysis were obtained by Huan et al. (2018) and Li et al. (2020), who applied a similar approach accounting for the groundwater intrinsic vulnerability and contaminant potential quantity, representing the hazard originating from land use activities, as two of the three risk factors considered. Generally, similar results were also obtained by Huan et al. (2020) in a risk analysis of groundwater sources due to the presence of livestock farms and landfills. They applied a similar process-based approach, considering mass transport through an unsaturated zone and an aquifer, via numerical simulations. Therefore, it seems feasible and effective to combine their method and tool with our approach.

5 Conclusions

Although the proposed method is extensive, the GSRA results obtained as a result of its application should provide a robust basis for policymakers when making decisions on GSPZ establishment.

As the performed GSRA concerns a specific period, another analysis is required after this period. This is attributed to possible changes in land use, technical conditions of the PSCs, agricultural production and related fertilization practices.

The reliable performance of GSRA requires the involvement of a multidisciplinary team and is a difficult task. The analysis complexity depends on the manner of land use assessment and diversity of the PSCs occurring within the projected GSPZ.

It is also necessary to improve the methods for assessment adaptation of the probability of industrial accidents and adverse natural, economic, and legal events to environmental risk analysis. This issue, although very difficult, must be resolved because without considering these probabilities, these assessments will inevitably be burdened by uncertainty.

The proposed process-based holistic GSRA method, which accounts for different types of PSCs, can also be applied, with minor modifications, to regional analysis of the groundwater contamination risk. Assessing the need for groundwater protection on a regional scale is important in light of the progressing depletion of groundwater resources.