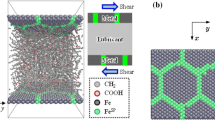
Abstract
In boundary lubrication, the detachment of lubricant molecules from a solid surface is likely to occur due to the presence of high compressive normal stress combined with shear stress exerted on the solid–liquid interface. This phenomenon often results in a delamination behavior at the interface. We aim to investigate the nanoscale roughness effect on the oil film delamination from sliding iron surfaces with grain boundaries by coarse-grained molecular dynamics simulations. As a result, the oil film delamination was effectively suppressed in higher roughness. Two distinct mechanisms of delamination were found depending on surface roughness when the critical normal stress is exceeded. High roughness enhanced the ability to prevent complete slip but had negligible influence on partial slip.
Graphical Abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In boundary lubrication, interaction of two sliding metal surfaces through super-thin lubricant film and local asperity contact would potentially lead to plastic deformation, severe wear, and even fracture. However, the continuum friction law at macroscale is known to break down in microscopic contact situation [1] due to the nanoscale surface roughness, which consequently spur further analysis into investigating the atomic roughness effect on friction contact [2,3,4,5,6,7,8,9]. It was found that the friction coefficient increased with roughness under dry sliding contact [5], and yet the relationship between nanoscale roughness and the coefficient of friction under boundary lubrication conditions is still inconclusive. Ewen et al. [2] found a slight increase in the friction coefficient on a rough iron surface of 0.5 nm. In contrast, Frérot et al. [10] observed that rough cobalt surface has a significantly larger friction coefficient than flat surface under boundary lubrication.
Furthermore, much research has been devoted to improving the frictional behavior and wear performance of metal surfaces in the past years [11,12,13,14,15,16,17,18,19,20,21]. One effective way to decrease the friction coefficient is to apply surface microstructure treatments, such as introducing grain boundaries [18,19,20,21]. The presumable mechanism for achieving a lower friction coefficient is that grain boundaries can serve as the preferential adsorption sites for lubricants and as a result it improves the coverage of the oil film on surface. In our previous simulations, we studied the relationship of surface microstructure and the friction properties [21]; it was found that grain boundaries can suppress the delamination of lubricant molecules from flat surfaces by increasing the critical normal stress. The normal stress and shear stress ware strongly influenced by surface roughness under sliding condition. It is necessary to explore the influence of surface roughness on interface delamination behavior in the presence of grain boundaries. Meanwhile, it was observed that atomistic roughness can resist interfacial slip between the fluid and wall surfaces even under a small roughness [15,16,17]. This phenomenon has the potential to enhance the adsorption of lubricants on metal surfaces. In addition, the interface slip between base oil and additive films were analyzed by Shi et al. [22, 23]. Although previous research include either surface hardening effect [11,12,13,14], grain boundary effect [18,19,20], or nanoscale roughness effect [2,3,4, 15,16,17], none of them pay attention to the temporal evolution of lubricant behavior between constant sliding nanostructured surfaces with nanoscale roughness. To have a better understanding of boundary lubrication, it is essential to investigate the dynamic interface behavior between oil film and sliding surfaces under a compressive load. Thus, in this work, we conducted a coarse-grained (CG) molecular dynamics simulation to analyze the contact of rough iron surfaces with nanostructured grain boundaries and arachidic acid as the lubricants.
2 Methodology
2.1 Model Set-up
Simulation system set-up. a A typical model with a root mean square (RMS) roughness of 0.3 nm. \({\text {Fe}}^{\text {SP}}\) denotes the grain boundary atoms. b The lower iron surfaces at different levels of RMS roughness. The colors of atoms represent their relative height based on the same model. The upper surfaces are a reflection of the lower surfaces (Color figure online)
The simulation system consists of a lubricant layer confined by two iron surfaces, as shown in Fig. 1a. The grain boundary is added to the metal surface to strengthen the adsorption of lubricant molecules [24] and those atoms are denoted as \({\text {Fe}}^{\text {SP}}\). Iron grains are arranged in a hexagonal pattern and the grain size is set to 7.5 nm. The saturated C\(_{20}\) fatty acid (arachidic acid, CH\(_{3}\)(CH\(_{2}\))\(_{18}\)COOH) is an effective organic friction modifier lubrication additive [25] and has been widely used in both experimental [26,27,28] and numerical studies [21]. Generally, the base oil is often utilized with additives in real machine components. However, in this study, in order to emphasize the interaction with grain boundary atoms, we only considered the adsorption of a single type of lubricant molecule on the surface for simplicity. As a result, the arachidic acid was selected as the lubricants. Lubricants have been modeled using both all-atom (AA) and united-atom (UA) methods for decades [29]. In the UA model, some hydrogen atoms are grouped with carbon atoms to increase computational efficiency up to an order of magnitude [30]. Thus, UA method has become very popular in the field of tribology due to the requirement of large and complicated simulation system [31,32,33]. The schematic illustration of the modeling method for arachidic acid molecule in this work is shown in Fig. 12 in “Appendix.” As is shown on the right of the figure, united-atom approach was used to develop the methylene and methyl group. \({\text {CH}}_{3}\) is regarded as \({\text {CH}}_{2}\) for simplicity. They were both treated as a same particle in our model. In addition, we replaced carboxyl group with another particle using coarse-grained (CG) method, as indicated on the left of the figure. As a result, the particle of a single arachidic acid molecule reduced from 62 in AA model to 20 in current model. Since our model contains both united-atom method and coarse-grained method, we considered it should be called, to be exact, a “UA-CG” hybrid model.
The lower bcc iron walls with (110) surfaces have a dimension of 11.5 \(\times\) 13.0 nm, as shown in Fig. 1b. We examined five cases of different root mean square (RMS) roughness from 0.1 to 0.5 nm. It should be noted that the rough surfaces represent a series of extremely flat surfaces because the substrate with RMS roughness of approximately 10 nm is regarded as the ‘flat’ surface in experiments. Hence, it revealed a single-asperity contact condition instead of multi-asperity contact. The atomically smooth surface was also conducted for comparison. The darker or lighter the shading (color online) of atoms, the lower or higher the valleys or peaks. The lower wall has a minimum 6 atom layers in all cases and a maximum 15 layers in Case 6 with a RMS roughness of 0.5 nm. Thus, the atom number of bottom surface varies from 15,360 in Case 1 to 27,144 in Case 6. The upper walls are the mirror reflection of the lower walls. The density of arachidic acid at 373 K in CG model is calculated as 0.97 g/cm\(^{3}\), while the experimental value is 15% smaller (0.824 g/cm\(^{3}\)) at the same temperature as reported in [34]. Former calculations of long-chain alkanes [29] have shown similar over-predictions of density, which have been linked to crystallization caused by the overestimation of the melting point.
The random surface topography modeling at different scales have been investigated for decades [35,36,37,38,39], but yet there is still not a perfect method to describe one rough surface either on microscale or macroscale. Each method for producing rough surfaces has its own set of advantages and disadvantages. For instance, the random midpoint displacement (RMD) algorithm is numerously used in many studies [2, 4,5,6] because the generated surface has a self-affine fractal scaling and the surface roughness can be directly quantified by Hurst exponent. However, RMD method cannot create a surface that has different lengths in the x- and y-direction, thus specific requirement exists regarding the lattice orientation of the model. Gaussian distribution is another common choice to generate a rough surface by means of height distribution function and auto-correlation function [3, 40]. But the Gaussian form of the auto-correlation function is insensitive to the nano/atomic scale asperities, thus only suitable for macroscopic surface generation. Besides, the sinusoidal wave has been adopted to establish analytical model and numerical model to analyze the tribological properties [15, 41, 42]. In this work, we used the sinusoidal wave to form random surfaces that are periodic across the boundaries. The position of wall atoms in the z-direction is derived from two-process traces in the x- and y-directions:
where z(x, y) denotes the accumulated roughness based on six layers of flat surface; \(A_{i}^{x}\), \(A_{i}^{y}\), \(B_{i}^{x}\), \(B_{i}^{y}\), \(C_{i}^{x}\), and \(C_{i}^{y}\) represent the amplitude, period, and phase of sinusoidal waves in x- and y-directions, respectively. The proper initial period \(B_{1}^{x}\) and \(B_{1}^{y}\) are set to make the sinusoidal wave exhibit a single period in both the x-direction and y-direction of the model. The initial amplitude \(A_{1}^{x}\) and \(A_{1}^{y}\) are set properly. \(k_{\text {A}}\) and \(k_{\text {B}}\) are the decay factor larger than one. i stands for the iteration number. Thus, the amplitude decays and the period grows during iteration, and the random phase \(C_{i}^{x}\) and \(C_{i}^{y}\) are set individually in each iteration. The iteration continues until the target roughness \({\text {RMS}}_{\text {target}}\) is reached. As a result, the random rough surfaces with desired RMS roughness are gradually generated.
2.2 Force Field
The potential function of the coarse-grained model is presented below:
here, r, \(\theta\), and \(\phi\) denote the bond length, bond angle, and dihedral angle between lubricant particles, respectively. The interaction parameters within lubricants are based on [21, 43, 44]. The last term represents the interactions between lubricants and the wall using the Lennard–Jones potential. The determined parameters between grain boundary atoms \({\text {Fe}}^{\text {SP}}\) and COOH groups, \(\alpha\) = 12.8 kcal/mol and \(\beta\) = 4.5675 Å, were utilized in this interaction. These parameters have been validated to ensure the occurrence of chemisorption between the lubricant and grain boundary atoms [45,46,47]. They have also been employed in previous non-equilibrium molecular dynamics (NEMD) simulations of tribological systems [21].
2.3 Simulation Procedure
The simulation system was fully relaxed at the temperature of 1000 K and cooled down to 300 K for 100 ps to minimize energy. It should be noted that there is no decomposition of lubricant molecules during relaxation process in our calculation system. Then, the compression process was conducted until the predetermined surface distances were reached. Note that such distance of rough surfaces denotes the distance between the top iron layer and the bottom iron layer. After the relaxation and compression, each system was ready for sliding process. The sliding velocity in boundary lubrication experiments (typically mm/s) is currently inaccessible in MD simulations of this scale. Thus, here the sliding velocity is set to 5 m/s which was a common choice in similar literature [2,3,4]. The surface distance remained constant as the surfaces moved in the y-direction. The upper surface moved in the y-positive direction, while the lower surface moved in the opposite direction. In order to improve the calculation efficiency, iron atoms were regarded as rigid during the simulation. The temperature was controlled at 300 K by the Nosé–Hoover thermostat [48, 49]. Shear heating is an important phenomena in industrial tribological contacts. It can also be understood by means of NEMD simulations [50]. However, in this work, we did not take friction heating into account for simplicity. Each system had 1600 lubricant molecules, with surface coverage falling within the experimental range [51]. Periodic boundary was applied in the x- and y-directions. In this work, we only analyzed the data during the sliding process where each surface moved a total of 250 nm in 50 ns. The calculation were conducted with the LAMMPS package [52] and the atomistic data from the MD simulations were visualized and analyzed using the OVITO package [53].
3 Results and Discussion
Variation in the average shear stress with the average compressive normal stress at the RMS roughness of 0, 0.1, 0.2, 0.3, 0.4, and 0.5 nm. Error bars are obtained from the standard deviation between the time-averages. The slope of the dashed lines represents the friction coefficient \(\mu\). Blue squares indicate the typical conditions that will be discussed in detail (Color figure online)
Figure 2 shows the average shear stress as a function of average compressive normal stress of all cases. The average stresses were calculated from the last 10 ns of total 100 ns, as shown in Fig. 13 in “Appendix.” Error bars, obtained from the standard deviation between the time-averages, are included in the figures. The relationships of shear stress and compressive stress in all cases can be roughly divided into three stages.
In the low stress region, it basically exhibits a linear distribution, characterized by a very low slope. The friction coefficient, which is obtained by the slope of linear fitting curves of the relationship of normal stress and shear stress, in this stage is extremely small (about 0.1). To understand this, radial distribution functions (RDFs) for CH\(_{2}\)–CH\(_{2}\) (a), COOH–CH\(_{2}\) (b), and COOH–COOH (c) pairs of Case 1 are shown in Fig. 3. The pair distribution function is normalized by the average number density of particles, i.e., the total number of particles divided by the simulation cell volume. RDF of different normal stresses are drawn in different shades of grayscale (colors online). In the RDF curves of this work, the outer range (r > 4 Å) is considered as the intermolecular distribution within lubricants. We will focus on this intermolecular interaction range. At low pressure, all of three pairs exhibit sharper peaks in longer separation distance than those at high pressure. It implies a similar oil film arrangement under low pressure and a more solid-like distribution. At high pressure, the peaks of intermolecular interactions become smoother and shifts of peaks to shorter pair separation distance can be observed. It indicates a liquid-like distribution with severe rearrangement of lubricant and density decline of oil film.
In the second stage, with increasing normal stress, the shear stress increased nearly linearly with a higher slope as the dashed lines show. The slope of the dashed line is regarded as the friction coefficient \(\mu\). Figure 4 illustrates the friction coefficient against the RMS roughness. It shows that the friction coefficient is at the same level under different RMS roughnesses.
Radial distribution function (RDF) for CH\(_{2}\)–CH\(_{2}\) (a), COOH–CH\(_{2}\) (b), and COOH–COOH (c) pairs in Case 1. Some curves are shifted upward for clarity. RDF of different normal stresses are drawn in different colors. Red-dashed line indicates the similarity under low stress but difference under high stress (Color figure online)
Temporal evolution of spatial-averaged velocity of lubricants at the RMS roughness 0.2 nm and 0.3 nm. Four typical conditions are selected based on the blue squares in Fig. 2. The top two (a and b) are from the RMS roughness of 0.2 nm and the below two (c and d) are from the RMS roughness of 0.3 nm (Color figure online)
In even higher stress conditions of Fig. 2, the stress curve exhibited distinct behaviors depending on the RMS roughness. A sudden slope variation even to a negative value is observed at three smaller RMS roughnesses, i.e., flat, 0.1 nm, and 0.2 nm, while the slope gradually decreases at three larger RMS roughnesses, i.e., 0.3 nm, 0.4 nm, and 0.5 nm. To further understand the difference, we selected four typical conditions (A, B, C, and D) indicated in squares in Fig. 2 to analyze the spatial-averaged velocity evolution, as shown in Fig. 5. The spatial-averaged velocity is calculated by the ratio of the average displacement over a time interval of 0.05 ns. And the average displacement is calculated as the mean change in position observed for all lubricant molecules over the past 0.05 ns.
The schematic illustration of spatial-averaged velocity is shown in Fig. 6. The colors of fluid particles stand for different lubricant molecules. The average velocities of 5 m/s and \(-5\) m/s mean that the lubricant molecules mainly follow the movement of one wall and detach from the other wall; a zero spatial-averaged velocity stands for the attachment on both surfaces. At a RMS roughness of 0.2 nm, Fig. 5a and b shows the representative conditions of the second and the third stages, respectively. The spatial-averaged velocity of A was close to \(-5\) m/s in the first 15 ns and oscillated around zero in the last 20 ns. This finding is in consistent with our previous study on the dynamic analysis of lubricant molecules between flat surfaces [54], where we observed that the formation of the oil film took a certain amount of time. In condition B, the spatial-averaged velocity was basically \(-5\) m/s and 5 m/s in the whole sliding process. It suggested that the detachment of the oil film always happened in the third stage at a RMS roughness of 0.2 nm. Figure 5c and d represents the typical conditions of the second and the third stages at a RMS roughness of 0.3 nm, respectively. The temporal evolution of the spatial-averaged velocity of C exhibited a similar pattern to that of A, wherein detachment occurred initially, followed by the formation of the oil film after a certain period of time. In contrast, the spatial-averaged velocity profile of D was quite different from that of B. The spatial-averaged velocity of lubricants oscillated between the top and bottom surface speed, owing to the alternating occurrences of oil film detachment and attachment. In [55], it was observed that wall slip occurred at both solid–liquid interfaces, resulting in the lubricant to become almost stationary. However, in this work, we only observed slip behavior at single surface, as shown in Fig. 5b, thus the lubricant moves with another surface.
To deeply reveal this phenomenon, the variation in the time-averaged velocities with the compressive normal stress at all roughness cases are shown in Fig. 7. The time-averaged velocities were determined based on the steady state of the temporal evolution of spatial-averaged velocities. The corresponding error bars were obtained from the standard deviation of such time-averaged process. For example, we defined the last 10 ns as the steady state in condition A as shown in Fig. 5a. The critical normal stress is defined as the maximum normal stress at which slip at either oil/metal interface does not occur, which represents the oil film’s capacity to resist delamination. A larger critical normal stress indicates a stronger anti-delamination capacity. In Fig. 7a–e, a critical compressive normal stress existed while it was absent in Case 6 with a RMS roughness of 0.5 nm in Fig. 7f because slip was not observed. At the RMS roughnesses of 0 nm, 0.1 nm, and 0.2 nm, the critical normal stress, which are indicated in squares, were determined by the variation of time-averaged velocity. When it was below the critical normal stress, the time-averaged velocity remained at zero, while above the critical normal stress, it was consistent with the wall speed due to the detachment of oil film on one surface. This full detachment of lubricant molecules on surface above the critical normal stress below a RMS roughness of 0.2 nm is defined as the complete slip. In contrast, another slip behavior was observed above the critical normal stress at the RMS roughness of 0.3 nm and 0.4 nm. The time-averaged velocity was near zero but had higher error bars when it exceeded the critical normal stress. In this slip condition, it is difficult to determine the accurate critical normal stress based on the time-averaged velocity. Thus, we further analyzed the time-averaged velocity fluctuation. Figure 8 shows the variation in the standard deviation of the time-averaged velocities with the compressive normal stress at the RMS roughness of 0.3 nm and 0.4 nm. It can be found that a low normal stress has a low standard deviation. The critical normal stress for the low standard deviation, \(\sigma _{\text {cr}}\), is determined by the maximum normal stress, as indicated in squares. When it was above the critical normal stress, the oil film alternately detached and adsorbed on surfaces, leading to a relative high standard deviation of time-averaged velocities. Thus, we defined this slip condition as the partial slip. In a rougher surface with a RMS roughness of 0.5 nm, we did not observe the detachment behavior even in high compressive normal stress. The time-averaged velocity (in Fig. 7f) maintains around zero due to the strong adsorption on both surfaces. The absence of detachment may be attributed to the storage of lubricants within the surface valley regions [56,57,58].
The average velocity profiles of complete slip, partial slip, and no slip condition are shown in Fig. 9. Velocity Y is defined as the ratio of the average displacement to time. When it is above critical normal stress, two slip mechanisms are identified. In complete slip, it shows a relatively uniform velocity distribution with the detachment of oil film in lower interface. It causes a decline of shear stress in Fig. 2a–c in high normal stress condition. While in no slip condition, it can be observed that a symmetrical velocity profile occurs with the fully adsorption of oil film on both surfaces. In partial slip, it is found that there is an alternate occurrence of detachment and adsorption of lubricants on metal surfaces. Thus, the shear stress shown in Fig. 2d, e still increases with increasing normal stress above the critical normal stress. It should be noted that the shear stress saturation under high pressure in Fig. 2a–c is similar with [59, 60]. However, we believe the mechanism behind the similar phenomenon is different. In [59, 60], the saturation of shear stress attributed to the phase transition from viscoelastic region to the plastic–elastic region which related to the suppression of the fluctuation in molecular motion. However, according to Fig. 7, time-averaged velocities shown higher error bars after the shear stress is saturated in this work. This implied that the saturation of shear stress attributed to the wall–liquid slip behavior which related to the enhancement of the fluctuation in molecular motion.
The density profile of arachidic acid of two typical conditions of slip and no slip is shown in Fig. 10. The oil film was divided into 100 groups along z-direction, and the number of particles in each groups were collected. The density at position z/\(z_{0}\) was calculated by dividing particle numbers by the volume of each groups and then averaging the obtained density over time in steady state. It should be noted that “slip” condition here denotes the complete slip condition, thus the density profile of partial slip condition is between slip and no slip condition. Both density profiles exhibit layer-like distribution, especially in boundary region. In slip condition, less layer of oil film was observed compared to those in no slip condition. It was found that a more uniform distribution of lubricant film occurred in no slip condition, while the lubricant molecules more concentrated on boundary layers in slip condition. This indicates that there is a local density difference in slip and no slip condition, but the general density pattern is similar. Similar layering density profile was also observed in [55].
The relationship of the critical normal stress and RMS roughness is summarized in Fig. 11. Basically, the critical normal stress became larger with increasing roughness. This effect varied with the specific delamination mechanism. When the roughness is smaller than 0.3 nm, the critical normal stress linearly increased with increasing RMS roughness in the complete slip region. But in the partial slip, the critical normal stress was higher than that in the complete slip and it nearly remained constant at two different RMS roughnesses. At a RMS roughness of 0.5 nm, no slip was observed even under a high compressive stress. It can be concluded that surface roughness mitigates the delamination of the oil film by increasing the wear resistance capacity.
As we mentioned in Introduction, previous studies reported that introducing nano-grains can reduce the friction coefficient in boundary lubrication [18,19,20,21, 24]. It was conjectured that the phenomenon is caused by the enhanced adsorption of lubricant molecules on grain boundaries. Our finding in this study, however, suggests that the surface roughness, which is likely to be introduced by nano-graining [61], might also contribute to such reduction of the friction coefficient. Thus, it is still an open question, what is the dominant mechanism behind the friction reduction by nano-graining. Further experimental and theoretical investigations are required to answer the question.
In this work, we did not take the base oil, friction heating, and elasticity of grains into account due to the limitation of calculation cost. The base oil can support the additive (fatty acid) and play a reliable role under severe industrial conditions. It makes our current model less realistic with the absence of base oil within additive layers. However, only two molecular layers of n-hexadecane remained between additive films under the contact pressure of 0.5 GPa according to [2, 62]. In higher contact pressure, most of base oil are expected to squeeze out of the contact asperities, thus only few n-hexadecane molecules remain. We believe such very few base oil molecules within additive films have negligible effect on the oil film slip behaviors occurring at the solid–liquid interface. Furthermore, the main purpose of this study is to understand the roughness effect on the adsorption of friction additive on metal surfaces. A more comprehensive investigation of lubricant slip behaviors in the presence of base oil including wall slip [63] and interfacial slip [22, 23] would certainly be an interesting objective of future MD simulations, but is beyond the scope of the current study. Moreover, the friction heating is an important issue under industrial tribological contacts. The local temperature rise may affect the friction behavior, leading to a squeeze out of lubricants and direct contact of asperities. Another critical factor is the elasticity of grains. The polycrystalline surface is likely to undergo an elastic deformation under boundary lubrication, which will further change its interaction with lubricants. Furthermore, the number of lubricant molecules will alter the surface coverage, which also has a strong relationship with the interaction between fatty acid and surface. In this work, a high coverage was employed to ensure an ample supply of lubricant molecules, especially for preferential adsorption with grain boundaries. Achieving a relatively lower coverage is technically feasible; future work needs to pay attention to the surface coverage effect. Lastly, temperature effect can also affect the interface behavior through the change of interaction strength between lubricant and surface. Subsequent studies should address above problems.
4 Conclusion
A series of coarse-grained dynamics simulations was carried out to investigate the nanoscale roughness effect on the oil film delamination between iron surfaces with grain boundaries. Five rough surfaces at the RMS roughness of 0.1 nm to 0.5 nm were generated and a flat surface was also set for comparison. As a result, the oil film delamination was effectively suppressed in higher roughness. Two delamination mechanisms were identified depending on the RMS roughness. The behaviors of oil film delamination at low roughness (\(\le\) 0.2 nm) and high roughness (0.3–0.4 nm) were attributed to the complete slip and the partial slip, respectively. The lubricant molecules fully detached from one surface in the complete slip, leading to a negative friction coefficient. However, the partial slip, where the detachment and attachment of oil film alternately happened, resulted in a gradual reduction of friction coefficient. At a RMS roughness of 0.5 nm, even no delamination was observed. Furthermore, the critical compressive stress for the oil film delamination increased with the surface roughness. Significant improvements in the complete slip resistance can be achieved with high roughness, whereas its impact on the partial slip was negligible.
Data Availability
Not applicable.
Code Availability
Not applicable.
References
Luan, B., Robbins, M.O.: The breakdown of continuum models for mechanical contacts. Nature 435(7044), 929–932 (2005)
Ewen, J.P., Restrepo, S.E., Morgan, N., Dini, D.: Nonequilibrium molecular dynamics simulations of stearic acid adsorbed on iron surfaces with nanoscale roughness. Tribol. Int. 107, 264–273 (2017)
Zheng, X., Zhu, H., Tieu, A.K., Kosasih, B.: A molecular dynamics simulation of 3D rough lubricated contact. Tribol. Int. 67, 217–221 (2013)
Zheng, X., Zhu, H., Tieu, A.K., Kosasih, B.: Roughness and lubricant effect on 3D atomic asperity contact. Tribol. Lett. 53, 215–223 (2014)
Spijker, P., Anciaux, G., Molinari, J.-F.: Dry sliding contact between rough surfaces at the atomistic scale. Tribol. Lett. 44, 279–285 (2011)
Spijker, P., Anciaux, G., Molinari, J.-F.: The effect of loading on surface roughness at the atomistic level. Comput. Mech. 50, 273–283 (2012)
Delogu, F.: Molecular dynamics of collisions between rough surfaces. Phys. Rev. B 82(20), 205415 (2010)
Kim, H., Strachan, A.: Nanoscale metal–metal contact physics from molecular dynamics: the strongest contact size. Phys. Rev. Lett. 104(21), 215504 (2010)
Kim, H., Strachan, A.: Molecular dynamics characterization of the contact between clean metallic surfaces with nanoscale asperities. Phys. Rev. B 83(2), 024108 (2011)
Frérot, L., Crespo, A., El-Awady, J.A., Robbins, M.O., Cayer-Barrioz, J., Mazuyer, D.: From molecular to multiasperity contacts: how roughness bridges the friction scale gap. ACS Nano 17(3), 2205–2211 (2023)
Wang, Z., Tao, N., Li, S.-S., Wang, W., Liu, G., Lu, J., Lu, K.: Effect of surface nanocrystallization on friction and wear properties in low carbon steel. Mater. Sci. Eng. A 352(1–2), 144–149 (2003)
Wang, X., Li, D.: Mechanical, electrochemical and tribological properties of nano-crystalline surface of 304 stainless steel. Wear 255(7–12), 836–845 (2003)
Zhang, Y., Han, Z., Wang, K., Lu, K.: Friction and wear behaviors of nanocrystalline surface layer of pure copper. Wear 260(9–10), 942–948 (2006)
Suh, C.-M., Song, G.-H., Suh, M.-S., Pyoun, Y.-S.: Fatigue and mechanical characteristics of nano-structured tool steel by ultrasonic cold forging technology. Mater. Sci. Eng. A 443(1–2), 101–106 (2007)
Jabbarzadeh, A., Atkinson, J., Tanner, R.: Effect of the wall roughness on slip and rheological properties of hexadecane in molecular dynamics simulation of Couette shear flow between two sinusoidal walls. Phys. Rev. E 61(1), 690 (2000)
Jabbarzadeh, A., Harrowell, P., Tanner, R.: Low friction lubrication between amorphous walls: unraveling the contributions of surface roughness and in-plane disorder. J. Chem. Phys. 125(3), 034703 (2006)
Ding, J., Chen, J., Yang, J.: The effects of surface roughness on nanotribology of confined two-dimensional films. Wear 260(1–2), 205–208 (2006)
Todaka, Y., Toda, K., Horii, M., Umemoto, M.: Effect of lattice defects on tribological behavior for low friction coefficient under lubricant in nanostructured steels. Tetsu-to-Hagané 101, 530–535 (2015)
Rydel, J.J., Pagkalis, K., Kadiric, A., Rivera-Díaz-del-Castillo, P.: The correlation between ZDDP tribofilm morphology and the microstructure of steel. Tribol. Int. 113, 13–25 (2017)
Lobzenko, I., Shiihara, Y., Sakakibara, A., Uchiyama, Y., Umeno, Y., Todaka, Y.: Chemisorption enhancement of single carbon and oxygen atoms near the grain boundary on Fe surface: ab initio study. Appl. Surf. Sci. 493, 1042–1047 (2019)
Albina, J.-M., Kubo, A., Shiihara, Y., Umeno, Y.: Coarse-grained molecular dynamics simulations of boundary lubrication on nanostructured metal surfaces. Tribol. Lett. 68, 1–9 (2020)
Shi, J., Wang, J., Yi, X., Fan, X.: Effect of film thickness on slip and traction performances in elastohydrodynamic lubrication by a molecular dynamics simulation. Tribol. Lett. 69, 1–9 (2021)
Shi, J., Li, H., Lu, Y., Sun, L., Xu, S., Fan, X.: Synergistic lubrication of organic friction modifiers in boundary lubrication regime by molecular dynamics simulations. Appl. Surf. Sci. 623, 157087 (2023)
Adachi, N., Matsuo, Y., Todaka, Y., Fujimoto, M., Hino, M., Mitsuhara, M., Oba, Y., Shiihara, Y., Umeno, Y., Nishida, M.: Effect of grain boundary on the friction coefficient of pure Fe under the oil lubrication. Tribol. Int. 155, 106781 (2021)
Spikes, H.: Friction modifier additives. Tribol. Lett. 60(1), 1–26 (2015)
Ossia, C., Han, H., Kong, H.: Response surface methodology for eicosanoic acid tribo properties in castor oil. Tribol. Int. 42(1), 50–58 (2009)
Cyriac, F., Yamashita, N., Hirayama, T., Yi, T.X., Poornachary, S.K., Chow, P.S.: Mechanistic insights into the effect of structural factors on film formation and tribological performance of organic friction modifiers. Tribol. Int. 164, 107243 (2021)
Zhang, S.-W., Lan, H.-Q.: Developments in tribological research on ultrathin films. Tribol. Int. 35(5), 321–327 (2002)
Ewen, J.P., Gattinoni, C., Thakkar, F.M., Morgan, N., Spikes, H.A., Dini, D.: A comparison of classical force-fields for molecular dynamics simulations of lubricants. Materials 9(8), 651 (2016)
Martin, M.G., Siepmann, J.I.: Transferable potentials for phase equilibria. 1. United-atom description of n-alkanes. J. Phys. Chem. B 102(14), 2569–2577 (1998)
Savio, D., Fillot, N., Vergne, P.: A molecular dynamics study of the transition from ultra-thin film lubrication toward local film breakdown. Tribol. Lett. 50, 207–220 (2013)
Liu, P., Yu, H., Ren, N., Lockwood, F.E., Wang, Q.J.: Pressure–viscosity coefficient of hydrocarbon base oil through molecular dynamics simulations. Tribol. Lett. 60, 1–9 (2015)
Berro, H., Fillot, N., Vergne, P.: Molecular dynamics simulation of surface energy and ZDDP effects on friction in nano-scale lubricated contacts. Tribol. Int. 43(10), 1811–1822 (2010)
Lide, D.R.: CRC Handbook of Chemistry and Physics, vol. 85. CRC Press, Boca Raton (2004)
Borodich, F.M., Pepelyshev, A., Savencu, O.: Statistical approaches to description of rough engineering surfaces at nano and microscales. Tribol. Int. 103, 197–207 (2016)
Pawlus, P., Reizer, R., Wieczorowski, M.: A review of methods of random surface topography modeling. Tribol. Int. 152, 106530 (2020)
Sista, B., Vemaganti, K.: Estimation of statistical parameters of rough surfaces suitable for developing micro-asperity friction models. Wear 316(1–2), 6–18 (2014)
Sabino, T.S., Carneiro, A.C., Carvalho, R.P., Pires, F.A.: The impact of non-Gaussian height distributions on the statistics of isotropic random rough surfaces. Tribol. Int. 173, 107578 (2022)
Mulakaluri, N., Persson, B.: Adhesion between elastic solids with randomly rough surfaces: comparison of analytical theory with molecular-dynamics simulations. Europhys. Lett. 96(6), 66003 (2011)
Garcia, N., Stoll, E.: Monte Carlo calculation for electromagnetic-wave scattering from random rough surfaces. Phys. Rev. Lett. 52(20), 1798 (1984)
Ji, J.-H., Guan, C.-W., Fu, Y.-H.: Effect of micro-dimples on hydrodynamic lubrication of textured sinusoidal roughness surfaces. Chin. J. Mech. Eng. 31(1), 1–8 (2018)
He, T., Ren, N., Zhu, D., Wang, J.: Plasto-elastohydrodynamic lubrication in point contacts for surfaces with three-dimensional sinusoidal waviness and real machined roughness. J. Tribol. 136(3), 031504 (2014)
Shin, S., Rice, S.A.: Comment on the influence of molecular flexibility on molecular packing in Langmuir monolayers. Langmuir 10(1), 262–266 (1994)
Muthukumar, M., Welch, P.: Modeling polymer crystallization from solutions. Polymer 41(25), 8833–8837 (2000)
Loehle, S.: Understanding of adsorption mechanism and tribological behaviors of C\(_{18}\) fatty acids on iron-based surfaces: a molecular simulation approach. PhD Thesis, Ecole Centrale de Lyon; Tōhoku Daigaku (Sendai, Japan) (2014)
Loehlé, S., Matta, C., Minfray, C., Le Mogne, T., Iovine, R., Obara, Y., Miyamoto, A., Martin, J.: Mixed lubrication of steel by C\(_{18}\) fatty acids revisited. Part I: toward the formation of carboxylate. Tribol. Int. 82, 218–227 (2015)
Loehlé, S., Matta, C., Minfray, C., Le Mogne, T., Iovine, R., Obara, Y., Miyamoto, A., Martin, J.: Mixed lubrication of steel by C\(_{18}\) fatty acids revisited. Part II: influence of some key parameters. Tribol. Int. 94, 207–216 (2016)
Nosé, S.: A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 52(2), 255–268 (1984)
Hoover, W.G.: Canonical dynamics: equilibrium phase-space distributions. Phys. Rev. A 31(3), 1695 (1985)
Ewen, J.P., Gao, H., Müser, M.H., Dini, D.: Shear heating, flow, and friction of confined molecular fluids at high pressure. Phys. Chem. Chem. Phys. 21(10), 5813–5823 (2019)
Ramachandran, S., Tsai, B.-L., Blanco, M., Chen, H., Tang, Y., Goddard, W.A.: Self-assembled monolayer mechanism for corrosion inhibition of iron by imidazolines. Langmuir 12(26), 6419–6428 (1996)
Thompson, A.P., Aktulga, H.M., Berger, R., Bolintineanu, D.S., Brown, W.M., Crozier, P.S., Veld, P.J., Kohlmeyer, A., Moore, S.G., Nguyen, T.D.: LAMMPS—a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 271, 108171 (2022)
Stukowski, A.: Visualization and analysis of atomistic simulation data with OVITO-the open visualization tool. Model. Simul. Mater. Sci. Eng. 18(1), 015012 (2009)
Deng, S., Kubo, A., Todaka, Y., Shiihara, Y., Mistuhara, M., Umeno, Y.: Oil film formation and delamination process on nanostructured surfaces in boundary lubrication: a coarse-grained molecular dynamics study. J. Tribol. 146(7), 1–34 (2024)
Zhang, H., Fukuda, M., Washizu, H., Kinjo, T., Yoshida, H., Fukuzawa, K., Itoh, S.: Shear thinning behavior of nanometer-thick perfluoropolyether films confined between corrugated solid surfaces: a coarse-grained molecular dynamics study. Tribol. Int. 93, 163–171 (2016)
Grützmacher, P.G., Profito, F.J., Rosenkranz, A.: Multi-scale surface texturing in tribology—current knowledge and future perspectives. Lubricants 7(11), 95 (2019)
Wang, L., Guo, S., Wei, Y., Yuan, G., Geng, H.: Optimization research on the lubrication characteristics for friction pairs surface of journal bearings with micro texture. Meccanica 54, 1135–1148 (2019)
Shi, R., Wang, B., Yan, Z., Wang, Z., Dong, L.: Effect of surface topography parameters on friction and wear of random rough surface. Materials 12(17), 2762 (2019)
Washizu, H., Ohmori, T., Suzuki, A.: Molecular origin of limiting shear stress of elastohydrodynamic lubrication oil film studied by molecular dynamics. Chem. Phys. Lett. 678, 1–4 (2017)
Katsukawa, R., Van Sang, L., Tomiyama, E., Washizu, H.: High-pressure lubrication of polyethylethylene by molecular dynamics approach. Tribol. Lett. 70(4), 101 (2022)
Perron, A., Politano, O., Vignal, V.: Grain size, stress and surface roughness. Surf. Interface Anal. Int. J. Devoted Dev. Appl. Tech. Anal. Surf. Interfaces Thin Films 40(3–4), 518–521 (2008)
Ewen, J.P., Gattinoni, C., Morgan, N., Spikes, H.A., Dini, D.: Nonequilibrium molecular dynamics simulations of organic friction modifiers adsorbed on iron oxide surfaces. Langmuir 32(18), 4450–4463 (2016)
Fillot, N., Berro, H., Vergne, P.: From continuous to molecular scale in modelling elastohydrodynamic lubrication: nanoscale surface slip effects on film thickness and friction. Tribol. Lett. 43, 257–266 (2011)
Acknowledgements
This research was conducted using the Fujitsu PRIMERGY CX400M1/CX2550M5 (Oakbridge-CX) at the Information Technology Center, The University of Tokyo. The first author greatly thanks the financial support from Chinese Scholarship Council (CSC). We acknowledge financial support from Japan Society for the Promotion of Science (JSPS) Grants-in-Aid for Scientific Research (KAKENHI) (Grant No. 22H00261). YU acknowledges financial support from JSPS KAKENHI (Grant No. 23H01295).
Funding
Open Access funding provided by The University of Tokyo. This research was funded by the Japan Society for the Promotion of Science (JSPS) through Grant-in-Aid for Scientific Research (KAKENHI) Program (Grant Nos. 22H00261 and 23H01295).
Author information
Authors and Affiliations
Contributions
Conceptualization, YU and AK; methodology, SD, YU, and AK; formal analysis and investigation, SD, YU, and AK; validation, SD, YU, and AK; writing—original draft preparation, SD; writing—review and editing, SD, YU, AK, YT, YS, and MM; visualization, SD; funding acquisition, YU, AK, and YT; resources, YU and AK; supervision, YU. All authors have read and agreed to the published version of the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no conflict of interest.
Ethical Approval
Not applicable.
Informed Consent
Not applicable.
Consent for Publication
Not applicable.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Deng, S., Kubo, A., Todaka, Y. et al. Coarse-Grained Molecular Dynamics Simulations of Nanoscale Roughness Effects on Oil Film Delamination. Tribol Lett 72, 73 (2024). https://doi.org/10.1007/s11249-024-01872-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11249-024-01872-2