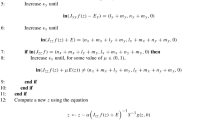Skip to main content
SpringerLink
Log in

Conservative Parametric Optimality and the Ridge Method for Tame Min-Max Problems

  • Published:
Set-Valued and Variational Analysis Aims and scope Submit manuscript

Abstract

We study the ridge method for min-max problems, and investigate its convergence without any convexity, differentiability or qualification assumption. The central issue is to determine whether the “parametric optimality formula” provides a conservative gradient, a notion of generalized derivative well suited for optimization. The answer to this question is positive in a semi-algebraic, and more generally definable, context. As a consequence, the ridge method applied to definable objectives is proved to have a minimizing behavior and to converge to a set of equilibria which satisfy an optimality condition. Definability is key to our proof: we show that for a more general class of nonsmooth functions, conservativity of the parametric optimality formula may fail, resulting in an absurd behavior of the ridge method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

We’re sorry, something doesn't seem to be working properly.

Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Similar content being viewed by others

References

  1. Ablin, P., Peyré, G., Moreau, T.: Super-efficiency of automatic differentiation for functions defined as a minimum. Presented at the (2020)

  2. Agrawal, A., Amos, B., Barratt, S., Boyd, S., Diamond, S., Kolter, Z. (2019). Differentiable convex optimization layers. Advances in neural information processing systems

  3. Aliprantis C.D., Border K.C. (2005) Infinite Dimensional Analysis (3rd edition) Springer

  4. Ambrosio L., Gigli N. and Savaré G. (2008). Gradient flows: in metric spaces and in the space of probability measures. Springer Science & Business Media

  5. Amos, B., Kolter, J. Z. (2017). Optnet: Differentiable optimization as a layer in neural networks. In International Conference on Machine Learning

  6. Arjovsky, Chintala, Bottou (2017). Wasserstein GAN. International Conference on Machine Learning

  7. Attouch, H., Bolte, J., Svaiter, B.F.: Convergence of descent methods for semi-algebraic and tame problems: proximal algorithms, forward-backward splitting, and regularized Gauss-Seidel methods. Mathematical Programming 137(1), 91–129 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  8. Benaïm, M., Hofbauer, J., Sorin, S.: Stochastic approximations and differential inclusions. SIAM Journal on Control and Optimization 44(1), 328–348 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  9. Bianchi, P., Hachem, W. and Schechtman, S. (2020). Convergence of constant step stochastic gradient descent for non-smooth non-convex functions. arXiv preprint arXiv:2005.08513

  10. Berthet, Q., Blondel, M., Teboul, O., Cuturi, M., Vert, J. P., Bach, F. (2020). Learning with differentiable perturbed optimizers. Advances in neural information processing systems

  11. Bertsekas D. P. (1971). Control of uncertain systems with a set-membership description of the uncertainty. Doctoral dissertation, Massachusetts Institute of Technology

  12. Bolte, J., Daniilidis, A., Lewis, A., Shiota, M.: Clarke subgradients of stratifiable functions. SIAM Journal on Optimization 18(2), 556–572 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  13. Bolte, J., Sabach, S., Teboulle, M.: Proximal alternating linearized minimization for nonconvex and nonsmooth problems. Mathematical Programming 146(1), 459–494 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  14. Bolte, J. and Pauwels, E. (2020). Conservative set valued fields, automatic differentiation, stochastic gradient methods and deep learning. Mathematical Programming

  15. Bolte, J. and Pauwels, E. (2020). A mathematical model for automatic differentiation in machine learning. Proceedings of the conference on neural information processing systems

  16. Borwein, J.M., Moors, W.B.: A chain rule for essentially smooth Lipschitz functions. SIAM Journal on Optimization 8(2), 300–308 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  17. Borwein, J., Moors, W., Wang, X.: Generalized subdifferentials: a Baire categorical approach. Transactions of the American Mathematical Society 353(10), 3875–3893 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  18. Borwein, J.M.: Generalisations, Examples, and Counter-examples in Analysis and Optimisation. Set-Valued and Variational Analysis 25(3), 467–479 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  19. C. Castera, J. Bolte, C. Févotte and E. Pauwels (2019). An inertial newton algorithm for deep learning. arXiv preprint http://arxiv.org/abs/1905.12278arXiv:1905.12278

  20. Clarke F. H. (1983). Optimization and nonsmooth analysis. Siam

  21. Coste, M.: An introduction to o-minimal geometry. RAAG notes, Institut de Recherche Mathématique de Rennes (1999)

    Google Scholar 

  22. Danskin, J.M.: The theory of max-min, with applications. SIAM Journal on Applied Mathematics 14(4), 641–664 (1966)

    Article  MathSciNet  MATH  Google Scholar 

  23. Davis D., Drusvyatskiy D., Kakade S., and Lee J. D. (2020). Stochastic subgradient method converges on tame functions, 20(1), 119-154. Foundations of Computational Mathematics

  24. Davis, D. and Drusvyatskiy, D. (2021). Conservative and semismooth derivatives are equivalent for semialgebraic maps. arXiv preprint http://arxiv.org/abs/2102.08484arXiv:2102.08484

  25. Dem’Yanov, V.F.: On the solution of several minimax problems. I. Cybernetics 2(6), 47–53 (1966)

    Article  Google Scholar 

  26. van den Dries, L., Miller, C.: Geometric categories and o-minimal structures. Duke Math. J 84(2), 497–540 (1996)

    MathSciNet  MATH  Google Scholar 

  27. Evans L. C. and Gariepy R. F. (2015). Measure theory and fine properties of functions. Revised Edition. Chapman and Hall/CRC

  28. Goodfellow, I.J., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., Courville, A., Bengio, Y. Generative adversarial nets. Advances in neural information processing systems

  29. Goodfellow, I. J., Shlens, J., Szegedy, C. (2015). Explaining and harnessing adversarial examples. International conference on learning representations

  30. Jin, C., Netrapalli, P. and Jordan, M. (2020). What is local optimality in nonconvex-nonconcave minimax optimization? In International Conference on Machine Learning (pp. 4880-4889). PMLR

  31. Kong, W. and Monteiro, R. D. (2019). An accelerated inexact proximal point method for solving nonconvex-concave min-max problems. arXiv preprint http://arxiv.org/abs/1905.13433arXiv:1905.13433

  32. Lewis, A., Tian, T.: The structure of conservative gradient fields. SIAM Journal on Optimization 31(3), 2080–2083 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  33. Lin, T., Jin, C. and Jordan, M. (2020). On gradient descent ascent for nonconvex-concave minimax problems. In International Conference on Machine Learning (pp. 6083-6093). PMLR

  34. Ostrovskii, D.M., Lowy, A., Razaviyayn, M.: Efficient search of first-order nash equilibria in nonconvex-concave smooth min-max problems. SIAM Journal on Optimization 31(4), 2508–2538 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  35. Rafique, H., Liu, M., Lin, Q. and Yang, T. (2021). Weakly-convex-concave min-max optimization: provable algorithms and applications in machine learning. Optimization Methods and Software, 1-35

  36. Rios-Zertuche R. (2020). Examples of pathological dynamics of the subgradient method for Lipschitz path-differentiable functions. arXiv preprint http://arxiv.org/abs/2007.11699arXiv:2007.11699

  37. Rockafellar, R.T.: Extensions of subgradient calculus with applications to optimization. Nonlinear Analysis: Theory, Methods & Applications 9(7), 665–698 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  38. Rockafellar R. T. and Wets R. J. B. (1998). Variational analysis (Vol. 317). Springer Science & Business Media

  39. H. Royden, P. Fitzpatrick (2010) Real Analysis Prentice Hall

  40. Szegedy, C., Zaremba, W., Sutskever, I., Bruna, J., Erhan, D., Goodfellow, I., Fergus, R. (2014). Intriguing properties of neural networks. International Conference on Learning Representations

  41. Thekumparampil, K. K., Jain, P., Netrapalli, P. and Oh, S. (2019). Efficient algorithms for smooth minimax optimization. arXiv preprint http://arxiv.org/abs/1907.01543arXiv:1907.01543

  42. Valadier, M.: Entraînement unilatéral, lignes de descente, fonctions lipschitziennes non pathologiques. Comptes rendus de l’Académie des Sciences 308, 241–244 (1989)

    MathSciNet  MATH  Google Scholar 

  43. Wang X. (1995). Pathological Lipschitz functions in \(\mathbb{R}_n\). Master Thesis, Simon Fraser University

  44. Wang Y. and Zhang G. and Ba J. (2020) On Solving Minimax Optimization Locally: A Follow-the-Ridge Approach International Conference on Learning Representations

  45. Whitney, H.: A function not constant on a connected set of critical points. Duke Mathematical Journal 1(4), 514–517 (1935)

    Article  MathSciNet  MATH  Google Scholar 

  46. Wilkie, A.J.: A theorem of the complement and some new o-minimal structures. Selecta Mathematica 5(4), 397–421 (1999)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The author would like to thank Jérôme Bolte and Rodolfo Rios-Zeruche for interesting discussions which helped putting this work together. The author acknowledge the support of ANR-3IA Artificial and Natural Intelligence Toulouse Institute under the grant agreement ANR-19-PI3A-0004, Air Force Office of Scientific Research, Air Force Material Command, USAF, under grant numbers FA9550-19-1-7026, FA8655-22-1-7012, and ANR MaSDOL - 19-CE23-0017-01.

Author information

Authors and Affiliations

  1. IRIT, Université de Toulouse, CNRS, Institut Universitaire de France (IUF), Toulouse, France

    Edouard Pauwels

Authors
  1. Edouard Pauwels
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Edouard Pauwels.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Pauwels, E. Conservative Parametric Optimality and the Ridge Method for Tame Min-Max Problems. Set-Valued Var. Anal 31, 19 (2023). https://doi.org/10.1007/s11228-023-00682-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11228-023-00682-3

Keywords

Search

Navigation