Introduction

In the current study, conventional hydrogen bonding has been investigated in two selected quinoline N-oxide derivatives in the gas phase and in the solid state using first-principle molecular dynamics [1] and metadynamics [2] methods. The motivation for this work is dictated by the fact that quinoline N-oxide derivatives contain short and strong intramolecular hydrogen bond, which is so-called resonance-assisted [3]. The dynamical nature of such kind of compounds has not been broadly investigated computationally; therefore, there is a lack of data concerning the hydrogen bridge dynamics at the ground state. Quinoline N-oxides exhibit excited state intramolecular proton transfer (ESIPT), which was an object of many studies, see, e.g., [4–6] and references therein.

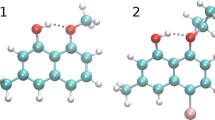
Knowing that quinoline derivatives are intensively investigated due to their potential practical applications in medicine and other branches of science, it could be of interest to examine their performance and perspective of chemical skeleton modification using steric and inductive effects. The excited state dynamics of intramolecular enol-keto proton-transfer tautomerism in 10-hydroxybenzoquinoline (HBQ) and its deuterated analog (DBQ) was studied by steady state absorption and fluorescence spectroscopy as well as computationally [4, 5]. On the basis of atoms in molecules (AIM) [7] and natural bond orbital (NBO) [8] theories, the excited state intramolecular proton transfer (ESIPT) was studied as well [6]. A series of quinoline/isoquinoline-pyrazole isomers was designed and synthesized, showing a system with five-membered intramolecular hydrogen bonding. As it was shown in the study, the similarity in molecular structure was not sufficient to predict the ESIPT effect in all investigated cases [9]. Some quinoline complexes with platinum were investigated theoretically as potential singlet oxygen photosensitizers in photodynamic therapy. The simulations were performed for the ground and excited states showing that the quinoline-based Pt(II) complexes with strong donor groups could be taken into account as potential candidates of novel photosensitizers in photodynamic therapy PDT of cancer [10]. Another study concerning potential application of quinoline derivatives in cancer therapy results with the development of highly active multidrug resistance (MDR) reversing drugs [11]. In quinoline derivatives, ESIPT effect is intensively studied, because it plays an important role in many photophysical processes and photochemical reactions. The electronic structure of the donor and acceptor molecules is reorganizing upon the electronic excitation, because of the charge distribution difference between the different electronic states [12]. The two quinoline N-oxides [8-hydroxyquinoline N-oxide (denoted as 1) and 2-carboxyquinoline N-oxide (denoted as 2)] chosen for the study are presented in Fig. 1, while their crystal unit cells are presented in the Figure S1 of the Online Resource [13, 14]. They possess two kinds of hydrogen bonding. The compound 1 known as 8HQNO exhibits biological activity—it is a bacterial inhibitor [15] and is a precursor of many antimalarial and cancer drugs [16]. The second compound (quinaldic acid N-oxide) contains very strong intramolecular hydrogen bond (2.435 Å) reported by Steiner et al. [14]. They found that the relevant hydrogen atoms are much closer to the acid than to the N-oxide oxygen atoms, so that the hydrogen bond is of the C–O–H···O–N type. The determined crystal structure showed that the compound is not planar. Moreover, according to Steiner [17], the compound is able to form intermolecular hydrogen bonds using present C–H and edge oxygen atoms. Stare et al. [18] performed IR measurements and density functional theory computations of the currently studied compound 1, as well as picolinic acid N-oxide and picolinic acid N-oxide derivatives. In both cases, a strong anharmonicity was found in the IR studies. The experimental findings were supported by the calculations in vacuo and with solvent reaction field (PCM) model, which have been in pretty good agreement with the experimental findings. However, hydrogen bond features and free energy profiles were not studied using dynamical models.

Fig. 1
figure 1

Structures of the investigated compounds: 8-hydroxyquinoline N-oxide (1) and 2-carboxyquinoline N-oxide (quinaldic acid N-oxide, 2)

Full size image

Car–Parrinello molecular dynamics (CPMD) [1] was applied to investigate the dynamical nature of the quinoline derivatives with special attention paid to the intramolecular hydrogen bonding features. The use of CPMD provides access to the dynamical description of the system on a DFT potential energy surface; this reveals details that cannot be seen in the static description [19]. However, by itself the CPMD uses approximation of classical nuclei (i.e., Newtonian dynamics)—see the Conclusions and perspectives section for a discussion on procedures going beyond that approximation. Further, the CPMD approach was used to probe vibrational dynamics of the bridge proton and C–O and N–O bonds by means of their contribution to the power spectra of atomic velocity. The signature of the bridge proton mobility and its strength is an absorption region in the IR spectrum. The free energy profile was computed on the basis of unconstrained CPMD runs as well as metadynamics method by Laio and Parrinello [2]. The organization of the paper is as follows: in section II, the applied computational methods are presented; section III contains results and discussion, whereas the final conclusions are given in the last paragraph.

Computational methods

First-principle simulations in vacuo and in the crystalline phase

First-principle molecular dynamics within the framework of Car–Parrinello (CPMD) [1] was performed for two quinoline N-oxide derivatives: 8-hydroxyquinoline N-oxide (1) and 2-carboxyquinoline N-oxide (2) [13, 14]. The models used for CPMD computations are presented in Figure S1 of the Online Resource. The simulations were carried out in vacuo and in the crystalline phase. The time-evolution simulations were employed to investigate the metric, vibrational, and energetic features of the two compounds. A special attention was paid to the intramolecular hydrogen bond properties derived from the fact that compound 1 is a derivative of quinoline N-oxide, but to be more precise, the compound 2 is a derivative of quinaldic acid N-oxide; therefore, the intramolecular hydrogen bonds have a different chemical origin. Initially, the geometry optimization was performed using the initial Hessian matrix proposed by Schlegel [20] in both phases to generate suitable conditions for the CPMD runs. The exchange correlation functional by Perdew, Burke, and Ernzerhof (PBE) [21] coupled with the plane-wave basis set was employed. A kinetic energy cutoff of 95 Ry was used for both compounds throughout the simulations. The kinetic energy cutoff value was chosen after tests performed for the compound 1 in the solid state (the plane waves are naturally suited for the use in periodic simulations, isolated systems need removal of periodic images, and this introduces additional artifacts—therefore the tests were performed only for the solid-state case). The tested cutoff value range was from 60 Ry up to 100 Ry. In addition, the geometry minimization was performed with Γ-point approximation (i.e., using only Bloch eigenfunctions with zero reciprocal vector k to represent the periodic states in the crystal) in the crystalline phase [22]. The pseudopotentials of N. Troullier and J. L. Martins [23] were used for all atoms in the investigated molecules.

Car–Parrinello molecular dynamics (CPMD) protocol in vacuo

Gas-phase molecular dynamics was performed in a cubic cell of a = 16 Å for compounds 1 and 2, respectively. The Hockney’s [24] scheme was applied to remove interactions with periodic images of the cell. The simulations were performed at 298 K. A Nosé–Hoover thermostat was applied to control the assigned conditions [25–27] for both compounds. The fictitious electron mass was set to 400 au. The time-step value was 3 au in both cases. The energy cutoff of 95 Ry was used. The mentioned above PBE functional and pseudopotentials were applied for the MD simulations as well. The CPMD runs were divided into two protocols: (I) using a classical one and (II) with inclusion of dispersion corrections (Grimme’s DFT-D2 method) [28]. Initially, the simulated models were equilibrated until a thermal equilibration was obtained (ca. 0.5 ps), and the trajectories were further collected for ca. 12 ps.

Crystalline phase CPMD simulations protocol

The solid-state models (see Figure S1) were constructed on the basis of available experimental X-ray data [13, 14]. The experimental monoclinic unit cell with a = 12.1364 Å, b = 4.9211 Å, c = 13.1384 Å, β = 109.26° for the 8-hydroxyquinoline N-oxide (1) was used for the simulations. In the case of 2-carboxyquinoline N-oxide (2), the experimental unit cell (monoclinic, a = 3.821 Å, b = 16.2406 Å, c = 13.062 Å, β = 91.010°) was extended by 5 % in the “a” direction (the correctness of this approach was confirmed by stress tensor monitoring during the MD run), and subsequently, a 2 × 1 × 1 supercell was constructed. Periodic boundary conditions (PBCs) were employed for the solid-state simulations, and the real space Ewald summation of electrostatic interactions was carried out by taking into consideration eight cell replicas in each direction. As it is described above, the simulation cells are relatively large and we mostly focus on strong, internal interactions. Therefore, our previous tests support the use of Γ-point approximation and the eight neighbors in the CPMD calculations. Following the gas-phase computational setup, the fictitious electron mass of 400 au, the time step of 3 au, and the cutoff of 95 Ry were employed to simulate both crystals. The simulations were carried out at 298 K controlled using the Nosé–Hoover thermostat. The solid-state models were equilibrated, and later the trajectories with data production were collected. The last part of the study contains solid-state simulations for both crystals with dispersion correction—Grimme’s DFT-D2 method [28]. The data were collected for 12 ps in the case of both N-oxides during all performed simulations. The trajectories served to obtain histograms (probability distributions) of variables of interest, from which the free energy profiles were derived.

Metadynamics simulations

Reproduction of free energy surfaces from unconstrained MD suffers from poor statistics of rare events. For this reason, we have used metadynamics in the Lagrangian formulation with accumulation of Gaussian-like hills [2, 29] to obtain the free energy maps for the motion of the bridged protons in the intramolecular HBs of 1 and 2 in the gas phase. The underlying electronic structure framework was the Car–Parrinello MD (for the setup details see the section on the CPMD in vacuo above); 150,000 CPMD steps were employed, and a placement of a new Gaussian-like hill in the potential energy of the system (in the Gaussian tube formalism, the hill height was 0.0005 au) took place between every 100–200 MD steps (depending on the movement of the collective variables, CVs). The initial velocities of the CVs were initialized to give the temperature of 298 K, and velocity rescaling algorithm was used to maintain these conditions for the CVs. Several choices of the CVs were tested, and the most successful results were obtained with a two-dimensional CV space consisting of r(OH) and r(H···O).

All plane-wave computations were performed using the CPMDv3.15.3 program [30]. The post-processing analyses were carried out using the VMD program [31], tools available from the CPMD Web site (www.cpmd.org) as well as using homemade scripts. The graphical presentation of the results was prepared within the framework of the VMD and Gnuplot [32] programs.

Results and discussion

Simulations in vacuo

Using the CPMD approach, the time evolution of the interatomic distances and spectroscopic features were investigated on the basis of simulated gas-phase trajectories. The interatomic distances involved in the intramolecular hydrogen bond formation were analyzed, and the obtained results are presented in Fig. 2 and Figure S2. As it is shown in Figure S2, for both compounds the bridged proton is localized most of the time on the donor side. The proton-transfer phenomenon does not occur during the simulations timescale in the ground state, but for the compound 1, short contacts with the acceptor side were noticed (e.g., it occurred ca. after 1.8 ps; see the left, upper graph in Figure S2). In both cases, the bridged proton exhibits a high mobility. According to the X-ray data, the investigated hydrogen bonds are classified as strong and short with O…O interatomic distance of 2.477 Å for 1 [13] and 2.435 Å for 2 [14]. Therefore, looking only at structural parameters, one can expect a spontaneous proton transfer in the ground state, but according to Lewis theory of acids and bases, the neighborhood of the acceptor atom should be modified accordingly by introduction of inductive effects. The 2D maps of O–H and O…O interatomic distances are presented in Fig. 2. Using the 2D presentation of the data, the idea was to show the contribution of the weak interactions. As it is shown, the computations of 1 with Grimme’s method [28] provide slight changes in the overall picture of the interatomic distances time evolution. The inclusion of dispersion correction resulted with a slight shortening of the O···O interatomic distance, whereas the O–H bond length changes were reproduced similarly in both simulations. Slightly different results were obtained for 2. It is visible (see Fig. 2, lower part, right graph) that the dispersion effects influenced the intramolecular hydrogen bond. The O···O distance was shortened, but the O–H bond length was elongated comparing to the results obtained for CPMD without dispersion corrections. At this point, it is worth to discuss the differences between hydrogen bonds present in the studied quinoline N-oxides. The compound 1 possesses hydrogen bonding attached to the atoms belonging to the phenyl and pyridine rings; therefore, it has a limited flexibility and it is nonlinear as it was confirmed experimentally [13]. The formed quasi-ring is rather planar. Moreover, the chemical composition of the molecule restricts the O···O interatomic distance fluctuations. 2-Carboxyquinoline N-oxide (2) is a derivative of quinaldinic acid N-oxide; therefore, the quasi-ring was formed between the N → O moiety and the carboxylic group. The chemical constitution of the quasi-ring and the HB location enables some spatial structure fluctuations, which have been reproduced by the CPMD simulations.

Fig. 2
figure 2

Joint probability density for the O–H and O···O distances from the gas-phase simulations of 8-hydroxyquinoline N-oxide (1) and 2-carboxyquinoline N-oxide (2) within classical nuclear dynamics (FPMD) (left) and within inclusion of dispersion effects (right). Probability density isocontours: inner—15 Å−2; outer—5 Å−2

Full size image

The spectroscopic properties of the two quinoline N-oxides were analyzed using a well-established approach, which is the power spectra of atomic velocity [33]. An important advantage of this method is the possibility to investigate particular motions (modes) by projecting atomic velocities onto specific vectors, planes, and so forth. The power spectra of 1 and 2 are presented in Figs. 3, S3 and S4, and they show both the all-atom and bridge hydrogen atom contributions. The bridged proton of 1 in the power spectrum (see Fig. 3, upper part) shows two regions of signal: ca. 880–1600 and 2550–2900 cm−1. The second region corresponds to the OH stretching, and the maximal power density was found at 2700 cm−1. The bridge proton power spectrum of 2 (see Fig. 3, lower part) exhibits signals in three regions: ca. 800–1100, 1400–1500 and 2500–2760 cm−1. The latter corresponds to the OH stretching, and most of the power density is located between ca. 2620 to 2760 cm−1. The bridge proton contribution is visible in the total atomic velocity power spectra concerning both compounds especially in regions with high frequencies. A different situation was observed for regions with lower wavenumbers partially due to overlap with other modes. As it is shown, the dispersion effects did not affect significantly the overall vibrational properties of the studied molecules. Their effect is visible for both compounds especially in the OH stretching region, but the impact of the dispersion corrections is opposite in the studied cases of 1 and 2. For more detailed insight into spectroscopic properties, the contribution of the bridge proton to the power spectrum was calculated with inclusion of dispersion effects. Figure S3 shows the superposition of the power spectra of all atoms with and without dispersion effect. In the case of 1, similarly to the above discussed results, two main regions are observed: ca. 840–1600 and 2400–3000 cm−1. Dziembowska et al. reported on IR spectra for the 8-hydroxyquinoline N-oxide (1) measured in Nujol at 300 and 14 K [34]. They detected the OH stretching region from 1800 to 3000 cm−1 and confirmed its presence with deuteration: the broad absorption for νOD moved to 2050–1750 cm−1. The experimental νOH and νOD band centers were assigned at 2330 and 1835 cm−1, respectively. Hansen and Spanget-Larsen [35] measured data for 1 in KBr tablets. According to them, the IR spectra of 1 are characterized by broad absorption from 2000 to 3000 cm−1. They claim that the OH stretching region is located from 2700 to 2900 cm−1. These results are in good agreement with our CPMD simulations, especially when one takes into account the use of classical (Newtonian) nuclear dynamics.

Fig. 3
figure 3

Fourier transforms of the atomic velocity autocorrelation function for the studied 8-hydroxyquinoline N-oxide (1) and 2-carboxyquinoline N-oxide (2). The results obtained from FPMD run in the gas phase. Upper line in each graph—all-atom power spectrum; lower line—the contribution of the bridge proton

Full size image

In the case of 2, the dispersion effects are also visible in the power spectra (see Figure S4, lower part). The bridge proton spectrum is divided into two main regions: 850–1680 and 2350–3100 cm−1. The experimental data were measured in hexachlorobutadiene, CHCl3 and in the Nujol mull [36]. The data obtained in the CHCl3 solvent could be used for the direct comparison of the experimental and computationally obtained wavenumbers, because the solvent is nonpolar and we can approximate there is no interaction between the solute and solvent molecules. The experimentally obtained regions of the OH stretching are: in hexachlorobutadiene—2000–2800 cm−1; in CHCl3—2100–2900 cm−1; and in the Nujol mull 2000–2800 cm−1. The calculated frequencies are always redshifted (ca. ~100 cm−1) due to the presence of various effects, e.g., DFT functional, finite cutoff and finally the Car–Parrinello “drag effect” inherent to the Car–Parrinello scheme [37]. Concluding the spectroscopic features, computations in the gas phase, for both compounds the dispersion effects, are visible in the power spectra by shifting the wavenumbers depending on the kind of bonding. The absorption region of the OH stretching is broad in the experimental data as well as in the computations and significantly redshifted with respect to the free OH (3500–3700 cm−1).This fact allows us to make a conclusion of the strength of the intramolecular HB, which in both cases is classified as short and strong. However, more recent measurement of the IR spectrum of 2 in CDCl3 [18] assigns the OH band to a sharp feature at ca. 1500 cm−1 (see Fig. 6C of [18]). In our simulation, such a band is present at 1450 cm−1, and its intensity (note: not corresponding to the observable IR intensity) is larger than that of the broader 2350–3100 cm−1 feature. The calculated vibrational features of 2 are even more interesting in the solid state—see the next section.

The free energy profiles for the proton motion resulting from the unconstrained CPMD runs are shown in Figs. 4 (one-dimensional) and 5 (two-dimensional). The gas-phase 1D profiles do not show dramatic differences between compounds 1 and 2; however, the potential well for 2 is less steep, which corresponds to slightly larger flexibility of the proton. This is well supported by the 2D results, which show that the classical oval shape of the potential energy surface is elongated for 2 (Fig. 5).

Fig. 4
figure 4

Free energy profiles for proton motion in the O–H···O hydrogen bridges in the studied compounds 1 and 2 computed for the gas phase and solid state. The proton-transfer (PT) coordinate on the horizontal axis is defined as r(A-H)–r(D-H), where D is the donor atom and A is the acceptor atom

Full size image
Fig. 5
figure 5

Two-dimensional free energy surfaces for proton motion in the O–H···O hydrogen bridges in the studied compounds 1 and 2. The color scale represents free energy values, in kcal/mol. The proton-transfer (PT) coordinate on the horizontal axis is defined as r(A-H)–r(D-H); the vertical axis represents the D···A distance, where D is the donor atom and A is the acceptor atom

Full size image

Crystalline phase simulations

This part of the section has been devoted to results and data analysis of CPMD simulations in the solid state. The models applied for the simulations are presented in Figure S1. The crystalline phase simulations allow us to discuss various effects, e.g., related to the crystal packing forces and their influence on the molecular features of the studied quinoline N-oxide derivatives. The graphical presentation of the propagation of the interatomic distances of hydrogen bonding is given in Figs. 6 and S2, respectively. The presented data were obtained without and with Grimme’s correction. Let us start the data analysis from the Figure S2 where the time evolution of interatomic distances of O···O, H···O and O–H are presented. The proton-transfer phenomenon does not occur in the case of both compounds. In 8-hydroxyquinoline N-oxide (1), the bridge proton is defined on the donor side. In the timescale of 12 ps, we observed only one short contact (after ca. 7.5 ps run) with the acceptor atom. Comparing the analysis of the interatomic distances time evolution for 1, it is visible that the behavior of the bridged proton is similar in both phases. In Fig. 6, the O–H versus O···O is presented. As it is shown, the dispersion effects are more visible in the solid state comparing with the gas-phase results. A slight shortening of the O···O (right upper panel in Fig. 6) comparing with the CPMD results obtained without inclusion of the dispersion and an elongation of the O–H bond length were observed. In the crystal unit cell, many short contacts between molecules were noticed [13]. The fact tentatively supports our computational findings in the crystalline phase where the dispersion effects are still subtle, but stronger than in the gas phase. Here, the crystal electric field contribution plays a secondary role, in the case of the hydrogen bridge atoms, because obtained results are very similar for both phases. In the compound 2, during the 12 ps of the CPMD run many short contacts with the acceptor side were noticed (see Figure S2 lower, right panel). The proton is localized mostly on the donor side, but it is more labile comparing to the bridged proton of 1. Here, the chemical character of the donor atom is different (the bridged proton derived from the OH group which is a part of the carboxylic group) and its properties are controlled by the overall acidity exhibited by the carboxylic group formation. Figure 6 provides a graphical presentation of O–H versus O···O distances calculated with and without Grimme’s correction. As it is shown, the dispersion effects influenced the crystalline phase results. When one compares these results with those obtained in the gas phase, one can easily see that the contribution of dispersion to the overall analysis of the interatomic distances time evolution cannot be neglected. The dispersion effects made the bridged proton more delocalized, which is shown by the O–H bond elongation, as depicted in Fig. 6 (right, lower panel).

Fig. 6
figure 6

Joint probability density for the O–H and O…O distances from the solid-state simulations of 8-hydroxyquinoline N-oxide (1) and 2-carboxyquinoline N-oxide (2) within classical nuclear dynamics (FPMD) (left) and within inclusion of dispersion effects (right). Probability density isocontours: inner—15 Å−2; outer—5 Å−2

Full size image

The classical fingerprint method in the H bond investigations is vibrational IR spectroscopy. Following available experimental data, we reconstructed the IR spectra of the studied quinoline derivatives on the basis of the Fourier transforms of atomic velocity autocorrelation function. The calculated spectra are presented in Figs. 7, S5 and S6. The figures present spectra of all atoms as well as only of the bridge proton. In addition, the influence of the dispersion on the obtained wavenumbers is shown. In agreement with the experimental data [38] predicting the O–H to be centered in the region 2900–2700 cm−1, the calculated spectrum of 1 has shown a broad adsorption and the OH stretching region was found from 2450 to 2800 cm−1. As shown in Figures S5 and S6, the presence of dispersion effects did not affect significantly the obtained wavenumbers. Therefore, we can conclude that the dispersion effects are very subtle in the case of 1 and the lack of their reproduction during the simulations does not affect the obtained results. The spectroscopic data computed for 2 provide a very broad OH region absorption. The obtained spectrum of the bridge proton (see lower graph in Fig. 7) shows one region which could be separated: from 850 to 2600 cm−1. The computed results can be directly compared only with those obtained in the Nujol mull [36]. The experimentally measured OH stretching region was reported to be from 2000 to 2800 cm−1. In the case of the computed spectrum, the OH stretching region was found from 1780 to 2800 cm−1. However, the CDCl3 solution of 2 has IR spectrum very similar to the one calculated in the solid state: a distinct feature centered at 1500 cm−1. The very broad and shallow feature of our calculated spectrum, reaching as far as 2600 cm−1, is not present in Fig. 6c of [18]—the difference in this region between the normal and deuterated sample is too small to be recognized as a part of the OH feature. This calls for further studies, possibly with the use of more complicated nuclear quantum treatment. As shown in Figure S5, the introduction of the dispersion correction did not provide significant quantitative changes. However, every time when it is possible, all effects should be taken into account, because it is not easy to detect a priori the cases in which they cannot be neglected [39]. Therefore, it is important to stress that further development of DFT and ab initio time-evolution methods is necessary to provide solutions to describe weak interactions. It was extremely important to be able to reproduce and check the weak interactions influence on molecular features in the crystalline phase for the studied quinoline N-oxide derivatives knowing of many intermolecular interactions present in the crystal cells. This part of the study has shown that still the intramolecular interaction is able to shield other possible weaker interactions.

Fig. 7
figure 7

Fourier transforms of the atomic velocity autocorrelation function for 8-hydroxyquinoline N-oxide (1) and 2-carboxyquinoline N-oxide (2). The results obtained from FPMD run in the solid state. Upper line in each graph—all-atom power spectrum; lower line—the contribution of the bridge proton

Full size image

Figure 8 presents contributions of two selected bond types, namely N-oxide N–O and phenolic or carboxylic C–O/C=O, to the total atomic velocity power spectrum of 1 and 2 in the gas phase and solid state, for calculations with dispersion correction. The technique of projecting the N and O atomic velocities onto the direction of the N–O bond reduces the impact of other modes, but does not provide “clean” stretching wavenumbers. For the N–O bond, it is known from experiment [40] and DFT calculations [34] that its stretching mode in variously substituted quinoline N-oxides lies between 1190 and 1233 cm−1. The CPMD results indicate strong contributions at 1150 cm−1 for 1 and 1140 cm−1 for 2. This redshift is associated with the unusual electronic structure of the N–O bond, leading to stronger than expected anharmonicity and lowering of the stretching frequency within the Car–Parrinello scheme. On the other hand, there is a strong mode at 1300–1310 cm−1, which was experimentally described as vibrational motion mainly involving the C–N bond [40]. The same picture follows from the potential energy distribution study based on the DFT results [34] and our analysis. The C–N motion involves large part of the pyridine ring moiety, and its motion is strongly modifying the instantaneous N–O vector. Hence, its presence in the N–O contribution is shown in Fig. 8. It is also visible that the solid-state inner electrostatic field has only moderate influence on the N–O stretching. Finally, we note that the C–O stretching wavenumbers are typical of the phenolic C–O for 1 (1230 cm−1) and carboxylic C–O for 2 (1090, 1170, 1290 cm−1—here the admixture of other oscillators is visible, as for the N–O), indicating that the CPMD scheme correctly reproduces the behavior of this bond. It is also true for the C=O in 2 (1660 cm−1), which is the least coupled to other oscillators. The above-mentioned couplings follow from the classical approach to the nuclear motion, on which the CPMD is based.

Fig. 8
figure 8

Contributions of the N–O and C–O bonds to the atomic velocity power spectra of compounds 1 and 2. The results obtained from FPMD run in the gas phase with Grimme’s dispersion corrections

Full size image

The free energy profiles for the proton motion resulting from the unconstrained CPMD runs are summarized in Figs. 5 and 6. The figures allow for a quick comparison between the gas-phase and solid-state behavior. It is visible that the crystal electrostatic field leads to softening of the potential well, which is stronger in case of the compound 2. It even leads to a plateau close to the “shared proton” location (PT coordinate close to 0). However, errors of statistical sampling are visible (undulations of the 1D curve); therefore, we proceeded with metadynamics simulation, which belongs to methods of enhanced sampling of the free energy surfaces.

Metadynamics in the gas phase

Metadynamics [2] was devised as a method of reproduction of free energy surfaces by extended sampling of the phase space, allowing for escaping the local energetic minima. Thus, it is a method a level of abstraction higher than the CPMD, i.e., metadynamics can be in principle run using any other MD scheme (classical MD, Born–Oppenheimer MD) as the underlying force field and method to propagate the nuclear positions. Metadynamics traces the trajectory of the chosen collective variables, introduces history-dependent potential terms to the system, and uses this history to recover free energy profiles. This way, the maps in Fig. 9, corresponds to the free energy surfaces. An inclusion of statistical effects means that structural fluctuations (e.g., donor–acceptor distance variations, vibrations of the aromatic rings) are properly taken care of. The chosen representative variables are r(OH) and r(H···O), that is donor-proton and proton-acceptor distances. Filling the potential well for the indicated collective variables is not straightforward, because the inflow of the artificial potential energy (on which the metadynamics is based) can easily result in rotation of the O–H bond in 1 and 2, or rotation of the whole carboxylic group in 2. The trajectories with such events were disregarded from further analysis; however, the presence of an additional degree of freedom in the system for 2 (the rotation of the carboxylic group as a whole) led to the broadening of the region close to minimum and shift of the minimum to lower O–H distances. It is also probably responsible for broadening and splitting the minimum in case of 2 into several centers connected by low energy regions. The data shown in Fig. 9 reveal that the rare events of short-lived proton movement into the acceptor zone are associated with free energy loss of ca. 6–8 kcal/mol, while the bottom of the well is located 14 kcal/mol below the surface for 1 and 16 kcal/mol for 2. Comparing this with energy scale of Fig. 4, one can appreciate that the CPMD simulation itself explores the free energy landscape to a smaller extent, and investigation of processes with larger barriers is best achieved using “enhanced sampling” schemes, such as metadynamics. On the other hand, metadynamics is more difficult to control because of additional dynamical degrees of freedom connected with collective variables, and artificial introduction of potential energy. The latter can dissipate along unwanted channels and lead to side reactions; we mentioned already the cases of rotations of hydroxyl or carboxyl groups connected with breaking of the hydrogen bond.

Fig. 9
figure 9

Free energy surfaces reproduced by the CPMD-based metadynamics simulations in the gas phase. Compound 1—top graph, compound 2—bottom graph

Full size image

Conclusions and perspectives

Two-phase simulations provided a description of dynamical nature of intramolecular hydrogen bridges present in the studied quinoline N-oxides. It was shown that during the simulation time, more short contacts were observed for 2 in the crystalline phase comparing with 1. These data are in agreement with our findings related to the kind of the intramolecular interaction and reduced flexibility of the hydrogen bridge in the case of 1. The computed spectra are in good agreement with the experimental IR data available. Some observed discrepancies are associated with the CPMD drag effects, which are well known in the literature. Inclusion of dispersion according to the Grimme’s formulation led only to small, but visible changes in the structural features of the systems. The free energy landscapes (1D and 2D) based on unconstrained CPMD runs suggest variations of proton flexibility, but can suffer from inaccurate statistical sampling. The application of metadynamics provided an accurate picture of the free energy profile. CPMD approach revealed a large structural flexibility of the hydrogen bond in the compound 2. Moreover, it is worth noticing that the crystal field has a significant influence on the hydrogen bridge dynamics in the studied cases. As an extension of the current study, the excited state dynamics could be of interest on the basis of surface hoping method. Another issue worth discussing is an influence of the nuclear motion quantization on the hydrogen bridge dynamics. It is well known that these effects are observable in spectroscopic behavior of strongly anharmonic systems with shallow potential energy surfaces. The fully quantum treatment of the system, including nuclei, is equivalent to the real nature of the molecule as found experimentally, with such phenomena as tunneling and Fermi resonances. However, it is not yet routinely possible. Many approximate treatments are known, such as path integral molecular dynamics (PIMD) coupled with CPMD, or methods to quantize a selected part of the system, e.g., proton motions in the hydrogen bridge. One of the recent examples of studies using the PIMD approach [19] shows impact of nuclear quantum effects on free energy profiles for proton transfer in double hydrogen bridges found in the crystal structure of KHCO3. A recent study on oxalic acid [41] shows the use of the latter methodology, based on quantization of a selected vibrational mode with the help of snapshots taken from the CPMD trajectory. This methodology evolved from 1D formulation [42, 43] into a two-dimensional version capable of reproduction of free energy [44] and vibrational features [45] of strongly anharmonic hydrogen-bonded systems. Further development of such methods is a path that must be necessarily followed in the quest for the most exact description of microscale behavior of chemical and biochemical species in various phases.