1 Introduction

Penalized splines are flexible and popular tools for estimating unknown smooth functions. They have been applied in many statistical modeling frameworks, including generalized additive models (Spiegel et al. 2019; Cao 2012), single-index models (Wang et al. 2018), functional single-index models (Jiang et al. 2020), generalized partially linear single-index models (Yu et al. 2017), functional mixed-effects models (Chen et al. 2018; Cao and Ramsay 2010; Liu et al. 2017), survival models (Orbe and Virto 2021; Bremhorst and Lambert 2016), trajectory modeling for longitudinal data (Koehler et al. 2017; Andrinopoulou et al. 2018; Nie et al. 2022), additive quantile regression models (Muggeo et al. 2021; Sang and Cao 2020), varying coefficient models (Hendrickx et al. 2018), quantile varying coefficient models (Gijbels et al. 2018), spatiotemporal models (Minguez et al. 2020; Goicoa et al. 2019), spatiotemporal quantile and expectile regression models (Franco-Villoria et al. 2019; Spiegel et al. 2020).

To explain the fundamental idea of a penalized spline, consider the following smoothing model for observations \((x_i, y_i)\), \(i = 1, \ldots , n\):

$$\begin{aligned} y_i = f(x_i) + e_i, \quad e_i \overset{\text {iid}}{\sim } \text {N}(0, \sigma ^2). \end{aligned}$$

After expressing \(f(x) = \sum _{j = 1}^{p}{\mathcal {B}}_j(x)\beta _j\) with some spline basis \({\mathcal {B}}_j(x)\), \(j = 1, \ldots , p\), we estimate basis coefficients \(\varvec{\beta } = (\beta _1, \beta _2, \ldots , \beta _p)^{\scriptscriptstyle \text {T}}\) by minimizing the penalized least squares (PLS) objective:

$$\begin{aligned} \Vert \varvec{y} - \varvec{B\beta }\Vert ^2 + \text {e}^{\rho }\varvec{\beta }^{\scriptscriptstyle \text {T}}\varvec{S}\varvec{\beta }. \end{aligned}$$
(1)

The first term is the least squares, where \(\varvec{y} = (y_1, y_2, \ldots , y_n)^{\scriptscriptstyle \text {T}}\) and \(\varvec{B}\) is a design matrix whose (i, j)th entry is \({\mathcal {B}}_j(x_i)\). The second term is the penalty, where \(\varvec{S}\) is a penalty matrix (such that \(\varvec{\beta }^{\scriptscriptstyle \text {T}}\varvec{S}\varvec{\beta }\) is a wiggliness measure for f) and \(\rho \in (-\infty , +\infty )\) is a smoothing parameter controlling the strength of the penalization. The choice of \(\rho \) is critical, as it trades off f’s closeness to data for f’s smoothness. The best \(\rho \) value often optimizes a smoothness selection criterion, like generalized cross-validation error (GCV) (Wahba 1990) and restricted likelihood (REML) (Wood 2017). Many strategies can be applied to this optimization task. However, to correctly identify the global optimum rather than being trapped in a local optimum, grid search is recommended. Specifically, we attempt an equidistant grid of \(\rho \) values in a search interval \([\rho _{\min }, \rho _{\max }]\) and pick the one that minimizes GCV or maximizes REML.

To illustrate that a criterion can have multiple local optima, and mistaking a local optimum for the global optimum may give undesirable result, consider smoothing daily new deaths attributed to COVID-19 in Finland from 2020-09-01 to 2022-03-01 and daily new confirmed cases of COVID-19 in Netherlands from 2021-09-01 to 2022-03-01 (data source: Our World in Data (Ritchie et al. 2020)). Figure 1 shows that the GCV (against \(\rho \)) in each example has a local minimum and a global minimum. The fitted spline corresponding to the local minimum is very wiggly, especially for Finland. Instead, the fit corresponding to the global minimum is smoother and more plausible; for example, it reasonably depicts the single peak during the first Omicron wave in Netherlands. In both cases, minimizing GCV via gradient descent or Newton’s method can be trapped in the local minimum, if the initial guess for \(\rho \) is in its neighborhood. By contrast, doing a grid search in \([-6, 5]\) guarantees that the global minimum can be found.

Fig. 1
figure 1

Daily COVID-19 data smoothing. Left column: new deaths in Finland from 2020-09-01 to 2022-03-01; Right column: new cases in Netherlands from 2021-09-01 to 2022-03-01. The first row shows that GCV has a local minimum (red) and a global minimum (blue). The second row shows that the fitted spline corresponding to the local minimum is wiggly. The last row shows that the fit corresponding to the global minimum is smoother and more plausible. (Color figure online)

Full size image

In general, to successfully identify the global optimum of a criterion function in grid search, the search interval \([\rho _{\min }, \rho _{\max }]\) must be sufficiently wide so that the criterion can be fully explored. Unfortunately, no guideline is available for pre-specifying this interval, so practitioners have to find it by trial and error. This inevitably causes two problems. First of all, the PLS problem (1) is not numerically solvable when \(\rho \) is too large, because the limiting linear system for \(\varvec{\beta }\) is rank-deficient. A \(\rho \) value too small triggers the same problem if \(p > n\), because the limiting unpenalized regression spline problem has no unique solution. As a result, practitioners do not even know what \(\rho \) range is numerically safe to attempt. Secondly, a PLS solver is often a computational kernel for more advanced smoothing problems, like robust smoothing with M-estimators (Dreassi et al. 2014; Osorio 2016) and backfitting-based generalized additive models (Eilers and Marx 2002; Oliveira and Paula 2021; Hernando Vanegas and Paula 2016). In these problems, a PLS needs be solved at each iteration for reweighted data, and it is more difficult to pre-specify a search interval because it changes from iteration to iteration.

To address these issues, we develop algorithms that automatically find a suitable \([\rho _{\min }, \rho _{\max }]\) for the grid search. Our automatic search interval has four advantages. (i) It gives a safe \(\rho \) range where the PLS problem (1) is numerically solvable. (ii) It is criterion-independent so that different smoothness selection criteria, including GCV and REML, can be explored on the same \(\rho \) range. (iii) It is wide enough to contain the global optimum of any selection criterion, such as the global minimum of GCV and the global maximum of REML. (iv) It is computationally cheap compared with the grid search itself, carrying no extra cost in practice.

We will introduce our method using penalized B-splines, because it is particularly challenging to develop algorithms for this class of penalized splines to achieve (iv). We will describe how to adapt our method for other types of penalized splines at the end of this paper. Our method is ready to use via our R package gps (\(\ge \) version 1.1) (Li and Cao 2022b). It may be embedded in more advanced statistical modeling methods that rely on penalized splines.

The rest of this paper is organized as follows: Sect. 2 introduces penalized B-splines and their estimation for any trial \(\rho \) value. Section 3 derives, discusses and illustrates several search intervals for \(\rho \). Section 4 conducts simulations for these intervals. Section 5 applies our search interval to practical smoothing by revisiting the COVID-19 example, with a comparison between GCV and REML in smoothness selection. The last section summarizes our method and addresses reviewers’ concerns. Our R code is available on the internet at https://github.com/ZheyuanLi/gps-vignettes/blob/main/gps2.pdf.

2 Penalized B-splines

There exists a wide variety of penalized splines, depending on the setup of basis and penalty. If we choose the basis functions \({\mathcal {B}}_j(x)\), \(j = 1, \ldots , p\) to be B-splines (de Boor 2001) and accompany them by either a difference penalty or a derivative penalty, we arrive at a particular class of penalized splines: the penalized B-splines family. This family has three members: O-splines (O’Sullivan 1986), standard P-splines (Eilers and Marx 1996) and general P-splines (Li and Cao 2022a); see the last reference for a good overview of this family. For this family, the matrix \(\varvec{S}\) in (1) can be induced by \(\varvec{S} = \varvec{D}_m^{\scriptscriptstyle \text {T}}\varvec{D}_m\). Therefore, the PLS objective can be expressed as:

$$\begin{aligned} \Vert \varvec{y} - \varvec{B\beta }\Vert ^2 + \text {e}^{\rho }\Vert \varvec{D}_m\varvec{\beta }\Vert ^2. \end{aligned}$$
(2)

In this context, \(\varvec{B}\) is an \(n \times p\) design matrix for B-splines of order \(d \ge 2\), and \(\varvec{D}_m\) is a \((p - m) \times p\) penalty matrix of order \(1 \le m \le d - 1\). Basically, the three family members only differ in (i) the type of knots for constructing B-splines; (ii) the penalty matrix \(\varvec{D}_m\) applied to B-spline coefficients \(\varvec{\beta }\). See Appendix A for concrete examples.

When estimating penalized B-splines, we can pre-compute some \(\rho \)-independent quantities that are reused over \(\rho \) values on a search grid. These include \(\Vert \varvec{y}\Vert ^2\), \(\varvec{B^{\scriptscriptstyle \text {T}}B}\), \(\varvec{D}_m^{\scriptscriptstyle \text {T}}\varvec{D}_m\), \(\varvec{B^{\scriptscriptstyle \text {T}}y}\) and the lower triangular factor \(\varvec{L}\) in the Cholesky factorization \(\varvec{B^{\scriptscriptstyle \text {T}}B} = \varvec{LL^{\scriptscriptstyle \text {T}}}\). In the following, we will consider them to be known quantities so that they do not count toward the overall computational cost of the estimation procedure.

Now, for any \(\rho \) value on a search grid, the PLS solution to (2) is \(\varvec{\hat{\beta }} = \varvec{C}^{\scriptscriptstyle -1}\varvec{B^{\scriptscriptstyle \text {T}}y}\), where \(\varvec{C} = \varvec{B^{\scriptscriptstyle \text {T}}B} + \text {e}^{\rho }\varvec{D}_m^{\scriptscriptstyle \text {T}}\varvec{D}_m\). The vector of fitted values is \(\varvec{\hat{y}} = \varvec{B\hat{\beta }} = \varvec{B}\varvec{C}^{\scriptscriptstyle -1}\varvec{B^{\scriptscriptstyle \text {T}}y}\). By definition, the sum of squared residuals is \(\text {RSS}(\rho ) = \Vert \varvec{y} - \varvec{\hat{y}}\Vert ^2\), but it can also be computed without using \(\varvec{\hat{y}}\):

$$\begin{aligned} \text {RSS}(\rho )&= \Vert \varvec{y} - \varvec{B\hat{\beta }}\Vert ^2 = (\varvec{y} - \varvec{B\hat{\beta }})^{\scriptscriptstyle \text {T}}(\varvec{y} - \varvec{B\hat{\beta }})\\&= \varvec{y^{\scriptscriptstyle \text {T}}y} - 2\varvec{\hat{\beta }^{\scriptscriptstyle \text {T}}B^{\scriptscriptstyle \text {T}}y} + \varvec{\hat{\beta }^{\scriptscriptstyle \text {T}}B^{\scriptscriptstyle \text {T}}B\hat{\beta }}\\&= \varvec{y^{\scriptscriptstyle \text {T}}y} - 2\varvec{\hat{\beta }^{\scriptscriptstyle \text {T}}B^{\scriptscriptstyle \text {T}}y} + \varvec{\hat{\beta }^{\scriptscriptstyle \text {T}}LL^{\scriptscriptstyle \text {T}}\hat{\beta }}\\&= \Vert \varvec{y}\Vert ^2 - 2\varvec{\hat{\beta }^{\scriptscriptstyle \text {T}}B^{\scriptscriptstyle \text {T}}y} + \Vert \varvec{L^{\scriptscriptstyle \text {T}}\hat{\beta }}\Vert ^2. \end{aligned}$$

The complexity of the fitted spline is measured by its effective degree of freedom (edf), defined as the trace of the hat matrix mapping \(\varvec{y}\) to \(\varvec{\hat{y}}\):

$$\begin{aligned} \textsf {edf}(\rho ) = \text {tr}\left( \varvec{B}\varvec{C}^{\scriptscriptstyle -1}\varvec{B^{\scriptscriptstyle \text {T}}}\right) = \text {tr}\left( \varvec{C}^{\scriptscriptstyle -1}\varvec{B^{\scriptscriptstyle \text {T}}B}\right) . \end{aligned}$$

The GCV error can then be calculated using RSS and edf:

$$\begin{aligned} \text {GCV}(\rho ) = \frac{n\cdot \text {RSS}}{(n - \textsf {edf})^2}. \end{aligned}$$

The restricted likelihood \(\text {REML}(\rho )\) has a more complicated from and is detailed in Appendix B. All these quantities vary with \(\rho \), explaining why the choice of \(\rho \) affects the resulting fit. It should also be pointed out that although edf depends on the basis \(\varvec{B}\) and the penalty \(\varvec{D}_m\), it depends on neither the response data \(\varvec{y}\) nor the choice of the smoothness selection criterion.

The actual computations of \(\varvec{\hat{\beta }}\) and edf do not require explicitly forming \(\varvec{C}^{\scriptscriptstyle -1}\). We can compute the Cholesky factorization \(\varvec{C} = \varvec{KK^{\scriptscriptstyle \text {T}}}\) for the lower triangular factor \(\varvec{K}\), then solve triangular systems \(\varvec{Kx} = \varvec{B^{\scriptscriptstyle \text {T}}y}\) and \(\varvec{K^{\scriptscriptstyle \text {T}}\hat{\beta }} = \varvec{x}\) for \(\varvec{\hat{\beta }}\). The edf can also be computed using the Cholesky factors:

$$\begin{aligned} \begin{aligned} \textsf {edf}(\rho )&= \text {tr}\left( \varvec{C}^{\scriptscriptstyle -1}\varvec{LL^{\scriptscriptstyle \text {T}}}\right) = \text {tr}\left( \varvec{L^{\scriptscriptstyle \text {T}}}\varvec{C}^{\scriptscriptstyle -1}\varvec{L}\right) \\&= \text {tr}\big ((\varvec{K}^{\scriptscriptstyle -1}\varvec{L})^{\scriptscriptstyle \text {T}}\varvec{K}^{\scriptscriptstyle -1}\varvec{L}\big ) = \Vert \varvec{K}^{\scriptscriptstyle -1}\varvec{L}\Vert _{\scriptscriptstyle F}^2, \end{aligned} \end{aligned}$$
(3)

where we solve the triangular system \(\varvec{KX} = \varvec{L}\) for \(\varvec{X} = \varvec{K}^{\scriptscriptstyle -1}\varvec{L}\), and calculate the squared Frobenius norm \(\Vert \varvec{X}\Vert _{\scriptscriptstyle F}^2\) (the sum of squared elements in \(\varvec{X}\)).

Penalized B-splines are sparse and computationally efficient. Notably, \(\varvec{B^{\scriptscriptstyle \text {T}}B}\), \(\varvec{D}_m^{\scriptscriptstyle \text {T}}\varvec{D}_m\), \(\varvec{C}\), \(\varvec{L}\) and \(\varvec{K}\) are band matrices, so the aforementioned Cholesky factorizations and triangular systems can be computed and solved in \(O(p^2)\) floating point operations. That is, both \(\varvec{\hat{\beta }}\) and edf come at \(O(p^2)\) cost. The computation of RSS (without using \(\varvec{\hat{y}}\)) has O(p) cost. Once RSS and edf are known, GCV is known. In addition, Appendix B shows that the REML score can be obtained at O(p) cost. Thus, computations for a given \(\rho \) value have \(O(p^2)\) cost. When \(\rho \) is selected over N trial values on a search grid to optimize GCV or REML, the overall computational cost is \(O(Np^2)\).

3 Automatic search intervals

To start with, we formulate edf in a different way that better reveals its mathematical property. Let \(q = p - m\). We form the \(p \times q\) matrix (at \(O(p^2)\) cost):

$$\begin{aligned} \varvec{E} = \varvec{L}^{\scriptscriptstyle -1}\varvec{D}_m^{\scriptscriptstyle \text {T}}, \end{aligned}$$
(4)

and express \(\varvec{C}\) as:

$$\begin{aligned} \varvec{C} = \varvec{LL^{\scriptscriptstyle \text {T}}} + \text {e}^{\rho }\varvec{D}_m^{\scriptscriptstyle \text {T}}\varvec{D}_m = \varvec{L}[\varvec{I} + \text {e}^{\rho }\varvec{EE^{\scriptscriptstyle \text {T}}}]\varvec{L^{\scriptscriptstyle \text {T}}} \end{aligned}$$

Plugging this into \(\textsf {edf}(\rho ) = \text {tr}\left( \varvec{L^{\scriptscriptstyle \text {T}}}\varvec{C}^{\scriptscriptstyle -1}\varvec{L}\right) \) (see (3)), we get:

$$\begin{aligned} \textsf {edf}(\rho ) = \text {tr}\big ([\varvec{I} + \text {e}^{\rho }\varvec{EE^{\scriptscriptstyle \text {T}}}]^{\scriptscriptstyle -1}\big ), \end{aligned}$$

where \(\varvec{I}\) is an identity matrix. The \(p \times p\) symmetric matrix \(\varvec{EE^{\scriptscriptstyle \text {T}}}\) is positive semi-definite with rank q. Thus, it has q positive eigenvalues \(\lambda _1> \lambda _2> \ldots > \lambda _q\), followed by m zero eigenvalues. Let its eigendecomposition be \(\varvec{EE^{\scriptscriptstyle \text {T}}} = \varvec{U\Lambda U}^{\scriptscriptstyle -1}\), where \(\varvec{U}\) is an orthonormal matrix with eigenvectors and \(\varvec{\Lambda }\) is a \(p \times p\) diagonal matrix with eigenvalues. Then,

$$\begin{aligned} \begin{aligned} \textsf {edf}(\rho )&= \text {tr}\big ([\varvec{U}\varvec{U}^{\scriptscriptstyle -1} + \text {e}^{\rho }\varvec{U\Lambda U}^{\scriptscriptstyle -1}]^{\scriptscriptstyle -1}\big )\\&= \text {tr}\big ([\varvec{U}(\varvec{I} + \text {e}^{\rho }\varvec{\Lambda })\varvec{U}^{\scriptscriptstyle -1}]^{\scriptscriptstyle -1}\big )\\&= \text {tr}\big (\varvec{U}(\varvec{I} + \text {e}^{\rho }\varvec{\Lambda })^{\scriptscriptstyle -1}\varvec{U}^{\scriptscriptstyle -1}\big )\\&= \text {tr}\big ((\varvec{I} + \text {e}^{\rho }\varvec{\Lambda })^{\scriptscriptstyle -1}\big )\\&= m + \textstyle \sum _{j = 1}^{q}(1 + \text {e}^{\rho } \lambda _j)^{\scriptscriptstyle -1}. \end{aligned} \end{aligned}$$

We call \((\lambda _j)_1^{q}\) the Demmler–Reinsch eigenvalues, in tribute to Demmler and Reinsch (1975) who first studied the eigenvalue problem of smoothing splines (Reinsch 1967, 1971; Wang 2011). We also define the restricted edf as:

$$\begin{aligned} \textsf {redf}(\rho ) = \textsf {edf}(\rho ) - m = \sum _{j = 1}^{q}\frac{1}{1 + \text {e}^{\rho } \lambda _j}, \end{aligned}$$
(5)

which is a monotonically decreasing function of \(\rho \). As \(\rho \rightarrow -\infty \), it increases to q; as \(\rho \rightarrow +\infty \), it decreases to 0. Given this one-to-one correspondence between \(\rho \) and redf, it is clear that choosing the optimal \(\rho \) is equivalent to choosing the optimal redf.

3.1 An exact search interval

The relation between \(\rho \) and redf is enlightening. Although it is difficult to see what \([\rho _{\min },\rho _{\max }]\) is wide enough for searching for \(\rho \), it is easy to see what \([\textsf {redf}_{\min },\textsf {redf}_{\max }]\) is adequate for searching for redf. For example,

$$\begin{aligned} \begin{aligned} \textsf {redf}_{\min }&= q\kappa ,\\ \textsf {redf}_{\max }&= q(1 - \kappa ), \end{aligned} \end{aligned}$$
(6)

with a small \(\kappa \) are reasonable. We interpret \(\kappa \) as a coverage parameter, as \([\textsf {redf}_{\min },\textsf {redf}_{\max }]\) covers \(100(1 - 2\kappa )\)% of [0, q]. In practice, \(\kappa = 0.01\) is good enough, in which case \([\textsf {redf}_{\min },\textsf {redf}_{\max }]\) covers 98% of [0, q]. It then follows that \(\rho _{\min }\) and \(\rho _{\max }\) satisfy

$$\begin{aligned} \begin{aligned} \textsf {redf}(\rho _{\min })&= \textsf {redf}_{\max },\\ \textsf {redf}(\rho _{\max })&= \textsf {redf}_{\min }, \end{aligned} \end{aligned}$$
(7)

and can be solved for via root-finding. As \(\textsf {redf}(\rho )\) is differentiable, we can use Newton’s method. See Algorithm 1 for an implementation of this method for a general root-finding problem \(g(x) = 0\).

figure a

It should be pointed out that Algorithm 1 is not fully automatic. To make it work, we need an initial \(\rho \) value, as well as a suitable \(\delta _{\max }\) for bounding the size of a Newton step (which helps prevent overshooting). This is not easy, though, since we don’t know a sensible range for \(\rho \) (in fact, we are trying to find such a range). We will come back to this issue in the next section. For now, let’s discuss the strength and weakness of this approach.

The interval \([\rho _{\min }, \rho _{\max }]\) is back-transformed from redf. As is stressed in Sect. 2, edf (and thus redf) does not depend on y values or the choice of the smoothness selection criterion; neither does the interval. This is a nice property. It is also an advantage of our method, for there is no need to find a new interval when y values or the criterion change. We call this idea of back-transformation the redf-oriented thinking.

Nevertheless, the interval is computationally expensive. To get \((\lambda _j)_1^{q}\), an eigendecomposition at \(O(p^3)\) cost is needed. Section 2 shows that solving PLS along with grid search only has \(O(Np^2)\) cost. Thus, when p is big, finding the interval is even more costly than the subsequent grid search. This is unacceptable and we need a better strategy.

3.2 A wider search interval

In fact, we don’t have to find the exact \([\rho _{\min }, \rho _{\max }]\) that satisfies (6) and (7). It suffices to find a wider interval:

$$\begin{aligned}{}[\rho _{\min }^*, \rho _{\max }^*] \supseteq [\rho _{\min }, \rho _{\max }]. \end{aligned}$$

That is, find \(\rho _{\min }^*\) and \(\rho _{\max }^*\) such that \(\rho _{\min }\ge \rho _{\min }^*\) and \(\rho _{\max }\le \rho _{\max }^*\). Surprisingly, in this way, we only need the maximum and the minimum eigenvalues (\(\lambda _1\) and \(\lambda _q\)) instead of all the eigenvalues.

We now derive this wider interval. From \(\lambda _1 \ge \lambda _j \ge \lambda _q\), we have:

$$\begin{aligned} \frac{1}{1 + \text {e}^{\rho } \lambda _1} \le \frac{1}{1 + \text {e}^{\rho } \lambda _j} \le \frac{1}{1 + \text {e}^{\rho } \lambda _q}. \end{aligned}$$

Then, applying \(\sum _{j = 1}^{q}\) to these terms, we get:

$$\begin{aligned} \frac{q}{1 + \text {e}^{\rho } \lambda _1} \le \textsf {redf}(\rho ) \le \frac{q}{1 + \text {e}^{\rho } \lambda _q}. \end{aligned}$$

Since the result holds for any \(\rho \), including \(\rho _{\min }\) and \(\rho _{\max }\), there are:

$$\begin{aligned} \begin{aligned} \textsf {redf}(\rho _{\min })&\ge \frac{q}{1 + \text {e}^{\rho _{\min }}\lambda _1},\\ \textsf {redf}(\rho _{\max })&\le \frac{q}{1 + \text {e}^{\rho _{\max }}\lambda _q}. \end{aligned} \end{aligned}$$

Together with (6) and (7), we see:

$$\begin{aligned} \begin{aligned} q(1 - \kappa )&\ge \frac{q}{1 + \text {e}^{\rho _{\min }}\lambda _1},\\ q\kappa&\le \frac{q}{1 + \text {e}^{\rho _{\max }}\lambda _q}. \end{aligned} \end{aligned}$$

These imply:

$$\begin{aligned} \begin{aligned} \rho _{\min }&\ge \log \left( \frac{\kappa }{(1 - \kappa )\lambda _1}\right) = \rho _{\min }^*,\\ \rho _{\max }&\le \log \left( \frac{1 - \kappa }{\kappa \lambda _q}\right) = \rho _{\max }^*. \end{aligned} \end{aligned}$$

Better yet, we can replace the maximum eigenvalue \(\lambda _1\) by the mean eigenvalue \({\bar{\lambda }} = \sum _{j = 1}^q\lambda _j/q\) for a tighter lower bound. In general, the harmonic mean of positive numbers \((a_j)_1^q\) is no larger than their arithmetic mean:

$$\begin{aligned} \frac{q}{\sum _{j = 1}^q\frac{1}{a_j}} \le {\bar{a}} \quad \Rightarrow \quad \frac{q}{{\bar{a}}} \le \sum _{j = 1}^q\frac{1}{a_j}. \end{aligned}$$

If we set \(a_j = 1 + \text {e}^{\rho } \lambda _j\), we get:

$$\begin{aligned} \frac{q}{1 + \text {e}^{\rho }{\bar{\lambda }}} \le \textsf {redf}(\rho ). \end{aligned}$$

This allows us to update \(\rho _{\min }^*\). In the end, we have:

$$\begin{aligned} \begin{aligned} \rho _{\min }^*&= \log \left( \frac{\kappa }{(1 - \kappa ){\bar{\lambda }}}\right) ,\\ \rho _{\max }^*&= \log \left( \frac{1 - \kappa }{\kappa \lambda _q}\right) . \end{aligned} \end{aligned}$$
(8)

At first glance, it appears that we still need all the eigenvalues in order to compute their mean \({\bar{\lambda }}\). But the trick is that \((\lambda _j)_1^q\) add up to:

$$\begin{aligned} \sum _{j = 1}^{q}\lambda _j = \text {tr}\left( \varvec{\Lambda }\right) = \text {tr}\left( \varvec{U\Lambda U}^{\scriptscriptstyle -1}\right) = \text {tr}\left( \varvec{EE^{\scriptscriptstyle \text {T}}}\right) = \Vert \varvec{E}\Vert _{\scriptscriptstyle F}^2, \end{aligned}$$

so we can easily compute \({\bar{\lambda }}\) (at \(O(p^2)\) cost):

$$\begin{aligned} {\bar{\lambda }} = \frac{1}{q}\sum _{j = 1}^{q}\lambda _j = \frac{\Vert \varvec{E}\Vert _{\scriptscriptstyle F}^2}{q}. \end{aligned}$$
(9)

This leaves the minimum eigenvalue \(\lambda _q\) the only nontrivial quantity to compute. As we will see in the next section, the computation of \(\lambda _q\) merely involves \(O(p^2)\) complexity. Therefore, the wider search interval \([\rho _{\min }^*, \rho _{\max }^*]\) is available at \(O(p^2)\) cost, much cheaper than the exact search interval \([\rho _{\min }, \rho _{\max }]\) that comes at \(O(p^3)\) cost.

Another advantage of the wider interval is its closed-form formula. The exact interval is defined implicitly by root-finding, and its computation is not automatic as Algorithm 1 requires \(\rho \)-relevant inputs. However, the wider interval can be directly computed using eigenvalues that are irrelevant to \(\rho \), so its computation is fully automatic.

In practice, we can utilize the wider interval to automate the computation of the exact interval. For example, when applying Algorithm 1 to find \(\rho _{\min }\) or \(\rho _{\max }\), we may use \((\rho _{\min }^* + \rho _{\max }^*)/2\) for its initial value, and bound the size of a Newton step by \(\delta _{\max } = (\rho _{\max }^* - \rho _{\min }^*)/4\). This improvement does not by any means make the computation of the exact interval less expensive, though.

3.3 Computational details

We now describe \(O(p^2)\) algorithms for computing the maximum and the minimum eigenvalues, i.e., \(\lambda _1\) and \(\lambda _q\), to aid the fast computation of the wider interval \([\rho _{\min }^*, \rho _{\max }^*]\). Note that although \(\lambda _1\) does not show up in (8), it is useful for assessing the credibility of the computed \(\lambda _q\), which will soon be explained.

Recall that \((\lambda _j)_1^q\) are the positive eigenvalues of the \(p \times p\) positive semi-definite matrix \(\varvec{EE^{\scriptscriptstyle \text {T}}}\), and the matrix also has m zero eigenvalues. To get rid of these nuisance eigenvalues, we can work with the \(q \times q\) positive-definite matrix \(\varvec{E^{\scriptscriptstyle \text {T}}E}\) instead. Here, the trick is that \(\varvec{E^{\scriptscriptstyle \text {T}}E}\) and \(\varvec{EE^{\scriptscriptstyle \text {T}}}\) have the same positive eigenvalues that equal the squared nonzero singular values of \(\varvec{E}\). This can be proved using the singular value decomposition of \(\varvec{E}\).

In general, given a positive definite matrix \(\varvec{A}\), we compute its maximum eigenvalue using power iteration and its minimum eigenvalue using inverse iteration. The two algorithms iteratively compute \(\varvec{Av}\) and \(\varvec{A^{\scriptscriptstyle -1}v}\), respectively. Unfortunately, when \(\varvec{A} = \varvec{E^{\scriptscriptstyle \text {T}}E}\), the latter operation is as expensive as \(O(p^3)\) because \(\varvec{A}\) is fully dense. Therefore, naively applying inverse iteration to compute \(\lambda _q\) is not any cheaper than a full eigendecomposition.

To obtain \(\lambda _q\) at \(O(p^2)\) cost, we are to exploit the following partitioning:

$$\begin{aligned} \varvec{E} = \begin{bmatrix} \varvec{E_1} \\ \varvec{E_2} \end{bmatrix}, \end{aligned}$$

where \(\varvec{E_1}\) is a \(q \times q\) lower triangular matrix and \(\varvec{E_2}\) is an \(m \times q\) rectangular matrix. Below is an illustration of such structure (with \(p = 6\), \(m = 2\) and \(q = 4\)), where ‘\(\times \)’ and ‘\(\circ \)’ denote the nonzero elements in \(\varvec{E_1}\) and \(\varvec{E_2}\), respectively.

$$\begin{aligned} \left[ \begin{array}{cccc} \times \\ \times &{} \times \\ \times &{} \times &{} \times \\ \times &{} \times &{} \times &{} \times \\ \hline \circ &{} \circ &{} \circ &{} \circ \\ \circ &{} \circ &{} \circ &{} \circ \end{array}\right] \end{aligned}$$

Such “trapezoidal” structure exclusively holds for the penalized B-splines family, and it allows us to express \(\varvec{A}\) as an update to \(\varvec{E_1^{\scriptscriptstyle \text {T}}E_1}\):

$$\begin{aligned} \varvec{A} = \varvec{E^{\scriptscriptstyle \text {T}}E} = \varvec{E_1^{\scriptscriptstyle \text {T}}E_1} + \varvec{E_2^{\scriptscriptstyle \text {T}}E_2}. \end{aligned}$$

Using Woodbury identity (Woodbury 1950), we obtain an explicit inversion formula:

$$\begin{aligned} \begin{aligned} \varvec{A}^{\scriptscriptstyle -1}&= (\varvec{E_1^{\scriptscriptstyle \text {T}}E_1})^{\scriptscriptstyle -1} - \varvec{F}(\varvec{I} + \varvec{R^{\scriptscriptstyle \text {T}}R})^{\scriptscriptstyle -1}\varvec{F^{\scriptscriptstyle \text {T}}}\\&= (\varvec{E_1^{\scriptscriptstyle \text {T}}E_1})^{\scriptscriptstyle -1} - \varvec{F}(\varvec{GG^{\scriptscriptstyle \text {T}}})^{\scriptscriptstyle -1}\varvec{F^{\scriptscriptstyle \text {T}}}, \end{aligned} \end{aligned}$$

where \(\varvec{R} = (\varvec{E_1^{\scriptscriptstyle \text {T}}})^{\scriptscriptstyle -1}\varvec{E_2^{\scriptscriptstyle \text {T}}}\) and \(\varvec{F} = \varvec{E_1^{\scriptscriptstyle -1}}\varvec{R}\) are both \(q \times m\) matrices, and \(\varvec{G}\) is the lower triangular Cholesky factor of the \(m \times m\) matrix \(\varvec{I} + \varvec{R^{\scriptscriptstyle \text {T}}R}\). We thus convert the expensive computation of \(\varvec{A}^{\scriptscriptstyle -1}\varvec{v}\) to solving triangular linear systems involving \(\varvec{E_1}\), \(\varvec{E_1^{\scriptscriptstyle \text {T}}}\), \(\varvec{G}\) and \(\varvec{G^{\scriptscriptstyle \text {T}}}\), which is much more efficient. See Algorithm 2 for implementation details as well as a breakdown of computational costs. The penalty order m is often very small (usually 1, 2 or 3) and the number of iterations till convergence is much smaller than q, so the overall cost remains \(O(q^2)\) in practice. Since \(q = p - m \approx p\), we report this complexity as \(O(p^2)\).

figure b

An important technical detail in Algorithm 2 is that it checks the credibility of the computed \(\lambda _q\). Although \(\varvec{E^{\scriptscriptstyle \text {T}}E}\) is positive definite, in finite precision arithmetic performed by our computers, it becomes numerically singular if \(\lambda _q / \lambda _1\) is smaller than the machine precision \(\varepsilon \) (the largest positive number such that \(1 + \varepsilon = 1\)). On modern 64-bit CPUs, this precision is about \(1.11 \times 10^{-16}\). In case of numerical singularity, \(\lambda _q\) can not be accurately computed for the loss of significant digits, and the output \(\lambda _q\) is fake. The best bet in this case, is to reset the computed \(\lambda _q\) to \(\lambda _1\varepsilon \) (see lines 29 to 31). Sometimes, the computed \({\tilde{\lambda }}\) at line 17 is negative. This is an early sign of singularity, and we can immediately stop the iteration (see lines 18 to 22). These procedures are necessary safety measures, without which the computed \(\lambda _q\) will be too small and the derived \(\rho _{\max }^*\) will be too big, making the PLS problem (2) unsolvable. In short, Algorithm 2 helps determine a search interval \([\rho _{\min }^*, \rho _{\max }^*]\) that is both sufficiently wide and numerically safe for grid search.

We need the maximum eigenvalue \(\lambda _1\) before applying Algorithm 2. The computation of \(\lambda _1\) is less challenging: even a direct application of power iteration by iteratively computing \(\varvec{E^{\scriptscriptstyle \text {T}}}(\varvec{Ev})\) is good enough at \(O(p^2)\) cost. But we can make it more efficient by exploiting the band sparsity behind the “factor form” (4) of matrix \(\varvec{E}\). See Algorithm 3 for details. The overall complexity is O(p) in practice.

figure c

3.4 An illustration of the intervals

We now illustrate search intervals \([\rho _{\min }, \rho _{\max }]\) and \([\rho _{\min }^*, \rho _{\max }^*]\) through a simple example. We set up p cubic B-splines (\(d = 4\)) on unevenly spaced knots and penalized them by a 2nd order (\(m = 2\)) difference penalty matrix \(\varvec{D}_2\). We then generated 10 uniformly distributed x values between every two adjacent knots and constructed the design matrix \(\varvec{B}\) at those locations. Figure 2 illustrates the resulting \(\textsf {redf}(\rho )\) for \(p = 50\) and \(p = 500\). The nominal mapping from \(\rho \) range to redf range is \((-\infty , +\infty ) \rightarrow [0, q]\) and here we have \(q = p - 2\). For the exact interval, the mapping is \([\rho _{\min }, \rho _{\max }] \rightarrow [0.01q, 0.99q]\). The wider interval \([\rho _{\min }^*, \rho _{\max }^*]\) is mapped to a wider range than [0.01q, 0.99q].

Fig. 2
figure 2

An example of \(\textsf {redf}(\rho )\) curve for p cubic B-splines (\(d = 4\)) on unevenly spaced knots, penalized by a 2nd order (\(m = 2\)) difference penalty. The black dots (\(\rho _{\min }^*\) and \(\rho _{\max }^*\)) lie beyond the red dashed lines (\(\rho _{\min }\) and \(\rho _{\max }\)) on both ends, implying that \([\rho _{\min }^*, \rho _{\max }^*]\) is wider than \([\rho _{\min }, \rho _{\max }]\). The text (with numbers rounded to 1 decimal place) state the actual mapping from \(\rho \) range to redf range. (Color figure online)

Full size image

Our search intervals do not depend on y values or the choice of the smoothness selection criterion. To illustrate this, we simulated two sets of y values for the \(p = 50\) case, and chose the optimal \(\rho \) by minimizing GCV or maximizing REML. Figure 3 shows that while the two datasets yield different GCV or REML curves, they share the same search interval for \(\rho \). Incidentally, both GCV and REML choose similar optimal \(\rho \) values in each example, leading to indistinguishable fit. This is not always true, though, and we will discuss more about this in Sect. 5.

Fig. 3
figure 3

Two sets of y values are simulated and smoothed for the \(p = 50\) case in Fig. 2. They yield different GCV or REML curves, but share the same search interval for \(\rho \). In the first row, red curves are the true functions and black curves are the optimal spline fit. (Color figure online)

Full size image

3.5 Heuristic improvementk

Let’s take a second look at Fig. 2. As the black circle on the right end is far off the red dashed line, \(\rho _{\max }^*\) is a loose upper bound. Moreover, the bigger p is, the looser it is. We now use some heuristics to find a tighter upper bound. Specifically, we seek approximated eigenvalues \((\hat{\lambda }_j)_1^q\) such that \(\hat{\lambda }_1 = \lambda _1\), \(\hat{\lambda }_q = \lambda _q\) and \(\sum _{j = 1}^q\hat{\lambda }_j = q{\bar{\lambda }}\). Then, replacing \(\lambda _j\) by \(\hat{\lambda }_j\) in (5) gives an approximated redf, with which we can solve (6) and (7) for an “exact” interval \([\hat{\rho }_{\min }, \hat{\rho }_{\max }]\). We are most interested in \(\hat{\rho }_{\max }\). If it is tighter than \(\rho _{\max }^*\), even if just empirically, we can narrow the search interval \([\rho _{\min }^*, \rho _{\max }^*]\) to \([\rho _{\min }^*, \hat{\rho }_{\max }]\). We hereafter call \(\hat{\rho }_{\max }\) the heuristic upper bound.

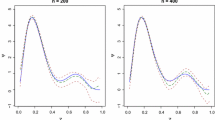
For reasonable approximation, knowledge on \(\lambda _j\)’s decay pattern is useful. Recently, Xiao (2019, Lemma 5.1) established an asymptotic decay rate at about \(O((1 - \frac{j}{q + m})^{2m}) \sim O((1 - \frac{j + m}{q + m})^{2m})\) (Xiao arranged \((\lambda _j)_1^q\) in ascending order and his original result is \(O((\frac{j}{q + m})^{2m}) \sim O((\frac{j + m}{q + m})^{2m})\)). So, \(\log (\lambda _j)\) roughly decays like \(z_j = \log (1 - t_j)\), where \(t_j = j / (q + 1)\). In practice, however, we observed that the first few eigenvalues often drop faster, while the decay of the remaining eigenvalues well follows the theory. Empirically, the actual decay resembles an “S”-shaped curve:

$$\begin{aligned} z_j = z(t_j, \gamma ) = \log (1 - t_j) + \gamma \log (1 / t_j), \end{aligned}$$

where \(\gamma \in [0, 1]\) is a shape parameter. For example, Fig. 4 illustrates the decay of \(\log (\lambda _j)\) against \(t_j\) for the examples in the previous section. The fast decay of the first few eigenvalues and the resulting “S”-shaped curve are most noticeable for \(p = 500\). The figure also plots \(z(t_j, \gamma )\) for various \(\gamma \) values. When \(\gamma = 0\), it is the asymptotic decay; when \(\gamma = 1\), it is a symmetric “S”-shaped curve similar to the quantile function of the logistic distribution. Moreover, it appears that we can tweak \(\gamma \) value to make \(z_j\) similar to \(\log (\lambda _j)\).

Fig. 4
figure 4

The asymptotic decay established by Xiao (2019) (red dashed) often does not reflect the actual decay (black solid) of \(\log (\lambda _j)\), because the first few eigenvalues may drop faster. Empirically, the actual decay of \(\log (\lambda _j)\) resembles an “S”-shaped curve \(z(t_j, \gamma )\), and we can tweak the value of the shape parameter \(\gamma \) to make this curve similar (but not identical) to \(\log (\lambda _j)\). (Note: the ranges of \(\log (\lambda _j)\) and \(z_j\) have been transformed to [0, 1] to aid shape comparison.) (Color figure online)

Full size image

As it is generally not possible to tweak \(\gamma \) value to make \(z_j\) identical to \(\log (\lambda _j)\), we chose to model \(\log (\lambda _j)\) as a function of \(z_j\), i.e., \(\log (\hat{\lambda }_j) = Q(z_j)\). For convenience, let \(a = \log (\lambda _q)\) and \(b = \log (\lambda _1)\). We also transform the range of \(z_j\) to [0, 1] by \(z_j \leftarrow (z_j - z_q) / (z_1 - z_q)\). As we require \(\hat{\lambda }_q = \lambda _q\) and \(\hat{\lambda }_1 = \lambda _1\), the function must satisfy \(Q(0) = a\) and \(Q(1) = b\). To be able to determine \(Q(z_j)\) with the last constraint \(\sum _{j = 1}^q\hat{\lambda }_j = q{\bar{\lambda }}\), we can only parameterize the function with one unknown. We now denote this function by \(Q(z_j, \alpha )\) and suggest two parametrizations that prove to work well in practice. The first one is a quadratic polynomial:

$$\begin{aligned} Q_1(z_j, \alpha ) = a + (b - a)z_j + \alpha (z_j ^ 2 - z_j). \end{aligned}$$

It is convex and monotonically increasing when \(\alpha \in [0, b - a]\). The second one is a cubic polynomial:

$$\begin{aligned} \begin{aligned} Q_2(z_j,\alpha ) =&\, [c_0(z_j) + c_2(z_j)]a + [c_2(z_j) + c_3(z_j)]b \\&+ [c_1(z_j) - c_2(z_j)]\alpha , \end{aligned} \end{aligned}$$

represented using cubic Bernstein polynomials:

$$\begin{aligned} c_0(z_j)&= (1 - z_j) ^ 3,&c_1(z_j)&= 3z_j(1 - z_j)^2,\\ c_2(z_j)&= 3z_j^2(1 - z_j),&c_3(z_j)&= z_j^3. \end{aligned}$$

It is an “S”-shaped curve and if \(\alpha \in [a, (2a + b)/3]\), it is monotonically increasing, concave on [0, 0.5] and convex on [0.5, 1]. See Fig. 5 for what the two functions look like as \(\alpha \) varies. To facilitate computation, we rewrite both cases as:

$$\begin{aligned} \log (\hat{\lambda }_j) = Q(z_j,\alpha ) = \theta _j + h_j\alpha , \quad \alpha \in [\alpha _l,\alpha _r]. \end{aligned}$$

Finding \(\alpha \) such that \(\sum _{j = 1}^q\hat{\lambda }_j = q{\bar{\lambda }}\) is equivalent to finding the root of \(g(\alpha ) = \sum _{j = 1}^q\exp (\theta _j + h_j\alpha ) - q{\bar{\lambda }}\). As \(g(\alpha )\) is differentiable, we use Newton’s method (see Algorithm 1) for this task. Obviously, a root exists in \([\alpha _l,\alpha _r]\) if and only if \(g(\alpha _l)\cdot g(\alpha _r) <= 0\). Therefore, we are not able to obtain approximated eigenvalues \((\hat{\lambda }_j)_1^q\) if this condition does not hold. Intuitively, the condition is met if \(\log (\lambda _j)\), when sketched against \(z_j\), largely lies on the “paths” of \(Q(z_j,\alpha )\) as \(\alpha \) varies (see Fig. 5). This in turn implies that \(\gamma \) value should be properly chosen for \(z_j = z(t_j, \gamma )\). For example, Fig. 5 shows that \(\gamma = 0.1\) is good for \(Q_1(z_j,\alpha )\), but not for \(Q_2(z_j,\alpha )\); whereas \(\gamma = 0.45\) is good for \(Q_2(z_j,\alpha )\), but not for \(Q_1(z_j,\alpha )\).

Fig. 5
figure 5

We can approximate \(\log (\lambda )\) by \(\log (\hat{\lambda }_j) = Q(z_j,\alpha )\), if \(\gamma \) value is properly chosen for \(z_j = z(t_j, \gamma )\) such that \(\log (\lambda _j)\) (sketched against \(z_j\)) largely lies on the “paths” of \(Q(z_j,\alpha )\) as \(\alpha \) varies. In this example (the \(p = 50\) case in Fig. 4), \(\gamma = 0.1\) is good for \(Q_1(z_j,\alpha )\), but not for \(Q_2(z_j,\alpha )\); whereas \(\gamma = 0.45\) is good for \(Q_2(z_j,\alpha )\), but not for \(Q_1(z_j,\alpha )\). (Note: the ranges of \(\log (\lambda _j)\) and \(z_j\) have been transformed to [0, 1] to aid shape comparison.) (Color figure online)

Full size image

In reality, we don’t know what \(\gamma \) value is good in advance, so we do a grid search in [0, 1], and for each trial \(\gamma \) value, we attempt both \(Q_1(z_j,\alpha )\) and \(Q_2(z_j,\alpha )\) (see Algorithm 4). We might have several successful approximations, so we take their average for the final \((\hat{\lambda }_j)_1^q\). Figure 6 shows \(\log (\lambda _j)\) and \(\log (\hat{\lambda }_j)\) (both transformed to range between 0 and 1) for the examples demonstrated through Figs. 2, 3, 4 and 5. The approximation is perfect for small p (which is not surprising because a smaller p means fewer eigenvalues to guess). As p grows, the approximation starts to deviate from the truth, but still remains accurate on both ends (which is important, since the quality of the heuristic upper bound \(\hat{\rho }_{\max }\) mainly relies on the approximation to extreme eigenvalues). Figure 7 displays (on top of Fig. 2) the approximated redf and the resulting \(\hat{\rho }_{\max }\). Clearly, \(\hat{\rho }_{\max }\) is closer to \(\rho _{\max }\) than \(\rho _{\max }^*\) is. Thus, it is a tighter bound. (More simulations of \(\rho _{\max }\), \(\rho _{\max }^*\) and \(\hat{\rho }_{\max }\) are conducted in Sect. 4.)

figure d
Fig. 6
figure 6

Log eigenvalues \(\log (\lambda _j)\) (solid) and their heuristic approximation \(\log (\hat{\lambda }_j)\) (dashed) against \(t_j\)

Full size image
Fig. 7
figure 7

Approximated \(\textsf {redf}(\rho )\) (black dashed) and heuristic upper bound \(\hat{\rho }_{\max }\) (black square). This figure enhances Fig. 2. As \(\hat{\rho }_{\max }\) is closer to \(\rho _{\max }\) (red dashed) than \(\rho _{\max }^*\) (black circle) is, it is a tighter upper bound. (Color figure online)

Full size image

In summary, to get the heuristic upper bound \(\hat{\rho }_{\max }\), we first apply Algorithm 4 to compute \((\hat{\lambda }_j)_1^q\) for approximating redf (5), then apply Algorithm 1 to solve the approximated redf for \(\hat{\rho }_{\max }\). Both steps are computationally efficient at O(p) cost, as they do not involve matrix computations. Thus, the overall computational cost of the heuristically improved interval \([\rho _{\min }^*, \hat{\rho }_{\max }]\) remains \(O(p^2)\). The computation is also fully automatic. In the first step, all variable inputs required by Algorithm 4, namely q, \(\lambda _1\), \(\lambda _q\) and \({\bar{\lambda }}\), can be obtained during the computation of the wider interval \([\rho _{\min }^*, \rho _{\max }^*]\). In the second step, we can automate Algorithm 1 by using \((\rho _{\min }^* + \rho _{\max }^*)/2\) for the initial \(\rho \) value, and bounding the size of a Newton step by \(\delta _{\max } = (\rho _{\max }^* - \rho _{\min }^*)/4\).

In rare cases, Algorithm 4 fails to approximate eigenvalues. On this occasion, \(\hat{\rho }_{\max }\) is not available and we have to stick to \(\rho _{\max }^*\). In principle, the chance of failure can be reduced by enhancing the heuristic. For example, we may introduce a shape parameter \(\nu \ge 1\) and model the “S”-shaped decay as \(z_j = z(t_j, \gamma , \nu ) = \log (1 - t_j) + \gamma [\log (1 / t_j)]^{\nu }\), which allows the first few eigenvalues to decrease even faster. We may also propose \(Q(z_j, \alpha )\) of new parametric forms. In short, Algorithm 4 can be easily extended for improvement.

3.6 Summary

We propose two search intervals for \(\rho \): the exact one \([\rho _{\min }, \rho _{\max }]\) and the wider one \([\rho _{\min }^*, \rho _{\max }^*]\). We prefer the wider one to the exact one for three reasons. Firstly, the wider one has a closed-form formula and its computation is fully automatic, whereas the exact one is implicitly defined by root-finding and its computation is not automatic by itself. Secondly, the wider one is computationally efficient. Its \(O(p^2)\) cost is no greater than the \(O(Np^2)\) cost for solving PLS over N trial \(\rho \) values, whereas the \(O(p^3)\) cost for computing the exact one is too expensive. Thirdly, the wider one, or rather, its upper bound \(\rho _{\max }^*\), can be tightened using simple heuristics, and the heuristic upper bound \(\hat{\rho }_{\max }\) can be computed at only O(p) cost. To reflect the practical impact of computational costs, we report in Table 1 the actual runtime of different computational tasks for growing p.

Table 1 Runtime (in seconds (s) or milliseconds (1 ms = 0.001 s) of different computational tasks for growing p, on an Intel i5-8250U CPU @ 1.60 GHz
Full size table

4 Simulations

The exact interval \([\rho _{\min }, \rho _{\max }]\) and the wider one \([\rho _{\min }^*, \rho _{\max }^*]\) have known theoretical property. By construction, we have (for \(\kappa = 0.01\)):

$$\begin{aligned} \rho _{\min }^*&\le \rho _{\min },&\textsf {redf}(\rho _{\min }^*)&\ge \textsf {redf}(\rho _{\min }) = 0.99q\\ \rho _{\max }^*&\ge \rho _{\max },&\textsf {redf}(\rho _{\max }^*)&\le \textsf {redf}(\rho _{\max }) = 0.01q. \end{aligned}$$

However, the heuristic bound \(\hat{\rho }_{\max }\) has unknown property. We expect it to be tighter than \(\rho _{\max }^*\), in the sense that it is closer to \(\rho _{\max }\). Ideally, it should satisfy \(\rho _{\max }\le \hat{\rho }_{\max }\le \rho _{\max }^*\). This is supported by Fig. 7, but we still need extensive simulations to be confident about this in general.

For comprehensiveness, let’s experiment every possible setup for penalized B-splines that affects \(\textsf {redf}(\rho )\). The placement of equidistant or unevenly spaced knots produces different \(\varvec{B}\). The choice of difference or derivative penalty gives different \(\varvec{D}_m\). We also consider weighted data where \((x_i, y_i)\) has weight \(w_i\). This leads to a penalized weighted least squares problem (PWLS) that can be transformed to a PLS problem by absorbing weights into \(\varvec{B}\): \(\varvec{B} \leftarrow \varvec{W}^{1/2}\varvec{B}\), where \(\varvec{W}\) is a diagonal matrix with element \(W_{ii} = w_i\). Altogether, we have 8 scenarios (see Table 2).

Table 2 The 8 scenarios for simulations
Full size table

Here are more low-level details for setting up \(\varvec{B}\), \(\varvec{D}_m\) and \(\varvec{W}\). In general, to construct order-d B-splines \({\mathcal {B}}_j(x)\), \(j = 1, \ldots , p\), we need to place \(p + d\) knots \((\xi _k)_1^{p + d}\). For our simulations, we take \(\xi _k = k\) for equidistant knots and \(\xi _k \sim \text {N}(k, [(p + d)/10]^2)\) for unevenly spaced knots. We then generate 10 uniformly distributed x values between every two nearby knots for constructing the design matrix \(\varvec{B}\) and the penalty matrix \(\varvec{D}_m\). For the weights, we use random samples from Beta(3, 3) distribution.

To finish our setup, we still need to specify the B-spline order d, the penalty order m and basis dimension p. By design, each combination of these parameters has 8 scenarios. For our simulations, we are to test different (d, m) pairs for growing p. We call each combination of d, m, p and scenario ID an experiment.

Fig. 8
figure 8

Estimated probability density function of \(\text {P}(\hat{\rho }_{\max })\), i.e., the proportion of [0, q] covered by \([\textsf {redf}(\hat{\rho }_{\max }), q]\). If \(\rho _{\max }\le \hat{\rho }_{\max }\le \rho _{\max }^*\), the density curve should lie between 0.99 (gray line) and \(\text {P}(\rho _{\max }^*)\) (yellow line). Numbers 1 to 8 refer to the scenarios in Table 2. (Color figure online)

Full size image

In principle, we want to run an experiment, say 200 times, and see how \(\hat{\rho }_{\max }\) is distributed relative to \(\rho _{\max }\) and \(\rho _{\max }^*\). But as none of these quantities stays fixed between runs, visualization is not easy. Back to our redf-oriented thinking, let’s compare the proportion of [0, q] covered by \([\textsf {redf}(\rho _{\max }), q]\), \([\textsf {redf}(\hat{\rho }_{\max }), q]\) and \([\textsf {redf}(\rho _{\max }^*), q]\):

$$\begin{aligned} \text {P}(\rho _{\max })&= 1 - \textsf {redf}(\rho _{\max }) / q = 0.99,\\ \text {P}(\hat{\rho }_{\max })&= 1 - \textsf {redf}(\hat{\rho }_{\max }) / q,\\ \text {P}(\rho _{\max }^*)&= 1 - \textsf {redf}(\rho _{\max }^*) / q. \end{aligned}$$

Since \(\textsf {redf}(\rho )\) is decreasing, we shall observe \(0.99 \le \text {P}(\hat{\rho }_{\max }) \le \text {P}(\rho _{\max }^*)\) if we expect \(\rho _{\max }\le \hat{\rho }_{\max }\le \rho _{\max }^*\). Interestingly, our simulations show that the variance of \(\text {P}(\rho _{\max }^*)\) is so low that its probability density function almost degenerates to a vertical line through its mean. This implies that we need to check if the density curve of \(\text {P}(\hat{\rho }_{\max })\) lies between two vertical lines. Figure 8 shows our simulation results for cubic splines with a 2nd order penalty and quadratic splines with a 1st order penalty as p grows. They look satisfying except for scenarios 1 and 5. In these cases, a non-negligible proportion of the density curve breaches 0.99, so we will get \(\hat{\rho }_{\max }< \rho _{\max }\) occasionally. Therefore, the resulting interval \([\rho _{\min }^*, \hat{\rho }_{\max }]\) is narrower than \([\rho _{\min }, \rho _{\max }]\). However, it is wide enough for grid search, as the corresponding redf range still covers a significant proportion of [0, q] (check out the numbers labeled along the x-axis of each graph in the figure). So, empirically, \(\hat{\rho }_{\max }\) is a fair tight upper bound.

One anonymous reviewer asked if lowering the value of \(\kappa \) would improve the performance of \(\hat{\rho }_{\max }\) for scenarios 1 and 5. The answer is no, because \(\kappa \) has no effect on the heuristic approximation to eigenvalues (see Algorithm 4). To really improve the performance of \(\hat{\rho }_{\max }\), we need to enhance our heuristics rather than alter the value of \(\kappa \). Figure S1 in the supplementary material shows further simulation results with \(\kappa = 0.005\) and 0.001. The results are very similar to Fig. 8, confirming that the value of \(\kappa \) is not critical.

5 Application

As an application of our automatic search interval to practical smoothing, we revisit the COVID-19 data example in the Introduction. To stress that our interval is criterion-independent, we illustrate smoothness selection using both GCV and REML.

The Finland dataset reports new deaths on 408 out of 542 days from 2020-09-01 to 2022-03-01. The Netherlands dataset reports new cases on 181 out of 182 days from 2021-09-01 to 2022-03-01. Let n be the number of data. For smoothing we set up cubic B-splines on n/4 knots placed at equal quantiles of the reporting days, and penalize them by a 2nd order difference penalty matrix. For the Finland example, our computed search interval is \([\rho _{\min }^*, \hat{\rho }_{\max }] = [-6.15, 14.93]\) (with \(\rho _{\max }^* = 20.25\)). For the Netherlands example, the search interval is \([\rho _{\min }^*, \hat{\rho }_{\max }] = [-6.26, 13.05]\) (with \(\rho _{\max }^* = 16.97\)). Figure 9 sketches \(\textsf {edf}(\rho )\), \(\text {GCV}(\rho )\) and \(\text {REML}(\rho )\) on the search intervals. For both examples, GCV has a local minimum and a global minimum (see Fig. 1 for a zoomed-in display), whereas REML has a single maximum. In addition, the optimal \(\rho \) value chosen by REML is bigger than that selected by GCV, yielding a smoother yet more plausible fit. In fact, theoretical properties of both criteria have been well studied by Reiss and Ogden (2009). In short, GCV is more likely to have multiple local optima. It is also more likely to underestimate the optimal \(\rho \) and cause overfitting. Thus, REML is superior to GCV for smoothness selection. But anyway, the focus here is not to discuss the choice of the selection criterion, but to demonstrate that our automatic search interval for \(\rho \) is wide enough for exploring any criterion.

Fig. 9
figure 9

Smoothing daily COVID-19 data in Finland (\(n = 408\) data; displayed in column 1) and Netherlands (\(n = 182\) data; displayed in column 2). A cubic general P-splines with n/4 knots and a 2nd order difference penalty is used for smoothing. For both examples, the optimal \(\rho \) value chosen by REML is bigger than that selected by GCV, resulting in a smoother yet more plausible fit

Full size image

The edf curves in Fig. 9 show that more than half of the B-spline coefficients are suppressed by the penalty in the optimal fit. In the Finland case, the maximum possible edf in Fig. 9 is 106, but the optimal edf (either 43.1 or 12.6) is less than half of that. To avoid such waste, we can halve the number of knots, i.e., place n/8 knots. This alters the design matrix, the penalty matrix and hence \(\textsf {edf}(\rho )\), so the search interval needs be recomputed. The new interval is \([\rho _{\min }^*, \hat{\rho }_{\max }] = [-6.16, 13.30]\) (with \(\rho _{\max }^* = 17.47\)) for the Finland example and \([\rho _{\min }^*, \hat{\rho }_{\max }] = [-6.43, 11.51]\) (with \(\rho _{\max }^* = 14.66\)) for the Netherlands example. Figure 10 sketches \(\textsf {edf}(\rho )\), \(\text {GCV}(\rho )\) and \(\text {REML}(\rho )\) on their new range. Interestingly, \(\text {GCV}(\rho )\) no longer has a second local minimum, yet it still underestimates the optimal \(\rho \) value when compared with REML. The fitted splines are almost identical to their counterparts in Fig. 9, and thus not shown in the figure.

Fig. 10
figure 10

The altered \(\textsf {edf}(\rho )\), \(\text {GCV}(\rho )\) and \(\text {REML}(\rho )\) after we halve the number of knots in the COVID-19 smoothing example. Interestingly, GCV no longer has a second local minimum, yet it still underestimates the optimal \(\rho \) value when compared with REML

Full size image

6 Discussion

We have developed algorithms to automatically produce a search interval for the grid search of the smoothing parameter \(\rho \) in penalized splines (1). Our search interval has four properties. (i) It gives a safe \(\rho \) range where the PLS problem is numerically solvable. (ii) It does not depend on the choice of the smoothness selection criterion. (iii) It is wide enough to contain the global optimum of any criterion. (iv) It is computationally cheap compared with the grid search itself.

The Demmler–Reinsch eigenvalues \((\lambda _j)_1^q\) play a pivotal role in our methodology development. They reveal a one-to-one correspondence between \(\rho \) (varying in \((-\infty , +\infty )\)) and redf (5) (varying in [0, q]), which motivates us to back-transform a target redf range \([q\kappa ,\ q(1-\kappa )]\) for a suitable \(\rho \) range \([\rho _{\min },\rho _{\max }]\), where \(\kappa \) is a coverage parameter such that the target redf range covers \(100(1 - 2\kappa )\)% of [0, q]. As such, the search interval satisfies (i)–(iii) naturally. To achieve (iv), the computational strategy for the interval needs to meet different goals, depending on whether the PLS problem (1) is dense or sparse.

  • A dense PLS problem has \(O(p^3)\) computational cost. This applies to penalized splines with a dense design matrix \(\varvec{B}\) and/or a dense penalty matrix \(\varvec{S}\). Examples are truncated power basis splines (Ruppert et al. 2003), natural cubic splines (Wood 2017, Sect. 5.3.1) and thin-plate splines (Wood 2017, Sect. 5.5.1);

  • A sparse PLS problem has \(O(p^2)\) computational cost. This applies to penalized B-splines (for which the PLS objective is (2)) with a sparse design matrix \(\varvec{B}\) and a sparse penalty matrix \(\varvec{D}_m\). Examples are O-splines (O’Sullivan 1986), standard P-splines (Eilers and Marx 1996) and general P-splines (Li and Cao 2022a).

Therefore, the computational costs of our search intervals need be no greater than \(O(p^3)\) and \(O(p^2)\), respectively.

We have made great efforts to optimize our computational strategy for the sparse penalized B-splines. The key is to give up computing all the eigenvalues (as an eigendecomposition has \(O(p^3)\) cost) and compute only the mean, the maximum and the minimum eigenvalues. This allows us to obtain a wider interval \([\rho _{\min }^*, \rho _{\max }^*] \supseteq [\rho _{\min }, \rho _{\max }]\) at \(O(p^2)\) cost. We can further tighten this interval using some heuristics. Precisely, step by step, we compute:

  1. 1.

    \({\bar{\lambda }}\), using (9);

  2. 2.

    \(\lambda _1\) and \(\lambda _q\), using Algorithms 3 and 2;

  3. 3.

    \([\rho _{\min }^*, \rho _{\max }^*]\), using (8);

  4. 4.

    \((\hat{\lambda }_j)_1^q\), using Algorithm 4;

  5. 5.

    \(\hat{\rho }_{\max }\), by applying Algorithm 1 to (5) (with \(\lambda _j\) replaced by \(\hat{\lambda }_j\)), (6) and (7). (To automatically start the algorithm, use \((\rho _{\min }^* + \rho _{\max }^*) / 2\) for the initial value and set \(\delta _{\max } = (\rho _{\max }^* - \rho _{\min }^*) / 4\).)

Steps 1-2 each have \(O(p^2)\) cost; step 3 is simple arithmetic; steps 4-5 each have O(p) cost. They are implemented by function gps2GS in our R package gps (\(\ge \) version 1.1). The function solves the PLS problem (2) for a grid of \(\rho \) values in \([\rho _{\min }^*, \hat{\rho }_{\max }]\). It can be embedded in more advanced statistical modeling methods that rely on penalized splines, such as robust smoothing and generalized additive models.

One anonymous reviewer commented that it appears possible to bypass the use of eigenvalues. It was noticed that the initial \(\textsf {edf}\) formula (3) is free of eigenvalues. So, it was suggested that we could work with \(\textsf {redf}= \textsf {edf}- m = \Vert \varvec{K}^{\scriptscriptstyle -1}\varvec{L}\Vert _F^2 - m\) instead of (5), when back-transforming a target redf range for \([\rho _{\min }, \rho _{\max }]\) via root-finding. Since the computational complexity of (3) is \(O(p^2)\), and a root-finding algorithm only takes a few iterations to converge, this method should have \(O(p^2)\) cost, too. While this is true, it is not practicable unless we automate the root-finding. If we use Newton’s method (see Algorithm 1) for this task, we need an initial value and a maximum stepsize for \(\rho \); if we use bisection or Brent’s method, we need a search interval for \(\rho \). Either way seems to be a deadlock, as we have to supply something relevant to what we hope to find. In fact, whether we express redf using eigenvalues or not, we will face this difficulty as long as the search interval is implicitly defined by root-finding. This difficulty is not eliminated, until we have a wider interval \([\rho _{\min }^*, \rho _{\max }^*]\) in closed form. This interval can be directly computed by (8) using eigenvalues. It can further be exploited to automate the root-finding (for example, see step 5 of our method). In summary, the wider interval and hence the Demmler–Reinsch eigenvalues are key to the automaticity of our method. There is no way to bypass the use of those eigenvalues. The best we can do, is to only compute the maximum, the minimum and the mean eigenvalues required for computing the wider interval.

Since we have to use eigenvalues anyway, we express \(\textsf {redf}(\rho )\) as (5) (the eigen-form) instead of \(\Vert \varvec{K}^{\scriptscriptstyle -1}\varvec{L}\Vert _F^2 - m\) (the PLS-form) when presenting our method. In addition, we prefer the eigen-form to the PLS-form for its simplicity. Given \((\lambda _j)_1^q\), it is easy to compute redf and its derivative if using the eigen-form, and Newton’s method has O(p) cost. By contrast, working with the PLS-form requires matrix computations and matrix calculus so that Newton’s method has \(O(p^2)\) cost. The difficulty with the eigen-form is the \(O(p^3)\) computational cost behind \((\lambda _j)_1^q\). However, once we replace them by their heuristic approximation \((\hat{\lambda }_j)_1^q\) that can be obtained at O(p) cost, the simplicity of the eigen-form becomes real computational efficiency.

It may still be asked why we would rather do some heuristic approximation to tighten our wider interval (as steps 4-5 of our method show), than compute the exact interval by applying Algorithm 1 to the PLS-form, (6) and (7) (where we can use the wider interval to automate the root-finding). After all, the \(O(p^2)\) cost behind the PLS-form, while greater the O(p) cost behind the eigen-form, is no greater than the \(O(p^2)\) cost for computing the wider interval. Thus, the overall computational cost of our method would still be \(O(p^2)\). While this is true, in our view, it is awkward to compute the exact interval; or at least, it is not worth it. The PLS-form is coupled with PLS solving. If we apply this idea, we would have to do PLS solving on three different sets of \(\rho \) grids: one for computing \(\rho _{\min }\), one for \(\rho _{\max }\) and one for the grid search on \([\rho _{\min }, \rho _{\max }]\). The first two rounds of PLS solving are a waste, given that we are only interested in the final grid search for smoothness selection. We want to separate the computation of our search interval from PLS solving and grid search, and thus deprecate this idea.

Another comment from the same reviewer, is that we have restricted the search for the optimal \(\rho \) in our bounded search interval, so that \(\rho = -\infty \) or \(+\infty \) can not be chosen. This is a good point. In terms of our redf-oriented thinking, it means that \(\textsf {redf}= 0\) and \(\textsf {redf}= q\) have been excluded. This is deliberately done. By construction, the minimum and the maximum \(\textsf {redf}\) we can reach are \(q\kappa \) and \(q(1 - \kappa )\), respectively. Apparently, if we want to approximately cover these two endpoints, we can choose a very small \(\kappa \) value. But this is not a good strategy (see the next paragraph for a discussion on the choice of \(\kappa \)). Instead, we compute the GCV error and the REML score for these limiting cases separately, then include them in our grid search. In either case, the PLS problem (2) degenerates to an ordinary least squares (OLS) problem. Thus, we can work with these OLS problems instead for these quantities. See Appendix C for details.

In this paper, the coverage parameter \(\kappa \) is fixed at 0.01. Although reducing this value would widen the target redf range, we don’t recommend it. In reality, \(\textsf {redf}(\rho )\) quickly plateaus as it gets close to either endpoint (for example, see Fig. 2). Setting \(\kappa \) too small will result in long flat “tails” on both sides. Moreover, \(\rho \) values on each “tail” give similar \(\textsf {redf}\) values, fitted splines, GCV errors and REML scores. This is undesirable for grid search. When a fixed number of equidistant grid points are positioned, the smaller \(\kappa \) is, the more trial \(\rho \) values fall on those “tails”, and thus, the fewer trial \(\rho \) values are available for exploring the “ramp” where \(\textsf {redf}(\rho )\) varies fast. The \(\kappa \) is to our method as the convergence tolerance is to an iterative algorithm. It needs to be small, but not unnecessarily small.

Our method has a limitation: it does not apply to a penalized spline whose design matrix \(\varvec{B}\) does not have full column rank. This is because we need matrix \(\varvec{L}\), the Cholesky factor of \(\varvec{B}^{\scriptscriptstyle \text {T}}\varvec{B}\), to derive the eigen-form of redf. While it is common to have a full rank design matrix in practical smoothing, a rank-deficient design matrix is not problematic at all. A typical example is when \(p > n\), i.e., there are more basis functions than (unique) x values. As Eilers and Marx (2021) put it, “It is impossible to have too many B-splines” (p. 15). Therefore, how to automatically produce a search interval for \(\rho \) in this case remains an interesting yet challenging question.

For dense penalized splines, it is acceptable to compute a full eigendecomposition for all the eigenvalues, because solving the PLS problem has \(O(p^3)\) cost anyway. It is not the decomposition of \(\varvec{EE}^{\scriptscriptstyle \text {T}}\), though, as the PLS objective reverts to (1) and neither \(\varvec{D}_m\) nor \(\varvec{E}\) is defined. So, we need to eliminate \(\varvec{D}_m\) and \(\varvec{E}\), and express the matrix using \(\varvec{S}\). First, (4) implies \(\varvec{EE}^{\scriptscriptstyle \text {T}} = \varvec{L}^{\scriptscriptstyle -1}\varvec{D}_m^{\scriptscriptstyle \text {T}}\varvec{D}_m(\varvec{L}^{\scriptscriptstyle -1})^{\scriptscriptstyle \text {T}}\). Then, replacing \(\varvec{D}_m^{\scriptscriptstyle \text {T}}\varvec{D}_m\) by \(\varvec{S}\) (which is the link between (1) and (2)) gives \(\varvec{EE}^{\scriptscriptstyle \text {T}} = \varvec{L}^{\scriptscriptstyle -1}\varvec{S}(\varvec{L}^{\scriptscriptstyle -1})^{\scriptscriptstyle \text {T}}\). Therefore, \((\lambda _j)_1^q\) are the positive eigenvalues of \(\varvec{L}^{\scriptscriptstyle -1}\varvec{S}(\varvec{L}^{\scriptscriptstyle -1})^{\scriptscriptstyle \text {T}}\). Our goal is to solve redf (5) for the exact interval, but to automate the root-finding, we need the wider interval first. Precisely, step by step, we compute:

  1. 1.

    \((\lambda _j)_1^q\), by computing a full eigendecomposition;

  2. 2.

    \([\rho _{\min }^*, \rho _{\max }^*]\), using (8);

  3. 3.

    \([\rho _{\min }, \rho _{\max }]\), by applying Algorithm 1 to (5), (6) and (7). (To automatically start the algorithm, use \((\rho _{\min }^* + \rho _{\max }^*) / 2\) for the initial value and set \(\delta _{\max } = (\rho _{\max }^* - \rho _{\min }^*) / 4\).)

We didn’t seek to optimize our method for dense penalize splines, so there is likely plenty of room for improvement.

ESM1[[Supplementary information.: The supplementary file contains simulation results when \(\kappa = 0.005\) and 0.001.]]