Importance sampling for non-Markovian tandem queues using subsolutions

Abstract

In this paper, we use importance sampling simulation to estimate the probability that the number of customers in a d-node GI|GI|1 tandem queue reaches some high level N in a busy cycle of the system. We present a state-dependent change of measure for a d-node GI|GI|1 tandem queue based on the subsolution approach, and we prove, under a mild conjecture, that this state-dependent change of measure gives an asymptotically efficient estimator for the probability of interest when all supports are bounded.

1 Introduction

In this paper, we will develop a simulation scheme to estimate the probability that the total number of customers in a d-node GI|GI|1 tandem queue exceeds some high level N in a busy cycle of the system. Two of the main methods used for rare event simulation are importance sampling and splitting: in this paper, we consider importance sampling. In importance sampling, we make the event of interest less rare by changing the underlying probability distribution.

Importance sampling for queueing networks has been studied since 1989, when a state-independentchange of measure for general queueing networks was proposed by Parekh and Walrand [11]. Sadowsky [12] showed that for the single queue this change of measure gives a so-called asymptotically efficient estimator. Afterwards, in [10], it has been shown that the change of measure that was proposed by Parekh and Walrand does not necessarily give an asymptotically efficient estimator for the two-node Markovian tandem queue. In [3, 10], necessary and sufficient conditions for asymptotic efficiency have been provided; thus, an extension to a state-dependent change of measure is required in order to get an asymptotically efficient estimator for all input parameters.

The subsolution approach is a method, developed by Dupuis and Wang [7], which can be used to construct a state-dependent change of measure. For the two-node Markovian tandem queue [6] and Jackson networks [8], this method has been applied to develop a state-dependent change of measure that gives an asymptotically efficient estimator for the probability of interest. Note that the subsolution approach is not limited in its use to importance sampling. It can also be used for splitting, see, for example, [5], but for this paper we choose not to address splitting and focus on importance sampling instead.

In [2], it has been shown that also for non-Markovian tandem queues an extension to a state-dependent change of measure is required in order to get an asymptotically efficient estimator. In that paper, necessary conditions for asymptotic efficiency have been provided. In this paper, we extend the existing work on d-node Markovian tandem queues to d-node non-Markovian tandem queues. This extension is important, because in many practical applications the Markov assumption is not realistic.

To construct a state-dependent change of measure for non-Markovian tandem queues using the subsolution approach, we extend the state description for Markovian tandem queues—consisting of the number of customers in each queue—with the residual inter-arrival and service times of all queues. By doing so, we have complete knowledge on the state of the system and it turns out that this is sufficient information to construct a state-dependent change of measure.

Firstly, we will analyse how the subsolution approach works for the single GI|GI|1 queue. Using this approach, we find the same change of measure as in [12], with a much shorter proof of asymptotic efficiency than the proof in [12]. Secondly, we consider the two-node GI|GI|1 tandem queue. In that case, the state description is relatively small and therefore the proofs are still quite clean. We end with statements for the d-node GI|GI|1 tandem queue, where we present the results but omit the proofs (which are natural extensions of the proofs for the two-node tandem queue).

The contribution of this paper is threefold. Firstly, we extend the subsolution approach from Markovian tandem queues to non-Markovian tandem queues and we present a state-(in)dependent change of measure that may give an asymptotically efficient estimator. Secondly, we prove asymptotic efficiency of the estimator for the single queue when the change of measure is based on this subsolution. For the d-node tandem queue, we prove that—when all supports are bounded and some conjecture holds—this state-dependent change of measure indeed gives an asymptotically efficient estimator. Lastly, we provide numerical examples to support our results.

This paper is structured as follows: In Sect. 2, we introduce the model and notation and we provide some background knowledge about the subsolution approach and importance sampling. Then, in Sect. 3 we present a state-dependent change of measure and we prove that this change of measure gives an asymptotically efficient estimator for the probability of interest. Section 4 concludes the paper with some numerical results.

2 Model and preliminaries

2.1 The model

In this paper, we consider a d-node GI|GI|1 tandem queue; see Fig. 1 for a graphical illustration. The inter-arrival times are i.i.d. and distributed according to some distribution A and the service times of queue j are i.i.d. and distributed according to some distribution $B^{(j)}$. All processes are assumed to be independent, and services at all queues follow a first-come first-served (FCFS) discipline. For notational convenience, we will denote the cumulative distribution function of any random variable X by $F_X(x)$, its moment generating function by $M_X(t)$ and the log-moment generating function by $\varLambda _X(t)$.

Fig. 1

The d-node tandem queue

We are interested in the probability of the event that the total number of customers in the system reaches some high level N in a busy cycle of the system.

Throughout this paper, we make the following assumptions with respect to the distributions of the inter-arrival time and service times.

Assumption 1

• (1) The moment generating functions for all service time distributions exist, i.e., for all j, $M_{B^{(j)}}(t) > 0$ for some $t> 0$;

• (2) The system is stable, i.e., for all j, $\mathbb {E}[B^{(j)}] < \mathbb {E}[A]$;

• (3) The probability of interest is non-trivial, i.e., for at least one queue j we have $\mathbb {P}(B^{(j)}> A) > 0$ and $\mathbb {P}(A> \sum _{j = 1}^d B^{(j)}) > 0$.

In addition, when considering the d-node tandem queue for $d > 1$, we make the following assumption.

Assumption 2

The supports of all distributions are bounded, i.e., there exist constants $Q^{(j)}< \infty$$\forall j = 0,\ldots ,d$ such that $\mathbb {P}(A_k < Q^{(0)}) = 1$, $\mathbb {P}(B_k^{(j)} < Q^{(j)}) = 1$.

When a Markovian system was studied in [6], the state description consisted of the number of customers in each queue. For a non-Markovian queue, we extend this state description by adding the residual inter-arrival time and the residual service times. Therefore, for the d-node tandem queue the state description is a vector with $2d+1$ components. As in [6], we define all processes embedded at a transition for the number of customers in a queue. For any vector $\mathbf {y}$ with $2d+1$ components $y_1, \ldots , y_{2d+1}$, we introduce shorthand notation $\bar{y}_j = y_{d+1+j}$, $j=0, \ldots , d$. Using this, we let

$$\begin{aligned} \mathbf {Z}_i = (Z_{1,i}, \ldots , Z_{d,i}, \bar{Z}_{0,i}, \ldots , \bar{Z}_{d,i}) \end{aligned}$$

denote the state of the system after i transitions. Here, $Z_{j,i}$, $j=1, \ldots , d,$ is the number of customers in queue j after i transitions, $\bar{Z}_{0,i}$ is the residual inter-arrival time after i transitions and $\bar{Z}_{j,i}$, $j=1, \ldots , d,$ is the residual service time at queue j after i transitions. If $Z_{j,i} = 0$ for some j, then we set $\bar{Z}_{j,i} = 0$. Throughout this paper, we let $\mathbf {Z}_0 = (1,0,\ldots ,0)$, i.e., we start with one customer in queue 1. We have $\mathbf {Z}_{i+1} = \mathbf {Z}_i + V_Z(\mathbf {Z}_i)$, where $V_Z(\mathbf {Z}_i)$ denotes the next transition when the state of the system after the ith transition is $\mathbf {Z}_i$. For $i > 0$, we define $V_Z(\mathbf {Z}_i)$ in terms of the shortest residual time $\mathcal {Z}(\mathbf {Z}_i)= \min _{k \in \{ 0\} \cup \{ j: Z_{j,i}> 0\}}\{\bar{Z}_{k,i}\}$, i.e., the minimum of the residual inter-arrival time and the residual service times of all customers in service. In other words, $\mathcal {Z}(\mathbf {Z}_i)$ is the time until the next transition. In Remark 1, we make a convention about what happens when $\mathcal {Z}(\mathbf {Z}_i)$ is not uniquely defined.

The possible transitions when the current state is $\mathbf {Z}_i$, corresponding to the cases in (1), are an arrival at queue 1, a customer going from queue j to queue $j+1$, $j \in \{1,\ldots ,d-1\}$ and a departure from queue d, which is a departure from the system. As the process starts at $(1,0,\ldots ,0)$, we need a different transition for $\mathbf {Z}_0$. It will become clear in Remarks 6 and 7 why this technicality is needed.

Let $\mathbf {e}_j$ denote the jth unit vector. Then, for all $i > 0$ we have

$$\begin{aligned}&V_Z(\mathbf {Z}_i) = -\mathcal {Z}(\mathbf {Z}_i)\left( \bar{\mathbf {e}}_0 + \sum _{k = 1}^d \bar{\mathbf {e}}_k \mathbb {1}\{Z_{k,i}> 0\}\right) \nonumber \\&\quad +\left\{ \begin{array}{ll} \mathbf {e}_1 + A_i \bar{\mathbf {e}}_0 + B^{(1)}_i\bar{\mathbf {e}}_1\mathbb {1}\{Z_{1,i} = 0\} &{}\qquad \text { if } \mathcal {Z}(\mathbf {Z}_i) = \bar{Z}_{0,i},\\ \mathbf {e}_{j+1} - \mathbf {e}_{j} + B^{(j)}_i \bar{\mathbf {e}}_j\mathbb {1}\{Z_{j,i}> 1\} \\ \qquad + B^{(j+1)}_i \bar{\mathbf {e}}_{j+1}\mathbb {1}\{Z_{j+1,i} = 0\} &{}\qquad \text { if } \mathcal {Z}(\mathbf {Z}_i) = \bar{Z}_{j,i}, \text { } j = 1,\ldots ,d-1,\\ -\mathbf {e}_{d} + B^{(d)}_i\bar{\mathbf {e}}_d\mathbb {1}\{Z_{d,i} > 1\} &{}\qquad \text { if } \mathcal {Z}(\mathbf {Z}_i) = \bar{Z}_{d,i}, \end{array}\right. \end{aligned}$$

(1)

and

$$\begin{aligned} V_Z(\mathbf {Z}_0) = A_0 \bar{\mathbf {e}}_0 + B^{(1)}_0\bar{\mathbf {e}}_1, \end{aligned}$$

where $A_i$ is the inter-arrival time if the ith transition is an arrival. If the ith transition is not an arrival, then $A_i = 0$. Similarly, we have that $B^{(j)}_i$ is the service time of a customer at queue jif a service is starting at queue j at the ith transition. If the ith transition is not a service at queue j, then $B^{(j)}_i = 0$. This means that, depending on the current state of the system, it is known which type of transition to take and each of them can have infinitely many possibilities in terms of the residuals (depending on the distribution).

We note that in (1) we consider $\mathbb {1}\{Z_{j,i} >1\}$ and not $\mathbb {1}\{Z_{j,i} >0\}$, since we do not need a new service time for queue j when queue j is empty after the transition. We do need a new service time for queue j when a customer departs from queue $j-1$ and queue j was empty before, i.e., $Z_{j,i} = 0$.

Remark 1

If $\mathcal {Z}(\mathbf {Z}_i)$ is not uniquely defined, it is not clear in which order the transitions should happen. However, in most cases it is not important for our probability of interest which of the transitions happens first. Only if $\mathcal {Z}(\mathbf {Z}_i) = \bar{Z}_{0,i} = \bar{Z}_{d,i}$, i.e., an arrival happens at the same time as a departure from the system, the order does matter, and we use the convention that the departure occurs first, i.e., $\mathcal {Z}(\mathbf {Z}_i) = \bar{Z}_{d,i}$.

As for the Markovian system in [6, 8], we will work with the scaled process. Therefore, we define

$$\begin{aligned} \mathbf {X}_i = (X_{1,i}, \ldots , X_{d,i}, \bar{X}_{0,i}, \ldots , \bar{X}_{d,i}) = \frac{1}{N} \mathbf {Z}_i, \end{aligned}$$

and we have

$$\begin{aligned} \mathbf {X}_{i+1} = \mathbf {X}_i + \frac{1}{N} V_X(\mathbf {X}_i), \end{aligned}$$

where $V_X(\mathbf {X}_i) = V_Z(\mathbf {X}_iN)$ is the $(i+1)$th transition when the state of the scaled system is $\mathbf {X}_i$. The advantage of the scaled system is that the first d elements of the state description are always in [0, 1], which does not increase as N increases. Note that for the scaled system we will use a similar convention as in Remark 1. Similarly to the unscaled system, we define $\mathcal {X}(\mathbf {X}_i) = \frac{\mathcal {Z}(\mathbf {X}_i)}{N}$. Hence, for $i > 0$, we have that

$$\begin{aligned}&V_X(\mathbf {X}_i) = -\mathcal {X}(\mathbf {X}_i)N\left( \bar{\mathbf {e}}_0 + \sum _{k =1}^d \bar{\mathbf {e}}_k \mathbb {1}\{X_{k,i}> 0\}\right) \nonumber \\&\quad +\left\{ \begin{array}{ll} \mathbf {e}_1 + A_i \bar{\mathbf {e}}_0 + B^{(1)}_i\bar{\mathbf {e}}_1\mathbb {1}\{X_{1,i} = 0\} &{}\qquad \text { if } \mathcal {X}(\mathbf {X}_i) = \bar{X}_{0,i},\\ \mathbf {e}_{j+1} - \mathbf {e}_j + B^{(j)}_i \bar{\mathbf {e}}_j\mathbb {1}\left\{ X_{j,i}> \frac{1}{N}\right\} \\ \qquad + B^{(j+1)}_i \bar{\mathbf {e}}_{j+1}\mathbb {1}\{X_{j+1,i} = 0\} &{}\qquad \text { if } \mathcal {X}(\mathbf {X}_i) = \bar{X}_{j,i}, \text { } j = 1,\ldots ,d-1,\\ -\mathbf {e}_{d} + B^{(d)}_i\bar{\mathbf {e}}_d \mathbb {1}\left\{ X_{d,i} > \frac{1}{N}\right\} &{}\qquad \text { if } \mathcal {X}(\mathbf {X}_i) = \bar{X}_{d,i}, \end{array}\right. \end{aligned}$$

(2)

and

$$\begin{aligned} V_X(\mathbf {X}_0) = A_0 \bar{\mathbf {e}}_0 + B^{(1)}_0\bar{\mathbf {e}}_1, \end{aligned}$$

where $\mathbf {X}_0 = (\frac{1}{N},0,\ldots ,0)$.

Now that we have defined the full state description, we define the goal set $\delta _e$ and taboo set $\delta _0$ in the following way:

$$\begin{aligned} \delta _e&= \left\{ \mathbf {x}: \sum _{k = 1}^d x_k= 1-\frac{1}{N}, \mathcal {X}(\mathbf {x}) = \bar{x}_{0}\right\} , \nonumber \\ \delta _0&= \left\{ \mathbf {x}: x_{k} = \bar{x}_{k} = 0\ \forall k \in \{1,\ldots , d\}\right\} , \end{aligned}$$

(3)

where the goal set is reached if there are $N-1$ customers in the system and the next event is an arrival to the system, and the taboo set is reached when there are no customers in the system.

Using the definitions above, we define the time to reach $\delta _e$ before $\delta _0$ as

$$\begin{aligned} \tau _N = \inf \{i > 0: \mathbf {X}_i \in \delta _e, \mathbf {X}_k \notin \delta _0 \ \forall k = 1,\dots ,i-1\}, \end{aligned}$$

and we set $\tau _N= \infty$ when $\delta _0$ is reached before $\delta _e$. Now we can write our probability of interest, $p_N$, in terms of $\tau _N$ as

$$\begin{aligned} p_N = \mathbb {P}\left( \tau _N < \infty \right) . \end{aligned}$$

Remark 2

Note that we could define $\delta _e$ and $\delta _0$ differently, i.e., there are more states for which we know that the total number of customers will reach N or that the system will be empty. However, the current definitions are easy to use and it turns out that these definitions are sufficient for our proofs; see Remarks 8 and 12.

From [1, 12], we know that the decay rate of $p_N$ equals

$$\begin{aligned} \gamma = - \lim _{N \rightarrow \infty } \frac{1}{N} \log p_N = - \varLambda _A(-\theta ^*), \end{aligned}$$

(4)

where $\theta ^* = \min _j\{\theta _j\}$ with

$$\begin{aligned} \theta _j = \sup \{\theta : \varLambda _A(-\theta ) + \varLambda _{B^{(j)}}(\theta ) \le 0\}, \end{aligned}$$

(5)

or equivalently $\theta _j = \sup \{\theta : M_A(-\theta )M_{B^{(j)}}(\theta ) \le 1\}$. Note that as a result of the stability and non-triviality assumption, $0< \theta ^* < \infty$; see [2] for a formal proof of $\mathbb {P}(B^{(j)} > A) \Leftrightarrow \theta ^* = \infty$. This gives rise to the following definition.

Definition 1

Queue j is a bottleneck queue when $\theta _j = \theta ^*$.

Which queue is the bottleneck also determines the form of the so-called most likely path to overflow: if the overflow level is reached, this is most likely done along a specific path (that dominates the probability of reaching the overflow level and hence determines the decay rate). When queue j is the bottleneck queue, it is therefore expected that along the most likely path $x_j > 0$.

2.2 Preliminaries

In order to estimate the probability of interest using simulation, we use importance sampling to make our event of interest less rare by changing the underlying probability distribution. In the current work, we make the change of measure state-dependent by using the subsolution approach.

2.2.1 Subsolution approach

The subsolution approach for importance sampling has been introduced in [7]. Later, in [6, 8], it has been used to find a state-dependent change of measure that results in an asymptotically efficient estimator for $p_N$ in the context of a Markovian tandem queue [6] and Jackson networks [8]. The definition of a classical subsolution is as follows.

Definition 2

A real-valued function $W(\mathbf {x})$ is called a classical subsolution if

• 1. $W(\mathbf {x})$ is continuously differentiable,

• 2. $\mathbb {H}(\mathbf {x},\hbox {DW}(\mathbf {x})) \ge 0$ for every $\mathbf {x}$,

• 3. $W(\mathbf {x}) \le 0$ for $\mathbf {x} \in \delta _e$,

where

$$\begin{aligned} \mathbb {H}(\mathbf {x},\hbox {DW}(\mathbf {x})) = -\log \left( \mathbb {E}\left[ e^{-\langle \hbox {DW}(\mathbf {x}), V_{X}(\mathbf {x}) \rangle }\right] \right) . \end{aligned}$$

(6)

In addition to this definition, in order to use the subsolution as a basis for a change of measure we require that

• 4. $W((\tfrac{1}{N},0,\ldots ,0)) = \gamma$,

so that the change of measure can be useful (i.e., asymptotically efficient; see Definition 3). This means that along the most likely path to reach the overflow level, subsolution properties 2 and 3 are satisfied with equality; see also [8].

In [6], there is an additional condition in the definition of a classical subsolution for the boundaries, when at least one of the queues is empty, and in [8] there are dedicated boundary functions for $\mathbb {H}(\mathbf {x}, \hbox {DW}(\mathbf {x}))$, which are used when one of the queues is empty. We will include the boundaries in $\mathbb {H}(\mathbf {x},\hbox {DW}(\mathbf {x}))$, as the boundaries are included in $V_X(\mathbf {x})$ by means of indicator functions.

Remark 3

The function $W(\mathbf {x})$ that we will construct in the sequel consists of (a combination of) affine functions so that for all these affine functions its derivative $\hbox {DW}(\mathbf {x})$ is a constant. Whenever we consider an affine function, we will denote the derivative by $\varvec{\alpha }$.

2.2.2 Importance sampling simulation

In this paper, we will propose a particular change of measure and prove that it results in an asymptotically efficient estimator for $p_N$; see Definition 3. In order to define the change of measure, we first introduce some notation for the probability measure. With some abuse of notation, we let ${\text {d}}F_{V_{X}(\mathbf {x})}(\mathbf {v})$ be the probability measure for some random vector $V_X(\mathbf {x})$. Typically, the vector $V_X(\mathbf {x})$ contains one random variable, see (2), but it may result in zero or two random variables as well, for example, when a customer moves from queue j to $j+1$ and queue $j+1$ is empty, there are two random variables in $V_X(\mathbf {x})$. For example, we can interpret ${\text {d}}F_{V_{X}(\mathbf {x})}(\mathbf {v})$ as ${\text {d}}F_A(a)$ if $\mathcal {X}(\mathbf {x}) = \bar{x}_0$ and $x_1 > 0$.

Remark 4

The probability measure of $V_X(\mathbf {x})$ can be written in a more formal way, which we illustrate by considering the arrival transition in a single queue. Thus, consider a state $\mathbf {x}=(x_1, \bar{x}_0, \bar{x}_1)$ for which $x_1>0$ and $\mathcal {X}(\mathbf {x})= \bar{x}_0$. Then, we have

$$\begin{aligned} F_{V_X(\mathbf {x})}(\mathbf {v} |\mathbf {x}: \bar{x}_0 < \bar{x}_1, x_1 > 0) = \mathbb {1}\{v_1 \ge 1\} \cdot F_A(\bar{v}_0 + \bar{x}_0N) \cdot \mathbb {1}\{\bar{v}_1 \ge -\bar{x}_0N\}, \end{aligned}$$

and thus the density

$$\begin{aligned} \frac{\partial ^3 F_{V_X(\mathbf {x})}(\mathbf {v} | \mathbf {x}: \bar{x}_0 < \bar{x}_1, x_1 > 0) }{\partial v_1 \partial \bar{v}_0 \partial \bar{v}_1} = \delta (v_1 - 1) \cdot {\text {d}}F_A(\bar{v}_0 + \bar{x}_0N) \cdot \delta (\bar{v}_1 + \bar{x}_0N). \end{aligned}$$

We remark that two of the three components of the transition $V_X(\mathbf {x})$ are deterministic, while the remaining component consists of a random sample from the inter-arrival time distribution $F_A$, added to the deterministic value $-\bar{x}_0 N$. Also, in larger models, most components of the transition are deterministic (cf. (2)); therefore, we prefer the shorter but less precise notation in which only the random component(s) are written down.

Let $W(\mathbf {x})$ be a classical subsolution; see Sect. 2.2.1. Then, we define the change of measure as

$$\begin{aligned} {\text {d}}\bar{F}_{V_{X}(\mathbf {x})}(\mathbf {v} | \mathbf {x}) = e^{\langle -\hbox {DW}(\mathbf {x}),\mathbf {v}\rangle } e^{\mathbb {H}(\mathbf {x}, \hbox {DW}(\mathbf {x}))}{\text {d}}F_{V_{X}(\mathbf {x})}(\mathbf {v}), \end{aligned}$$

(7)

where $\bar{F}_{V_{X}(\mathbf {x})}(\mathbf {v} | \mathbf {x})$ is the distribution function under the new measure and $\mathbb {H}(\mathbf {x}, \hbox {DW}(\mathbf {x}))$ is defined in (6). Note that the latter quantity can be interpreted as a normalization constant. In fact, (7) means that we apply an exponential tilt to a random variable (that depends on the random vector $V_X(\mathbf {x})$), for example, when $\mathcal {X}(\mathbf {x}) = \bar{x}_0$ and $x_1 > 0$ we are tilting the inter-arrival times exponentially with some parameter.

While performing a simulation run and changing the underlying probability distributions at every step, we keep track of the likelihood ratio. The likelihood ratio for a successful path $\mathcal {P}= (\mathbf {X}_i, i = 0,\ldots ,\tau _N)$ is

$$\begin{aligned} L(\mathcal {P}) = \prod _{i=0}^{\tau _N-1}\frac{{\text {d}}F_{V_{X}(\mathbf {X}_i)}(V_{X}(\mathbf {X}_i))}{{\text {d}}\bar{F}_{V_{X}(\mathbf {X}_i)}(V_{X}(\mathbf {X}_i) | \mathbf {X}_i)} = \prod _{i=0}^{\tau _N-1} e^{\langle \hbox {DW}(\mathbf {X}_i),V_{X}(\mathbf {X}_i)\rangle } e^{-\mathbb {H}(\mathbf {X}_i,\hbox {DW}(\mathbf {X}_i))}, \end{aligned}$$

(8)

where the second equality follows by using (7).

We now define the estimator of $p_N$ to be $L(\mathcal {P})I(\mathcal {P})$, where $I(\mathcal {P})$ indicates whether we have reached level N or not, i.e., $I(\mathcal {P})= \mathbb {1}\{\tau _N < \infty \}$. This estimator is unbiased under the new measure, denoted by $\mathbb {Q}$, since

$$\begin{aligned} p_N = \mathbb {E}\left[ I(\mathcal {P})\right] = \mathbb {E}^\mathbb {Q}\left[ L(\mathcal {P})I(\mathcal {P})\right] . \end{aligned}$$

We use the following definition for asymptotic efficiency.

Definition 3

The estimator for $p_N$ is asymptotically efficient if and only if

$$\begin{aligned} \liminf _{N \rightarrow \infty }\frac{\log \mathbb {E}^{\mathbb {Q}}\left[ L(\mathcal {P})^2I(\mathcal {P})\right] }{\log p_N} \ge 2. \end{aligned}$$

Using the decay rate of $p_N$, see (4), we find that Definition 3 is equivalent to the following definition.

Corollary 1

The estimator for $p_N$ is asymptotically efficient if and only if

$$\begin{aligned} \limsup _{N \rightarrow \infty } \frac{1}{N} \log \mathbb {E}^{\mathbb {Q}}\left[ L(\mathcal {P})^2I(\mathcal {P})\right] \le -2 \gamma . \end{aligned}$$

3 Asymptotically efficient change of measure

In this section, we present our main result. For readability, we present it for three cases separately. In Sect. 3.1, we start with $d=1$, i.e., the single queue, where the subsolution approach results in a state-independent change of measure. Although this change of measure has been proven to be asymptotically efficient in [12], we present an alternative proof using the method that will be extended to a state-dependent change of measure for the d-node tandem queue. Secondly, we consider $d=2$ in Sect. 3.2 in detail, as in this case the state vector consists of five dimensions only. Lastly, in Sect. 3.3, we present the result for the d-node tandem queue, but we omit the proofs since they are very similar to the two-node case.

The approach of the subsolution method, as developed in [7], is the same in all cases defined above and is as follows:

• 1. For all possible $\mathbf {x}$, we find solutions $\varvec{\alpha }$ to $\mathbb {H}(\mathbf {x},\varvec{\alpha }) \ge 0$.

• 2. We construct a function $W(\mathbf {x})$ that both is continuously differentiable and satisfies properties 3 and 4 in and below Definition 2, as $N\rightarrow \infty$. The function $W(\mathbf {x})$ will be as indicated in Remark 3; more precisely, for each $\mathbf {x}$ we will have $\hbox {DW}(\mathbf {x}) \approx \varvec{\alpha }$, where $\varvec{\alpha }$ is a solution corresponding to $\mathbf {x}$ as found in Step 1.

• 3. We then use the function $W(\mathbf {x})$ to define a change of measure as in (7).

After we have proposed the change of measure, we will prove asymptotic efficiency of this change of measure.

3.1 The single GI|GI|1 queue

For the single queue, the model, as presented in Sect. 2.1, simplifies significantly. We will highlight the most important simplifications. To start with, the state description reduces to $\mathbf {x} = (x_1, \bar{x}_0, \bar{x}_1)$. Furthermore, queue 1 is never empty during a busy cycle of the system and so $\mathcal {X}(\mathbf {x}) = \min \{\bar{x}_{0}, \bar{x}_{1}\}$. Due to the same reason, we always have $\mathbb {1}\{x_{1} = 0\} = 0$ and, when there is a departure from the system, $\mathbb {1}\{x_{1} > \frac{1}{N}\} = 1$ (otherwise, $\mathbf {x} \in \delta _0$, i.e., the system will become empty after the transition). In view of Remark 6, we do not yet substitute $\mathbb {1}\{x_{1} = 0\} = 0$ in the remainder. Thus, (2) in the case $d=1$ becomes

$$\begin{aligned} V_X(\mathbf {x}) =&-\mathcal {X}(\mathbf {x})N\left( \bar{\mathbf {e}}_0 + \bar{\mathbf {e}}_1 \mathbb {1}\{x_{1}> 0\}\right) \\&+{\left\{ \begin{array}{ll} \mathbf {e}_1 + A_i \bar{\mathbf {e}}_0 + B^{(1)}_i\bar{\mathbf {e}}_1\mathbb {1}\{x_{1} = 0\} &{}\text { if } \mathcal {X}(\mathbf {x}) = \bar{x}_{0},\\ -\mathbf {e}_{1} + B^{(1)}_i\bar{\mathbf {e}}_1 \mathbb {1}\left\{ x_{1} > \frac{1}{N}\right\} &{}\text { if } \mathcal {X}(\mathbf {x}) = \bar{x}_{1}. \end{array}\right. } \end{aligned}$$

In the next sections, we will follow the subsolution approach step by step and conclude with a proof of asymptotic efficiency of the change of measure based on the developed subsolution.

3.1.1 Solution to $\mathbb {H}(\mathbf {x},\varvec{\alpha }) \ge 0$ for all $\mathbf {x}$

We have, for all possible $\mathbf {x} \ne (\tfrac{1}{N},0,0)$, from (6) and the above, that

and

$$\begin{aligned} \mathbb {H}\left( \left( \tfrac{1}{N}, 0,0\right) , \varvec{\alpha }\right) = -\varLambda _A(-\bar{\alpha }_0) - \varLambda _{B^{(1)}}(-\bar{\alpha _1}). \end{aligned}$$

Then, using that $\mathbb {1}\{x_{1} = 0\} = 0$, a solution to $\mathbb {H}(\mathbf {x},\varvec{\alpha })\ge 0$ for all $\mathbf {x}$ during a busy cycle of the system is

$$\begin{aligned} \varvec{\alpha } = (\alpha _1,\bar{\alpha }_0, \bar{\alpha }_1) = (-\gamma , \theta ^*, -\theta ^*), \end{aligned}$$

where $\theta ^*$ equals $\theta _1$ in (5).

Remark 5

Another solution to $\mathbb {H}(\mathbf {x},\varvec{\alpha }) \ge 0$ is $\varvec{\alpha } = (0,0,0)$. As this is equivalent to no change of measure, we will not use this solution.

Remark 6

To justify the necessity of $\mathbf {X}_0 \ne (0,0,0)$, we note that when $\mathbf {X}_0$ would be equal to  (0, 0, 0) our proposed solution does not satisfy $\mathbb {H}(\mathbf {x},\varvec{\alpha }) \ge 0$ for $\mathcal {X}(\mathbf {x}) = \bar{x}_{0}$. Using $\mathbf {X}_0$ solves this issue. We will justify our specific choice of $\mathbf {X}_0 = (\frac{1}{N},0,0)$ in Remark 7.

3.1.2 Construction of $W(\mathbf {x})$

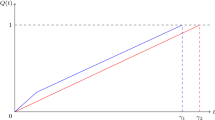
To use the subsolution approach, we want to choose the function $W(\mathbf {x})$ such that $W(\mathbf {x}) \le 0$ for $\mathbf {x} \in \delta _e$ and $W((\tfrac{1}{N},0,0)) = \gamma$; see properties 3 and 4 in and below Definition 2. For the single queue, we have $\delta _e = \{\mathbf {x}: x_{1} = 1-\frac{1}{N}, \mathcal {X}(\mathbf {x}) = \bar{x}_{0} \}$; see (3). Combining these, together with $\hbox {DW}(\mathbf {x}) = \varvec{\alpha } = (-\gamma ,\theta ^*, -\theta ^*)$, we find

$$\begin{aligned} W(\mathbf {x}) = -\gamma x_{1} + \theta ^*(\bar{x}_{0} - \bar{x}_{1}) +\gamma , \end{aligned}$$

satisfying all the requirements when $N \rightarrow \infty$: indeed, $W(\mathbf {x}) = -\gamma (1-\frac{1}{N}) + \theta ^*(\bar{x}_{0} - \bar{x}_{1}) +\gamma \le \frac{\gamma }{N}$ for all $\mathbf {x} \in \delta _e$, and $W((\tfrac{1}{N},0,0)) = \gamma \left( 1-\frac{1}{N}\right)$, and so when $N \rightarrow \infty$ the boundary conditions for $W(\mathbf {x})$ are satisfied. In Fig. 2, the function $W(\mathbf {x})$ is displayed as a function of $x_1$ and $\bar{x}_0 - \bar{x}_1$.

Fig. 2

The classical subsolution $W(\mathbf {x})$ for the single queue as a function of $x_1$ and $\bar{x}_0 - \bar{x}_1$

Remark 7

To justify the specific choice of $\bar{x}_0 = \bar{x}_1 = 0$ in $\mathbf {X}_0 = (\tfrac{1}{N},0,0)$, we note that any other choice does not satisfy $W((\tfrac{1}{N},\bar{x}_0,\bar{x}_1)) = \gamma$ when $N \rightarrow \infty$. For the choice $x_1 = \tfrac{1}{N}$, we note that this is equivalent to starting with 1 customer in the system, and hence this is a natural choice.

3.1.3 The change of measure

We now find that, using (7), the change of measure is, for $\mathbf {x} \ne (\tfrac{1}{N}, 0,0)$,

$$\begin{aligned} {\text {d}}\bar{F}_{V_{X}(\mathbf {x})}(\mathbf {v} | \mathbf {x}) =&{\left\{ \begin{array}{ll} \frac{e^{-a\theta ^*}}{M_A(-\theta ^*)} {\text {d}}F_A(a) &{} \text { if } \mathcal {X}(\mathbf {x}) = \bar{x}_{0},\\ \frac{e^{b_1\theta ^*}}{M_{B^{(1)}}(\theta ^*)} {\text {d}}F_{B^{(1)}}(b_1)&{} \text { if } \mathcal {X}(\mathbf {x}) = \bar{x}_{1}, \end{array}\right. } \end{aligned}$$

(9)

and

$$\begin{aligned} {\text {d}}\bar{F}_{V_{X}((\tfrac{1}{N},0,0))}(\mathbf {v} | (\tfrac{1}{N},0,0))=&\frac{e^{-a\theta ^*+b_1\theta ^*}}{M_A(-\theta ^*)M_{B^{(1)}}(\theta ^*)} {\text {d}}F_A(a) {\text {d}}F_{B^{(1)}}(b_1). \end{aligned}$$

(10)

Proposition 1

The change of measure provided in (9) and (10) is the same change of measure as the state-independent change of measure from [12].

Proof

The proof is straightforward by noting that the inter-arrival times are exponentially tilted with parameter $-\theta ^*$ and the service times are exponentially tilted with parameter $\theta ^*$. $\square$

3.1.4 Asymptotic efficiency

In [12], it has been shown that the change of measure as mentioned above is asymptotically efficient under the condition that $\mathbb {P}(B_k^{(1)} < M) = 1$ for some finite constant M. This restriction to bounded service times is said to be a technicality, but the paper is not clear about how to remove it. Instead, we will give a different proof without the need for this condition.

Theorem 1

Under Assumption 1, the state-independent change of measure based on $\hbox {DW}(\mathbf {x}) = (-\gamma ,\theta ^*,-\theta ^*)$, see (9) and (10), is asymptotically efficient for the single GI|GI|1 queue.

Proof

We start with the log likelihood, $\log L(\mathcal {P})$, of any path $\mathcal {P}= (\mathbf {X}_i, i = 0,\ldots ,\tau _N)$ such that $\tau _N < \infty$. By using (8), we find

$$\begin{aligned} \log L(\mathcal {P})&= N\sum _{i=0}^{\tau _N -1} \langle \hbox {DW}(\mathbf {X}_i), \mathbf {X}_{i+1}-\mathbf {X}_i \rangle - \sum _{i=0}^{\tau _N -1} \mathbb {H}(\mathbf {X}_i, \hbox {DW}(\mathbf {X}_i)) \nonumber \\&\le N\sum _{i=0}^{\tau _N -1} \langle \hbox {DW}(\mathbf {X}_i), \mathbf {X}_{i+1}-\mathbf {X}_i \rangle \nonumber \\&= N \langle \hbox {DW}(\mathbf {X}_0), \mathbf {X}_{\tau _N} - \mathbf {X}_0 \rangle \nonumber \\&= N \left( -\gamma \left( 1 - \frac{1}{N}-\frac{1}{N}\right) + \theta ^* (\bar{X}_{0,\tau _N} - \bar{X}_{0,0}) - \theta ^*(\bar{X}_{1,\tau _N} - \bar{X}_{1,0})\right) \nonumber \\&= N \left( -\gamma \left( 1-\frac{2}{N}\right) + \theta ^* (\bar{X}_{0,\tau _N} - \bar{X}_{1,\tau _N}) \right) \nonumber \\&< -(N-2)\gamma , \end{aligned}$$

(11)

where we note that $\mathbf {X}_0 = (\frac{1}{N}, 0, 0)$, $\mathbf {X}_{\tau _N} = (1-\frac{1}{N}, \bar{X}_{0,\tau _N}, \bar{X}_{1,\tau _N})$ and $\bar{X}_{0, \tau _N} < \bar{X}_{1, \tau _N}$ by the definition of $\tau _N$ and $\delta _e$. So we have

$$\begin{aligned} \lim _{N \rightarrow \infty } \frac{1}{N}\log \mathbb {E}\left[ L(\mathcal {P})I(\mathcal {P})\right]&= \lim _{N \rightarrow \infty } \frac{1}{N} \log \left( \mathbb {E}\left[ L(\mathcal {P})I(\mathcal {P})| I(\mathcal {P}) = 1\right] \mathbb {P}(I(\mathcal {P}) = 1)\right) \\&\le \lim _{N \rightarrow \infty } \frac{1}{N} \log \left( \mathbb {E}\left[ e^{-(N-2)\gamma }\right] p_N\right) \\&= -2 \gamma , \end{aligned}$$

where the inequality follows from (11) and by the definition of $p_N$, and the second equality follows by using (4). $\square$

Remark 8

In the proof of Theorem 1, we see why we defined $\delta _e$ as in (3), and not simply $\delta _e = \{\mathbf {x}: x_1 = 1\}$; this allows for the second (strict) inequality to hold.

3.2 The two-node GI|GI|1 tandem queue

Although the subsolution approach for the single queue results in a state-independent and asymptotically efficient change of measure, it is known from both [2] (general distributions) and [3, 10] (Markovian distribution) that a state-independent change of measure for the GI|GI|1 tandem queue cannot be asymptotically efficient for all input parameters. We will see that the subsolution method, as it did for the Markovian case in [6, 8], results in a state-dependent change of measure.

In this section, we will use the same approach as in Sect. 3.1 and we conclude by proving asymptotic efficiency of the constructed change of measure.

3.2.1 Solutions to ${\pmb {\mathbb {H}}} (\mathbf {x},\varvec{\alpha }) \ge 0$ for all possible $\mathbf {x}$

We start the method by finding a solution to $\mathbb {H}(\mathbf {x},\varvec{\alpha }) \ge 0$ for all possible $\mathbf {x}$. As before, we let $\hbox {DW}(\mathbf {x})=(\alpha _1, \alpha _2, \bar{\alpha }_0, \bar{\alpha }_1, \bar{\alpha }_2)$ and recall that $\mathcal {X}(\mathbf {x}) = \min _{k \in \{0\} \cup \{j: x_{j} > 0\}} \{\bar{x}_{k}\}$. Then, we have from (6), for all possible $\mathbf {x} \ne (\tfrac{1}{N},0,0,0,0)$,

(12)

and

$$\begin{aligned} \mathbb {H}((\tfrac{1}{N},0,0,0,0),\varvec{\alpha }) = -\varLambda _A(-\bar{\alpha }_0) - \varLambda _{B^{(1)}}(-\bar{\alpha }_1). \end{aligned}$$

Table 1 Some solutions to $\mathbb {H}(\mathbf {x},\varvec{\alpha }) \ge 0$ for all possible $\mathbf {x}$

The solutions to $\mathbb {H}(\mathbf {x},\varvec{\alpha }) \ge 0$ that we describe depend on the number of customers in queue 1 and the number of customers in queue 2. Note that there may be more solutions possible, but in order to find a state-dependent change of measure the current solutions turn out to be sufficient. Clearly, $\varvec{\alpha } = \mathbf {0}$ is always a solution to $\mathbb {H}(\mathbf {x},\varvec{\alpha }) \ge 0$ and is equivalent to no change of measure. However, using $\hbox {DW}(\mathbf {x}) = \varvec{\alpha } = \mathbf {0}$ does not give a subsolution, since in that case it is impossible to satisfy properties 3 and 4 in Definition 2.

In Table 1, $\widetilde{\theta }^{(1)} = \sup \{\theta : \varLambda _A(-\theta ^*) + \varLambda _{B^{(1)}}(\theta ) \le 0\}$ and $\widetilde{\theta }^{(2)} = \sup \{\theta : \varLambda _A(-\theta ^*) + \varLambda _{B^{(2)}}(\theta ) \le 0\}$; see Figs. 3 and 4 for a graphical illustration of $\theta _1$, $\theta _2$, $\widetilde{\theta }^{(1)}$ and $\widetilde{\theta }^{(2)}$. Note that for all solutions proposed in Table 1 we have

$$\begin{aligned} \mathbb {H}\left( \left( \tfrac{1}{N},0,0,0,0\right) , \varvec{\alpha }\right) = -\varLambda _A(-\bar{\alpha }_0) - \varLambda _{B^{(1)}}(-\bar{\alpha }_1) \ge 0. \end{aligned}$$

Fig. 3

Illustration of $\theta _1$, $\theta _2$, $\widetilde{\theta }^{(1)}$ and $\widetilde{\theta }^{(2)}$ when queue 1 is the bottleneck queue

Fig. 4

Similar to Fig. 3, but when queue 2 is the bottleneck queue

Remark 9

All solutions presented in Table 1 satisfy subsolution property 2 along the most likely path (as defined below Definition 1) with equality. Recall that, along the most likely path, $x_j > 0$ when queue j is the bottleneck queue. Note that the only solutions that do not necessarily satisfy $\mathbb {H}(\mathbf {x},\varvec{\alpha }) = 0$ are those along the boundary $x_j = 0$ when queue j is the bottleneck queue (except for $\varvec{\alpha } = \varvec{0}$, which is always possible).

Remark 10

We see from Table 1 that in some cases there is a possibility to choose $\bar{\alpha }_j > 0$. It is not obvious to do so, because then the service times of queue j are tilted in the ‘wrong’ way, since it would imply that on average the service times of queue j are even shorter than under the original measure. Nevertheless, it is a solution that satisfies $\mathbb {H}(\mathbf {x},\varvec{\alpha }) \ge 0$.

3.2.2 Construction of $W(\mathbf {x})$

Since there is no non-trivial solution for $\mathbb {H}(\mathbf {x},\varvec{\alpha }) \ge 0$ that holds for all $\mathbf {x}$, that is, there is not a single affine function $W(\mathbf {x})$ such that for its derivative $\varvec{\alpha }$ this condition holds for all $\mathbf {x}$, it turns out that a different change of measure needs to be applied in different ‘regions’ of the state space that are specified precisely later.

From Table 1, we can extract two non-trivial solutions that are dependent on the bottleneck queue: one which we can use for $x_1 > 0$ (and any $x_2$) and one which we can use for $x_2 > 0$ (and any $x_1$). These solutions, along with the trivial solution, can be found in Table 2 and are sufficient to obtain an asymptotically efficient estimator (as we will prove in Sect. 3.2.4; see Theorem 2). In the construction that is explained below, we will also see that cases in which both $x_j > 0$ can be handled using these subsolutions; see Eq. (14). As it turns out, when both $x_j > 0$, either the solution for $x_1 > 0$or the solution for $x_2 > 0$ will be used.

Table 2 Solutions extracted from Table 1 that are used for the state-dependent change of measure

Remark 11

The other solutions that are described in Table 1 can also be used to find a state-dependent change of measure that is proven to be asymptotically efficient using the same method that is described below; see Theorem 3.

Remember that $\gamma = -\varLambda _A(-\theta ^*)$, and so we define

$$\begin{aligned} \varvec{\alpha }_1= & {} (-\gamma , -\gamma , \theta ^*, 0, -\theta ^*), \\ \varvec{\alpha }_2= & {} (-\gamma , 0, \theta ^*, -\theta ^*,0),\\ \varvec{\alpha }_3= & {} (0,0,0,0,0), \end{aligned}$$

which are used to determine the different changes of measure in each of the ‘regions’ of the state space. Thus, ‘region’ 1—corresponding to $\varvec{\alpha }_1$—has to cover $x_1 = 0$, ‘region’ 2—corresponding to $\varvec{\alpha }_2$—has to cover $x_2 = 0$ and, finally, ‘region’ 3—corresponding to $\varvec{\alpha }_3$—has to cover $x_1 = x_2 = 0$. Note that $\varvec{\alpha }_k$ is the notation for a solution to $\mathbb {H}(\mathbf {x},\varvec{\alpha }) \ge 0$, whereas $\alpha _k$ is the notation for a component of some vector $\varvec{\alpha }$. From these solutions $\varvec{\alpha }_k$, we define three functions

$$\begin{aligned} W_k^{\delta }(\mathbf {x}) = \langle \varvec{\alpha }_k ,\mathbf {x} \rangle + \gamma - k\delta , \quad \text { for } k = 1,2,3, \end{aligned}$$

(13)

for some $\delta > 0$, and their minimum

$$\begin{aligned} W^{\delta }(\mathbf {x}) = W_1^\delta (\mathbf {x}) \wedge W_{2}^\delta (\mathbf {x}) \wedge W_{3}^\delta (\mathbf {x}). \end{aligned}$$

(14)

The idea of this construction, as in [6,7,8], and in particular subtracting $k\delta$, is that the minimum function $W^\delta (\mathbf {x})$ has gradient $\varvec{\alpha }_1$ near $x_1 = 0$, gradient $\varvec{\alpha }_2$ near $x_2 = 0$ and gradient $\varvec{\alpha }_3$ near $x_1 =x_2 =0$, as desired.

Fig. 5

Main dimensions $(x_1, x_2)$ (the scaled queue sizes) of the state space, neglecting $\bar{x}_0, \bar{x}_1, \bar{x}_2$ (the scaled residuals) by setting them equal to 0. The figure shows the three regions where the different $W^{\delta }_k(\mathbf {x})$, $k=1,2,3$, are the minimum function

In Figs. 5 and 6, we give a rough illustration of the behaviour of the function $W^{\delta }(\mathbf {x})$, considering the dependence on the scaled queue lengths $x_1$ and $x_2$ while neglecting the dependence on the scaled residuals $\bar{x}_0$, $\bar{x}_1$ and $\bar{x}_2$. For large N, these can indeed be neglected due to scaling, in particular in the case of bounded supports of the inter-arrival time and service times. However, for unbounded supports there can be exceptions to this idea due to a very large residual inter-arrival time or a very large residual service time. For example, at $x_1 = 0$ we have $W_3^\delta (\mathbf {x}) < \min \{W_1^\delta (\mathbf {x}), W_2^\delta (\mathbf {x})\}$ if and only if $x_2 < \frac{2\delta + \theta ^* (\bar{x}_0 - \bar{x}_2)}{\gamma }$. When $\bar{x}_0 - \bar{x}_2$ is large, $W_3^\delta (\mathbf {x})$ is the minimum function even when $x_2$ is not near 0. Indeed, in this case it is very likely that the system empties before the next arriving customer, and hence it makes sense that $W^\delta (\mathbf {x}) = W_3^\delta (\mathbf {x})$ (and no change of measure will be applied).

Fig. 6

Illustration of the dependence of $W^{\delta }(\mathbf {x})$ on $(x_1, x_2)$, neglecting the scaled residuals as in Fig. 5. The figure here shows how for $\mathbf {x}$ in region k we have $W^{\delta }(\mathbf {x})=W^{\delta }_k(\mathbf {x})$, and hence $\hbox {DW}^{\delta }(\mathbf {x})=\varvec{\alpha }_k$

Note that $W^\delta (\mathbf {x})$ satisfies properties 2–4 in and below Definition 2 by construction. As we have different functions for different regions, $W^\delta (\mathbf {x})$ is not a continuously differentiable function, which is the first property of a classical subsolution. Therefore, we apply a similar mollification procedure as in previous work on Markovian systems; see [6, 8]. This mollification ensures that a derivative exists throughout the whole parameter space. We let

$$\begin{aligned} W^{\varepsilon , \delta }(\mathbf {x}) = -\varepsilon \log \sum _{k=1}^3 e^{-W_k^\delta (\mathbf {x})/\varepsilon }. \end{aligned}$$

(15)

When $\varepsilon \rightarrow 0$, $W^{\varepsilon , \delta }(\mathbf {x})$ converges to $W^\delta (\mathbf {x})$. Another result of this choice of $W^{\varepsilon ,\delta }(\mathbf {x})$ is that

$$\begin{aligned} \hbox {DW}^{\varepsilon ,\delta }(\mathbf {x})&= \sum _{k=1}^3 \rho _k(\mathbf {x}) \varvec{\alpha }_k\nonumber \\&= (-(\rho _1(\mathbf {x}) + \rho _2(\mathbf {x}))\gamma , -\rho _1(\mathbf {x})\gamma , (\rho _1(\mathbf {x}) + \rho _2(\mathbf {x}))\theta ^*, \nonumber \\&\quad -\rho _2(\mathbf {x})\theta ^*, -\rho _1(\mathbf {x})\theta ^*), \end{aligned}$$

(16)

with

$$\begin{aligned} \rho _k(\mathbf {x}) = \frac{e^{-W_k^{\delta }(\mathbf {x})/\varepsilon }}{\sum _j e^{-W_j^\delta (\mathbf {x})/\varepsilon }}. \end{aligned}$$

(17)

Throughout this paper, we make the following assumptions on $\varepsilon$ and $\delta$, as in [6]. We remark that we let $\varepsilon$ and $\delta$ depend on N, though for brevity we do not explicitly write this dependence.

Assumption 3

We choose $\varepsilon$ and $\delta$ dependent on N, such that

$$\begin{aligned}&\bullet \lim _{N \rightarrow \infty } \varepsilon = 0,\\&\bullet \lim _{N \rightarrow \infty } \delta = 0,\\&\bullet \lim _{N \rightarrow \infty } \varepsilon N = \infty ,\\&\bullet \lim _{N \rightarrow \infty } \frac{\varepsilon }{\delta } = 0. \end{aligned}$$

As a result, $W^{\varepsilon , \delta }(\mathbf {x})$ satisfies properties 3 and 4 in and below Definition 2 as $N \rightarrow \infty$, which follows immediately from the following lemma.

Lemma 1

Under Assumption 1, we have, for the two-node GI|GI|1 tandem queue, that $W^{\varepsilon ,\delta }(\mathbf {x}) \le \frac{\gamma }{N}-\delta$ for $\mathbf {x} \in \delta _e$ and $\gamma (1 -\frac{1}{N}) - 3\delta -\varepsilon \log (3) \le W^{\varepsilon ,\delta }(\mathbf {X}_0) \le \gamma -3 \delta$.

Proof

We have, for $\mathbf {x} \in \delta _e$, by (15),

$$\begin{aligned} W^{\varepsilon ,\delta }(\mathbf {x}) \le W_1^\delta (\mathbf {x}) = -\gamma (x_{1} + x_{2}) + \theta ^*(\bar{x}_{0} - \bar{x}_{2}) + \gamma - \delta \le \frac{\gamma }{N}-\delta , \end{aligned}$$

where the final inequality follows as $x_{1} + x_{2} = 1 - \frac{1}{N}$ and $\bar{x}_{0} - \bar{x}_{2} \le 0$ for $\mathbf {x} \in \delta _e$.

For $W^{\varepsilon , \delta }(\mathbf {X}_0)$, we note that $\mathbf {X}_0 = (\tfrac{1}{N},0,0,0,0)$. By (15), we have

$$\begin{aligned} W^{\varepsilon ,\delta }(\mathbf {X}_0) \le&\, W_3^\delta (\mathbf {X}_0) = \gamma - 3\delta ,\\ W^{\varepsilon ,\delta }(\mathbf {X}_0) =&-\varepsilon \log \left( e^{\left( -\gamma \left( 1-\frac{1}{N}\right) + \delta \right) /\varepsilon } + e^{\left( -\gamma \left( 1- \frac{1}{N}\right) + 2\delta \right) /\varepsilon } + e^{(-\gamma + 3\delta )/\varepsilon }\right) \\ \ge&-\varepsilon \log \left( 3e^{\left( -\gamma +\frac{\gamma }{N} + 3\delta \right) /\varepsilon }\right) \\ =&\, \gamma \left( 1- \frac{1}{N}\right) - 3\delta - \varepsilon \log (3). \end{aligned}$$

$\square$

Remark 12

The proof of Lemma 1 again explains our choice of $\delta _e$: it is chosen such that $W^{\varepsilon ,\delta }(\mathbf {x})$ can be upper bounded for $\mathbf {x} \in \delta _e$.

Note that, by construction, we expect that also the second property of a classical subsolution is satisfied for $W^{\varepsilon ,\delta }(\mathbf {x})$, i.e., $\mathbb {H}(\mathbf {x}, \hbox {DW}^{\varepsilon ,\delta }(\mathbf {x})) \ge 0$ when $N \rightarrow \infty$, which we will prove in Lemma 2.

3.2.3 The change of measure

In this section, we will give examples of the change of measure based on $W_k^{\delta }(\mathbf {x})$, see (13), for some parts of the state description. This gives some insight into the change of measure that is applied in the mollified function $W^{\varepsilon ,\delta }(\mathbf {x})$ and how the change of measure that we use in the current paper relates to previous work. When choosing $\hbox {DW}^\delta _k(\mathbf {x})$ in (7) as a constant vector $\varvec{\alpha } = (\alpha _1,\alpha _2, \bar{\alpha }_0, \bar{\alpha }_1, \bar{\alpha }_2)$, the change of measure can be written in terms of $\bar{\alpha }_0$, $\bar{\alpha }_1$ and $\bar{\alpha }_2$ as

$$\begin{aligned}&{\text {d}}\bar{F}_{V_{X}(\mathbf {x})}(\mathbf {v} | \mathbf {x}) = \nonumber \\&\quad \begin{array}{ll} \frac{e^{-a\bar{\alpha }_0- b_1\bar{\alpha }_1\mathbb {1}\{x_{1} = 0\} }}{M_A(-\bar{\alpha }_0) M_{B^{(1)}}(-\bar{\alpha }_1\mathbb {1}\{x_{1} = 0\})}{\text {d}}F_A(a){\text {d}}F_{B^{(1)}}(b_1) &{} \text { if } \mathcal {X}(\mathbf {x}) = \bar{x}_{0},\\ \frac{e^{-b_1\bar{\alpha }_1\mathbb {1}\left\{ x_{1}> \frac{1}{N}\right\} - b_2 \bar{\alpha }_2\mathbb {1}\{x_{2} = 0\}}}{ M_{B^{(1)}}\left( -\bar{\alpha }_1\mathbb {1}\left\{ x_{1}> \frac{1}{N}\right\} \right) M_{B^{(2)}}(-\bar{\alpha }_2\mathbb {1}\{x_{2} = 0\})}{\text {d}}F_{B^{(1)}}(b_1){\text {d}}F_{B^{(2)}}(b_2) &{} \text { if } \mathcal {X}(\mathbf {x}) = \bar{x}_{1},\\ \frac{e^{-b_2\bar{\alpha }_2\mathbb {1}\left\{ x_{2}> \frac{1}{N}\right\} }}{M_{B^{(2)}}\left( -\bar{\alpha }_2\mathbb {1}\left\{ x_{2} > \frac{1}{N}\right\} \right) }{\text {d}}F_{B^{(2)}}(b_2) &{}\text { if } \mathcal {X}(\mathbf {x}) = \bar{x}_{2}, \end{array} \end{aligned}$$

(18)

for $\mathbf {x} \ne \mathbf {X}_0$ and

$$\begin{aligned} {\text {d}}\bar{F}_{V_{X}(\mathbf {X}_0)}(\mathbf {v} | \mathbf {X}_0)&= \frac{e^{-a\bar{\alpha }_0- b_1 \bar{\alpha }_1}}{M_A(-\bar{\alpha }_0) M_{B^{(1)}}(-\bar{\alpha }_1)} {\text {d}}F_A(a){\text {d}}F_{B^{(1)}}(b_1). \end{aligned}$$

(19)

In each of the examples below, we consider the cases where our change of measure based on $W^{\varepsilon ,\delta }(\mathbf {x})$ gets close, as $N \rightarrow \infty$, to an ‘affine’ change of measure as above, that is, based on some $W^\delta _k(\mathbf {x})$ with constant gradient $\varvec{\alpha }$. It is two of these latter ‘limiting’ change of measures that we consider in the following.

Examples of the change of measure

Example 1

Where $W^{\varepsilon ,\delta }(\mathbf {x})$ gets close to $W^\delta _2(\mathbf {x})$, we let $\varvec{\alpha } = \hbox {DW}_2^\delta (\mathbf {x}) = (-\gamma ,0,\theta ^*, -\theta ^*,0)$. Then (18) and (19) reduce to

$$\begin{aligned}&{\text {d}}\bar{F}_{V_{X}(\mathbf {x})}(\mathbf {v} | \mathbf {x}) \\&\quad = {\left\{ \begin{array}{ll} \frac{e^{-a\theta ^*+b_1\theta ^*}}{M_A(-\theta ^*) M_{B^{(1)}}(\theta ^*)}{\text {d}}F_A(a){\text {d}}F_{B^{(1)}}(b_1)&{} \text { if } \mathcal {X}(\mathbf {x}) = \bar{x}_{0} \text { and}\ x_1 = 0,\\ \frac{e^{-a\theta ^*}}{M_A(-\theta ^*) }{\text {d}}F_A(a)&{} \text { if } \mathcal {X}(\mathbf {x}) = \bar{x}_{0} \text { and}\ x_1> 0,\\ \frac{e^{b_1\theta ^*\mathbb {1}\left\{ x_{1}> \frac{1}{N}\right\} }}{ M_{B^{(1)}}\left( \theta ^*\mathbb {1}\left\{ x_{1}> \frac{1}{N}\right\} \right) }{\text {d}}F_{B^{(1)}}(b_1){\text {d}}F_{B^{(2)}}(b_2)&{} \text { if } \mathcal {X}(\mathbf {x}) = \bar{x}_{1} \text { and}\ x_2 = 0,\\ \frac{e^{b_1\theta ^*\mathbb {1}\left\{ x_{1}> \frac{1}{N}\right\} }}{ M_{B^{(1)}}\left( \theta ^*\mathbb {1}\left\{ x_{1}> \frac{1}{N}\right\} \right) }{\text {d}}F_{B^{(1)}}(b_1)&{} \text { if } \mathcal {X}(\mathbf {x}) = \bar{x}_{1} \text { and}\ x_2 > 0,\\ {\text {d}}F_{B^{(2)}}(b_2)&{} \text { if } \mathcal {X}(\mathbf {x}) = \bar{x}_{2}, \end{array}\right. } \end{aligned}$$

for $\mathbf {x} \ne \mathbf {X}_0$ and

$$\begin{aligned} {\text {d}}\bar{F}_{V_{X}(\mathbf {X}_0)}(\mathbf {v} | \mathbf {X}_0)&= \frac{e^{-a\theta ^* + b_1 \theta ^*}}{M_A(-\theta ^*) M_{B^{(1)}}(\theta ^*)} {\text {d}}F_A(a){\text {d}}F_{B^{(1)}}(b_1). \end{aligned}$$

When queue 1 is the bottleneck queue, this corresponds to the state-independent change of measure that has been studied in [2, 9, 11]. On the other hand, when queue 2 is the bottleneck queue, the inter-arrival times are still exponentially tilted with parameter $-\theta ^* = -\theta _2$ and so it also corresponds to the state-independent change of measure studied in those papers. However, it is not the service times of queue 2 that are exponentially tilted, but the service times of queue 1 that are exponentially tilted with parameter $\theta ^* = \theta _2$.

Remark 13

We note that the change of measure used here along the horizontal boundary is different from the one in [6] for a two-node Markovian tandem queue. Let $\lambda$, $\mu _1$ and $\mu _2$ be the exponential rates for the inter-arrival times, and service times of queue 1 and queue 2 under the original measure. If we would consider $\hbox {DW}_2^{\delta }(\mathbf {x}) \equiv \varvec{\alpha }_2 = (-\gamma ,0,\theta ^*, -\widetilde{\theta }^{(1)},0)$, which is a solution to $\mathbb {H}(\mathbf {x},\varvec{\alpha }) \ge 0$ according to Table 1, then we find that under the change of measure the service times of queue 1 have an exponential distribution with rate $\frac{\mu _1\lambda }{\mu _2}$. This does correspond with the results from [6], although they consider the embedded discrete-time Markov chain, while we consider the continuous-time Markov chain.

Example 2

Where $W^{\varepsilon ,\delta }(\mathbf {x})$ gets close to $W^\delta _1(\mathbf {x})$, we let $\varvec{\alpha } = \hbox {DW}_1^\delta (\mathbf {x}) = (-\gamma ,-\gamma ,\theta ^*,0,-\theta ^*)$. Then, (18) and (19) reduce to

$$\begin{aligned} {\text {d}}\bar{F}_{V_{X}(\mathbf {x})}(\mathbf {v} | \mathbf {x})&= {\left\{ \begin{array}{ll} \frac{e^{-a\theta ^* }}{M_A(-\theta ^*) }{\text {d}}F_A(a){\text {d}}F_{B^{(1)}}(b_1)&{} \text { if } \mathcal {X}(\mathbf {x}) = \bar{x}_{0} \text { and}\ x_1 = 0,\\ \frac{e^{-a\theta ^* }}{M_A(-\theta ^*) }{\text {d}}F_A(a)&{} \text { if } \mathcal {X}(\mathbf {x}) = \bar{x}_{0} \text { and}\ x_1> 0,\\ {\text {d}}F_{B^{(1)}}(b_1){\text {d}}F_{B^{(2)}}(b_2)&{} \text { if } \mathcal {X}(\mathbf {x}) = \bar{x}_{1} \text { and}\ x_2 = 0,\\ {\text {d}}F_{B^{(1)}}(b_1)&{} \text { if } \mathcal {X}(\mathbf {x}) = \bar{x}_{1}\text { and}\ x_2> 0,\\ \frac{e^{b_2\theta ^*\mathbb {1}\left\{ x_{2}> \frac{1}{N}\right\} }}{M_{B^{(2)}}\left( \theta ^*\mathbb {1}\left\{ x_{2} > \frac{1}{N}\right\} \right) }{\text {d}}F_{B^{(2)}}(b_2)&{} \text { if } \mathcal {X}(\mathbf {x}) = \bar{x}_{2}, \end{array}\right. } \end{aligned}$$

for $\mathbf {x} \ne \mathbf {X}_0$ and

$$\begin{aligned} {\text {d}}\bar{F}_{V_{X}(\mathbf {X}_0)}(\mathbf {v} | \mathbf {X}_0)&= \frac{e^{-a\theta ^*}}{M_A(-\theta ^*) } {\text {d}}F_A(a){\text {d}}F_{B^{(1)}}(b_1). \end{aligned}$$

When queue 1 is the bottleneck queue, this change of measure corresponds to the state-independent change of measure studied in [2, 9, 11] in the sense that the inter-arrival times are exponentially tilted with parameter $-\theta ^* = -\theta _1$. In contrast to an exponential tilt for the service times of queue 1, which happens for the state-independent change of measure, here we exponentially tilt the service times of queue 2 with parameter $\theta ^* = \theta _1$. When queue 2 is the bottleneck queue, the change of measure described above corresponds to the state-independent change of measure that has been studied in [2, 9, 11].

3.2.4 Asymptotic efficiency

Using (16), we can find a lower bound on $\mathbb {H}(\mathbf {x}, \hbox {DW}^{\varepsilon ,\delta }(\mathbf {x}))$ which goes to 0 when $N \rightarrow \infty$.

Remark 14

Since we assume bounded supports of the various service time distributions, we note that equality is achieved in (5) for all queues j. That is, we have $\varLambda _A(-\theta ^{(j)}) + \varLambda _{B^{(j)}}(\theta ^{(j)}) = 0$ for all queues j. In particular, equality holds for the bottleneck queue. Similarly, equality in the definition of $\widetilde{\theta }^{(1)}$ and $\widetilde{\theta }^{(2)}$ also holds.

Lemma 2

Under Assumptions 1 and 2, we have, for the two-node GI|GI|1 tandem queue, for all possible $\mathbf {x}$,

$$\begin{aligned} \mathbb {H}(\mathbf {x}, \hbox {DW}^{\varepsilon ,\delta }(\mathbf {x})) \ge - (\theta ^*\max \{Q^{(0)},Q^{(1)},Q^{(2)}\} +\gamma )e^{-\delta /\varepsilon }. \end{aligned}$$

Proof

We substitute (16) in (12) to find $\mathbb {H}(\mathbf {x}, \hbox {DW}^{\varepsilon , \delta }(\mathbf {x}))$ for $\mathbf {x} \ne \mathbf {X}_0$ equal to

$$\begin{aligned}&-\mathcal {X}(\mathbf {x})N((\rho _1(\mathbf {x})+\rho _2(\mathbf {x}))\theta ^* - \rho _2(\mathbf {x})\theta ^*\mathbb {1}\{x_1> 0\} -\rho _1(\mathbf {x})\theta ^*\mathbb {1}\{x_2> 0\}) \nonumber \\&\qquad +{\left\{ \begin{array}{ll} -(\rho _1(\mathbf {x}) + \rho _2(\mathbf {x}))\gamma - \varLambda _A(-(\rho _1(\mathbf {x})+\rho _2(\mathbf {x}))\theta ^*)\\ \qquad - \mathbb {1}\{ x_1 = 0\}\varLambda _{B^{(1)}}(\rho _2(\mathbf {x})\theta ^*) \text { if } \mathcal {X}(\mathbf {x}) = \bar{x}_0, \\ (\rho _1(\mathbf {x}) + \rho _2(\mathbf {x}))\gamma -\rho _1(\mathbf {x})\gamma -\mathbb {1}\left\{ x_1> \frac{1}{N}\right\} \varLambda _{B^{(1)}}(\rho _2(\mathbf {x})\theta ^*) \\ \qquad - \mathbb {1}\{x_2 = 0\}\varLambda _{B^{(2)}}(\rho _1(\mathbf {x})\theta ^*) \text { if } \mathcal {X}(\mathbf {x}) = \bar{x}_1,\\ \rho _1(\mathbf {x})\gamma - \mathbb {1}\left\{ x_2> \frac{1}{N}\right\} \varLambda _{B^{(2)}}(\rho _1(\mathbf {x})\theta ^*) \text { if } \mathcal {X}(\mathbf {x}) = \bar{x}_2, \end{array}\right. }\nonumber \\&\quad \ge -\mathcal {X}(\mathbf {x})N( \rho _1(\mathbf {x})\theta ^*\mathbb {1}\{x_2 = 0\} +\rho _2(\mathbf {x})\theta ^*\mathbb {1}\{x_1 = 0\}) \nonumber \\&\qquad +{\left\{ \begin{array}{ll} - \rho _2(\mathbf {x})\mathbb {1}\{x_1 = 0\}\varLambda _{B^{(1)}}(\theta ^*) \text { if } \mathcal {X}(\mathbf {x}) = \bar{x}_0, \\ \rho _2(\mathbf {x})\gamma - \rho _2(\mathbf {x}) \mathbb {1}\left\{ x_1> \frac{1}{N}\right\} \varLambda _{B^{(1)}}(\theta ^*) \\ \qquad - \rho _1(\mathbf {x})\mathbb {1}\{x_2 = 0\}\varLambda _{B^{(2)}}(\theta ^*) \text { if } \mathcal {X}(\mathbf {x}) = \bar{x}_1,\\ \rho _1(\mathbf {x})\gamma - \rho _1(\mathbf {x})\mathbb {1}\left\{ x_2 > \frac{1}{N}\right\} \varLambda _{B^{(2)}}(\theta ^*) \text { if } \mathcal {X}(\mathbf {x}) = \bar{x}_2, \end{array}\right. } \end{aligned}$$

(20)

where the inequality follows from convexity of the log-moment generating functions, $\rho _k(\mathbf {x}) \in [0,1]$ and by the definition of $\gamma =-\varLambda _A(-\theta ^*) \ge 0$. By using $\mathbb {1}\{x_{k} > \frac{1}{N}\} \le 1$ for $k = 1,2$, $\varLambda _A(-\theta ^*) + \varLambda _{B^{(j)}}(\theta ^*) \le 0$ for all queues j by the definition of $\theta ^*$, $\gamma$ and the bounded supports (and hence bounded $\mathcal {X}(\mathbf {x})$), we find that (20) is greater than or equal to

$$\begin{aligned}&-\max \{Q^{(0)}, Q^{(1)}, Q^{(2)}\}( \rho _1(\mathbf {x})\theta ^*\mathbb {1}\{x_2 = 0\} +\rho _2(\mathbf {x})\theta ^*\mathbb {1}\{x_1 = 0\}) \nonumber \\&\quad +{\left\{ \begin{array}{ll} - \rho _2(\mathbf {x})\mathbb {1}\{x_1 = 0\} \varLambda _{B^{(1)}}(\theta ^*) &{}\text { if } \mathcal {X}(\mathbf {x}) = \bar{x}_0, \\ - \rho _1(\mathbf {x})\mathbb {1}\{x_2 = 0\}\varLambda _{B^{(2)}}(\theta ^*) &{}\text { if } \mathcal {X}(\mathbf {x}) = \bar{x}_1,\\ 0 &{}\text { if } \mathcal {X}(\mathbf {x}) = \bar{x}_2. \end{array}\right. } \end{aligned}$$

(21)

For any $\mathbf {x}$ with $x_2 = \bar{x}_2 = 0$, we have, from (17),

$$\begin{aligned} \rho _1(\mathbf {x}) =&\frac{e^{-W_1^{\delta }(\mathbf {x})/\varepsilon }}{\sum _j e^{-W_j^\delta (\mathbf {x})/\varepsilon }} \le \frac{e^{-(\langle \varvec{\alpha }_1,\mathbf {x} \rangle + \gamma - \delta )/\varepsilon }}{e^{-(\langle \varvec{\alpha }_2,\mathbf {x} \rangle + \gamma - 2\delta )/\varepsilon }} = e^{- (\bar{x}_1\theta ^* + \delta )/\varepsilon } \le e^{-\delta /\varepsilon }, \end{aligned}$$

(22)

and, for any $\mathbf {x}$ with $x_1 = \bar{x}_1 = 0$,

$$\begin{aligned} \rho _2(\mathbf {x}) =&\frac{e^{-W_2^{\delta }(\mathbf {x})/\varepsilon }}{\sum _j e^{-W_j^\delta (\mathbf {x})/\varepsilon }} \le \frac{e^{-(\langle \varvec{\alpha }_2,\mathbf {x} \rangle + \gamma - 2\delta )/\varepsilon }}{e^{-(\langle \varvec{\alpha }_3,\mathbf {x} \rangle + \gamma - 3\delta )/\varepsilon }} = e^{-(\bar{x}_0\theta ^*+\delta )/\varepsilon } \le e^{-\delta /\varepsilon }. \end{aligned}$$

(23)

Substituting (22) and (23) in (21), we find, for $\mathbf {x} \ne \mathbf {X}_0$, that

$$\begin{aligned} \mathbb {H}&(\mathbf {x}, \hbox {DW}^{\varepsilon , \delta }(\mathbf {x}))\\ \ge&-\max \{Q^{(0)}, Q^{(1)}, Q^{(2)}\}( \rho _1(\mathbf {x})\theta ^*\mathbb {1}\{x_2 = 0\} +\rho _2(\mathbf {x})\theta ^*\mathbb {1}\{x_1 = 0\})\\ {}&- \rho _2(\mathbf {x})\mathbb {1}\{x_1 = 0\} \varLambda _{B^{(1)}}(\theta ^*)\mathbb {1}\{\mathcal {X}(\mathbf {x}) = \bar{x}_0\}\\ {}&-\rho _1(\mathbf {x})\mathbb {1}\{x_2 = 0\} \varLambda _{B^{(2)}}(\theta ^* )\mathbb {1}\{\mathcal {X}(\mathbf {x}) = \bar{x}_1\}\\ \ge&- e^{-\delta /\varepsilon } \left( \theta ^*\max \{Q^{(0)}, Q^{(1)}, Q^{(2)}\} \right. \\ {}&\qquad \quad \qquad + \left. \varLambda _{B^{(1)}}(\theta ^*)\mathbb {1}\{\mathcal {X}(\mathbf {x}) = \bar{x}_0\} + \varLambda _{B^{(2)}}(\theta ^*)\mathbb {1}\{\mathcal {X}(\mathbf {x}) = \bar{x}_1\}\right) \\ \ge&- e^{-\delta /\varepsilon } \left( \theta ^*\max \{Q^{(0)}, Q^{(1)}, Q^{(2)}\} + \max \left( \varLambda _{B^{(1)}}(\theta ^*), \varLambda _{B^{(2)}}(\theta ^*)\right) \right) \\ =&-\left( \theta ^*\max \{Q^{(0)}, Q^{(1)}, Q^{(2)}\} +\gamma \right) e^{-\delta /\varepsilon }, \end{aligned}$$

where the second and the third inequalities follow as at most one of the indicators equals 1 at any time during a busy cycle of the system and the final equality follows by the definition of $\theta ^*$. To conclude the proof, we write for the initial state that

$$\begin{aligned} \mathbb {H}(\mathbf {X}_0, \hbox {DW}^{\varepsilon , \delta }(\mathbf {X}_0)) =&-\varLambda _A(-(\rho _1(\mathbf {X}_0) + \rho _2(\mathbf {X}_0))\theta ^* ) - \varLambda _{B^{(1)}}(\rho _2(\mathbf {X}_0)\theta ^*)\\ \ge&-(\rho _1(\mathbf {X}_0) + \rho _2(\mathbf {X}_0))\varLambda _A(-\theta ^* ) - \rho _2(\mathbf {X}_0)\varLambda _{B^{(1)}}(\theta ^*) \ge 0. \end{aligned}$$

$\square$

Next we show that $\sum _{i=0}^{\tau _N -1} \langle \hbox {DW}^{\varepsilon ,\delta }(\mathbf {X}_i), \mathbf {X}_{i+1} - \mathbf {X}_i \rangle$ approximates $W^{\varepsilon ,\delta }(\mathbf {X}_{\tau _N}) - W^{\varepsilon ,\delta }(\mathbf {X}_0)$ and provide an upper bound for the error term, similar to Lemma 2 in [4].

Lemma 3

Consider a two-node GI|GI|1 tandem queue satisfying Assumptions 1 and 2. Then, for any successful path $\mathbf {X}_i$, $i = 0,\ldots , \tau _N$, it holds that

$$\begin{aligned} \left| N \sum _{i=0}^{\tau _N -1} \langle \hbox {DW}^{\varepsilon ,\delta }(\mathbf {X}_i), \mathbf {X}_{i+1} - \mathbf {X}_i \rangle - N( W^{\varepsilon ,\delta }(\mathbf {X}_{\tau _N}) - W^{\varepsilon ,\delta }(\mathbf {X}_0)) \right| \le \frac{2C_1^2}{\varepsilon N}\tau _N, \end{aligned}$$

where $C_1 = \sqrt{2}(\gamma + \theta ^*)(\sqrt{2} + \sqrt{3}\max _j\{Q^{(j)}\}) < \infty$.

Proof

We can bound $|\langle \hbox {DW}^{\varepsilon ,\delta }(\mathbf {X}_i), \mathbf {X}_{i+1} - \mathbf {X}_i \rangle - ( W^{\varepsilon ,\delta }(\mathbf {X}_{i+1}) - W^{\varepsilon ,\delta }(\mathbf {X}_i)) |$ for each step i by using the mean value theorem. Let $\mathbf {x} = \mathbf {X}_i$ and $\mathbf {y} = \mathbf {X}_{i+1} - \mathbf {X}_i$. By the mean value theorem, we have $W^{\varepsilon ,\delta }(\mathbf {x} + \mathbf {y}) - W^{\varepsilon ,\delta }(\mathbf {x}) = \langle \hbox {DW}^{\varepsilon ,\delta }(\mathbf {x}+\eta \mathbf {y}), \mathbf {y} \rangle$ for some $\eta \in [0,1]$. For convenience, we denote $R_k(\mathbf {x}) = e^{-W_k^\delta (\mathbf {x})/\varepsilon }$, so that $\rho _k(\mathbf {x}) = \frac{R_k(\mathbf {x})}{\sum _{j=1}^3 R_j(\mathbf {x})}$, and $R_k(\mathbf {x} + \eta \mathbf {y}) = R_k(\mathbf {x}) e^{-\langle \varvec{\alpha }_k, \mathbf {y} \rangle \eta /\varepsilon }$, which implies that $\hbox {DW}^{\varepsilon ,\delta }(\mathbf {x} + \eta \mathbf {y}) = \sum _{k} \rho _k(\mathbf {x}+\eta \mathbf {y}) \varvec{\alpha }_k = \sum _k \frac{R_k(\mathbf {x} + \eta \mathbf {y})}{\sum _{j=1}^3 R_j(\mathbf {x} + \eta \mathbf {y})} \varvec{\alpha }_k$. Thus,

$$\begin{aligned}&|\langle \hbox {DW}^{\varepsilon ,\delta }(\mathbf {x}),\mathbf {y} \rangle - \left( W^{\varepsilon ,\delta }(\mathbf {x} + \mathbf {y}) - W^{\varepsilon ,\delta }(\mathbf {x}) \right) |\nonumber \\&\quad = \left| \frac{\sum _{k=1}^3 R_k(\mathbf {x}) \langle \varvec{\alpha }_k, \mathbf {y} \rangle }{\sum _{j = 1}^3 R_j(\mathbf {x})} - \frac{\sum _{k=1}^3 R_k(\mathbf {x} + \eta \mathbf {y}) \langle \varvec{\alpha }_k, \mathbf {y} \rangle }{\sum _{j=1}^3 R_j(\mathbf {x} + \eta \mathbf {y})} \right| \nonumber \\&\quad = \left| \sum _{k=1}^3 \frac{ R_k(\mathbf {x})\langle \varvec{\alpha }_k, \mathbf {y} \rangle }{\sum _{j=1}^3 R_j(\mathbf {x})} \left( 1-e^{-\langle \varvec{\alpha }_k, \mathbf {y} \rangle \eta / \varepsilon } \frac{\sum _{j=1}^3 R_j(\mathbf {x})}{\sum _{j=1}^3 R_j(\mathbf {x} + \eta \mathbf {y})}\right) \right| \nonumber \\&\quad \le \left| \langle \hbox {DW}^{\varepsilon ,\delta }(\mathbf {x}), \mathbf {y} \rangle \right| \cdot \nonumber \\&\qquad \; \left| \max \{1 - e^{\left( \min _k \langle \varvec{\alpha }_k, \mathbf {y} \rangle - \max _k \langle \varvec{\alpha }_k, \mathbf {y} \rangle \right) \eta /\varepsilon }, e^{\left( \max _k \langle \varvec{\alpha }_k, \mathbf {y} \rangle - \min _k \langle \varvec{\alpha }_k, \mathbf {y} \rangle \right) \eta /\varepsilon } -1\}\right| , \end{aligned}$$

(24)

where the inequality follows by the definition of $\hbox {DW}^{\varepsilon ,\delta }(\mathbf {x})$, see (16), $\rho (\mathbf {x})$ and $R_j(\mathbf {x} + \eta \mathbf {y})$, and by bounding $\langle \varvec{\alpha }_k, \mathbf {y} \rangle$ by the minimum or maximum over k (whichever is appropriate). We use the crude bounds

$$\begin{aligned} |\hbox {DW}^{\varepsilon ,\delta }(\mathbf {x})|\le&\max _k |\varvec{\alpha }_k |\le \sqrt{2 \gamma ^2 + 2(\theta ^*)^2} \le \sqrt{2}(\gamma + \theta ^*),\\ |\mathbf {y} |\le&\frac{1}{N}\max \left\{ \sqrt{1 + 2(Q^{(0)})^2 + (\max \{Q^{(0)}, Q^{(1)}\})^2}, \right. \\&\left. \sqrt{2 + 2(Q^{(1)})^2 + (\max \{Q^{(1)},Q^{(2)}\})^2}, \sqrt{1 + 3(Q^{(2)})^2}\right\} \\ \le&\frac{1}{N}\sqrt{2 + 3\max _j\{(Q^{(j)})^2\}} \le \frac{\sqrt{2} + \sqrt{3}\max _j\{Q^{(j)}\}}{N}, \end{aligned}$$

where the second inequality follows by considering all possible transitions. For example, in the case of an arrival the number of customers in the system changes by 1, the residual inter-arrival time and the residual service time at queue 2 change by at most $Q^{(0)}$ and the residual service time at queue 1 changes by at most $\max \{Q^{(0)}, Q^{(1)}\}$. Letting $C_1 = \sqrt{2}(\gamma + \theta ^*)(\sqrt{2} + \sqrt{3}\max _j\{Q^{(j)}\})$, we find $|\langle \varvec{\alpha }_k, \mathbf {y} \rangle |\le C_1$ for all $k = 1,2,3$, and so we can upper bound (24) by

$$\begin{aligned} \frac{C_1}{N} \left|\max \left\{ 1-e^{-2\frac{C_1\eta }{\varepsilon N}}, e^{2\frac{C_1\eta }{\varepsilon N}}-1\right\} \right|&= \frac{C_1}{N}\left( e^{2\frac{C_1\eta }{\varepsilon N}}-1\right) \\&= \frac{C_1}{N} \left( \frac{C_1 \eta }{\varepsilon N} + \mathcal {O}\left( \frac{C_1^2 \eta ^2}{\varepsilon ^2 N^2}\right) \right) \le \frac{2C_1^2}{\varepsilon N^2}, \end{aligned}$$

where the inequality holds for sufficiently large $\varepsilon N$, and hence we have found

$$\begin{aligned} \left| N \sum _{i=0}^{\tau _N -1} \langle \hbox {DW}^{\varepsilon ,\delta }(\mathbf {X}_{i}),\mathbf { X}_{i+1} - \mathbf {X}_{i} \rangle - N( W^{\varepsilon ,\delta }(\mathbf {X}_{\tau _N}) - W^{\varepsilon ,\delta }(\mathbf {X}_0)) \right| \le \frac{2C_1^2}{\varepsilon N}\tau _N. \end{aligned}$$

$\square$

Remark 15

The bound in Lemma 3 is very crude and better bounds can be obtained by considering all possible transitions separately. However, in order to show asymptotic efficiency the current bound is sufficient.

Remark 16

Some solutions to $\mathbb {H}(\mathbf {x}, \varvec{\alpha }) \ge 0$ in Table 1 use different values rather than $\theta ^*$, for example,  $\widetilde{\theta }^{(1)}$. It is easy to verify that for these different values, similar bounds as in Lemmas 2 and 3 can be obtained by using their definition. The only additional requirement is that the value replacing $\theta ^*$ is finite. Note that $\theta ^*$ is finite by Assumption 1.

In order to show asymptotic efficiency, we need an asymptotic result involving $\tau _N$, the total number of steps to reach level N (given that level N is reached before the system is empty). This is the subject of the following conjecture.

Conjecture 1

If $\sigma _N$ is a sequence of real numbers such that $\sigma _N \rightarrow 0$ when $N \rightarrow \infty$, then

$$\begin{aligned} \limsup _{N \rightarrow \infty }\frac{1}{N} \log \mathbb {E}^{\mathbb {Q}}\left[ e^{\tau _N \sigma _N}| \tau _N < \infty \right] = 0. \end{aligned}$$

(25)

Intuition

We note that we can upper bound $\tau _N$ by $3K_N$, where $K_N$ is the index of the first customer who reaches the overflow level N. Along the major part of the most likely path to reach the overflow level, the change of measure is very close to the state-independent change of measure as discussed in [2] (see also Examples 1 and 2). In Lemmas 3.2 and 4.1 of that same paper, it is shown that under this state-independent change of measure the system is unstable and $\frac{K_N}{N} \rightarrow C < \infty$ with probability 1. This means that the left-hand side of (25) would be upper bounded by $\limsup _{N \rightarrow \infty }\frac{1}{N} \log \mathbb {E}^{\mathbb {Q}}\left[ e^{3K_N \sigma _N}| \tau _N < \infty \right]$, which behaves as $\limsup _{N \rightarrow \infty }\frac{1}{N} \log \mathbb {E}^{\mathbb {Q}}\left[ e^{3 C N \sigma _N}\right] = \lim _{N \rightarrow \infty } 3 C \sigma _N = 0$. Also, suppose that (25) does not hold, i.e. $\limsup _{N \rightarrow \infty }\frac{1}{N} \log \mathbb {E}^{\mathbb {Q}}\left[ e^{\tau _N \sigma _N} | \tau _N < \infty \right] > 0$. This means that the random variable $\tau _N$, and also the random variable $K_N$, would grow much faster than N as $N \rightarrow \infty$, which does not seem plausible.

For a mathematical proof of the conjecture, two problems remain. The first one is to show that the difference between the actual change of measure and the state-independent change of measure (which is small along the most likely path) does not influence the validity of (25). The second problem is to show that for the state-independent change of measure we indeed have $\limsup _{N \rightarrow \infty }\frac{1}{N} \log \mathbb {E}^{\mathbb {Q}}\big [e^{3K_N\sigma _N}| \tau _N < \infty \big ] = 0$. Even if the change of measure were equal to the state-independent change of measure along the whole state space, we could not show this relation. Of course, there may be other possibilities to show that (25) holds.

We can now prove the main theorem of this section.

Theorem 2

Suppose we have a two-node GI|GI|1 tandem queue satisfying Assumptions 1 and 2. Then, under Conjecture 1 and Assumption 3, the change of measure based on $\hbox {DW}^{\varepsilon , \delta }(\mathbf {x})$ in Eq. (16) is asymptotically efficient.

Proof

For a successful path $\mathcal {P}$, we have

$$\begin{aligned} \log L(\mathcal {P})&= N \sum _{i=0}^{\tau _N -1} \langle \hbox {DW}^{\varepsilon ,\delta }(\mathbf {X}_i), \mathbf {X}_{i+1} - \mathbf {X}_i \rangle - \sum _{i=0}^{\tau _N -1} \mathbb {H}(\mathbf {X}_{i}, \hbox {DW}^{\varepsilon ,\delta }(\mathbf {X}_{i}))\\&\le \frac{2C_1^2}{\varepsilon N}\tau _N + NW^{\varepsilon ,\delta }(\mathbf {X}_{\tau _N}) - NW^{\varepsilon ,\delta }(\mathbf {X}_0)\\&\quad +\, (\theta ^*\max \{Q^{(0)},Q^{(1)},Q^{(2)}\} +\gamma ) e^{-\delta /\varepsilon }\tau _N, \end{aligned}$$

where the second step follows from Lemmas 2 and 3. Define $\sigma _N = \frac{2C_1^2}{\varepsilon N} + (\theta ^*\max \{Q^{(0)},Q^{(1)},Q^{(2)}\} +\gamma ) e^{-\delta /\varepsilon }$. Then it follows that

$$\begin{aligned} \log L(\mathcal {P}) \le \tau _N \sigma _N + NW^{\varepsilon ,\delta }(\mathbf {X}_{\tau _N}) - NW^{\varepsilon ,\delta }(\mathbf {X}_0). \end{aligned}$$

Since $\mathbf {X}_{\tau _N} \in \delta _e$ for the successful path $\mathcal {P}$, we find, by using Lemma 1,

$$\begin{aligned} \log L(\mathcal {P})&\le \tau _N \sigma _N + N\left( \frac{\gamma }{N} - \delta \right) - N\left( \gamma \left( 1-\frac{1}{N}\right) - 3\delta -\varepsilon \log (3)\right) \\&= \tau _N \sigma _N + 2N\delta - \gamma (N-2) + \varepsilon N \log (3), \end{aligned}$$

and so we have

$$\begin{aligned}&\limsup _{N \rightarrow \infty } \frac{1}{N}\log \mathbb {E}^{\mathbb {Q}}\left[ L(\mathcal {P})^2I(\mathcal {P})\right] \\&\qquad \le \limsup _{N \rightarrow \infty } \frac{1}{N}\log \mathbb {E}^{\mathbb {Q}}\left[ e^{2\tau _N \sigma _N + 4N\delta - 2\gamma (N-2) + 2\varepsilon N \log (3)}I(\mathcal {P})\right] \\&\qquad =-2\gamma + \limsup _{N \rightarrow \infty } \frac{1}{N} \log \left( \mathbb {E}^{\mathbb {Q}} \left[ e^{2\tau _N \sigma _N}| I(\mathcal {P}) =1\right] \mathbb {P}^{\mathbb {Q}}(I(\mathcal {P}) =1)\right) \\&\qquad \le -2\gamma + \limsup _{N \rightarrow \infty } \frac{1}{N} \log \mathbb {E}^{\mathbb {Q}} \left[ e^{2\tau _N \sigma _N}| \tau _N < \infty \right] , \end{aligned}$$

where the equality follows by Assumption 3 and the last step follows by noting that $\mathbb {P}^{\mathbb {Q}}(I(\mathcal {P}) =1) \le 1$. Using Conjecture 1 concludes the proof. $\square$

Remark 17

In the proof of Theorem 2, we bounded $N \sum _{i=0}^{\tau _N -1} \langle \hbox {DW}^{\varepsilon ,\delta }(\mathbf {X}_i), \mathbf {X}_{i+1} - \mathbf {X}_i \rangle$ and $\sum _{i=0}^{\tau _N -1} \mathbb {H}(\mathbf {X}_{i}, \hbox {DW}^{\varepsilon ,\delta }(\mathbf {X}_{i}))$ separately, resulting in bounds involving the maximum support of the various distributions. Looking at Eqs. (18) and (19), we see, for example, that the new probability density functions themselves do not depend on $\mathcal {X}(\mathbf {X}_i)N$, and thus the likelihood ratio in (8) does not depend on $\mathcal {X}(\mathbf {X}_i)N$, even though $\mathcal {X}(\mathbf {X}_i)$ is needed in order to determine which probability density function is used. However, to use the mean value theorem in Lemma 3 we do need to keep this quantity throughout the proofs.

We can extend Theorem 2 to the following set of changes of measure; see also Remarks 11 and 16. We restrict ourselves to three regions only, since this is the easiest from an implementation perspective. Let

$$\begin{aligned} \hbox {DW}^{\varepsilon ,\delta }(\mathbf {x})&= (-(\rho _1(\mathbf {x}) + \rho _2(\mathbf {x}))\gamma , -\rho _1(\mathbf {x})\gamma , (\rho _1(\mathbf {x}) + \rho _2(\mathbf {x}))\theta ^*,\nonumber \\&\quad -\rho _1(\mathbf {x})\bar{\alpha }_{1,1}-\rho _2(\mathbf {x})\bar{\alpha }_{1,2}, -\rho _1(\mathbf {x})\bar{\alpha }_{2,1} - \rho _2(\mathbf {x})\bar{\alpha }_{2,2}), \end{aligned}$$

(26)

where

$$\begin{aligned} \bar{\alpha }_{1,1}\in & {} [0,-\bar{\alpha }_{2,1}-\theta ^*],\\ \bar{\alpha }_{2,1}\in & {} [-\widetilde{\theta }^{(2)},-\theta ^*], \\ \bar{\alpha }_{1,2}\in & {} [-\widetilde{\theta }^{(1)}, -\theta ^*], \\ \bar{\alpha }_{2,2}\in & {} [0,-\bar{\alpha }_{1,2} - \theta ^*] . \end{aligned}$$

Note that when queue j is the bottleneck queue, $\widetilde{\theta }^{(j)} = \theta ^*$ and hence along the most likely path still the state-independent change of measure studied in [2, 9, 11] is used.

We leave the proof of the following theorem to the reader, as this only requires some small modifications in the proofs of Lemmas 2, 3 and Theorem 2.

Theorem 3

Suppose we have a two-node GI|GI|1 tandem queue satisfying Assumptions 1 and 2. Then, under Conjecture 1 and Assumption 3, the change of measure based on $\hbox {DW}^{\varepsilon , \delta }(\mathbf {x})$ in Eq. (26) is asymptotically efficient.

3.3 The d-node GI|GI|1 tandem queue

In this section, we present the steps to follow in order to find a state-dependent change of measure for the d-node GI|GI|1 tandem queue. As we needed a conjecture for the case $d=2$, we also need a conjecture for the more general case. We will formulate similar lemmas as in Sect. 3.2 but omit the proofs, as these are just extensions of the proofs for the two-node tandem queue and therefore do not require any additional techniques.

3.3.1 Solutions to ${\pmb {\mathbb {H}}}(\mathbf {x},\varvec{\alpha }) \ge 0$ for all possible $\mathbf {x}$

For the d-node tandem queue we have, for $\mathbf {x}\ne \mathbf {X}_0$,

$$\begin{aligned}&\mathbb {H}(\mathbf {x}, \varvec{\alpha }) = -\mathcal {X}(\mathbf {x})N\left( \bar{\alpha }_0 + \sum _{k =1}^d \bar{\alpha }_k \mathbb {1}\{x_{k}> 0\}\right) \\&\quad + \left\{ \begin{array}{ll} \alpha _1 - \varLambda _A(-\bar{\alpha }_0) -\varLambda _{B^{(1)}}(-\bar{\alpha }_1\mathbb {1}\{x_{1} = 0\}) &{}\quad \text { if } \mathcal {X}(\mathbf {x}) = \bar{x}_{0},\\ \alpha _{j+1} - \alpha _j -\varLambda _{B^{(j)}}\left( -\bar{\alpha }_{j} \mathbb {1}\left\{ x_{j}> \frac{1}{N}\right\} \right) \\ \qquad -\varLambda _{B^{(j+1)}}\left( -\bar{\alpha }_{j+1}\mathbb {1}\left\{ x_{j+1} = 0\right\} \right) &{}\quad \text { if } \mathcal {X}(\mathbf {x}) = \bar{x}_{j} \text {, } j = 1,...,d-1,\\ -\alpha _{d} - \varLambda _{B^{(d)}}\left( -\bar{\alpha }_d\mathbb {1}\left\{ x_{d} > \frac{1}{N}\right\} \right) &{}\quad \text { if } \mathcal {X}(\mathbf {x}) = \bar{x}_{d}, \end{array}\right. \end{aligned}$$

and for $\mathbf {x} = \mathbf {X}_0$

$$\begin{aligned} \mathbb {H}(\mathbf {X}_0, \varvec{\alpha }) = -\varLambda _A(-\bar{\alpha }_0) - \varLambda _{B^{(1)}}(-\bar{\alpha }_1). \end{aligned}$$

Some possible solutions to $\mathbb {H}(\mathbf {x},\varvec{\alpha }) \ge 0$, similar to the solutions presented in Table 2, can be found in Table 3 (including the trivial solution $\varvec{\alpha } = \mathbf {0}$). Similarly to Table 2, the solutions presented consider cases where some $x_j > 0$. Due to the construction that is used, using the minimum of all subsolutions, these solutions also cover the interior of the state space.

Table 3 Some solutions to $\mathbb {H}(\mathbf {x},\varvec{\alpha }) \ge 0$ for all $\mathbf {x}$

Clearly, solutions similar to the other solutions presented in Table 1 also exist. For example, define $\widetilde{\theta }^{(1)} = \sup \{\theta : \varLambda _A(-\theta ^*) + \varLambda _{B^{(1)}}(\theta ) \le 0 \}$. When $x_1 > 0$, another possibility would be $\bar{\alpha }_1 \in [-\widetilde{\theta }^{(1)}, -\theta ^*]$ and $\bar{\alpha }_j \in [0, -\sum _{i \ne j} \bar{\alpha }_i]$, $j > 1$. Thus, when $x_j > 0$, we define $\widetilde{\theta }^{(j)} = \sup \{\theta : \varLambda _A(-\theta ^*) + \varLambda _{B^{(j)}}(\theta ) \le 0 \}$ and another possibility would be $\bar{\alpha }_j \in [-\widetilde{\theta }^{(j)}, -\theta ^*]$ and, for $k > 0$, $\bar{\alpha }_k \in [0, -\sum _{i \ne k}\bar{\alpha }_i]$, $k \ne j$.

3.3.2 Construction of $W(\mathbf {x})$

As for the two-node tandem queue, there is no solution for $\mathbb {H}(\mathbf {x},\varvec{\alpha }) \ge 0$ that holds for all $\mathbf {x}$. Therefore, a different change of measure needs to be applied in different ‘regions’. In this case, the following vectors are used to specify the different changes of measure in each of the ‘regions’:

$$\begin{aligned} \varvec{\alpha }_1= & {} -\gamma (\mathbf {e}_1+\cdots + \mathbf {e}_d) + \theta ^*(\bar{\mathbf {e}}_0 - \bar{\mathbf {e}}_d), \nonumber \\&\vdots&\nonumber \\ \varvec{\alpha }_j= & {} -\gamma (\mathbf {e}_1 + \cdots + \mathbf {e}_{d-(j-1)}) + \theta ^*(\bar{\mathbf {e}}_0 - \bar{\mathbf {e}}_{d-(j-1)}),\nonumber \\&\vdots&\nonumber \\ \varvec{\alpha }_d= & {} -\gamma \mathbf {e}_1 + \theta ^*(\bar{\mathbf {e}}_0 - \bar{\mathbf {e}}_1),\nonumber \\ \varvec{\alpha }_{d+1}= & {} (0,\ldots ,0). \end{aligned}$$

(27)

From this, we find $d+1$ functions $W_k^{\delta }(\mathbf {x}) = \langle \varvec{\alpha }_k , \mathbf {x} \rangle + \gamma - k\delta$, for $k = 1,\ldots ,d+1$, for $\delta > 0$, and their minimum

$$\begin{aligned} W^{\delta }(\mathbf {x}) = W_1^\delta (\mathbf {x}) \wedge \cdots \wedge W_{d+1}^\delta (\mathbf {x}), \end{aligned}$$

which again is a piecewise affine function that equals $W_k^\delta (\mathbf {x})$ in ‘region’ k. The constant $\gamma$ in $W_k^\delta (\mathbf {x})$ is included to satisfy the properties of the subsolution, and the subtraction of $k\delta$ is needed so that the minimum function $W^\delta (\mathbf {x})$ is uniquely attained at each of the boundaries.

To make the minimum function a continuously differentiable function, we apply a similar mollification procedure as for the two-node GI|GI|1 tandem queue. This mollification ‘removes’ the regions and ensures that a derivative exists throughout the whole parameter space. We let

$$\begin{aligned} W^{\varepsilon , \delta }(\mathbf {x}) = -\varepsilon \log \sum _{k=1}^{d+1} e^{-W_k^\delta (\mathbf {x})/\varepsilon }. \end{aligned}$$

(28)

When $\varepsilon \rightarrow 0$, $W^{\varepsilon , \delta }(\mathbf {x}) \rightarrow W_1^\delta (\mathbf {x}) \wedge \cdots \wedge W_{d+1}^\delta (\mathbf {x})$. The assumptions on $\varepsilon$ and $\delta$ can be found in Assumption 3. Similarly to Lemma 1, we see that $W^{\varepsilon ,\delta }(\mathbf {x})$ satisfies properties 3 and 4 in and below Definition 2.

Lemma 4

Under Assumption 1, we have, for the d-node GI|GI|1 tandem queue, that $W^{\varepsilon ,\delta }(\mathbf {x}) \le \frac{\gamma }{N}-\delta$ for $\mathbf {x} \in \delta _e$ and $\gamma (1 -\frac{1}{N}) - (d+1)\delta -\varepsilon \log (d+1) \le W^{\varepsilon ,\delta }(\mathbf {X}_0) \le \gamma -(d+1) \delta$.

The change of measure will be based on the gradient of $W^{\varepsilon ,\delta }(\mathbf {x})$. From (28), it follows that

$$\begin{aligned} \hbox {DW}^{\varepsilon ,\delta }(\mathbf {x}) = \sum _{k = 1}^{d+1} \rho _k(\mathbf {x})\varvec{\alpha }_k, \end{aligned}$$

(29)

where $\rho _k(\mathbf {x})$ is defined similarly to in (17).

3.3.3 The change of measure

As for the 2-node tandem queue, we show that the change of measure based on $W_k^\delta (\mathbf {x})$ results in the state-independent change of measure studied in [2, 9, 11] in some particular cases. This gives some insight into the change of measure that is applied in the mollified function $W^{\varepsilon ,\delta }(\mathbf {x})$.

Choosing $\hbox {DW}(\mathbf {x})$ in (7) as a constant vector $\varvec{\alpha } = (\alpha _1,\ldots ,\alpha _d,\bar{\alpha }_0,\ldots , \bar{\alpha }_d)$, the change of measure can be written in terms of $\bar{\alpha }_0,\ldots ,\bar{\alpha }_d$ as

$$\begin{aligned}&{\text {d}}\bar{F}_{V_{X}(\mathbf {x})}(\mathbf {v} | \mathbf {x}) \nonumber \\&\quad = \left\{ \begin{array}{l@{\quad }l} \frac{e^{-a\bar{\alpha }_0- b_1\bar{\alpha }_1\mathbb {1}\{x_{1} = 0\} }}{M_A(-\bar{\alpha }_0) M_{B^{(1)}}(-\bar{\alpha }_1\mathbb {1}\{x_{1} = 0\})}{\text {d}}F_A(a){\text {d}}F_{B^{(1)}}(b_1) &{} \text { if } \mathcal {X}(\mathbf {x}) = \bar{x}_{0},\\ \frac{e^{-b_j\bar{\alpha }_1\mathbb {1}\left\{ x_{j}> \frac{1}{N}\right\} - b_{j+1} \bar{\alpha }_{j+1}\mathbb {1}\{x_{j+1} = 0\}}}{ M_{B^{(j)}}\left( -\bar{\alpha }_j\mathbb {1}\left\{ x_{j}> \frac{1}{N}\right\} \right) M_{B^{(j+1)}}(-\bar{\alpha }_{j+1}\mathbb {1}\{x_{j+1} = 0\})}{\text {d}}F_{B^{(j)}}(b_j){\text {d}}F_{B^{(j+1)}}(b_{j+1}) &{} \text { if } \mathcal {X}(\mathbf {x}) = \bar{x}_{j}, j = 1,\ldots d-1,\\ \frac{e^{-b_{\text {d}}\bar{\alpha }_d\mathbb {1}\left\{ x_{d}> \frac{1}{N}\right\} }}{M_{B^{(d)}}\left( -\bar{\alpha }_d\mathbb {1}\left\{ x_{d} > \frac{1}{N}\right\} \right) }{\text {d}}F_{B^{(d)}}(b_d) &{} \text { if } \mathcal {X}(\mathbf {x}) = \bar{x}_{d}, \end{array}\right. \nonumber \\ \end{aligned}$$

(30)

for $\mathbf {x} \ne \mathbf {X}_0$ and

$$\begin{aligned} {\text {d}}\bar{F}_{V_{X}(\mathbf {X}_0)}(\mathbf {v} | \mathbf {X}_0)&= \frac{e^{-a\bar{\alpha }_0- b_1 \bar{\alpha }_1}}{M_A(-\bar{\alpha }_0) M_{B^{(1)}}(-\bar{\alpha }_1)} {\text {d}}F_A(a){\text {d}}F_{B^{(1)}}(b_1). \end{aligned}$$

(31)

We now consider the cases where our change of measure based on $W^{\varepsilon ,\delta }(\mathbf {x})$ gets close, as $N \rightarrow \infty$, to an ‘affine’ change of measure as above, that is, based on some $W_k^\delta (\mathbf {x})$ with constant gradient. Then, if we let $\varvec{\alpha } =W_{d-(j-1)}^\delta (\mathbf {x}) = \varvec{\alpha }_{d-(j-1)}$, see (27), it follows that indeed the resulting change of measure equals the state-independent change of measure studied in [2, 9, 11] if queue j is the bottleneck queue.

3.3.4 Asymptotic efficiency

To show that asymptotic efficiency also holds for the d-node GI|GI|1 tandem queue, assuming that Conjecture 1 is correct, we need the following two lemmas.

Lemma 5

Under Assumptions 1 and 2, we have, for the d-node GI|GI|1 tandem queue, for all possible $\mathbf {x}$,

$$\begin{aligned} \mathbb {H}(\mathbf {x}, \hbox {DW}^{\varepsilon ,\delta }(\mathbf {x})) \ge - (\theta ^* \max \{Q^{(0)},\ldots ,Q^{(d)}\}+ \gamma ) e^{-\delta /\varepsilon }. \end{aligned}$$

Lemma 6

Suppose we have a d-node GI|GI|1 tandem queue satisfying Assumptions 1 and 2. Then, for any successful path $\mathbf {X}_i$, $i = 0,\ldots , \tau _N$, it holds for all $\mathbf {X}_{\tau _N}$ that

$$\begin{aligned} \left| N \sum _{i=0}^{\tau _N -1} \langle \hbox {DW}^{\varepsilon ,\delta }(\mathbf {X}_i), \mathbf {X}_{i+1} - \mathbf {X}_i \rangle - N( W^{\varepsilon ,\delta }(\mathbf {X}_{\tau _N}) - W^{\varepsilon ,\delta }(\mathbf {X}_0)) \right| \le \frac{2C_2^2}{\varepsilon N} \tau _N, \end{aligned}$$

where $C_2 = \sqrt{2}(\gamma + \theta ^*)(\sqrt{2} + \sqrt{3}\max _j\{Q^{(j)}\}) < \infty$.

Using Lemmas 4–6, we can prove the following result.

Theorem 4

Suppose we have a d-node GI|GI|1 tandem queue satisfying Assumptions 1 and 2. Then, under Conjecture 1 and Assumption 3, the change of measure based on $\hbox {DW}^{\varepsilon , \delta }(\mathbf {x})$ in Eq. (29) is asymptotically efficient.

Remark 18

We could also extend Theorem 4, as we did for the two-node tandem queue in Theorem 3, and we claim that asymptotic efficiency also holds in that case under the same conditions as in Theorem 4.

4 Numerical results for the two-node tandem queue

In this section, we present numerical results for the two-node tandem queue to illustrate that the proposed method indeed works. In each of the examples below, we use (16) for the change of measure. We recall that the estimator for $p_N$ is $L(\mathcal {P})I(\mathcal {P})$ and hence we will define the following estimator, which is obtained via simulation,

$$\begin{aligned} \hat{p}_N = \frac{1}{S} \sum _{i=1}^S L(i)I(i), \end{aligned}$$

where S is the total number of simulation runs, L(i) is the likelihood ratio in simulation i and I(i) indicates whether level N has been reached in simulation i or not.

In all tables given below, RE is the relative error, i.e., the standard deviation of the estimator divided by its mean,

$$\begin{aligned} {\text {RE}} = \frac{\sqrt{\frac{1}{S-1} \sum _{i=1}^S (L(i)I(i) - \hat{p}_N)^2}}{\sqrt{S}\hat{p}_N}, \end{aligned}$$

and AE denotes

$$\begin{aligned} {\text {AE}} = \frac{\log \frac{1}{S} \sum _{i=1}^S L^2(i)I(i)}{\log \frac{1}{S} \sum _{i=1}^S L(i)I(i)}. \end{aligned}$$

Thus, if the change of measure is asymptotically efficient, AE should converge to 2 when N tends to infinity; see Definition 3. Furthermore, in our tables we will include the number of times the overflow level has been reached (out of a total of $S = 10^6$ simulation runs) and the (rounded) simulation time in seconds. Note that the latter quantity is only there for reference and does not indicate if the estimator is asymptotically efficient or not.

To use the change of measure based on (16), we need to choose $\varepsilon$ and $\delta$ so that they satisfy Assumption 3. It is not trivial to find suitable $\varepsilon$ and $\delta$ that satisfy all requirements; we only explored several possibilities, while many more exist. In all the examples below, we set $\varepsilon$ proportional to $\frac{1}{\sqrt{N}}$ and $\delta = - \varepsilon \log \varepsilon$, unless the condition in Remark 19 is not satisfied.

Remark 19

For the choice $\delta = -\varepsilon \log \varepsilon$, it may happen for small values of N that $W^\delta (\mathbf {x})$ does not attain $W_k^\delta (\mathbf {x})$ for some k in the ‘region’ where it is supposed to be attained. For example, consider $W_2^\delta (\mathbf {x}) < W_1^\delta (\mathbf {x})$, which is equivalent to

$$\begin{aligned}x_2 < \frac{\theta ^*(\bar{x}_1 -\bar{x}_2)}{\gamma } + \frac{\delta }{\gamma }.\end{aligned}$$

Taking into account that $W_2^\delta (\mathbf {x})$ is designed for the case $x_2 = 0$, the right-hand side of this equation should be positive. Thus, we need $\delta > \frac{Q^{(2)}}{N} \theta ^*$ (recall that $Q^{(2)}$ is an upper bound on the support of the service times at queue 2). When we also consider $W_1^\delta (\mathbf {x}) < W_3^\delta (\mathbf {x})$ and $W_2^\delta (\mathbf {x}) < W_3^\delta (\mathbf {x})$, it turns out that we actually need

$$\begin{aligned} \delta > \frac{\max \{Q^{(1)}, Q^{(2)}\}\theta ^*}{N}. \end{aligned}$$

(32)

Therefore, when $\delta = -\varepsilon \log \varepsilon$ does not satisfy (32), in our numerical experiments, we actually set $\delta = \frac{\max \{Q^{(1)}, Q^{(2)}\}\theta ^*}{N^{0.95}}$. We choose the denominator to be $N^{0.95}$, but of course other choices are possible to obtain the strict inequality in (32). Unless mentioned otherwise, only for $N =20$ this different value for $\delta$ is used. (Note that for a d-node tandem queue, a similar condition exists; $\delta > \frac{\max \{Q^{(1)},\ldots , Q^{(d)}\}\theta ^*}{N}$.)

Table 4 $D|U|1-\cdot |U|1$ tandem queue when both queues are the bottleneck queue. We choose $A =1.1$, $B^{(1)}\sim U[0,2]$, $B^{(2)} \sim U[0,2]$ and $\varepsilon = \frac{0.06}{\sqrt{N}}$. We find $\theta ^* = \theta _1 = \theta _2 = 0.6073$. The number of simulations is $10^6$

We consider two types of tandem queues, a $D|U|1-\cdot |U|1$ tandem queue and a $M|U|1-\cdot |U|1$ tandem queue, and in both cases we vary the bottleneck queue. Starting with a $D|U|1-\cdot |U|1$ tandem queue, we first consider the case where the $\theta$-bottleneck queue is not unique, i.e., the service times at both queues have the same distribution with the same parameters. In our case, both service times have a uniform distribution on the interval [0, 2]. Similar cases are known to fail when using a state-independent change of measure, see [2, 3], and thus this is an interesting case to consider. The results can be found in Table 4. In this table, we see results that clearly support the theoretical results of the estimator being asymptotically efficient; at first the relative error is decreasing, after which it slowly increases. We also see that the number of times the overflow level N is reached is decreasing with N. This behaviour may seem strange, but it can be seen in all of the results in this section. Given our assumptions on $\varepsilon$ and $\delta$, we note that $\delta N \rightarrow \infty$ and hence ‘region’ 3—where no change of measure is applied—is increasing in size. Therefore, we can expect that as N increases it becomes increasingly more difficult to reach the overflow level, even though we have asymptotic efficiency. In particular, we observed that when a system has small server utilizations, it may be hard to escape the ‘region’ of the state space where (almost) no change of measure is applied.

Table 5 $D|U|1-\cdot |U|1$ tandem queue when queue 1 is the bottleneck queue. We choose $A =1.1$, $B^{(1)}\sim U[0,2]$, $B^{(2)} \sim U[0.5,1.5]$ and $\varepsilon = \tfrac{0.07}{\sqrt{N}}$. We find $\theta ^* = \theta _1 = 0.6073$, $\theta _2 = 2.5215$. The number of simulations is $10^6$

Table 6 $D|U|1-\cdot |U|1$ tandem queue when queue 2 is the bottleneck queue. We choose $A = 1.1$, $B^{(1)}\sim U[0.5,1.5]$, $B^{(2)} \sim U[0,2]$ and $\varepsilon = \frac{0.01}{\sqrt{N}}$. We find $\theta ^* = \theta _2 = 0.6073$, $\theta _1 = 2.5215$. The number of simulations is $10^6$

Table 7 $M|U|1-\cdot |U|1$ tandem queue when both queues are the bottleneck queue. We choose $A \sim \exp (0.5)$, $B^{(1)}\sim U[0,3]$, $B^{(2)} \sim U[0,3]$ and $\varepsilon = \frac{0.025}{\sqrt{N}}$. We find $\theta ^* = \theta _1 = \theta _2 = 0.2690$. The number of simulations is $10^6$

Next, we let one of the queues be the bottleneck queue. In Tables 5 and 6, queue 1 and queue 2 are the bottleneck queue, respectively. Here, we changed one of the service time distributions of the previous example from U[0, 2] to U[0.5, 1.5] so that there is a unique $\theta$-bottleneck queue, but the server utilizations of both queues remain the same. When queue 1 is the bottleneck queue, we see that the relative error is still very large for $N = 20$, but for larger values of N the theoretical results are supported. Note that in this case $\delta = -\varepsilon \log \varepsilon$ for all values of N. We also see from this table that the simulation time is increasing, even though the number of times the overflow level is reached is decreasing. This is due to the fact that we have to reach a higher overflow level N. When queue 2 is the bottleneck queue, we have considered a much smaller value for $\varepsilon$, and thus $\delta$ differs from being $-\varepsilon \log \varepsilon$ for $N = 20,\ldots ,260$. This can also be seen from the table, by noting that both the number of times the overflow is reached and the simulation time increase at $N = 300$. Besides this difference, the results in the table clearly support the theoretical results.

Lastly, we consider a $M|U|1-\cdot |U|1$ tandem queue in Tables 7, 8 and 9. We emphasize that the inter-arrival times are exponentially distributed, which means an unbounded support, and, hence, this is not covered by our theoretical results. Again, we start with the case where there is no unique bottleneck queue in Table 7. We see from this table that the relative error remains roughly constant, suggesting asymptotic efficiency. In Table 8, when queue 1 is the bottleneck queue, and in Table 9, when queue 2 is the bottleneck queue, we see that the relative error is slightly increasing, but still suggesting asymptotic efficiency. We remark that in Table 9$\delta$ does not equal $-\varepsilon \log \varepsilon$ for $N = 20,\ldots ,100$, which can be seen by an increasing number of times level N is reached for $N = 140$.

Even though we do not have a proof of asymptotic efficiency for unbounded supports, which is the case for the inter-arrival times in Tables 7, 8 and 9, all these tables show good results that suggest asymptotic efficiency of the estimator. We also did some experiments with exponentially distributed service times, where, regardless of (32) in Remark 19, we set $\delta = -\varepsilon \log \varepsilon$, but we did not obtain good results there. This is most likely due to the fact that for Markovian service times (and unbounded service times in general), the condition on $\delta$, see (32), cannot hold. As a result, it could happen that, for example, $W_2^\delta (\mathbf {x}) > W_1^\delta (\mathbf {x})$ when $x_2 = 0$, see also Remark 19, leading for $x_2 = 0$ to $\mathbb {H}(\mathbf {x}, \hbox {DW}^{\varepsilon ,\delta }(\mathbf {x})) \approx \mathbb {H}(\mathbf {x}, \varvec{\alpha }_1)$, which is negative for $x_2 = 0$ (and hence violates property 2 in Definition 2).

Table 8 $M|U|1-\cdot |U|1$ tandem queue when queue 1 is the bottleneck queue. We choose $A \sim \exp (0.5)$, $B^{(1)}\sim U[0,3]$, $B^{(2)} \sim U[0,2]$ and $\varepsilon = \frac{0.025}{\sqrt{N}}$. We find $\theta ^* = \theta _1 = 0.2690$, $\theta _2 = 0.8966$. The number of simulations is $10^6$

Table 9 $M|U|1-\cdot |U|1$ tandem queue when queue 2 is the bottleneck queue. We choose $A \sim \exp (0.5)$, $B^{(1)}\sim U[0,2]$, $B^{(2)} \sim U[0,3]$ and $\varepsilon = \frac{0.01}{\sqrt{N}}$. We find $\theta ^* = \theta _2 = 0.2690$, $\theta _1 = 0.8966$. The number of simulations is $10^6$