Introduction

Chiral symmetry breaking in Life or why all living organisms are built from \(L\) amino acids and \(D\) sugars has been the subject of active academic research for the last about 150 years since the discovery of enantiomers. Many theories have been considered over the years and many outstanding reviews of these matters have been written, for example: Frank 1953; Joyce et al. 1984; Kondepudi et al. 1985; Kauffman 1986; Avetisov and Goldanskii 1996; Steel 2000; Sandars 2003; Plasson et al. 2004; Saito and Hyuga 2004; Wattis and Coveney 2005; Weissbuch et al. 2005; Brandenburg et al. 2007; Plasson et al. 2007; Gleiser et al. 2008; van der Meijden et al. 2009; Karfi et al. 2010; Noorduin et al. 2010; Blackmond 2011; Blanco and Hochberg 2011; Hordijk et al. 2011; Coveney et al. 2012; Hein et al. 2012; Ribó et al. 2013; Sczepanski and Joyce 2014; Higgs and Lehman 2015, Brandenburg 2019, Hawbaker and Blackmond 2019; Konstantinov and Konstantinova 2018, 2020, Martínez et al. 2022. It is also often mentioned that chiral symmetry breaking requires far from equilibrium systems (Kondepudi and Nelson 1983; Plasson et al. 2007) and, in fact, some of the works considered how temporary chiral symmetry breaking occurs in specially prepared far from equilibrium systems (Blanco and Hochberg 2011). A good example of autocatalytic reaction producing large enantiomeric excess is Soai reaction (Soai et al. 1995), where large enantiomeric excess of 5-pyrimidyl alkanol is achieved from a small initial imbalance.

Many models of chiral symmetry breaking utilize some form of autocatalysis coupled with mutual inhibition. This can be traced back to Frank’s model (Frank 1953) and its various further extensions (Sandars 2003; Wattis and Coveney 2005; Karfi et al. 2010; Blanco and Hochberg 2011, Buhse and Micheau 2022). However, such mutual inhibition is a very energy expensive process, especially when complex organic structures are involved. If applied to some complex organic structures, then we would rather call the process, as in Frank’s model, a “fierce competition” to illustrate the fact that two opposite organic structures have to “die off” to make it work. There are also some other models, which utilize different approaches (Kauffman 1986; Steel 2000; Hordijk et al. 2011). However, the most interesting point is that organic life operates on a slightly different set of reactions.

To start, synthesis of amino acids in organic life produces only left amino acids, whereas a catalytic synthesis of amino acids is bound by enantioselectivity of catalysts and cannot be 100%. This is due to the energy differences between catalytic reactions with two enantiomer catalysts and the estimates of enantioselectivity (\({\eta }_{c}\)) of such catalysts are from around \({\eta }_{c}\approx 0.2\) to \(0.75\) (Gellman and Ernst 2018) to as high as \({\eta }_{c}\approx 0.95\) (Cherney et. al. 2015). However, organic life reaches nearly perfect 100%. To achieve such perfect enantioselectivity in synthesis of amino acids organic life requires approximately from 12 to 74 high-energy phosphate bods per amino acid molecule (Akashi and Gojobori 2002). That means that such synthesis can no longer be called purely catalytic because the energy is spent during such reactions. We can call it catalytic synthesis with energy consumption to distinguish from just catalytic synthesis. This has very deep consequences. To start from, a catalyst cannot change the equilibrium due to thermodynamic constraints. In addition, a catalyst cannot be 100% enantioselective, as mentioned above. And so, if organic life used purely catalytic synthesis of amino acids, then it would have produced some noticeable amounts of right amino acids and it would have just faster produced some thermodynamically equilibrium state. But it does neither of that. Spending energy during synthesis of amino acids allows organic life to produce the result, which is far from thermodynamic equilibrium.

Second, once amino acids are made, the next crucial step of organic life is peptide synthesis or, to be more precise, a directed peptide synthesis, where peptides are synthesized as needed rather than at random. It is an energetically unfavorable process and so a concentration of even random peptides would form a decreasing geometric progression in the absence of energy inflow. However, peptides of any needed length and needed, non-random constitution are synthesized by all living organisms. Again, organic life uses energy to synthesize peptides that it needs, and some simple unicellular life forms could use substantial portion of their energy budget on that process. The result is also shifted far from the thermodynamic equilibrium by consuming energy. Similar to the terminology above, we can call such reactions ligation with energy consumption.

Third, all living organisms possess the ability to discard what they don’t need. To maintain a chiral state, they must constantly decrease the entropy inside them. This is achieved by changing whatever can be properly changed inside the organisms and removing whatever cannot be and then discarding that into the environment. Probably one of the simplest examples is a sodium–potassium pump, discovered in 1957 by Jens Christian Skou (Skou 1957). The pump consumes energy from ATP and pushes sodium out from the region of lower concentration into the region of higher concentration and captures potassium from the region of lower concentration into the region of higher concentration, both of which are against diffusion. This is also achieved by spending energy. We can call such reactions as destruction with energy consumption. Given that prebiotic “soup” did not yet have cell boundaries, discarding whatever was not needed could only happen in one of two ways: releasing some gas into the atmosphere or forming some sediment, which would fall into the ocean floor.

Fourth, as the chemical systems consist of finite number of molecules, that results in stochastic behavior in chemical kinetics (e.g., McQuarrie 1967; Gillespie 1992, 2007). Differential equations, which are often used to describe chemical kinetics, including the reactions used to study chiral symmetry breaking, cannot describe that stochasticity. Subsequently, the scenarios, which consider transition through a bifurcation point, need to perform some additional statistical analysis to determine if chiral symmetry breaking could be directed or random in the presence of some global asymmetry factor (e.g., Kondepudi and Nelson 1985).

In addition, as discussed in detail in Konstantinov and Konstantinova 2020, all models of chiral symmetry breaking, which considered a very limited set of reactions, rely on some favorable set of parameters to make the models work. However, since the number of substances and reactions on prebiotic Earth were extremely large, that requires that models should statistically result in chiral symmetry breaking rather than rely on some specifically chosen parameters.

The situation changes drastically when protocells started to appear. The most important part there was the appearance of closed boundary between protocells and the environment. The boundary substantially decreased diffusion between the inside and the outside of protocells, and that allowed synthesizing something inside protocells without letting hard to synthesize (at that time) organic parts get lost in the immense amounts of surrounding water, e.g., Monnard and Walde 2015. From another point, as the number of molecules in a protocell was many orders of magnitude smaller than total number of molecules in the primordial soup, stochastic fluctuations inside protocells were far more substantial than in the surrounding environment.

Finally, even many modern unicellular organisms do not participate in a “fierce competition” as required in Frank’s model or similar models. Rather, they simply coexist and the only competition that they have is in consumption of food and / or other resources. And it is even more questionable to imagine “fierce competition” on a prebiotic Earth when organic structures were much simpler than now and had much less ability to capture and use low-entropy energy. It is therefore interesting and challenging to try explaining how chiral symmetry breaking could occur on a prebiotic Earth under the following conditions:

  • The number of substances and reactions was extremely large and, therefore, effective averaging of enantioselectivity rules out “favorable” choices of reaction rates.

  • Given that organic life operates in far from thermodynamic equilibrium state, low-entropy energy storage and consumption must be taken into account.

  • Greatly increased stochasticity of chemical reactions inside the protocells should be considered.

  • It seems important to explain chiral symmetry breaking without using “fierce competition”.

  • The question whether chiral symmetry breaking was directed or just by a pure chance should be answered.

Evolution of Protocells Without Competition

In the current work we would like to consider a half-way from chemistry to biology and that is consider a very simple model of protocells: there is no biology yet, but the chemistry is already complicated enough. We can take a view that a protocell is a relatively simple and small open system capable of storing and processing low entropy energy (e.g., sunlight) and which is also capable of producing a near copies of itself. In fact, the need for energy in the process of transitioning from chemical to biological evolution is explicitly or implicitly discussed in many works, e.g., Plasson and Brandenburg 2010, Dibrova et. al. 2012. A protocell has some kind of a closed boundary, which substantially hinders diffusion-like processes between the inside and the outside of the protocell. Some experiments (Bahadur 1964; Gupta 2014) showed that such small structures with closed boundaries can appear under relatively simple conditions.

A reasonable assumption then is that the prebiotic soup should have been close to thermodynamic equilibrium as a whole when the protocell boundaries started to close and actually did form the protocells. This is since diffusion would spread out any substantial irregularities including the ones related to the energy inflow when there were no boundaries. Once the boundaries of the protocells were closed and diffusion between the inside and the outside slowed down substantially, then further evolution inside protocells could become dependent on energy transformations.

We can further look at a protocell as a black box, which consumes some “food” and low-entropy energy out of the environment and produces another protocell. This looks nearly identical to catalytic synthesis reactions except that a new protocell does not have to be an exact copy of the original one. We shall note that this is one of the points where enantiomeric excess can change in the system. Therefore, we can write:

$$n\; X+U\to U+U^{\prime}$$
(1)

where \(X\) is some achiral food (e.g., \(C{O}_{2}\)), \(U\) is a “catalyzing” protocell, \(U^{\prime}\) is a new protocell, and we assumed that \(n\) molecules of food are needed to create one protocell. The Eq. (1) assumes that all amino acid needed for a new protocell are synthesized only inside the original protocell. The real process is much more complicated, and the protocells come in different sizes and types. However, even this simplified consideration is sufficient for the model to work.

Since the number of amino acids, including the ones inside the protocell is finite, all “internal” reactions, which result in the replication in Eq. (1), are subject to statistical fluctuations. This impact of finiteness, which, in turn, results in stochastic evolution of chemical systems, is well known (see, e.g., Gillespie 1992). Here it results in the change of enantiomeric excess in the new protocell, which we can call mutations. This illustrates the fact that finiteness alone is sufficient to explain such mutations in protocells.

We can further model that protocells just “die off” without any mutual inhibition as:

$$U\to W$$
(2)

where \(W\) is some “waste”. This is another point where enantiomeric excess can change in the system because all chiral amino acids are considered as completely lost in this process.

To complete the model, we then need to either “recycle” the “waste” or assume that there is a nearly infinite amount of food. The latter was the case of \(C{O}_{2}\) on a prebiotic Earth. However, even though the amount of \(C{O}_{2}\) was nearly infinite, there are always some other constraints that limit the growth of organic systems and therefore models, which recycle the waste instead of considering an infinite amount of food seem to be more appropriate. The equation for that can be written as:

$$W\to n\; X$$
(3)

The smallest unicellular organisms known today contain on the order of \({\left(1 \;to \;100\right)\times 10}^{12}\) atoms. However, primordial protocells were very likely much smaller than that, though it is hard to estimate what could have been their size. We can take the reported minimum size of experimentally obtained by Gupta and Rai 2013 protocell-like particles of about \(d\approx 0.5 \mu m\) in diameter as a starting point. Assuming \({p}_{w}\approx 70\mathrm{\%}\) water (and non-amino acids) content and \(\left(1-p_w\right)\approx30\%\) amino acid content and using average amino acid density \({\rho }_{a}\approx 1.3 \;g/ml\), average molar mass \({m}_{a}\approx 110\; g/mol\), we can estimate the number of amino acids \(n\) in such reported protocells-like particles as:

$$n \sim \frac{\frac{4\pi }{3}{\left(\frac{d}{2}\right)}^{3} \left(1-{p}_{w}\right) {\rho }_{a}{ N}_{A}}{{m}_{a}}\approx 1.4 \times {10}^{8}$$
(4)

where \({N}_{A}\) is the Avogadro number. Even if primordial protocells had a few orders of magnitude less amino acids, this number is still large enough to replace summations needed when dealing with discreet variables by integrations. And this significantly simplifies the consideration without introducing too large errors, except certain cases, which we consider below. Then we can write the kinetics of Eqs. (1) and (2) as:

$$\frac{dU\left(\eta ,t\right)}{dt}= {\rho }_{X}{\left(t\right)}^{n}\underset{-1}{\overset{1}{\int }}K\left(\eta ,{\eta }^{\mathrm{^{\prime}}}\right) U\left({\eta }^{\mathrm{^{\prime}}},t\right) d{\eta }^{\mathrm{^{\prime}}}-{\gamma }_{0} U\left(\eta ,t\right)$$
(5)

where \({\rho }_{X}\left(t\right)\) is the concentration of the “food” substance \(X\) at time \(t\), \(U\left(\eta ,t\right)\) describes the concentration of protocells with total enantiomeric excess \(\eta\) at time \(t\), \(K\left(\eta ,{\eta }^{\mathrm{^{\prime}}}\right)\) is the rate coefficient at which \(U\left({\eta }^{\mathrm{^{\prime}}},t\right)\) can produce \(U\left(\eta ,t\right)\) and \({\gamma }_{0}\) is the decay rate, which we assumed here as independent on \(\eta\) for simplicity.

There should be also a linear term corresponding to a spontaneous initial formation of protocells:

$$n\; X\to U$$
(6)

However, this process can be safely considered as very slow. Therefore, we can ignore it and consider that the system evolves from some very small initial fluctuation \(U\left(\eta ,0\right)\) created by that linear process. This initial fluctuation \(U\left(\eta ,0\right)\) should be some narrow peak centered around \(\eta =0\) with a standard deviation \({\sigma }_{0}\approx \frac{1}{\sqrt{n}}\), Plasson and Brandenburg 2010, because the prebiotic soup was close to thermodynamic equilibrium as a whole.

The changes in \(X\) and \(W\) can be written as:

$$\frac{d{\rho }_{X}\left(t\right)}{dt}=-n \;{\rho }_{X}{\left(t\right)}^{n}\underset{-1}{\overset{1}{\int }}\underset{-1}{\overset{1}{\int }}K\left(\eta ,{\eta }^{\mathrm{^{\prime}}}\right) U\left({\eta }^{\mathrm{^{\prime}}},t\right) d\eta\; d{\eta }^{\mathrm{^{\prime}}}+s\; {\rho }_{W}\left(t\right)$$
(7)

and

$$\frac{d\,{\rho }_{W}\left(t\right)}{dt}=-s\; {\rho }_{W}\left(t\right)+{\gamma }_{0}\underset{-1}{\overset{1}{\int }}U\left({\eta }^{\mathrm{^{\prime}}},t\right) d{\eta }^{\mathrm{^{\prime}}}$$
(8)

where \(s\) is the “recycling” rate.

We can look at the stationary point of these equations when \(\frac{dU\left(\eta ,t\right)}{dt}=0\). Then we can rewrite Eq. (5) as:

$$\underset{-1}{\overset{1}{\int }}K\left(\eta ,{\eta }^{\mathrm{^{\prime}}}\right) u\left({\eta }^{\mathrm{^{\prime}}}\right) d{\eta }^{\mathrm{^{\prime}}}=\lambda\; u\left(\eta \right)$$
(9)

where \(\lambda =\frac{{\gamma }_{0}}{{{\rho }_{X}}^{n}}\), \(U\left(\eta \right)\equiv {U}_{0} u\left(\eta \right)\) and \(u\left(\eta \right)\) is \({L}_{2}\) normalized so that:

$$\underset{-1}{\overset{1}{\int }}u{\left(\eta \right)}^{2} d\eta =1$$
(10)

This is an eigenvalue problem for Fredholm integral operator of the first kind. The eigenvalues \({\lambda }_{i}\) determine stationary concentration of \({\rho }_{X}\) and eigenvectors \({u}_{i}\left(\eta \right)\). The largest value of \({\lambda }_{i}\) corresponds to the smallest concentration of and it is therefore the one toward which the system should evolve. All eigenvectors are orthonormal, and they form a basis on the interval \(\left[-1, 1\right]\):

$$\underset{-1}{\overset{1}{\int }} {u}_{i}\left(\eta \right) {u}_{j}\left(\eta \right) d\eta ={\delta }_{ij}$$
(11)

where \({\delta }_{ij}\) is Kronecker delta symbol.

To show that the system evolves toward eigenvector with the highest eigenvalue, we can decompose the distribution of protocells at any moment \(t\) into \({u}_{i}\left(\eta \right)\):

$$U\left(\eta ,t\right)=\sum_{i=1}^{\infty }{A}_{i}\left(t\right){u}_{i}\left(\eta \right)$$
(12)

where \({A}_{i}\left(t\right)\) is the amplitude of \(i\)-th eigenvector at time \(t\) and it can be determined using orthonormality condition:

$${A}_{i}\left(t\right)=\underset{-1}{\overset{1}{\int }} U\left(\eta ,t\right) {u}_{i}\left(\eta \right) d\eta$$
(13)

Then multiplying Eq. (5) by \({u}_{i}\left(\eta \right)\) and integrating by \(d\eta\) we can obtain:

$$\frac{d{A}_{i}\left(t\right)}{dt}= \left({{\lambda }_{i} \;\rho }_{X}{\left(t\right)}^{n}-{\gamma }_{0}\right) {A}_{i}\left(t\right)$$
(14)

from which it follows that \({A}_{i}\left(t\right)\) evolves with a local in time exponential coefficient \(\left({{\lambda }_{i}\; \rho }_{X}{\left(t\right)}^{n}-{\gamma }_{0}\right)\). As the food is consumed and \({\rho }_{X}\left(t\right)\) decreases, more and more eigenvalues will have \(\left({{\lambda }_{i}\; \rho }_{X}{\left(t\right)}^{n}-{\gamma }_{0}\right)<0\) and that means that such eigenvectors start to die off at some point in time. This process will continue until the stationary point is reached, at which point the value of \(\left({{\lambda }_{1}\; \rho }_{X}{\left(t\right)}^{n}-{\gamma }_{0}\right)\) for the largest eigenvalue \({\lambda }_{1}\) reaches zero and the system reaches its final state: \({A}_{1} {u}_{1}\left(\eta \right)\). Since Eq. (5) is linear in \(u\left(\eta \right)\), it does not fix the overall multiplier \({A}_{1}\). It is determined by using the matter conservation condition:

$${\rho }_{X}\left(t\right)+n\left({\rho }_{W}\left(t\right)+\underset{-1}{\overset{1}{\int }}U\left(\eta ,t\right) \;d\eta \right)\equiv const={\rho }_{0}$$
(15)

where \({\rho }_{0}\) can be called the total amount of matter in the system. Substituting stationary conditions into this equation and denoting:

$$\underset{-1}{\overset{1}{\int }}U\left(\eta ,t\right) \;d\eta ={A}_{1}\underset{-1}{\overset{1}{\int }}{u}_{1}\left(\eta \right) \;d\eta \equiv {A}_{1} {c}_{1}$$
(16)

where \({c}_{1}\) is \({L}_{1}\) norm of the first eigenvector we can obtain:

$$\sqrt[n]{\frac{{\gamma }_{0}}{{\lambda }_{1}}}+n\; {c}_{1}\; {A}_{1}\left(1+\frac{{\gamma }_{0}}{s}\right)={\rho }_{0}$$
(17)

From which it follows that:

$${A}_{1}=\frac{{\rho }_{0}-\sqrt[n]{\frac{{\gamma }_{0}}{{\lambda }_{1}}}}{n {c}_{1}\left(1+\frac{{\gamma }_{0}}{s}\right)}$$
(18)

The following should be noted. Because of the global symmetry \(L\leftrightarrow D\), if \(u\left(\eta \right)\) is some eigenvector of Eq. (9), then \(u\left(-\eta \right)\) is also an eigenvector with the same eigenvalue. That means that the eigenvectors are either even or odd functions of \(\eta:u\left(-\eta \right)=\pm u\left(\eta \right)\) because if \(u\left(-\eta \right)\ne \pm u\left(\eta \right)\) then since \(u\left(-\eta \right)\) must have the same eigenvalue as \(u\left(\eta \right)\), we can make two linear combinations: \({u}_{+}\left(\eta \right)=\frac{u\left(\eta \right)+u\left(-\eta \right)}{\sqrt{2}}\) and \({u}_{-}\left(\eta \right)=\frac{u\left(\eta \right)-u\left(-\eta \right)}{\sqrt{2}}\), which will also have the same eigenvalues and are orthogonal. The new eigenvectors \({u}_{+}\left(\eta \right)\) and \({u}_{-}\left(\eta \right)\) are even and odd functions correspondingly. The global symmetry imposes some constraints on \(K\left(\eta ,{\eta }^{\mathrm{^{\prime}}}\right)\), which we will use shortly. If initial concentration \({\rho }_{0}\) is sufficiently small so that \(\left({\rho }_{0}-\sqrt[n]{\frac{{\gamma }_{0}}{{\lambda }_{1}}}\right)<0\), then \(\left({{\lambda }_{i} \;\rho }_{0}^{n}-{\gamma }_{0}\right)<0\) for any value of \(i\) and that means that all protocells just die off.

To proceed further we need to determine the shape of the kernel function \(K\left(\eta ,{\eta }^{^{\prime}}\right)\). First, we can write:

$$\underset{-1}{\overset{1}{\int }}K\left(\eta ,{\eta }^{\mathrm{^{\prime}}}\right) d\eta \equiv {k}_{0} \;{k}_{a}\left({\eta }^{\mathrm{^{\prime}}}\right)$$
(19)

where \({k}_{a}\left({\eta }^{\mathrm{^{\prime}}}\right)\) can be called normalized replication rate multiplier and:

$${k}_{0}=\underset{-1}{\overset{1}{\int }}K\left(\eta ,0\right) d\eta$$
(20)

is a normalization coefficient chosen so that \({k}_{a}\left(0\right)\equiv 1\). The physical meaning of \({k}_{a}\left({\eta }^{\mathrm{^{\prime}}}\right)\) is how much more (or less) efficient are the species with total enantiomeric excess \({\eta }^{\mathrm{^{\prime}}}\) in comparison to the species with equal number of left and right amino acids (\({\eta }^{\mathrm{^{\prime}}}=0\)).

We can note that when a protocell produces a copy of itself then there are some small chances of mutations, as discussed above, and that the probability of such mutations rapidly decreases if a copy is substantially different. Therefore, we can rewrite:

$$K\left(\eta ,{\eta }^{\mathrm{^{\prime}}}\right)\equiv {{k}_{0} \;k}_{a}\left({\eta }^{\mathrm{^{\prime}}}\right) p\left(\eta ,{\eta }^{\mathrm{^{\prime}}}\right)$$
(21)

and then we can express that \(p\left(\eta ,{\eta }^{\mathrm{^{\prime}}}\right)\) as:

$$p\left(\eta ,{\eta }^{\mathrm{^{\prime}}}\right)\equiv \frac{K\left(\eta ,{\eta }^{\mathrm{^{\prime}}}\right)}{{{k}_{0} \;k}_{a}\left({\eta }^{\mathrm{^{\prime}}}\right)}$$
(22)

from which it follows that:

$$\underset{-1}{\overset{1}{\int }}p\left(\eta ,{\eta }^{\mathrm{^{\prime}}}\right) d\eta =\underset{-1}{\overset{1}{\int }}\frac{K\left(\eta ,{\eta }^{\mathrm{^{\prime}}}\right)}{{{k}_{0} \;k}_{a}\left({\eta }^{\mathrm{^{\prime}}}\right)} d\eta =\frac{1}{{{k}_{0} \;k}_{a}\left({\eta }^{\mathrm{^{\prime}}}\right)}\underset{-1}{\overset{1}{\int }}K\left(\eta ,{\eta }^{\mathrm{^{\prime}}}\right) d\eta \equiv 1$$
(23)

which means that \(p\left(\eta ,{\eta }^{^{\prime}}\right)\) is the probability that species with total enantiomeric excess \({\eta }^{^{\prime}}\) would produce species with total enantiomeric excess \(\eta\).

The shape of \(p\left(\eta ,{\eta }^{\mathrm{^{\prime}}}\right)\) substantially depends on the models of protocell existence and replication. In the current work we consider that \(p\left(\eta ,{\eta }^{^{\prime}}\right)\) is a very narrow peak centered around \(\eta ={\eta }^{^{\prime}}\). We can model such probability using normal distribution and that leads to the following expression for \(p\left(\eta ,{\eta }^{^{\prime}}\right)\):

$$p\left(\eta ,{\eta }^{\mathrm{^{\prime}}}\right)=\frac{2 {e}^{- \frac{{\left(\eta -{\eta }^{\mathrm{^{\prime}}}\right)}^{2}}{{\epsilon }^{2}}}}{\epsilon \sqrt{\pi } \left(\mathrm{erf}\left(\frac{1-{\eta }^{\mathrm{^{\prime}}}}{\epsilon }\right)+\mathrm{erf}\left(\frac{1+{\eta }^{\mathrm{^{\prime}}}}{\epsilon }\right)\right)}$$
(24)

where \(\epsilon \ll 1\) is some small parameter defining the mutation rate, \(\mathrm{erf}\) is the error function and the normalization coefficient follows from normalization condition Eq. (23). Following the same reasoning as in Plasson and Brandenburg 2010, the value of \(\epsilon\) is likely \(\sim \frac{1}{\sqrt{n}}\). However, as mentioned above, that depends on the models of protocell existence and replication. Therefore, we just varied parameter \(\epsilon\) within a certain range without attempting to translate it into the value of \(n\). The choice of normal distribution is justified when \(\epsilon \ll 1\) and \({\eta }^{\mathrm{^{\prime}}}\) is far from \(\pm 1\). This is the scenario that we are interested in, as we would like to investigate how does the system evolve away from \(\eta =0\) and are not concerned much about the actual final shape when / if the system approaches the states near \(\eta =\pm 1\). Then we can rewrite Eq. (9) as:

$$\underset{-1}{\overset{1}{\int }}{k}_{a}\left({\eta }^{\mathrm{^{\prime}}}\right) p\left(\eta ,{\eta }^{\mathrm{^{\prime}}}\right) u\left({\eta }^{\mathrm{^{\prime}}}\right) d{\eta }^{\mathrm{^{\prime}}}= \widetilde{\lambda } u\left(\eta \right)$$
(25)

where \(\widetilde{\lambda }=\frac{{\gamma }_{0}}{{k}_{0}\,{ {\rho }_{X}}^{n}}\) is the normalized eigenvalue. We shall note that function \({k}_{a}\left({\eta }^{\mathrm{^{\prime}}}\right)\) must be even due to a global \(L\leftrightarrow D\) symmetry and \(p\left(\eta ,{\eta }^{\mathrm{^{\prime}}}\right)\) is invariant under transformation \(\left(\eta ,{\eta }^{\mathrm{^{\prime}}}\right)\to \left(-\eta ,-{\eta }^{\mathrm{^{\prime}}}\right)\) by construction. This means that \(L\leftrightarrow D\) symmetry is maintained by this kernel, as expected. Performing Taylor expansion up to second powers of \(\eta\) around \(\eta =0\) leads to the following form of \({k}_{a}\):

$${k}_{a}\left(\eta \right)=1+a\; {\eta }^{2}$$
(26)

Then we can investigate what are the eigenvalues and eigenvectors of Eq. (25) for different values of parameter \(a\). This equation can be solved numerically by discretizing the integral in that equation and then finding the eigenvalues and eigenvectors of the resulting matrix. We performed calculation using 1,000 points and 200 digits of precision. Using 1,000 points imposed some constraints on how small we could take some small parameters (like \(\epsilon\)) to be able to “resolve” functions with narrow peaks. Using substantially more than 1,000 points would make computation times prohibitive.

The physical meaning of parameter \(a\) is replication efficiency. When \(a>0\), then homochiral species (species with total enantiomeric content near \(\eta =\pm 1\)) are more efficient in replication (have larger replication rate) than the species with total enantiomeric content \(\eta =0\), and when \(a<0\), then it is the other way around.

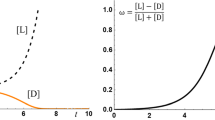
The situation when \(a\le 0\) is not interesting. The eigenvector corresponding to the largest eigenvalue is a Gaussian-like peak centered around \(\eta =0\). The situation when \(a>0\) does result in two species with total enantioselectivity near \(\eta =\pm 1\). Figure 1 shows the first two eigenvectors for the largest eigenvalues for \(a=0.5\) and \(\epsilon =0.005\). The eigenvectors were \({L}_{2}\) normalized. The eigenvector \({u}_{1}\left(\eta \right)\) is an even function, \({u}_{2}\left(\eta \right)\) is an odd function, and they are nearly indistinguishable on the interval \(\eta \in \left[-1, 0\right]\) so that only \({u}_{2}\left(\eta \right)\) peak is effectively visible on the left side of the chart.

Fig. 1
figure 1

Eigenvectors for the largest two eigenvalues for replication efficiency parameter \(a=0.5\)and mutation rate \(\epsilon =0.005\)

Full size image

To test if the largest two eigenvalues are the same or different, we performed calculations with 200 digits of precision. The difference turned out to be extremely small: \({\lambda }_{1}-{\lambda }_{2} \sim {10}^{-177}\) and even though we still had about 23 digits of precision left before hitting the precision limit of 200, our view is that such difference can be safely considered as exact zero for practical purposes. That means that the eigenvalues are nearly degenerate, and any linear combinations are possible. In other words that means that any mix of protocells made from nearly all left or nearly all right amino acids can coexist in such a model. And even if the eigenvalues are not degenerate (that means that symmetric eigenvector has a slightly larger eigenvalue), the difference in eigenvalues is so tiny that it will take a very large amount of time for some arbitrary mix of protocells made from nearly all left and nearly all right amino acids to wear out the asymmetry and transition to an equal mix of left and right species.

The first two largest eigenvectors have narrow peaks near \(\eta =\pm 1\) and it is therefore interesting to calculate how the mutation rate \(\epsilon\) and replication efficiency parameter \(a\) affect the widths and positions of these peaks. To do so we varied \(a\) in the range from 0.01 to 1, \(\epsilon\) in the range from 0.005 to 0.02 and then calculated mean (\(\mu\)) and standard deviation (\(\sigma\)) for the right peak of the even eigenvector. The value of \(\epsilon =0.005\) is approximately the smallest, which can be resolved without significant errors using 1,000 grid points. The results are shown on Figs. 2 and 3.

Fig. 2
figure 2

Dependence of \(\mu\) on replication efficiency parameter \(a\) and mutation rate \(\epsilon\)

Full size image
Fig. 3
figure 3

Dependence of \(\sigma\) on replication efficiency parameter \(a\) and mutation rate \(\epsilon\)

Full size image

As the mutation rate \(\epsilon\) decreases, the peaks in the largest two eigenvectors become more and more narrow and shift closer and closer to \(\eta =\pm 1\). On the other hand, decreasing the value of parameter \(a\) widens the peaks and pushes them away from \(\eta =\pm 1\). However, that impact is smaller for smaller values of \(\epsilon\).

Impact of Global Asymmetry

The \(L\leftrightarrow D\) symmetric model described above does evolve from protocells with nearly racemic content (\(\eta \approx 0\)) toward two nearly homochiral species with \(\eta \approx \pm 1\). However, one may argue that symmetry breaking does not really occur in such a model because there are two species, and their combined total enantiomeric excess is around zero. In fact, we will take this statement further and state that the whole concept of symmetry breaking does not apply to evolutionary models, like this one. We discuss that in detail below when we talk about differences in topologies of the spaces used in bifurcation-based models and current evolutionary model. Subsequently, when considering evolutionary models, we should only talk about two aggregate parameters describing the system: average total enantiomeric excess:

$${\mu }_{\eta }=\underset{-1}{\overset{1}{\int }}{\eta }^{\mathrm{^{\prime}}} {\widetilde{u}}_{1}\left({\eta }^{\mathrm{^{\prime}}}\right) d{\eta }^{\mathrm{^{\prime}}}$$
(27)

and standard deviation of total enantiomeric excess in the system:

$${{\sigma }_{\eta }}^{2}=\left(\underset{-1}{\overset{1}{\int }}{\left({\eta }^{\mathrm{^{\prime}}}\right)}^{2} {\widetilde{u}}_{1}\left({\eta }^{\mathrm{^{\prime}}}\right) d{\eta }^{\mathrm{^{\prime}}}\right)-{{\mu }_{\eta }}^{2}$$
(28)

where \({\widetilde{u}}_{1}\left(\eta \right)\) is \({L}_{1}\) renormalized strictly non-negative eigenvector \({u}_{1}\left(\eta \right)\) corresponding to the largest eigenvalue:

$${\widetilde{u}}_{1}\left(\eta \right)=\frac{{u}_{1}\left(\eta \right)}{\int_{-1}^1{u}_{1}\left({\eta }^{^{\prime}}\right) d{\eta }^{^{\prime}}}\equiv \frac{{u}_{1}\left(\eta \right)}{{c}_{1}}$$
(29)

from which it follows that \({\widetilde{u}}_{1}\left(\eta \right)\) can be interpreted as a probability to find a protocell with total enantiomeric excess \(\eta\) in a final state.

Subsequently, it is then important to investigate what happens if \(L\leftrightarrow D\) symmetry is slightly broken due to some external mechanism. It is a known fact that \(L\) amino acids and \(D\) sugars are slightly more energy stable due to weak interaction (for review see, e.g., Bonner 1991). However, the difference is extremely tiny, and it was always a mystery why the biological evolution went that way and whether it was just by chance or that tiny difference did matter. The analysis above seems to provide a definite answer on that question. When discussing eigenvalues of Eq. (25) we mentioned that due to global \(L\leftrightarrow D\) symmetry the largest two eigenvalues are likely degenerate and there are two eigenvectors (even and odd) corresponding to them. However, once weak integration is taken into account, then this degenerate pair splits and subsequently the combination based on \(L\) amino acids and \(D\) sugars gets the largest eigenvalue. That means that the other combination based on \(D\) amino acids and \(L\) sugars (as well as the other two pairs) will eventually die off.

To test that we introduced a very small asymmetry parameter \(g\) into \({k}_{a}\left(\eta \right)\):

$${k}_{g,a}\left(\eta \right)=\left(1+g\; \eta \right) {k}_{a}\left(\eta \right)$$
(30)

and then calculated eigenvalues and eigenvectors using \({k}_{g,a}\left(\eta \right)\) instead of \({k}_{a}\left(\eta \right)\) in Eq. (25) for the value of \(g={10}^{-20}\), \(a=0.5\), and \(\epsilon =0.005\). The difference between the first two eigenvalues turned out: \(\left({\lambda }_{1}-{\lambda }_{2}\right) \sim {10}^{-20} \sim g\) and the eigenvectors are no longer nearly even and odd functions. Rather, they split into distinct left and right species. The result is shown on Fig. 4 and it illustrates the statement above. We used 200 digits of precision for this calculation as well.

Fig. 4
figure 4

Eigenvectors for the largest two eigenvalues for global asymmetry parameter \(g={10}^{-20}\), replication efficiency parameter \(a=0.5\), and mutation rate \(\epsilon =0.005\)

Full size image

We can also compare the amplitudes \({\widetilde{A}}_{i}\left(0\right)\equiv {\widetilde{A}}_{{0}_{i}}\) for initial fluctuation \(U\left(\eta ,0\right)\) and kernel with the broken symmetry Eq. (30) with the amplitudes \({A}_{i}\left(0\right)\equiv {A}_{{0}_{i}}\) obtained using a symmetric kernel (\(g=0\)). The largest absolute difference is very small:

$$\left|{\widetilde{A}}_{{0}_{i}}-{A}_{{0}_{i}}\right|<2.5\times {10}^{-11}$$
(31)

and it happens around \(i\approx 50\). This illustrates the fact that only the eigenvectors, which correspond to the first few largest eigenvalues, are split into distinct left and right species. However, since the corresponding amplitudes are extremely small, then so are the differences \(\left|{\widetilde{A}}_{{0}_{i}}-{A}_{{0}_{i}}\right|\) for small values of \(i\).

It should be noted that even though the energy difference between individual \(L\) and \(D\) amino acids is extremely small and so if we take just one \(L\) and \(D\) amino acid, then they are nearly indistinguishable in their stability, the situation changes when we consider large chains of amino acids. The errors in less stable species (\(D\) amino acids) will start to add up faster than in more stable species (\(L\) amino acids) and that results in effective asymmetry parameter for \(n\) amino acids \({g}_{n}\), which can be estimated using binomial distribution:

$${{g}_{n}=1-\left(1-g\right)}^{n}\approx 1-{e}^{-\left(n g\right)}\approx \left(n g\right), \;\; \left(n g\right)\ll 1$$
(32)

To estimate the time needed for the system to transition from the state with two distinct species with total enantiomeric excess centered around \(\eta =\pm 1\) into the state where only one of the species survives, consider Eq. (14) for two largest eigenvalues, \({\lambda }_{1}\) and \({\lambda }_{2}\):

$${\lambda }_{\mathrm{1,2}}={k}_{0}\left(1\pm f {g}_{n}\right) {\widetilde{\lambda }}_{0}$$
(33)

where \({\widetilde{\lambda }}_{0}\equiv \frac{{\widetilde{\lambda }}_{1}+{\widetilde{\lambda }}_{2}}{2}\), \(f\equiv \frac{{\widetilde{\lambda }}_{1}-{\widetilde{\lambda }}_{2}}{\left({\widetilde{\lambda }}_{1}+{\widetilde{\lambda }}_{2}\right) {g}_{n}} \sim 1\) (because \(\left({\widetilde{\lambda }}_{1}-{\widetilde{\lambda }}_{2}\right) \sim {g}_{n}\), as shown by numerical calculations), and \({\widetilde{\lambda }}_{\mathrm{1,2}} \sim 1\) (as also shown by numerical calculations) are normalized eigenvalues from Eq. (25) and then consider the scenario when:

$${\widetilde{\lambda }}_{0} {{\rho }_{X}}^{n}-{\gamma }_{0}=0$$
(34)

This corresponds to the state when all other eigenvectors except \({u}_{1}\) and \({u}_{2}\) are no longer present in the system and the food is scarce enough. Then we can obtain (ignoring changes in \({\rho }_{X}\) and \({\rho }_{w}\) for simplicity as we are only interested in the estimate of the exponential factor here):

$$\frac{d{A}_{1}\left(t\right)}{dt}=f\; {g}_{n} \;{\gamma }_{0} \;{A}_{1}\left(t\right), \;\;\frac{d{A}_{2}\left(t\right)}{dt}=-f\; {g}_{n}\; {\gamma }_{0}\; {A}_{2}\left(t\right)$$
(35)

from which it follows that initially \({A}_{1}\) will experience exponential growth with the rate \(f\; {g}_{n} \;{\gamma }_{0}\) and \({A}_{2}\) will experience exponential decay with the same (but negative) rate. Since the system is non-linear when we consider \({A}_{1}\), \({A}_{2}\), and \({\rho }_{X}\), the overall dependence is more complicated. However, we can use that initial growth / decay rate to estimate the time needed for such a system to reach a homochiral state as:

$${T}_{h}=\frac{1}{f \;{g}_{n} \;{\gamma }_{0} }\approx \frac{{T}_{\gamma }}{f \;n \;g}\sim \frac{{T}_{\gamma }}{n \;g},\quad \left(n\; g\right)\ll 1$$
(36)

where \({T}_{\gamma }\equiv \frac{1}{ {\gamma }_{0}}\) is the average lifespan of the species and we used Eq. (32) to estimate \({g}_{n}\). This means that the larger are the protocells and the smaller is their lifespan, the faster they reach homochirality. Given that the condition on prebiotic Earth were harsh, it is reasonable to assume that the average lifespan of protocells was reasonably small. Assuming the value of global asymmetry factor \(g \sim {10}^{-17}\) (Kondepudi and Nelson 1983), number of amino acids in the protocell \(n \sim {10}^{9}\), \(f \sim 1\), \({T}_{\gamma } \sim 1\) day (the fastest growing modern bacteria can have doubling time as short as 10 min under optimal conditions, Elsgaard and Prieur, 2011) leads to an estimate \({T}_{h} \sim 300\) thousand years and it can easily go back and forth a few orders of magnitude if the lifespan and / or the number of chiral centers in the protocells change. The value of \({T}_{h}\) can shrink to \(\sim {T}_{\gamma }\) if much larger species are involved. To illustrate that consider some species with about 1 mg of weight and about \({p}_{w}=70\mathrm{\%}\) water and non-amino acid content. Then using average molar mass of amino acid of about \({m}_{a}\approx 110\) g/mol leads to an estimate of the total number of chiral centers in such species as \(\sim 1.6\times {10}^{18}\) and subsequently a value of \(\left(n g\right) \sim 16\). That results in \({g}_{n}\approx 1-{e}^{-\left(n g\right)}\approx 1\) and subsequently \({T}_{h}\approx {T}_{\gamma }\). This illustrates that the process can be extremely quick on a geological scale when species become larger and larger.

One may argue that the calculated above time estimate to reach homochirality could be too large compared to racemization time of amino acids under conditions on prebiotic Earth. However, the amino acids in the considered model only exist for the duration of the protocell lifespans, not for the duration of the whole transition period. Therefore, racemization does not affect this model.

Interplay of Global Asymmetry and Efficiency

The analysis above considers a specific case where global asymmetry parameter (the linear coefficient in the kernel near \(\eta =0\)) and the efficiency near \(\eta =\pm 1\) are skewed the same way. Here we would like to consider that in more details. In fact, one may argue that why it is not possible that e.g., mostly right species evolve to be more efficient in producing copies of themselves than left species just by chance when the system initially evolves toward distinct left and right species. Then they would dominate in the considerations above. To address this question, we need to get back to finding stationary points (eigenvectors and eigenvalues) of Eq. (5) but consider that the decay rate \(\gamma\) is now a function of \(\eta\):

$${\gamma }_{0}\to {\gamma }_{0} \,\gamma \left(\eta \right), \quad \gamma \left(0\right)\equiv 1$$
(37)

where \({\gamma }_{0}\) is now some normalizing decay rate coefficient and \(\gamma \left(\eta \right)\) can be called a relative decay rate of the species. Then the eigenvalue problem Eq. (25) becomes:

$$\underset{-1}{\overset{1}{\int }}\frac{k\left({\eta }^{\mathrm{^{\prime}}}\right) p\left(\eta ,{\eta }^{\mathrm{^{\prime}}}\right)}{\gamma \left(\eta \right)} u\left({\eta }^{\mathrm{^{\prime}}}\right) d{\eta }^{\mathrm{^{\prime}}}=\frac{{\gamma }_{0}}{{{\rho }_{X}}^{n}{k}_{0}} u\left(\eta \right)$$
(38)

We can estimate the ratio of two largest eigenvalues \(\frac{{\lambda }_{1}}{{\lambda }_{2}}\) (assuming that corresponding eigenvectors \({u}_{1}\) and \({u}_{2}\) are narrow peaks centered near \(\pm 1\)) as:

$$\frac{{\lambda }_{1}}{{\lambda }_{2}}\approx \left(\frac{k\left(1\right)}{k\left(-1\right)}\right)\left(\frac{\gamma \left(-1\right)}{\gamma \left(1\right)}\right)$$
(39)

So, even if right species turn out to be slightly more efficient just by chance: \(k\left(-1\right)>k\left(1\right)\), there is a limit on how much more efficient they could be due to effective averaging because of a very large number or reactions. Therefore, this term is \(\approx 1\) and the difference from \(1\) should be very small. However, the relative decay rate can easily become very different for left and right species and that means that \(\gamma \left(-1\right)\) can be substantially greater than \(\gamma \left(1\right)\). Subsequently \(\frac{{\lambda }_{1}}{{\lambda }_{2}}\) becomes greater than one. Further research is needed to check this statement in detail.

It is then interesting to look at how the eigenvector corresponding to the largest eigenvalue changes when efficiency parameter \(a\) is varied in the kernel with broken symmetry (Eq. 30). The results are shown on Fig. 5 (\(g={10}^{-20}\), \(\epsilon =0.02\)) and Fig. 6 (\(g={10}^{-20}\), \(\epsilon =0.005\)).

Fig. 5
figure 5

First eigenvector for different values of replication efficiency parameter \(a\) for global asymmetry parameter \(g={10}^{-20}\) and mutation rate \(\epsilon =0.02\)

Full size image
Fig. 6
figure 6

First eigenvector for different values of replication efficiency parameter \(a\) for global asymmetry parameter \(g={10}^{-20}\) and mutation rate \(\epsilon =0.005\)

Full size image

The value of \(a\to 0\) corresponds to the situation when there is no difference in efficiency based on enantiomeric content of the protocells. The resulting eigenvector at that value of \(a\) is a very wide even function, which spawns the whole region \(\left[-1, 1\right]\). As the parameter \(a\) increases, the eigenvector starts to run toward both \(\eta \pm 1\). That means that there is a range of parameter \(a\) where both species (made from mostly left and mostly right amino acids) can coexist. However, it is still nearly symmetric and the peaks near \(\eta \pm 1\) are wide until some critical value of \(a\), after which less efficient species disappear quickly and only the most efficient species remain. The eigenvector then becomes a narrow peak near \(\eta \approx 1\) (because we used a positive value of parameter \(g\), which makes species with \(\eta \approx 1\) more efficient in replication).

It is also interesting to look at the dependence of cut off value of parameter \(a\) at which the right species (\(\eta =-1\)) completely disappear. Figures 5 and 6 visually provide two points to estimate that: \({a}_{1}\approx 0.1\) for \({\epsilon }_{1}=0.02\) and \({a}_{2}\approx 0.006\) for \({\epsilon }_{2}=0.005\), from which it follows that \(\frac{{a}_{1}}{{a}_{2}}\approx {\left(\frac{{\epsilon }_{1}}{{\epsilon }_{2}}\right)}^{2}\). We also checked that ratio for values of \(g={10}^{-10}\) and \(g={10}^{-5}\). The charts for \(g={10}^{-10}\) exhibit similar dependency, though it is harder to determine the cut off because it becomes more spread out. The chart for \(g={10}^{-5}\) and \(\epsilon =0.005\), which is shown on Fig. 7 looks interesting. There is no visible region in parameter \(a\) where left and right species can coexist. Rather, when value of \(a\) increases, the eigenvector just transitions into left species straight away.

Fig. 7
figure 7

First eigenvector for different values of replication efficiency parameter \(a\) for global asymmetry parameter \(g={10}^{-5}\) and mutation rate \(\epsilon =0.005\)

Full size image

There are three parameters at play here: replication efficiency parameter \(a\), mutation rate \(\epsilon\), and global asymmetry parameter \(g\) that together determine the shape of the first eigenvector.

To continue the discussion about what if the right species evolve to be more efficient than the left species, whereas the global asymmetry parameter \(g\) favors the left species, we can consider a scenario when the value of \(g\) is not “enough” to overcome the efficiency of the right species near \(\eta =\pm 1\). To model such a scenario, we can introduce an extra parameter into a kernel, call it \({k}_{g,a,b}\):

$${k}_{g,a,b}\left(\eta \right)=1+g\; \eta +a\; {\eta }^{2}\left(1-b\; \eta \right)$$
(40)

where such parameter choice was made to make the part of the kernel made of quadratic and cubic powers of \(\eta\) rescale without changing shape when parameter \(a\) is varied. Parameter \(b\) can be called efficiency asymmetry parameter. The chart for some interesting combination of parameters is presented on Fig. 8.

Fig. 8
figure 8

First eigenvector for different values of replication efficiency parameter \(a\) for global asymmetry parameter \(g={10}^{-5}\), efficiency asymmetry parameter \(b=0.0005\), and mutation rate \(\epsilon =0.005\)

Full size image

The chart is interesting because it shows that while only one of the species always remains (after the value of parameter \(a\) becomes large enough), now it could be different species based on the value of the replication efficiency. The sudden transition from left species into right species happens when right species become more efficient than left species near points \(\eta =\pm 1\), which means that: \({k}_{g,a,b}\left(1\right)\approx {k}_{g,a,b}\left(-1\right)\), from which it follows that a critical value \({a}_{c}\) of parameter \(a\) should be:

$${a}_{c}\approx \frac{g}{b}$$
(41)

The actual value \({a}_{c}\approx 0.02155\) for the values of parameters \(g\) and \(b\) used on Fig. 8 and it is very close to the estimated value of \(\frac{g}{b}=0.02\) used to generate the chart. The eigenvector on Fig. 8 looks almost the same as on Fig. 7 up to \({a}_{c}\) and then it transitions to the right species. The transition from left to right species near \({a}_{c}\) point is very sharp, and it shows that the system slides into one or the other direction once the critical value \({a}_{c}\) is passed.

Impact of Discreteness

Continuous representation of the model described above is convenient for performing analysis because it allows us to use a well-known machinery of Fredholm equations. However, as chemical systems stochastically evolve in integers (number of molecules), rather than in continuous real functions, there are certain peculiarities, which must be accounted for.

When there is a global \(L\leftrightarrow D\) symmetry but some asymmetry of the initial state, then continuous model will first evolve into an asymmetric state made of some possibly unequal number of left and right species. The proportionality is the same as in the original decomposition of the initial state as determined by Eq. (13). Since the first two eigenvalues are nearly degenerate (the value \({\lambda }_{1}-{\lambda }_{2} \sim {10}^{-177}\) in one of the examples), that mix will coexist for extremely long time and for practical purposes it can be considered as forever. The real chemical systems are discrete, and they evolve stochastically. That means that Eq. (1) is effectively a random walk on a 1-D lattice where each step could be some small number of lattice nodes (number of left amino acids in a protocell) at a time. Such random walks are equivalent to diffusion processes and that ensures that a discrete model will spread out in the whole range in \(\eta\). In addition, as it is a random walk, the system could evolve into a random mix of left and right species, regardless, which mix is supposed to dominate in potentially asymmetric initial state according to Eq. (13). This is different from continuous representation where initial state completely determines the final state.

The most interesting behavior appears when there is a global asymmetry parameter pointing in one direction, but the efficiency factor: \(a\; {\eta }^{2}\left(1-b\; \eta \right)\) is tilted in the other direction: Eq. (40) and as illustrated on Fig. 8. When efficiency parameter \(a\) is gradually increasing and is crossing the value of \({a}_{c}\), then continuous system experiences a sudden transition from left to right species. This is because there are species with any total enantiomeric excess in continuous representation, even though some of the species (e.g., near \(\eta =-1\) when left species still dominate before reaching \({a}_{c}\)) have diminishingly small amplitudes. That does not happen in discrete evolution, as all small real numbers become exact zeros. That means that when efficiency parameter \(a\) crosses the value of \({a}_{c}\), there are no right species, which could have driven left species into extinction due to increased efficiency of the right species. Subsequently left species still stays. That means that it is the linear coefficient in the kernel function \({k}_{g,a,b}\left(\eta \right)\) near \(\eta =0\), which determines the direction into which the system will evolve, and that coefficient is a global asymmetry parameter \(g\).

Replication with Errors and Normalized Replication Rate Multiplier

Given that normalized replication rate multiplier \({k}_{a}\) with replication efficiency parameter \(a>0\) is crucial for the considered model to work, it is, therefore, important to perform analysis of the replication process for various total enantiomeric content of the protocells. Before proceeding further, we need to clarify what do we mean here by replication. For the purposes of further considerations, a replication is a process of creating a near copy of an “input” peptide chain (template). While it is tempting to bring parallels with DNA and RNA replication, where a so-called replication fork moves along the template and produces a copy of the DNA, the replication process on primordial Earth must have been much simpler than that because DNA and RNA have not existed yet. Therefore, without speculating about what chemical reactions could have been used at that time to perform a replication, we consider an abstract replication process in the following simplified form:

  • The replication happens at the replication site.

  • The template is “read” one amino acid at a time.

  • The replication site waits for matching amino acid to collide with the replication site and attempts to attach it to the copy.

  • If the process is unsuccessful (the amino acid is not attached), then replication site waits for another collision.

  • If the process is successful, then the replication site moves to the next amino acid of the template.

It is a known fact that the replication site does not have to carry the same chirality as a template. For example, Sczepanski and Joyce 2014, developed cross-chiral RNA polymerase where D-RNA enzyme catalyzes joining of L-mono or oligonucleotide substrates on a complimentary L-RNA template. Subsequently, we will not attempt to speculate what could be an effect of replication errors on the viability of the replicated structures. Here we only analyze collision events and their effect on the replication rate. In the current work we are also only interested in tracing amino acid enantiomers rather than types. Subsequently, we will not be considering errors due to replacement of amino acid types, but rather trace only errors due to incorrect enantiomers.

It is a well-known fact that rates of chemical reactions are proportional to the concentration of reagents. Consider a protocell with total internal enantiomeric excess \(\eta\) and consider that this protocell needs to replicate some complicated structure (e.g., create a copy of the protocell) with approximately the same total enantiomeric excess. The collision process between replication site and amino acids in the solution can be modeled using exponential distribution with probability density function: \(P\left(t\right)=\frac{1}{{T}_{c}}{e}^{\frac{t}{{T}_{c}}}\), where \({T}_{c}\) is the average collision time between any amino acid and the replication site. The probability that a left amino acid collides with the replication site is \(p=\frac{1+\eta }{2}\) when collision happens and the probability that a right amino acid collides with the replication site is \(\left(1-p\right)\).

As we are talking about protocells on primordial Earth where organic structures were much simpler than now, it is, therefore, reasonable to assume that such replication process was not completely precise at that time. To describe that we need to introduce two dimensionless parameters: \(q\) – the probability that a correct amino acid enantiomer is not attached to the structure when it successfully collides with the replication site and \(r\) – the probability that incorrect amino acid enantiomer is attached to the structure when it successfully collides with the replication site. We can call parameter \(q\) as skip probability and \(r\) as error probability. Then, we can calculate total enantiomeric excess of replicated structure \({\eta }_{w}\) by considering collision events:

$$\begin{aligned}P_{LLA}=&\,p\;(1-q)\;-\;\mathrm{probability\;to\;get\;}L\mathrm{\;amino\;acid\;and\;attach\;it\;when}\;L\;\mathrm{is\;needed}\\&P_{LLN}=p\;q\;-\;\mathrm{probability\;to\;get}\;L\;\mathrm{amino\;acid\;and\;do\;not\;attach\;it\;when}\;L\;\mathrm{is\;needed}\\&P_{LDA}=(1-p)\;r\;-\;\mathrm{probability\;to\;get}\;D\;\mathrm{amino\;acid\;and\;attach\;it\;when}\;L\;\mathrm{is\;needed}\\&P_{LDN}=(1-p)\;(1-r)\;-\;\mathrm{probability\;to\;get}\;D\;\mathrm{amino\;acid\;and\;do\;not\;attach\;it\;when}\;L\;\mathrm{is\;needed}\end{aligned}$$
(42)

and similar when \(D\) amino acid is needed:

$$\begin{aligned}P_{DDA}=&\,(1-p)\;(1-q)\;-\;\mathrm{probability\;to\;get}\;D\;\mathrm{amino\;acid\;and\;attach\;it\;when}\;D\;\mathrm{is\;needed}\\&P_{DDN}=(1-p)\;q\;-\;\mathrm{probability\;to\;get}\;\mathrm{D}\;\mathrm{amino\;acid\;and\;do\;not\;attach\;it\;when}\;D\;\mathrm{is\;needed}\\&P_{DLA}=p\;r\;-\;\mathrm{probability\;to\;get}\;L\;\mathrm{amino\;acid\;and\;attach\;it\;when}\;D\;\mathrm{is\;needed}\\&P_{DLN}=p\;(1-r)\;-\;\mathrm{probability\;to\;get}\;L\;\mathrm{amino\;acid\;and\;do\;not\;attach\;it\;when}\;D\;\mathrm{is\;needed}\end{aligned}$$
(43)

from which we can calculate the following probabilities:

$$\begin{aligned}P_{LA}=&\,r+p\;(1-q-r)-\;\mathrm{probability\;to\;attach\;any\;amino\;acid\;when}\;L\;\mathrm{is\;needed}\\&P_{LN}=1-r-p\;(1-q-r)-\;\mathrm{probability\;to}\;\boldsymbol{do}\;\boldsymbol{not}\;\mathrm{attach\;any\;amino\;acid\;when}\;L\;\mathrm{is\;needed}\\&P_{DA}=1-q-p\;(1-q-r)-\;\mathrm{probability\;to\;attach\;any\;amino\;acid\;when}\;D\;\mathrm{is\;needed}\\&P_{DN}=q+p\;(1-q-r)-\;\mathrm{probability\;to}\;\boldsymbol{do}\;\boldsymbol{not}\;\mathrm{attach\;any\;amino\;acid\;when}\;D\;\mathrm{is\;needed}\end{aligned}$$
(44)

and from which it follows that “expected value” of attached amino acid enantiomeric excess (taking that “enantiomeric excess” of \(L\) is \(e{e}_{L}=1\), and of \(D\) is \(e{e}_{D}=-1\)) after attachment on the first try when \(L\) is needed and expected value after attachment on the first try when \(D\) is needed are:

$$\begin{aligned}E_{L1}&=ee_LP_{LLA}+ee_DP_{LDA}=p\left(1-q\right)-\left(1-p\right)r\\E_{D1}&=ee_DP_{DDA}+ee_LP_{DLA}=-\left(1-p\right)\left(1-q\right)+p\;r\end{aligned}$$
(45)

We can note that \({E}_{L1}\leftrightarrow \left({-E}_{D1}\right)\) when \(p\leftrightarrow \left(1-p\right)\), as expected. When, e.g., \(L\) is needed, then the following events are possible at each collision: the amino acid is attached (which is described by two events captured in \({E}_{L1}\): the probability to get \(L\) and attach it: \({P}_{LLA}\), and the probability to get \(D\) and attach it: \({P}_{LDA}\)) or not (which has the probability \(1-\left({P}_{LLA}+{P}_{LDA}\right)\equiv 1-{P}_{LA}\equiv {P}_{LN}\)). Then, we can calculate expected values of attached amino acid enantiomeric excess after any number of tries when \(L\) is needed and when \(D\) is needed as:

$$\begin{aligned}E_L=E_{L1}\sum_{k=0}^\infty\left(P_{LN}\right)^k=\frac{E_{L1}}{1-P_{LN}}=\frac{p\left(1-q+r\right)-r}{p\left(1-q-r\right)+r}\\E_D=E_{D1}\sum_{k=0}^\infty\left(P_{DN}\right)^k=\frac{E_{D1}}{1-P_{DN}}=\frac{(1-p)\;\left(1-q+r\right)-r}{(1-p)\;\left(1-q-r\right)+r}\end{aligned}$$
(46)

and, finally, expected total enantiomeric excess of the replicated structure as:

$${\eta }_{w}\left(\eta ,w\right)=p\; {E}_{L} + \left(1-p\right) {E}_{D}=\eta \left(1+\frac{w \left(1-w\right)\left(1-{\eta }^{2}\right)}{1-{w}^{2} {\eta }^{2}}\right)$$
(47)

assuming that the amino acids in the solution are abundant enough so that we can neglect changes to enantiomeric excess in the solution due to replication, and that parameters \(q\) and \(r\) are independent on enantiomeric content, and where parameter \(w\) was introduced for the convenience as:

$$w=\frac{1-q-r}{1-q+r}\equiv \frac{1-\left(\frac{r}{1-q}\right)}{1+\left(\frac{r}{1-q}\right)}\equiv \frac{1-\widetilde{r} }{1+\widetilde{r}}$$
(48)

where \(\widetilde{r}=\left(\frac{r}{1-q}\right)\) is an adjusted error rate. It shall be noted that the physical meaning of \(w\) is the enantioselectivity of the replication site.

To calculate total expected replication time \({T}_{w}\) we note that total \(\left(p n\right)\) left amino acids and \(\left(\left(1-\mathrm{p}\right) n\right)\) right amino acids need to be attached, consider the same replication events as above, and note that when amino acids it not attached then we need to wait for another \({T}_{c}\) (on average) before the next collision event happens. The expected times to attach some amino acid when \(L\) is needed and when \(D\) is needed are:

$$\begin{aligned}T_L=T_cP_{LA}\sum_{k=0}^\infty\left(k+1\right)\left(P_{LN}\right)^k\\T_D=T_cP_{DA}\sum_{k=0}^\infty\left(k+1\right)\left(P_{DN}\right)^k\end{aligned}$$
(49)

from which it follows that total expected replication time is:

$${T}_{w}\left(\eta ,w,r\right)=p\; n \;{T}_{L} +\left(1-\mathrm{p}\right) \;n \;{T}_{D}=\frac{\left(1-w\right)\left(1-w {\eta }^{2}\right)}{r \left(1-{w}^{2} {\eta }^{2}\right)} {T}_{c} \;n$$
(50)

We can further define normalized replication rate multiplier due to different replication time as:

$${k}_{w}\left(\eta ,w\right)=\frac{{T}_{w}\left(0,w,r\right)}{{T}_{w}\left(\eta ,w,r\right)}=1+\frac{w\left(1-w\right) {\eta }^{2}}{1-w {\eta }^{2}}$$
(51)

The value of \(\Delta {\eta }_{w}=\left({\eta }_{w}-\eta \right)\), which can be called extra total enantiomeric excess, shows the difference between total enantiomeric excess of the original structure and replicated structure and the value of \({k}_{w}\) shows how much faster the replication process should take in comparison to a protocell with an equal mix of left and right amino acids (\(\eta =0\)) for a given value of \(w\). The charts for \(\Delta {\eta }_{w}\) and \({k}_{w}\), are shown on Figs. 9 and 10.

Fig. 9
figure 9

Dependence of extra total enantiomeric excess \(\Delta {\eta }_{w}\) on enantioselectivity of replication site \(w\)and enantiomeric excess \(\eta\)

Full size image
Fig. 10
figure 10

Dependence of normalized rate multiplier \({k}_{w}\) on enantioselectivity of replication site \(w\)and enantiomeric excess \(\eta\)

Full size image

The following should be noted. The value of \(\Delta {\eta }_{w}\) is an odd function, which is strictly positive in the interval \(\eta \in \left(0, 1\right)\) for any \(w\in \left(0, 1\right)\) and the value of \({k}_{w}\) is an even convex function with a minimum at \(\eta =0\) for any value of \(w>0\). Both have the same reason, and it is the non-zero parameter \(r\) that results in that. Parameter \(r\) is effectively an error rate that amino acid of wrong chirality will be attached to the replicated structure. If, e.g., \(\eta >0\), then the probably of collision with left amino acid is larger than with the right amino acid, at which point the left amino acid could be attached instead of right amino acid (where right was needed). The same explains why \({k}_{w}\) does not stay constant when \(\eta\) is varied: amino acid of incorrect chirality is simply attached to the chain and replication moves on to the next element. The fact that values of \({k}_{w}\) and \(\Delta {\eta }_{w}\) depend only on parameter \(w\) and not on individual values of parameters \(q\) and \(r\) makes it irrelevant whether parameters \(q\) and \(r\) are related or not.

Since, as shown above, replication with errors amplifies the enantiomeric excess in the replicated structure, the surrounding solution experiences the opposite, that is the enantiomeric excess should decrease in absolute value. Therefore, without any mechanism to restore enantiomeric excess in the solution inside the protocell, the net effect must be zero. However, there is a well-known effect, which ensures that at least some amino acids can maintain high level of enantiomeric excess inside protocells. That is formation of highly insoluble diastereomeric salts. While it is often mentioned that only 5–10% of amino acids form such highly insoluble diastereomeric salts and so it is not enough to reach homochirality (Klussmann et al. 2006; Blackmond 2011), this statement should be rephrased as follows when applied to replication inside protocells: there are at least about 5–10% of amino acids, which should participate in replication process in nearly homochiral form. Therefore, it would be interesting to look at solubilities of nearly racemic mixtures of 20 to 22 amino acids that comprise proteins and especially of adenine, thymine, guanine, and cytosine, which are used in the DNA. Unfortunately, we were unable to find detailed information in this regard. It shall be also noted that formation of such diastereomeric salts is mutual inhibition mechanism as described in Frank’s model.

The analysis above shows a very interesting phenomena: while modern Life has error rate \(\widetilde{r}\) nearly identically zero, it is substantially different from zero value of \(\widetilde{r}\) that pushes replicated structures in primitive protocells toward homochirality. It is also interesting that apart from a very low error rate, modern Life utilizes “error correction” mechanisms in the form of, e.g., \(D\)-amino acid oxidase, which destroys all natural \(D\)-amino acid except the acidic ones (e.g., Pollegioni et al. 2018).

Topology of the Model

Here we would like to discuss the topological differences between, e.g., Frank’s or similar models and the current model. The systems in Frank’s or similar models experience bifurcation when some control parameter crosses certain critical value regardless the absence or presence of some small global asymmetry factor. The model considered here can be called evolutionary. The protocells do not experience a bifurcation point even in case of a global \(L\leftrightarrow D\) symmetry where left and right species can coexist (which is not the case in bifurcation-based models). This can be illustrated by calculating average total enantiomeric excess in the system, \({\mu }_{\eta }\) (Eq. 27) and standard deviation, \({\sigma }_{\eta }\) (Eq. 28). The average total enantiomeric excess is \({\mu }_{\eta }\equiv 0\) and the standard deviation is \({\sigma }_{\eta }\approx 1\) for the evolutionary model discussed here, whereas \({\mu }_{\eta }\approx \pm 1\) and \({\sigma }_{\eta }\approx 0\) for bifurcation-based models when there is a global \(L\leftrightarrow D\) symmetry.

Once a small global asymmetry parameter is introduced, the current model just “evolves” toward the most efficient species, and it happens in a smooth way when the control parameter (replication efficiency parameter \(a\)) is varied. This difference in behavior can be explained once we consider the spaces in which bifurcation-based models and current model operate. A typical bifurcation-based model has, e.g., some \(L\) and \(D\) species. Topologically, this is a set of two zero-dimensional disconnected spaces (points with \(\eta =-1\) and \(\eta =1\)). Current model (when viewed in continuous form) operates in one-dimensional connected space (the whole interval \(\eta \in \left[-1, 1\right]\)) and so the points \(\eta =-1\) and \(\eta =1\) are connected. This is what makes it possible for the system to smoothly evolve on the interval \(\left[-1, 1\right]\) in the relevant direction based on values of the coefficients (small global asymmetry parameter \(g\), replication efficiency parameter \(a\), and efficiency asymmetry parameter \(b\)). When discretization is introduced (whether considering that protocells have some finite number of amino acids or discretizing function \(u\left({\eta }^{\mathrm{^{\prime}}}\right)\) in the integral), then it is no longer possible to use the term “connected”, as it is only used for continuous spaces. However, it is still possible to make a “path” between \(\eta =-1\) and \(\eta =1\) points by making small steps (replacing one \(D\) amino acid by one \(L\) amino acid in a protocell). That difference in topology of the spaces, in which bifurcation models and evolutionary models, like considered here, operate is what makes the difference.

Subsequently, from the topology point of view, we can further say that the concept of symmetry breaking is not applicable to evolutionary models, like considered here. The change in control parameter in bifurcation models results in a sudden split of a symmetric racemic state into either only left or only right species. That split is random in case of global symmetry or directed in case of some global asymmetry parameter. The evolutionary models can have any values of total enantiomeric excess in between purely left and purely right species and that allows them to gradually transition to, e.g., nearly all left species when control parameter (the efficiency parameter \(a\)) is varied.

Further Research

As a final note we would like to discuss some possible directions of further research.

Considering that some percentage of amino acids is taken out of the environment and the rest is synthesized inside the protocells is an interesting and important question. That will require introducing several more parameters and reactions. One of the reactions, which must be considered in such a case, is racemization. The larger percentage of amino acids is reused, the larger will be effect of racemization. Another reaction that might be worth considering is an internal “error correction” mechanism, as discussed above.

Better analysis of effect of global asymmetry, like weak interaction, on stability of long peptide chains is needed to come up with a better time estimate to reach homochirality. This becomes especially important when some amino acids are reused, and racemization is taken into account.

Dynamic evolution with gradually increasing efficiency parameter \(a\) for model described by Eq. (40) is also interesting. If parameter \(a\) is slowly increasing (which would model the scenario when protocells evolve to become more efficient), then the system will first transition into purely \(L\) species. The question is what will happen when parameter \(a\) goes above \({a}_{c}\). Since protocells are measured in non-negative integers, then there will likely be no \(D\) protocells at all. Subsequently, the sudden transition to purely right species, as shown on Fig. 8 is likely never going to happen.

Experimentally, it is interesting to look at the solubilities of diastereomeric salts made of 20–22 amino acids used in organic life and especially the four used in the DNA.

It is also interesting to look not only on chirality of amino acids but also on their type and then investigate how that affects replication with errors.

Conclusion

There have been numerous discussions over many years whether chiral symmetry breaking on primordial Earth occurred first followed by biological evolution or it happened the other way around and whether that symmetry breaking was directed or happened just by chance.

Our current view is as follows. Given that reactions with energy consumptions are crucial for organic life to maintain order, it seems unlikely that substantial and consistent chiral symmetry breaking could occur before the ability to store and process energy has evolved, even if it was in a very primitive form.

We considered a very simple linear model of protocell evolution and showed such model should evolve into a mix of almost purely left and almost purely right species when there is a global \(L\leftrightarrow D\) symmetry. This is very different from bifurcation-based models, which exhibit spontaneous symmetry breaking. However, when a tiny global asymmetry factor is introduced into the model, then only one, more efficient, species survive. We traced down the difference in behavior of evolutionary models and bifurcation-based models to the differences in the topologies of the spaces, in which the models operate. Bifurcation-based models operate in disjoint set of two zero-dimensional spaces (two points \(L\) and \(D\)), whereas evolutionary models (in continuous representation) operate in one-dimensional connected space (any value of total enantioselectivity is possible between \(\eta =-1\) and \(\eta =1\)). Subsequently, we argued that the concept of symmetry breaking is not applicable to evolutionary models. Rather, more efficient species simply outperform less efficient species either in increased replication rate, or decreased decay rate, or both and that results in less efficient species simply dying off from “starvation” when the “food” becomes scarce in the model.

We performed an estimate of the time needed to achieve homochirality in such a model and showed that it could be on the order of a few hundred thousand years plus or minus a couple of orders of magnitude. Despite this seemingly large time, the model is immune to racemization because amino acids in the model exist only for the duration of protocells lifespan.

We then proceeded with the analysis of replication with errors and showed that homochiral protocells should have a faster replication time in comparison to racemic protocells. In addition, we showed that replication with errors results in higher enantiomeric excess in replicated structures in comparison to the original structure, though at the expense of depleting enantiomeric excess inside the protocell and / or in the environment.