1 Introduction

Nonlinear partial differential equations (NPDEs) are powerful tools for modeling nonlinear physical phenomena that occur in science and engineering problems. Obtaining numerical or exact solutions for NPDEs (Bilal and Ren 2022; Bilal et al. 2021b, 2023b, 2024; Rizvi et al. 2023, 2024a, b) has attracted the attention of the scientific community from many different fields in recent years, more than ever before, in terms of understanding these models in detail due to their use in scientific experiments that lead to technological breakthroughs. Therefore, improving methods in the process of obtaining solutions is of vital importance in supporting scientific advances. Particularly, the optical solitons arising from a wide variety of experimental and theoretical studies have pervasive significance in diverse physical applications such as in water waves, nonlinear acoustics, plasma physics, astrophysics, hydrodynamics, telecommunications, quantum field theory, the dynamics of particles, and nonlinear optics. In terms of maintaining their shape and energy without distortion over long distances and transmitting high-speed data through an optical fiber, these soliton solutions have contributed to the efficiency of optical communication systems in recent years. One of the most important integrable equations as a well-known soliton problem in the physical and engineering sciences is the classical nonlinear Schrödinger (NLS) equation given by:

$$\begin{aligned} iq_{t}+\frac{1}{2}q_{xx}+|q|^2 q=0. \end{aligned}$$
(1.1)

The NLS equation and its various forms play an important role in the understanding of optical solitons (Bilal et al. 2021, 2021a, 2023a, b; Geng et al. 2023; Chen 2023; Bo et al. 2023; Xu et al. 2023; Wen et al. 2023; Rizvi et al. 2024c). Due to its versatile application in many engineering problems such as in the field of transcontinental services and transoceanic transmission, several generic deformations of the NLS equation under higher-order perturbations have been proposed depending on the nature of the problems. Some of these NLS equations have been derived from the following system (Abhinav et al. 2018; Zhu and Chen 2021), called the derivative nonlinear Schrödinger (DNLS) family.

$$\begin{aligned} {\left\{ \begin{array}{ll} q_{t}=iq_{xx}-(4\beta +1)q^2r_{x}-4\beta q q_{x}r+\frac{i}{2}(1+2\beta )(4\beta +1)q^3r^2 , \\ r_{t}=-ir_{xx}-(4\beta +1)r^2q_{x}-4\beta r r_{x}q-\frac{i}{2}(1+2\beta )(4\beta +1)q^2r^3,\\ \end{array}\right. } \end{aligned}$$
(1.2)

where \(q=q(x,t)\) and \(r=r(x,t)\) are complex-valued functions with x and t being independent variables that are spatial and temporal variables respectively. Some of the important DNLS equations derived from Eq. (1.2) with some special parameters are presented below.

Taking \(\beta =-\frac{1}{2}\) and \(r=-q^*\) reduces the system (1.2) to the Kaup–Newell (KN) equation (Kaup et al. 1978), also called DNLS I

$$\begin{aligned} iq_{t}+q_{xx}-i(|q|^2 q)_x=0, \end{aligned}$$
(1.3)

modeling to the description of sub-pico-second pulse which spreads via the single-mode optical fibers (Triki et al. 2019; Jawad et al. 2019a; Arshed et al. 2018).

Taking \(\beta =-\frac{1}{4}\) and \(r=-q^*\) reduces the system (1.2) to the Chen–Lee–Liu (CLL) equation (Chen 2023), also called DNLS II

$$\begin{aligned} iq_{t}+q_{xx}-i|q|^2 q_x=0, \end{aligned}$$
(1.4)

modeling to the transmission of ultrashort optical pulses (Khater 2023a, b; Ouahid et al. 2023).

Taking \(\beta =0\) and \(r=-q^*\) reduces the system (1.2) to the Gerdjikov–Ivanov (GI) equation (Gerdjikov and Ivanov 1982), also called DNLS III

$$\begin{aligned} iq_{t}+q_{xx}-iq^2 q_x^*+\frac{1}{2}|q|^4 q=0, \end{aligned}$$
(1.5)

modeling to the propagation parallel to the ambient magnetic field for the Alfvén waves (Mjølhus 1989; Xu et al. 2023; Ding et al. 2019). Here asterisk(*) sign denotes complex conjugation.

These three well-known DNLS equations, which play critical roles in various applied fields by modeling physics, mathematics, and engineering problems, have received increasing attention recently. Particularly, the effects of high-order perturbations arising in the modern telecommunication industry and social media communications are being investigated extensively. Optical soliton solutions of the KN equation were found by Biswas et al. (2018) using modified simple equation method and trial equation method, by Esen et al. (2022) using new Kudryashovs method and generalized projective Riccati equations, by Jawad et al. (2019b) using csch-function method. The CLL equation studied by Akinyemi et al. (2021) using \(\left( \frac{G^{\prime }}{G}\right)\)-expansion method, by Mohamed et al. (2022) using modified generalized exponential rational function method, by Arnous et al. (2022) using the enhanced Kudryashov and improved extended tanh-function methods. Moreover, Bilal et al. (2021) not only investigated optical soliton solutions of the CLL equation of monomode fibers by applying three different exact solution methods, which are the extended sinh-Gordon equation expansion method, logarithmic transformation, and the ansatz functions method but also discussed modulation instability analysis of the CLL equation. Manafian and Lakestani (2016) applied the improved \(\tan (\frac{\phi }{2})\)-expansion method to study optical soliton solutions for the GI equation. The bright soliton solutions were employed for the GI equation with Lie symmetry analysis by Biswas et al. (2017). Optical soliton perturbation of the GI equation was studied by Biswas et al. (2018b) by using modified simple equation method. Zhang and Fan (2020) applied the inverse scattering method for the GI equation with a nonzero boundary at infinity. Li et al. (2021) studied the nonlocal GI equation by constructing its 2nd-fold Darboux transformation and had the bright-dark soliton, breather, rogue wave, kink, W-shaped soliton, and periodic solutions. The GI equation with nonzero boundary at infinity was studied by Luo and Fan (2021) by applying the Dbar-dressing method. The nonlinear GI equation with the M-fractional operator was studied by implementing the modified exponential function method by Ismael et al. (2023). Rizvi et al. (2023) studied the GI equation using the polynomial method’s complete discrimination system, which plays a crucial role in performing quantitative and qualitative evaluations, and studying equilibrium points, phase diagrams, bifurcation behavior.

In this study, we are dealing with the perturbed Kaup–Newell (KN), the perturbed Chen–Lee–Liu (CLL) equation, and the perturbed Gerdjikov–Ivanov (GI) equation with three Hamiltonian-type perturbation terms that come with full nonlinearity. The mathematical forms of the perturbed KN equation, the perturbed CLL equation and the perturbed GI equation are given as follows, respectively:

$$\begin{aligned}{} & {} iq_{t}+aq_{xx}-ib(|q|^2 q)_x=i \left[ \alpha q_x+\beta (|q|^{2m} q)_x+\gamma (|q|^{2m})_x q\right] . \end{aligned}$$
(1.6)
$$\begin{aligned}{} & {} iq_{t}+a q_{xx}+ib|q|^2 q_x=i \left[ \alpha q_x+\beta (|q|^{2m} q)_x+\gamma (|q|^{2m})_x q\right] , \end{aligned}$$
(1.7)

The perturbed KN equation and the perturbed CLL equation describe the propagation of sub-picosecond pulses in the optical fiber. The terms on the left-hand side in Eqs. (1.6) and (1.7) stand for the time evolution, the group velocity dispersion, and a special form of nonlinearity, respectively.

$$\begin{aligned} iq_{t}+a q_{xx}+b|q|^4 q+i cq^2 q_x^*= i\left[ \alpha q_x+\beta (|q|^{2m} q)_x+\gamma (|q|^{2m})_x q\right] , \end{aligned}$$
(1.8)

The perturbed GI equation describes the dynamics of soliton propagation of the ultrashort signal through optical fibers, photonic crystal fibers (PCF), and metamaterial. The terms on the left-hand side in Eq. (1.8) stand for the time evolution, the group velocity dispersion, quintic nonlinearity, and nonlinear dispersion, respectively. The terms on the right-hand side for these three equations are coming from the perturbation effects account for the intermodal dispersion, the self-steepening, and the nonlinear dispersion, respectively. Also, the full nonlinearity parameter is demonstrated by m for these three equations.

Various approaches by many scientists have been developed to solve the perturbed KN equation, the perturbed CLL equation, and the perturbed GI equation. Stability analysis and conservation laws were investigated by Yusuf et al. (2018) for the perturbed KN equation. Elliptic periodic, chirped solitons and trigonometric solutions were obtained based on the Jacobian elliptic functions theory for the perturbed KN equation by Salas et al. (2020). Arshad et al. (2023); Qian et al. (2021) found analytical solutions of the fractional-order perturbed KN equation by employing generalized exp\((-\phi (\xi ))\)-expansion method and improved F-expansion. Hu et al. (2021) used the modified extended simple equation method to obtain the solution on bright-dark and multi-wave novel soliton structures. Esen et al. (2021) obtained solitary wave solutions of the CLL equation using the Sardar subequation method, taking the full nonlinear parameter \(m=1\). After obtaining exact solutions for the CLL equation with \(m=1\), Abdel-Gawad (2022) demonstrated the behavior of these solutions represented by figures. Khater et al. (2023) investigated analytical and semi-analytical solutions of the CLL equation with the full nonlinear parameter \(m=1\) and depicted them graphically. The perturbed CLL equation was solved by seven exact solution methods, which are the sine-Gordon equation method, F-expansion method, functional variable method, exp-expansion method, method, trial equation method, modified simple equation method by Yildirim et al. (2020). The optical soliton solutions for the perturbed CLL equation were constructed by Baskonus et al. (2021) with the exp\((-\phi (\xi ))\)-expansion method and by Yokus et al. (2021) with modified \(\left( \frac{1}{G^{\prime }}\right)\)-expansion method and modified Kudryashov methods. Optical solitons of the perturbed CLL equation with arbitrary refractive index were obtained by Kudryashov (2021) via the Jacobi and the Weierstrass elliptic functions. Houwe et al. (2021) studied the perturbed CLL equation to obtain the chirped solitary waves. The semi-inverse variational principle applied to the perturbed GI equation by Biswas et al. (2017) to get Chirp-free bright optical solitons solutions. Obtaining optical soliton solutions for perturbed GI equation was investigated by Kaur and Wazwaz (2018) using the exp\((-\phi (\xi ))\)-expansion method and \(\left( \frac{G^{\prime }}{G}\right)\)-expansion method, by Biswas et al. (2018) using the extended trial equation method, by Biswas et al. (2018a) using the trial equation method, by Biswas et al. (2018) using the extended Kudryashov’s method, and by Onder et al. (2023) using the Sardar sub-equation and the modified Kudryashov’s methods. Arshed (2018) developed traveling wave solutions for the perturbed GI equation by using exp\((-\phi (\xi ))\)-expansion method and the Kudryashov method. The bright, dark, dark-bright, singular, and combined singular optical solitons are investigated for Hamiltonian type perturbed GI equation using the sine-Gordon equation method by Yasar et al. (2018). Improved projective Riccati equations method applied to the perturbed GI equation by Al-Kalbani et al. (2021) to obtain bright, kink, and singular optical soliton solutions. Shehata et al. (2021) developed the new optical solitons of the perturbed GI equation with the balanced modified extended tanh-function and the non-balanced Riccati-Bernoulli Sub-ODE methods. Hassan et al. (2021) applied the collective variables technique to the perturbed GI equation for obtaining novel optical solitons. The modified extended tanh expansion method and exp-function approach were used to construct M-fractional optical solitons to the perturbed GI equation by Zafar et al. (2022). Rehman et al. (2023) investigated the new soliton solutions of the perturbed GI equation with the aid of the hyperbolic extended function method and generalized Kudryashovs method. They produced the dark, bright, periodic, and singular solitons deriving the considered solutions with the appropriate choice of parameters.

To the best of our knowledge, there is no study in which these three problems with perturbed terms of the DNLS family are studied simultaneously. The purpose of this paper is to construct the general exact solutions with free parameters based on the generalized unified method (GUM) for the three members of the DNLS family, which are the perturbed Kaup–Newell equation, the perturbed Chen–Lee–Liu equation, and the perturbed Gerdjikov–Ivanov equation. Considering the studies in the past which mostly studied unperturbed DNLS family, we have obtained more general exact solutions with free parameters for the DNLS family with perturbed terms such that hyperbolic, trigonometric, and exponential function solutions can be also derived from these solutions. Therefore, the obtained results will be useful to explain better the propagation of ultrashort optical pulses in fibers in problems modeled by the family such as the modern telecommunication industry and social media communications.

The organization of this paper is as follows. Firstly, we give a brief description of the generalized unified method (GUM) in Sect. 2. Then, the exact optical soliton solutions of the perturbed KN, the perturbed GI, and the perturbed CLL equations are presented in Sect. 3. After summarizing the obtained solutions, physical structures and graphical illustrations of some selected solutions for these equations are displayed in the result and discussion part. Lastly, conclusive remarks are given in Sect. 5.

2 Outline of The Generalized Unified Method

In this short section, we describe briefly the generalized unified method (GUM) for solving nonlinear partial differential equations (NPDEs). The reader is referred to these articles Aydemir (2023a, 2023b) for a more detailed discussion. The basic principle of exact solution methods based on the Ansatz method for finding exact solutions of NPDEs after reducing them to ordinary differential equations (NODEs) is to model the solution forms by finite series expansions, mostly represented by various Riccati differential equations (RDEs). The GUM expresses the solution of reduced ODEs by finite series expansion as below:

$$\begin{aligned} Q(\eta ) =a_{0}+\sum _{m=1}^{M}\left[ a_{m}\psi ^{m}+b_{m}\psi ^{-m}\right] , \end{aligned}$$
(2.1)

where \(\psi =\psi (\eta )\) satisfies the RDE defined \(\psi ^{\prime }(\eta ) =\psi ^{2}(\eta )-\mu ^2\) with \(\psi ^{\prime }=\frac{d\psi }{d\eta }\) and \(\mu =(\mu _1+i\mu _2)\) where \(\mu _1\) and \(\mu _2\) are parameters. The degree of this finite series expansion, called the balance parameter, is calculated by using the highest-order linear derivative term and the highest nonlinear term. Substituting the finite series expansion and its derivatives with respect to wave variable into reduced ODE gives a system of algebraic equations. This system can be solved by any computer algebra systems (CAS) such as Maple or Mathematica to determine the coefficients of the finite series expansion. Lastly, the combinations of these coefficients and the solutions of the RDE provide exact solutions of NPDE with free parameters. The general solutions of this RDE are as follows:

$$\begin{aligned} \psi (\eta ) =\left\{ \begin{array}{c} \psi _1=\frac{(\mu _1+i\mu _2)\left( \sqrt{A^{2}+(B+iC)^{2}}-A(\cosh \left( 2(\mu _1+i\mu _2) (\eta +\eta _{0} )\right) \right) }{(B+iC)+A\sinh \left( 2(\mu _1+i\mu _2)( \eta +\eta _{0} ) \right) }, \\ \psi _2=\frac{-(\mu _1+i\mu _2)\left( \sqrt{A^{2}+(B+iC)^{2}}+A(\cosh \left( 2(\mu _1+i\mu _2) (\eta +\eta _{0} )\right) \right) }{(B+iC)+A\sinh \left( 2(\mu _1+i\mu _2)( \eta +\eta _{0} ) \right) }, \\ \psi _3=\frac{(\mu _1+i\mu _2)\left( -A+e^{-2(\mu _1+i\mu _2)(\eta +\eta _{0} )}\right) }{A+e^{-2(\mu _1+i\mu _2)(\eta +\eta _{0} )}}, \\ \psi _4=\frac{-(\mu _1+i\mu _2)\left( -A+e^{2(\mu _1+i\mu _2)(\eta +\eta _{0} )}\right) }{A+e^{2(\mu _1+i\mu _2)(\eta +\eta _{0} )} },\\ \psi _5=-\frac{1}{\eta +\eta _{0} } \end{array} \right. \end{aligned}$$
(2.2)

where \(A\ne 0\), B and C are real arbitrary parameters.

3 Applications

Obtaining exact solutions provides valuable information for the problems modeled with these equations such as the structure of the wave shape and the propagation of nonlinear waves. This section contains exact optical soliton solutions of the perturbed Kaup–Newell equation (KN), the perturbed Chen–Lee–Liu (CLL) equation, and the Gerdjikov–Ivanov (GI) equation which have been obtained by applying the generalized unified method (GUM).

3.1 Exact Optical Soliton Solutions of The Perturbed Kaup–Newell Equation

The perturbed KN equation is given by

$$\begin{aligned} iq_{t}+aq_{xx}-ib(|q|^2 q)_x-i \left[ \alpha q_x+\beta (|q|^{2m} q)_x+\gamma (|q|^{2m})_x q\right] =0. \end{aligned}$$
(3.1)

Firstly, the wave transformation \(q(x,t)=Q(\eta )e^{-i\Omega }\) is applied to the perturbed KN equation to reduce it to the form of a nonlinear ordinary differential equation (NODE). \(Q(\eta )\) represents the shape of the wave pulse in this transformation with the wave variable \(\eta = x-vt+\eta _0\) and the phase of wave \(\Omega =px-wt+\Omega _0\), where \(\Omega _0\), \(\eta _0\) are arbitrary free parameters. Substituting \(\displaystyle {q(x,t)=Q(\eta )e^{-i\Omega }}\) and its derivatives into Eq. (3.1), the perturbed KN equation is reduced to the NODE. By uncoupling this equation of real and imaginary parts, the following two equations are obtained, respectively.

$$\begin{aligned} {\left\{ \begin{array}{ll} a Q''-(w+\alpha p+ap^2)Q-bp Q^3 -\beta pQ^{2m+1}=0,\\ -(v+2ap+\alpha )-3bQ^2-\left( (2m+1)\beta +2m\gamma \right) Q^{2m}=0. \end{array}\right. } \end{aligned}$$
(3.2)

The statement \(Q^{2m}=\displaystyle {\frac{-(v+2ap+\alpha )-3bQ^2}{(2m+1)\beta +2m\gamma }}\) obtained from the imaginary part is substituted into the real part to get the following final equation used for finding exact solutions.

$$\begin{aligned} a Q''-\left( w+\alpha p+ap^2-\frac{\beta p(v+2ap+\alpha )}{(2m+1)\beta +2m\gamma }\right) Q-\left( bp-\frac{3\beta bp}{(2m+1)\beta +2m\gamma }\right) Q^3=0. \end{aligned}$$
(3.3)

The coefficients of Eq. (3.3) are defined as \(D=\displaystyle {\left( w+\alpha p+ap^2-\frac{\beta p(v+2ap+\alpha )}{(2\,m+1)\beta +2\,m\gamma }\right) }\) and

\(E=\displaystyle {\left( bp-\frac{3\beta bp}{(2\,m+1)\beta +2\,m\gamma }\right) }\) for simplicity. Hence, Eq. (3.3) is stated as follows:

$$\begin{aligned} a Q''-DQ-E Q^3=0. \end{aligned}$$
(3.4)

Balancing between nonlinear and linear effects \(Q^3\) and \(Q''\) gives this simple equation \(3M=M+2\). From here, the balance parameter is \(\displaystyle {M=1}\). Using this balance parameter, we get the following finite series expansion for Q to explore the solutions.

$$\begin{aligned} Q(\eta ) =a_{0}+ a_{1}\psi (\eta ) +b_{1}\psi ^{-1}(\eta ) \end{aligned}$$
(3.5)

where \(a_0,a_1\) and \(b_1\) are coefficients of \(\psi\) which are determined later. Substituting Eq. (3.5) and its derivatives into Eq. (3.4) gives different power of \(\psi\). All the expressions having the same order of \(\psi\) are brought together, then equating the coefficients of the same power of \(\psi\) to zero gives a system of nonlinear algebraic equations with \(a_0,a_1,b_1\), and \(\mu\). We obtain the following sets of parameters solving this algebraic equations system under the constraint \((2m+1)\beta +2m\gamma \ne 0\).

Set 1.

\(a_{0}=0\),      \(a_{1}=\mp \sqrt{\frac{2a}{E}}\)      \(b_{1}=0\),      \(\mu =\mp \sqrt{\frac{-D}{2a}}\),

Set 2.

\(a_{0}=0\),      \(a_{1}=0\),      \(b_{1}=\mp \sqrt{\frac{2a}{E}}\mu ^2\)      \(\mu =\mp \sqrt{\frac{-D}{2a}}\),

Set 3.

\(a_{0}=0\),      \(a_{1}=\frac{b1}{\mu ^2}\),      \(b_{1}=\mp \sqrt{\frac{2a}{E}}\mu ^2\)      \(\mu =\mp \sqrt{\frac{-D}{8a}}\),

Set 4.

\(a_{0}=0\),      \(a_{1}=- \frac{b1}{\mu ^2}\),      \(b_{1}=\mp \sqrt{\frac{2a}{E}}\mu ^2\)      \(\mu =\mp \sqrt{\frac{D}{4a}}\).

Before expressing briefly the representative general exact solutions for the perturbed KN equation, we list all solutions derived from (3.5) plugging these 4 coefficient sets along with Eq. (2.2) for providing clarity in the application of the method. Throughout this section, the first index n indicates which one of \(\psi\) solution in (2.2) is used and the second index m shows the set number above used in \(u_{n,m}\). In this context, substituting the coefficients from set 1 to set 4 along with \(\psi _1\) into (3.5) gives solutions respectively as follows:

$$\begin{aligned} q_{1,1}(x,t)= & {} \mp \sqrt{\frac{-D}{E}} \begin{pmatrix}\frac{\sqrt{A^{2}+(B+iC)^{2}}-A\cosh \left( \sqrt{\frac{-2D}{a}} \eta \right) }{(B+iC)\mp A\sinh \left( \sqrt{\frac{-2D}{a}} \eta \right) } \end{pmatrix}e^{-i\Omega }, \end{aligned}$$
(3.6)
$$\begin{aligned} q_{1,2}(x,t)= & {} \mp \sqrt{\frac{-D}{E}} \begin{pmatrix} \frac{(B+iC)\mp A\sinh \left( \sqrt{\frac{-2D}{a}}\eta \right) }{\sqrt{A^{2}+(B+iC)^{2}}-A\cosh \left( \sqrt{\frac{-2D}{a}} \eta \right) } \end{pmatrix}e^{-i\Omega }, \end{aligned}$$
(3.7)
$$\begin{aligned} q_{1,3}(x,t)= & {} \mp \frac{1}{2}\sqrt{\frac{-D}{E}} \begin{pmatrix}\frac{\sqrt{A^{2}+(B+iC)^{2}}-A\cosh \left( \sqrt{\frac{-D}{2a}} ( \eta +\eta _{0} ) \right) }{(B+iC)\mp A\sinh \left( \sqrt{\frac{-D}{2a}}( \eta ) \right) } \\ +\frac{(B+iC)\mp A\sinh \left( \sqrt{\frac{-D}{2a}}\eta \right) }{\sqrt{A^{2}+(B+iC)^{2}}-A\cosh \left( \sqrt{\frac{-D}{2a}} \eta \right) } \end{pmatrix}e^{-i\Omega }, \end{aligned}$$
(3.8)
$$\begin{aligned} q_{1,4}(x,t)= & {} \mp \sqrt{\frac{D}{2E}} \begin{pmatrix}\frac{\sqrt{A^{2}+(B+iC)^{2}}-A\cosh \left( \sqrt{\frac{D}{a}} \eta \right) }{(B+iC)\mp A\sinh \left( \sqrt{\frac{D}{a}}( \eta ) \right) } \\ -\frac{(B+iC)\mp A\sinh \left( \sqrt{\frac{D}{a}}\eta \right) }{\sqrt{A^{2}+(B+iC)^{2}}-A\cosh \left( \sqrt{\frac{D}{a}} \eta \right) } \end{pmatrix}e^{-i\Omega }. \end{aligned}$$
(3.9)

Substituting the coefficients from set 1 to set 4 along with \(\psi _2\) into (3.5) gives the following solutions:

$$\begin{aligned} q_{2,1}(x,t)= & {} \mp \sqrt{\frac{-D}{E}} \begin{pmatrix}\frac{\sqrt{A^{2}+(B+iC)^{2}}+A\cosh \left( \sqrt{\frac{-2D}{a}} \eta \right) }{(B+iC)\mp A\sinh \left( \sqrt{\frac{-2D}{a}} \eta \right) } \end{pmatrix}e^{-i\Omega }, \end{aligned}$$
(3.10)
$$\begin{aligned} q_{2,2}(x,t)= & {} \mp \sqrt{\frac{-D}{E}} \begin{pmatrix} \frac{(B+iC)\mp A\sinh \left( \sqrt{\frac{-2D}{a}}\eta \right) }{\sqrt{A^{2}+(B+iC)^{2}}+A\cosh \left( \sqrt{\frac{-2D}{a}} \eta \right) } \end{pmatrix}e^{-i\Omega }, \end{aligned}$$
(3.11)
$$\begin{aligned} q_{2,3}(x,t)= & {} \mp \frac{1}{2}\sqrt{\frac{-D}{E}} \begin{pmatrix}\frac{\sqrt{A^{2}+(B+iC)^{2}}+A\cosh \left( \sqrt{\frac{-D}{2a}} \eta \right) }{(B+iC)\mp A\sinh \left( \sqrt{\frac{-D}{2a}}( \eta ) \right) } \\ +\frac{(B+iC)\mp A\sinh \left( \sqrt{\frac{-D}{2a}}\eta \right) }{\sqrt{A^{2}+(B+iC)^{2}}+A\cosh \left( \sqrt{\frac{-D}{2a}} \eta \right) } \end{pmatrix}e^{-i\Omega }, \end{aligned}$$
(3.12)
$$\begin{aligned} q_{2,4}(x,t)= & {} \mp \sqrt{\frac{D}{2E}} \begin{pmatrix}\frac{\sqrt{A^{2}+(B+iC)^{2}}+A\cosh \left( \sqrt{\frac{D}{a}} \eta \right) }{(B+iC)\mp A\sinh \left( \sqrt{\frac{D}{a}}( \eta ) \right) } \\ -\frac{(B+iC)\mp A\sinh \left( \sqrt{\frac{D}{a}}\eta \right) }{\sqrt{A^{2}+(B+iC)^{2}}+A\cosh \left( \sqrt{\frac{D}{a}} \eta \right) } \end{pmatrix}e^{-i\Omega }. \end{aligned}$$
(3.13)

Substituting the coefficients from set 1 to set 4 along with \(\psi _3\) and \(\psi _4\) into (3.5), that gives

$$\begin{aligned} q_{3,1}(x,t)= & {} \mp \sqrt{\frac{-D}{E}}\left( \frac{-A+e^{\mp \sqrt{\frac{-2D}{a}}\eta }}{A+e^{\mp \sqrt{\frac{-2D}{a}}\eta }}\right) e^{-i\Omega }, \end{aligned}$$
(3.14)
$$\begin{aligned} q_{3,2}(x,t)= & {} \mp \sqrt{\frac{-D}{E}}\left( \frac{A+e^{\mp \sqrt{\frac{-2D}{a}}\eta }}{-A+e^{\mp \sqrt{\frac{-2D}{a}}\eta }}\right) e^{-i\Omega }, \end{aligned}$$
(3.15)
$$\begin{aligned} q_{3,3}(x,t)= & {} \mp \sqrt{\frac{-D}{E}} \left( \frac{A^2+e^{\mp \sqrt{\frac{-2D}{a}}\eta }}{-A^2+e^{\mp \sqrt{\frac{-2D}{a}}\eta }}\right) e^{-i\Omega }, \end{aligned}$$
(3.16)
$$\begin{aligned} q_{3,4}(x,t)= & {} \mp \sqrt{\frac{D}{2E}} \left( \frac{4A e^{\mp \sqrt{\frac{D}{a}}\eta }}{-A^2+e^{\mp 2\sqrt{\frac{D}{a}}\eta }}\right) e^{-i\Omega } \end{aligned}$$
(3.17)

where the wave variable \(\eta = x-vt+\eta _0\), the phase of wave \(\Omega =px-wt+\Omega _0\), \(D=\displaystyle {\left( w+\alpha p+ap^2-\frac{\beta p(v+2ap+\alpha )}{(2\,m+1)\beta +2\,m\gamma }\right) }\) and \(E=\displaystyle {\left( bp-\frac{3\beta bp}{(2\,m+1)\beta +2\,m\gamma }\right) }\) under the constraint \((2m+1)\beta +2m\gamma \ne 0\).

3.2 Exact Optical Soliton Solutions of The Perturbed Chen–Lee–Liu Equation

The perturbed CLL equation is given by

$$\begin{aligned} iq_{t}+a q_{xx}+ib|q|^2 q_x-i \left[ \alpha q_x+\beta (|q|^{2m} q)_x+\gamma (|q|^{2m})_x q\right] =0. \end{aligned}$$
(3.18)

The perturbed CLL equation is reduced to NODE using the wave transformation \(q(x,t)=Q(\eta )e^{-i\Omega }\) similarly. Substituting \(\displaystyle {q(x,t)=Q(\eta )e^{-i\Omega }}\) and its derivatives into Eq. (3.18), then the reduced NODE is obtained. Splitting the real and imaginary parts of the NODE, the following two equations are obtained, respectively.

$$\begin{aligned} {\left\{ \begin{array}{ll} a Q''-(w+\alpha p+ap^2)Q+bp Q^3 -\beta pQ^{2m+1}=0,\\ -(v+2ap+\alpha )+bQ^2-\left( (2m+1)\beta +2m\gamma \right) Q^{2m}=0. \end{array}\right. } \end{aligned}$$
(3.19)

Substituting \(Q^{2m}=\displaystyle {\frac{-(v+2ap+\alpha )+bQ^2}{(2m+1)\beta +2m\gamma }}\) statement obtained from the imaginary part into the real part that gives

$$\begin{aligned} a Q''-\left( w+\alpha p+ap^2-\frac{\beta p(v+2ap+\alpha )}{(2m+1)\beta +2m\gamma }\right) Q-\left( -bp+\frac{\beta bp}{(2m+1)\beta +2m\gamma }\right) Q^3=0. \end{aligned}$$
(3.20)

The coefficients of Eq. (3.20) are defined as \(D=\displaystyle {\left( w+\alpha p+ap^2-\frac{\beta p(v+2ap+\alpha )}{(2\,m+1)\beta +2\,m\gamma }\right) }\) and

\(E=\displaystyle {\left( -bp+\frac{\beta bp}{(2\,m+1)\beta +2\,m\gamma }\right) }\) for simplicity. Hence, Eq. (3.20) is stated as follows:

$$\begin{aligned} a Q''-DQ-E Q^3=0. \end{aligned}$$
(3.21)

Balancing between nonlinear and linear terms \(Q^3\) and \(Q''\) gives this simple equation \(3M=M+2\). From here, the balance parameter is \(\displaystyle {M=1}\). Using this balance parameter, we get the following finite series expansion for Q to explore the solutions

$$\begin{aligned} Q(\eta ) =a_{0}+ a_{1}\psi (\eta ) +b_{1}\psi ^{-1}(\eta ) \end{aligned}$$
(3.22)

where \(a_0,a_1\) and \(b_1\) are coefficients of \(\psi\) which are determined later. Substituting Eq. (3.22) and its derivatives into Eq. (3.21) gives different power of \(\psi\). Because of having the same NODE equation for perturbed KN and CLL equations, we obtain also the same coefficients and solution structures from Eqs. (3.6) to (3.17) for perturbed CLL equation but under different statement for D and E.

3.3 Exact Optical Soliton Solutions of The Perturbed Gerdjikov–Ivanov Equation

The perturbed GI equation is given by

$$\begin{aligned} iq_{t}+a q_{xx}+b|q|^4 q+i \left[ cq^2 q_x^*-\alpha q_x-\beta (|q|^{2m} q)_x-\gamma (|q|^{2m})_x q\right] =0. \end{aligned}$$
(3.23)

Firstly, the wave transformation \(q(x,t)=Q(\eta )e^{-i\Omega }\) is applied to reduce the perturbed GI equation to the form of a nonlinear ordinary differential equation. \(Q(\eta )\) represents the shape of the wave pulse in this transformation with the wave variable \(\eta = x-vt+\eta _0\) and the phase of wave \(\Omega =px-wt+\Omega _0\), where \(\Omega _0\), \(\eta _0\) are arbitrary free parameters. Substituting \(\displaystyle {q(x,t)=Q(\eta )e^{-i\Omega }}\), \(\displaystyle {q^*(x,t)=Q(\eta )e^{i\Omega }}\) and its derivatives into Eq. (3.23), then the reduced NODE is obtained. By decomposing the NODE into real and imaginary parts, the following two equations are obtained, respectively.

$$\begin{aligned} {\left\{ \begin{array}{ll} a Q''-(w+\alpha p+ap^2)Q-cp Q^3+b Q^5 -\beta pQ^{2m+1}=0,\\ -(v+2ap+\alpha )+cQ^2-\left( (2m+1)\beta +2m\gamma \right) Q^{2m}=0. \end{array}\right. } \end{aligned}$$
(3.24)

The statement \(Q^{2m}=\displaystyle {\frac{-(v+2ap+\alpha )+cQ^2}{(2m+1)\beta +2m\gamma }}\) obtained from the imaginary part is substituted into the real part to get the following final equation used for finding exact solutions.

$$\begin{aligned} a Q''-\left( w+\alpha p+ap^2-\frac{\beta p(v+2ap+\alpha )}{(2m+1)\beta +2m\gamma }\right) Q-\left( cp+\frac{\beta cp}{(2m+1)\beta +2m\gamma }\right) Q^3+b Q^5=0. \end{aligned}$$
(3.25)

The coefficients of Eq. (3.25) are defined as \(D=\displaystyle {\left( w+\alpha p+ap^2-\frac{\beta p(v+2ap+\alpha )}{(2\,m+1)\beta +2\,m\gamma }\right) }\) and

\(E=\displaystyle {\left( cp+\frac{\beta cp}{(2\,m+1)\beta +2\,m\gamma }\right) }\) for simplicity. Therefore, Eq. (3.25) is stated as follows:

$$\begin{aligned} a Q''-DQ-E Q^3+b Q^5=0. \end{aligned}$$
(3.26)

Balancing between the linear term of the highest order \(Q''\) with the nonlinear term of the highest degree \(Q^5\) gives this simple equation \(5M=M+2\). From here, it is \(\displaystyle {M=\frac{1}{2}}\). However, Eq. (3.26) requires the transformation \(\displaystyle {Q(\eta )=R^{\frac{1}{2}}(\eta )}\) to obtain a useful balance number for finite series expansion, then

$$\begin{aligned} \frac{a}{4} \left( -R^{\frac{-3}{2}}R'^2+2R^{\frac{-1}{2}}R''\right) -D R^{\frac{1}{2}}-E R^{\frac{3}{2}}+b R^{\frac{5}{2}}=0. \end{aligned}$$
(3.27)

After simplifying the Eq. (3.27) that gives:

$$\begin{aligned} \frac{a}{4} \left( -R'^2+2RR''\right) -D R^2-ER^3 +b R^{4}=0. \end{aligned}$$
(3.28)

Balancing between nonlinear and linear effects \(R^4\) and \(RR''\) in Eq. (3.28), we find \(4K=2K+2\) so that \(K=1\). Using this balance number, we get the following finite series expansion for R to explore the solutions.

$$\begin{aligned} R(\eta ) =a_{0}+ a_{1}\psi (\eta ) +b_{1}\psi ^{-1}(\eta ) \end{aligned}$$
(3.29)

where \(a_0,a_1\) and \(b_1\) are coefficients of \(\psi\) which are determined later. Substituting Eq. (3.29) and its derivatives into Eq. (3.26) with \(\displaystyle {Q(\eta )=R^{\frac{1}{2}}(\eta )}\) gives different power of \(\psi\). All the expressions having the same order of \(\psi\) are brought together, then equating the coefficients of the same power of \(\psi\) to zero gives a system of nonlinear algebraic equations with \(a_0,a_1,b_1\), and \(\mu\). Solving this algebraic equations system under the constraints \(3E^2+16Db=0\) and \((2m+1)\beta +2m\gamma \ne 0\), we obtain the following sets of parameters:

Set 1.

\(a_{0}=\frac{3E}{8b}\),      \(a_{1}=\frac{\sqrt{-3ab}}{2b}\)      \(b_{1}=a1\mu ^2\),      \(\mu =\frac{\sqrt{-ab(9E^2+32Db)}}{8ab}\),

Set 2.

\(a_{0}=\frac{3E}{8b}\),      \(a_{1}=-\frac{\sqrt{-3ab}}{2b}\)      \(b_{1}=a1\mu ^2\),      \(\mu =\frac{\sqrt{-ab(9E^2+32Db)}}{8ab}\),

Set 3.

\(a_{0}=\frac{3E}{8b}\),      \(a_{1}=\frac{\sqrt{-3ab}}{2b}\)      \(b_{1}=a1\mu ^2\),      \(\mu =-\frac{\sqrt{-ab(9E^2+32Db)}}{8ab}\),

Set 4.

\(a_{0}=\frac{3E}{8b}\),      \(a_{1}=-\frac{\sqrt{-3ab}}{2b}\)      \(b_{1}=a1\mu ^2\),      \(\mu =-\frac{\sqrt{-ab(9E^2+32Db)}}{8ab}\),

Before expressing briefly the representative general solutions for the perturbed GI equation, we list all derived solutions plugging these 4 coefficient sets along with Eq. (2.2) for providing clarity in the application of the method. Throughout this section, the first index n indicates which one of \(\psi\) solution in (2.2) is used and the second index m shows the set number above used in \(u_{n,m}\). In this context, substituting the coefficients from set 1 to set 4 along with \(\psi _1\) into (3.29) with \(q(x,t)=Q(\eta )e^{-i\Omega }\) and \(\displaystyle {Q(\eta )=R^{\frac{1}{2}}(\eta )}\) gives solutions respectively as follows:

$$\begin{aligned} q_{1,1}(x,t)= & {} \begin{pmatrix}\frac{3E}{8b} + \sqrt{\frac{-3D}{16b}}\begin{pmatrix}\frac{\sqrt{A^{2}+(B+iC)^{2}}-A\cosh \left( \sqrt{\frac{D}{a}} \eta \right) }{(B+iC)+A\sinh \left( \sqrt{\frac{D}{a}} \eta \right) } \\ +\frac{(B+iC)+A\sinh \left( \sqrt{\frac{D}{a}} \eta \right) }{\sqrt{A^{2}+(B+iC)^{2}}-A\cosh \left( \sqrt{\frac{D}{a}} \eta \right) } \end{pmatrix}\end{pmatrix}^{\frac{1}{2}}e^{-i\Omega }, \end{aligned}$$
(3.30)
$$\begin{aligned} q_{1,2}(x,t)= & {} \begin{pmatrix}\frac{3E}{8b} - \sqrt{\frac{-3D}{16b}}\begin{pmatrix}\frac{\sqrt{A^{2}+(B+iC)^{2}}-A\cosh \left( \sqrt{\frac{D}{a}} \eta \right) }{(B+iC)+A\sinh \left( \sqrt{\frac{D}{a}}\eta \right) } \\ +\frac{(B+iC)+A\sinh \left( \sqrt{\frac{D}{a}}\eta \right) }{\sqrt{A^{2}+(B+iC)^{2}}-A\cosh \left( \sqrt{\frac{D}{a}} \eta \right) } \end{pmatrix}\end{pmatrix}^{\frac{1}{2}}e^{-i\Omega }, \end{aligned}$$
(3.31)
$$\begin{aligned} q_{1,3}(x,t)= & {} \begin{pmatrix}\frac{3E}{8b} - \sqrt{\frac{-3D}{16b}}\begin{pmatrix}\frac{\sqrt{A^{2}+(B+iC)^{2}}-A\cosh \left( \sqrt{\frac{D}{a}} \eta \right) }{(B+iC)-A\sinh \left( \sqrt{\frac{D}{a}}( \eta ) \right) } \\ +\frac{(B+iC)-A\sinh \left( \sqrt{\frac{D}{a}}\eta \right) }{\sqrt{A^{2}+(B+iC)^{2}}-A\cosh \left( \sqrt{\frac{D}{a}} \eta \right) } \end{pmatrix}\end{pmatrix}^{\frac{1}{2}}e^{-i\Omega }, \end{aligned}$$
(3.32)
$$\begin{aligned} q_{1,4}(x,t)= & {} \begin{pmatrix}\frac{3E}{8b} + \sqrt{\frac{-3D}{16b}}\begin{pmatrix}\frac{\sqrt{A^{2}+(B+iC)^{2}}-A\cosh \left( \sqrt{\frac{D}{a}} \eta \right) }{(B+iC)-A\sinh \left( \sqrt{\frac{D}{a}}\eta \right) } \\ +\frac{(B+iC)-A\sinh \left( \sqrt{\frac{D}{a}}\eta \right) }{\sqrt{A^{2}+(B+iC)^{2}}-A\cosh \left( \sqrt{\frac{D}{a}} \eta \right) } \end{pmatrix}\end{pmatrix}^{\frac{1}{2}}e^{-i\Omega }. \end{aligned}$$
(3.33)

Substituting the coefficients from set 1 to set 4 along with \(\psi _2\) gives the following solutions:

$$\begin{aligned} q_{2,1}(x,t)= & {} \begin{pmatrix}\frac{3E}{8b} - \sqrt{\frac{-3D}{16b}}\begin{pmatrix}\frac{\sqrt{A^{2}+(B+iC)^{2}}+A\cosh \left( \sqrt{\frac{D}{a}} \eta \right) }{(B+iC)+A\sinh \left( \sqrt{\frac{D}{a}}\eta \right) } \\ +\frac{(B+iC)+A\sinh \left( \sqrt{\frac{D}{a}}\eta \right) }{\sqrt{A^{2}+(B+iC)^{2}}+A\cosh \left( \sqrt{\frac{D}{a}} \eta \right) } \end{pmatrix}\end{pmatrix}^{\frac{1}{2}}e^{-i\Omega }, \end{aligned}$$
(3.34)
$$\begin{aligned} q_{2,2}(x,t)= & {} \begin{pmatrix}\frac{3E}{8b} + \sqrt{\frac{-3D}{16b}}\begin{pmatrix}\frac{\sqrt{A^{2}+(B+iC)^{2}}+A\cosh \left( \sqrt{\frac{D}{a}} \eta \right) }{(B+iC)+A\sinh \left( \sqrt{\frac{D}{a}}\eta \right) } \\ +\frac{(B+iC)+A\sinh \left( \sqrt{\frac{D}{a}}\eta \right) }{\sqrt{A^{2}+(B+iC)^{2}}+A\cosh \left( \sqrt{\frac{D}{a}} \eta \right) } \end{pmatrix}\end{pmatrix}^{\frac{1}{2}}e^{-i\Omega }, \end{aligned}$$
(3.35)
$$\begin{aligned} q_{2,3}(x,t)= & {} \begin{pmatrix}\frac{3E}{8b} +\sqrt{\frac{-3D}{16b}}\begin{pmatrix}\frac{\sqrt{A^{2}+(B+iC)^{2}}+A\cosh \left( \sqrt{\frac{D}{a}} \eta \right) }{(B+iC)-A\sinh \left( \sqrt{\frac{D}{a}}\eta \right) } \\ +\frac{(B+iC)-A\sinh \left( \sqrt{\frac{D}{a}}\eta \right) }{\sqrt{A^{2}+(B+iC)^{2}}+A\cosh \left( \sqrt{\frac{D}{a}} \eta \right) } \end{pmatrix}\end{pmatrix}^{\frac{1}{2}}e^{-i\Omega }, \end{aligned}$$
(3.36)
$$\begin{aligned} q_{2,4}(x,t)= & {} \begin{pmatrix}\frac{3E}{8b} -\sqrt{\frac{-3D}{16b}}\begin{pmatrix}\frac{\sqrt{A^{2}+(B+iC)^{2}}+A\cosh \left( \sqrt{\frac{D}{a}} \eta \right) }{(B+iC)-A\sinh \left( \sqrt{\frac{D}{a}}\eta \right) } \\ +\frac{(B+iC)-A\sinh \left( \sqrt{\frac{D}{a}}\eta \right) }{\sqrt{A^{2}+(B+iC)^{2}}+A\cosh \left( \sqrt{\frac{D}{a}} \eta \right) } \end{pmatrix}\end{pmatrix}^{\frac{1}{2}}e^{-i\Omega }. \end{aligned}$$
(3.37)

Substituting the coefficients from set 1 to set 4 along with \(\psi _3\) and \(\psi _4\) gives

$$\begin{aligned} q_{3,1}(x,t)= & {} \begin{pmatrix}\frac{3E}{8b} + \sqrt{\frac{-3D}{4b}}\left( \frac{A^2+e^{-2\sqrt{\frac{D}{a}}\eta }}{-A^2+e^{-2\sqrt{\frac{D}{a}}\eta }}\right) \end{pmatrix}^{\frac{1}{2}}e^{-i\Omega }, \end{aligned}$$
(3.38)
$$\begin{aligned} q_{3,2}(x,t)= & {} \begin{pmatrix}\frac{3E}{8b} - \sqrt{\frac{-3D}{4b}}\left( \frac{A^2+e^{-2\sqrt{\frac{D}{a}}\eta }}{-A^2+e^{-2\sqrt{\frac{D}{a}}\eta }}\right) \end{pmatrix}^{\frac{1}{2}}e^{-i\Omega }, \end{aligned}$$
(3.39)
$$\begin{aligned} q_{3,3}(x,t)= & {} \begin{pmatrix}\frac{3E}{8b} - \sqrt{\frac{-3D}{4b}}\left( \frac{A^2+e^{2\sqrt{\frac{D}{a}}\eta }}{-A^2+e^{2\sqrt{\frac{D}{a}}\eta }}\right) \end{pmatrix}^{\frac{1}{2}}e^{-i\Omega }, \end{aligned}$$
(3.40)
$$\begin{aligned} q_{3,4}(x,t)= & {} \begin{pmatrix}\frac{3E}{8b} + \sqrt{\frac{-3D}{4b}}\left( \frac{A^2+e^{2\sqrt{\frac{D}{a}}\eta }}{-A^2+e^{2\sqrt{\frac{D}{a}}\eta }}\right) \end{pmatrix}^{\frac{1}{2}}e^{-i\Omega }, \end{aligned}$$
(3.41)

where the wave variable \(\eta = x-vt+\eta _0\), the phase of wave \(\Omega =px-wt+\Omega _0\), \(D=\left( w+\alpha p+ap^2-\frac{\beta p(v+2ap+\alpha )}{(2\,m+1)\beta +2\,m\gamma }\right)\) and \(E=\left( cp+\frac{\beta cp}{(2m+1)\beta +2m\gamma }\right)\) under the constraints \(3E^2+16Db=0\) and \((2\,m+1)\beta +2\,m\gamma \ne 0\).

4 Result and Discussion

We have obtained the general exact solutions for three Schrödinger-type reductions in the previous section. In this section, first of all, the solutions are summarized and described briefly. Moreover, we will plot the 3D and 2D graphs of some selected solutions with suitable values of the physical parameters by considering the constraints and definitions of the proposed method and equations. Therefore, these graphical representations will be beneficial to give insight into the physical interpretation of the solutions and the behaviors of some optical solitons.

We have found and listed the general exact solutions of the perturbed KN equation from Eqs. (3.6) to (3.17). These solutions are summarized under the following 6 solution forms:

$$\begin{aligned} q_{KN_1}(x,t)= & {} \mp \sqrt{\frac{-D}{E}} \begin{pmatrix}\frac{\sqrt{A^{2}+(B+iC)^{2}}\mp A\cosh \left( \sqrt{\frac{-2D}{a}} \eta \right) }{(B+iC)\mp A\sinh \left( \sqrt{\frac{-2D}{a}} \eta \right) } \end{pmatrix}e^{-i\Omega }, \end{aligned}$$
(4.1)
$$\begin{aligned} q_{KN_2}(x,t)= & {} \mp \sqrt{\frac{-D}{E}} \begin{pmatrix} \frac{(B+iC)\mp A\sinh \left( \sqrt{\frac{-2D}{a}}\eta \right) }{\sqrt{A^{2}+(B+iC)^{2}}\mp A\cosh \left( \sqrt{\frac{-2D}{a}} \eta \right) } \end{pmatrix}e^{-i\Omega }, \end{aligned}$$
(4.2)
$$\begin{aligned} q_{KN_3}(x,t)= & {} \mp \frac{1}{2}\sqrt{\frac{-D}{E}} \begin{pmatrix}\frac{\sqrt{A^{2}+(B+iC)^{2}}\mp A\cosh \left( \sqrt{\frac{-D}{2a}} \eta \right) }{(B+iC)\mp A\sinh \left( \sqrt{\frac{-D}{2a}}( \eta ) \right) } \\ +\frac{(B+iC)\mp A\sinh \left( \sqrt{\frac{-D}{2a}}\eta \right) }{\sqrt{A^{2}+(B+iC)^{2}}\mp A\cosh \left( \sqrt{\frac{-D}{2a}} \eta \right) } \end{pmatrix}e^{-i\Omega }, \end{aligned}$$
(4.3)
$$\begin{aligned} q_{KN_4}(x,t)= & {} \mp \sqrt{\frac{D}{2E}} \begin{pmatrix}\frac{\sqrt{A^{2}+(B+iC)^{2}}\mp A\cosh \left( \sqrt{\frac{D}{a}} \eta \right) }{(B+iC)\mp A\sinh \left( \sqrt{\frac{D}{a}}( \eta ) \right) } \\ -\frac{(B+iC)\mp A\sinh \left( \sqrt{\frac{D}{a}}\eta \right) }{\sqrt{A^{2}+(B+iC)^{2}}\mp A\cosh \left( \sqrt{\frac{D}{a}} \eta \right) } \end{pmatrix}e^{-i\Omega }, \end{aligned}$$
(4.4)
$$\begin{aligned} q_{KN_5}(x,t)= & {} \mp \sqrt{\frac{-D}{E}} \left( \frac{A+e^{\mp \sqrt{\frac{-2D}{a}}\eta }}{-A+e^{\mp \sqrt{\frac{-2D}{a}}\eta }}\right) e^{-i\Omega }, \end{aligned}$$
(4.5)
$$\begin{aligned} q_{KN_6}(x,t)= & {} \mp \sqrt{\frac{D}{2E}} \left( \frac{4A e^{\mp \sqrt{\frac{D}{a}}\eta }}{-A^2+e^{\mp 2\sqrt{\frac{D}{a}}\eta }}\right) e^{-i\Omega }, \end{aligned}$$
(4.6)

where the wave variable \(\eta = x-vt+\eta _0\), the phase of wave \(\Omega =px-wt+\Omega _0\), \(D=\displaystyle {\left( w+\alpha p+ap^2-\frac{\beta p(v+2ap+\alpha )}{(2\,m+1)\beta +2\,m\gamma }\right) }\) and \(E=\displaystyle {\left( bp-\frac{3\beta bp}{(2\,m+1)\beta +2\,m\gamma }\right) }\) under the constraint \((2m+1)\beta +2m\gamma \ne 0\). Taking \(A=1\), \(B=0\) and \(C=0\) in Eqs.(4.1)–(4.6) and considering the hyperbolic identities \(\sinh (2y)=2\sinh (y)\cosh (y)\) and \(\cosh (2y)=\cosh ^2(y)+\sinh ^2(y)=2\cosh ^2(y)-1=2\sinh ^2(y)+1\) give us the following hyperbolic and exponential function solutions. Besides deriving these reduced hyperbolic and exponential function solutions from the general exact solutions, trigonometric function solutions can also be obtained depending on the coefficient of \(\eta\) with the aid of \(\sinh (iy)=i\sin (y)\) and \(\cosh (iy)=\cos (y)\).

$$\begin{aligned} q_{KN}(x,t)\longrightarrow \left\{ \begin{array}{lll} \displaystyle {q_{KN_1}=\mp \sqrt{\frac{-D}{E}} \tanh \left( \sqrt{\frac{-D}{2a}} \eta \right) }e^{-i\Omega }, \\ \displaystyle {q_{KN_2}=\mp \sqrt{\frac{-D}{E}} \coth \left( \sqrt{\frac{-D}{2a}} \eta \right) }e^{-i\Omega },\\ \displaystyle {q_{KN_3}=\mp \sqrt{\frac{-D}{E}} \coth \left( \sqrt{\frac{-2D}{a}} \eta \right) }e^{-i\Omega },\\ \displaystyle {q_{KN_4}=\mp \sqrt{\frac{2D}{E}} \text {cosech} \left( \sqrt{\frac{4D}{a}} \eta \right) }e^{-i\Omega },\\ \displaystyle {q_{KN_5}}= \mp \sqrt{\frac{-D}{E}} \left( 1+\frac{2}{-1+e^{\mp \sqrt{\frac{-2D}{a}}\eta }}\right) e^{-i\Omega },\\ \displaystyle {q_{KN_6}}=\mp \sqrt{\frac{D}{2E}} \left( \frac{4e^{\mp \sqrt{\frac{D}{a}}\eta }}{-1+e^{\mp 2\sqrt{\frac{D}{a}}\eta }}\right) e^{-i\Omega }. \end{array} \right. \end{aligned}$$
(4.7)
Fig. 1
figure 1

The 3-D graphs of the perturbed Kaup–Newell solution \(q_{31}\) are plotted above for the parameter choices \(m=1,~a=1,~b=1,~p=1,~w=1,~\alpha =1,~\beta =1,~\gamma =1,~v=5\), \(A=5\), \(B=4\), \(C=3\) over the intervals \(-10<x<10\), \(0<t<10\)

Full size image

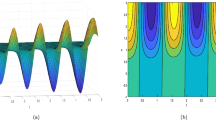
In the first row of the Fig. 1, 3D graphs of modulus, real part, and imaginary part of the obtained solutions \(q_{31}\) for the Kaup–Newell equation are plotted for the values \(m=1,~a=1,~b=1,~p=1,~w=1,~\alpha =1,~\beta =1,~\gamma =1,~v=5\), \(A=5\), \(B=4\), \(C=3\) over the intervals \(-10<x<10\), \(0<t<10\). In the second row of the Fig. 1, 2D line plots are plotted with the same parameters at \(x=0\). It can be seen from the Fig. 1 that the obtained optical soliton solutions behave periodically.

Similarly, we have summarized the general exact solutions of the perturbed CLL equation under the following 6 solution forms, then reduced them to hyperbolic, trigonometric, and exponential function solutions in (4.14).

$$\begin{aligned} q_{CLL_1}(x,t)= & {} \mp \sqrt{\frac{-D}{E}} \begin{pmatrix}\frac{\sqrt{A^{2}+(B+iC)^{2}}\mp A\cosh \left( \sqrt{\frac{-2D}{a}} \eta \right) }{(B+iC)\mp A\sinh \left( \sqrt{\frac{-2D}{a}} \eta \right) } \end{pmatrix}e^{-i\Omega }, \end{aligned}$$
(4.8)
$$\begin{aligned} q_{CLL_2}(x,t)= & {} \mp \sqrt{\frac{-D}{E}} \begin{pmatrix} \frac{(B+iC)\mp A\sinh \left( \sqrt{\frac{-2D}{a}}\eta \right) }{\sqrt{A^{2}+(B+iC)^{2}}\mp A\cosh \left( \sqrt{\frac{-2D}{a}} \eta \right) } \end{pmatrix}e^{-i\Omega }, \end{aligned}$$
(4.9)
$$\begin{aligned} q_{CLL_3}(x,t)= & {} \mp \frac{1}{2}\sqrt{\frac{-D}{E}} \begin{pmatrix}\frac{\sqrt{A^{2}+(B+iC)^{2}}\mp A\cosh \left( \sqrt{\frac{-D}{2a}} \eta \right) }{(B+iC)\mp A\sinh \left( \sqrt{\frac{-D}{2a}}( \eta ) \right) } \\ +\frac{(B+iC)\mp A\sinh \left( \sqrt{\frac{-D}{2a}}\eta \right) }{\sqrt{A^{2}+(B+iC)^{2}}\mp A\cosh \left( \sqrt{\frac{-D}{2a}} \eta \right) } \end{pmatrix}e^{-i\Omega }, \end{aligned}$$
(4.10)
$$\begin{aligned} q_{CLL_4}(x,t)= & {} \mp \sqrt{\frac{D}{2E}} \begin{pmatrix}\frac{\sqrt{A^{2}+(B+iC)^{2}}-A\cosh \left( \sqrt{\frac{D}{a}} \eta \right) }{(B+iC)\mp A\sinh \left( \sqrt{\frac{D}{a}}( \eta ) \right) } \\ -\frac{(B+iC)\mp A\sinh \left( \sqrt{\frac{D}{a}}\eta \right) }{\sqrt{A^{2}+(B+iC)^{2}}\mp A\cosh \left( \sqrt{\frac{D}{a}} \eta \right) } \end{pmatrix}e^{-i\Omega }, \end{aligned}$$
(4.11)
$$\begin{aligned} q_{CLL_5}(x,t)= & {} \mp \sqrt{\frac{-D}{E}} \left( \frac{A+e^{\mp \sqrt{\frac{-2D}{a}}\eta }}{-A+e^{\mp \sqrt{\frac{-2D}{a}}\eta }}\right) e^{-i\Omega }, \end{aligned}$$
(4.12)
$$\begin{aligned} q_{CLL_6}(x,t)= & {} \mp \sqrt{\frac{D}{2E}} \left( \frac{4A e^{\mp \sqrt{\frac{D}{a}}\eta }}{-A^2+e^{\mp 2\sqrt{\frac{D}{a}}\eta }}\right) e^{-i\Omega }, \end{aligned}$$
(4.13)

where the wave variable \(\eta = x-vt+\eta _0\), the phase of wave \(\Omega =px-wt+\Omega _0\), \(D=\displaystyle {\left( w+\alpha p+ap^2-\frac{\beta p(v+2ap+\alpha )}{(2\,m+1)\beta +2\,m\gamma }\right) }\) and \(E=\displaystyle {\left( -bp+\frac{\beta bp}{(2\,m+1)\beta +2\,m\gamma }\right) }\) under the constraint \((2m+1)\beta +2m\gamma \ne 0\). Taking \(A=1\), \(B=0\) and \(C=0\) in Eqs. (4.8)–(4.13) and considering the hyperbolic identities give us the following hyperbolic and exponential function solutions.

$$\begin{aligned} q_{CLL}(x,t)\longrightarrow \left\{ \begin{array}{lll} \displaystyle {q_{CLL_1}=\mp \sqrt{\frac{-D}{E}} \tanh \left( \sqrt{\frac{-D}{2a}} \eta \right) }e^{-i\Omega }, \\ \displaystyle {q_{CLL_2}=\mp \sqrt{\frac{-D}{E}} \coth \left( \sqrt{\frac{-D}{2a}} \eta \right) }e^{-i\Omega },\\ \displaystyle {q_{CLL_3}=\mp \sqrt{\frac{-D}{E}} \coth \left( \sqrt{\frac{-2D}{a}} \eta \right) }e^{-i\Omega },\\ \displaystyle {q_{CLL_4}=\mp \sqrt{\frac{2D}{E}} \text {cosech} \left( \sqrt{\frac{2D}{a}} \eta \right) }e^{-i\Omega },\\ \displaystyle {q_{CLL_5}}= \mp \sqrt{\frac{-D}{E}} \left( 1+\frac{2}{-1+e^{\mp \sqrt{\frac{-2D}{a}}\eta }}\right) e^{-i\Omega },\\ \displaystyle {q_{CLL_6}}=\mp \sqrt{\frac{D}{2E}} \left( \frac{4e^{\mp \sqrt{\frac{D}{a}}\eta }}{-1+e^{\mp 2\sqrt{\frac{D}{a}}\eta }}\right) e^{-i\Omega }. \end{array} \right. \end{aligned}$$
(4.14)
Fig. 2
figure 2

The 3-D graphs of the perturbed Chen–Lee–Liu solution \(q_{21}\) are plotted above for the parameter choices \(m=1,~a=1,~b=1,~p=1,~w=1,~\alpha =1,~\beta =1,~\gamma =1,~v=5\),\(A=5\), \(B=4\), \(C=3\) over the intervals \(-10<x<10\), \(0<t<10\)

Full size image

In the first row of the Fig. 2, 3D graphs of modulus, real part, and imaginary part of the obtained solutions \(q_{21}\) for the Chen–Lee–Liu equation are plotted for the values \(m=1,~a=1,~b=1,~p=1,~w=1,~\alpha =1,~\beta =1,~\gamma =1,~v=5\), \(A=5\), \(B=4\), \(C=3\) over the intervals \(-10<x<10\), \(0<t<10\). In the second row of the Fig. 2, 2D line plots are plotted with the same parameters at \(x=0\). It can be seen from the Fig. 2 that the obtained optical soliton solutions behave periodically.

Many different powerful and effective exact solution methods such as \(\tan (\frac{\phi }{2})\)-expansion method, \(\left( \frac{G^{\prime }}{G}\right)\)-expansion method, the extended sinh-Gordon equation expansion method, modified generalized exponential rational function method, modified simple equation method, trial equation method, new Kudryashovs method, generalized projective Riccati equations, csch-function method have been used by mathematicians to find exact solutions for the perturbed or unperturbed KN equation and the perturbed or unperturbed CLL equation in Biswas et al. (2018); Esen et al. (2022); Jawad et al. (2019b); Akinyemi et al. (2021); Mohamed et al. (2022); Arnous et al. (2022); Bilal et al. (2021); Salas et al. (2020); Hu et al. (2021); Esen et al. (2021); Khater et al. (2023); Yildirim et al. (2020); Baskonus et al. (2021); Yokus et al. (2021); Kudryashov (2021); Houwe et al. (2021). Each method is tailored to a certain sort of solution that gives bright, dark, singular, hyperbolic, trigonometric, and periodic solutions such that these can be already derived from the general exact solutions obtained by the GUM as shown in Eqs. (4.7) and (4.14). Additionally, the solutions of the unperturbed forms obtained aforementioned studies can be also derived from Eqs. (4.1)–(4.6) and Eqs. (4.8)–(4.13) removing the last terms of D and E taking \(\alpha =0\).

Lastly, summarizing the general exact solutions of the perturbed GI equation under the following 2 solution forms, we have reduced them to hyperbolic, trigonometric, and exponential function solutions in (4.17), in a similar way.

$$\begin{aligned} q_{GI_1}(x,t)= & {} \begin{pmatrix}\frac{3E}{8b} \mp \sqrt{\frac{-3D}{16b}}\begin{pmatrix}\frac{\sqrt{A^{2}+(B+iC)^{2}}\mp A\cosh \left( \sqrt{\frac{D}{a}} \eta \right) }{(B+iC)\mp A\sinh \left( \sqrt{\frac{D}{a}} \eta \right) } \\ +\frac{(B+iC)\mp A\sinh \left( \sqrt{\frac{D}{a}} \eta \right) }{\sqrt{A^{2}+(B+iC)^{2}}\mp A\cosh \left( \sqrt{\frac{D}{a}} \eta \right) } \end{pmatrix}\end{pmatrix}^{\frac{1}{2}}e^{-i\Omega }, \end{aligned}$$
(4.15)
$$\begin{aligned} q_{GI_2}(x,t)= & {} \begin{pmatrix}\frac{3E}{8b} \mp \sqrt{\frac{-3D}{4b}}\left( \frac{A^2+e^{\mp 2\sqrt{\frac{D}{a}}\eta }}{-A^2+e^{\mp 2\sqrt{\frac{D}{a}}\eta }}\right) \end{pmatrix}^{\frac{1}{2}}e^{-i\Omega }, \end{aligned}$$
(4.16)

where the wave variable \(\eta = x-vt+\eta _0\), the phase of wave \(\Omega =px-wt+\Omega _0\), \(D=\left( w+\alpha p+ap^2-\frac{\beta p(v+2ap+\alpha )}{(2\,m+1)\beta +2\,m\gamma }\right)\) and \(E=\left( cp+\frac{\beta cp}{(2m+1)\beta +2m\gamma }\right)\) under the constraints \(3E^2+16Db=0\) and \((2\,m+1)\beta +2\,m\gamma \ne 0\).

$$\begin{aligned} q_{GI}(x,t)\longrightarrow \left\{ \begin{array}{lll} u_{GI_1}(x,t)=\begin{pmatrix}\frac{3E}{8b} \mp \sqrt{\frac{-3D}{16b}}\coth \left( \sqrt{\frac{D}{a}} \eta \right) \end{pmatrix}^{\frac{1}{2}}e^{-i\Omega },\\ u_{GI_2}(x,t)=\begin{pmatrix}\frac{3E}{8b} \mp \sqrt{\frac{-3D}{4b}}\left( 1+\frac{2}{-1+e^{\mp 2\sqrt{\frac{D}{a}}\eta }}\right) \end{pmatrix}^{\frac{1}{2}}e^{-i\Omega }. \end{array} \right. \end{aligned}$$
(4.17)
Fig. 3
figure 3

The 3-D graphs of the perturbed Gerdjikov–Ivanov solution \(q_{12}\) are plotted above for the parameter choices \(m=1,~a=1,~b=1,~c=1,~p=1,~w=1,~\alpha =1,~\beta =1,~\gamma =1,~v=-\frac{387}{20}\), \(A=5\), \(B=4\), \(C=3\) over the intervals \(-10<x<10\), \(0<t<10\)

Full size image
Fig. 4
figure 4

The 3-D graphs of the perturbed Gerdjikov–Ivanov solution \(q_{31}\) are plotted above for the parameter choices \(m=1,~a=1,~b=1,~c=1,~p=1,~w=1,~\alpha =1,~\beta =1,~\gamma =1,~v=-\frac{387}{20}\), \(A=5\), \(B=4\), \(C=3\) over the intervals \(-10<x<10\), \(0<t<10\)

Full size image

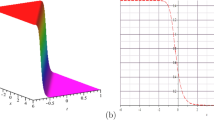
In the first row of the Figs. 3 and 4, 3D graphs of modulus, real part, and imaginary part of the obtained solutions \(q_{12}\), \(q_{31}\) for the Gerdjikov–Ivanov equation are plotted for the values \(m=1,~a=1,~b=1,~p=1,~w=1,~\alpha =1,~\beta =1,~\gamma =1,~v=-\frac{387}{20}\), \(A=5\), \(B=4\), \(C=3\) over the intervals \(-10<x<10\), \(0<t<10\). In the second row of the Figs. 3 and 4, 2D line plots are plotted with the same parameters at \(x=0\). It can be seen from the Fig. 3 and 4 that the obtained optical soliton solutions behave periodically. The coefficients a and c represent the group velocity dispersion and nonlinear dispersion, respectively. Therefore, as these parameters increase, the wave amplitude will decrease and the wavelength will increase.

Comparing other studies in Manafian and Lakestani (2016); Arshed (2018); Yasar et al. (2018); Zafar et al. (2022); Shehata et al. (2021); Ismael et al. (2023); Biswas et al. (2018b); Zhang and Fan (2020); Rizvi et al. (2023); Li et al. (2021); Rehman et al. (2023) used several exact solution methods such as \(\tanh\)-function method, the exp\((-\phi (\xi ))\)-expansion method, the sine-Gordon equation method, the modified extended tanh expansion method, exp-function approach, the modified simple equation method, the modified exponential function method, the balanced modified extended tanh-function, the inverse scattering method, the polynomial method’s complete discrimination system, 2nd-fold Darboux transformation, the hyperbolic extended function method, generalized Kudryashovs method, the GUM gives more general exact solutions for the perturbed or unperturbed GI equation as shown in Eq. (4.17). The solutions of the unperturbed forms of the GI equation can be also obtained from Eqs. (4.15) and (4.16) removing the last terms of D and E taking \(\alpha =0\).

It has been concluded that the obtained solutions provide more solution sets in compact form with free parameters. Certain types of solutions obtained by different methods that give bright, dark, singular, hyperbolic, trigonometric, and periodic solutions can be produced from these general exact solutions as shown in this section. The 3D and 2D profiles of some selected of these obtained solutions have been plotted for the special values as above.

5 Conclusions

In this study, we have obtained general exact solutions for the three Schrödinger-type reductions using the generalized unified method (GUM). The aims of this study are twofold in terms of the application of the GUM and obtaining the general exact solutions of three members of the DNLS family.

One of the most fundamental purposes of exact solution methods is to obtain an exact solution family by finding a concise, direct, effective, and elegant way. The GUM provides more general exact solutions with free parameters in compact forms. The obtained solutions are valuable for a comprehensive insight into the dynamics of the mentioned family using free parameters. Compared to previous studies that give hyperbolic, trigonometric, and exponential function solutions, the solutions obtained by the GUM can be converted to these aforementioned function-type solutions. Consequently, considering the obtained results, the proposed exact solution method can be easily applied to the derivative nonlinear Schrödinger family as well as more complex nonlinear problems in various fields for future studies without having tedious calculation complexity.

Due to explaining the transmission of the pulses through optical fibers, the three members of the DNLS family called the perturbed Kaup–Newell equation, the perturbed Chen–Lee–Liu equation, and the Gerdjikov–Ivanov equation play a significant role in modeling telecommunication problems. Particularly, the optical soliton solutions obtained here will be very useful in depicting the propagation of solitons through optical fibers due to their wide applications in nonlinear optics. Considering the contributions of finding solutions to these equations in applied sciences such as the telecommunication industry that uses these equations to model their problems, the obtained solutions give promising results for computational tools for further analysis.

The graphical representations of some obtained solutions are plotted to demonstrate the behaviors of optical solitons. These solutions indicate various and rich wave structures for selections of different parameters.

In this study, computations and verifications were made with Maple 12, and graphical illustrations were plotted by Mathematica. In future studies, we intend to focus on a theoretical comparative study of the GUM and other exact solution methods.