A mathematical study of electromagnetic waves diffraction by a slit in non-thermal plasma

Abstract

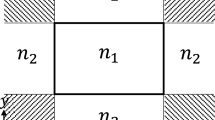
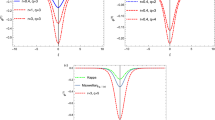
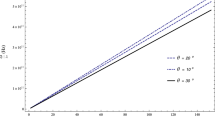
This research presents the wave propagation analysis due to the interaction between electromagnetic waves and a finite-width slit embedded in an anisotropic medium. The separated field results are obtained in the case of Neumann boundary conditions while employing Fourier transform and Wiener–Hopf analysis. The numerical findings using the rectangular and polar plots of the far-field are presented to investigate the impacts of various physical parameters and characteristics of the anisotropic medium. The results provide significant insights, including the amplification of oscillations with changes in wave number and slit width, the reduction of wave dispersion in anisotropic media, and the observation of an extended wavelength with an expanding electron charge density in the separated field. Notably, nullity occurs at observation angles of 0 and ?, offering valuable directions for future research. These findings enhance comprehension of electromagnetic wave diffraction in anisotropic media, with implications for optics and telecommunications.

Appendices

Appendix A

$$\begin{aligned}{} & \tilde {{\mathcal{F}}}_{l}^{\prime }(\beta ,0)=\frac{1}{2}\left( {\mathcal {F}}_{l}^{\prime } (\beta ,0^{+})-{\mathcal {F}}_{l}^{\prime }(\beta ,0^{-})\right), \end{aligned}$$

(33)

$$\begin{aligned}{} & {} {\mathcal {G}}(\beta )=\frac{\exp [i l(\beta -k_{eff}\cos \theta _{0})]-\exp [-i l(\beta -k_{eff}\cos \theta _{0})]}{\sqrt{2\pi }(\beta -k_{eff}\cos \theta _{0})}, \end{aligned}$$

(34)

Kernel function:

$$\begin{aligned} {\mathcal {K}}(\beta )=\frac{1}{i{\gamma (\beta )}}, \end{aligned}$$

(35)

Factorisation of kernel function:

$$\begin{aligned} {\mathcal {K}}(\beta )=\frac{1}{i{\gamma (\beta )}}={\mathcal {K}}_{+} (\beta ) {\mathcal {K}}_{-} (\beta )\text { with }\gamma (\beta )=\gamma _{+} (\beta )\gamma _{-} (\beta ), \end{aligned}$$

(36)

where $K_{\pm }(\beta )$ are,

$$\begin{aligned}{} & {} {\mathcal {K}}_{\pm }(\beta )=\frac{\exp (-i{\frac{\pi }{4}})}{\gamma _{\pm }(\beta )}\text { with }\gamma _{\pm }(\beta )=\sqrt{k_{eff}{\pm }\beta }. \end{aligned}$$

(37)

$$\begin{aligned}{} & {} {\mathcal {G}}_{1,2}(\beta )=\frac{\exp ({\mp }i{k_{eff}l\cos \theta _{0}} )}{\beta {\mp }k_{eff}\cos \theta _{0}}\left( \frac{1}{{\mathcal {K}}_{+}(\beta )}-\frac{1}{{\mathcal {K}}_{+}({\pm }k_{eff}\cos \theta _{0})}\right) -\exp ({\pm }{i}k_{eff}l\cos \theta _{0}){\mathcal {R}}_{1,2}(\beta ), \end{aligned}$$

(38)

$$\begin{aligned}{} & {} {\mathcal {C}}_{1,2}={\mathcal {K}}_{+}(k_{eff})\frac{{\mathcal {G}}_{2,1} (k_{eff})+{\mathcal {K}}_{+}(k_{eff}){\mathcal {G}}_{1,2}(k_{eff}){\mathcal {T}} (k_{eff})}{1-{\mathcal {K}}_{+}^{2}(k_{eff}){\mathcal {T}}^{2}(k_{eff})}, \end{aligned}$$

(39)

$$\begin{aligned}{} & {} {\mathcal {R}}_{1,2}(\beta )=\frac{E_{-1}}{2\pi {i}(\beta \mp k_{eff}\cos \theta _{0})}[{\mathcal {W}}_{-1}(-{i}(k_{eff}\pm k_{eff}\cos \theta _{0}))-{\mathcal {W}}_{-1}(-{i}(k_{eff}+\beta ))], \end{aligned}$$

(40)

$$\begin{aligned}{} & {} {\mathcal {T}}(\beta )=\frac{E_{-1}}{2\pi }{\mathcal {W}}_{-1}[-i(k_{eff} +\beta )l],\quad E_{-1}=2\sqrt{\frac{l}{i}}e^{i{k_{eff}+\beta }}, \end{aligned}$$

(41)

$$\begin{aligned}{} & {} {\mathcal {W}}_{n-1/2}(q)=\int \limits _{0}^{\infty }\frac{v^{n}e^{-v}}{v+q}dv=\Gamma (n+1)e^{ \left( \frac{q}{2}\right) } q^{(n-1)/2}{\mathcal {W}}_{-(n+1)/2,n/2}(q), \end{aligned}$$

(42)

where $q=-i(k_{eff}+\beta )l$, $n=-\frac{1}{2}$ and ${\mathcal {W}}$ is the Whittaker function.

Appendix B

$$\begin{aligned}{} & {} f_{sep}(-k_{eff}\cos \phi )=\frac{{\mathcal {A}}}{{\mathcal {K}}(-k_{eff}\cos \phi )}\left\{ \begin{array}{c} \frac{{\mathcal {K}}_{+}(-k_{eff}\cos \phi )\exp [-ik_{eff}l(\cos \phi +\cos \theta _{0})]}{{\mathcal {K}}_{+}(k_{eff}\cos \theta _{0})(-k_{eff}\cos \phi -k_{eff}\cos \theta _{0})}\\ -\frac{{\mathcal {K}}_{+}(k_{eff}\cos \phi )\exp [ilk_{eff}(\cos \phi +\cos \theta _{0})]}{{\mathcal {K}}_{+}(-k_{eff}\cos \theta _{0})(-k_{eff}\cos \phi -k_{eff}\cos \theta _{0})} \end{array} \right\}, \end{aligned}$$

(43)

$$\begin{aligned}{} & {} f_{int}(-k_{eff}\cos \phi )=\frac{{\mathcal {A}}}{{\mathcal {K}}(-k_{eff}\cos \phi )}\left\{ \left. \begin{array}{c} \exp (-ik_{eff}l\cos \phi ){\mathcal {K}}_{+}(-k_{eff}\cos \phi )\\ \times {\mathcal {T}}(-k_{eff}\cos \phi ){\mathcal {C}}_{1}\\ -\exp [il(-k_{eff}\cos \phi +k_{eff}\cos \theta _{0})]\\ \times {\mathcal {K}}_{+}(-k_{eff}\cos \phi ){\mathcal {R}}_{1}(-k_{eff}\cos \phi )\\ +{\mathcal {K}}_{-}(-k_{eff}\cos \phi )\exp (ik_{eff}l\cos \phi )\\ \times {\mathcal {T}}(k_{eff}\cos \phi ){\mathcal {C}}_{2}\\ -\exp \left[ -il(-k_{eff}\cos \phi +k_{eff}\cos \theta _{0})\right] \\ \times {\mathcal {K}}_{-}(-k_{eff}\cos \phi ){\mathcal {R}}_{2}(k_{eff}\cos \phi ) \end{array} \right. \right\}. \end{aligned}$$

(44)