Efficient parametric family of fourth-order Jacobian-free iterative vectorial schemes

Abstract

In this work, a multiparametric family of iterative vectorial fourth-order methods free of Jacobian matrices is proposed. A convergence analysis of this family is carried out as well as a study of its efficiency. Several numerical experiments are made in order to compare the behaviour of the proposed family with other competitive methods of the literature.

1 Introduction

Newton’s method, see [1], is one of the best known methods and has the following structure for vectorial non-linear problems:

$$\begin{aligned} \begin{array}{ll} y^{(k)}&=x^{(k)}-\left[ F'(x^{(k)})\right] ^{-1}F(x^{(k)}), \ k=0,1,\ldots , \end{array} \end{aligned}$$

(1)

where $F:D\subseteq \mathbb {R}^n\rightarrow \mathbb {R}^n$ is a non-linear vectorial function describing the non-linear system $F(x)=0$.

This method has quadratic convergence, and it is computationally very efficient. Many methods have been designed in an attempt to improve Newton’s convergence and its computational efficiency, see for instance [2].

On the other hand, Newton’s method is the first optimal method for vectorial problems according to the following conjecture for vectorial methods proposed in [3].

Conjecture 1

The order of convergence of any iterative method, without memory, for solving non-linear systems cannot exceed $2^{k_1+k_2-2}$, where $k_1$ is the number of evaluations of the Jacobian matrix and $k_2$ the number of evaluations of the non-linear function per iteration, and $k_1\le k_2$. When the scheme reaches this upper bound, we say that it is optimal.

In the literature, up to our knowledge, only one other optimal method for vectorial problems has been proposed according to the above conjecture and it is the family proposed in [4]. In it, the authors proposed a parametric family of optimal methods of order 4 which has the following structure:

$$\begin{aligned} \begin{array}{ll} y^{(k)}&{}=x^{(k)}-\left[ F'(x^{(k)})\right] ^{-1}F(x^{(k)}), \ k=0,1,\ldots , \\ x^{(k+1)}&{}=y^{(k)}-\left[ F'(x^{(k)})\right] ^{-1}\left( p_kF(y^{(k)})+q_kF(x^{(k)})\right) , \end{array} \end{aligned}$$

(2)

where $\lambda$ and $\psi$ are free real parameters,

$$\begin{aligned} \begin{array}{llllllll} \nu _k&{}=\dfrac{\Vert F(y^{(k)})\Vert _2^2}{\Vert F(x^{(k)})\Vert _2^2}, \qquad &{} K_k&{}=\dfrac{1}{1+\lambda \nu _k},\qquad &{}p_k&{}=K_k(1+\psi \nu _k), \qquad &{} q_k&{}=2K_k\nu _k.\\ \end{array} \end{aligned}$$

The idea of using such a definition of the variable $\nu _k$ comes from the article [5].

The iterative class (2) has a Jacobian matrix in its iterative expression, so it is not a Jacobian-free family. The aim of this work is to modify this family to obtain a new class of Jacobian-free schemes, which maintains the convergence order. In addition, we intend to make the modifications without considerably increasing the computational cost in order to obtain an efficient and competitive family compared to methods with the same characteristics.

In this article, a Jacobian-free multiparametric class of iterative methods for solving non-linear systems is presented. In Sect. 2, the parametric family is presented and an analysis of the convergence order is performed. Section 3 presents an analysis of the efficiency of the proposed family and compares it with other known methods in the literature with similar characteristics. In Sect. 4, several numerical experiments are carried out to see the behaviour of the family and to compare it with other iterative methods. The article concludes with some conclusions and references used in it.

2 Design of the parametric family

The only part we need to replace to obtain a derivative-free method is the Jacobian matrix $F'(x^{(k)})$ of the family (2). For that reason, we are going to keep the previous structure by replacing the Jacobian matrix with a divided difference operator. If we replace the matrix by a forward or backward divided difference operator, the order of convergence is not maintained, so we choose the following symmetrical divided difference operator $\left[ x^{(k)}+rF(x^{(k)}),x^{(k)}-rF(x^{(k)});F\right]$, which has a parameter r that can be any real number different from 0.

The parametric family obtained is denoted by CRTT and has the following iterative structure

$$\begin{aligned} \begin{array}{ll} y^{(k)}&{}=x^{(k)}\!-\!\left[ x^{(k)}+rF(x^{(k)}),x^{(k)}-rF(x^{(k)});F\right] ^{-1}F(x^{(k)}),\\ \\ x^{(k+1)}&{}=y^{(k)}\!-\!\left[ x^{(k)}+rF(x^{(k)}),x^{(k)}-rF(x^{(k)});F\right] ^{-1}\left( p_kF(y^{(k)})+q_kF(x^{(k)})\right) , \end{array} \end{aligned}$$

(3)

where $r\in \mathbb {R}$, $r\ne 0$ and

$$\begin{aligned} \begin{array}{llll} \nu _k&{}=\dfrac{F(y^{(k)})^T F(y^{(k)})}{F(x^{(k)})^T F(x^{(k)})},\qquad \qquad &{} K_k&{}=\dfrac{1}{1+\lambda \nu _k},\\ p_k&{}=K_k(1+\psi \nu _k), &{} q_k&{}=2K_k\nu _k.\\ \end{array} \end{aligned}$$

We prove that the parametric family CRTT has fourth order of convergence for any value of real parameters r, $\lambda$ and $\psi$.

Theorem 2

Let us consider $F: D \subseteq \mathbb {R}^n \longrightarrow \mathbb {R}^n$ a differentiable enough function defined in a neighbourhood D of $\alpha$, such that $F(\alpha )=0$. Let us also assume that $F'(\alpha )$ is non-singular. Therefore, being $x^{(0)}$ an initial guess close enough to $\alpha$, sequence $\{x^{(k)}\}$ defined by CRTT converges to $\alpha$ with order 4, for any non-zero value of parameter r and for any values of $\lambda$ and $\psi$.

Proof

We first obtain the Taylor development of $F(x^{(k)})$, $F'(x^{(k)})$, $F''(x^{(k)})$ and $F'''(x^{(k)})$ around $\alpha$, where $e_k=x^{(k)}-\alpha$ and $C_i=\frac{1}{i!}[F'(\alpha )]^{-1}F^{(i)}(\alpha )$, $i=2, 3,\ldots$

$$\begin{aligned} F(x^{(k)})&=F'(\alpha )(e_k+C_2e_k^2+C_3e_k^3)+O\left( e_k^4\right) ,\\ F'(x^{(k)})&=F'(\alpha )(I+2C_2e_k+3C_3e_k^2)+O\left( e_k^3\right) ,\\ F''(x^{(k)})&=F'(\alpha )(2C_2+6C_3e_k)+O\left( e_k^2\right) ,\\ F'''(x^{(k)})&=F'(\alpha )6C_3+O(e_k). \end{aligned}$$

From [6], it is obtained the following expansion using the Genocchi-Hermite formula:

$$\begin{aligned} {\begin{matrix} [x^{(k)}\!+rF(x^{(k)}),x^{(k)}\!-rF(x^{(k)});F]&{}\!=\!F'(x^{(k)})+\dfrac{1}{6}F'''(x^{(k)})(rF(x^{(k)}))^2+O(rF(x^{(k)})^3)\\ &{}\!=\!F'(\alpha )(I\!+\!2C_2e_k\!+\!3C_3e_k^2)+ \dfrac{1}{6}F'(\alpha )(6C_3)r^2F'(\alpha )^2(e_k^2)+\\ {} &{}\quad +O\left( e_k^3\right) \\ &{}\!=\!F'(\alpha )\left( I+ 2C_2e_k+C_3\left( 3I+r^2F'(\alpha )^2\right) e_k^2\right) +O\left( e_k^3\right) . \end{matrix}} \end{aligned}$$

It can be simply checked that the inverse operator of $[x^{(k)}+rF(x^{(k)}),x^{(k)}-rF(x^{(k)});F]$ has the following expression

$$\begin{aligned} {\begin{matrix} [x^{(k)}+rF(x^{(k)}),x^{(k)}-rF(x^{(k)});F]^{-1} &{}=\left( I- 2C_2e_k+\left( 4C_2^2-C_3\left( 3I+r^2F'(\alpha )^2\right) \right) e_k^2\right) F'(\alpha )^{-1}\\ &{}\quad +O\left( e_k^3\right) . \end{matrix}} \end{aligned}$$

(4)

From expression (4) and the Taylor development of $F(x^{(k)})$, we obtain that $e_{y,k}=y^{(k)}-\alpha$ satisfies the following equality

$$\begin{aligned} e_{y,k}&=x^{(k)}-\alpha - [x^{(k)}+rF(x^{(k)}),x^{(k)}-rF(x^{(k)});F]^{-1}F(x^{(k)})\\&=e_k-\left( I- 2C_2e_k+\left( 4C_2^2-C_3\left( 3I+r^2F'(\alpha )^2\right) \right) e_k^2\right) \left( e_k+C_2e_k^2+C_3e_k^3\right) +O\left( e_k^4\right) \\&=e_k-e_k-C_2e_k^2-C_3e_k^3+2C_2e_k^2+2C_2^2e_k^3-\left( 4C_2^2-C_3\left( 3I+r^2F'(\alpha )^2\right) \right) e_k^3+O\left( e_k^4\right) \\&=C_2e_k^2+ \left( -2C_2^2+C_3\left( 2I+r^2F'(\alpha )^2\right) \right) e_k^3+O\left( e_k^4\right) . \end{aligned}$$

To simplify the notation, we define $Y_3$ as follows

$$\begin{aligned} Y_3=-2C_2^2+C_3\left( 2I+r^2F'(\alpha )^2\right) . \end{aligned}$$

For any $x\in \mathbb {R}^n$, we have that $F(x)=(f_1(x),f_2(x),\ldots , f_n(x))^T$, where $f_i(x):\mathbb {R}^n\rightarrow \mathbb {R}$ for $i=1,2,\ldots ,n$.

Also, it is verified that

$$\begin{aligned} \dfrac{F(y^{(k)})^TF(y^{(k)})}{F(x^{(k)})^TF(x^{(k)})} =\dfrac{\sum \limits _{i=1}^n f_i^2(y^{(k)}) }{\sum \limits _{i=1}^n f_i^2(x^{(k)})}, \end{aligned}$$

(5)

where the developments of $f_i(x^{(k)})$ and $f_i(y^{(k)})$ around $\alpha$ for $i=1,2,\ldots ,n$ are

$$\begin{aligned} f_i(x^{(k)})&=f_i'(\alpha )e_k+\dfrac{1}{2}f_i''(\alpha )e_k^2+O\left( e_k^3\right) ,\\ f_i(y^{(k)})&=f_i'(\alpha )e_{y,k}+\dfrac{1}{2}f_i''(\alpha )e_{y,k}^2+O\left( e_{y,k}^3\right) , \end{aligned}$$

being $f_i'(x)=\left( \frac{\partial f_i}{\partial x_1},\frac{\partial f_i}{\partial x_2},\ldots ,\frac{\partial f_i}{\partial x_n} \right)$ and $f_i''(x)$ is the Hessian matrix with components $\frac{\partial ^2 f_i}{\partial x_j \partial x_k}$, for $j,k\in \{1,2,\ldots ,n\}$.

To simplify the notation, we can rewrite it in the following way

$$\begin{aligned} f_i(x^{(k)})&=R_ie_k+H_ie_k^2+O\left( e_k^3\right) ,\\ f_i(y^{(k)})&=R_ie_{y,k}+H_ie_{y,k}^2+O\left( e_{y,k}^3\right) , \end{aligned}$$

with $R_i=f_i'(\alpha )$ and $H_i=\dfrac{1}{2}f_i''(\alpha )$.

In order to obtain $\nu _k$, we compute now $f_i^2(x^{(k)})$ and $f_i^2(y^{(k)})$, for $i=1,2,\ldots ,n$:

$$\begin{aligned} {\begin{matrix} f_i^2(x^{(k)})&{}=f_i(x^{(k)})^Tf_i(x^{(k)})\\ &{}=R_i^TR_ie_k^2+(R_i^TH_i+H_i^TR_i)e_k^3+O\left( e_k^4\right) ,\\ f_i^2(y^{(k)})&{}=f_i(y^{(k)})^Tf_i(y^{(k)})\\ &{}=R_i^TR_ie_{y,k}^2+(R_i^TH_i+H_i^TR_i)e_{y,k}^3+O\left( e_{y,k}^4\right) .\\ \end{matrix}} \end{aligned}$$

(6)

By denoting $P_i=R_i^TR_i$ and $Q_i=R_i^TH_i+H_i^TR_i$, the relations (6) can be rewritten as

$$\begin{aligned} {\begin{matrix} f_i^2(x^{(k)}) &{}=P_ie_k^2+Q_ie_k^3+O\left( e_k^4\right) ,\\ f_i^2(y^{(k)}) &{}=P_ie_{y,k}^2+Q_ie_{y,k}^3+O\left( e_{y,k}^4\right) .\\ \end{matrix}} \end{aligned}$$

(7)

Since $e_{y,k}=C_2e_k^2+Y_3e_k^3+O\left( e_k^4\right)$, therefore $e_{y,k}^2=C_2^2e_k^4+(C_2Y_3+Y_3C_2)e_k^5+O\left( e_{k}^6\right) .$ Substituting this relation in (7), we obtain

$$\begin{aligned} {\begin{matrix} f_i^2(y^{(k)}) &{}=P_ie_{y,k}^2+Q_ie_{y,k}^3+O\left( e_{y,k}^4\right) \\ &{}=P_i\left( C_2^2e_k^4+(C_2Y_3+Y_3C_2)e_k^5\right) +O(e_{k}^6).\\ \end{matrix}} \end{aligned}$$

(8)

If we denote $P=\sum \limits _{i=1}^nP_i$ and $Q=\sum \limits _{i=1}^nQ_i$, and substituting the results of (7) and (8) in (5), we obtain

$$\begin{aligned} \nu _k= & {} \dfrac{Pe_{y,k}^2+Qe_{y,k}^3+ O\left( e_{y,k}^4\right) }{Pe_k^2+Qe_k^3+O\left( e_k^4\right) }\nonumber \\= & {} \dfrac{P(C_2^2e_k^4+(C_2Y_3+Y_3C_2)e_k^5)+O\left( e_{k}^6\right) }{Pe_k^2+Qe_k^3+O\left( e_k^4\right) }\\= & {} \dfrac{P(C_2^2e_k^2+(C_2Y_3+Y_3C_2)e_k^3)+O\left( e_k^4\right) }{P+Qe_k+O\left( e_k^2\right) }.\nonumber \end{aligned}$$

(9)

Since

$$\begin{aligned}{}[P+Qe_k+O\left( e_k^2\right) ]^{-1}=P^{-1}-P^{-1}Qe_k+O\left( e_k^2\right) , \end{aligned}$$

we obtain that

$$\begin{aligned} {\begin{matrix} \nu _k&{}=(P^{-1}-P^{-1}Qe_k)P(C_2^2e_k^2+(C_2Y_3+Y_3C_2)e_k^3)+O\left( e_k^4\right) \\ &{}=C_2^2e_k^2+(C_2Y_3+Y_3C_2)e_k^3-P^{-1}QPC_2^2e_k^3+O\left( e_k^4\right) \\ &{}=C_2^2e_k^2+(C_2Y_3+Y_3C_2-P^{-1}QPC_2^2)e_k^3+O\left( e_k^4\right) . \end{matrix}} \end{aligned}$$

(10)

In order to simplify the notation, we denote $V_3$ as follows

$$\begin{aligned} V_3=(C_2Y_3+Y_3C_2-P^{-1}QPC_2^2), \end{aligned}$$

obtaining then that $\nu _k=C_2^2e_k^2+V_3e_k^3+O\left( e_k^4\right)$.

Therefore, the expression of $K_k$ is as follows

$$\begin{aligned} K_k=I\left( \dfrac{1}{1+\lambda \nu _k}\right) =I-\lambda C_2^2e_k^2+\lambda (C_2^4-V_3)e_k^3+O\left( e_k^4\right) . \end{aligned}$$

(11)

From (10) and (11), we obtain that the expressions of $p_k$ and $q_k$ are

$$\begin{aligned} {\begin{matrix} p_k&{}=K_k(1+\psi \nu _k)=(I-\lambda C_2^2e_k^2 +\lambda (C_2^4-V_3)e_k^3)(1+\psi \nu _k)+O\left( e_k^4\right) \\ &{}=I+(\psi -\lambda )C_2^2e_k^2+((-\lambda +\psi )V_3 + \lambda C_2^4)e_k^3+O\left( e_k^4\right) ,\\ q_k&{}=2K_k\nu _k=2(I-\lambda C_2^2e_k^2+\lambda (C_2^4-V_3)e_k^3)\nu _k+O\left( e_k^4\right) \\ &{}=2C_2^2e_k^2+2V_3e_k^3+O\left( e_k^4\right) . \end{matrix}} \end{aligned}$$

(12)

Therefore,

$$\begin{aligned} {\begin{matrix} p_kF(y^{(k)})+q_kF(x^{(k)})&{}=C_2 e_k^2 + C_3(2I + r^2F'(\alpha )^2)e_k^3 + \\ {} &{}(-C_4 + 2 V_3 + 2C_2C_3+ 3 C_3C_2 +(-1-\lambda +\psi )C_2^3+ r^2 C_3 F'(\alpha )^2C_2)e_k^4\\ &{}+O\left( e_{k}^5\right) . \end{matrix}} \end{aligned}$$

(13)

Therefore, from (4) and (13), the error equation is

$$\begin{aligned} e_{k+1}= & {} y^{(k)}-\alpha -\left[ x^{(k)}+rF(x^{(k)}),x^{(k)}-rF(x^{(k)});F\right] ^{-1}\left( p_kF(y^{(k)})+q_kF(x^{(k)})\right) \\= & {} \left( -2 V_3 + 4 C_2C_3+ 3 C_3C_2 +(- 7 + \lambda - \psi )C_2^3 + 2 r^2 C_2C_3F'(\alpha )^2 + r^2 C_3 F'(\alpha )^2 C_2\right) e_k^4\\{} & {} +O\left( e_{k}^5\right) . \end{aligned}$$

Since

$$\begin{aligned} V_3&= (C_2Y_3+Y_3C_2-P^{-1}QPC_2^2)\\&=C_2(-2C_2^2+C_3\left( 2I+r^2F'(\alpha )^2\right) )+(-2C_2^2+C_3\left( 2I+r^2F'(\alpha )^2\right) )C_2-P^{-1}QPC_2^2\\&=-2C_2^3+C_2C_3\left( 2I+r^2F'(\alpha )^2\right) )-2C_2^3+C_3\left( 2I+r^2F'(\alpha )^2\right) C_2-P^{-1}QPC_2^2\\&=-4C_2^3+C_2C_3\left( 2I+r^2F'(\alpha )^2\right) )+C_3\left( 2I+r^2F'(\alpha )^2\right) C_2-P^{-1}QPC_2^2, \end{aligned}$$

the error equation can be rewritten as

$$\begin{aligned} {\begin{matrix} e_{k+1}&{}=y^{(k)}-\alpha -\left[ x^{(k)}+rF(x^{(k)}),x^{(k)}-rF(x^{(k)});F\right] ^{-1}\left( p_kF(y^{(k)})+q_kF(x^{(k)})\right) \\ &{}= \left( 8C_2^3-2C_2C_3\left( 2I+r^2F'(\alpha )^2\right) -2C_3\left( 2I+r^2F'(\alpha )^2\right) C_2+2P^{-1}QPC_2^2 +\right. \\ {} &{}\quad +\left. 4 C_2C_3+ 3 C_3C_2 +(- 7 + \lambda - \psi )C_2^3 + 2 r^2 C_2C_3F'(\alpha )^2 + r^2 C_3 F'(\alpha )^2 C_2\right) e_k^4\\ {} &{}\quad +O\left( e_{k}^5\right) \\ &{}=\left( 2P^{-1}Q P C_2^2 +(1 + \lambda - \psi )C_2^3 - C_3(I+ r^2 F'(\alpha )^2 )C_2\right) e_k^4+O\left( e_{k}^5\right) .\\ \end{matrix}} \end{aligned}$$

Therefore, it is proven that the members of the parametric family (3) have order of convergence 4. $\square$

3 Efficiency index

To compare different iterative methods, the efficiency index suggested by Ostrowski is widely used. The formula of this index is the following

$$I_E=p^{1/d},$$

where p is the order of convergence of the method and d represents the number of functional evaluations needed to perform the method per iteration.

Another classical measure of the efficiency of iterative methods is the operational efficiency index proposed by Traub, with the expression:

$$I_O=p^{1/op},$$

where op is the number of operations, expressed in units of product, needed to calculate each iteration.

In several occasions, a combination of both is also used, called the computational efficiency index, whose expression is

$$I_{EC}=p^{1/(d+op)}.$$

In this section, we will study these different indices for our parametric family, as well as compare the results obtained with the efficiency indices of other methods known in the literature, which are S2S from [7], CJTS5 from [8], WF6S from [9] and WZ7S from [10].

When working on systems of size $n\times n$, the number of functional evaluations used in calculating F(z) is n while the number used in calculating a divided difference operator as used in the iterative method is $n^2-n$.

In the case of the CRTT parametric family, we compute $F(x^{(k)})$, $F(y^{(k)})$, $F(x^{(k)}+rF(x^{(k)}))$ and $F(x^{(k)}-rF(x^{(k)}))$ and just one divided difference operator, so the number of functional evaluations is:

$$\begin{aligned} 4n+n^2-n=n^2+3n. \end{aligned}$$

Below is a list of the number of products and quotients needed to perform the operations involved:

• Each scalar/vector product costs n.

• Each transpose vector/vector product costs n.

• Each matrix/vector product costs $n^2$.

• Each matrix/matrix product costs $n^3$.

• The number of quotients of a divided difference operator is $n^2$.

• Each LU decomposition costs $\frac{1}{3}(n^3-n)$.

• Each system resolution costs $n^2$.

In this case, we calculate three scalar/vector products, two transpose vector/vector products, a divided difference operator, and a single LU decomposition and we solve two systems, so the number of operations is:

$$\begin{aligned} 3n+2n+n^2+\frac{1}{3}(n^3-n)+2n^2=\frac{1}{3}(n^3-n)+3n^2+5n. \end{aligned}$$

Then, the addition of evaluations and operations is:

$$\begin{aligned} \frac{1}{3}(n^3-n)+3n^2+5n+n^2+3n=\frac{1}{3}(n^3-n)+4n^2+8n. \end{aligned}$$

In the following, we present and compute the efficiency of the methods with which we compare the indices.

The S2S method has the following iterative expression:

$$\begin{aligned} y^{(k)}=x^{(k)}-\left[ [x^{(k)}+F(x^{(k)}),x^{(k)}-F(x^{(k)});F]\right] ^{-1}F(x^{(k)}), \end{aligned}$$

There are 3 evaluations and a divided difference, so the number of functional evaluations is:

$$ 3n+n^2-n=n^2+2n. $$

On the other hand, a divided difference operator is calculated and a single system is solved, so the number of operations is:

$$ n^2+\frac{1}{3}(n^3-n)+n^2=\frac{1}{3}(n^3-n)+2n^2. $$

Thus, the total number of functional evaluations and operations is:

$$ n^2+2n+\frac{1}{3}(n^3-n)+2n^2=\frac{1}{3}(n^3-n)+3n^2+2n. $$

The iterative expression of CJTS5 is:

$$\begin{aligned} {\begin{matrix} y^{(k)}&{}=x^{(k)}-[a^{(k)},b^{(k)};F]^{-1}F(x^{(k)}),\\ z^{(k)}&{}=y^{(k)}-\alpha [a^{(k)},b^{(k)};F]^{-1}F(y^{(k)}),\\ t^{(k)}&{}=z^{(k)}-\beta [a^{(k)},b^{(k)};F]^{-1}F(z^{(k)}),\\ x^{(k+1)}&{}=z^{(k)}-\gamma [a^{(k)},b^{(k)};F]^{-1}F(t^{(k)}),\\ \end{matrix}} \end{aligned}$$

where $a^{(k)}=x^{(k)}+F(x^{(k)})$ and $b^{(k)}=x^{(k)}-F(x^{(k)})$.

This method calculates 6 functional evaluations and a divided difference, then the number of evaluations is:

$$\begin{aligned} 6n+n^2-n=n^2+5n. \end{aligned}$$

On the other hand, it performs 3 scalar/vector products, a divided difference operator, and a single LU decomposition and solves 4 systems with the same matrix; therefore, the number of operations is:

$$\begin{aligned} 3n+n^2+\frac{1}{3}(n^3-n)+4n^2=\frac{1}{3}(n^3-n)+5n^2+3n. \end{aligned}$$

The total number of evaluations and operations is:

$$\begin{aligned} n^2+5n +\frac{1}{3}(n^3-n)+5n^2+3n=\frac{1}{3}(n^3-n)+6n^2+8n. \end{aligned}$$

The iterative expression of the WF6S method is as follows:

$$\begin{aligned} {\begin{matrix} y^{(k)}&{}=x^{(k)}-[w^{(k)},s^{(k)};F]^{-1}F(x^{(k)}),\\ \mu _1&{}=(3I-2[w^{(k)},s^{(k)};F]^{-1}[y^{(k)},x^{(k)};F])[w^{(k)},s^{(k)};F]^{-1}\\ z^{(k)}&{}=y^{(k)}-\mu _1 F(y^{(k)}),\\ x^{(k+1)}&{}=z^{(k)}-\mu _1F(z^{(k)}),\\ \end{matrix}} \end{aligned}$$

where $w^{(k)}=x^{(k)}+F(x^{(k)})$ and $s^{(k)}=x^{(k)}-F(x^{(k)})$.

This method calculates 5 functional evaluations and 2 divided difference operators. Then, the number of functional evaluations is:

$$\begin{aligned} 5n+2n^2-2n=2n^2+3n. \end{aligned}$$

The number of operations performed is as follows: two divided difference operators are calculated, 3 systems are solved with the same coefficient matrix, a multiplication between 2 matrices is done, a scalar matrix multiplication is done and a vector matrix multiplication is done, so the number of operations is:

$$\begin{aligned} 2n^2+\frac{1}{3}(n^3-n)+3n^2+n^2+n^2+n^3=\frac{1}{3}(n^3-n)+n^3+7n^2. \end{aligned}$$

The total of evaluations and operations is:

$$\begin{aligned} 2n^2+3n+\frac{1}{3}(n^3-n)+n^3+7n^2=\frac{1}{3}(n^3-n)+n^3+9n^2+3n. \end{aligned}$$

Finally, the iterative expression of the method WZ7S is:

$$\begin{aligned} {\begin{matrix} y^{(k)}&{}=x^{(k)}-[w^{(k)},x^{(k)};F]^{-1}F(x^{(k)}),\\ z^{(k)}&{}=y^{(k)}-\left( [y^{(k)},x^{(k)};F]+[y^{(k)},w^{(k)};F]-[w^{(k)},x^{(k)};F]\right) ^{-1}F(y^{(k)}),\\ x^{(k+1)}&{}=z^{(k)}-\left( [z^{(k)},x^{(k)};F]+[z^{(k)},y^{(k)};F]-[y^{(k)},x^{(k)};F]\right) ^{-1}F(z^{(k)}),\\ \end{matrix}} \end{aligned}$$

being $w^{(k)}=x^{(k)}+F(x^{(k)})$.

In this case, 4 evaluations of F and 5 divided difference operators are calculated, so the number of functional evaluations is:

$$\begin{aligned} 4n+5(n^2-n)=5n^2-n. \end{aligned}$$

The number of operations performed is as follows: 5 different divided difference operators are calculated and 2 different LU decompositions are performed and a system is solved with each of the decompositions. Thus, the total number of operations is:

$$ 5n^2+\frac{2}{3}(n^3-n)+2n^2=\frac{2}{3}(n^3-n)+7n^2. $$

Thus, the number of total evaluations and operations is:

$$\begin{aligned} 5n^2-n+\frac{2}{3}(n^3-n)+7n^2=\frac{2}{3}(n^3-n)+12n^2-n. \end{aligned}$$

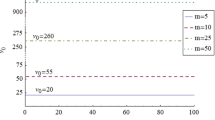
Below are some images showing the efficiency index, the operational index and the computational efficiency index of the previously mentioned methods for different sizes of the system to be solved, in order to compare the different methods.

Figure 1 illustrates the efficiency rate of the different methods for different system sizes. In these figures, we can see that the methods with the highest efficiency rates are CJTS5 and CRTT.

Fig. 1

Efficiency index (a) For $n = 1$ to $n = 10$, (b) For $n = 10$ to $n = 50$, (c) For $n = 50$ to $n = 100$

Fig. 2

Operational efficiency index (a) For $n = 1$ to $n = 10$, (b) For $n = 10$ to $n = 50$, (c) For $n = 50$ to $n = 100$

Fig. 3

Computational efficiency index (a) For $n = 1$ to $n = 10$, (b) For $n = 50$ to $n = 100$, (c) For $n = 2000$ to $n = 2500$

Figure 2 illustrates the operational efficiency index of the different methods for different system sizes. In these figures, we can see that for small sizes the methods CJTS5 and CRTT are not as competitive, but when the size is greater than or equal to 10, these are the two methods with the highest operational efficiency index.

Figure 3 illustrates the computational efficiency index for different system sizes. As with the other indices, the methods CJTS5 and CRTT stand out for system sizes greater than 1.

4 Numerical performance of CRTT

We compare some methods of CRTT class, namely CJF4S, TJF4S and CRTT4, with values of the parameters $\psi =0, \;r=1$ in all cases and $\lambda =\{-4,\; -5, \; 0\},$ respectively, with others, of high efficiency or order, S2S, CJTS5, WF6S and WZ7S, of orders 2, 5, 6 and 7, respectively, in the same problems, which have been define in the previous section. Note that CRTT4 is the version with the least computational effort of all of the family.

The maximum number of iterations considered is 50 and the stopping criterion is $\left\| x^{(k+1)}-x^{(k)}\right\| < 10^{-100}$ or $\left\| F (x^{(k+1)}) \right\| < 10^{-100}$. Each calculation was performed using Matlab R2022b with variable-precision arithmetic with a 500-digit mantissa to minimize round-off errors.

We must take into account that the approximate computational order of convergence (ACOC), see [11]:

$$ p \approx A C O C=\frac{\ln \left( \left\| x^{(k+1)}-x^{(k)}\right\| / {\left\| x^{(k)}-x^{(k-1)}\right\| }\right) }{\ln \left( \left\| x^{(k)}-x^{(k-1)}\right\| / \left\| x^{(k-1)}-x^{(k-2)}\right\| \right) }, $$

will be calculated that gives the numerical approximation of the theoretical order of an iterative method.

4.1 Academical problems

Consider the system of equations:

$$ -x_i-3+\sum _{j=1}^m {x_j} -e^{x_i} +4 \cos \left( 2 \ln \left( |x_i+1|\right) \right) =0, \quad i=1,2, \ldots , m. $$

By taking $m=200,$ the initial estimate that we chose is $x^{(0)}=\left( \frac{1}{100}, \ldots , \frac{1}{100}\right) ^T$ to obtain the solution

$$ \alpha =(0, 0, \ldots , 0)^T.$$

In Table 1, the results obtained by the different methods for the academic problem are shown. The table shows that the elements of the CRTT family take the least computational time to reach the required tolerance, being considerably less than other methods that double their ACOC. Moreover, excluding the S2S method, they require the same iterations as the other methods with the highest order of convergence.

Table 1 Academic problem

Fig. 4

Numerical approximation of the solution of the non-linear and non-homogeneous transport equation $u_t+u_x=-2\, u\,|u|$

4.2 Application to boundary value problem

We consider a particular case of the partial derivative equation, called the transport equation (see [12]). This case is non-linear and non-homogeneous. This equation models physical phenomena, referring to the movement of different entities, such as inertial moment, mass or energy, through a medium, solid or fluid, with particular conditions that exist within the medium and it is expressed by the non-differentiable partial differential equation:

$$u_t+u_x=-2\, u\,|u|, $$

for $x \in [0,1]$, $t \ge 0$. The boundary conditions on u(x, t) are imposed as $u(0,t)=\frac{1}{1+t}, \; u(1,t)=\frac{1}{2+t}$ for all $t \ge 0,$ along with the initial condition as $u(x,0)=\frac{1}{1+x}$, for $0 \le x \le 1.$

Applying the method of characteristics, we have the system of ordinary differential equations:

$$ \left\{ \begin{array}{lll} \frac{dt}{ds}=1,\\ \frac{dx}{ds}=1, \\ \frac{du}{ds}=-2\, u\,|u| \end{array} \right. $$

We solve the system numerically applying in each case the trapezium method (or second-order implicit Runge-Kutta). With the first two equations, we have that $\Delta x +\Delta t=2 \Delta s.$

From the third equation, we form a system of $n = 500$ equations, taking as step size $\Delta s=(b-a)/(n-1)$, we obtain our initial approximation, applying the initial condition.

Now, we must solve the system of size $500 \times 500$, numerically:

$$\begin{aligned} {\begin{matrix} u_1&{}-1=0,\\ u_i&{}-u_{1-1}+\Delta s \; (u_i \;|u_i|+u_{i-1} \; |u_{i-1}|)=0, \quad i=2, 3 \ldots , 500. \end{matrix}} \end{aligned}$$

(14)

We take the same stopping criteria as in the academic problem. Next, we form the corresponding mesh, considering the domain

$$D = \{(x,t),\ (x,t) \in [0,1] \times [0,1]\},$$

with the partition of spatial step $\Delta x =1/(n-1)$ and time step $\Delta t =1/(n-1),$ respectively, for the domains, from the solution of the first two equations, and we obtain the solution shown in Fig. 4.

In Table 2, the results obtained for the boundary value problem by the different methods are shown, where ‘-’ denotes lack of convergence or unstable value of the ACOC. In this table, we can see that the WZ7S method only requires a single iteration, while the rest require 3 iterations or more. We can also see that the TJF4S element of the CRTT family increases the ACOC by one unit for this problem.

Table 2 Boundary value problem

The methods of the CRTT family maintain the theoretical order in very large systems, considering sizes 200 and 500. They can also compete with methods of equal or higher order, as can be seen in Tables 1 and 2.

About computational effort, note that the methods of CRTT family make much better use of the computational effort compared to the others.

5 Conclusion

In this work, a parametric family of Jacobian-free fourth-order convergence iterative methods has been presented. This class has been designed from the family defined in [4] in order to maintain the properties by modifying the Jacobian matrix by a divided difference operator, to make it suitable for non-differentiable problems. An efficiency study and several numerical experiments have been carried out, showing that it is a family of competitive methods compared to other known methods in the literature with similar characteristics.