Bifurcation and Turing instability of the solutions of the diffusive Lauffenburger–Kennedy bacterial infection model with phagocyte and bacterial chemotactic terms

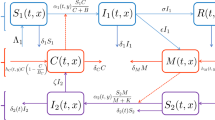
Abstract

It is well known that diffusion could have a destabilizing effect on the otherwise stable solution (including the spatially homogenous periodic solutions), which is called Turing instability. This paper analyzes dynamic behavior of the reaction–diffusion Lauffenburger–Kennedy bacterial infection system, and the focus is on the Turing instability of constant equilibrium solutions and spatially homogeneous Hopf bifurcating periodic solutions. The specific conditions about the diffusion rates under which constant equilibrium solutions and spatially homogeneous periodic solutions occur Turing instability are obtained. Then, the results of theoretical analysis are verified by the examples of numerical simulation.

Appendices

Appendix A

In this “Appendix,” we shall state some well-known conclusions for the dynamics of ODEs (A.1).

The ODE system consistent with reaction–diffusion system (1.4) is represented as follows:

$$\begin{aligned} \dfrac{du}{dt} = \varrho (1+\gamma v-u),\, \, \, \, \, \, \, \dfrac{dv}{dt} = \displaystyle \frac{\eta v}{1+v}-\displaystyle \frac{uv}{\kappa +v}.\nonumber \\ \end{aligned}$$

(A.1)

System (A.1) has a semi-trivial equilibrium solution (1, 0). Solving

$$\begin{aligned} 1+\gamma v-u=0,\, \, \, \displaystyle \frac{\eta }{1+v}-\displaystyle \frac{u}{\kappa +v}=0, \end{aligned}$$

(A.2)

we find that the existence of positive equilibrium solutions for ODEs (A.1) is equivalent to solving

$$\begin{aligned} h(v):=\displaystyle \frac{(1+v)(1+\gamma v)}{\kappa +v}=\eta , \end{aligned}$$

(A.3)

and $u=1+\gamma v>0$.

In [21], for the existence of positive equilibrium solutions, the authors obtained the following results:

Lemma A.1

([21]) The following statements hold true:

• 1. Assume $\kappa \ge 1/(1+\gamma )$.

  • (a) when $\eta \le 1/\kappa$, system (A.1) has no positive equilibrium solutions;

  • (b) when $\eta >1/\kappa$, system (A.1) has a unique positive equilibrium solution $(u_\mu ,\mu )$, where $\mu >0$ solves the equation $\eta =h(v)$ and $u_\mu =1+\gamma \mu$.

• 2. Assuming $0<\kappa <1/(1+\gamma )$, then $h(\mu )$ has a minimum point

  $$\begin{aligned} \mu _0:=\sqrt{\kappa ^2-(\kappa +\kappa \gamma -1)/\gamma }-\kappa >0. \end{aligned}$$

  • (a) when $\eta <h(\mu _0)$, system (A.1) has no positive equilibrium solutions;

  • (b) when $\eta =h(\mu _0)$, system (A.1) has a unique positive equilibrium solution $(u_{\mu _0},\mu _0)$;

  • (c) when $h(\mu _0)<\eta <1/\kappa$, system (A.1) has two positive equilibrium solutions $(u_{\mu ^-},{\mu ^-})$ and $(u_\mu ,\mu )$, where $0<{\mu ^-}<\mu _0<\mu$ satisfy $h({\mu ^-})=h(\mu )=\eta$, and $u_{\mu ^-}=1+\gamma {\mu ^-}, u_\mu =1+\gamma \mu$;

  • (d) when $\eta \ge 1/\kappa$, system (A.1) has a unique positive equilibrium solution $(u_\mu ,\mu )$, where $\mu \ge \mu _*>\mu _0$, $h(\mu _*)=1/\kappa$, and $u_\mu =1+\gamma \mu$.

Define

$$\begin{aligned} W(\mu ):=\displaystyle \frac{\mu (1+\gamma \mu )(1-\kappa )}{(1+\mu )(\kappa +\mu )^2}. \end{aligned}$$

(A.4)

Then, we have the following lemma about $W(\mu )$:

Lemma A.2

([21]) If $0<\kappa <1$, then there must be a unique $\mu _{**}>0$, such that $W(\mu )$ is increasing (resp. decreasing) in $(0, \mu _{**})$ (resp. $(\mu _{**}, \infty )$).

The proof of the above lemma is easy. We can get $W'(\mu )=(1-\kappa )B(\mu )/\big ((1+\mu )^2(\kappa +\mu )^3\big )$, here, $B(\mu ):=-\gamma \mu ^3+(\kappa \gamma -2)\mu ^2+(2\kappa \gamma -1)\mu +\kappa$. Clearly, if $0<\kappa <1$, then $W'(\mu )B(\mu )>0$. In fact, $B'(\mu )=-3\gamma \mu ^2+2(\kappa \gamma -2)\mu +2\kappa \gamma -1$, that means when $2\kappa \gamma -1>0$, $B'(\mu )=0$ has two roots with different signs; when $2\kappa \gamma -1\le 0$, $B'(\mu )=0$ has two different non-positive roots. Combined with $B(0)=\kappa$, we observe there must be a unique $\hat{\mu }>0$, satisfying $B(\mu )>0$ for $\mu \in (0, \hat{\mu })$ and $B(\mu )<0$ for $\mu \in (\hat{\mu }, +\infty )$. Note $W(0)=0$, thus the conclusion clearly holds.

Following [21], the stability of equilibrium solutions, the existence of Hopf bifurcations and the stability of periodic solutions are summarized, and then, we state the following conclusions:

Lemma A.3

([21]) Let h(v) and $W(\mu )$ be defined in (A.3) and (A.4), respectively, the following statements hold true:

• 1. When $\eta \kappa <1$, (1, 0) is stable; when $\eta \kappa >1$, (1, 0) is unstable; when $\eta \kappa =1$, (1, 0) is stable if $\kappa \ge 1$; and it is unstable if $0<\kappa <1$.

• 2. Assuming 1(b) of Lemma (A.1) hold. The unique positive equilibrium solution $(u_\mu ,\mu )$ is stable for $\mu >0$ if $\kappa \ge 1$ or $1/(1+\gamma )<\kappa <1$ but $\varrho >W(\mu _{**})$, or for $\mu \in (0,\mu _1)\cup (\mu _2,\infty )$ if $1/(1+\gamma )<\kappa <1$ but $0<\varrho <W(\mu _{**})$. In addition, $(u_\mu ,\mu )$ is unstable for $\mu \in (\mu _1,\mu _2)$ if $1/(1+\gamma )<\kappa <1$ but $0<\varrho <W(\mu _{**})$. In particular, system (A.1) has two Hopf bifurcation points at $\mu =\mu _1 \,and\, \mu _2$, where both $\mu _1$ and $\mu _2$ satisfy the equation $W(\mu )=\varrho$ and $\mu _1<\mu _2$.

• 3. Assuming 2(b) of Lemma (A.1) hold. The unique positive equilibrium solution $(u_{\mu _0},\mu _0)$ is unstable.

• 4. Assuming 2(c) of Lemma A.1 hold. $(u_{\mu ^-},{\mu ^-})$ must be unstable, and $(u_\mu ,\mu )$ is stable for $\mu >0$ if $\varrho >W(\mu _{**})$, or $0<\varrho <W(\mu _{**})$ but $\mu \in \Lambda _1$, and it is unstable if $0<\varrho <W(\mu _{**})$ but $\mu \in \Lambda _2$, where

  $$\begin{aligned} \Lambda _1:= & {} {\left\{ \begin{array}{ll} (\mu _0,\mu _1)\cup (\mu _2,\infty ),\,\,\text {if}\,\,\mu _1>\mu _0;\\ (\mu _2,\infty ),\,\,\text {if}\,\,\mu _2>\mu _0>\mu _1;\\ (\mu _0,\infty ),\,\,\text {if}\,\,\mu _0>\mu _2; \end{array}\right. }\nonumber \\ \Lambda _2:= & {} {\left\{ \begin{array}{ll} (\mu _1,\mu _2),\,\,\text {if}\,\,\mu _1>\mu _0,\\ (\mu _0,\mu _2),\,\,\text {if}\,\,\mu _2>\mu _0>\mu _1.\\ \end{array}\right. } \end{aligned}$$

  (A.5)

  If $0<\varrho <W(\mu _{**})$ holds: when $\mu _0<\mu _1$, system (A.1) has two Hopf bifurcation points at $\mu =\mu _1 \,and\, \mu _2$; when $\mu _1<\mu _0<\mu _2$, system (A.1) has a Hopf bifurcation point at $\mu =\mu _2$; when $\mu _0>\mu _2$, system (A.1) does not have Hopf bifurcation point.

• 5. Assuming 2(d) of Lemma (A.1) hold. Then, $(u_\mu ,\mu )$ is stable for $\mu >0$ if $\varrho >W(\mu _{**})$, or $0<\varrho <W(\mu _{**})$ but $\mu \in \Lambda _3$, and it is unstable if $0<\varrho <W(\mu _{**})$ but $\mu \in \Lambda _4$, where

  $$\begin{aligned} \Lambda _3:= & {} {\left\{ \begin{array}{ll} (\mu _*,\mu _1)\cup (\mu _2,\infty ),\,\,\text {if}\,\,\mu _1>\mu _*;\\ (\mu _2,\infty ),\,\,\text {if}\,\,\mu _2>\mu _*>\mu _1;\\ (\mu _*,\infty ),\,\,\text {if}\,\,\mu _*>\mu _2; \end{array}\right. }\nonumber \\ \Lambda _4:= & {} {\left\{ \begin{array}{ll} (\mu _1,\mu _2),\,\,\text {if}\,\,\mu _1>\mu _*;\\ (\mu _*,\mu _2),\,\,\text {if}\,\,\mu _2>\mu _*>\mu _1. \\ \end{array}\right. } \end{aligned}$$

  (A.6)

  If $0<\varrho <W(\mu _{**})$ hold: when $\mu _*<\mu _1$, system (A.1) has two Hopf bifurcation points at $\mu =\mu _1 \,and\, \mu _2$; when $\mu _1<\mu _*<\mu _2$, system (A.1) has a Hopf bifurcation point at $\mu =\mu _2$; when $\mu _*>\mu _2$, system (A.1) does not have Hopf bifurcation point.

• 6. Assuming the conditions for system (A.1) that undergoes Hopf bifurcations hold. Then, the periodic solution bifurcating from $(u_\mu , \mu )$ is supercritical if $\mathcal {A}(\mu )<0$, but subcritical if $\mathcal {A}(\mu )>0$, where $\mathcal {A}(\mu )$ is defined in Eq. (3.23).

Appendix B

In this “Appendix”, the simple prove process of Proposition 2.3 will be shown.

The proof of Proposition 2.3 We know that the positive constant equilibrium solution could be expressed as $(u_{\mu }, \mu )=(1+\gamma \mu , \mu )$(see Lemma A.1). At $(1+\gamma \mu , \mu )$, the Jacobian matrix for the linearization of system (A.1) is

$$\begin{aligned} J(\mu ):=\begin{pmatrix} -\varrho &{} \varrho \gamma \\ -\displaystyle \frac{\mu }{\kappa +\mu } &{} \displaystyle \frac{\mu (1+\gamma \mu )(1-\kappa )}{(1+\mu )(\kappa +\mu )^2} \end{pmatrix}. \end{aligned}$$

(B.1)

Just like the proof of Proposition 2.1, we know that, at $(u_{\mu }, v_{\mu })=(1+\gamma \mu , \mu )$, the eigenvalues of linearized operator $L(\mu )$ for system (1.4) depend on those of the operator $L_n(\mu )$, where

$$\begin{aligned} L_n(\mu ):=\begin{pmatrix} {-}\displaystyle \frac{n^2}{\ell ^2}d_1{-}\varrho &{} \displaystyle \frac{n^2}{\ell ^2}\alpha _1(1{+}\gamma \mu ){+}\varrho \gamma \\ {-}\displaystyle \frac{n^2}{\ell ^2}\alpha _2\mu {-}\displaystyle \frac{\mu }{\kappa {+}\mu } &{} {-}\displaystyle \frac{n^2}{\ell ^2}d_2{+}\displaystyle \frac{\mu (1{+}\gamma \mu )(1{-}\kappa )}{(1{+}\mu )(\kappa {+}\mu )^2} \end{pmatrix}.\nonumber \\ \end{aligned}$$

(B.2)

Let $\sigma ^2-\sigma T_n(\mu )+D_n(\mu )=0, n\in \mathbb {N}_0,$ are the characteristic equation of $L_n(\mu )$, where

$$\begin{aligned} T_n(\mu ):= & {} -\displaystyle \frac{n^2}{\ell ^2}(d_1+d_2)-\varrho +W(\mu ),\nonumber \\ D_n(\mu ):= & {} \big (d_2\displaystyle \frac{n^2}{\ell ^2}-W(\mu )\big )d_1\displaystyle \frac{n^2}{\ell ^2}+S(\mu ),\nonumber \\ \end{aligned}$$

(B.3)

where $W(\mu )$ is defined in (A.4), and

$$\begin{aligned} S(\mu ):= & {} \alpha _1\alpha _2(1+\gamma \mu )\mu \displaystyle \frac{n^4}{\ell ^4}\nonumber \\{} & {} +\big (\displaystyle \frac{\alpha _1(1+\gamma \mu )\mu }{\kappa +\mu }+\alpha _1\mu \varrho \gamma \nonumber \\{} & {} +d_2\varrho \big )\displaystyle \frac{n^2}{\ell ^2}-\varrho W(\mu )+\displaystyle \frac{\varrho \gamma \mu }{\kappa +\mu }.\nonumber \\ \end{aligned}$$

(B.4)

Since $(u_{\mu }, \mu )=(1+\gamma \mu , \mu )$ is stable for system (A.1), then, for the Jacobian $J(\mu )$, $T(\mu )<0$ and $D(\mu )>0$, where

$$\begin{aligned} \begin{aligned} T(\mu ):&=\displaystyle \frac{\mu (1+\gamma \mu )(1-\kappa )}{(1+\mu )(\kappa +\mu )^2}-\varrho =W(\mu )-\varrho ,\\ D(\mu ):&=-\varrho W(\mu )+\displaystyle \frac{\varrho \gamma \mu }{\kappa +\mu }\\&=\displaystyle \frac{\varrho \mu (\gamma \mu ^2+2\kappa \gamma \mu +\kappa \gamma +\kappa -1)}{(1+\mu )(\kappa +\mu )^2}. \end{aligned}\nonumber \\ \end{aligned}$$

(B.5)

Obviously, $T_n(\mu )<0$, and $S(\mu )>0$. Then, we analysis the sign of $D_n(\mu )$ ($n=1,2,...$).

If $d_2\ge \ell ^2W(\mu )$ holds, then we have $D_n(\mu )\ge \big (\displaystyle \frac{d_2}{\ell ^2}-W(\mu )\big )d_1\displaystyle \frac{n^2}{\ell ^2}+S(\mu )>0$ for any $n\in \mathbb {N}_0$. This means that $(u_{\mu }, \mu )$ remains stable for system (1.4). Obviously, Turing instability of $(u_{\mu }, \mu )$ is impossible to occur.

If $d_2<\ell ^2W(\mu )$ holds, then by the definition of $n_{d_2}$, for any integer $n>n_{d_2}$, we can get $D_n(\mu )>0$. Then, for any $d_1<\hat{d_1}$, $D_n(\mu )>0$, where $\hat{d_1}$ is defined in (2.4). Thus, $(u_{\mu }, \mu )$ is also stable for system (1.4). However, when $d_1>\hat{d_1}$, there exists at least an $n\in [1, n_{d_2}]$, such that $D_n(\mu )<0$. Thus, $(u_{\mu }, \mu )$ is unstable, and undergoes Turing instability. This completes the proof.