Elimination approach toward normalization constraint for Euler parameters

Abstract

It is known that three-parameter representations of spatial rotation suffer from kinematic singularities. Euler parameters (unit quaternions) are a four-parameter solution for this issue. However, a normality constraint needs to be enforced while implementing this set of four parameters, otherwise the mass matrix in the equations of motion will be singular. This paper discusses an approach to enforce this normality constraint using a redefinition of the state space in terms of quasi-velocities, along with the standard elimination of dependent variables at the velocity and acceleration level. The approach is implemented on a 3D double pendulum example.

Appendices

Appendix 1: Double-pendulum equations of motion

The equations of motion for the double pendulum example are computed using Kane’s method. Because the final EOMs are too large, this section does not derive complete EOMs. Rather, it provides important equations in a format discussed in [4], which when evaluated result in the EOMs for the double pendulum.

Rigid Bodies: There are two rigid bodies, the two cylindrical rods of double pendulum.

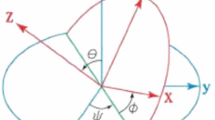
Inertial Reference Frame and Point: The inertial reference point is N, and N $= \left( {\widehat{\mathbf {N}}_{1}},{\widehat{\mathbf {N}}_{2}},{\widehat{\mathbf {N}}_{3}} \right)$ is the inertial reference frame shown in Fig. 2.

Other Points and Frames: Points A and B are body-attached points, and they are also the center of gravity of bodies A and B, respectively. Point C represents the spherical joint between two rods. A $= \left( {\widehat{\mathbf {A}}_{1}},{\widehat{\mathbf {A}}_{2}},{\widehat{\mathbf {A}}_{3}} \right)$ and B $= \left( {\widehat{\mathbf {B}}_{1}},{\widehat{\mathbf {B}}_{2}},{\widehat{\mathbf {B}}_{3}} \right)$ are body-attached frames shown in Fig. 2 (Tables 2, 3 and 4).

Location Descriptions: The location descriptions provide a formal way of specifying the position of every point that comprises the rigid bodies in the system.

$$\begin{aligned} L_A = \left\{ {\mathbf {P}_{NA}}, {}^{}_{A}{\,}^{N}_{}R \right\} + geom. L_B = \left\{ {\mathbf {P}_{CB}}, {}^{}_{B}{\,}^{A}_{}R \right\} + geom. \end{aligned}$$

(23)

$$\begin{aligned} {\mathbf {P}_{NA}} = {\mathbf {P}_{AC}} = l_A {\widehat{\mathbf {A}}_{1}} {\mathbf {P}_{NC}} = 2l_A {\widehat{\mathbf {A}}_{1}} {\mathbf {P}_{CB}} = l_B {\widehat{\mathbf {B}}_{1}} \end{aligned}$$

(24)

$$\begin{aligned} {}^{}_{A}{\,}^{N}_{}R = \frac{1}{e_{A_0}^2 + e_{A_1}^2 + e_{A_2}^2 + e_{A_3}^2} \begin{bmatrix} e_{A_0}^2 + e_{A_1}^2 - e_{A_2}^2 - e_{A_3}^2 &{} 2e_{A_1}e_{A_2} - 2e_{A_0}e_{A_3} &{} 2e_{A_0}e_{A_2} + 2e_{A_1}e_{A_3} \\ 2e_{A_1}e_{A_2} + 2e_{A_0}e_{A_3} &{} e_{A_0}^2 - e_{A_1}^2 + e_{A_2}^2 - e_{A_3}^2 &{} 2e_{A_2}e_{A_3} - 2e_{A_0}e_{A_1} \\ 2e_{A_1}e_{A_3} - 2e_{A_0}e_{A_2} &{} 2e_{A_2}e_{A_3} + 2e_{A_0}e_{A_1} &{} e_{A_0}^2 - e_{A_1}^2 - e_{A_2}^2 + e_{A_3}^2 \end{bmatrix} \end{aligned}$$

(25)

$$\begin{aligned} {}^{}_{B}{\,}^{A}_{}R = \frac{1}{e_{B_0}^2 + e_{B_1}^2 + e_{B_2}^2 + e_{B_3}^2} \begin{bmatrix} e_{B_0}^2 + e_{B_1}^2 - e_{B_2}^2 - e_{B_3}^2 &{} 2e_{B_1}e_{B_2} - 2e_{B_0}e_{B_3} &{} 2e_{B_0}e_{B_2} + 2e_{B_1}e_{B_3} \\ 2e_{B_1}e_{B_2} + 2e_{B_0}e_{B_3} &{} e_{B_0}^2 - e_{B_1}^2 + e_{B_2}^2 - e_{B_3}^2 &{} 2e_{B_2}e_{B_3} - 2e_{B_0}e_{B_1} \\ 2e_{B_1}e_{B_3} - 2e_{B_0}e_{B_2} &{} 2e_{B_2}e_{B_3} + 2e_{B_0}e_{B_1} &{} e_{B_0}^2 - e_{B_1}^2 - e_{B_2}^2 + e_{B_3}^2 \end{bmatrix} \end{aligned}$$

(26)

Coordinates: Eight coordinates appear in the location descriptions, where $e_{A_{0-3}}$ and $e_{B_{0-3}}$ are Euler parameters representing body A’s and body B’s orientation, respectively. The vector of generalized coordinates, $\mathbf{q}$, is defined as:

$$\begin{aligned} \mathbf {q} = [ \mathbf {e}_A^T \ \ \mathbf {e}_B^T ]^T = [ e_{A_0} \ e_{A_1} \ e_{A_2} \ e_{A_3} \ e_{B_0} \ e_{B_1} \ e_{B_2} \ e_{B_3} ]^T \end{aligned}$$

Constraints: The normalization constraints associated with both the Euler parameter sets are given as

$$\begin{aligned} q_1^2 + q_2^2 + q_3^2 + q_4^2&= 1&,&q_5^2 + q_6^2 + q_7^2 + q_8^2&= 1 \end{aligned}$$

Table 2 Euler parameters for approach in Ref.  [8]

Table 3 Euler parameters for the proposed approach

Table 4 Euler parameters when the rotation matrices are integrated directly

Degrees of Freedom (DOFs):

8 coordinates - 2 constraints = 6 DOFs

Velocity: The angular velocity of body A and body B is

$$\begin{aligned} {^\mathrm{N} \varvec{\omega }^\mathrm{A}}&= 2 \left( u_1 {\widehat{\mathbf {A}}_{1}} + u_2 {\widehat{\mathbf {A}}_{2}} + u_3 {\widehat{\mathbf {A}}_{3}} \right) \nonumber \\&= 2( q_1 \dot{q}_2 - q_2 \dot{q}_1 - q_3 \dot{q}_4 + q_4 \dot{q}_3 ) {\widehat{\mathbf {A}}_{1}} \nonumber \\&\quad + 2( q_1 \dot{q}_3 + q_2 \dot{q}_4 - q_3 \dot{q}_1 - q_4 \dot{q}_2 ) {\widehat{\mathbf {A}}_{2}} \nonumber \\&\quad + 2( q_1 \dot{q}_4 - q_2 \dot{q}_3 + q_3 \dot{q}_2 - q_4 \dot{q}_1 ) {\widehat{\mathbf {A}}_{3}} \end{aligned}$$

(27)

$$\begin{aligned} {^\mathrm{A} \varvec{\omega }^\mathrm{B}}&= 2 \left( u_5 {\widehat{\mathbf {B}}_{1}} + u_6 {\widehat{\mathbf {B}}_{2}} + u_7 {\widehat{\mathbf {B}}_{3}} \right) \nonumber \\&= 2( q_5 \dot{q}_6 - q_6 \dot{q}_5 - q_7 \dot{q}_8 + q_8 \dot{q}_7 ) {\widehat{\mathbf {B}}_{1}} \nonumber \\&\quad + 2( q_5 \dot{q}_7 + q_6 \dot{q}_8 - q_7 \dot{q}_5 - q_8 \dot{q}_6 ) {\widehat{\mathbf {B}}_{2}} \nonumber \\&\quad + 2( q_5 \dot{q}_8 - q_6 \dot{q}_7 + q_7 \dot{q}_6 - q_8 \dot{q}_5 ) {\widehat{\mathbf {B}}_{3}} \end{aligned}$$

(28)

$$\begin{aligned} {^\mathrm{N} \varvec{\omega }^\mathrm{B}}&= {}^{}_{B}{\,}^{A}_{}R^T {^\mathrm{N} \varvec{\omega }^\mathrm{A}} + {^\mathrm{A} \varvec{\omega }^\mathrm{B}} \end{aligned}$$

(29)

The translational velocity of the mass centers A and B and point C is given as

$$\begin{aligned} {\mathbf {V}_{A}}&= \frac{d{\mathbf {P}_{NA}}}{dt} = {^\mathrm{N} \varvec{\omega }^\mathrm{A}} \times {\mathbf {P}_{NA}} \end{aligned}$$

(30)

$$\begin{aligned} {\mathbf {V}_{C}}&= \frac{d{\mathbf {P}_{NC}}}{dt} = {^\mathrm{N} \varvec{\omega }^\mathrm{A}} \times {\mathbf {P}_{NC}} \end{aligned}$$

(31)

$$\begin{aligned} {\mathbf {V}_{B}}&= \frac{d{\mathbf {P}_{NB}}}{dt} = {}^{}_{B}{\,}^{A}_{}R^T {\mathbf {V}_{C}} + {^\mathrm{N} \varvec{\omega }^\mathrm{B}} \times {\mathbf {P}_{CB}} \end{aligned}$$

(32)

The quasi-velocities required to compute partial derivatives in Kane’s equations of motion are $\mathbf {u}_A$ and $\mathbf {u}_B$ which are already defined in Sect. 3.

Acceleration: The angular acceleration of body A and body B is

$$\begin{aligned} {^\mathrm{N}\dot{\varvec{\omega }}^\mathrm{A}}&= 2( q_1 \ddot{q}_2 - q_2 \ddot{q}_1 - q_3 \ddot{q}_4 + q_4 \ddot{q}_3 ) {\widehat{\mathbf {A}}_{1}} \nonumber \\&\quad + 2( q_1 \ddot{q}_3 + q_2 \ddot{q}_4 - q_3 \ddot{q}_1 - q_4 \ddot{q}_2 ) {\widehat{\mathbf {A}}_{2}} \nonumber \\&\quad + 2( q_1 \ddot{q}_4 - q_2 \ddot{q}_3 + q_3 \ddot{q}_2 - q_4 \ddot{q}_1 ) {\widehat{\mathbf {A}}_{3}} \end{aligned}$$

(33)

$$\begin{aligned} {^\mathrm{A}\dot{\varvec{\omega }}^\mathrm{B}}&= 2( q_5 \ddot{q}_6 - q_6 \ddot{q}_5 - q_7 \ddot{q}_8 + q_8 \ddot{q}_7 ) {\widehat{\mathbf {B}}_{1}} \nonumber \\&\quad + 2( q_5 \ddot{q}_7 + q_6 \ddot{q}_8 - q_7 \ddot{q}_5 - q_8 \ddot{q}_6 ) {\widehat{\mathbf {B}}_{2}} \nonumber \\&\quad + 2( q_5 \ddot{q}_8 - q_6 \ddot{q}_7 + q_7 \ddot{q}_6 - q_8 \ddot{q}_5 ) {\widehat{\mathbf {B}}_{3}} \end{aligned}$$

(34)

$$\begin{aligned} {^\mathrm{N}\dot{\varvec{\omega }}^\mathrm{B}}&= {}^{}_{B}{\,}^{A}_{}R^T {^\mathrm{N}\dot{\varvec{\omega }}^\mathrm{A}} + {^\mathrm{A}\dot{\varvec{\omega }}^\mathrm{B}} + {^\mathrm{N} \varvec{\omega }^\mathrm{B}} \times {^\mathrm{A} \varvec{\omega }^\mathrm{B}} \end{aligned}$$

(35)

The translational acceleration of mass centers A and B and point C is given as

$$\begin{aligned} {\dot{\mathbf {V}}_{A}}&= \frac{d{\mathbf {V}_{A}}}{dt} = {^\mathrm{N}\dot{\varvec{\omega }}^\mathrm{A}} \times {\mathbf {P}_{NA}} + {^\mathrm{N} \varvec{\omega }^\mathrm{A}} \times \left( {^\mathrm{N} \varvec{\omega }^\mathrm{A}} \times {\mathbf {P}_{NA}} \right) \end{aligned}$$

(36)

$$\begin{aligned} {\dot{\mathbf {V}}_{C}}&= \frac{d{\mathbf {V}_{C}}}{dt} = {^\mathrm{N}\dot{\varvec{\omega }}^\mathrm{A}} \times {\mathbf {P}_{NC}} + {^\mathrm{N} \varvec{\omega }^\mathrm{A}} \times \left( {^\mathrm{N} \varvec{\omega }^\mathrm{A}} \times {\mathbf {P}_{NC}} \right) \end{aligned}$$

(37)

$$\begin{aligned} {\dot{\mathbf {V}}_{B}}&= \frac{d{\mathbf {V}_{B}}}{dt} = {}^{}_{B}{\,}^{A}_{}R^T {\dot{\mathbf {V}}_{C}} + {^\mathrm{N}\dot{\varvec{\omega }}^\mathrm{B}} \times {\mathbf {P}_{CB}} \nonumber \\&+ {^\mathrm{N} \varvec{\omega }^\mathrm{B}} \times \left( {^\mathrm{N} \varvec{\omega }^\mathrm{B}} \times {\mathbf {P}_{CB}} \right) \end{aligned}$$

(38)

Mass Properties: Mass of body A and body B is assumed to be $m_A$ and $m_B$, respectively, while the spherical joint is assumed to be massless. The inertia matrix of body A and body B can be given as

$$\begin{aligned} {I_\mathrm{AA}}&= \begin{bmatrix} \frac{1}{2}m_A r^2 &{} 0 &{} 0 \\ 0 &{} \frac{1}{12}m_A(3r^2+L^2) &{} 0 \\ 0 &{} 0 &{} \frac{1}{12}m_A(3r^2+L^2) \end{bmatrix} \end{aligned}$$

(39)

$$\begin{aligned} {I_\mathrm{BB}}&= \begin{bmatrix} \frac{1}{2}m_B r^2 &{} 0 &{} 0 \\ 0 &{} \frac{1}{12}m_B(3r^2+L^2) &{} 0 \\ 0 &{} 0 &{} \frac{1}{12}m_B(3r^2+L^2) \end{bmatrix} \end{aligned}$$

(40)

Forces and Moments: No external moments are acting on the bodies. Only the gravitational force acts on both the bodies. Note that both resultant force and moment vectors given below are expressed in inertial frame. Moments were taken about the mass center of each body.

$$\begin{aligned} {\mathbf {F}_{A}}&= -m_A g {\widehat{\mathbf {N}}_{3}},&{\mathbf {F}_{B}}&= -m_B g {\widehat{\mathbf {N}}_{3}} \end{aligned}$$

(41)

$$\begin{aligned} {\mathbf {M}_{AA}}&= \mathbf {0},&{\mathbf {M}_{BB}}&= \mathbf {0} \end{aligned}$$

(42)

Equations of Motion: The equations of motion can be computed using the Kane’s equations given below. All the necessary terms are already defined in this appendix.

$$\begin{aligned} \begin{aligned} 0&= F_i - F_i^*\\ F_i&= \sum _{K=1}^{bodies} \left[ {\mathbf {F}_{K}} \cdot \frac{\partial {\mathbf {V}_{K}}}{\partial u_i} + {\mathbf {M}_{KK}} \cdot \frac{\partial {^\mathrm{N} \varvec{\omega }^\mathrm{K}}}{\partial u_i} \right] \\ F_i^*&= \sum _{K=1}^{bodies} \left[ m_K {\dot{\mathbf {V}}_{K}} \cdot \frac{\partial {\mathbf {V}_{K}}}{\partial u_i} + {\dot{\mathbf {H}}_{KK}} \cdot \frac{\partial {^\mathrm{N} \varvec{\omega }^\mathrm{K}}}{\partial u_i} \right] \end{aligned} \end{aligned}$$

(43)

where $i= \{ 1,2,3,5,6,7 \}$ and,

$$\begin{aligned} {\dot{\mathbf {H}}_{KK}} = {I_\mathrm{KK}} {^\mathrm{N}\dot{\varvec{\omega }}^\mathrm{K}} + {^\mathrm{N} \varvec{\omega }^\mathrm{K}} \times \left( {I_\mathrm{KK}} {^\mathrm{N} \varvec{\omega }^\mathrm{K}} \right) \end{aligned}$$

(44)

Appendix 2: Online constraint embedding method

The virtual work done by the system can be calculated from (43) as follows:

$$\begin{aligned} 0 = \delta W= & {} \sum _{i = 1}^n \sum _{K = 1}^{bodies} \\&\left[ {\mathbf {F}_{K}} \cdot \frac{\partial {\mathbf {V}_{K}}}{\partial u_i} - m_K {\dot{\mathbf {V}}_{K}} \cdot \frac{\partial {\mathbf {V}_{K}}}{\partial u_i} \right. \\&\left. + {\mathbf {M}_{KK}} \cdot \frac{\partial {^\mathrm{N} \varvec{\omega }^\mathrm{K}}}{\partial u_i} - {\dot{\mathbf {H}}_{KK}} \cdot \frac{\partial {^\mathrm{N} \varvec{\omega }^\mathrm{K}}}{\partial u_i} \right] \delta q_i \end{aligned}$$

The equation above can also be expressed as

$$\begin{aligned} 0 = \sum _{i = 1}^n (F_i - F_i^*) \delta q_i \end{aligned}$$

(45)

Here, the $F_i$ and $F_i^*$ are generated for both the dependent and independent generalized coordinates. Note that any holonomic constraint can be expressed in a form that is linear in the virtual displacements. Let’s say that we are solving for a system that has five generalized coordinates and two constraints. Thus, the relationship between dependent and independent virtual displacements can be given as

$$\begin{aligned} \begin{bmatrix} \delta q_{D_4} \\ \delta q_{D_5} \end{bmatrix} = \begin{bmatrix} C_{41} &{} C_{42} &{} C_{43} \\ C_{51} &{} C_{52} &{} C_{53} \end{bmatrix} \begin{bmatrix} \delta q_{I_1} \\ \delta q_{I_2} \\ \delta q_{I_3} \end{bmatrix} \end{aligned}$$

(46)

where the subscripts ‘$D$’ and ‘$I$’ denote a dependent or independent virtual displacement, respectively. Substituting the equation above in Eq. (45) yields

$$\begin{aligned} 0&= (F_1 - F_1^*)\delta q_1 \ + \ (F_2 - F_2^*)\delta q_2 \nonumber \\&\quad \, + \ (F_3 - F_3^*)\delta q_3 \quad \ + \ (F_4 - F_4^*)\delta q_4 \ \nonumber \\&\quad \,+ \ (F_5 - F_5^*)\delta q_5 \nonumber \\&= (F_1 - F_1^*)\delta q_1 \ + \ (F_2 - F_2^*)\delta q_2 \ \nonumber \\&\quad \ + \ (F_3 - F_3^*)\delta q_3 + \ (F_4 - F_4^*)(C_{41} \delta q_1 \nonumber \\&\quad \ + \ C_{42} \delta q_2 \ + \ C_{43} \delta q_3) \nonumber \\&\quad \ + \ (F_5 - F_5^*)(C_{51} \delta q_1 \ + \ C_{52} \delta q_2 \nonumber \\&\quad \ + \ C_{53} \delta q_3) \nonumber \\&= (F_1 - F_1^*\ + \ C_{41} (F_4 - F_4^*) \nonumber \\&\quad \ + \ C_{51} (F_5 - F_5^*))\delta q_1 \nonumber \\&\quad \ + \ (F_2 - F_2^*\ + \ C_{42} (F_4 - F_4^*) \nonumber \\&\quad \ + \ C_{52} (F_5 - F_5^*))\delta q_2 \nonumber \\&\quad \ + \ (F_3 - F_3^*\ + \ C_{43} (F_4 - F_4^*) \nonumber \\&\quad \ + \ C_{53} (F_5 - F_5^*))\delta q_3 \end{aligned}$$

(47)

Because the virtual displacements in the equation above are independent, the only way for the virtual work to be equal to zero for any values they may take is when their coefficients are zero for all time. Thus, it can be shown that

$$\begin{aligned} \bar{F}_i - \bar{F}_i^*&= 0 \quad \bar{F}_i = F_i + \sum _{j = p+1}^{p+q} C_{ji} F_j, \nonumber \\ \bar{F}_i^*&= F_i^*+ \sum _{j = p+1}^{p+q} C_{ji} F_j^*\end{aligned}$$

(48)

where $p$ and $q$ are the number of independent and dependent generalized coordinates, respectively. And, $i = \{1,2,3,...,p\}$.