Double mode model of size-dependent chaotic vibrations of nanoplates based on the nonlocal elasticity theory

Abstract

In this paper vibrations of the isotropic micro/nanoplates subjected to transverse and in-plane excitation are investigated. The governing equations of the problem are based on the von Kármán plate theory and Kirchhoff–Love hypothesis. The small-size effect is taken into account due to the nonlocal elasticity theory. The formulation of the problem is mixed and employs the Airy stress function. The two-mode approximation of the deflection and application of the Bubnov–Galerkin method reduces the governing system of equations to the system of ordinary differential equations. Varying the load parameters and the nonlocal parameter, the bifurcation analysis is performed. The bifurcations diagrams, the maximum Lyapunov exponents, phase portraits as well as Poincare maps are constructed based on the numerical simulations. It is shown that for some excitation conditions the chaotic motion may occur in the system. Also, the small-scale effects on the character of vibrating regimes are illustrated and discussed.

1 Introduction

In recent years, a large number of studies of micro- and nanoobjects, such as micro/nanobeams, micro/nanoplates, and micro/nanoshells, have appeared. This is primarily due to their widespread use in various modern applications as nano-electromechanical systems (NEMS), micro-electromechanical systems (MEMS), nano-optomechanical structures, sensors, resonators, DNA detectors, energy storage systems and so on [7, 8, 16, 19, 23, 50]. In this paper we consider a graphene sheet subjected to in-plane and transverse excitation. It is known that this material has excellent mechanical, thermal, electrical and magnetic properties, which makes it useful in mechanical, chemical and biomedical applications. It should be noted that experimental and numerical studies helped to find out that the classical theory for such problems is insufficient, and gives incorrect outcomes [9, 22]. Moreover, in the case of micro/nanostructures it is needed to pay attention to small-scale effects appearing when the sizes of plates are in micro/nanoscale. This fact led to the development of higher-order continuum theories: the theory of micropolar elasticity [10], the couple stress theory [18, 27, 38], the nonlocal elasticity theory, the strain gradient theory [22] and the modified couple stress theory [49]. The presented investigation is based on the nonlocal elasticity theory proposed by Eringen [12] and on the fact that the stress at a given point is a function of strains at all other points in the body. The governing equations, in that case, contain the nonlocal parameter, which depends on the internal characteristic length (distance between C–C bonds, lattice parameter), and constant corresponding to the material for adjusting the model to experimental results or molecular dynamics results [11, 12].

A number of studies devoted to the behaviour of nanotubes based on the nonlocal theory were carried out. It needs to be mentioned the work of Nematollahi et al. [30], where fluttering and divergence instability of functionally graded viscoelastic nanotubes conveying fluid are discussed. The vibrations of carbon nanotubes are considered in works of Wang et al. [44,45,46] including the cases of viscous fluid loading and the parametric excitation. Concerning the investigation of nanoplate vibrations, based on the nonlocal elasticity theory, most of the researches studied linear vibrations and analysed the influence of certain parameters on the linear frequency values. Lu et al. [24] analysed the vibrations and bending of simply supported plates and compared the results of the nonlocal theory with corresponded local solutions. The classical plate theory as well as the first-order shear deformation theory are applied by Pradhan and Phadikar [31] for linear analysis of nanoplates vibration problems. Vibrations and buckling of nanoplates are investigated with the finite strip method by Analooei et al. [2]. Aghababaei and Reddy [1] used the nonlocal third-order shear deformation plate theory in the analysis of bending and vibration of plates. Influence of elastic medium on the vibrating process is studied in [6, 36, 37].

It is worth to mention a number of works, where geometrically nonlinear stability and vibrations of plates are investigated. These works include the paper of Jomehzadeh et al. [17], where the nonlinear vibrations of isotropic nanoplates are studied. The nonlinear stability of orthotropic single-layered graphene sheet is studied by Asemi et al. [3]. Setoodeh et al. [34] investigated the nonlinear vibrations of the orthotropic Mindlin plate by the differential quadrature method. Gholami et al. [14] studied the nonlinear vibrations of multiferroic composite rectangular nanoplates resting on an elastic foundation by the generalized differential quadrature method. The nonlinear vibrations of viscoelastic double-layered plates with several types of boundary conditions were studied by Wang et al. [41, 43]. The influence of magnetic and electric excitation on the nonlinear vibrations was studied in [13, 25].

In the above-mentioned works devoted to the micro/nanoplates dynamics, the regular vibrations are analysed. However, as shown in works [5, 15, 21, 35] vibrating process in dissipative systems under certain loading conditions can change its character and transition from periodic regimes to chaos is possible. The detection of such chaotic zones is a very important study, by reason of the fact, that in the case of chaotic vibrations, the behaviour of a dynamic system becomes poorly predicted, which may have undesirable consequences. The complicated nonlinear dynamics in micro/nanosystems has not been studied sufficiently until now. There is a small number of such works among which the paper of Krysko et al. [20], where chaotic vibrations based on the modified couple stress theory are considered and the effect of the material length-scale parameter on nanoshell vibrations is studied. Wang et al. [42] performed the nonlocal chaotic and homoclinic investigation of double-layered viscoelastic nanoplates.

In the present work, the nonlinear vibrations of micro/nanoplates are studied. The formulation of the problem is based on the nonlocal elasticity theory, von Kármán plate theory, and employs the Airy stress function. The proposed algorithm implies double mode approximation of deflection and presentation of stress function as a solution of nonlocal compatibility equation. The application of Bubnov–Galerkin method reduces the governing system to the system of the ordinary differential equations, where coefficients contain the nonlocal parameter. The numerical simulation of the problem is performed for isotropic simply supported graphene sheet. The approaches of nonlinear dynamics for detection of chaotic regimes are applied [4, 28, 29]. Therefore, the bifurcation diagrams, phase plots, Poincare maps and the largest Lyapunov exponents are presented and the obtained results are discussed.

The manuscript consists of five sections. Following the introduction, Sect. 2 describes the mathematical formulation of the problem. The method of investigation is discussed in Sect. 3. The validation of the problem and the results of the numerical investigation are included in Sect. 4. . The last section is aimed at the conclusion of the study.

Fig. 1

Rectangular plate subjected to in-plane loads and transverse periodic force

Fig. 2

Bifurcation diagrams for $y_1$ (a), $y_2$ (b) with bifurcation parameter $\xi _p$ and fixed parameters $\mu =0, \sigma =2$

2 Mathematical formulation

For geometrically nonlinear vibrations analysis of the isotropic micro/nanoplates the von Kármán theory, the Kirchhoff’s hypotheses and the nonlocal elasticity theory are employed. Based on the nonlocal theory of elasticity the constitutive relation for the nonlocal stress tensor at a point x is presented in integral form as follows:

$$\begin{aligned} \sigma = \int _V K \left( |{X}^{\prime } -X|,\tau \right) \sigma ^{\prime }(X^{\prime })\mathrm{d}X^{\prime }, \end{aligned}$$

(1)

where $\sigma$, $\sigma '$ are nonlocal and local stress tensors, $K \left( || {X}^{\prime } -X|| ,\tau \right)$ is the nonlocal modulus, $\tau =e_0\alpha /l$, $\alpha$ stands for the internal characteristic length, $e_0$ is a constant appropriate to material and l is external characteristics length. The differential form [12] of the nonlocal constitutive relation, which is more often used, has the following form:

$$\begin{aligned} \left( 1-\mu \nabla ^2 \right) \sigma =\sigma ', \end{aligned}$$

(2)

where $\mu =(e_0 \alpha )^2$ is nonlocal parameter, and $\nabla ^2$ is the Laplacian operator. For isotropic micro/nanoplate the relation (2) is transformed to the form:

$$\begin{aligned} \begin{aligned} \begin{bmatrix} \sigma _{xx}\\ \sigma _{yy}\\ \sigma _{xy} \end{bmatrix}-\mu \nabla ^2 \begin{bmatrix} \sigma _{xx}\\ \sigma _{yy}\\ \sigma _{xy} \end{bmatrix}= \begin{bmatrix} \frac{E}{1-\nu ^2 }&{} \frac{\nu E}{1-\nu ^2}&{} 0\\ \frac{\nu E}{1-\nu ^2}&{} \frac{E}{1-\nu ^2}&{} 0\\ 0&{} 0&{}\frac{E}{2(1+\nu )}\\ \end{bmatrix} \begin{bmatrix} \varepsilon _{xx}\\ \varepsilon _{yy}\\ \varepsilon _{xy} \end{bmatrix}. \end{aligned}\nonumber \\ \end{aligned}$$

(3)

In (3) E is Young’s modulus and $\nu$ is Poisson’s ratio. As follows from the von Kármán nonlinear theory, the components of strain tensor for Kirchhoff’s plate are presented as follows [40]:

$$\begin{aligned} \begin{aligned}&\varepsilon _{ xx }=\varepsilon _{ xx }^0+z k_{xx}, \quad \varepsilon _{ yy }=\varepsilon _{ yy }^0+z k_{yy}, \\&\quad \varepsilon _{ xy }=\varepsilon _{ xy }^0+z k_{xy}, \\&\quad \varepsilon _{ xx }^0=\frac{{\partial }u}{{\partial }x}+\frac{1}{2}\left( \frac{{\partial }w}{{\partial }x}\right) ^2,\quad k_{xx}=-\frac{{\partial }^2w}{{\partial }x^2},\\&\quad \varepsilon _{ yy }^0=\frac{{\partial }v}{{\partial }y}+\frac{1}{2}\left( \frac{{\partial }w}{{\partial }y}\right) ^2,\quad k_{yy}=-\frac{{\partial }^2w}{{\partial }y^2},\\&\quad \varepsilon _{ xy }^0=\frac{{\partial }u}{{\partial }y}+\frac{{\partial }v}{{\partial }x}+\frac{{\partial }w}{{\partial }x}\frac{{\partial }w}{{\partial }y},\quad k_{xy}=-2\frac{{\partial }^2w}{{\partial }x{\partial }y}. \end{aligned} \end{aligned}$$

(4)

Differentiation and transformation of the relations (4) give the compatibility equation for strains in the middle surface:

$$\begin{aligned} \frac{\partial ^2 \varepsilon _{xx}^0}{\partial y^2 } +\frac{\partial ^2 \varepsilon _{yy}^0}{\partial x^2 }-\frac{\partial ^2 \varepsilon _{xy}^0}{\partial x \partial y }=\left( \frac{{\partial }^2w}{{\partial }x{\partial }y}\right) ^2-\frac{{\partial }^2w}{{\partial }x^2}\frac{{\partial }^2w}{{\partial }y^2}.\nonumber \\ \end{aligned}$$

(5)

The system of the governing equations is employed based on the Hamilton’s principle:

$$\begin{aligned}&\frac{{\partial }N_x}{{\partial }x}+\frac{{\partial }N_{ xy }}{{\partial }y}=\rho h\frac{{\partial }^2u}{{\partial }t^2},\nonumber \\&\quad \frac{{\partial }N_{ xy }}{{\partial }x}+\frac{{\partial }N_y}{{\partial }y}=\rho h\frac{{\partial }^2v}{{\partial }t^2}, \end{aligned}$$

(6)

$$\begin{aligned}&\frac{{\partial }^2M_x}{{\partial }x^2}+2\frac{{\partial }^2M_{ xy }}{{\partial }x{\partial }y}+\frac{{\partial }^2M_y}{{\partial }y^2}=\nonumber \\&\quad -\frac{{\partial }}{{\partial }x}\left( N_x\frac{{\partial }w}{{\partial }x}+N_{ xy }\frac{{\partial }w}{{\partial }y}\right) \nonumber \\&\quad -\frac{{\partial }}{{\partial }y}\left( N_{ xy }\frac{{\partial }w}{{\partial }x}+N_y\frac{{\partial }w}{{\partial }y}\right) +\nonumber \\&\quad +\delta _0 \frac{{\partial }w}{{\partial }t}+\rho h \frac{{\partial }^2w}{{\partial }t^2}-q_t, \end{aligned}$$

(7)

where h is the thickness of the micro/nanoplate, $\rho$ stands for the density of the plate, $\delta _0$ is damping coefficient, whereas $q_t$ is the transverse force. The resultant in-plane forces and moments are derived by the following formulas:

$$\begin{aligned} \begin{aligned}&N_x=\int _\frac{-h}{2}^\frac{h}{2} \sigma _{xx}\mathrm{d}z, \quad N_y=\int _\frac{-h}{2}^\frac{h}{2} \sigma _{yy}\mathrm{d}z,\quad \\&\quad N_{xy}=\int _\frac{-h}{2}^\frac{h}{2} \sigma _{xy}\mathrm{d}z, \end{aligned} \end{aligned}$$

(8)

$$\begin{aligned} \begin{aligned}&M_x=\int _\frac{-h}{2}^\frac{h}{2} \sigma _{xx}z\mathrm{d}z, \quad M_y=\int _\frac{-h}{2}^\frac{h}{2} \sigma _{yy}z\mathrm{d}z,\quad \\&\quad M_{xy}=\int _\frac{-h}{2}^\frac{h}{2} \sigma _{xy}z\mathrm{d}z. \end{aligned} \end{aligned}$$

(9)

Taking into account relations (3) and (8), (9) one can obtain the following equations:

$$\begin{aligned} \begin{aligned}&\begin{bmatrix} N_{x}\\ N_{y}\\ N_{xy} \end{bmatrix}-\mu \nabla ^2 \begin{bmatrix} N_{x}\\ N_{y}\\ N_{xy} \end{bmatrix}\\ {}&\quad = h\begin{bmatrix} \frac{E}{1-\nu ^2 }&{} \frac{\nu E}{1-\nu ^2}&{} 0\\ \frac{\nu E}{1-\nu ^2 }&{} \frac{E}{1-\nu ^2}&{} 0\\ 0&{} 0&{}\frac{E}{2(1+\nu )}\\ \end{bmatrix} \begin{bmatrix} \varepsilon _{xx}^0\\ \varepsilon _{yy}^0\\ \varepsilon _{xy}^0 \end{bmatrix}, \end{aligned} \end{aligned}$$

(10)

$$\begin{aligned} \begin{aligned}&\begin{bmatrix} M_{x}\\ M_{y}\\ M_{xy} \end{bmatrix}-\mu \nabla ^2 \begin{bmatrix} M_{x}\\ M_{y}\\ M_{xy} \end{bmatrix}=\\ {}&\quad = \frac{h^3}{12}\begin{bmatrix} \frac{E}{1-\nu ^2}&{} \frac{\nu E}{1-\nu ^2}&{} 0\\ \frac{\nu E}{1-\nu ^2}&{} \frac{E}{1-\nu ^2}&{} 0\\ 0&{} 0&{}\frac{E}{2(1+\nu )}\\ \end{bmatrix} \begin{bmatrix} k_{xx}\\ k_{yy}\\ k_{xy} \end{bmatrix}. \end{aligned} \end{aligned}$$

(11)

The formulas (4) allow to rewrite equations (11) into the following counterpart form:

$$\begin{aligned}&M_{x} -\mu \nabla ^2 M_{x}=-D(\frac{\partial ^2 w}{\partial x^2}+\nu \frac{\partial ^2 w}{\partial y^2}),\nonumber \\&\quad M_{y} -\mu \nabla ^2 M_{y}=-D(\nu \frac{ \partial ^2 w}{\partial x^2}+\frac{\partial ^2 w}{\partial y^2}),\nonumber \\&\quad M_{xy} -\mu \nabla ^2 M_{xy}=-D(1-\nu )\frac{\partial ^2 w}{\partial x \partial y}, \end{aligned}$$

(12)

where $D=\frac{Eh^3}{12(1-\nu ^2)}$ acts as flexural nanoplate rigidity.

Following the study [21, 35, 40], let us introduce the Airy stress function F as follows:

$$\begin{aligned} N_x=\frac{\partial ^2F}{\partial y^2}, \quad N_y=\frac{\partial ^2F}{\partial x^2}, \quad N_{ xy }=-\frac{\partial ^2F}{\partial x\partial y}. \end{aligned}$$

(13)

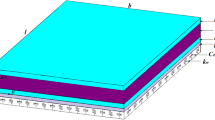
Assuming that the in-plane inertia terms are neglected and considering formulas (12), the governing equation (7) for plate under in-plane uniform forces $N_1, N_2$ as well as transverse periodic force $q_t=q\cos \omega t$ (see Fig. 1) can be transformed to the following mixed form including the deflection w and stress function F:

$$\begin{aligned} \begin{aligned}&D\Delta ^2 w=\left( 1-\mu {\nabla }^2\right) (-N_{1}\frac{\partial ^2 w}{\partial x^2}-N_{2}\frac{\partial ^2 w}{\partial y^2}+\\&\quad +L\left( w,F\right) -\rho h\frac{\partial ^{2,}w}{\partial t^2}-\delta _0\frac{\partial w}{\partial t}+q \cos \omega t), \end{aligned} \end{aligned}$$

(14)

where

$$\begin{aligned} L\left( w,F\right) =\frac{{\partial }^2w}{{\partial }x^2}\frac{{\partial }^2F}{{\partial }y^2}+\frac{{\partial }^2F}{{\partial }x^2}\frac{{\partial }^2w}{{\partial }y^2}-2\frac{{\partial }^2w}{{\partial }x{\partial }y}\frac{{\partial }^2F}{{\partial }x{\partial }y},\nonumber \\ \end{aligned}$$

(15)

and $\Delta ^2=(\frac{\partial ^2}{\partial x^2}+\frac{\partial ^2}{\partial y^2})^2$. The additional equation linking unknown functions w, F is yielded by the compatibility equation (5) and the relations (10), i.e. we have

$$\begin{aligned} \begin{aligned} (1-\mu \nabla ^2 )\frac{1}{E}\Delta ^2 F=-\frac{h}{2}L\left( w,w\right) , \end{aligned} \end{aligned}$$

(16)

where

$$\begin{aligned} L\left( w,w\right) =2\left( \frac{{\partial }^2w}{{\partial }x^2}\frac{{\partial }^2w}{{\partial }y^2}-\left( \frac{{\partial }^2w}{{\partial }x{\partial }y}\right) ^2\right) . \end{aligned}$$

(17)

We consider the simply supported plate, and hence, the following relations are satisfied:

$$\begin{aligned} \begin{aligned}&w=0,\frac{{\partial }^2w}{{\partial }x^2}+\nu \frac{{\partial }^2w}{{\partial }y^2}=0,\\&\quad \frac{{\partial }^2F}{{\partial }x{\partial }y}=0,\int _0^b\frac{{\partial }^2F}{{\partial }y^2}\mathrm{d}y=0,\quad x=0,a, \\&\quad w=0,\frac{\partial ^2w}{\partial y^2}+\nu \frac{{\partial }^2w}{{\partial }x^2}=0,\\&\quad \frac{{\partial }^2F}{{\partial }x{\partial }y}=0,\int _0^a\frac{{\partial }^2F}{{\partial }x^2}\mathrm{d}x=0, \quad y=0,b. \end{aligned} \end{aligned}$$

(18)

3 Method of solution

To apply the Bubnov–Galerkin method, we present the deflection of the micro/nanoplate $w\left( x,y,t\right)$ as follows [21, 35]:

$$\begin{aligned} \begin{aligned}&w\left( x,y,t\right) =w_1 (t) \sin \frac{ \pi x }{a}\sin \frac{ \pi y }{b}+\\&\quad +w_2 (t) \sin \frac{ 2\pi x }{a}\sin \frac{ 2\pi y }{b}, \end{aligned} \end{aligned}$$

(19)

where $w_1, w_2$ are bi-modal amplitudes, and $\sin \frac{ \pi x }{a}\sin \frac{ \pi y }{b}$ and $\sin \frac{ 2\pi x }{a}\sin \frac{ 2\pi y }{b}$ are shape functions, which satisfy the chosen boundary conditions. In order to get the expression for stress function, the substitution of the deflection (19) into (16) is performed:

$$\begin{aligned} \begin{aligned}&(1-\mu \nabla ^2 )\Delta ^2 F=Eh((w_1 \frac{\pi ^2}{a b}\cos \frac{\pi x}{a}\cos \frac{\pi y}{b}+\\&\quad +w_2 \frac{4\pi ^2}{a b}\cos \frac{2\pi x}{a}\cos \frac{2\pi y}{b})^2-\\&\quad -(w_1 \frac{\pi ^2}{a ^2}\sin \frac{\pi x}{a}\sin \frac{\pi y}{b}\\&\quad +w_2 \frac{4\pi ^2}{a^2}\sin \frac{2\pi x}{a}\sin \frac{2\pi y}{b})\times \\&\quad \times (w_1 \frac{\pi ^2}{b ^2}\sin \frac{\pi x}{a}\sin \frac{\pi y}{b}\\&\quad +w_2 \frac{4\pi ^2}{b^2}\sin \frac{2\pi x}{a}\sin \frac{2\pi y}{b})) , \end{aligned} \end{aligned}$$

$$\begin{aligned} \begin{aligned}&(1-\mu \nabla ^2 )\Delta ^2 F=\\&\quad =Eh(w_1^2 \frac{\pi ^4}{a^2 b^2}(\cos ^2 \frac{\pi x}{a}\cos ^2\frac{\pi y}{b}\\&\quad -\sin ^2 \frac{\pi x}{a}\sin ^2\frac{\pi y}{b})+\\&\qquad +w_2^2 \frac{16\pi ^4}{a^2 b^2}(\cos ^2 \frac{2\pi x}{a}\cos ^2\frac{2\pi y}{b}\\&\quad -\sin ^2 \frac{2\pi x}{a}\sin ^2\frac{2\pi y}{b})+\\&\qquad +w_1w_2 \frac{8\pi ^4}{a ^2 b ^2}(\cos \frac{\pi x}{a}\cos \frac{\pi y}{b}\cos \frac{2\pi x}{a}\cos \frac{2\pi y}{b}-\\&\qquad -\sin \frac{\pi x}{a}\sin \frac{\pi y}{b}\sin \frac{2\pi x}{a}\sin \frac{2\pi y}{b})) , \end{aligned} \end{aligned}$$

and application of trigonometric formulas yields

$$\begin{aligned} \begin{aligned}&(1-\mu \nabla ^2 )\Delta ^2 F=\\&\quad =Eh(w_1^2 \frac{\pi ^4}{4a^2 b^2}((1+\cos \frac{2\pi x}{a})(1+\cos \frac{2\pi y}{b})-\\&\qquad -(1-\cos \frac{2\pi x}{a})(1-\cos \frac{2\pi y}{b}))+\\&\qquad +w_2^2 \frac{4\pi ^4}{a^2 b^2}((1+\cos \frac{4\pi x}{a})(1+\cos \frac{4\pi y}{b})-\\&\qquad -(1-\cos \frac{4\pi x}{a})(1-cos\frac{4\pi y}{b}))+\\&\qquad +w_1w_2 \frac{2\pi ^4}{a ^2 b ^2}((\cos \frac{\pi x}{a}\\&\qquad +\cos \frac{3\pi x}{a})(\cos \frac{\pi y}{b}+\cos \frac{3\pi y}{b})-\\&\qquad -(\cos \frac{\pi x}{a}-\cos \frac{3\pi x}{a})(\cos \frac{\pi y}{b}-\cos \frac{3\pi y}{b}))) , \end{aligned} \end{aligned}$$

Performing some transformation the following equation is obtained:

$$\begin{aligned} \begin{aligned}&(1-\mu \nabla ^2) \Delta F\!=\!\frac{h E \pi ^4}{2 a^2b^2}(w_1^2\cos \frac{2 \pi x }{a}\!+\!w_1^2\cos \frac{2 \pi y }{b}\\&\quad +16w_2^2\cos \frac{4 \pi x }{a}+16w_2^2\cos \frac{4 \pi y }{b}\\&\quad +8w_1w_2(\cos \frac{3 \pi x }{a}\cos \frac{ \pi y }{b} +\cos \frac{ \pi x }{a}\cos \frac{3 \pi y }{b})). \end{aligned}\nonumber \\ \end{aligned}$$

(20)

The equation (20) was solved, as it was done based on the classical theory in [21, 47]. Solution of the nonlocal equation (20) gives us the stress function in the following form:

$$\begin{aligned} \begin{aligned}&F=f_1\cos \frac{2\pi x}{a}+f_2\cos \frac{2\pi y}{b}+f_3\cos \frac{4\pi x}{a}\\&\quad +f_4\cos \frac{4\pi y}{b}+f_5\cos \frac{3\pi x}{a} \cos \frac{\pi y}{b}\\&\quad +f_6\cos \frac{\pi x}{a}\cos \frac{3\pi y}{b}+p_1 x^2+p_2y^2, \end{aligned} \end{aligned}$$

(21)

where

$$\begin{aligned} \begin{aligned}&f_1 = \frac{w_1^2 Eha^4}{32b^2(a^2+4\mu \pi ^2)}, f_2=\frac{w_1^2 Eh b^4}{32a^2 (b^2+4\mu \pi ^2)}, \\&\quad f_3 \!=\! \frac{w_2^2 Eh a^4}{32b^2(a^2\!+\!16\mu \pi ^2)}, f_4\!=\!\frac{w_2^2 Eh b^4}{32a^2 (b^2+16\mu \pi ^2)},\\&\quad f_5 = \frac{4w_1w_2 Eha^4b^4 }{(a^2+9b^2)^2(a^2b^2+\mu \pi ^2(a^2+9b^2))},\\&\quad f_6=\frac{4w_1w_2 Eh a^4b^4}{(9a^2+b^2)^2(a^2b^2+\mu \pi ^2(9a^2+b^2))}. \end{aligned}\nonumber \\ \end{aligned}$$

(22)

Considering simply supported movable boundary conditions (18) allows to find the coefficients $p_1=0$ and $p_2=0$ occurring in formula (21).

Fig. 3

The largest Lyapunov exponent as a function of in-plane load parameter $\xi _p$, $\mu =0, \sigma =2$

Fig. 4

Bifurcation diagrams for $y_1$ (a), $y_2$ (b) with bifurcation parameter $\xi _p$ and fixed parameters $\mu =2 \text { nm}^2, \sigma =2$

Fig. 5

The largest Lyapunov exponent as a function of in-plane load parameter $\xi _p$, $\mu =2 \text { nm}^2, \sigma =2$

Fig. 6

Bifurcation diagrams for $y_1$ (a), $y_2$ (b) with bifurcation parameter $\xi _p$ and fixed parameters $\mu =5 \text { nm}^2, \sigma =2$

Fig. 7

The largest Lyapunov exponent as a function of in-plane load parameter $\xi _p$, $\mu =5 \text { nm}^2, \sigma =2$

Fig. 8

Bifurcation diagrams for $y_1$ (a), $y_2$ (b) with bifurcation parameter $\sigma$ and fixed parameters $\mu =2 \text { nm} ^{2}, \xi _p=2.5.$

According to Bubnov–Galerkin procedure, we substitute the deflection of the plate (19) and Airy stress function (21) into the equation (14), multiply the obtained equation by shape functions and integrate over considered domain [21, 26, 40]:

$$\begin{aligned} \begin{aligned}&\int _0^a\int _0^bX(x,y)\sin (\frac{\pi x}{a})\sin (\frac{\pi y}{b}) \mathrm{d}x \mathrm{d}y =0,\\&\quad \int _0^a\int _0^bX(x,y)\sin (\frac{2\pi x}{a})\sin (\frac{2\pi y}{b}) \mathrm{d}x \mathrm{d}y =0, \end{aligned} \end{aligned}$$

(23)

where

$$\begin{aligned} \begin{aligned}&X=D\Delta w-\left( 1-\mu {\nabla }^2\right) (-N_{1}\frac{\partial ^2 w}{\partial x^2}-N_{2}\frac{\partial ^2 w}{\partial y^2}+\\&\quad +L\left( w,F\right) -\rho h\frac{\partial ^{2}w}{\partial t^2}-\delta _0\frac{\partial w}{\partial t}+q \cos \omega t). \end{aligned} \end{aligned}$$

(24)

Implementation of the listed operations yields the system of the following nonlinear ordinary differential equations (ODEs):

$$\begin{aligned} \begin{aligned}&w_1^{''}+\bar{\delta } w_1^{'}+\alpha _0 w_1-\alpha _p w_1+\alpha _1 w_1w_2^2+\alpha _2 w_1^3+\\&\quad +\bar{q} \cos \omega t=0,\\&\quad w_2^{''}+\bar{\delta } w_2^{'}+\beta _0 w_2-\beta _p w_2+\beta _1 w_2 w_1^2+\beta _2 w_2^3=0, \end{aligned}\nonumber \\ \end{aligned}$$

(25)

where

$$\begin{aligned}&\alpha _0=\frac{\pi ^4D(a^2+b^2)^2}{\rho h a^2b^2(a^2b^2+\mu \pi ^2(a^2+b^2))}, \nonumber \\&\qquad \beta _0=\frac{16\pi ^4D(a^2+b^2)^2}{\rho h a^2b^2(a^2b^2+4\mu \pi ^2(a^2+b^2))},\nonumber \\&\qquad \alpha _p=\frac{1}{\rho h}(N_1\frac{\pi ^2 }{a^2}+N_2\frac{\pi ^2 }{b^2}),\nonumber \\&\qquad \beta _p =\frac{4}{\rho h}(N_1\frac{\pi ^2 }{a^2}+N_2\frac{\pi ^2 }{b^2}),\nonumber \\&\qquad \alpha _1=\beta _1\nonumber \\&\quad =\frac{16a^2b^2E\pi ^4}{\rho }\Big (\frac{1}{(9a^2+b^2)^2(a^2 b^2+\mu \pi ^2(9a^2+b^2))}+\nonumber \\&\qquad +\frac{1}{(a^2+9b^2)^2(a^2 b^2+\mu \pi ^2(a^2+9b^2))}\Big ), \end{aligned}$$

(26)

$$\begin{aligned} \begin{aligned}&\alpha _2= \frac{a^2b^2E\pi ^4}{16\rho }\Big (\frac{1}{a^6( b^2+4\mu \pi ^2)}+\frac{1}{b^6( a^2+4\mu \pi ^2)}\Big ),\\&\quad \beta _2=\frac{a^2b^2E\pi ^4}{\rho }\Big (\frac{1}{a^6( b^2+16\mu \pi ^2)}+\frac{1}{b^6( a^2+16\mu \pi ^2)}\Big ),\\&\quad \bar{\delta }=\frac{\delta _0}{\rho h}, \bar{q}=-\frac{16a^2b^2q}{\rho h\pi ^2(a^2b^2+\mu \pi ^2(a^2+b^2))}. \end{aligned} \end{aligned}$$

It is worth to mention that taking the nonlocal coefficient as $\mu = 0$ in (25), (26) leads to the system discussed in [21] for plates in the framework of the classical theory, which validates our approach. Also, it should be added that in case of one-mode approximation ($w_2=0$) the system (25) is reduced to the Duffing-type equation, where coefficient $\alpha _0$ stands for squared fundamental linear frequency of the micro/nanoplate.

Table 1 Dimensionless linear frequency of isotropic simply supported square micro/nanoplate for various values of the nonlocal parameter $\mu (nm^2)$

Fig. 9

The largest Lyapunov exponent as a function of transverse load parameter $\sigma$, $\mu =2 \text { nm} ^{2}, \xi _p=2.5.$

Fig. 10

Bifurcation diagrams for $y_1$ (a), $y_2$ (b) with bifurcation parameter $\mu$ and fixed parameters $\xi _p=2.5$, $\sigma =2$

By introducing the dimensionless parameters as follows:

$$\begin{aligned} y_1=\frac{w_1}{h}, \quad y_2=\frac{w_2}{h}, \quad \tau =\omega t, \end{aligned}$$

(27)

the ODEs (25) are recast to the following dimensionless form

$$\begin{aligned} \begin{aligned}&y_1^{''}+\delta y_1^{'}\!+\!(\xi _0-\xi _p) y_1+\xi _1 y_1y_2^2\!+\!\xi _2 y_1^3\!+\!\sigma \cos \tau \!=\!0,\\&\quad y_2^{''}+\delta y_2^{'}+(\eta _0 -\eta _p) y_2+\eta _1 y_2 y_1^2+\eta _2 y_2^3=0, \end{aligned}\nonumber \\ \end{aligned}$$

(28)

with the following dimensionless coefficients:

$$\begin{aligned} \begin{aligned}&\delta =\frac{\bar{\delta }}{\omega }, \xi _0=\frac{\alpha _0}{\omega ^2}, \xi _1=\frac{\alpha _1 h^2}{\omega ^2},\\&\quad \xi _p=\frac{\alpha _p}{\omega ^2}, \xi _2=\frac{\alpha _2 h^2}{\omega ^2}, \eta _0=\frac{\beta _0}{\omega ^2},\eta _p=\frac{\beta _p}{\omega ^2},\\&\quad \eta _1=\frac{\beta _1 h^2}{\omega ^2}, \eta _2=\frac{\beta _2 h^2}{\omega ^2},\sigma =\frac{\bar{q}}{\omega ^2 h}. \end{aligned} \end{aligned}$$

(29)

4 Numerical simulations

In order to test and validate the proposed approach, we compared results with those published in [1]. On particular, we calculated the linear frequency for graphene sheet with the following material properties:

$$\begin{aligned} \begin{aligned}&E=30 \text {MPa},\quad \nu =0.3, \quad \rho =1220 \text { kg/m}^3, \\&\quad a=10 \text { nm}, \quad b=a, \quad h=a/10. \end{aligned} \end{aligned}$$

(30)

In Table 1 the dimensionless frequency parameters corresponded to two modes taken in approximation of deflection (19) are presented for various values of the nonlocal parameter $\mu$:

$$\begin{aligned} \lambda _1=h\sqrt{\frac{\alpha _0 \rho }{G}}, \lambda _2=h\sqrt{\frac{\beta _0 \rho }{G}}. \end{aligned}$$

(31)

In (31) the shear modulus is determined as $G=\frac{E}{2(1+\nu )}$. Obviously, these results totally coincide with ones received in [1], which validates the developed approach.

Another validation task is the nonlinear vibrations problem for simply supported isotropic plate, considered in the works [32, 33, 39]. To carry out this study, we took into account one mode in the expansion of the plate deflection (19), while ignoring the nonlocal parameter, damping and load parameters as well. It should be noted that the comparison of the results is carried out for a immovable plate [25, 48]; in this case, $p_1, p_2$ in (21) can be found as in [43, 48]. The nonlinear ratio $\omega _n/\omega _l$ is calculated and presented in Table 2, where $\omega _l=\sqrt{\alpha _0}$ and $\omega _n$ stand for linear and nonlinear frequencies, respectively.

Fig. 11

The largest Lyapunov exponent as a function of the nonlocal parameter $\mu$, $\xi _p=2.5$, $\sigma =2$

Fig. 12

Phase plots and Poincaré sections for $y_1$ (a) and $y_2$ (b) with fixed parameters $\mu =0, \xi _p=9.9$ and $\sigma =2$

Table 2 Nonlinear frequency ratio $\omega _n/\omega _l$ for simply supported rectangular isotropic plate ($\nu =0.3, h/a=0.1$)

Fig. 13

The largest Lyapunov exponent as a function of number of periods of external forcing n for $\mu =0, \xi _p=9.9$ and $\sigma =2$

Fig. 14

Phase plots and Poincar sections for $y_1$ (a) and $y_2$ (b) with fixed parameters $\mu =2 \text { nm}^2, \xi _p=2.4$ and $\sigma =2$

In the following numerical simulations it is assumed that the parameters values (30) are fixed. Moreover, it is assumed that the damping parameter $\delta =1$, and the exciting frequency of the transverse load coincides with natural frequency of the nanoplate $\omega =\sqrt{\alpha _0}$, i.e. we consider resonance case. Bifurcation dynamics of the system (28) is then investigated for variations of the transverse load parameter $\sigma$, in-plane load parameter $\xi _p$ ($\eta _p=4\xi _p$) and the nonlocal parameter $\mu$, observe that occurrence of small-size effect can significantly change the character of the vibration regime.

Fig. 15

The largest Lyapunov exponent as a function of number of periods of external forcing n for $\mu =2 \text { nm}^{2}, \xi _p=2.4$ and $\sigma =2$

Fig. 16

Phase plots and Poincar sections for $y_1$ (a) and $y_2$ (b) with $\mu =2 \text { nm} ^2, \xi _p=3.47$ and $\sigma =2$

Bifurcation diagrams and Poincaré sections presented in this paper are based on sampling the system state at instances $\tau =2\pi i$ $(i\in {\mathbb {N}})$. Each bifurcation diagram consists of 600 Poincaré sections computed for 600 constant values of the bifurcation parameter, spanned equally in the range of its changes. Each Poincaré section of the bifurcation diagram consists of 300 points of steady state motion shown in the diagram, after ignoring the initial 100 points of the transient motion starting from the final state of the previous Poincaré section.

The presented in this work results of computation of the largest Lyapunov exponent are based on the classical algorithm utilizing numerical solution of analytical form of the linearized differential equations of motion describing behaviour of infinitesimal perturbations from the nominal trajectory. The system of perturbations is periodically re-orthonormalized based on the Gram–Schmidt algorithm. In this work the period of re-orthonormalization is chosen as 0.2T, where T is period of forcing. Note that in our algorithm we have omitted computation of the Lyapunov exponent, which is always equal to zero and corresponds to the phase of external forcing (perturbation along the trajectory).

Fig. 17

The largest Lyapunov exponent as a function of number of periods of external forcing n for $\mu =2 \text { nm}^{2}, \xi _p=3.47$ and $\sigma =2$

Fig. 18

Phase plots and Poincar sections for $y_1$ (a) and $y_2$ (b) with $\mu =2 \text { nm}^2, \xi _p=2.5$ and $\sigma =2.8$

The bifurcation diagrams for variables $y_1$ and $y_2$ obtained as a result of numerical simulation with increasing bifurcation parameter $\xi _p$ in the range 112, for constant parameters $\mu = 0$ (without small-scale effect), $\sigma = 2$, are presented in Fig. 2, respectively. It is observed that for $\xi _p < 8.75$ the coordinate $y_2$ tends to zero, while the variable $y_1$ undergoes a rich bifurcation scenario in the range $\xi _p\in (1.8,2.7)$. In the zone $\xi _p\in (8.75,10.3)$ both the coordinates $y_1$ and $y_2$ behave in a complicated manner, including chaotic motion. For $\xi _p >10.3$ the system behaves periodically. Figure 3 exhibits the bifurcation diagram of the largest Lyapunov exponent corresponding to the bifurcation diagram presented in Fig. 2, computed for each attractor over 1200 periods of forcing. One can observe intervals of negative and positive values of the largest Lyapunov exponent corresponding to periodic and chaotic zones of the system behaviour, with good agreement of the results reported in Fig. 2. The same analysis for the same parameters as in Figs. 2, 3, but with small-scale effect for $\mu = 2 \text { nm}^2$, is shown in Figs. 4, 5. It is now observed that $\xi _p < 2.32$ the variable $y_2$ tends to zero and simultaneously the variable $y_1$ undergoes a rich bifurcation scenario consisting, among others, of period doubling bifurcation cascade leading to chaotic behaviour of only one part of the dynamical system. This chaotic zone is then interrupted by 3-periodic window. Further increase in bifurcation parameter leads to second chaotic zone, initially observed only for $y_1$ variable, but starting from $\xi _p = 2.32$ also for the coordinate $y_2$. This chaotic window ends with inverse period doubling cascade. For higher values of $\xi _p$ one can observe two more narrow chaotic zones for both variables $y_1$ and $y_2$. This distinction between periodic and chaotic zones is confirmed by the diagram of the largest Lyapunov exponent shown in Fig. 5. Zero values of the exponent correspond to bifurcation points. Behaviour of the system in the same bifurcation parameter $\xi _p$ range 1, , 12 for higher value of the small-scale parameter $\mu = 5 \text { nm}^2$ and $\sigma = 2$ can be observed in Figs.  6, 7. First of all one can notice that the coordinate $y_2$ tends to zero for $\xi _p < 1.7$, while the variable $y_1$ behaves in a periodical manner. For $\xi _p > 1.7$ one can observe rich bifurcation dynamics including periodic and chaotic motion in both the coordinates $y_1$ and $y_2$. Moreover, there are many more areas of chaotic motion than in the case of system dynamics for smaller values of $\xi _p$, which is also confirmed in the diagram of the largest Lyapunov exponent in Fig. 7.

Fig. 19

The largest Lyapunov exponent as a function of number of periods of external forcing n for $\mu =2 \text { nm}^2, \xi _p=2.5$ and $\sigma =2.8$

Fig. 20

Phase plots and Poincar sections for $y_1$ (a) and $y_2$ (b) with $\mu =3.7 \text { nm} ^2$, $\xi _p=2.5$ and $\sigma =2$

The influence of transverse load parameter $\sigma$ (in the range $1 \ldots 5$) is analysed for fixed nonlocal parameter $\mu =2 \text { nm}^2$ and $\xi _p=2.5$. The corresponding bifurcation diagrams for increasing parameter $\sigma$ are presented in Fig. 8. One can observe one wide chaotic zone interrupted by some periodic windows. Again, for $\sigma <1.76$, one can see the variable $y_2$ tending to zero. This bifurcation scenario is confirmed by the corresponding bifurcation diagram of the largest Lyapunov exponent presented in Fig. 9.

Fig. 21

Phase plots and Poincar sections as a function of number of periods of external forcing n for $\mu =3.7 \text { nm}^2$, $\xi _p=2.5$ and $\sigma =2$

Bifurcation diagrams with increasing nonlocal parameter $\mu$ in the range 0...5 ($nm^2$) there are presented in Fig. 10. The corresponding bifurcation diagram of the largest Lyapunov exponent as a function of $\mu$ is depicted in Fig. 11. For these numerical simulations the following parameters are fixed: $\xi _p=2.5$, $\sigma =2$. The obtained results allow for observation that small-scale effects crucially influence the behaviour of the nanoplate. If for classical theory ($\mu =0$) one observes the periodic regimes, for some other values of the nonlocal parameter the complex chaotic motion is detected. One can see two intervals of bifurcation parameter corresponding to chaotic regimes separated by intervals of periodicity. The two main chaotic zones are connected by two period adding cascades. Also, on can observe that for higher values of the nonlocal parameter starting from $\mu \approx 3.8 \text { nm}^2$ the periodic regimes play a crucial role. In Fig. 12 there are presented projections of phase plot and Poincaré section of a chaotic attractor without the small-scale effect and corresponding to the bifurcation diagrams seen in Figs. 2, 3 for in-plane force parameter $\xi _p=9,9$. The chaotic character of the solution is confirmed by positive largest Lyapunov exponent with computation process presented in Fig. 13, where n is the number of periods of external forcing. Figure 14 exhibits the projections of phase plot and Poincaré section of exemplary chaotic attractor associated with bifurcation diagram presented in Fig. 4, for in-plane force parameter $\xi _p=2.4$. The corresponding largest Lyapunov exponent, as a function of the number of periods of forcing, there is presented in Fig. 15. Analysis of another example of chaotic attractor corresponding to bifurcation diagram shown Fig. 4, for $\xi _p=3.47$, there is presented in Fig. 16 (phase plots and Poincaré sections) and in Fig. 17 (the largest Lyapunov exponent). Analogously, Figs. 18–21 exhibit analysis of two chaotic attractors corresponding to bifurcation diagrams presented in Fig. 8 (for $\sigma =2.8$, see Figs. 18-19) and in Fig. 10 (for $\mu =3.7 \text { nm}^2$, see Figs. 20–21). In all cases, the character of phase plots and Poincaré sections, as well as positive Lyapunov exponents, confirm chaotic nature of the detected attractors.

5 Conclusions

The geometrically nonlinear dynamics of the isotropic simply supported micro/nanoplate is considered in the present work. In order to take into account the small-scale effects, the nonlocal elasticity theory is used. The studied plate is supposed to be under the action of transverse periodic force and uniform in-plane forces. The base of the developed approach is the application of the Bubnov–Galerkin method with a two-mode approximation of the plate deflection. The employed bifurcation diagrams, the largest Lyapunov exponents, phase portraits as well as Poincare sections allowed to detect chaotic vibrations of the studied mechanical object. It is shown a significant influence of the excitation parameters on the vibrations regimes. Another work achievement is an indication of the nonlocal parameter influence on vibration regimes, which means that the small-scale effects can change the character of the vibrations and provoke chaotic behaviour of the object that can give undesirable consequences for the nanostructure used in engineering applications. It is shown that in-plane load ($\xi _p>0$) is necessary for oscillations of the coordinate $y_2$. Moreover, an increase in the small-scale effect lowers the threshold for the onset of the coordinate $y_2$ oscillations. Finally, this bifurcation and chaotic dynamics are detected and validated via classical apparatus of nonlinear dynamics systems.