1 Introduction

The rapid development of high-tech industry gave a significant impetus to the study of micro- and nano-structures. The widespread use of micro/nanobeams, micro/nanoplates, micro/nanoshells in modern industry (in micro/nano-electromechanical systems, nano-optomechanical structures, energy storage systems, DNA detectors, and so on) [1,2,3,4,5,6] forced the necessity to study the dynamics of micro/nano structural members. The experimental and theoretical investigations show that the classical (local) theory may lead to incorrect outcomes in the analysis of micro/nanostructures due to appearance of size-effect [7], and that is why it cannot be used. This problem has led to the development of the nonclassical continuum theories, among them the theory of micropolar elasticity [8], the couple stress theory [9,10,11], the nonlocal elasticity theory [12], and the strain gradient theory [7] should be mentioned. In our work, the micro/nanoplates are studied on a base of the model which uses the nonlocal elasticity theory and whence it follows that the stress state at a given point is dependent on the strains in all points of the body. It is worth mentioning that recently a large number of publications aimed at the dynamics of the micro/nanoplate have been published. Among them a key role plays the paper of Pradhan and Phadikar [13], where the Navier approach is applied to linear vibrations of small-scale plates based on the classical plate theory and first-order shear deformation theory. Aghababaei and Reddy [14] employed third-order shear deformation plate theory in bending and vibration of nano/microplates problems. Ritz method was applied to the free vibration analysis of a rectangular nanoplate resting on the Winkler and Pasternak foundations by Bastami and Behjat [15]. Zhang et al. [16] analyzed vibrations of flexoelectric nanoplates by the differential quadrature method. Influence of elastic foundations on dynamics of small-scale plates is also studied in [17,18,19,20].

It should be noticed that most of the papers devoted to the considering problem contain investigations of the behavior of the plates with square and rectangular shape, but obviously in practical applications, an object may have a complex shape with internal or external cutouts, and therefore, it becomes necessary to develop new approaches. Among a small number of works including studies of micro/nanoplates with nonstandard form, it can be listed the paper by Shahidi et al. [21] which studied linear vibrations of orthotropic triangular plate by Bubnov–Galerkin approach within the nonlocal elasticity theory. The non-uniform circular nanoplate vibrations based on the nonlocal elasticity theory are investigated by Ritz method in the work of Zarei et al. [22]. Axisymmetric free vibrations of annular and circular Mindlin plates are studied based on the nonlocal continuum theory by Sari [23]. Li et al. [24] devoted their work to the research of vibrations of rotating composite nano-annular plates based on Kirchhoff plate theory, Mindlin plate theory, and Reddy plate theory, combined with the nonlocal theory. Shahriari and Shirvani [25] analyzed buckling of skew nanoplates based on nonlocal elasticity theory as well as second-order strain gradient theory. Isogeometric analysis was applied to the study of large amplitude free vibration of porous skew and elliptical nanoplates based on nonlocal elasticity by Tao and Dai [26] . The studies devoted to the micro/nanoplates of complex geometry also include works [27,28,29] (plates with a hole, and L-shaped plate, and skew plate, respectively), where the authors use the modified couple stress theory accounting for the small-scale effects.

In the present work, our research is carried out by the Ritz method. The problem of construction of the system of basic functions is solved by application of R-functions theory. It should be mentioned that the application of R-functions is novel for the micro/nanoobjects based on the nonlocal elasticity theory. At the same time the combination of Ritz method and R-function theory (RFM) works well for plate and shell problems in the framework of the classical (local) theory. A description of R-functions theory and review of works in which it is successively employed for various problems of dynamics of plates and shells with complex form can be found in [30,31,32]. Thus, the novelty of this work is application of RFM to developing the approach of investigation for a new class of problems, namely vibrations of micro/nanoplates with complex shape and several types of boundary conditions based on the small-scale nonlocal governing equations. The proposed method is applied to the study of an orthotropic plate with two cutouts, the influence of small-scale parameter and size parameter is analyzed.

The present paper is organized in the following way. In the first Section, a short review of the known results is outlined. The mathematical formulation of the considered problem including variational statement based on nonlocal constitutive relations is given in the second Section. The next Section is aimed at the R-function theory description. The application of the proposed approach and numerical results are reported in the fourth Section. The last Section contains conclusions.

2 Mathematical formulation

2.1 The governing system

In the present work, we consider orthotropic Kirchhoff’s micro/nanoplate with nonclassical shape. In order to indicate the small-scale effects, we are going to use the nonlocal elasticity theory. Owing to the mentioned theory, the constitutive relation in an integral form for the nonlocal stress tensor at a point x has the following form:

$$\begin{aligned} \sigma = \int _V K \left( |{X} ^ {'} -X|,\tau \right) \sigma '(X') \mathrm{d}X', \end{aligned}$$
(1)

where \(\sigma \), \(\sigma '\) are nonlocal and local stress tensors, \( K \left( |{X} ^ {'} -X|,\tau \right) \) is the nonlocal modulus, \( \tau =e_0\alpha /l\), \(\alpha \) is the internal characteristic length, \(e_0\) is a constant corresponding to material, and l is an external characteristic length. Since the integral form is quite complicated, the following differential form [33] of the nonlocal constitutive relations is often used:

$$\begin{aligned} \left( 1-\mu \nabla ^2 \right) \sigma =\sigma ', \end{aligned}$$
(2)

where \(\mu =(e_0 \alpha )^2\) stands for the nonlocal parameter. Note that the components of the strain tensor are as follows [34]:

$$\begin{aligned} \begin{aligned} \varepsilon _{ xx }&= -z\frac{{\partial }^2w}{{\partial }x^2}, \varepsilon _{ yy }&= -z \frac{{\partial }^2w}{{\partial }y^2}, \varepsilon _{ xy }&= -2\frac{{\partial }^2w}{{\partial }x{\partial }y}. \end{aligned} \end{aligned}$$
(3)

For orthotropic micro/nanoplate, one can rewrite the relation (2) into the following counterpart form:

$$\begin{aligned} \begin{bmatrix} \sigma _{xx}\\ \sigma _{yy}\\ \sigma _{xy} \end{bmatrix}-\mu \nabla ^2 \begin{bmatrix} \sigma _{xx}\\ \sigma _{yy}\\ \sigma _{xy} \end{bmatrix}= \begin{bmatrix} \frac{E_1}{1-\nu _1 \nu _2}&{}\,\,\, \frac{\nu _1 E_2}{1-\nu _1 \nu _2}&{}\,\,\, 0\\ \frac{\nu _2E_1}{1-\nu _1 \nu _2}&{}\,\,\, \frac{E_2}{1-\nu _1 \nu _2}&{}\,\,\, 0\\ 0&{} 0&{}G\\ \end{bmatrix} \begin{bmatrix} \varepsilon _{xx}\\ \varepsilon _{yy}\\ \varepsilon _{xy} \end{bmatrix}, \end{aligned}$$
(4)

where \(E_1, E_2\) are Young’s modules, \(\nu _1, \nu _2\) are Poisson’s ratios, and G is shear modulus. Moreover, moments are defined as follows [13, 16, 35]:

$$\begin{aligned} M_x=\int _\frac{-h}{2}^\frac{-h}{2} \sigma _{xx}z\mathrm{d}z, M_y=\int _\frac{-h}{2}^\frac{-h}{2} \sigma _{yy}z\mathrm{d}z, M_{xy}=\int _\frac{-h}{2}^\frac{-h}{2} \sigma _{xy}z\mathrm{d}z. \end{aligned}$$
(5)

Formulas (3)–(5) yield the following relations

$$\begin{aligned}&\begin{gathered} M_{x} - \mu \nabla ^{2} M_{x} = - D_{{11}} \left( {\frac{{\partial ^{2} w}}{{\partial x^{2} }} + \nu _{2} \frac{{\partial ^{2} w}}{{\partial y^{2} }}} \right) , \\ \quad M_{y} - \mu \nabla ^{2} M_{y} = - D_{{22}} \left( {\nu _{1} \frac{{\partial ^{2} w}}{{\partial x^{2} }} + \frac{{\partial ^{2} w}}{{\partial y^{2} }}} \right) , \\ \quad M_{{xy}} - \mu \nabla ^{2} M_{{xy}} = - 2D_{{66}} \frac{{\partial ^{2} w}}{{\partial x\partial y}}, \\ \end{gathered} \end{aligned}$$
(6)

where

$$\begin{aligned} D_{11}=\frac{E_1h^3}{12(1-\nu _1\nu _2)}, D_{22}=\frac{E_2h^3}{12(1-\nu _1\nu _2)}, D_{66}=\frac{Gh^3}{12}. \end{aligned}$$
(7)

The governing equation of the considered linear vibration micro/nanoplate problem takes the following form:

$$\begin{aligned} D_{11}\frac{{\partial }^4w}{{\partial }x^4}+2\left( D_{12}+2D_{66}\right) \frac{{\partial }^4w}{{\partial }x^2{\partial }y^2}+D_{22}\frac{{\partial }^4w}{{\partial }y^4} =\left( 1-\mu {\nabla }^2\right) \left( -\rho h\frac{\partial ^{2}w}{\partial t^2}\right) . \end{aligned}$$
(8)

Equation (8) is supplemented with the corresponding boundary conditions [30]:

  1. 1.

    Simple support

    $$\begin{aligned} w=0, M_n=0, \end{aligned}$$
    (9)
  2. 2.

    Clamping

    $$\begin{aligned} w=0, \frac{\partial w}{\partial n}=0, \end{aligned}$$
    (10)

where n stands for a normal to the boundary, and \(M_n\) is bending moment.

2.2 The variational approach

Following the work of Phadikar and Pradhan [36] based on using calculus of variation, one can get the variational statement of the vibration problem for a micro/nanoplate as follows:

$$\begin{aligned} F= & {} \iint _{{\Omega }}\Bigg [\Bigg (D_{11}{\frac{{\partial }^2w}{\partial x^2}}\frac{{\partial }^2 w}{\partial x^2}+D_{22}{\frac{{\partial }^2w}{\partial y^2}}\frac{{\partial }^2 w}{\partial y^2}+D_{12}\left( \frac{{\partial }^2w}{\partial x^2}\frac{{\partial }^2 w}{\partial y^2}+\frac{{\partial }^2w}{\partial x^2}\frac{{\partial }^2 w}{\partial y^2}\right) \nonumber \\&+4D_{66}\left( \frac{{\partial }^2w}{\partial x\partial y}\right) \left( \frac{{\partial }^2w}{\partial x\partial y}\right) \Bigg )-\rho h{\omega }^2_L \Bigg ( w^2 +\mu \Bigg (\frac{\partial w}{\partial x} \frac{\partial w}{\partial x}+\frac{\partial w}{\partial y}\frac{\partial w}{\partial y}\Bigg )\Bigg )\Bigg ] \mathrm{d}{\Omega }, \end{aligned}$$
(11)

where \({\omega }_L\) is the vibration frequency. The minimization of the functional (11) is performed by the Ritz method. Observe that the Ritz method requires constructions of coordinate functions, satisfying boundary conditions. Namely, the deflection of the plate is represented as

$$\begin{aligned} w=\sum _{i=1}^{n}c_i w_i(x,y), \end{aligned}$$
(12)

where \(c_i\) are unknown coefficients, \(w_i=g(x,y)\varphi _i\) are a system of coordinate (basis) functions, whereas g(x, y) is a shape function depending on the boundary conditions and shape of the plate, \(\varphi _i\) is a complete system of functions (in particular, the set of power polynomials). Obviously, construction of the shape functions is a difficult problem when the shape of the plate is complicated, for example, contains cutouts. In contrast to the standard representation of coordinate functions for rectangular regions, as it was done in the work [15], we propose to construct the basis functions within the R-function theory.

3 R-functions method

In this Section, some details of the R-functions theory are presented [30,31,32]. This theory was proposed by V.L. Rvachev [30]. The main advantage of this theory is the ability to represent geometric information about the plate analytically. The R-functions method is often referred to as a structural method because the main concept of this method relies on definition of the solution structure of the boundary value problems. The application of the RFM begins with the construction of the solution structure. The structure of the solution of the boundary value problem is a set of the functions

$$\begin{aligned} W=B(P,\omega ,\omega _i) \end{aligned}$$

which exactly satisfies all (or part) of the boundary conditions at any choice of the uncertain component P. The operator B depends on the shape of the region and sections of its border, the equations of which are \(\omega , \omega _i\), respectively. A number of works [30, 31] are devoted to the construction of such solution structures for boundary value problems of the plate theory.

Further, according to the R-functions method it is needed to construct the logical predicate of the domain \({{\Omega }}\) consisting of the characteristic functions \({{\Omega }}_i\) of its subdomains. Furthermore, based on the theorem proved by V.L. Rvachev we replace \({{\Omega }}_i\) by corresponding continuous functions \(f_i\) and Boolean operators \({\vee },{\wedge }\), \(^{-}\) by R-functions. In result, we get the equation of the boundary of domain \(\omega (x,y)=0\) [30]. The equation constructed in such way is normalized upto 1\({}^{st}\) order, that is,

$$\begin{aligned}&\omega =0, \frac{\partial \omega }{\partial n}=1, \forall (x,y)\in \partial {\Omega },N, \nonumber \\&\quad \omega >0, \forall (x,y)\in {\Omega }. \end{aligned}$$
(13)

In this paper, we apply the following R-functions system:

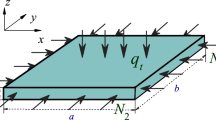
$$\begin{aligned} x{{\vee }}_0y=x+y+\sqrt{x^2+y^2}, (R-\mathrm{disjunction}),\nonumber \\ x{{\wedge }}_0y=x+y-\sqrt{x^2+y^2}, (R-\mathrm{conjunction}),\nonumber \\ \overline{x}=-x, ({R}-\mathrm{negation}). \end{aligned}$$
(14)

Let us consider the rectangular plate with two cutouts on opposite sides (see Fig. 1).

Fig. 1
figure 1

Shape of the studied plate with cutouts

Full size image

The logical predicate of the domain is constructed as follows:

$$\begin{aligned} \Omega =(\Omega _1{{\wedge }}\Omega _2)\wedge (\Omega _3{{\vee }}\Omega _4). \end{aligned}$$
(15)

According to the algorithm mentioned above (see description of the Theorem by Rvachev [30]), one can obtain the equation of the boundary domain as

$$\begin{aligned} \omega =(f_1{{\wedge }}_0f_2){{\wedge }}_0(f_3{{\vee }}_0f_4), \end{aligned}$$
(16)

where

$$\begin{aligned} f_1=\frac{1}{2a}\left( a^2-x^2\right) \ge 0, f_2=\frac{1}{2b}\left( b^2-y^2\right) \ge 0 \end{aligned}$$
(17)

are the region between \(x=\pm {a}\) and the region between \(y=\pm {b}\), whereas

$$\begin{aligned} f_3=\frac{1}{2c_1}\left( c_1^2-x^2\right) \ge 0, f_4=\frac{1}{2c_2}\left( y^2-c_2^2\right) \ge 0 \end{aligned}$$
(18)

define the region between \(x=\pm c_1\) and the region outside the lines \(y=\pm c_2\). For considering in the current work types of the boundary conditions, the structures of solutions were constructed in [30, 31]. Thus, if a plate is clamped, then the structure of the solution is

$$\begin{aligned} w={\omega }^2P, \end{aligned}$$
(19)

while for the case of a simply supported plate a more useful simplified variant of structure of solution, satisfying the main boundary conditions, is

$$\begin{aligned} w=\omega P. \end{aligned}$$
(20)

If a part of the plate is clamped (\(\omega _1\)), and the remaining part is simply supported, the structure of the solution takes the form

$$\begin{aligned} w=\omega \omega _1 P. \end{aligned}$$
(21)

Here, we consider mixed boundary conditions with clamped edges \(y=\pm {b}\), whereas \(\omega _1= f_2\). Structures (19), (20), (21) contain an uncertain component P. It is represented as a truncated series in some complete system of functions \(\{{\varphi }_i\}\):

$$\begin{aligned} P=\sum _{i=1}^{n}c_i\varphi _i(x,y), \end{aligned}$$
(22)

such as power polynomials, trigonometrical polynomials, Chebyshev polynomials, and splines. Due to the symmetry of the geometric shape of the considered nanoplate, integration was performed over 1/4 of the region, and power polynomials were used as a complete system of functions:

$$\begin{aligned} \{{\varphi }_i\}:1,x^2,y^2,x^4,x^2y^2,y^4,\ldots \end{aligned}$$
(23)

while the coordinate functions in (12) for simply supported boundary conditions (9) take the form

$$\begin{aligned} w_1=\omega , w_2=x^2 \omega , w_3=y^2 \omega , w_4=x^4 \omega ,w_5= x^2y^2 \omega ,\ldots , \end{aligned}$$
(24)

whereas for clamped boundary conditions (10)

$$\begin{aligned} w_1=\omega ^2, w_2=x^2 \omega ^2, w_3=y^2 \omega ^2, w_4=x^4 \omega ^2,w_5= x^2y^2 \omega ^2,\ldots \end{aligned}$$
(25)

For mixed boundary conditions, one can apply the structure of solution (21); thus, the basis functions are

$$\begin{aligned} w_1=\omega \omega _1, w_2=x^2 \omega \omega _1, w_3=y^2 \omega \omega _1, w_4=x^4 \omega \omega _1,w_5= x^2y^2 \omega \omega _1,\ldots \end{aligned}$$
(26)
Table 1 Dimensionless linear frequency \({\overline{\omega }}\) of the isotropic simply supported square plate
Full size table
Table 2 Dimensionless linear frequency \({\overline{\omega }}\) of the orthotropic clamped square plate
Full size table
Fig. 2
figure 2

Vibration modes associated with the first (a), second (b) and third (c) vibration frequencies of simply supported plate

Full size image
Fig. 3
figure 3

Dimensionless frequencies \(\bar{\omega }\) in terms of cutout size ratio \(c_2/a\) and nonlocal parameter \(\mu (\mathrm{nm}^2)\) for an isotropic nanoplate; a simply supported, b clamped

Full size image
Fig. 4
figure 4

Dimensionless frequencies \(\bar{\omega }\) for three types of boundary conditions versus nonlocal parameter \(\mu \); a \(c_1/a=0.7; c_2/a=0.3\), b \(c_1/a=0.5, c_2/a=0.5\)

Full size image
Fig. 5
figure 5

Dimensionless frequencies \(\bar{\omega }\) in terms of cutout size ratio \(c_2/a\) and nonlocal parameter \(\mu (\mathrm{nm}^2)\) for an orthotropic nanoplate; a simply supported, b clamped

Full size image
Fig. 6
figure 6

Dimensionless frequencies \(\bar{\omega }\) for different boundary conditions versus nonlocal parameter \(\mu \); \(c_1/a=0.5, c_2/a=0.5\)

Full size image

4 Numerical results

Validation of the proposed method has been performed by solving several testing problems and by comparison obtained results with existing ones. The first case study describes the linear vibrations of an isotropic square nanoplate with simply supported boundary conditions. The analytical estimation of the linear frequency can be found in [13]. It should be mentioned that for isotropic material we have to take \(E=E_1=E_2, \nu =\nu _1=\nu _2, G={E}/{(2(1+\nu ))}\). The following mechanical parameters are fixed:

$$\begin{aligned} E=30\,\mathrm{MPa},\rho =1220\,\mathrm{kg/m}^3,\nu =0.3. \end{aligned}$$
(27)

The dimensionless frequency parameter \({\overline{\omega }}=\omega _L h \sqrt{\frac{\rho }{G}}\) calculated for various values of the nonlocal parameter \(\mu \) is presented in Table 1. The obtained results have been compared with the ones presented in [14].

Further, we consider the problem studied in [21, 36]. Namely, vibrations of the clamped orthotropic graphene sheet with the following mechanical parameters:

$$\begin{aligned} E_1=1765\,\mathrm{GPa},E_2=1588\,\mathrm{GPa},G=678.85\,\mathrm{GPa},\rho =2300\,\mathrm{kg/m}^3,\nu _1=0.3,\nu _2=0.27, \end{aligned}$$
(28)

and geometrical parameters: \(2a=10.2\,\mathrm{nm}, h=0.34\,\mathrm{nm}, b/a=1\) have been investigated. The dimensionless frequencies \({\overline{\omega }}=\frac{(2 a)^2 \omega _L}{h} \sqrt{\frac{\rho }{E_1}}\) are provided for the nonlocal parameter \(\mu \) (in the range 0–4 \(\mathrm{nm}^2\)), see Table 2.

Comparison of the results obtained by the proposed approach with published results by other researchers allows to make a conclusion about the reliability of the presented method and developed software.

In what follows, numerical calculations are performed for a simply supported small-scale plate (see Fig. 1), with the following fixed geometrical parameters:

$$\begin{aligned} a=5\,\mathrm{nm}, h/{2a}=0.1, b/a=1, \end{aligned}$$

and the plate is supposed to be made from isotropic material with the properties (27). The presented results contain the first three vibration modes calculated for \(\mu =1\,\mathrm{nm}^2\) and size of cutouts associated with the following ratio: \(c_1/a=0.7, c_2/a=0.3\). The corresponding frequency parameters (\({\overline{\omega }}_i=\frac{(2 a)^2 \omega _{Li}}{h} \sqrt{\frac{\rho }{E_1}},i=1,2,3\)) are shown as well in Fig. 2.

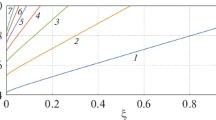
Figure 3 demonstrates the results of studying the effect of the size of the cutouts on the frequency parameter \({\overline{\omega }}=\frac{(2 a)^2 \omega _L}{h} \sqrt{\frac{\rho }{E_1}}\) depending on the change in the nonlocal parameter, see Fig. 3. It is assumed that \(c_1/a+c_2/a=1\). One can note that an increase in the size of cutouts leads to an increase in the frequency parameter, while an increase in the small-scale parameter decreases the value of the frequency parameter. A similar behavior is characteristic of both the simply supported plate and the clamped plate; furthermore, the clamped plate is associated with higher values of the frequency parameter.

The influence of the boundary conditions is investigated for two cutout sizes, \(c_1/a=0.7, c_2/a=0.3\), and \(c_1/a=0.5, c_2/a=0.5\), see Fig. 4. Here, we consider the above-mentioned boundary conditions, where the plate is simply supported or clamped along the entire edge, as well as mixed conditions with clamped part of the boundary (\(\omega _2=f_2\)) and remaining simply supported part of the edge, that corresponds to the structure of solution (21). Analyzing the obtained results, we come to the conclusion that an increase in the size of the nanoplate cutouts increases the value of the frequency parameter while for large values of the nonlocal parameter the influence of the boundary conditions decreases. It should also be noted that for a larger cutout size the values of the frequency parameter for the simply supported edge and mixed boundary conditions are very close and differ significantly from the values obtained for the clamped edges.

Next, we consider an orthotropic nanoplate (mechanical properties (28)) with a complex shape and geometrical ratios \(2a=10\,\mathrm{nm}, h=1\,\mathrm{nm}, b/a=1, c_1/a+c_2/a=1\). By varying the values of the nonlocal parameter \(\mu \) and size of the cutouts, the frequency parameter \({\overline{\omega }}=\frac{(2 a)^2 \omega _L}{h} \sqrt{\frac{\rho }{E_1}}\) is calculated, and the obtained values are presented in Fig. 5.

Figure 6 shows the values of the frequency parameter for isotropic (27) and orthotropic (28) plates in the case of simply supported and clamped nanoplates. Geometrical parameters here are taken as \(c_1/a=0.5, c_2/a=0.5\). One can observe that the results obtained for isotropic (see Fig. 3) and orthotropic nanoplates are close, and the behavior of the system is the same for both materials.

5 Concluding remarks

The presented work is devoted to the study of vibrations of orthotropic nano/microplates of complex shapes. The governing equations are based on the Kirchhoff–Love hypothesis, and the nonlocal theory is used to take into account small-scale effects. The proposed approach uses a variational statement in combination with the Ritz method. At the same time, the approach to constructing a coordinate system based on the R-functions theory is fundamentally new for this class of problems, and it allows one to study plates of various geometric shapes, as well as the influence of different types of boundary conditions. A numerical simulation was performed for an isotropic and orthotropic square nanoplate with cutouts on opposite sides. Moreover, we considered three types of boundary conditions, including mixed ones. The developed approach allowed us to observe that an increase in the nonlocal parameter decreases the value of the frequency parameter for a complex shape plate for all types of boundary conditions considered, while the small-scale effect is more pronounced for large plate cutouts and clamped boundary conditions.