Skip to main content
SpringerLink
Log in

Bäcklund transformation and N-shock-wave solutions for a (3+1)-dimensional nonlinear evolution equation

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

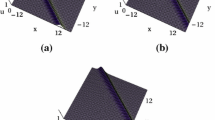
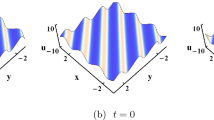
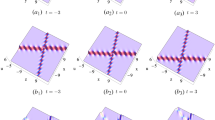
In this paper, a (3+1)-dimensional nonlinear evolution equation is investigated, which can be used to describe reacting mixtures and shallow water waves. Through the Hirota method and symbolic computation, bilinear forms and Bäcklund transformation are derived, which are different from those in the existing literature. Moreover, N-shock-wave solutions are obtained. Based on those shock-wave solutions, propagation and collision of the shock waves are discussed via the asymptotic and graphic analysis on different planes: (1) oblique elastic collisions between/among the two/three shock waves will arise on the x–y and y–z planes, while parallel elastic collisions exist on the x–z plane; (2) shock waves maintain their original directions, amplitudes and velocities except for some small phase shifts after each collision; (3) the shock wave with higher amplitude travels faster and moves across the slower.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Notes

  1. Oblique collision means that the angle of the collision between two shock waves is nonzero [36].

References

  1. Agrawal, G.P.: Nonlinear Fiber Optics. Academic Press, San Diego (2012)

    MATH  Google Scholar 

  2. Tian, B., Gao, Y.T.: Spherical Kadomtsev–Petviashvili equation and nebulons for dust ion-acoustic waves with symbolic computation. Phys. Lett. A 340, 243–250 (2005)

    Article  MATH  Google Scholar 

  3. Tian, B., Gao, Y.T., Zhu, H.W.: Variable-coefficient higher-order nonlinear Schrödinger model in optical fibers: Variable-coefficient bilinear form, Bäcklund transformation, brightons and symbolic computation. Phys. Lett. A 366, 223–229 (2007)

    Article  MATH  Google Scholar 

  4. Gao, Y.T., Tian, B.: Cosmic dust-ion-acoustic waves, spherical modified Kadomtsev–Petviashvili model, and symbolic computation. Phys. Plasmas 13, 112901–112906 (2006)

    Article  Google Scholar 

  5. Gao, Y.T., Tian, B.: Cylindrical Kadomtsev–Petviashvili model, nebulons and symbolic computation for cosmic dust ion-acoustic waves. Phys. Lett. A 349, 314–319 (2006)

    Article  Google Scholar 

  6. Gao, Y.T., Tian, B.: Reply to: Comment on: ‘Spherical Kadomtsev–Petviashvili equation and nebulons for dust ion-acoustic waves with symbolic computation’. Phys. Lett. A 361, 523–528 (2007)

    Article  MATH  Google Scholar 

  7. Whitham, G.B.: Linear and Nonlinear Waves. Wiley, New York (1974)

    MATH  Google Scholar 

  8. Wang, Y.F., Tian, B., Wang, P., Li, M., Jiang, Y.: Bell-polynomial approach and soliton solutions for the Zhiber–Shabat equation and (2+1)-dimensional Gardner equation with symbolic computation. Nonlinear Dyn. 69, 2031–2040 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  9. Zuo, D.W., Gao, Y.T., Meng, G.Q., Shen, Y.J., Yu, X.: Multi-soliton solutions for the three-coupled KdV equations engendered by the Neumann system. Nonlinear Dyn. 75, 701–708 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  10. Calogero, F.: A method to generate solvable nonlinear evolution equations. Lettere Al Nuovo Cimento 14, 443–448 (1975)

    Article  MathSciNet  Google Scholar 

  11. Radhakrishnan, R., Lakshmanan, M.: Dromion like structures in the (2+1)-dimensional breaking soliton equation. Phys. Lett. A 197, 7–12 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  12. Calogero, F., Degasperis, A.: Nonlinear evolution equations solvable by the inverse spectral transform. I. Nuovo Cimento B 31, 201–242 (1976)

    Article  MathSciNet  Google Scholar 

  13. Calogero, F., Degasperis, A.: Nonlinear evolution equations solvable by the inverse spectral transform. II. Nuovo Cimento B 39, 1–54 (1977)

    Article  MathSciNet  Google Scholar 

  14. Bogoyavlenskii, O.I.: Breaking solitons in (2+1)-dimensional integrable equations. Russ. Math. Surv. 45, 1–86 (1990)

    Article  MathSciNet  Google Scholar 

  15. Li, Y.S., Zhang, Y.J.: Symmetries of a (2+1)-dimensional breaking soliton equation. J. Phys. A 26, 7487–7494 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  16. Lou, S.Y.: A (2+1)-dimensional extension for the sine-Gordon equation. J. Phys. A 26, L789–L791 (1993)

    Article  MathSciNet  Google Scholar 

  17. Qin, Y., Gao, Y.T., Shen, Y.J., Sun, Y.H., Meng, G.Q., Yu, X.: Solitonic interaction of a variable-coefficient (2+1)-dimensional generalized breaking soliton equation. Phys. Scr. 88(045004), 1–7 (2013)

    Google Scholar 

  18. Geng, X.G., Cao, C.W.: Explicit solutions of the (2+1)-dimensional breaking soliton equation. Chaos Solitons Fract. 22, 683–691 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  19. Schiff, J.: Painlevé Transendent, Their Asymptotics and Physical Applications. Plenum, New York (1992)

    Google Scholar 

  20. Yan, Z.Y., Zhang, H.Q.: Constructing families of soliton-like solutions to a (2+1)-dimensional breaking soliton equation using symbolic computation. Comput. Math. Appl. 44, 1439–1444 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  21. Yu, S.J., Toda, K., Sasa, N., Fukuyama, T.: N soliton solutions to the Bogoyavlenskii–Schiff equation and a quest for the soliton solution in (3+1) dimensions. J. Phys. A 31, 3337–3347 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  22. Hamed, Y.S., Sayed, M., Elagan, S.K., El-Zahar, E.R.: The improved \((\frac{G^{\prime }}{G})\)-expansion method for solving (3+1)-dimensional potential-YTSF equation. J. Mod. Methods Numer. Math. 2, 32–38 (2011)

    Article  MATH  Google Scholar 

  23. Yan, Z.Y.: New families of nontravelling wave solutions to a new (3+1)-dimensional potential-YTSF equation. Phys. Lett. A 318, 78–83 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  24. Wang, Y.P.: Solving the (3+1)-dimensional potential-YTSF equation with Exp-function method. J. Phys.: Conf. Ser. 96(012186), 1–7 (2008)

    Google Scholar 

  25. Li, Z.T., Dai, Z.D.: Exact periodic cross-kink wave solutions and breather type of two-solitary wave solutions for the (3+1)-dimensional potential-YTSF equation. Comput. Math. Appl. 61, 1939–1945 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  26. Bai, C.L., Liu, X.Q., Zhao, H.: Bäcklund transformation and multiple soliton solutions for (3+1)-dimensional potential-YTSF equation. Commun. Theor. Phys. 42, 827–830 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  27. Ma, W.X., Huang, T.W., Zhang, Y.: A multiple exp-function method for nonlinear differential equations and its application. Phys. Scr. 82(065003), 1–8 (2010)

    Google Scholar 

  28. Hirota, R.: The Direct Method in Soliton Theory. Cambridge University Press, Cambridge (2004)

    Book  MATH  Google Scholar 

  29. Tian, B., Gao, Y.T.: Variable-coefficient higher-order nonlinear Schrödinger model in optical fibers: new transformation with burstons, brightons and symbolic computation. Phys. Lett. A 359, 241–248 (2006)

    Article  Google Scholar 

  30. Tian, B., Gao, Y.T.: Cylindrical nebulons, symbolic computation and Bäcklund transformation for the cosmic dust acoustic waves. Phys. Plasmas 12(70703), 1–4 (2005)

    MathSciNet  Google Scholar 

  31. Gao, Y.T., Tian, B.: (3+1)-Dimensional generalized Johnson model for cosmic dust-ion-acoustic nebulons with symbolic computation. Phys. Plasmas (Lett.) 13, 120703–120706 (2006)

    Article  Google Scholar 

  32. Gao, Y.T., Tian, B.: Reply to: Comment on: ‘Spherical Kadomtsev–Petviashvili equation and nebulons for dust ion-acoustic waves with symbolic computation’. Phys. Lett. A 361, 523–528 (2007)

    Article  MATH  Google Scholar 

  33. Barnett, M.P., Capitani, J.F., Gathen, Von Zur, Gerhard, J.: Symbolic calculation in chemistry: selected examples. Int. J. Quant. Chem 100, 80–104 (2004)

    Article  Google Scholar 

  34. Wadati, M., Sanuki, H., Konno, K.: Relationships among inverse method, Bäcklund transformation and an infinite number of conservation laws. Prog. Theor. Phys. 53, 419–436 (1975)

    Article  MathSciNet  MATH  Google Scholar 

  35. Rogers, C., Shadwick, W.F.: Bäcklund Transformations and Their Applications. Academic Press, New York (1982)

    MATH  Google Scholar 

  36. Zhang, H.Q., Meng, X.H., Li, J., Tian, B.: Soliton resonance of the (2+1)-dimensional Boussinesq equation for gravity water waves. Nonlinear Anal. Real World Appl. 9, 920–926 (2008)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

This work has been supported by the National Natural Science Foundation of China under Grant No. 11272023, by the Open Fund of State Key Laboratory of Information Photonics and Optical Communications (Beijing University of Posts and Telecommunications), and by the Fundamental Research Funds for the Central Universities of China under Grant No. 2011BUPTYB02.

Author information

Authors and Affiliations

  1. School of Science, Beijing University of Posts and Telecommunications, Beijing, 100876, China

    Ya Sun, Bo Tian, Yu-Feng Wang & Hui-Ling Zhen

  2. State Key Laboratory of Information Photonics and Optical Communications, School of Science, Beijing University of Posts and Telecommunications, Beijing, 100876, China

    Bo Tian

Authors
  1. Ya Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Bo Tian
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yu-Feng Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Hui-Ling Zhen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ya Sun.

Appendix: Some exchange formulas of the Hirota bilinear operator

Appendix: Some exchange formulas of the Hirota bilinear operator

The following exchange formulas of the Hirota bilinear operator hold for the real arbitrary functions f and \(f'\) [28–30]:

$$\begin{aligned}&(D_{y}^{2}f'\cdot f')f^{2}-(D_{y}^{2}f\cdot f)f'^{2}=2D_{y}(D_{y}f'\cdot f)\cdot (f'f),\\&D_{x}(D_{z}f'\cdot f)\cdot (f'f)=D_{z}(D_{x}f'\cdot f)\cdot (f'f),\\&D_{x}^{3}(D_{z}f'\cdot f)\cdot (f'f) \\&\quad =D_{z}(D_{x}^{3}f'\cdot f)\cdot (f'f)-3D_{z}(D_{x}^{2}f'\cdot f)\cdot (D_{x}f'\cdot f),\\&(D_{z}D_{t}f'\cdot f')f^{2}-(D_{z}D_{t}f\cdot f)f'^{2} \\&\quad =2D_{z}(D_{t}f'\cdot f)\cdot (f'f),\\&4(D_{x}^{3}D_{z}f'\cdot f')f^{2}-4(D_{x}^{3}D_{z}f\cdot f)f'^{2} \\&\quad =2D_{z}(D_{x}^{3}f'\cdot f)\cdot (f'f)+6D_{x}(D_{x}^{2}D_{z}f'\cdot f)\cdot (f'f)\\&\qquad -\,6D_{x}(D_{x}^{2}f'\cdot f)\cdot (D_{z}f'\cdot f){-}\,6D_{z}(D_{x}^{2}f'\cdot f)\cdot (D_{x}f'\cdot f) \\&\qquad -\,12D_{x}(D_{x}D_{z}f'\cdot f)\cdot (D_{x}f'\cdot f),\\&4D_{z}(D_{x}^{2}f'\cdot f)\cdot (D_{x}f'\cdot f)+D_{x}^{3}(D_{z}f'\cdot f)\cdot (f'f) \\&\quad =D_{x}[(D_{x}^{2}D_{z}f'\cdot f)-(D_{x}^{2}f'\cdot f)\cdot (D_{z}f'\cdot f) \\&\qquad +\,2(D_{x}D_{z}f'\cdot f)\cdot (D_{x}f'\cdot f)]. \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sun, Y., Tian, B., Wang, YF. et al. Bäcklund transformation and N-shock-wave solutions for a (3+1)-dimensional nonlinear evolution equation. Nonlinear Dyn 84, 851–861 (2016). https://doi.org/10.1007/s11071-015-2531-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-015-2531-1

Keywords

Search

Navigation