Skip to main content
SpringerLink
Log in

Bäcklund transformations and soliton solutions for a (2 + 1)-dimensional Korteweg–de Vries-type equation in water waves

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

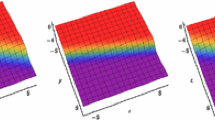
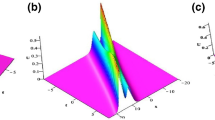
Under investigation in this paper is a \((2+1)\)-dimensional Korteweg–de Vries-type equation, which can describe the propagation of nonlinear waves such as the shallow-water waves, surface and internal waves. By virtue of the Bell polynomials, symbolic computation and auxiliary independent variable, the bilinear forms, Bäcklund transformations and soliton solutions are obtained. Solitonic propagation and elastic collisions between/among the two- and three-solitons are discussed analytically and graphically. It can be seen that, after each collision, solitonic shapes and amplitudes keep invariant except for some phase shifts, and the smaller-amplitude soliton moves faster and overtakes the larger.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Notes

  1. This operator is defined as \(R=D^{2}+4U+2U_{x}D^{-1}\) with \(D\) denoting the total derivative with respect to \(x\), \(D^{-1}u=\int u dx\), and \(U\) being a function of \(x\) and \(t\) [34–38].

References

  1. Korteweg, D.J., de Vries, G.: On the change of form of long waves advancing in a rectangular channel, and on a new type of long stabilizing wave. Phil. Mag. 39, 422 (1895)

    Article  MATH  Google Scholar 

  2. Zabusky, N.J., Kruskal, M.D.: Interaction of solitons in a collisionless plasma and the recurrence of initial states. Phys. Rev. Lett. 15, 240–243 (1965)

    Article  MATH  Google Scholar 

  3. Gardner, C.S., Greene, J.M., Krustal, M.D., Miura, R.M.: Method for solving the Korteweg–de Vries equation. Phys. Rev. Lett. 19, 1095–1097 (1967)

    Article  Google Scholar 

  4. Zhang, Y., Yang, S., Li, C., Ge, J.Y., Wei, W.W.: Exact solutions and Painleve analysis of a new (2+1)-dimensional generalized KdV equation. Nonlin. Dyn. 68, 445–458 (2012)

    Article  MATH  Google Scholar 

  5. Zhang, S.: Exact solutions of a KdV equation with variable coefficients via Exp-function method. Nonlin. Dyn. 52, 11–17 (2008)

    Article  Google Scholar 

  6. Ablowitz, M.J., Clarkson, P.A.: Soliton, Nonlinear Evolution Equations and Inverse Scattering. Cambridge University, Cambridge (1991)

    Book  Google Scholar 

  7. Biswas, A.: Solitary wave solution for KdV equation with power-law nonlinearity and time-dependent coefficients. Nonlin. Dyn. 58, 345–348 (2009)

    Article  MATH  Google Scholar 

  8. Ismail, M.S., Biswas, A.: 1-Soliton solution of the generalized KdV equation with generalized evolution. Appl. Math. Comput. 216, 1673–1679 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  9. Johnpillai, A.G., Khalique, C.M., Biswas, A.: Exact solutions of KdV equation with time-dependent coefficients. Appl. Math. Comput. 216, 3114–3119 (2010)

    Article  MathSciNet  Google Scholar 

  10. Biswas, A., Ismail, M.S.: 1-Soliton solution of the coupled KdV equation and GearCGrimshaw model. Appl. Math. Comput. 216, 3662–3670 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  11. Sturdevant, B.J.M., Biswas, A.: Topological 1-soliton solution of the generalized KdV equation with generalized evolution. Appl. Math. Comput. 217, 2289–2294 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  12. Lü, X., Tian, B., Qi, F.H.: Bell-polynomial construction of Bäcklund transformations with auxiliary independent variable for some soliton equations with one Tau-function. Nonlin. Anal. 13, 1130–1138 (2012)

    Article  MATH  Google Scholar 

  13. Triki, H., Biswas, A.: Soliton solutions for a generalized fifth-order KdV equation with t-dependent coefficients. Wave Random Complex 21, 151–160 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  14. Johnpillai, A.G., Khalique, C.M., Biswas, A.: Exact solutions of the mKdV equation with time-dependent coefficients. Math. Commun. 16, 509–518 (2011)

    MathSciNet  Google Scholar 

  15. Triki, H., Milovic, D., Biswas, A.: Solitary waves and shock waves of the KdV6 equation. Ocean Eng. 73, 119–125 (2013)

    Article  Google Scholar 

  16. Triki, H., Milovic, D., Hayat, T., Aldossary, O.M., Biswas, A.: Topological soliton solutions of (2+1)-dimensional KdV equation with power law nonlinearity and time-dependent coefficient. Int. J. Nonlin. Sci. Num. 12, 45–50 (2011)

    Article  MathSciNet  Google Scholar 

  17. Wang, G.W., Xu, T.Z., Ebadi, G., Johnson, S., Strong, A.J., Biswas, A.: Singular solitons, shock waves, and other solutions to potential KdV equation. Nonlin. Dyn. 76, 1059–1068 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  18. Sassaman, R., Biswas, A.: Topological and non-topological solitons of the KleinCGordon equations in 1+2 dimensions. Nonlin. Dyn. 61, 23–28 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  19. Ebadi, G., Mojaver, A., Triki, H., Yildirim, A., Biswas, A.: Topological solitons and other solutions of the Rosenau–KdV equation with power law nonlinearity. Rom. J. Phys. 58, 1–10 (2013)

    MathSciNet  Google Scholar 

  20. Biswas, A.: 1-Soliton solution of the K(m, n) equation with generalized evolution and time-dependent damping and dispersion. Comput. Math. Appl. 59, 2536–2540 (2010)

    Article  MathSciNet  Google Scholar 

  21. Ebadi, G., Mojaver, A., Kumar, S., Biswas, A.: Solitons and other solutions of the long-short wave equation. Int. J. Numer. Method H. 25, 129–145 (2015)

    Article  MathSciNet  Google Scholar 

  22. Wang, Y.Y., Dai, C.Q.: Elastic interactions between multi-valued foldons and anti-foldons for the (2+1)-dimensional variable coefficient Broer–Kaup system in water waves. Nonlin. Dyn. 74, 429–438 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  23. Antonova, M., Biswas, A.: Adiabatic parameter dynamics of perturbed solitary waves. Commun. Nonlin. Sci. Numer. Simul. 14, 734–748 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  24. Krishnan, E.V., Triki, H., Labidi, M., Biswas, A.: A study of shallow water waves with Gardners equation. Nonlin. Dyn. 66, 497–507 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  25. Biswas, A., Milovic, D., Ranasinghe, A.: Solitary waves of Boussinesq equation in a power law media. Commun. Nonlin. Sci. Numer. Simul. 14, 3738–3742 (2009)

  26. Hirota, R.: The Direct Method in Soliton Theory. Cambridge University, Cambridge (2004)

    Book  MATH  Google Scholar 

  27. Ma, W.X., Fan, E.: Linear superposition principle applying to Hirota bilinear equations. Comput. Math. Appl. 61, 950–959 (2011)

    Article  MathSciNet  Google Scholar 

  28. Razborova, P., Kara, A.H., Biswas, A.: Additional conservation laws for Rosenau–KdV–RLW equation with power law nonlinearity by Lie symmetry. Nonlin. Dyn. 79, 743–748 (2014)

    Article  MathSciNet  Google Scholar 

  29. Biswas, A.: Solitary waves for power-law regularized long-wave equation and R(m, n) equation. Nonlin. Dyn. 59, 423–426 (2010)

    Article  MATH  Google Scholar 

  30. Triki, H., Yildirim, A., Hayat, T., Aldossary, O.M., Biswas, A.: Shock wave solution of Benney–Luke equation. Rom. J. Phys. 57, 1029–1034 (2012)

    MathSciNet  Google Scholar 

  31. Wadati, M.: Wave propagation in nonlinear lattice. Phys. Soc. Jpn. 38, 673–680 (1975)

    Article  MathSciNet  Google Scholar 

  32. Barnett, M.P., Capitani, J.F., Gathen, J.V.Z., Gerhard, J.: Symbolic calculation in chemistry: selected examples. Int. J. Quantum Chem. 100, 80–104 (2004)

    Article  Google Scholar 

  33. Wazwaz, A.M.: A study on the (2+1)-dimensional KdV4 equation derived by using the KdV recursion operator. Math. Methods Appl. Sci. 36, 1760–1767 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  34. Baldwin, D.E., Hereman, W.A.: Symbolic algorithm for computing recursion operators of nonlinear partial differential equations. Int. J. Comput. Math. 87, 1094–1119 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  35. Fokas, A.S.: Symmetries and integrability. Stud. Appl. Math. 77, 253–299 (1987)

    MathSciNet  MATH  Google Scholar 

  36. Gürse, M., Pekcan, A.: 2+1 KdV (N) equations. J. Math. Phys. 52, 083516 (2011)

    Article  MathSciNet  Google Scholar 

  37. Matveev, V.B.: Positon–positon and soliton-positon collisions: KdV case. Phys. Lett. A 166, 209–212 (1992)

    Article  MathSciNet  Google Scholar 

  38. Jaworski, M., Zagrodzinski, J.: Positon and positon-like solutions of the Korteweg–de Vries and Sine–Gordon equations. Chaos Solitons Fract. 5, 2229–2233 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  39. Bell, E.T.: Exponential polynomials. Ann. Math. 35, 258–277 (1934)

    Article  Google Scholar 

  40. Gilson, C., Lambert, F., Nimmo, J., Willox, R.: On the combinatorics of the Hirota D-operators. Proc. R. Soc. Lond. A 452, 223–234 (1996)

    Article  MathSciNet  Google Scholar 

  41. Wang, Y.F., Tian, B., Wang, P., Li, M., Jiang, Y.: Bell-polynomial approach and soliton solutions for the Zhiber–Shabat equation and (2+1)-dimensional Gardner equation with symbolic computation. Nonlin. Dyn. 69, 2031–2040 (2012)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

Thank you very much for editors and referees’ kind letter with valuable comments. This work has been supported by the National Natural Science Foundation of China under Grant No. 11272023, by the Open Fund of State Key Laboratory of Information Photonics and Optical Communications (Beijing University of Posts and Telecommunications) and by the Fundamental Research Funds for the Central Universities of China under Grant No. 2011BUPTYB02.

Author information

Authors and Affiliations

  1. School of Science, Beijing University of Posts and Telecommunications, Beijing, 100876, China

    Yun-Po Wang, Bo Tian, Ming Wang, Yu-Feng Wang, Ya Sun & Xi-Yang Xie

  2. State Key Laboratory of Software Development Environment, Beijing University of Aeronautics and Astronautics, Beijing, 100191, China

    Bo Tian

  3. Key Laboratory of Information Photonics and Optical Communications, Ministry of Education, Beijing University of Posts and Telecommunications, Beijing, 100876, China

    Bo Tian

Authors
  1. Yun-Po Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Bo Tian
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ming Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yu-Feng Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Ya Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Xi-Yang Xie
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yun-Po Wang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, YP., Tian, B., Wang, M. et al. Bäcklund transformations and soliton solutions for a (2 + 1)-dimensional Korteweg–de Vries-type equation in water waves. Nonlinear Dyn 81, 1815–1821 (2015). https://doi.org/10.1007/s11071-015-2109-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-015-2109-y

Keywords

Search

Navigation