Introduction

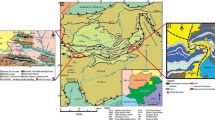
Decreasing discovery rates (Groves et al., 2023), a continually diminishing supply of current mineral resources (Vidal et al., 2022), and a growing demand for various metals (Calvo & Valero, 2022; Yu et al., 2023), all have the potential to disrupt the supply chains for many commodities (Ali et al., 2017). This is in particular pertinent to the so-called suite of “critical” minerals—metals, elements, or minerals that play a pivotal role in modern technologies (Knobloch et al., 2018; Jowitt & McNulty, 2021; Williams-Jones & Vasyukova, 2023) and might face potential supply chain disruptions (Jowitt et al., 2017). Although different countries maintain their own lists of critical minerals, Canada′s list (NRCan – RNCan, 2022) include niobium (Nb) and rare earth elements (REEs). REEs are a group of 17 elements, consisting of scandium (Sc), yttrium (Y), and lanthanides—elements from lanthanum (La) to lutetium (Lu) corresponding to atomic numbers 57 to 71. Some 60% of the world′s REE resources (Zhou et al., 2017) and the majority of world′s global Nb production are associated with carbonatites (de Oliveira Cordeiro et al., 2011; Mitchell, 2015). These silica-poor igneous rocks are distinguished by their composition comprising over 50% total carbonates (Le Maître, 2002) and serve as the primary sources of Nb and REEs (Simandl & Paradis, 2018). Mineralized carbonatites exhibit enrichment in light rare earth elements (LREEs: Verplanck et al., 2014), spanning from La to europium (Eu), and can be potentially enriched in iron, thorium, uranium, strontium, barium, zirconium, copper, fluorite, and apatite (Laznicka, 2006). Some of the world′s renowned carbonatite-associated REE deposits include the Bayan Obo deposit in Inner Mongolia, China (Berger et al., 2009; Smith et al., 2015), the Mountain Pass deposit in California, USA (Castor, 2008), and the Mount Weld deposit in Australia (Lottermoser, 1990). Also, carbonatite-associated complexes in Brazil (de Oliveira Cordeiro et al., 2011) produce a majority of world′s Nb (Mitchell, 2015). There are examples of Canadian REE +/− Nb occurrences associated with carbonatites (Fig. 1); Saint-Honoré (Fournier, 1993; Mitchell, 2015; Néron et al., 2018), Oka (Eby, 1975; Treiman & Essene, 1985), and Ashram (Mitchell & Smith, 2017; Beland & Williams-Jones, 2021) are hosted within the Canadian Shield (Rukhlov & Bell, 2010), encompassing the Grenville, Superior, and Churchill geological provinces (Wheeler et al., 1996), whereas Wicheeda (Dalsin et al., 2015; Mackay et al., 2016; Trofanenko et al., 2016) and associated occurrences within the Blue River complex (Simandl et al., 2001; Mitchell et al., 2017) are hosted within the Canadian Cordillera.

Figure 1
figure 1

Spatial distribution of Canadian carbonatite-hosted REE +/− Nb occurrences (see Supplementary Material 1) superimposed on the geological provinces of Canada (after Wheeler et al., 1996). These occurrences are distributed across multiple geological provinces, notably the Cordilleran Orogen, Superior, and Grenville Provinces

Full size image

The wide-ranging industrial applications of REEs and Nb (Mitchell, 2015; Dushyantha et al., 2020) coupled with the ever-increasing demand for these commodities render carbonatites highly appealing exploration targets. Accordingly, the primary goal of this study was to exploit machine learning algorithms to identify potential regions of interest for Canadian carbonatite-hosted REE +/− Nb deposits with national-scale mineral prospectivity modeling (MPM). The findings of this study complement existing national-scale prospectivity models of Canadian critical metals (Lawley et al., 2021, 2022). They can also be used to compare the geological prospectivity of Canadian mineralized carbonatites with those of Australia (Ford et al., 2023), India (Aranha et al., 2022a, b; Aranha et al., 2023), and beyond (e.g., Morgenstern et al., 2018).

Examples of machine learning-based mineral prospectivity models abound in the literature (e.g., Porwal et al., 2003; Carranza & Laborte, 2015; Harris et al., 2015; Ford, 2020; Chen et al., 2020, 2021; Chen and Sui, 2022; Zuo & Xu, 2023; Zuo et al., 2023). Yet, machine learning-based predictive modeling of Canadian carbonatite-hosted REE +/− Nb systems is intrinsically faced with challenges. The primary challenge is a widespread issue in MPM, characterized by a significant imbalance between the target features (Li et al., 2021). In this study, it is evident while comparing a very small number of true positives (n = 71), the location of Canadian carbonatite-hosted REE +/− Nb occurrences, with areas not associated with such occurrences in Canada. In this study, employing different unique cell sizes yielded a ratio of cells containing true positives to the remaining cells ranging from 0.005 to 0.05%. This extreme imbalance is more pronounced than in previously developed Canadian national-scale prospectivity models (Lawley et al., 2021, 2022), which is linked to the scarcity of mineralized carbonatites compared to other mineral systems in Canada, such as sediment-hosted Zn–Pb and magmatic Ni mineral systems. This target feature label imbalance problem potentially leads to poor generalization or over-fitting of predictive models (cf. Kuhn & Johnson, 2013). Additionally, as elaborated in the forthcoming sections, inherent disparities exist between carbonatite-hosted REE +/− Nb occurrences in the Canadian Cordillera and those in the Canadian Shield, adversely affecting the predictive capability of prospectivity models (cf. Parsa & Carranza, 2021; Lawley et al., 2022). Moreover, the application of machine learning algorithms to MPM as a binary classification problem requires the incorporation of true negative labels (Zuo & Wang, 2020). Lastly, there is also the problem of interpretability of some machine learning-based predictive models; that is, it is not directly possible to determine which variables have the most significant impact on neural network-based models′ predictions.

A multi-step approach to tackling the above challenges is presented herein, leveraging global hierarchical tessellations (Dutton, 1991) to alleviate the target feature label imbalance issue. Concurrently, an ensemble learning approach is introduced to assist in quantifying the inherent stochastic uncertainties of predictive models and mitigating potential model artifacts arising from label discrepancies. Moreover, data space similarity measures (Mathisen et al., 2020) were employed to handle ′true negatives′ within prospectivity models. Additionally, Shapley additive explanations (SHAP: Lundberg & Lee, 2017) were employed to evaluate the impact of individual variables on predictive models.

Publicly available geophysical (Bradley, 2008; Miles & Oneschuk, 2016; Jobin et al., 2017; Czarnota et al., 2020; Lawley et al., 2021, 2022), geological (Lawley et al., 2022 and references therein), and geochronological (NRCan – RNCan, 2023) data were exploited in this study to define a set of vectors that represent potential drivers, sources, and fluid flow architectures for carbonatite-hosted REE +/− Nb deposits. These vectors were then used as input for predictive models, coupled with the adopted methodologies in this study to narrow the exploration search space for carbonatite-hosted REE +/− Nb deposits. We opted to use convolutional neural networks (CNN: O′Shea & Nash, 2015) and random forest (RF: Breiman, 2001) because these are two popular, robust tools, applied to MPM (Zuo & Carranza, 2023). Finally, some conclusions are drawn based on these models′ performance, generalization, and predicting ability.

Carbonatite-hosted REE +/− NB deposits

Carbonatites and peralkaline suites are two categories of alkaline igneous rocks associated with REE mineralization (Verplanck et al., 2014; Dostal, 2016). The former group are mostly LREE-enriched (Verplanck et al., 2016), intrusive bodies supplying a majority of world′s Nb (Mitchell, 2015) and REEs (Zhou et al., 2017). Documented carbonatites are distributed over all continents and have diverse ages (Humphreys-Williams & Zahirovic, 2021). Nevertheless, their occurrence is frequent in Archean or Proterozoic rock formations or in Phanerozoic rocks underlain by Precambrian basement (Simandl & Paradis, 2018). The shape and size of carbonatites are influenced by the configuration of magmatic systems with which they are associated, resulting in significant variability (Verplanck et al., 2014). Supplementary Material 1 offers an overview of the Canadian carbonatite-hosted REE +/− Nb occurrences utilized in this study. These occurrences were used as positive labels that feed machine learning algorithms.

At least three mechanisms (Yaxley et al., 2021) are required to produce silica-poor, high-temperature, low-viscosity carbonatite magmas (Fig. 2). These are: (1) high-pressure mantle-derived primary carbonate melts (Wallace & Green, 1988; Yaxley and Brey, 2004), (2) immiscible carbonate melts (Freestone & Hamilton, 1980; Kjarsgaard & Peterson, 1991; Brooker & Kjarsgaard, 2011), and (3) residual-carbonate melts (Watkinson & Wyllie, 1971). The first mechanism posits that the emplacement of carbonatite magmas is a direct consequence of the partial melting of carbonate-bearing material in the mantle (Fig. 2a). According to the second mechanism, an immiscible carbonatite magma forms through segregation from CO2-rich, silica-deficient peralkalic magmas. This immiscibility arises due to the fractionation of the initial or a more evolved liquid, altering its composition toward a two-liquid solvus. This process results in the division of the silica-poor silicate melt and the carbonatite melt (Fig. 2b). The third mechanism proposes that the fractional crystallization of a silica-deficient, carbonated silicate melt leads to the creation of an advanced, highly evolved carbonatite liquid, bypassing the interaction with a solvus boundary (Fig. 2c).

Figure 2
figure 2

Schematic representation of diverse scenarios for the genesis of carbonatites (after Yaxley et al., 2021). This includes (a) direct partial melting of carbonated lithosphere near rift zones or along cratonic margins, as well as (b) fractional crystallization of minerals such as olivine, clinopyroxene, nepheline, and calcite from a of a silica-poor carbonated melt that leads to a solvus with two distinct liquids, triggering the separation of a carbonatite liquid, and (c) fractional crystallization of minerals such as a silica-deficient, carbonated melt leading to an evolved carbonatite phase, bypassing any interaction with a solidus

Full size image

Considering the above three mechanisms, we employed a mineral systems framework (Knox-Robinson & Wyborn, 1997) to define a suite of spatial vectors (i.e., mappable criteria or their proxies) that could be used as input for MPM. This framework offers a holistic approach that extends beyond the immediate environment of a mineral deposit to encompass the fundamental processes that are responsible for concentrating ore components from source to trap (Knox-Robinson & Wyborn, 1997). The spatial vectors defined herein explain all the essential components necessary for the formation of a carbonatite-hosted REE +/− Nb mineral system. These include drivers, sources of metals, as well as deep and crustal architectures that focus melts and mechanisms controlling mineral trapping (e.g., Skirrow et al., 2019; Lawley et al., 2021, 2022; Ford et al., 2023). The specifics of these vectors are summarized in Table 1 and elaborated in the subsequent sections.

Table 1 Vectors used for prospectivity modeling of carbonatite-hosted REE +/− Nb occurrences deposits
Full size table

Triggers and Energy Sources

Carbonatites are typically formed in extensional tectonic settings (Verplanck et al., 2014; Simandl & Paradis, 2018). They may exhibit spatial association with features such as cratonic margins, rifts, and extensional faults (see Fig. 2a), offering the requisite conditions for the partial melting of mantle materials (Verplanck et al., 2014). To model such tectonic environments, we delineated the boundaries of geological provinces (Wheeler et al., 1996) and passive margins (Bradley, 2008), quantified the proximity to these boundaries, and considered them as vectors in our models (Table 1). We, however, refrained from including faults in our prospectivity models because mapping these structures, which is primarily conducted through field surveys and remote sensing techniques in Canada (e.g., Behnia et al., 2013), depends on their surficial exposure. And, since a significant portion of Canada is covered by vegetation and glacial sediments (Shilts, 1993), relying on such a fault inventory might introduce a bias into our models.

Major mantle melting events represent the drivers of carbonatite-hosted deposit formation. These events can be mapped in time using the geological ages available in bedrock map compilations (e.g., Lawley et al., 2021, 2022) (Table 1). We converted the geochronological vectors developed by Lawley et al. (2021) into binary vectors with one-hot encoding—the process of transforming a categorical vector (i.e., geological ages referenced to the international chronostratigraphic chart) into a set of binary vectors that indicate the presence or absence of individual categories (Seger, 2018).

Sources

Per stable and radiogenic isotopic data (Bell, 1989), carbonatites′ metal content is linked to low degrees of partial melting (Yaxley et al., 2021), derived from carbonate-bearing eclogite or peridotite in the upper mantle (Hunter & McKenzie, 1989). Also, stable REE-bearing complexes are transported with orthomagmatic fluids expelled from parental carbonatite magmas (Rankin, 2005). To map mantle sources of ore-bearing complexes, we applied one-hot encoding to the compilation of Canadian bedrock geology (Lawley et al., 2021, 2022) to construct a spatial vector representing alkaline suites, indicative of potential mantle sources (Table 1).

Deep and Crustal Architectures

Lithospheric thickness exerts control on fractional crystallization and thereby metal enrichment of carbonatite magmas (Beard et al., 2023). Depth to lithosphere–asthenosphere boundary, defined based on deep reflection seismic data (Czarnota et al., 2020), was, therefore, used as a vector to model favorable deep-seated structures (Table 1). In addition, deep-seated fault systems serve as primary crustal architectures facilitating the ascent of carbonatite melts to the surface, as outlined by Berger et al. (2009). Magnetic and gravity anomalies can be used as proxies to map these deep structures in the subsurface, as described in Table 1.

Trapping Mechanism and Ore Emplacement

Carbonatites might be components of larger alkaline suites, typically being younger than the surrounding alkaline rocks (Verplanck et al., 2014). The widespread spatial association between carbonatites and alkaline suites is well-documented, although the possibility of a genetic link between these two categories remains a topic of debate (Gittins & Harmer, 2003). Alkaline igneous suites, therefore, can act as vectors, indicating the presence of carbonatites. Similarly, positive spatial associations exist between Canadian carbonatite-hosted REE +/− Nb occurrence and igneous suites, prompting us to consider igneous suites and mafic-to-ultramafic igneous suites as additional vectors associated with the trapping mechanism (Table 1).

Mafic alkalic sequences with high magnetic susceptibility are associated with magnetic highs (Satterly, 1970), rendering magnetic anomaly maps as a proxy for favorable emplacement environments. In this study, a reduced-to-pole magnetic anomaly map was utilized to showcase these anomalies (Table 1). Also, some carbonatite-hosted REE +/− Nb occurrences are associated with gravity anomaly highs (Carlson & Treves, 2005), potentially because of the presence of dolomitic carbonatites, syenites, and basalts. In this study, a Bouguer anomaly map was used to capture these geophysical anomalies (Table 1).

Methods

Gridding and Labeling

The common procedure in data-driven mineral prospectivity modeling using tabular datasets involves establishing a tessellation of cells to which values of spatial vectors are assigned. For this purpose, traditional latitude–longitude and discrete global tessellations (Lawley et al., 2021) were utilized. The latter, often referred to as discrete global gridding systems (Dutton, 1991), represents a comprehensive mosaic that spans the entire Earth′s surface. This system is essentially a method of space partitioning, consisting of numerous polygons that collectively segment the Earth′s surface. During the process of recursive partitioning, this grid evolves into a series of discrete global grids with increasingly finer resolution, thereby creating a hierarchical grid structure, commonly known as a global hierarchical tessellation (Dutton, 1991). In the context of this study, we employed S2 hierarchical tessellations (https://github.com/google/s2geometry). The hierarchical nature of these quadrilateral cells enables efficient data storage and retrieval, which is particularly beneficial in handling large datasets used for a national-scale MPM. It also allows for quicker processing and analysis of mineral prospectivity data, compared to traditional latitude–longitude tessellations. In a S2 tessellation, each parent S2 cell at a given level of the hierarchy can be subdivided into four equal-sized child cells (Dunnington et al., 2020). This is beneficial for defining augmented positive samples for MPM as practiced in this study.

For selecting negative samples, we considered selecting cells that are the least similar, in terms of multi-dimensional geospatial features, to positive labels. This was practiced by measuring the similarity of positive labels to the rest of S2 cells using cosine similarity measures. Cosine similarity is a metric used to determine the similarity between two vectors in a multi-dimensional space. The cosine similarity index calculates the cosine of the angle between two vectors, which indicates how closely aligned these vectors are. The index ranges from − 1 to 1, where 1 indicates perfect similarity and values below or equal to 0 represent dissimilarity. Further details on cosine similarity measures can be found elsewhere (e.g., Han et al., 2012). We measured the similarity between each augmented positive label and the rest of S2 cells in our data cube. It was followed by average voting to determine the average similarity of S2 cells with carbonatite-hosted REE +/− Nb occurrences. The average similarity model was visualized and used to demarcate the boundaries of areas containing the lowermost 5% of average similarity indices. Having delineated these boundaries, randomly distributed S2 cells were selected within the delineated boundaries and considered negative labels. Following Porwal et al. (2003), an equal number of positive and negative labels was selected to account for the balance of labeled samples. The random selection process was adopted based on the rationale that, in contrast to the typically clustered distribution of mineral deposits, negative labels are expected to exhibit a random spatial distribution (Carranza, 2009).

Modeling

Two algorithms, namely RF and CNN, were employed to generate prospectivity models for carbonatite-hosted REE +/− Nb occurrences. These algorithms were selected in light of their robustness and demonstrated performance in the literature for MPM (Zuo & Carranza, 2023). RF, a shallow ensemble learning algorithm, is a popular algorithm of choice for MPM (e.g., Carranza & Laborte, 2015; Harris et al., 2015; Ford, 2020), which applies majority voting to a forest of random decision trees, yielding high predictive performance and reliable model generalization. Robust pattern recognition and the ability to extract information from large datasets have also led many to apply different variations of CNNs, including one- and two-dimensional architectures, to MPM (Zhang et al., 2021; Li et al., 2021, 2022; 2023). Owing to the premise that both one-dimensional CNNs and RF could be applied to tabular data (Li et al., 2023; Zuo and Xu, 2023), we were inclined to use one-dimensional CNNs in our study. Both RF and CNN are well-documented in the literature (e.g., Harris et al., 2015; Li et al., 2021). For both algorithms, we re-scaled our data cube using the MinMaxScaler transformation, which is commonly used in data science and machine learning (e.g., Kim et al., 2020). This transformation re-scales data to the range [0, 1] ensuring that the minimum and maximum values correspond to these endpoints.

Also, as carbonatites and their mineralized components are mantle-related (Fig. 2), it was deemed essential for this study to have base prospectivity models that potentially capture deeper signatures of carbonatites. Base prospectivity models are the least sensitive to surface sampling bias, because only the most complete geophysical datasets were used for training these models. Base models were exclusively constructed utilizing spatial vectors pertinent to magnetic, gravimetric, and seismic surveys (Table 1). These vectors are indicative of the deeper sub-surface regions associated potentially with carbonatite-hosted REE +/− Nb mineralization (Fig. 2). In contrast, comprehensive models incorporate all spatial vectors, including geological datasets that are biased by the availability and quality of bedrock exposure. Nevertheless, the comprehensive models include data supporting each component of the mineral system and have the potential to outperform the base model for well-mapped areas.

Risk and Return Values of Prospectivity Models

Notable disparities in geospatial features of labels can induce bias in machine learning-based predictive models (Parsa and Carranza, 2021). To mitigate this issue, instead of using only one set of labels for training and testing algorithms, we used an iterative methodology, sampling different labels for training and testing algorithms in each iteration. This process introduces more diversity to labels, making the models less sensitive to carbonatite-hosted REE +/− Nb occurrences hosted within the Cordillera. To achieve this, before each iteration, labels underwent a shuffling process to ensure that the training and testing labels differed in every iteration. This was achieved by selecting a unique random seed, an initial value fed into the algorithm for generating pseudo-random numbers, for each iteration (Hastie et al., 2009). In each iteration, stratified random sampling (Cochran, 1946) was used to split training (70% of labels) and testing (30% of labels) labels to minimize the bias by sampling an equal number of positive and negative labels in the training and testing sets. In this study, models generated with both RF and CNN were implemented with 50 iterations. This higher number of iterations made the processing time longer and hindered our experimentations.

The above iterative procedure results in estimating n (the number of iterations) different sets of prospectivity values, P1, P2, …, Pn, for any given S2 cells, allowing for measuring the stochastic uncertainty of prospectivity values (Parsa and Carranza, 2021). This uncertainty is linked to significant differences of geophysical and geological features associated with Canadian carbonatite-hosted REE +/− Nb occurrences. Having a set of prospectivity values for any given location also allows for a risk–return analysis (Wang et al., 2020), which can help with the interpretation of prospectivity models. As such, a high return S2 cell is one with high average prospectivity value. A high variation in the estimated prospectivity values for a given cell, however, results in high uncertainty or high-risk value. From a mathematical point of view, at a given location, the estimated prospectivity value can be explained by odds as logO (P) = log (P/1 − P). At a given S2 cell, j, one can quantify the values of return and risk using, respectively, the following equations:

$${\text{return}}\left( j \right) \, = \overline{{\log \,{\text{O}} }} = \frac{1}{L} \log \,{\text{O}}\left( {P\left( {j^{l} } \right)} \right)$$
(1)
$${\text{risk}}\left( j \right) \, = \frac{1}{L - 1} \mathop \sum \limits_{l = 1}^{L} \left( {{\text{log}}\,{\text{O}}\left( {P\left( {j^{l} } \right)} \right) - \overline{{{\text{log}}\,{\text{O }}}} } \right)^{2}$$
(2)

where L and \(P\left({j}^{l}\right)\) are the number of iterations and the prospectivity value for location j, respectively (Wang et al., 2020).

The procedure explained above is an ensemble modeling procedure, which allows to (1) quantify the values of risk (i.e., stochastic uncertainty linked to diversity of positive cells) and return for individual cells and (2) help with model′s generalization (Parsa & Carranza, 2021). It is, however, important to note that this procedure is different from the one applied by Parsa and Carranza (2021), in that they employed bootstrapping (Mooney et al., 1993) to quantify the stochastic uncertainties of their models. The primary distinction between the method we employed here and bootstrapping lies in the sampling technique. The latter involves repeatedly drawing samples from the original dataset with replacement, whereas our method here selects samples randomly without replacement. Consequently, our approach is more suited to enhancing the diversity of labels for machine learning algorithms.

Fine Tuning and Network Architecture

The CNN model designed and used in this study was a one-dimensional CNN, comprising an input layer, a one-dimensional convolutional layer (Conv1D), a one-dimensional pooling layer, a flatten layer, fully connected dense layers, and an output layer. One-dimensional CNNs are typically used for signal processing (e.g., Kiranyaz et al., 2020), but they are also effective tools for processing tabular data (e.g., Li et al., 2023). In this regard, the data cube was fed into the input layer. In the convolutional layer, one-dimensional convolutional filters apply the convolution to a portion of the array as defined by the shape of kernels in this layer. The Conv1D applied herein constitutes 512 filters and a kernel size of 5. This layer is adept at feature extraction from input data, utilizing filters and being activated by a rectified linear unit (ReLU) activation function (see Ramachandran et al., 2017). Following this, a pooling layer, namely the MaxPooling layer (see Gholamalinezhad & Khosravi, 2020), steps in to condense the data dimensionality, encapsulating the features identified by the convolutional layer. Subsequently, the data undergo transformation via a flatten layer, thereby priming the data for the subsequent fully connected dense layers. Post-flattening, the model incorporates three dense layers with 256, 128, and 64 neurons, respectively, each employing the ReLU activation function. These layers are engineered to interpret the features delineated by the convolutional layer. Culminating the model is a dense output layer, consisting of a single neuron activated by a sigmoid function (see Ramachandran et al., 2017), dedicated to rendering the predicted output. The model employs the Adam optimizer, which is widely favored for its adaptive learning rate mechanism (Kingma & Ba, 2014). The mean squared error function, as the loss function, was used to quantify the average of the squares of discrepancies between predicted and actual values. To reduce over-fitting and pinpoint the optimal stopping point for training, an early stopping mechanism was integrated as a callback (see Prechelt, 2002), halting the training when the monitored metric, in this case, validation loss, ceased to improve. To further lower the probability of over-fitting, the connection between convolutional layers and activation functions was facilitated by batch normalization (e.g., Chen et al., 2019) and dropouts (Khan et al., 2020). The architecture presented above was honed through a systematic trial-and-error aiming to refine the models′ efficacy and to secure the most robust results. Modeling was implemented within a Python environment (version 3.9.13), exploiting a variety of different packages, including Scikit-learn (https://github.com/scikit-learn/scikit-learn) and TensorFlow (https://github.com/tensorflow/tensorflow).

Hyperparameter optimization of RF was implemented by a method called Grid Search (GS: Bergstra & Bengio, 2012). Some hyperparameters of the RF algorithm require optimization, namely the number of trees, the maximum depth of trees, and the minimum number of samples required to form a leaf in the tree, and the minimum number of samples required to split an internal node (Breiman, 2001). The maximum depth of each tree was allowed to vary within a range of 0 to 20. Additionally, the minimum number of samples required at each leaf node was set within a range of 1 to 4, while the minimum number of samples needed to split an internal node fell within a range of 1–10. The number of trees in the forest was also variable, ranging from 1000 to 2000. For these parameters, GS starts with defining a set of initial parameters and then systematically tests combinations of different settings to find the most robust model in terms of performance, which was evaluated using area under the curve (AUC) of receiver operating characteristics (ROC: Swets, 2014). The GS was combined with cross-validation to provide a robust estimate of a model′s performance. All models were run with fivefold cross-validation, meaning that each model was derived with 50 iterations of fivefold cross-validation.

Performance Evaluation

A models′ performance was evaluated with the AUC of ROC for testing labels, offering insights into the models′ generalization capabilities by showcasing their predictive performance (i.e., models′ return) on unseen data (e.g., Parsa, 2021). This index, however, does not measure a models′ efficiency in narrowing down the search area for mineral exploration. To evaluate how well a model reduced the exploration search space, we employed success-rate curves (Chung & Fabbri, 2003; Agterberg & Bonham-Carter, 2005), providing a more specific assessment of the models′ effectiveness in this context. In both ROC and fitting-rate curves, higher AUC values indicate a generally better performance (e.g., Parsa, 2021).

Feature Importance

In this study, we used Shapley additive explanation (SHAP: Lundberg & Lee, 2017; Molnar, 2020) for assessing the importance of our input vectors in prospectivity models generated by CNNs (e.g., Yang et al., 2024; Zuo et al., 2024). We used SHAP given the premise that assessing the importance of features is not directly possible with CNN-based models (Zhang et al., 2021). Utilizing game theory principles, SHAP assigns an importance value to each input vector based on its impact on a model′s prediction outcome. In MPM, SHAP considers a tabular dataset′s vectors (features) as a coalition, with each vector contributing differently to the overall prospectivity score. Shapley values are used to measure the average contribution of each coalition member to the prospectivity score of each sample, allowing for comparison of the coalition′s performance with and without specific members. As a local explanation method (Molnar, 2020), SHAP focuses on explaining the effects of individual samples on a model’s prediction, but it can also provide global explanations through the aggregation of individual predictions. Shapely values (Φi) are quantified as (Molnar, 2020):

$$\Phi_{i} \left( {f, x} \right) = g\left( x \right) = \mathop \sum \limits_{{z^{\prime} \subset x^{\prime}}} \frac{{\left| {z^{\prime}} \right|!\left( {M - \left| {z^{\prime}} \right| - 1} \right)!}}{M!} . \left[ { f_{x} \left( {z^{\prime}} \right) - f_{x} \left( {z^{\prime}\backslash i} \right)} \right]$$
(3)

where Φi is the Shapely value for the ith vector (feature) in a tabular dataset, f is the black box model, x is a single row in the tabular dataset, \({z}{\prime}\) is a subset of all possible combinations of vectors in the coalition, \(x{\prime}\) denotes all possible combinations of vectors, and \({f}_{x} \left({z}{\prime}\right)\) is the output of the black box while including the ith vector, whereas \({f}_{x} \left({z}{\prime}\backslash i\right)\) refers to the output of the black box excluding the ith vector. In this context, \(\left[{f}_{x} \left({z}{\prime}\right)- {f}_{x} \left({z}{\prime}\backslash i\right)\right]\) is referred to as the marginal value, which is calculated for each permutation of all possible subsets. \(\left|{z}{\prime}\right|\) and M are the number of vectors in the subset and total number of vectors, respectively. The explainer function, g(x), can be regarded as a tool that analyzes the black box of complex neural network models. In this study, we used the DeepExplainer of the SHAP Python package (https://github.com/shap/shap) as our explainer function, which is employed for measuring Shapely values for CNN-based predictive models (Lundberg & Lee, 2017).

For RF-based models, feature importance was assessed by the Gini index (Breiman, 2001). As an ensemble modeling was practiced in this study, feature importance was assessed per iteration. The average of Gini indices and Shapely values was then considered as the importance of a given vector. To further assist the interpretation of vectors and their potential contribution in our predictive models, we quantified the spatial associations of vectors (Table 1) with the carbonatite-hosted REE +/− Nb deposits using the AUC for the ROC plot (Table 1).

Visualization and Interpretation

As explained in previous sections, two values were derived per model for individual S2 cells, namely risk and return. In this study, risk and return were classified into three classes using 33% and 66% quantiles. It was followed by using bivariate choropleth risk–return plots to simultaneously demonstrate models′ risk and return. Generally, low-risk, high-return cells should be considered as the highest priority for further exploration surveys, whereas high-risk, high-return and low-return classes present less-reliable exploration targets.

Results

Utilizing the s2sphere Python package (https://github.com/sidewalklabs/s2sphere), we defined a tessellation consisting of level 12 cells within the S2 system. This tessellation comprised 1,939,898 cells, collectively encompassing the entirety of Canada′s terrestrial areas. Each S2 level 12 cell spanned an approximate area of 5 km2. MPM was conducted using both finer (s2 level 13) and coarser (s2 level 14) cells for comparison. The latter produced inferior results relative to those presented here. Conversely, the finer cells led to a significantly increased cell count (approximately 4 ×), which rendered the modeling process computationally expensive, thereby hindering experimentation with models. Zonal statistics were subsequently performed using the rasterstats Python package (https://github.com/perrygeo/python-rasterstats) to assign the values of spatial vectors (Table 1) to S2 level 12 cells. This process resulted in a data cube comprising: (1) 1,939,898 rows or S2 cells; (2) 25 columns, each representing a spatial vector (Table 1); (3) a target variable indicating the presence or absence of carbonatite-hosted REE +/− Nb mineralization in S2 cells; and (4) a column containing unique S2 cell IDs that can be used for joining operations. This step was succeeded by the designation of labels for the training and validation of models. Within the data cube, cells containing at least one carbonatite-hosted REE +/− Nb occurrence were deemed positive labels, resulting in only 71 positive cells. The number of carbonatite-hosted REE +/− Nb occurrences reported in Supplementary Material 1 is higher than this due to the fact that many entries in Supplementary Material 1 represent drill holes that are relatively close to each other or different zones within a single mineral deposit. Such entries were considered as a single positive label. A significant target feature label imbalance issue arises when comparing the quantity of labeled data to the total number of S2 cells, which could hinder the generalization capability of models (cf. Kuhn and Johnson, 2013). The models generated using only 71 positive labels performed poorly in terms of generalization and predictive capability, inclining us to leverage the hierarchical relationship between child and parent cells to augment the dataset with additional labels. Therefore, S2 level 13 child cells corresponding to positive labeled cells were identified and considered as 248 augmented positive labels. Following the procedure explained in the METHODS section above, 248 negative labels were also selected. The 248 augmented positive labels and the selected negative labels underwent zonal statistics analysis, resulting in a matrix comprising 496 rows and 27 variables, encompassing spatial vectors, the target variable, and S2 cell IDs.

Canadian carbonatite-hosted REE +/− Nb occurrences are distributed across various geological provinces, each exhibiting distinct geospatial characteristics. This diversity was elucidated through their representation on a multi-dimensional scale, as demonstrated by multi-dimensional scaling (MDS)—a statistical technique that analyzes and visualizes similarity or dissimilarity in a condensed dimensional space. Readers are referred to Kruskal (1964) for further details on MDS. Derived from the spatial vectors utilized in this study (Table 1), Figure 3 color-codes carbonatite-hosted REE +/− Nb occurrences according to the geological provinces they inhabit on a MDS plot. This figure reveals a distinct clustering pattern of carbonatite-hosted REE +/− Nb occurrences situated in the Cordillera, setting them apart from deposits in other geological provinces. When implementing data-driven MPM, this observation translates into models proficiently predicting carbonatite-hosted REE +/− Nb occurrences within the Cordillera but exhibiting limited accuracy elsewhere. This discrepancy arises because the geospatial features of these deposits are more readily discernible by machine learning algorithms. We, therefore, used the procedure introduced in the METHODS section to add more diversity to our labels. Base and comprehensive models were produced from 50 iterations, allowing for quantifying the values of risk and return. Tables 2 and 3 summarize the optimized parameters obtained for each iteration, detailing the configuration of base and comprehensive RF models, respectively.

Figure 3
figure 3

Multidimensional scaling of Canadian carbonatite-hosted REE +/− Nb occurrences. Colors are based on host geological provinces, and key occurrences are labeled for identification. A distinct separation is evident between the occurrences located in the Cordilleran Orogen and those within the Canadian Shield, including Grenville, Superior, and Churchill

Full size image
Table 2 Optimized hyperparameters per iteration for the RF-based base model
Full size table
Table 3 Optimized hyperparameters per iteration for the RF-based comprehensive model
Full size table

Bivariate choropleth risk–return plots were used to visualize the RF-based models (Fig. 4a, c). High-return, low-risk cells covered approximately 9% of Canada in the base RF model; whereas 33% of Canada was classified as low-return. Likewise, high-return, low-risk cells accounted for merely 6% of total S2 cells in the comprehensive RF model, whereas low-return cells accounted for some 30% of the cells in this model. High-return, low-risk S2 cells covered 7% of Canada in the CNN-based model, whereas 9% of Canada was covered by such S2 cells in the comprehensive CNN-based model. Low-return S2 cells accounted for 33% of total cells in both CNN-based models (Fig. 4b, d).

Figure 4
figure 4

Bivariate choropleth risk–return maps representing prospectivity models of Canadian carbonatite-hosted REE +/− Nb deposits: (a) RF-derived base prospectivity model; (b) CNN-derived base prospectivity model; (c) RF-derived comprehensive prospectivity model; and (d) CNN-derived comprehensive prospectivity model. Black lines depict the boundaries of Canada’s geological provinces (after Wheeler et al., 1996)

Full size image

The average AUC of ROC for the testing labels was 0.91 for the RF-based model. This number, however, was 0.95 for the comprehensive RF-based model. The CNN-based models performed slightly differently from the RF-based models. The average AUC of ROC for the testing labels was 0.93 and 0.96 for base and comprehensive CNN-based models, respectively (Fig. 5). As per the success-rate curves (Fig. 6), the base RF model was the worst-performing model with an AUC of fitting-rate of 0.86, whereas the comprehensive CNN-based model was the best-performing model with an AUC of success-rate curve of 0.97.

Figure 5
figure 5

Average AUC of ROC values derived with testing labels

Full size image
Figure 6
figure 6

Success-rate curves of prospectivity models

Full size image

Given the AUC of ROC values and the AUC of success-rate curves, comprehensive models performed better than the base models (Figs. 5 and 6). These models were used for assessing the importance of vectors contributing to the model. For this, ensemble modeling was employed, whereby the importance of features was evaluated in each iteration. Subsequently, the average importance assigned to each variable was regarded as the definitive value for feature significance. This was achieved by the Gini indices (Fig. 7) and Shapely values (Fig. 8) for RF- and CNN-based comprehensive prospectivity models, respectively; Shapely values presented in Figure 8 were calculated for all labeled samples. Bouguer and magnetic anomalies as well as geological provinces were among most influential vectors in the RF- based comprehensive model (Fig. 7). Such results were similar to those reported in the bee swarm summary plot (Fig. 8a) and the bar chart representing the average Shapely values for each vector (Fig. 8b). Each point in the bee swarm summary plot (Fig. 8a) presents the measured Shapely value of a labeled sample for a given vector, whereas the bar chart (Fig. 8b) represents the mean absolute Shapley values for each vector (Molnar, 2020).

Figure 7
figure 7

Average variable importance derived through Gini indices for the comprehensive RF-based model. Table 1 describes the spatial vectors, to which readers are referred

Full size image
Figure 8
figure 8

(a) Shapely values derived for labeled samples of the CNN-based comprehensive prospectivity model, and (b) mean Shapely values calculated for each vector, showing the average impact of each vector on the CNN-based comprehensive prospectivity model. Table 1 describes the spatial vectors, to which readers are referred

Full size image

Furthermore, the performance of the models for carbonatite-hosted REE +/− Nb prospectivity was assessed using the AUC of success-rate curves (Fig. 9) in the geological provinces in which they reside, namely Canadian Cordillera, Superior, and Grenville (Fig. 1). As per Figure 9, all predictive models exhibited marginally lower performance in the Grenville and Cordillera provinces compared to Superior province, prompting a detailed evaluation of these models in key areas of the former. The comprehensive CNN-based model, which surpassed other models in terms of the AUC of the ROC plot (Fig. 5) and the AUC the fitting-rate curves (Fig. 6), was selected for detailed analysis in the provinces of Cordillera (Fig. 10) and Grenville (Fig. 11). As per Figures 10 and 11, prominent mineralized carbonatites including Saint-Honoré and Blue River complexes are within high-return cells.

Figure 9
figure 9

AUC of fitting rate curves for different geological provinces

Full size image
Figure 10
figure 10

(a) Bivariate risk–return map of the CNN model (Fig. 4d) zoomed in on the Canadian Cordillera and its Blue River Complex and (b) the location of Fig. 10a in Canada. Yellow circles represent carbonatite-hosted REE + /− Nb occurrences

Full size image
Figure 11
figure 11

(a) Bivariate choropleth risk–return map of the CNN model (Fig. 4d) zoomed in on the Grenville province and its Saint Honoré REE +/− Nb zone and (b) the location of Fig. 11a in Canada. Yellow circles represent carbonatite-hosted REE + /− Nb occurrences

Full size image

Discussion

From different spatial vectors available from publicly available geophysical, geochronological, and geological datasets, we opted to use only the ones presented in Table 1. This was because these vectors are among the higher resolution available datasets that are genetically linked to carbonatite-hosted REE +/− Nb occurrences and/or demonstrate positive spatial associations with these occurrences, as evidenced by their AUC of ROC values (Table 1). The term ′average AUC values′ in Table 1 indicate that these values were calculated with positive labels and different sets of negative labels. Negative labels were generated following the procedure outlined in the Gridding and Labeling sub-section above. The purpose of employing diverse sets of negative labels was to acknowledge that each set may yield marginally different AUC values. Consequently, the AUC values displayed in Table 1 represent the mean of all AUC values obtained using distinct sets of negative labels, thereby accommodating the inherent uncertainty associated with the selection of negative labels (Zuo & Wang, 2020). As per Table 1, the horizontal gradient magnitude of gravity data and the Bouguer anomaly map demonstrate the most significant positive spatial associations with carbonatite-hosted REE +/− Nb occurrences. This is partly consistent with the results of feature importance for RF-based comprehensive model (Fig. 7) and the Shapely values of the CNN-based comprehensive model (Fig. 8), as the Bouguer anomaly map is among the top vectors contributing to both models. Also notable in Figures 7 and 8 and in Table 1 is the fact that the AUC values presented in Table 1, Shapely values of the CNN-based model, and Gini indices of the RF-based model are not necessarily consistent. Such differences can be attributed to distinct mathematical frameworks underlying CNN and RF.

The formation of carbonatite magmas and their associated REE +/− Nb mineralization is linked to mantle-related processes (Fig. 2). This study′s base models (Fig. 4a, b) were pivotal for capturing potential signatures associated with these mantle processes. Moreover, the specific vectors analyzed here can potentially indicate deep and crustal structures related to REE +/− Nb mineralization. For example, vectors denoting proximity to gravity anomalies (′gravity worms′) and magnetic anomalies (′magnetic worms′) have average AUC of ROC values of 0.71 and 0.60, respectively (Table 1), highlighting their potential substantial contributions to the comprehensive models, as conformed by their Gini indices (Fig. 7) and Shapely values (Fig. 8). Each of these geophysical derivative products highlighted the edges of geophysical boundaries that were likely important for focusing magmas at multiple crustal levels. The high-return areas in the western Canada sedimentary basin largely reflect these favorable structures underneath thick sequences (a few km) of non-prospective sedimentary rocks (Fig. 10).

As highlighted in the INTRODUCTION section, this study confronted four principal challenges in employing supervised machine learning algorithms for predictive modeling of prospectivity for Canadian carbonatite-hosted REE +/− Nb deposits: (1) poor generalization; (2) selection of negative labels; (3) diversity of geological settings hosting mineralized carbonatites across Canada; and (4) interoperability of machine learning models. Poor generalization (i.e., over-fitting) remains a critical obstacle for data-driven prospectivity models. This issue stems from target feature label imbalance, the complexity of models, and their hyperparameters (Parsa et al., 2022). Over-fitting was assessed by comparing the AUC of ROC for the testing labels (unseen data), with scores of 0.96 and 0.95 (Fig. 5), indicating that this study’s comprehensive models were less affected by over-fitting. This is because a high AUC value suggests that a model in effective at predicting unseen data and are not over-fit (Parsa et al., 2023). Additionally, we observed that the AUC of ROC for training labels was not significantly higher than that for testing labels, further indicating that our comprehensive models were less affected by over-fitting. This achievement is attributed to leveraging the hierarchical structure of S2 grids; by designating each S2 level 12 cell containing a carbonatite-hosted REE +/− Nb occurrence as a ′parent′ cell and its S2 level 13 ′child′ cells as positive labels, we quadrupled the number of positive labels. This strategy notably enhanced the models′ performances, as the models developed without augmented labels performed worse than those presented herein. To tackle the challenge of selecting negative labels, this study introduced an approach using the cosine similarity index. This metric measures the similarity among data points, in this case, geophysical, geological, and geochronological characteristics of cells, to ensure that selected negative labels are markedly dissimilar from positive labels, which are indicative of carbonatite-hosted REE +/− Nb occurrences. The commonly used methods for selecting negative labels in MPM (Carranza and Laborte, 2015; Nykänen et al., 2015; Ford, 2020) include (1) choosing negative labels at a certain distance from positive labels and (2) employing other mineral deposit types as negative labels. In our study, the first approach resulted in prospectivity models riddled with a significant number of false positive cells. Such models inaccurately labeled a considerable portion of Canada as being prospective for carbonatite-hosted REE +/− Nb deposits—an unrealistic outcome. The second approach involved experimentation with sedimentary-hosted Zn–Pb deposits, which yielded bipolar models that identified favorable zones for carbonatite-hosted REE +/− Nb deposits at higher prospectivity values, while indicating areas favorable for sedimentary-hosted Zn–Pb deposits in less favorable zones. It is important to note that using other mineral deposit types that bear similarities to the targeted mineral systems as negative labels may not be advisable for prospectivity modeling. This is because the two mineral systems might share commonalities, which could lead to erroneous results. Consequently, due to the issues identified in the results of the above methods, we refrained from reporting them in our work. Instead, the methodology proposed in this work secures a more reliable selection of negative labels by ensuring that they (1) exhibit minimal similarity to positive samples based on the input data and (2) are selected in feature space rather than using their spatial coordinates. This approach significantly mitigates inherent biases in predictive modeling, thereby enhancing the models′ reliability and performance by ensuring that the training data accurately reflect the complexity and variability of the geological settings being modeled. Moreover, Canadian carbonatite-hosted REE +/− Nb occurrences exhibit distinct geospatial characteristics (Fig. 3), which results in predictive outcomes disproportionately favoring carbonatite-hosted REE +/− Nb occurrences located within the Canadian Cordillera. To counteract this bias, this study employed an ensemble modeling approach to diversifying the labels, effectively mitigating the skewness toward any single deposit group within the labels. This approach also facilitated the estimation of stochastic uncertainty (Parsa and Carranza, 2021) associated with the variability in mineral deposits utilized as labels, enabling a risk–return analysis. Furthermore, SHAP (Lundberg & Lee, 2017; Molnar, 2020) helped with assessing the importance of vectors contributing to predictive models, addressing the fourth challenge.

Bivariate choropleth risk–return plots were utilized to visualize prospectivity models (Figs. 4, 10, and 11). Within these visual representations, cells were categorized into three classes—low-return, medium-return, and high-return—based on their prospectivity values. Similarly, cells were also designated as belonging to one of three risk categories: low-risk, medium-risk, and high-risk based on the variability of prospectivity scores for S2 cell and model iteration. For both risk and return, we calculated two thresholds on the basis of 33% and 66% quantiles and applied these thresholds to categorize the values. This methodology stratifies the results into nine distinct classifications, encompassing combinations such as low-risk, high-return (illustrated as pale pink), high-risk, high-return (depicted as grayish blue), and low-risk, low-return (represented as light gray) cells (Fig. 4). This approach to interpreting prospectivity models posits that cells characterized by low-risk and high-return are prime candidates for subsequent exploratory surveys. This assertion holds irrespective of the labels used for training, as these cells consistently exhibit elevated prospectivity values. Conversely, the decision to pursue exploratory surveys in cells classified as high-risk, high-return warrants careful reconsideration, given that variability in training labels can lead to significant fluctuations in their prospectivity values.

The algorithms used in this study are among those with demonstrated effectiveness in MPM (Zuo & Carranza, 2023). The AUC of ROC values for all four models exceeded 0.9, indicating that both RF- and CNN-based models were effective. Figure 5 illustrates that the comprehensive CNN-based model outperformed its RF-based counterpart—a trend also observed when comparing base models. Moreover, the comprehensive models surpassed the base models in AUC of ROC for testing labels (Fig. 5). Success-rate curves in Fig. 6 also confirm the superiority of the comprehensive models over the base models and the CNN-based models over the RF-based ones. These results were similarly observed when comparing the performances of models across individual geological provinces (Fig. 9). Consequently, we conclude that the CNN-based comprehensive model (Fig. 4d) was the most effective, thereby selecting it for further analysis (Figs. 10 and 11). A detailed examination of this model within the Canadian Cordillera (Fig. 10) revealed that the majority of carbonatite-hosted REE +/− Nb occurrences, notably those within the Blue River Complex, Perry River, Mount Grace, and Wicheeda, are situated in S2 cells characterized by low-risk and high-return. However, several deposits are located in areas associated with medium-risk and high-return. Likewise, the Saint-Honoré complex in the Grenville geological province (Fig. 11) is situated within the low-risk, high-return, contrasting with some other carbonatite-hosted REE +/− Nb occurrences of Grenville that do not share this classification.

This study contributed to an initiative to develop national-scale predictive models for Canada′s critical commodities, with specific focus on mineralized carbonatites due to their significance as primary sources of REE and Nb. As discussed in the INTRODUCTION section, predictive modeling of prospectivity for such mineral deposits encountered numerous challenges. The methodology employed here was designed to address these challenges effectively. Nonetheless, it is important to acknowledge that there are limitations associated with both the methodology and the outcomes of this research. Firstly, publicly available seismic velocity profiles based on global compilations (Debayle & Ricard, 2012) are associated with relatively poor spatial resolutions, which can have a negative impact on the accuracy and reliability of the prospectivity models. Although these global seismic data compilations have the potential to contain valuable information pertinent to the exploration of carbonatites, such vectors were omitted from the analysis conducted in this study. Secondly, many machine learning algorithms were exploited for this study. However, this paper only reported the results of two algorithms, as the results of other algorithms were either similar or inferior to those included here. Another limitation of our models is related to the input dataset we used. The bedrock map that we created to develop many of our spatial vectors (Table 1), for example, was generated by merging various bedrock maps. Occasionally, these bedrock maps may not be consistent, leading to artifacts in our prospectivity models, such as those observed in Figure 10 at around 60°N. A further caveat of our CNN-based models is linked to the one-dimensional (1D) architecture we employed. Unlike two-dimensional (2D) CNNs that work with image data (2D data) (Zuo & Carranza, 2023), 1D CNNs cannot capture the spatial pattern characteristics of mineral deposits. In this study, we did not present the results of 2D CNNs because the focal point of our study—introducing global hierarchical tessellations to address the target feature imbalance problem in MPM— is only applicable to tabular (i.e., 1D) data and 1D CNNs. For comparison purposes, we experimented with 2D CNNs; however, they yielded inferior models compared to those presented in this paper. This was due to the insufficiency of positive labels, which could potentially be addressed using methodologies proposed for 2D CNN-based MPM, such as the random-drop data augmentation (Li et al., 2021). Therefore, further research could focus on applying image-based CNN architectures with proper data augmentation tools to the datasets used in this work.

Conclusions

This study was undertaken to develop national-scale prospectivity models for carbonatite-hosted REE +/− Nb deposits, utilizing publicly available geophysical, geological, and geochronological data. The modeling of prospectivity for these deposits faces several obstacles: (1) scarcity of positive labels; (2) selecting appropriate negative labels; (3) varied geospatial characteristics of positive labels; and (4) complexity of interpreting machine learning-based prospectivity models. To overcome these challenges, a multi-stage methodology was employed, incorporating global hierarchical tessellations, data space similarity measures, ensemble modeling, and Shapley additive explanation. Bivariate choropleth risk–return plots were employed to facilitate the visualization and interpretation of the prospectivity models. Comparing different predictive models derived in this study revealed that the best-performing model is a convolutional neural network-based model resulting from the combination of publicly available geodatabases. This model is mostly affected by magnetic and gravimetric vectors. Although this model performs slightly worse in the geological province of Grenville compared to the rest of Canadian geological provinces, these models predict most mineralized carbonatites within high-return (i.e., high prospectivity) and low-risk zones.