1 Introduction

1.1 Multibody dynamics and differential algebraic equations

Nonlinear computational dynamics theory has been developed for systematically deriving the equations of motion of multibody systems from the perspective of analytical mechanics [1, 2]. In the 1980s, commercial software with functions for modeling, simulation, and animation of multibody systems was developed, and multibody dynamics began to be used in practical situations [3]. Since the 1990s, the interest in multibody dynamics has shifted towards the deformation of bodies [4]. The theory of multibody dynamics, which incorporates the deformation of bodies, has been developed into flexible multibody dynamics [5, 6].

The same multibody system can be modeled in independent or dependent coordinates. The number of independent coordinates coincides with that of the degrees of freedom of the system and, hence, is minimal, which leads to high computational efficiency. However, they cannot directly determine the position of the system. Therefore, studies on this subject tend to conclude that independent coordinates are not appropriate for general-purpose analysis [7]. The model of multibody system dynamics often appears as a set of algebraic, ordinary differential, or differential algebraic equations (DAEs) [8]. DAEs are formulated in dependent coordinates and are generally used in analysis software for multibody systems. They are advantageous as they facilitate the calculation of forces associated with constraints via the Lagrange multipliers with minimal additional effort [7].

1.2 Kalman filters and their applications to constrained systems

The Kalman filter theory was published in the 1960s [9]. This is a minimum-variance state observer for linear systems with Gaussian noise [10]. To consider the nonlinearities of real-world problems, state observers for nonlinear systems have been developed based on the theory of Kalman filters, such as the extended Kalman filter (EKF) and unscented Kalman filter (UKF) [11, 12].

In case of the availability of information on systems that Kalman filters do not incorporate into their schemes, it can be employed to improve the filtering performance [13]. In the 2000s, Kalman filters were developed for constrained systems. Simon and Chia [14] presented a method to incorporate linear state constraints into a Kalman filter. The effectiveness of this method was demonstrated using a vehicle-tracking simulation. Julier and LaViola [15] categorized the previous approaches into pseudo-observation and projection methods. They proposed using the projection method twice to constrain the entire distribution and its statistics. Yang and Blasch [16] proposed a method that specifically facilitated using second-order nonlinear constraints between states. For second-order constraints, there is a trade-off between reducing the approximation errors and maintaining tractable computational costs.

1.3 Combination of Kalman filters and multibody dynamics

Many approaches for combining Kalman filters and multibody dynamics have been studied over the past 20 years [17].

Cuadrado et al. [18] used the continuous-time extended Kalman filter (CEKF) to estimate the states of a multibody system. In their study, DAEs were converted into state equations via two methods. One method involved using the matrix-R method to reduce the dependent generalized coordinates and Lagrange multipliers. The other involved using the penalty method to eliminate the Lagrange multipliers. The observer constructed using the matrix-R method exhibited better results than that constructed using the penalty method. Cuadrado et al. [19] developed real-time automotive observers based on the work presented in [18]. Although a good convergence was demonstrated, the computational cost was high. Pastorino et al. [20] compared the performance of Kalman filters implemented using multibody models. The state observers considered in their study were CEKF, UKF, and spherical simplex UKF (SSUKF). The matrix-R method was used to transform the DAEs into state equations. The UKF and SSUKF approximated the system nonlinearities better than the CEKF and hence exhibited better results in terms of accuracy with an additional computational cost. Sanjurjo et al. [21] introduced state observers built by combining multibody models with an error-state extended Kalman filter (errorEKF). It was compared with previously proposed state observers, namely the discrete-time extended Kalman filter (DEKF), CEKF, and UKF. These observers were tested on four- and five-bar linkages using several sensor configurations and sampling rates. They considered the position and velocity sensors. The results showed that the errorEKF was the most computationally efficient. Furthermore, it was one of the methods whose computational cost was less affected by an increase in the system size from four- to five-bar linkages. Sanjurjo et al. [22] improved their previous work by proposing two state observers for multibody models: errorEKF with the exact Jacobian matrix of the plant (errorEKF-EJ) and errorEKF with force estimation (errorEKF-FE). The errorEKF-FE follows the same structure as the errorEKF-EJ and provides input force estimation. The performances of the state observers were compared with those of the errorEKF and UKF. They were tested using four- and five-bar linkages. Regarding the accuracy, the errorEKF-EJ outperformed the errorEKF with a slight increase in the computational time. Moreover, it achieved nearly identical accuracy to the UKF, with a much shorter computational time. The errorEKF-FE was the only method that yielded reliable estimation results when accelerometers were used. Its computational cost was slightly higher than that of the errorEKF-EJ. Rodríguez et al. [23] presented a state-parameter-input observer for vehicle dynamics. As a considerable number of parameters was involved in vehicle modeling, state and parameter estimations were combined for accuracy improvement. This combination approach is referred to as the dual Kalman filter method. The state and parameter estimators used were errorEKF-FE and UKF, respectively. Rodríguez et al. [24] also proposed an adaptive errorEKF-FE (AerrorEKF-FE) method, known as the maximum likelihood method, which was adjusted to the errorEKF-FE. The accuracy of the Kalman filters is dependent on noise covariance matrices, which are usually unknown; therefore, they are estimated via adaptive techniques.

Various studies on state and parameter estimations of systems based on multibody dynamics and hydraulics have been conducted, recently. Jaiswal et al. [25] extended the use of the errorEKF-EJ to hydraulically actuated systems, where a monolithic approach was used to couple the multibody system and the hydraulic subsystem. A hydraulically actuated four-bar linkage was employed in the case study. The work cycle of the system and hydraulic pressures were accurately estimated. Khadim et al. [26] developed a state observer based on the UKF and a multiphysics model of a forestry crane. The state observer was experimentally investigated, and the non-measured states were estimated with reasonable accuracy. Pyrhönen et al. [27] proposed an online algorithm for identifying the load mass of a hydraulically driven crane. The algorithm was divided into two parts. First, states were estimated using mechanism kinematics and hydraulic system dynamics. Second, the unknown load mass was estimated using inverse dynamics. The states and mass were accurately estimated using the proposed method.

Naets et al. [28] proposed the subsystem global modal parametrization (SS-GMP) approach. Using SS-GMP reduced the variables of multibody models such that real-time capable modes could be achieved without a drastic decrease in accuracy. The augmented DEKF (ADEKF) was used to estimate the states and inputs of the reduced multibody model. Notably, their approach was not robust against incorrect initial conditions. Hagh et al. [29] investigated the application of four different, adaptive, sigma-point Kalman filters to a simulated, rigid–flexible four-bar linkage and experimental, servo-hydraulic actuator; these were as follows: the adaptive UKF, adaptive square-root UKF, adaptive scaled spherical simplex UKF, and adaptive square-root scaled spherical simplex UKF. The performance of these filters was examined under various operating conditions. Pyrhönen et al. [30] proposed an accurate state-transition model employed in the DEKF framework. The state-transition model presented in their study was based on the coordinate-partitioning method and linearized using an exponential integration scheme. Their approach was more accurate and numerically stable than the forward Euler linearization methods. Palomba et al. [31] proposed a general theory for designing state observers based on kinematic models of multibody systems under the assumption of rigid bodies and negligible joint clearance. A simple formulation was obtained using this approach. This was validated through numerical and experimental tests on open- and closed-chain multibody systems. The EKF and UKF were employed as state observers. A two-stage approach was presented in [32]. The estimation was processed by two observers that ran simultaneously. In the first stage, the states were estimated using a state observer based on kinematic models [31]. In the second stage, unknown inputs were estimated using a force observer based on dynamic models. Their study was numerically validated using a closed-chain multibody system. Risaliti et al. [33] presented an ADEKF for flexible multibody models governed by DAEs. The penalty method was used to convert DAEs into ordinary differential equations (ODEs), eliminating the Lagrange multipliers from the equations and introducing additional effort to select effective penalty factors. It was applied to estimate the six-wheel center loads and strain fields on the vehicle suspension system. All six loads and strain fields were accurately estimated when the model incorporated the accurate relationships between the estimated and measured loads. In [34], the UKF was used to estimate the states of a flexible cable, and the state estimates were then used to obtain control inputs. Both ends of the cable body, modeled by the absolute nodal coordinate formulation [35–37], were attached to an unmanned aerial vehicle and a rigid body by pin joints. This yielded a multibody system that could be used for construction inspection and disaster monitoring. Cuadrado et al. [38] used acceleration measurements to tune the EKF parameters for optical-motion capture. This study offered two key advantages. One, when employing a marker-based optical system, the EKF significantly contributed to enhancing the efficiency of motion capture and reconstruction. Two, using inertial-sensor-based acceleration measurements assists in tuning-parameter adjustments, improving the overall reliability of the accelerations obtained. Adduci et al. [39] presented a generalized approach to the methodology described in [33], eliminating the efforts to determine effective penalty factors. A linearization approach for DAEs to extract the system matrices required in the DEKF scheme was proposed. In addition, output equations, augmented by the constraint equations of the DAEs, were introduced. The state and output equations were used in the DEKF scheme. This was experimentally validated using a slider-crank mechanism. Mohammadi et al. [40] incorporated the UKF into multibody dynamics to estimate states of flexible multibody systems. Both reference and modal coordinates were used to form the equations of motion. As sensor measurements do not have a physical meaning, a novel technique for converting them into non-physical coordinates was proposed. Capalbo et al. [41] presented an approach for estimating states, inputs, and parameters of flexible structures. Their approach integrated a parametric model order reduction into an augmented EKF. Both numerical and experimental validations were conducted. Tamarozzi et al. [42] proposed an augmented manifold differential-algebraic extended Kalman filter (AMANDA-EKF) for multibody systems. The AMANDA-EKF has two steps. The first involved the removal of the Lagrange multipliers from the state vector through a null-space projection. The second was the solution of a constrained optimization problem.

1.4 Differences between proposed and conventional methods

Various approaches for incorporating multibody dynamics into the Kalman filter scheme have been studied. Although the commonly used method that describes the dynamics of multibody systems involves using DAEs, Kalman filters have been formulated for systems described by ODEs. Thus, to apply Kalman filters to multibody systems formulated by DAEs, DAEs must be converted to ODEs.

In [18–22], the matrix-R method was used to obtain the form of ODEs in minimal coordinates. The constraint equations of DAEs must be eliminated while maintaining the mathematical and physical correctness of the systems to convert DAEs in dependent coordinates into ODEs in minimal coordinates. Eliminating the constraint equations is an additional effort for users. Moreover, the information that can be obtained via the Kalman filter scheme was reduced. To the best of our knowledge, the method presented in [39] is the only method that applies the Kalman filter to multibody systems described by DAEs, where all the variables of the DAEs, namely generalized coordinates, generalized velocities, and Lagrange multipliers, remain in the states and are estimated using the Kalman filters. The Lagrange multipliers facilitate the calculation of forces that are associated with constraints [7]. These forces contribute to the designs and strength analyses of multibody systems [43]. The Lagrange multipliers can be algebraically calculated as a post process, using the generalized coordinates and velocities that are estimated by the Kalman filters. However, the errors generated in the scheme of Kalman filters are amplified by the post calculation because the Kalman filters assume that errors are independent of the states. In contrast, when the state vector includes the Lagrange multipliers, the Kalman filters estimate them directly and contribute to error reduction in each step, and the problem mentioned above does not occur.

However, it should be noted that systems using minimal coordinates tend to be more computationally efficient than those using dependent coordinates. Thus, both dependent- and reduced-coordinate usages have their own advantages and disadvantages. For clarity, conversion methods that reduce the number of states were not considered in this study.

The common feature of the proposed method and the method in [39] was that the constraint equations of DAEs need not be eliminated. Instead, they were exploited in the output equations as perfect measurements, thereby enforcing kinematic constraints in the estimation schemes. Further comparisons between the proposed and conventional methods are summarized in Table 1. In their study, unknown input forces further augmented the states, assuming that random-walk models were associated. The control input was accurately estimated during validation. However, this was not considered in this study and will be addressed in future work. Another point to mention is the difference between the output models. The output model in their study comprised a sensor model and a constraint vector, which is sufficient to achieve observable systems when used in a state-space model, along with the state equations in their work. However, observable systems were not achieved when they were used in conjunction with the proposed state equations. Therefore, we propose a Lagrange multiplier constraint vector and employ it in the output model, thereby improving the system observability. Although their study offers several advantages, it has three limitations that should be addressed. First, the state equations were expressed only in a discrete-time form. However, the proposed state equations can be expressed in continuous- and discrete-time forms. Second, forward discretization schemes could not apply to the linearization approach. By contrast, the proposed state equations do not have such limitations. Third, the linearization approach was specific to the DEKF scheme. However, as the proposed approach achieves the general form of state-space models, the schemes formulated for state-space models are applicable to the proposed state-space model. Therefore, the proposed method provides more choices for the users.

Table 1 Comparisons between proposed and conventional methods (GC: generalized coordinate, GV: generalized velocity, LM: Lagrange multiplier, UI: unknown input, SM: sensor model, CV: constraint vector, LMCV: Lagrange multiplier constraint vector, RK4: fourth-order Runge–Kutta method, BE: backward Euler method, BDS: backward discretization scheme, CEKF: continuous-time extended Kalman filter, DEKF: discrete-time extended Kalman filter)
Full size table

1.5 Research objectives

This study has two primary research objectives.

The first objective is the proposal of a novel method for converting DAEs into a state-space model. We propose a transition model of the time derivatives of the Lagrange multipliers used in the proposed state equations. In addition, we propose a Lagrange multiplier constraint vector and use it in the proposed output equations, thereby improving the system observability.

The second objective is the verification of the proposed state-space model. State estimations are simulated on benchmark four- and five-bar linkages. The CEKF and DEKF are constructed using the proposed state-space model. The Popov–Belevitch–Hautus rank test [44] is employed for observability analysis. Tests with errors in the parameters and initial positions are conducted.

The remainder of this paper is organized as follows. Section 2 explains the derivation of the proposed state-space model. Section 3 describes the structures of CEKF and DEKF. Section 4 presents the verification method and the results. Finally, Sect. 5 presents the conclusions drawn from this study.

2 Novel method for converting DAEs into a state-space model

The dynamics of holonomic multibody systems can be described by DAEs that are composed of second-order differential and algebraic equations. The differential equations represent the dynamics of multibody systems, whereas the algebraic equations represent the kinematic constraints of the systems. Index-3 DAEs [7] are formulated as

$$ \left \{ \textstyle\begin{array}{c} \mathbf{M}\ddot{\mathbf{q}} + \boldsymbol{\Phi}_{\mathbf{q}}^{\mathrm{T}}\boldsymbol{\lambda} = \mathbf{Q} \\ \boldsymbol{\Phi} \left ( \mathbf{q} \right ) = \mathbf{0}_{m \times 1} \end{array}\displaystyle \right ., $$
(1)

where \(\mathbf{M}\) is a mass matrix, \(\mathbf{Q}\) is a generalized force vector, \(\mathbf{q}\) is a generalized coordinate vector, \(\boldsymbol{\lambda}\) is a Lagrange multiplier vector, \(\boldsymbol{\Phi}\) is a constraint vector, \(\boldsymbol{\Phi}_{\mathbf{q}}\) is a Jacobian matrix of the constraint vector with respect to the generalized coordinate vector, and \(m\) is the number of constraints. Index-1 DAEs in matrix form [7] are formulated as

$$ \left [ \textstyle\begin{array}{c@{\quad } c} \mathbf{M} & \boldsymbol{\Phi}_{\mathbf{q}}^{\mathrm{T}} \\ \boldsymbol{\Phi}_{\mathbf{q}} & \mathbf{0}_{m \times m} \end{array}\displaystyle \right ]\left \{ \textstyle\begin{array}{c} \ddot{\mathbf{q}} \\ \boldsymbol{\lambda} \end{array}\displaystyle \right \} = \left \{ \textstyle\begin{array}{c} \mathbf{Q} \\ \boldsymbol{\gamma} \end{array}\displaystyle \right \}, $$
(2)

where \(\boldsymbol{\gamma}\) is a vector associated with the second-order time derivative of the constraint vector.

The DAEs must be converted into a state-space model composed of the state and output equations to fit the Kalman filter scheme. In this section, we propose a method for converting the DAEs into state and output equations.

2.1 Proposed state equations

State equations are first-order ODEs that describe the dynamics of systems. The DAEs, which represent the dynamics of multibody systems, include both algebraic and differential equations. In addition, the Lagrange multipliers are included in the differential equations. The derivation of the proposed state equations begins with index-1 DAEs, as expressed by Eq. (2). If the mass matrix is a nonsingular matrix, then the coefficient matrix in Eq. (2) can be inverted in the block matrix form; hence, the generalized acceleration and Lagrange multiplier vectors can be expressed as

$$ \begin{aligned}\left \{ \textstyle\begin{array}{c} \ddot{\mathbf{q}} \\ \boldsymbol{\lambda} \end{array}\displaystyle \right \} &= \left [ \textstyle\begin{array}{c@{\quad }c} \mathbf{M}^{ - 1} - \mathbf{M}^{ - 1}\boldsymbol{\Phi}_{\mathbf{q}}^{\mathrm{T}}\left ( \boldsymbol{\Phi}_{\mathbf{q}}\mathbf{M}^{ - 1}\boldsymbol{\Phi}_{\mathbf{q}}^{\mathrm{T}} \right )^{ - 1}\boldsymbol{\Phi}_{\mathbf{q}}\mathbf{M}^{ - 1} & \mathbf{M}^{ - 1}\boldsymbol{\Phi}_{\mathbf{q}}^{\mathrm{T}}\left ( \boldsymbol{\Phi}_{\mathbf{q}}\mathbf{M}^{ - 1}\boldsymbol{\Phi}_{\mathbf{q}}^{\mathrm{T}} \right )^{ - 1} \\ \left ( \boldsymbol{\Phi}_{\mathbf{q}}\mathbf{M}^{ - 1}\boldsymbol{\Phi}_{\mathbf{q}}^{\mathrm{T}} \right )^{ - 1}\boldsymbol{\Phi}_{\mathbf{q}}\mathbf{M}^{ - 1} & {-}\! \left ( \boldsymbol{\Phi}_{\mathbf{q}}\mathbf{M}^{ - 1}\boldsymbol{\Phi}_{\mathbf{q}}^{\mathrm{T}} \right )^{ - 1} \end{array}\displaystyle \right ]\left \{ \textstyle\begin{array}{c} \mathbf{Q} \\ \boldsymbol{\gamma} \end{array}\displaystyle \right \} \\ &= \left \{ \textstyle\begin{array}{c} \mathbf{M}^{ - 1}\mathbf{Q} - \mathbf{M}^{ - 1}\boldsymbol{\Phi}_{\mathbf{q}}^{\mathrm{T}}\left ( \boldsymbol{\Phi}_{\mathbf{q}}\mathbf{M}^{ - 1}\boldsymbol{\Phi}_{\mathbf{q}}^{\mathrm{T}} \right )^{ - 1}\left ( \boldsymbol{\Phi}_{\mathbf{q}}\mathbf{M}^{ - 1}\mathbf{Q} - \boldsymbol{\gamma} \right ) \\ \left ( \boldsymbol{\Phi}_{\mathbf{q}}\mathbf{M}^{ - 1}\boldsymbol{\Phi}_{\mathbf{q}}^{\mathrm{T}} \right )^{ - 1}\left ( \boldsymbol{\Phi}_{\mathbf{q}}\mathbf{M}^{ - 1}\mathbf{Q} - \boldsymbol{\gamma} \right ) \end{array}\displaystyle \right \} \\ &\equiv \left \{ \textstyle\begin{array}{c} \mathbf{f}_{\mathrm{acc}}\left ( \mathbf{q},\dot{\mathbf{q}} \right ) \\ \mathbf{f}_{\mathrm{Lag}}\left ( \mathbf{q},\dot{\mathbf{q}} \right ) \end{array}\displaystyle \right \}, \end{aligned} $$
(3)

where \(\mathbf{f}\)acc() and \(\mathbf{f}\)Lag() are continuous-time transition models of the acceleration and Lagrange multipliers, respectively. They are summarized as

$$\begin{aligned} &\ddot{\mathbf{q}} = \mathbf{f}_{\mathrm{acc}}\left ( \mathbf{q},\dot{\mathbf{q}} \right ), \end{aligned}$$
(4)
$$\begin{aligned} &\boldsymbol{\lambda} = \mathbf{f}_{\mathrm{Lag}}\left ( \mathbf{q},\dot{\mathbf{q}} \right ). \end{aligned}$$
(5)

Exploiting the fact that they are only dependent on generalized coordinates and velocities, we propose a transition model of the time derivatives of the Lagrange multipliers. By differentiating both sides of Eq. (5) with respect to time and substituting Eq. (4), we obtain the following:

$$\begin{aligned} \dot{\boldsymbol{\lambda}} &= \frac{\partial \mathbf{f}_{\mathrm{Lag}}\left ( \mathbf{q},\dot{\mathbf{q}} \right )}{\partial \mathbf{q}}\dot{\mathbf{q}} + \frac{\partial \mathbf{f}_{\mathrm{Lag}}\left ( \mathbf{q},\dot{\mathbf{q}} \right )}{\partial \dot{\mathbf{q}}}\ddot{\mathbf{q}} \\ &= \frac{\partial \mathbf{f}_{\mathrm{Lag}}\left ( \mathbf{q},\dot{\mathbf{q}} \right )}{\partial \mathbf{q}}\dot{\mathbf{q}} + \frac{\partial \mathbf{f}_{\mathrm{Lag}}\left ( \mathbf{q},\dot{\mathbf{q}} \right )}{\partial \dot{\mathbf{q}}}\mathbf{f}_{\mathrm{acc}}\left ( \mathbf{q},\dot{\mathbf{q}} \right ) \\ &\equiv \mathbf{f}_{\mathrm{LagDyn}}\left ( \mathbf{q},\dot{\mathbf{q}} \right ), \end{aligned}$$
(6)

where \(\mathbf{f}\)LagDyn() is a continuous-time transition model of the time derivatives of the Lagrange multipliers. As the generalized acceleration vector is replaced by its transition model, the transition model of the time derivatives of the Lagrange multipliers depends only on the generalized coordinates and velocities. The partial derivatives are obtained analytically as explained in Appendix A. Although analytical differentiations are the most computationally efficient for derivative evaluation, substantial effort is required for implementation [45]. These terms can have complex expressions, particularly for relative coordinates. Hence, the approximations of these terms will be addressed in future research. Using the proposed transition model, we define a continuous-time transition model of the states, where the state vector is defined as

$$ \mathbf{x} \equiv \left \{ \mathbf{q}^{\mathrm{T}} \quad \dot{\mathbf{q}}^{\mathrm{T}} \quad \boldsymbol{\lambda}^{\mathrm{T}} \right \}^{\mathrm{T}}. $$
(7)

Using Eqs. (4) and (6), the proposed state equations can be formulated as

$$ \dot{\mathbf{x}} = \left \{ \textstyle\begin{array}{c} \dot{\mathbf{q}} \\ \ddot{\mathbf{q}} \\ \dot{\boldsymbol{\lambda}} \end{array}\displaystyle \right \} = \left \{ \textstyle\begin{array}{c} \dot{\mathbf{q}} \\ \mathbf{f}_{\mathrm{acc}}\left ( \mathbf{q},\dot{\mathbf{q}} \right ) \\ \mathbf{f}_{\mathrm{LagDyn}}\left ( \mathbf{q},\dot{\mathbf{q}} \right ) \end{array}\displaystyle \right \} \equiv \mathbf{f}_{\mathrm{cont}}\left ( \mathbf{x} \right ), $$
(8)

where \(\mathbf{f}\)cont() is a continuous-time transition model of the states.

2.2 Conventional output equations

The state vector, defined in Eq. (7), includes dependent variables, which may result in a lack of observability. Thus, the output equations must be improved to guarantee the observability of the systems. The general output equations indicating the relationship between the states and physical quantities measured by the sensors are expressed as

$$ \mathbf{y}_{\mathrm{sensor}} = \mathbf{h}_{\mathrm{sensor}}\left ( \mathbf{q},\dot{\mathbf{q}} \right ), $$
(9)

where \(\mathbf{y}\)sensor is an output vector containing physical quantities measured by the sensors, and \(\mathbf{h}\)sensor() is a sensor model. Equation (9) contains general output equations that only include the sensor models. Thus, it is referred to as sensor output equations in this study. Because the proposed state equations include dependent variables, many states must be measured to render the system observable. Thus, many sensors are required. Moreover, certain states are difficult to measure, such as Lagrange multipliers. Hence, it is not realistic to measure all the states required to render the system observable. The general output equations are augmented using the algebraic equations of the DAEs to solve this problem. In [13], various methods for exploiting state constraints in the Kalman filter schemes were introduced.

In [39], the constraint equations of the DAEs were treated as perfect measurements (PMs) and used to augment the general output equations of Eq. (9), that is,

$$ \left \{ \textstyle\begin{array}{c} \mathbf{y}_{\mathrm{sensor}} \\ \mathbf{0}_{m \times 1} \end{array}\displaystyle \right \} = \left \{ \textstyle\begin{array}{c} \mathbf{h}_{\mathrm{sensor}}\left ( \mathbf{q},\dot{\mathbf{q}} \right ) \\ \boldsymbol{\Phi} \left ( \mathbf{q} \right ) \end{array}\displaystyle \right \} \equiv \mathbf{h}_{\mathrm{conv}}\left ( \mathbf{q},\dot{\mathbf{q}} \right ), $$
(10)

where \(\mathbf{h}\)conv() expresses a conventional PM output model. Equation (10) expresses the output equations presented by Adduci et al. [39] and is referred to as conventional PM output equations in this study.

2.3 Proposed output equations

The output equations in Eq. (10) enforce the kinematic constraints and provide information regarding the dependent generalized coordinates in the estimation schemes. However, it does not provide any information regarding the Lagrange multipliers. The lack of this information renders the systems unobservable when used along with the proposed state equations of Eq. (8). Consequently, we propose a Lagrange multiplier constraint vector. Moving the Lagrange multiplier vector in Eq. (5) to the right side, the Lagrange multiplier constraint equations are formulated as

$$ \boldsymbol{\Phi}_{\mathrm{Lag}}\left ( \mathbf{q},\dot{\mathbf{q}},\boldsymbol{\lambda} \right ) \equiv \mathbf{f}_{\mathrm{Lag}}\left ( \mathbf{q},\dot{\mathbf{q}} \right ) - \boldsymbol{\lambda} = \mathbf{0}_{m \times 1}, $$
(11)

where \(\boldsymbol{\Phi}\)Lag denotes a Lagrange multiplier constraint vector. We propose treating the equations as perfect measurements and augmenting the output equations of Eq. (10), that is,

$$ \left \{ \textstyle\begin{array}{c} \mathbf{y}_{\mathrm{sensor}} \\ \mathbf{0}_{m \times 1} \\ \mathbf{0}_{m \times 1} \end{array}\displaystyle \right \} = \left \{ \textstyle\begin{array}{c} \mathbf{h}_{\mathrm{sensor}}\left ( \mathbf{q},\dot{\mathbf{q}} \right ) \\ \boldsymbol{\Phi} \left ( \mathbf{q} \right ) \\ \boldsymbol{\Phi}_{\mathrm{Lag}}\left ( \mathbf{q},\dot{\mathbf{q}},\boldsymbol{\lambda} \right ) \end{array}\displaystyle \right \} \equiv \mathbf{h}_{\mathrm{prop}}\left ( \mathbf{q},\dot{\mathbf{q}},\boldsymbol{\lambda} \right ), $$
(12)

where \(\mathbf{h}\)prop() denotes a proposed PM output model. Equation (12) expresses the output equations originally proposed in this study and is referred to as the proposed PM output equations. In the Kalman filter scheme, the output equations of Eq. (12) provide information regarding the dependent generalized coordinates as well as Lagrange multipliers. Hence, they play an important role in improving system observability when used along with the proposed state equations of Eq. (8). To prove this, studies on system observability are presented in Sect. 4.2.

3 Structures of state observers

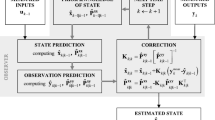
As state observers of multibody systems, CEKF and DEKF [11] were employed in this study. The following explains the structures of the CEKF and DEKF.

3.1 Structure of CEKF

Using the state and output equations, the CEKF is formulated as

$$ \begin{aligned} \hat{\dot{\mathbf{x}}} &= \mathbf{f}_{\mathrm{cont}}\left ( \hat{\mathbf{x}} \right ) + \mathbf{PH}^{\mathrm{T}}\left ( \hat{\mathbf{x}} \right )\boldsymbol{\Sigma}_{\mathrm{measure}}^{ - 1}\left \{ \mathbf{y} - \mathbf{h}\left ( \hat{\mathbf{x}} \right ) \right \}, \\ \dot{\mathbf{P}} &= \mathbf{F}_{\mathrm{cont}}\left ( \hat{\mathbf{x}} \right )\mathbf{P} + \mathbf{PF}_{\mathrm{cont}}^{\mathrm{T}}\left ( \hat{\mathbf{x}} \right ) + \boldsymbol{\Sigma}_{\mathrm{sys}}^{\mathrm{CEKF}} - \mathbf{PH}^{\mathrm{T}}\left ( \hat{\mathbf{x}} \right )\boldsymbol{\Sigma}_{\mathrm{measure}}^{ - 1}\mathbf{H}\left ( \hat{\mathbf{x}} \right )\mathbf{P}, \end{aligned} $$
(13)

where \(\hat{\mathbf{x}}\) is a state estimate vector, \(\mathbf{P}\) is an error covariance matrix, \(\boldsymbol{\Sigma}_{\mathrm{sys}}^{\mathrm{CEKF}}\) is a covariance matrix of the system noise for the CEKF, \(\boldsymbol{\Sigma}\)measure is a covariance matrix of the measurement noise, \(\mathbf{y}\) is an output vector, \(\mathbf{h}\)() is an output model, \(\mathbf{H}\)() is a Jacobian matrix of the output model with respect to the state vector, and \(\mathbf{F}\)cont() is a Jacobian matrix of the continuous-time transition model with respect to the state vector. The Jacobian matrix \(\mathbf{F}\)cont() is expressed as

$$ \mathbf{F}_{\mathrm{cont}}\left ( \mathbf{x} \right ) \equiv \frac{\partial \mathbf{f}_{\mathrm{cont}}}{\partial \mathbf{x}} = \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} \mathbf{0}_{n \times n} & \mathbf{I}_{n} & \mathbf{0}_{n \times m} \\ \partial \mathbf{f}_{\mathrm{acc}} / \partial \mathbf{q} & \partial \mathbf{f}_{\mathrm{acc}} / \partial \dot{\mathbf{q}} & \mathbf{0}_{n \times m} \\ \partial \mathbf{f}_{\mathrm{LagDyn}} / \partial \mathbf{q} & \partial \mathbf{f}_{\mathrm{LagDyn}} / \partial \dot{\mathbf{q}} & \mathbf{0}_{m \times m} \end{array}\displaystyle \right ], $$
(14)

where \(n\) is the number of generalized coordinates. The partial derivatives are analytically obtained as explained in Appendix A. As mentioned earlier, the analytical expressions of partial derivatives can be complicated. Hence, the approximations of these terms will be investigated in future. In addition, the UKF application will also be considered because the Jacobian matrices are not required for the implementation. The output vector \(\mathbf{y}\) and output model \(\mathbf{h}\)() are represented by Eq. (9), (10), or (12). The Jacobian matrices of the output models with respect to the state vector are respectively shown as

$$\begin{aligned} \mathbf{H}_{\mathrm{sensor}}\left ( \mathbf{x} \right ) &\equiv \frac{\partial \mathbf{h}_{\mathrm{sensor}}}{\partial \mathbf{x}} = \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} \partial \mathbf{h}_{\mathrm{sensor}} / \partial \mathbf{q} & \partial \mathbf{h}_{\mathrm{sensor}} / \partial \dot{\mathbf{q}} & \mathbf{0}_{s \times m} \end{array}\displaystyle \right ], \\ \mathbf{H}_{\mathrm{conv}}\left ( \mathbf{x} \right ) &\equiv \frac{\partial \mathbf{h}_{\mathrm{conv}}}{\partial \mathbf{x}} = \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} \partial \mathbf{h}_{\mathrm{sensor}} / \partial \mathbf{q} & \partial \mathbf{h}_{\mathrm{sensor}} / \partial \dot{\mathbf{q}} & \mathbf{0}_{s \times m} \\ \boldsymbol{\Phi}_{\mathbf{q}} & \mathbf{0}_{m \times m} & \mathbf{0}_{m \times m} \end{array}\displaystyle \right ], \\ \mathbf{H}_{\mathrm{prop}}\left ( \mathbf{x} \right ) &\equiv \frac{\partial \mathbf{h}_{\mathrm{prop}}}{\partial \mathbf{x}} = \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} \partial \mathbf{h}_{\mathrm{sensor}} / \partial \mathbf{q} & \partial \mathbf{h}_{\mathrm{sensor}} / \partial \dot{\mathbf{q}} & \mathbf{0}_{s \times m} \\ \boldsymbol{\Phi}_{\mathbf{q}} & \mathbf{0}_{m \times m} & \mathbf{0}_{m \times m} \\ \partial \mathbf{f}_{\mathrm{Lag}} / \partial \mathbf{q} & \partial \mathbf{f}_{\mathrm{Lag}} / \partial \dot{\mathbf{q}} & - \mathbf{I}_{m} \end{array}\displaystyle \right ], \end{aligned}$$
(15)

where \(s\) is the number of physical quantities measured by sensors.

3.2 Structure of DEKF

To apply the DEKF, the state equations must be discretized in time. In this study, the fourth-order explicit Runge–Kutta method (RK4) was used to discretize Eq. (8), that is,

$$ \mathbf{x}_{k + 1} = \mathbf{x}_{k} + \Delta t\mathbf{f}_{\mathrm{RK}4}\left ( \mathbf{x}_{k} \right ) \equiv \mathbf{f}_{\mathrm{disc}}\left ( \mathbf{x}_{k} \right ), $$
(16)

where \(\Delta t\) is a time step, \(\mathbf{f}\)RK4() is a gradient vector of the RK4, explained in Appendix B, and \(\mathbf{f}\)disc() is a discrete-time transition model of the states.

The DEKF comprises two stages: prediction and update. States are first predicted using transition models in the prediction stage, and the outputs are then used to improve the predicted states in the update stage. The prediction stage involves the following:

$$ \begin{aligned} \hat{\mathbf{x}}_{k + 1|k} &= \mathbf{f}_{\mathrm{disc}}\left ( \hat{\mathbf{x}}_{k|k} \right ), \\ \mathbf{P}_{k + 1|k}& = \mathbf{F}_{\mathrm{disc}}\left ( \hat{\mathbf{x}}_{k|k} \right )\mathbf{P}_{k|k}\mathbf{F}_{\mathrm{disc}}^{\mathrm{T}}\left ( \hat{\mathbf{x}}_{k|k} \right ) + \boldsymbol{\Sigma}_{\mathrm{sys}}^{\mathrm{DEKF}}, \end{aligned} $$
(17)

where \(\boldsymbol{\Sigma}_{\mathrm{sys}}^{\mathrm{DEKF}}\) is a covariance matrix of the system noise for the DEKF, and \(\mathbf{F}\)disc() is a Jacobian matrix of the discrete-time transition model with respect to the state vector, as explained in Appendix B. The update stage involves the following:

$$\begin{aligned} \mathbf{G}_{k + 1} &= \mathbf{P}_{k + 1|k}\mathbf{H}^{\mathrm{T}}\left ( \hat{\mathbf{x}}_{k + 1|k} \right )\left \{ \mathbf{H}\left ( \hat{\mathbf{x}}_{k + 1|k} \right )\mathbf{P}_{k + 1|k}\mathbf{H}^{\mathrm{T}}\left ( \hat{\mathbf{x}}_{k + 1|k} \right ) + \boldsymbol{\Sigma}_{\mathrm{measure}} \right \}^{ - 1}, \\ \hat{\mathbf{x}}_{k + 1|k + 1} &= \hat{\mathbf{x}}_{k + 1|k} + \mathbf{G}_{k + 1}\left \{ \mathbf{y}_{k + 1} - \mathbf{h}\left ( \hat{\mathbf{x}}_{k + 1|k} \right ) \right \}, \\ \mathbf{P}_{k + 1|k + 1} &= \mathbf{P}_{k + 1|k} - \mathbf{G}_{k + 1}\mathbf{H}\left ( \hat{\mathbf{x}}_{k + 1|k} \right )\mathbf{P}_{k + 1|k}, \end{aligned}$$
(18)

where \(\mathbf{G}\) is a Kalman gain matrix.

3.3 Covariance matrices of system and measurement noises

For the EKFs, the optimal combinations of tuning parameters (covariance matrices) differ depending on the initial conditions. Considerable time is required to determine these parameters for each initial condition. In [24, 38], adaptive techniques were combined with the EKF to estimate covariance matrices. However, this is beyond the scope of this study. The optimal combinations of the tuning parameters have not been explored. The covariance matrices are simplified as follows.

The covariance matrices of system noise for the CEKF and DEKF are respectively defined as

$$\begin{aligned} \begin{aligned} \boldsymbol{\Sigma}_{\mathrm{sys}}^{\mathrm{CEKF}} &\equiv \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} \sigma _{\mathrm{vel}}\mathbf{I}_{n} & \mathbf{0}_{n \times n} & \mathbf{0}_{n \times m} \\ \mathbf{0}_{n \times n} & \sigma _{\mathrm{acc}}\mathbf{I}_{n} & \mathbf{0}_{n \times m} \\ \mathbf{0}_{m \times n} & \mathbf{0}_{m \times n} & \sigma _{\mathrm{LagDyn}}\mathbf{I}_{m} \end{array}\displaystyle \right ], \\ \boldsymbol{\Sigma}_{\mathrm{sys}}^{\mathrm{DEKF}} &\equiv \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} \sigma _{\mathrm{coord}}\mathbf{I}_{n} & \mathbf{0}_{n \times n} & \mathbf{0}_{n \times m} \\ \mathbf{0}_{n \times n} & \sigma _{\mathrm{vel}}\mathbf{I}_{n} & \mathbf{0}_{n \times m} \\ \mathbf{0}_{m \times n} & \mathbf{0}_{m \times n} & \sigma _{\mathrm{Lag}}\mathbf{I}_{m} \end{array}\displaystyle \right ], \end{aligned} \end{aligned}$$
(19)

where \(\sigma \)coord, \(\sigma \)vel, \(\sigma \)acc, \(\sigma \)Lag, and \(\sigma \)LagDyn are variances of the system noises for the coordinates, velocities, accelerations, Lagrange multipliers, and time derivatives of the Lagrange multipliers, respectively.

Three types of covariance matrices for the measurement noise are prepared corresponding to the output models. These are defined as

$$ \begin{aligned} \boldsymbol{\Sigma}_{\mathrm{measure}}^{\mathrm{sensor}} &\equiv \sigma _{\mathrm{sensor}}\mathbf{I}_{s}, \\ \boldsymbol{\Sigma}_{\mathrm{measure}}^{\mathrm{conv}}& \equiv \left [ \textstyle\begin{array}{c@{\quad }c} \sigma _{\mathrm{sensor}}\mathbf{I}_{s} & \mathbf{0}_{s \times m} \\ \mathbf{0}_{m \times s} & \sigma _{\mathrm{constr}}\mathbf{I}_{m} \end{array}\displaystyle \right ], \\ \boldsymbol{\Sigma}_{\mathrm{measure}}^{\mathrm{prop}}& \equiv \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} \sigma _{\mathrm{sensor}}\mathbf{I}_{s} & \mathbf{0}_{s \times m} & \mathbf{0}_{s \times m} \\ \mathbf{0}_{m \times s} & \sigma _{\mathrm{constr}}\mathbf{I}_{m} & \mathbf{0}_{m \times m} \\ \mathbf{0}_{m \times s} & \mathbf{0}_{m \times m} & \sigma _{\mathrm{LagConstr}}\mathbf{I}_{m} \end{array}\displaystyle \right ], \end{aligned} $$
(20)

where \(\sigma \)sensor, \(\sigma \)constr, and \(\sigma \)LagConstr are variances of the measurement noises for the sensors, constraints, and Lagrange multiplier constraints, respectively. In each state estimation, one of them is employed depending on the output model.

Therefore, the parametric study described herein involves the determination of the values of \(\sigma \)vel, \(\sigma \)acc, \(\sigma \)LagDyn, \(\sigma \)sensor, \(\sigma \)constr, and \(\sigma \)LagConstr for the CEKF and \(\sigma \)coord, \(\sigma \)vel, \(\sigma \)Lag, \(\sigma \)sensor, \(\sigma \)constr, and \(\sigma \)LagConstr for the DEKF.

4 State estimations using four- and five-bar linkages

The three-simulation method [17] was employed to evaluate the accuracy of state observers. The first simulation was conducted by numerically solving the index-1 DAEs shown as Eq. (2). The reference values of the generalized coordinates, generalized velocities, and Lagrange multipliers were obtained by this simulation and used to evaluate the state observers and create sensor outputs. In this study, noise was created according to [22] and added to the sensor outputs for recreating real-world noise conditions. The same noise sequence was used throughout for fair comparison. The second simulation, referred to as the model, was also conducted by numerically solving the index-1 DAEs; however, this simulation involved several errors, such as initial positions and parameters that were different from the first simulation. The third simulation was the state estimation using the state observers. This simulation included the same errors as the second simulation. In addition, the initial values of the Lagrange multipliers were set to zero to represent zero energy; zero energy cannot exist in dynamics systems.

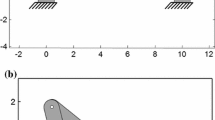
The state estimations were simulated on planar four- and five-bar linkages. The four-bar linkage with a gyroscope on its coupler is shown in Fig. 1a, where \(L_{1}\), \(L_{2}\), and \(L_{3}\) represent the lengths of the crank, coupler, and rocker, respectively, \(\theta _{0}\) indicates the initial angle between the \(x\)-axis and crank, and \(X_{1}\), \(Y_{1}\), \(X_{2}\), and \(Y_{2}\) indicate the coordinates of the joints. The initial angle was set as \(\pi /3\) rad. The five-bar linkage with gyroscopes on its couplers is shown in Fig. 1b, where \(L_{1}\), \(L_{2}\), \(L_{3}\), and \(L_{4}\), respectively, represent the lengths of the left crank, left coupler, right coupler, and right crank, \(\theta _{01}\) indicates the initial angles between the \(x\)-axis and left crank, \(\theta _{02}\) indicates the initial angles between the \(x\)-axis and right crank, and \(X_{1}\), \(Y_{1}\), \(X_{2}\), \(Y_{2}\), \(X_{3}\), and \(Y_{3}\) indicate the coordinates of the joints. The initial angles were set to 0 and \(\pi \) rads, respectively. The outputs of gyroscopes are angular velocities denoted as \(\omega \), \(\omega _{1}\), and \(\omega _{2,}\) respectively. The properties of the four- and five-bar linkages were determined according to [21] and summarized in Tables 2 and 3, respectively. The ground element specifies the distance between the two joints attached to the ground. The four- and five-bar linkages were formulated in natural coordinates according to [7], and their generalized coordinate vectors are defined as

$$ \begin{aligned} \mathbf{q}_{\text{four-bar}} &\equiv \left \{ \textstyle\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} X_{1} & Y_{1} & X_{2} & Y_{2} \end{array}\displaystyle \right \}^{\mathrm{T}}, \\ \mathbf{q}_{\text{four-bar}} &\equiv \left \{ \textstyle\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} X_{1} & Y_{1} & X_{2} & Y_{2} & X_{3} & Y_{3} \end{array}\displaystyle \right \}^{\mathrm{T}}. \end{aligned} $$
(21)
Fig. 1
figure 1

Mechanisms employed in this study

Full size image
Table 2 Properties of the four-bar linkage [21]
Full size table
Table 3 Properties of the five-bar linkage [21]
Full size table

The gyroscope model was formulated according to [22]. The gyroscopes were installed on couplers or cranks. In this study, analytical differentiation was used to obtain the partial derivatives of the four- and five-bar linkages. However, numerical differentiation may be required for more complex multibody systems, and it will be addressed in our future research.

The RK4 was employed to numerically integrate the differential equations of the CEKF. The time step of the RK4 and sampling rate of the gyroscope were respectively set to \(5\times 10^{-3}\) s and 200 Hz, indicating that the gyroscope output was available at every time step. In this study, the initial value of the error covariance matrix \(\mathbf{P}_{0}\) is defined as

$$ \mathbf{P}_{0} \equiv \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} P_{0}^{\mathrm{coord}}\mathbf{I}_{n} & \mathbf{0}_{n \times n} & \mathbf{0}_{n \times m} \\ \mathbf{0}_{n \times n} & P_{0}^{\mathrm{vel}}\mathbf{I}_{n} & \mathbf{0}_{n \times m} \\ \mathbf{0}_{m \times n} & \mathbf{0}_{m \times n} & P_{0}^{\mathrm{Lag}}\mathbf{I}_{m} \end{array}\displaystyle \right ], $$
(22)

where the parameters \(P_{0}^{\mathrm{coord}}\), \(P_{0}^{\mathrm{vel}}\), and \(P_{0}^{\mathrm{Lag}}\) are summarized in Table 4. The tuning parameters of the CEKF and DEKF are summarized in Tables 5 and 6, respectively. As aforementioned, discovering the optimal combinations of tuning parameters is beyond the scope of this study.

Table 4 Parameters for the initial values of the error covariance matrices
Full size table
Table 5 Tuning parameters for CEKF
Full size table
Table 6 Tuning parameters for DEKF
Full size table

In this study, two evaluation approaches were employed. The first was to analyze the L2 norms of errors in generalized coordinates, generalized velocities, and Lagrange multipliers at each time step. These values were calculated using the following equations:

$$ \begin{aligned} q_{\mathrm{e}}\left ( t \right )& \equiv \left | \mathbf{q}\left ( t \right ) - \hat{\mathbf{q}}\left ( t \right ) \right | = \sqrt{\sum _{i = 1}^{n} \left | q_{\mathrm{e}}^{\left ( i \right )}\left ( t \right ) \right |^{2}}, \\ \dot{q}_{\mathrm{e}}\left ( t \right ) &\equiv \left | \dot{\mathbf{q}}\left ( t \right ) - \hat{\dot{\mathbf{q}}}\left ( t \right ) \right | = \sqrt{\sum _{i = 1}^{n} \left | \dot{q}_{\mathrm{e}}^{\left ( i \right )}\left ( t \right ) \right |^{2}}, \\ \lambda _{\mathrm{e}}\left ( t \right ) &\equiv \left | \boldsymbol{\lambda} \left ( t \right ) - \hat{\boldsymbol{\lambda}} \left ( t \right ) \right | = \sqrt{\sum _{i = 1}^{m} \left | \lambda _{\mathrm{e}}^{\left ( i \right )}\left ( t \right ) \right |^{2}}, \end{aligned} $$
(23)

where \(q_{\mathrm{e}}^{\left ( i \right )}\left ( t \right ) \equiv q^{\left ( i \right )}\left ( t \right ) - \hat{q}^{\left ( i \right )}\left ( t \right )\), \(\dot{q}_{\mathrm{e}}^{\left ( i \right )}\left ( t \right ) \equiv \dot{q}^{\left ( i \right )}\left ( t \right ) - \hat{\dot{q}}^{\left ( i \right )}\left ( t \right )\), and \(\lambda _{\mathrm{e}}^{\left ( i \right )}\left ( t \right ) \equiv \lambda ^{\left ( i \right )}\left ( t \right ) - \hat{\lambda}^{\left ( i \right )}\left ( t \right )\). The other evaluation was to investigate the total normalized root mean square error (NRMSEs), defined as

$$ \begin{gathered} \mathrm{NRMSE}_{\mathrm{total}} \equiv \sqrt{\sum _{i = 1}^{2n + m} \left ( \mathrm{NRMSE}^{\left ( i \right )} \right )^{2}}, \\ \mathrm{NRMSE}^{\left ( i \right )} \equiv \frac{1}{x_{\max}^{\left ( i \right )} - x_{\min}^{\left ( i \right )}}\sqrt{\frac{1}{N}\sum _{k = 1}^{N} \left | x_{k}^{\left ( i \right )} - \hat{x}_{k}^{\left ( i \right )} \right |^{2}}, \end{gathered} $$
(24)

where \(N\) is the amount of data of each state. The reference values of generalized coordinates, generalized velocities, and Lagrange multipliers were obtained from the first simulation. The purpose of this calculation was the evaluation of the state observers, and the estimated values originated from the third simulation.

4.1 State estimations and computational costs

The initial positions for the reference and estimated mechanisms of the four- and five-bar linkage are shown in Fig. 2, where \(\theta _{\mathrm{e}}\) indicates an error in the initial angle of the estimated mechanism. As \(\theta _{\mathrm{e}}\) was set to \(\pi /6\) rad, the initial generalized coordinates of the estimated mechanism provided to the state observers differed from the initial generalized coordinates of the reference mechanism. The proposed output equations were used in the test. State estimations were simulated for 10 s under these conditions. The gyroscope was installed on the coupler.

Fig. 2
figure 2

Initial positions for the reference and estimated mechanisms with the error in the initial angle of the estimated mechanism

Full size image

The estimation results of the four-bar linkage for generalized coordinates, generalized velocities, and Lagrange multipliers are shown in Figs. 3, 4, and 5, respectively. The results include the errors and 95% credible intervals (CIs) for the CEKF and DEKF. The state estimates for both the CEKF and DEKF converged to the reference values of the states, verifying the proposed state-space model. For the DEKF, the 95% CIs immediately decreased and remained small till the end of the simulation. In contrast, for the CEKF, the 95% CIs remained large. This is attributed to \(\boldsymbol{\Sigma}_{\mathrm{sys}}^{\mathrm{CEKF}}\) being a constant matrix containing large values. Owing to the importance of the ratio of \(\boldsymbol{\Sigma}_{\mathrm{sys}}^{\mathrm{CEKF}}\) to \(\boldsymbol{\Sigma}\)measure for CEKF tuning, a reduction in \(\boldsymbol{\Sigma}_{\mathrm{sys}}^{\mathrm{CEKF}}\) necessitates a reduction in \(\boldsymbol{\Sigma}\)measure. However, if \(\boldsymbol{\Sigma}\)measure becomes further smaller, the term: \(\mathbf{PH}^{\mathrm{T}}\left ( \hat{\mathbf{x}} \right )\boldsymbol{\Sigma}_{\mathrm{measure}}^{ - 1}\mathbf{H}\left ( \hat{\mathbf{x}} \right )\mathbf{P}\) in the second equation of Eq. (13) becomes excessively large in the first step. Consequently, the state estimation diverges.

Fig. 3
figure 3

Estimation results of the generalized coordinates of the four-bar linkage

Full size image
Fig. 4
figure 4

Estimation results of the generalized velocities of the four-bar linkage

Full size image
Fig. 5
figure 5

Estimation results of the Lagrange multipliers of the four-bar linkage

Full size image

In this test, one gyroscope was installed on the coupler of the four-bar linkage, and two were installed on the right and left couplers of the five-bar linkage, as shown in Fig. 1. The outputs of gyroscopes are angular velocities denoted as \(\omega \), \(\omega _{1}\), and \(\omega _{2,}\) respectively. The angular velocities were also calculated using the estimation results of the model and state observers. In Fig. 6, they were compared with the reference sensor outputs. The results of both the CEKF and DEKF converged to the reference sensor outputs, which also verifies the proposed state-space model.

Fig. 6
figure 6

Comparison of the angular velocities of the couplers

Full size image

Computational costs are summarized in Fig. 7 for investigating the real-time ability of the state observers. The results show that the state observers achieved real-time performance in all the four cases. However, computational costs significantly depend on target systems and computer specifications. Hence, these results should only be taken as a reference when selecting a state observer for multibody systems. The state estimations were conducted using MATLAB 2024a on a computer with a 12th Gen Intel(R) Core(TM) i7-12700 processor @ 2.10 GHz and 16.0 GB of RAM. The results indicate that the DEKF is more computationally efficient than the CEKF. This trend was also reported in [21].

Fig. 7
figure 7

Computational costs of the state observers on the four- and five-bar linkages

Full size image

4.2 Tests with errors in parameter and initial angle

Modeling-error sensitivity was investigated using four- and five-bar linkages. This was evaluated using the total NRMSEs defined in Eq. (24). State estimations were simulated for 100 s. High and low modeling errors were prepared [21, 22]. The low modeling error was 0.5 m/s2 when measuring acceleration due to gravity and \(\pi /32\) rad for the initial angle. The high modeling error was 1 m/s2 in measuring acceleration due to gravity and \(\pi /16\) rad in the initial angle.

The state estimates converged well to the states of the reference mechanism. The total NRMSEs are summarized in Fig. 8; the NRMSEs of the low modeling errors are smaller than those of the high modeling errors in all the cases. This test shows that the state observers constructed using the proposed state-space model are not affected much by errors in parameter and initial angle.

Fig. 8
figure 8

Total NRMSEs of the CEKF and DEKF with high and low modeling errors, in which the gyroscopes are installed on either the couplers or cranks (low modeling error: 0.5 m/s2 in measuring acceleration due to gravity and \(\pi /32\) rad in the initial angle, high modeling error: 1 m/s2 in measuring acceleration due to gravity and \(\pi /32\) rad in the initial angle)

Full size image

4.3 Demonstration of system observability

Three types of output equations are introduced in Eqs. (9), (10), and (12); here, Eq. (12) was originally derived in this study. The system observability, depending on the output equations, was investigated.

The initial position errors provide simple demonstrations of system observability; if the errors are corrected by a state observer, the system can be considered observable under these conditions [22]. The four-bar linkage with the gyroscope on the coupler was employed in this test. The results of the CEKF and DEKF are presented in Fig. 9. The errors were calculated using Eq. (23). In both cases, the state observer with the proposed output model is the only one that corrects all the initial errors. This indicates that the Lagrange multiplier constraint vector in Eq. (11) has a significant role in the proposed output equations. Therefore, when the proposed state equations are used, the proposed output equations must be employed to obtain observable systems.

Fig. 9
figure 9

L2 norms of the errors in the generalized coordinates, generalized velocities, and Lagrange multipliers for the state observers using different output equations (Eqs. (12), (10), and (9) that are the proposed PM, conventional PM [39], and sensor output equations, respectively)

Full size image

The Popov–Belevitch–Hautus observability test [44] was conducted for further investigation. This test does not perfectly explain observability of nonlinear systems as it was originally designed for linear systems; however, it does have a certain value when combined with the previous test. The matrix for the observability test is defined as follows:

$$ \mathbf{M}_{\mathrm{obs}}\left ( e_{i},\hat{\mathbf{x}} \right ) \equiv \left [ \textstyle\begin{array}{c} e_{i}\mathbf{I} - \mathbf{F}\left ( \hat{\mathbf{x}} \right ) \\ \mathbf{H}\left ( \hat{\mathbf{x}} \right ) \end{array}\displaystyle \right ], $$
(25)

where \(\mathbf{F}\)() is the Jacobian matrix of the continuous- or discrete-time transition model with respect to the state vector, and \(e_{i}\) denotes eigenvalues of \(\mathbf{F}\)() at a current time step. The system is observable at the time step if the matrix defined by Eq. (25) has a rank of (2\(n + m\)) for every eigenvalue \(e_{i}\) (\(i = 1\), 2, …, 2\(n + m\)). Hence, the system is observable if the following equation is satisfied for every time step:

$$ \begin{aligned} r_{\mathrm{sum}} &\equiv \operatorname{rank}\left ( \mathbf{M}_{\mathrm{obs}}\left ( e_{1},\hat{\mathbf{x}} \right ) \right ) + \operatorname{rank}\left ( \mathbf{M}_{\mathrm{obs}}\left ( e_{2},\hat{\mathbf{x}} \right ) \right ) + \cdots \\ &\quad + \operatorname{rank}\left ( \mathbf{M}_{\mathrm{obs}}\left ( e_{2n + m},\hat{\mathbf{x}} \right ) \right ) = \left ( 2n + m \right )^{2}, \end{aligned} $$
(26)

where rank(\(\mathbf{M}\)obs) represents a rank of \(\mathbf{M}\)obs. This test employed the four-bar linkage with two different sensor configurations: the gyroscope on either the coupler or crank. Thus, if \(r\)sum = \((2\times 4+ 3)^{2} = 121\) for every time step, the system is observable. The time histories of \(r\)sum are shown in Figs. 10 and 11, respectively. In all the cases, the state observer with the proposed output model satisfies \(r\)sum = 121 for every time step. The results of this test also indicate that, when the proposed state equations are used, the proposed output equations must be employed to achieve observable systems.

Fig. 10
figure 10

Time histories of \(r\)sum of the four-bar linkage with the gyroscope on the coupler (Eqs. (12), (10), and (9) that are the proposed PM, conventional PM [39], and sensor output equations, respectively)

Full size image
Fig. 11
figure 11

Time histories of \(r\)sum of the four-bar linkage with the gyroscope on the crank (Eqs. (12), (10), and (9) that are the proposed PM, conventional PM [39], and sensor output equations, respectively)

Full size image

Among the three output equations introduced in this study, the proposed output equations are the only ones that explicitly contain the Lagrange multipliers. The proposed output equations provide the information regarding the Lagrange multipliers, and hence the errors of the Lagrange multipliers can be corrected via the scheme of Kalman filters. This contributes to the improvement of the system observability.

4.4 Tests with wide error ranges in initial generalized coordinates

The sensitivity to errors in the initial generalized coordinates of the estimated mechanism was studied using four- and five-bar linkages. This was evaluated using the total NRMSEs defined in Eq. (24). The gyroscopes were installed on the couplers, state estimations were simulated for 100 s. Two types of initial errors were prepared.

In one test, the errors in the initial angles \(\theta _{\mathrm{e}}\) were assigned to the estimated mechanisms of the four- and five-bar linkages, as shown in Fig. 2. The initial generalized coordinates of the estimated mechanisms satisfied the constraint equations. The error was increased from \(-\pi \) to \(\pi \) rad at intervals of \(\pi /6\) rad, and the total NRMSE was calculated for each case. The results are summarized in Fig. 12. In the case of four-bar linkage, the results converged for every attempt, and the trends in the total NRMSEs did not differ significantly. However, in the case of five-bar linkage, a significant difference in the trends of the total NRMSEs was observed. In case of a small initial error, the total NRMSEs for DEKF were smaller. On the other hand, when the initial error was large, the total NRMSEs for CEKF were smaller. It should also be noted that the estimation result of CEKF diverged for the case of \(\pi /3\) rad. When dealing with nonlinear systems, state observers can be unstable if the tuning parameters are not set properly [21, 22]. To discuss the robustness of the CEKF and DEKF, the tuning parameters must be properly set for each system with specific initial conditions. However, exploring the best tuning-parameter combination is beyond the scope of this study. Recently, adaptive EKFs [24, 38] that do not require tuning were proposed. The integration of the adaptive techniques into our proposed formulation is to be expected; and will be addressed in our future research.

Fig. 12
figure 12

Total NRMSE of CEKF and DEKF when changing the errors in the initial angle of the estimated mechanism

Full size image

In the other test, errors in the initial length for each rigid bar were assigned to the estimated mechanisms of the four- and five-bar linkages, as shown in Fig. 13, where \(L_{\mathrm{e}}\) represents the error. The errors were used only to calculate the initial generalized coordinates of the estimated mechanisms, implying that the estimated mechanisms themselves were constructed using the true lengths. In this test, the initial generalized coordinates of the estimated mechanisms did not satisfy the constraint equations. The error was increased from −1 to 1 m with step size of 0.1 m for the four-bar linkage and from −0.5 to 0.4 m with step size of 0.1 m for the five-bar linkage. The smaller range of the five-bar linkage was owing to the following geometrical limitations. The shortest bar has a length of 0.5 m, and the five-bar linkage has no geometrically possible positions when \(L_{\mathrm{e}}\) = 0.5 m or longer. The total NRMSE was calculated for each case. The estimation results are summarized in Fig. 14, both of which exhibit the same trend. The total NRMSE of the DEKF was lower than that of the CEKF in every case, and the convergent range of the DEKF was as wide as or wider than that of the CEKF. This trend clearly indicates that the DEKF is more robust than the CEKF when errors in the initial length for each rigid bar are assigned to the estimated mechanisms.

Fig. 13
figure 13

Initial positions for the reference and estimated mechanisms with the error in the initial length for each rigid bar of the estimated mechanism

Full size image
Fig. 14
figure 14

Total NRMSE of CEKF and DEKF when changing the errors in the initial length for each rigid bar of the estimated mechanism

Full size image

These tests demonstrate that, although convergence depends on the system and initial conditions, both the CEKF and DEKF, constructed using the proposed state-space model, can estimate the states accurately when the wide range of errors in the initial generalized coordinates are provided to the estimated mechanisms.

5 Conclusions

In this study, we developed a novel method for converting DAEs into a state-space model, where the state vector comprises generalized coordinates, generalized velocities, and Lagrange multipliers. The transition model of the time derivatives of the Lagrange multipliers was derived from index-1 DAEs and employed in the transition model of the states. The proposed state equations were successfully expressed in continuous- and discrete-time forms. As the states include dependent variables, the output equations must be improved to render the system observable. To address this problem, we proposed a Lagrange multiplier constraint vector and used it to augment the output equations.

State estimations were simulated using the benchmark four- and five-bar linkages. The CEKF and DEKF were constructed using the proposed state-space model. Demonstrations of system observability were performed. Three types of output equations were prepared, and observability was investigated for each output equation. The test demonstrated that when the proposed state equations were used, the proposed output equations were necessary to achieve observable systems. The sensitivity to the initial state estimates was also studied. This test revealed that when the proposed state-space model was used to construct state observers, and the RK4 was employed as a discretization scheme, both the CEKF and DEKF presented good convergence.

In future research, the proposed state-space model will be employed to construct other types of Kalman filters, and their performances will be compared. Applications to input estimation, parameter identification, and control of multibody systems will be expected. State estimations of flexible multibody systems, approximations of partial derivatives, and integration of adaptive techniques will also be addressed.