Kalman filters based on multibody models: linking simulation and real world. A comprehensive review

Abstract

The Kalman filter algorithm estimates variables of linear systems combining information from real sensors and a mathematical model of the system. It may be applied to observe nonlinear systems by means of a linearization of the system model. Multibody system dynamics constitutes a methodology for the analysis and design of mechanical systems. During the last twenty years, many ways of employing a multibody model as the Kalman filter model have been explored.

This paper gathers up diverse algorithms, from the first ones based on the continuous expressions of the filter, to the indirect methods that enable real-time implementations of the observation of mechanical systems with a large number of variables. A detailed explanation of the methods and a description of the strengths and weaknesses of each one is presented along this paper, including a benchmark evaluating the performance of the methods.

An important aspect of the Kalman filter is the characterization of the system uncertainty by means of white Gaussian noise. Sometimes, the statistical properties of the noise are unknown. Several methods to determine these properties are described, and a new methodology to model systems perturbed by colored noise (time-correlated noise) is presented.

In Kalman filters based on multibody models, the information from a real mechanical system can be employed to keep the model behaving like the actual system with a great level of accuracy, linking the simulation to the real behavior of the system.

List of symbols

The symbols used throughout the whole document are defined here. The symbols employed only in specific parts of the document are defined locally.

$\varDelta t$:

Time step

${\mathbf{x}}$:

State

${\dot{\mathbf{x}}}$:

Time derivative of the state

${\hat{\mathbf{x}}}$:

Estimation of the state

${\hat{\dot{\mathbf{x}}}}$:

Estimation of the time derivative of the state

$\mathbf{z}$:

Vector of independent coordinates

$\dot{\mathbf{z}}$:

Vector of independent velocities

$\ddot{\mathbf{z}}$:

Vector of independent accelerations

${\hat{\mathbf{z}}}$:

Estimated vector of independent coordinates

${\hat{\dot{\mathbf{z}}}}$:

Estimated vector of independent velocities

$\hat{\ddot{\mathbf{z}}}$:

Estimated vector of independent accelerations

$\mathbf{R}$:

Matrix relating the dependent and independent velocities of a multibody system in the matrix-R formulation

$\mathbf{K}$:

Stiffness matrix

$\mathbf{C}$:

Damping matrix

$\mathbf{f}$:

Transition function

$\mathbf{F}$:

Discrete system transition matrix

$\boldsymbol{\mathfrak{F}}$:

Continuous system matrix

${\mathbf{f}_{\mathbf{x}}}$:

Jacobian of discrete system transition function with respect to states

$\boldsymbol{\mathfrak{f}}_{\mathbf{x}}$:

Jacobian of continuous system function with respect to states

$\mathbf{h}$:

Measurement function

$\mathbf{h}_{\mathbf{x}}$:

Jacobian of measurement function with respect to states

$\mathbf{H}$:

Discrete system measurement sensitivity matrix

$\mathbf{G}$:

Discrete system input matrix

$\mathbf{B}$:

Continuous system input matrix

$\boldsymbol{\mathcal{K}}$:

Kalman gain

$\mathbf{P}$:

Covariance matrix of state estimation uncertainty

$\boldsymbol {\varSigma }$:

Discrete system innovation covariance matrix

$\boldsymbol {\varSigma }^{P}$:

Discrete system covariance matrix of plant noise

$\boldsymbol {\varSigma }^{P}_{c}$:

Power spectral density matrix of continuous plant noise

$\boldsymbol {\varSigma }^{S}$:

Covariance matrix of sensor noise

$\boldsymbol{{}\hat{\varSigma}}{}^{P}$:

Discrete system estimation of the covariance matrix of plant noise

$\boldsymbol{{}\hat{\varSigma}}{}^{S}$:

Discrete system estimation of the covariance matrix of sensor noise

$\boldsymbol{q}_{c}$:

Vector of power spectral density of continuous acceleration noise

$\mathbf{u}$:

Vector of inputs

$\mathbf{y}$:

Vector of outputs

$\tilde{\mathbf{y}}$:

Vector of innovation

$\mathbf{o}$:

Vector of observations

$\mathbf{w}$:

Vector of process noise

$\mathbf{v}$:

Vector of measurement noise

$n$:

Size of the vector of dependent coordinates $\mathbf{q}$

$l$:

Size of the vector of states $\mathbf{x}$

$g$:

Number of degrees of freedom

$\boldsymbol{\chi}$:

Matrix containing the sigma points of the unscented Kalman filter

$\boldsymbol{\xi}$:

Weakening matrix

1 Introduction

Since Rudolf E. Kálmán wrote his articles in 1960 [23, 24], the Kalman filter (KF) has been employed in a wide range of applications, such as the acquisition of the position and attitude in navigation systems. The KF is a statistically optimal estimator of the states of a linear dynamic system perturbed by white noise. To achieve these estimations, it employs measurements linearly related to the states but also corrupted by white noise together with a model of the system. By doing so, it can estimate variables that are difficult to obtain by means of physical sensors. The extended Kalman filter (EKF) allows a similar approach for nonlinear systems by substituting the model of the system by a linearization of the system around a working point. Both KF and EKF take into account the noise of the system and the sensors. Many applications have been developed and have originated a wide knowledge about estimation [4, 17, 18, 61].

At the same time, multibody (MB) dynamics modeling arose as a powerful tool for the analysis and design of mechanical systems [15, 58, 60]. MB dynamics covers all the required elements for simulating the motion of a mechanical system: modeling, formulations, numerical integrators, etc. Because of this, it has been strongly influenced by the growth of computational efficiency. Achieving real time in MB simulations started as a challenge but, nowadays, complex systems can be simulated in real time on personal computers without special capabilities [2, 12, 20, 28, 59].

The improvements of these two disciplines, estimators and MB dynamics simulation, suggested the idea of merging them by including the MB model in the estimation algorithm. The hypothesis behind this procedure is that a more detailed description of the system may contribute to a more accurate estimation of the observed variables. Through the KF and a set of sensors, the possible drift between an MB model of the system can be corrected, and the MB model can be synchronized with the real system. Therefore, the MB model can be used as an additional source of measurements or virtual sensors. The abundant information about the system provided by the observer based on an MB model can be useful for other tasks, such as control or maintenance. For control purposes, it is of particular interest to obtain this information in real time. In addition, such a procedure is of great interest for enabling the development of digital twins of mechanical systems: a simulation running at the same time as the real system and linked to it by exchanging the information of the real sensors and the observer. As an example, [27] presents a digital twin of a mobile log crane developed by using a KF based on MB simulation.

The next sections of this paper, after revisiting the formulation of the observers and the dynamics of an MB problem, describe different approaches, developed to the date, for the design of observers based on MB models. This review systematizes the different methods following their chronology. In addition, many applications for force estimation are presented simultaneously with the different state estimation methodologies since they do not imply specific methods. The first approach tried to merge the formulation of filter and MB dynamics, combining their continuous equations and solving the resulting system, thus leading to the continuous-time extended Kalman filter (Sect. 3). Difficulties arisen from this formulation suggested the idea of solving the model equations and the filter equations separately. The first implementation of this methodology employed the sigma-point Kalman filter (Sect. 4), which opened the way to the discrete-time extended Kalman filters (Sect. 5). After that, it was sought to implement multibody formulations in dependent coordinates (Sect. 6) and reduce the execution time by means of the indirect filters (Sect. 7), pursuing formulations that achieved real time for complex dynamical problems on conventional computers. These indirect filters do not use the coordinates or their derivatives of the system degrees of freedom in the state vector. Instead, they estimate the errors, at the degrees of freedom, between model and the real system. As a novelty, the direct estimator derived from these filters is described in Sect. 7.4. Section 8 addresses a peculiar methodology that employs kinematic models. Properly, it does not follow the MB dynamics methodology, but it is close to it. Kalman filters are typically employed for the estimation of states, but it is also possible to employ them for the estimation of parameters and/or forces. Parameter estimation is described in Sect. 9. As mentioned above, Kalman filters require knowledge of the statistical properties of system and measurements. The uncertainties of system and measurements are modeled by means of white Gaussian noise, but it is common that the exact properties of these noises are unknown. Section 10 presents an approach to estimate and model the noise. Section 11 presents a methodology to characterize the noise in the case of not being white noise. This methodology is a novel contribution of the paper. Finally, Sect. 12 shows the results of a benchmark evaluating ten of the filters analyzed in this work. The accuracy of each approach is compared, together with their computational cost, giving practical information of the performance of each method.

2 Stating the problem

2.1 Multibody formalisms

The dynamics of an MB system are described in its most basic form by a set of $n$ generalized coordinates ${\mathbf{q}}$ and the $m$ constrained Lagrangian equations [15]:

$$\mathbf{M}\ddot{\mathbf{q}}+{\mathbf{\Phi }}_{\mathbf{q}}^{\mathrm{T}}\mathit{\lambda }=\mathbf{Q}$$

(1a)

$$\begin{aligned} {\boldsymbol{\Phi}}\left({\mathbf{q}},t\right) &= {\mathbf{0}}, \end{aligned}$$

(1b)

where ${\mathbf{M}}$ is the $n \times n$ mass matrix, $\ddot{\mathbf {q}}$ is the acceleration vector, $\boldsymbol{\varPhi}$ is the constraints vector, ${\boldsymbol{\Phi}}_{{\mathbf{q}}}= \partial{\boldsymbol{\Phi}}/ \partial{ \mathbf{q}}$ is the $m \times n$ Jacobian matrix of the constraints, $\boldsymbol{\lambda}$ is the Lagrange multipliers vector, and ${\mathbf {Q}}$ is the applied forces vector.

Vector ${\mathbf{q}}$ includes the variables that describe the position of the mechanism. If that set is minimum, it will only include the independent variables $\mathbf{z}$ that measure the evolution of the degrees of freedom (DOFs) of the mechanism. However, it is very common that more variables than those representing the DOFs are employed.

The equations of motion showed in Eq. (1a), (1b) are a set of differential algebraic equations (DAEs) of second order. Many formulations convert these DAEs into a set of ordinary differential equations (ODEs) [15]. For that purpose, each formulation can follow different techniques to define the model and its constraints.

However, MB models do not fulfill the requirements for being used as KF models. The set of Eq. (1a), (1b) is nonlinear, while the KF expects linear systems. Several approaches have been developed to combine MB models with the KF. Each approach follows different techniques to adapt the MB equations in the structure of the KF: modeling in dependent or independent coordinates, using different integrators, defining different force and constraint models, etc. The next subsection revisits the formulation of the Kalman filter and its related expressions.

2.2 The Kalman filter

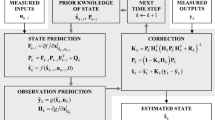
Kalman filters estimate some variables through the propagation of the mean and covariance of these variables through the time [61]. This propagation is conditioned by the measurements provided by sensors that monitor the system. The KF was initially developed for linear systems and independent state variables. The first formulation of the filter was developed in discrete-time form, and it is presented here. To derive the equations, a generic linear model is defined:

$$\begin{aligned} {\mathbf{x}} _{k} &= \mathbf{F} {\mathbf{x}} _{k-1} + \mathbf{G} \mathbf{u} _{k-1}+ \mathbf{w} _{k} \end{aligned}$$

(2a)

$$\begin{aligned} \mathbf{y} _{k} &= \mathbf{H} {\mathbf{x}} _{k} + \mathbf{v} _{k} \end{aligned}$$

(2b)

$$\begin{aligned} \mathbf{w} & \sim N(0, \boldsymbol {\varSigma }^{P} ) \end{aligned}$$

(2c)

$$\begin{aligned} \mathbf{v} & \sim N(0, \boldsymbol {\varSigma }^{S} ), \end{aligned}$$

(2d)

where ${\mathbf{x}}$ is the state vector, $\mathbf{u}$ is the vector of the inputs to the model, $\mathbf{y}$ is the vector containing the outputs of the model (referred to as $\mathbf{o}$ hereafter), $\mathbf{w}$ is the process noise with mean zero and covariance $\boldsymbol {\varSigma }^{P}$, $\mathbf{v}$ is the noise from the measurements with mean zero and covariance $\boldsymbol {\varSigma }^{S}$, $\mathbf{F}$ is the transition matrix, $\mathbf{G}$ is the input matrix, and $\mathbf{H}$ is the measurement sensitivity matrix. The product of this last matrix by the states $\mathbf{H} {\mathbf{x}}$ produces the calculated values equivalent to the output of the sensors.

The filter consists of two main steps: prediction and correction. The state and the estimation error covariance are propagated during the prediction according to a linear model

$$\begin{aligned} {\hat{\mathbf{x}}} ^{-}_{k} =& \mathbf{F} {\hat{\mathbf{x}}} ^{+}_{k-1} + \mathbf{G} \mathbf{u} _{k-1} \end{aligned}$$

(3)

$$\begin{aligned} \mathbf{P} ^{-}_{k} =& \mathbf{F} \mathbf{P} ^{+}_{k-1} \mathbf{F} ^{\mathrm {{T}}} + \boldsymbol {\varSigma }^{P} , \end{aligned}$$

(4)

where ${\hat{\mathbf{x}}}$ is the vector of the estimated states, $\mathbf{P}$ is the covariance matrix of the estimation error, and the superindices ‘−’ and ‘+’ mean $\mathit{a\,priori}$ (before measurements of the current time step are taken into account) and $\mathit{a\,posteriori}$ (after applying the measurements), respectively.

After this prediction step, the measurements (if available) are taken into account to obtain the innovation $\tilde{\mathbf{y}}$ (the difference between the measurements of the sensors $\mathbf{o}$ and the virtual sensors $\mathbf{H} {\hat{\mathbf{x}}}$) and the Kalman gain $\boldsymbol{\mathcal{K}}$ as follows:

$$\begin{aligned} \tilde{\mathbf{y}} _{k} =& \mathbf{o} _{k}- \mathbf{H} {\hat{\mathbf{x}}} ^{-}_{k} \end{aligned}$$

(5)

$$\begin{aligned} \boldsymbol {\varSigma } _{k} =& \mathbf{H} \mathbf{P} ^{-}_{k} \mathbf{H} ^{\mathrm{{T}}} + \boldsymbol {\varSigma }^{S} \end{aligned}$$

(6)

$$\begin{aligned} \boldsymbol{\mathcal{K}} _{k} =& \mathbf{P} ^{-}_{k} \mathbf{H} ^{\mathrm{{T}}} \boldsymbol {\varSigma } _{k}^{-1}, \end{aligned}$$

(7)

where $\boldsymbol {\varSigma } _{k}$ represents the uncertainty in the system state projected through the measurement sensitivity matrix $\mathbf{H}$ with the addition of the covariance $\boldsymbol {\varSigma }^{S}$, which is the Gaussian noise due to the sensors or measurements.

Finally, the correction stage employs the Kalman gain to obtain the final values of the estimated states and the covariance matrix of the estimation error:

$$\begin{aligned} {\hat{\mathbf{x}}} ^{+}_{k} =& {\hat{\mathbf{x}}} ^{-}_{k} + \boldsymbol{\mathcal{K}} _{k} \tilde{\mathbf{y}} _{k} \end{aligned}$$

(8)

$$\begin{aligned} \mathbf{P} ^{+}_{k} =& ({\mathbf{I}}- \boldsymbol{\mathcal{K}} _{k} \mathbf{H} ) \mathbf{P} ^{-}_{k}. \end{aligned}$$

(9)

These equations represent the discrete formulation of the KF presented in the initial Kalman papers in 1960 [23, 24]. In 1961, Kalman and Bucy presented the continuous-time formulation, also known as Kalman–Bucy filter [25]. Although this formulation is hardly employed, several MB-based state observers that will be presented in the following sections are based on it.

First, the considered linear system is written in differential form:

$$\begin{aligned} {\dot{\mathbf{x}}} =& { \boldsymbol{\mathfrak{F}} } {\mathbf{x}} + \mathbf{B} \mathbf{u} + \mathbf{w} \end{aligned}$$

(10)

$$\begin{aligned} \mathbf{y} =& \mathbf{H} {\mathbf{x}} + \mathbf{v} \end{aligned}$$

(11)

$$\begin{aligned} \mathbf{w} \sim& (0, \boldsymbol {\varSigma }^{P}_{c} ) \end{aligned}$$

(12)

$$\begin{aligned} \mathbf{v} \sim& (0,\boldsymbol {\Sigma }^{S}_{c}), \end{aligned}$$

(13)

where $\boldsymbol{\mathfrak{F}}$ represents the continuous system matrix and $\mathbf{B}$ the continuous input matrix. The continuous-time white noises in Eq. (12) and Eq. (13) are characterized by a null mean and a power spectral density matrix of $\boldsymbol {\varSigma }^{P}_{c}$ and $\boldsymbol {\Sigma }^{S}_{c}$, respectively. Now, the continuous-time KF equations become

$$\begin{aligned} \boldsymbol{\mathcal{K}} =& \mathbf{P} \mathbf{H} ^{\mathrm{{T}}} [\boldsymbol {\Sigma }^{S}_{c}]^{-1} \end{aligned}$$

(14)

$$\begin{aligned} {\hat{\dot{\mathbf{x}}}} =& \boldsymbol{\mathfrak{F}} {\hat{\mathbf{x}}} + \mathbf{B} \mathbf{u} + \boldsymbol{\mathcal{K}} ( \mathbf{y} - \mathbf{H} {\hat{\mathbf{x}}} ) \end{aligned}$$

(15)

$$\begin{aligned} \dot{ \mathbf{P} } =& \boldsymbol{\mathfrak{F}} \mathbf{P} + \mathbf{P} \boldsymbol{\mathfrak{F}} ^{\mathrm {{T}}} - \mathbf{P} \mathbf{H} ^{\mathrm{{T}}} [\boldsymbol {\Sigma }^{S}_{c}]^{-1} \mathbf{H} \mathbf{P} + \boldsymbol {\varSigma }^{P}_{c} . \end{aligned}$$

(16)

As it can be deduced from the previous equations, the KF was developed for linear systems with independent variables. Therefore, its application to MB models is not trivial since, in this case, the system is highly nonlinear. To overcome this difficulty, several approaches have been followed that take into account the nonlinearity of the system.

One of the most popular approaches is the extended Kalman filter (EKF), where the nonlinearities are dealt with by using a Jacobian matrix (${\mathbf{f}_{\mathbf{x}}}$ for the discrete equations and $\boldsymbol{\mathfrak{f}}_{\mathbf{x}}$ for the continuous formulation) to propagate the mean and the covariance of the state vector [61] instead of using the transition matrix ($\mathbf{F}$ in the discrete formulation or $\boldsymbol{\mathfrak{F}}$ in the continuous case). Several methods included in this paper are based on the EKF due to its efficiency and accuracy.

3 Continuous-time extended Kalman filter: CEKF

The first estimators based on MB models merged MB equations, commonly expressed in the form of continuous-time differential equations [54], and the continuous-time extended KF formulation. However, simulations are normally performed in discrete time steps. Therefore, the equations of the continuous-time extended Kalman filter (CEKF) combined with the equations of the MB must be numerically integrated.

Despite the compatibility of the EKF with nonlinear systems, there are additional issues when combining it with an MB model. First, the EKF is formulated for first-order systems, while the equations of motion of an MB model are second order. This issue is overcome by including both positions and velocities of the MB model in the state vector (${\mathbf{x}} ^{\mathrm{{T}}}=\left\lbrace{\mathbf {q}}^{\mathrm{{T}}} \mathbf{v}^{\mathrm{{T}}} \right\rbrace$, where $\mathbf{v} = \dot{\mathbf{q}}$), at the cost of duplicating the problem size. Therefore, Eq. (1a), (1b) becomes

$$\begin{aligned} \dot{\mathbf{q}}&= \mathbf{v} \end{aligned}$$

(17a)

$$\begin{aligned} \dot{\mathbf{v}} &= {\mathbf{M}}^{-1} \left( {\mathbf{Q}}- {\boldsymbol{\Phi}}_{{ \mathbf{q}}}^{\mathrm{T}}\lambda\right). \end{aligned}$$

(17b)

This equation can be considered as ${\dot{\mathbf{x}}} = \mathbf{f \left( {\mathbf{x}} \right)}$. However, to match Eq. (17a), (17b) to Eq. (10), several difficulties arise: the Lagrange multipliers are unknown and the mass matrix is not always invertible. In addition, the EKF applies to independent states, whereas most MB formulations are set in dependent coordinates related by constraint equations. Thus, tailored MB formulations must be developed so that the dynamic equations can be expressed in independent coordinates.

In [8], two different approaches are presented. The first one is a state-space reduction method known as matrix-R method [15], and the second one is the penalty method [15].

The main idea of matrix-R method is to obtain an ODE system with a dimension equal to the actual number of DOFs by using a set $\mathbf{z}$ of independent coordinates. The starting point is the following relation between velocities (assuming no rheonomic constraints exist):

$$ \dot{\mathbf{q}}= \mathbf{R} \dot{\mathbf{z}} , $$

(18)

where ${\mathbf{q}}$ is the full set of dependent variables and $\mathbf{z}$ is the set of independent variables. Differentiating Eq. (18), the accelerations are

$$ \ddot{\mathbf{q}}= \mathbf{R} \ddot{\mathbf{z}} + \dot{ \mathbf{R} } \dot{\mathbf{z}} . $$

(19)

Substituting Eq. (18) and Eq. (19) into Eq. (17b), the accelerations of the independent variables can be rewritten as

$$ \ddot{\mathbf{z}} = ( \mathbf{R} ^{\mathrm{{T}}} {\mathbf{M}} \mathbf{R} )^{-1} [ \mathbf{R} ^{\mathrm{{T}}}({ \mathbf{Q}}-{\mathbf{M}}\dot{ \mathbf{R} } \dot{\mathbf{z}} )] = \bar{{\mathbf {M}}}^{-1} \bar{{\mathbf{Q}}}. $$

(20)

And finally, including the velocities in the state vector as ${\mathbf{x}} ^{\mathrm{{T}}}=\left[ \mathbf{z} ^{\mathrm{{T}}} \mathbf {w}^{\mathrm{{T}}} \right]$, where $\mathbf{w} = \dot{\mathbf{z}}$, Eq. (17a), (17b) takes the form of

$$ \begin{bmatrix} \dot{\mathbf{z}} \\ \mathbf{\dot{w}} \end{bmatrix} = \begin{bmatrix} \mathbf{w} \\ \bar{{\mathbf{M}}}^{-1}\bar{{\mathbf{Q}}} \end{bmatrix} . $$

(21)

These equations match Eq. (17a), (17b) and, after their linearization, they can be included as the Jacobian matrix in the EKF:

$$ \boldsymbol{\mathfrak{f}}_{\mathbf{x}} = \frac{\partial\mathbf{f}(\mathbf{x})}{\partial\mathbf{x}} = \begin{bmatrix} {\mathbf{0}}& \mathbf{I} \\ \frac{\partial(\bar{{\mathbf{M}}}^{-1}\bar{{\mathbf{Q}}})}{\partial \mathbf{z} } & \frac{\partial(\bar{{\mathbf{M}}}^{-1}\bar{{\mathbf{Q}}})}{\partial\mathbf{w}} \end{bmatrix} . $$

(22)

This expression can be approximated by

$$\begin{aligned} \boldsymbol{\mathfrak{f}}_{\mathbf{x}} &\simeq \begin{bmatrix} {\mathbf{0}}& \mathbf{I} \\ \boldsymbol{\mathfrak{F}}_{\mathbf{x}}^{21} & \boldsymbol{\mathfrak{F}}_{\mathbf{x}}^{22} \end{bmatrix} \end{aligned}$$

(23a)

$$\begin{aligned} \boldsymbol{\mathfrak{F}}_{\mathbf{x}}^{21} &= -\bar{{\mathbf{M}}}^{-1} \mathbf{R} ^{\mathrm{{T}}} ( \mathbf{K} \mathbf{R} +2{\mathbf{M}} \mathbf{R} _{q} \mathbf{R} \mathbf{\dot{w}}) \end{aligned}$$

(23b)

$$\begin{aligned} \boldsymbol{\mathfrak{F}}_{\mathbf{x}}^{22} &= -\bar{{\mathbf{M}}}^{-1} \mathbf{R} ^{\mathrm{{T}}} ( \mathbf{C} \mathbf{R} +{\mathbf{M}}\dot{ \mathbf{R} }), \end{aligned}$$

(23c)

where $\mathbf{K}$ and $\mathbf{C}$ are the stiffness and damping matrices of the system, respectively. At this point, the correction step starts by adding the sensor information into the filter:

$$\begin{aligned} \dot{\mathbf{z}} -\mathbf{w}+\mathcal{K}_{1}( \mathbf{h} ( {\mathbf{x}} )- \mathbf{o} ) &= {\mathbf{0}} \end{aligned}$$

(24a)

$$\begin{aligned} \bar{{\mathbf{M}}} \ddot{\mathbf{z}} -\bar{{\mathbf{Q}}}+\bar{{\mathbf {M}}}\mathcal{K}_{2}( \mathbf{h} ( {\mathbf{x}} )- \mathbf{o} ) &= {\mathbf{0}}, \end{aligned}$$

(24b)

where $\mathbf{h}$ is the measurement function evaluated in the states of the KF.

In these equations, $\boldsymbol{\mathcal{K}}_{1}$ and $\boldsymbol{\mathcal{K}}_{2}$ are the upper and lower parts of the Kalman gain matrix $\boldsymbol{\mathcal{K}}$, where $\boldsymbol{\mathcal{K}}_{1}$ corresponds to $\mathbf{z}$ and $\boldsymbol{\mathcal{K}}_{2}$ corresponds to $\dot{\mathbf{z}}$. Once the integrator (in this case, the trapezoidal rule integrator (TR) seeking high efficiency) is introduced in Eq. (24a), (24b), the nonlinear system of the states becomes

$$ \left\lbrace \textstyle\begin{array}{c} \mathbf{g}_{1}( {\mathbf{x}} _{n+1}) = {\mathbf{0}} \\ \mathbf{g}_{2}( {\mathbf{x}} _{n+1}) = {\mathbf{0}}\end{array}\displaystyle \right. \;\Longrightarrow\;\mathbf{g}( {\mathbf{x}} _{n+1}) = {\mathbf{0}}. $$

(25)

This system can be iteratively solved by means of the Newton–Raphson method, being the tangent matrix as follows:

$$ \frac{\partial\mathbf{g}}{\partial {\mathbf{x}} } = \begin{bmatrix} \frac{2}{ \varDelta t } {\mathbf{I}}& -{\mathbf{I}} \\ \mathbf{R} ^{\mathrm{{T}}} \mathbf{K} \mathbf{R} \; & \; \mathbf{R} ^{\mathrm {{T}}} ( \mathbf{C} \mathbf{R} + {\mathbf{M}}\dot{ \mathbf{R} }) + \frac{2}{ \varDelta t } \bar {{\mathbf{M}}}\end{bmatrix} + \begin{bmatrix} \mathcal{K}_{1}\mathbf{h}_{x_{1}} & \mathcal{K}_{1}\mathbf{h}_{x_{2}} \\ \bar{{\mathbf{M}}}\mathcal{K}_{2}\mathbf{h}_{x_{1}} & \bar {{\mathbf{M}}} \mathcal{K}_{2}\mathbf{h}_{x_{2}} \end{bmatrix} , $$

(26)

where $\mathbf{h}_{x_{1}}$ and $\mathbf{h}_{x_{2}}$ are the upper and lower parts of the measurement Jacobian matrix $\mathbf{h}_{\mathbf{x}}$.

The second approach presented in [8] merges the penalty formulation, which is a typical formulation for MB dynamics, and the continuous EKF. The penalty method hypothesizes that the constraining forces in Eq. (1a), (1b) are proportional to the violation of the constraints and their derivatives. Hence, the Lagrange multipliers can be written as

$$ \lambda= \alpha(\ddot{\boldsymbol{\Phi}}+2\zeta\omega \dot{\boldsymbol{\Phi}}+\omega^{2}{\boldsymbol{\Phi}}), $$

(27)

where $\alpha$ is the penalty factor that commonly takes values between $10^{7}$ and $10^{10}$.

As it can be seen, the expression has the form of a second-order oscillating system with damping coefficient $\zeta$ and natural frequency $\omega$ (typically, $\zeta=1$, $\omega=10$). Introducing Eq. (27) into Eq. (1a), (1b), the dynamic equations become an ODE:

$$ \ddot{\mathbf{q}}= ({\mathbf{M}}+{\boldsymbol{\Phi}}_{{\mathbf {q}}}^{\mathrm{T}}\alpha{ \boldsymbol{\Phi}}_{{\mathbf{q}}})^{-1}[{\mathbf{Q}}-{\boldsymbol{\Phi}}_{{\mathbf{q}}}^{ \mathrm{T}}\alpha(\dot{\boldsymbol{\Phi}}_{{\mathbf{q}}}\dot{\mathbf {q}}+2\zeta \omega\dot{\boldsymbol{\Phi}}+\omega^{2}{\boldsymbol{\Phi}})]. $$

(28)

In this case, the number of variables is greater than in the matrix-R method: dependent coordinates are employed instead of independent coordinates (equal in number to the number of DOFs). However, following this approach, Eq. (28) can be directly integrated. The next step consists in expressing the equation as a first-order equation:

$$\begin{aligned} \dot{\mathbf{q}}&= \mathbf{v} \end{aligned}$$

(29a)

$$\begin{aligned} \dot{\mathbf{v}} &= ({\mathbf{M}}+{\boldsymbol{\Phi}}_{{\mathbf {q}}}^{\mathrm{T}} \alpha{\boldsymbol{\Phi}}_{{\mathbf{q}}})^{-1}[{\mathbf{Q}}-{\boldsymbol{\Phi}}_{{ \mathbf{q}}}^{\mathrm{T}}\alpha(\dot{\boldsymbol{\Phi}}_{{\mathbf {q}}}\dot{\mathbf{q}}+2 \zeta\omega\dot{\boldsymbol{\Phi}}+\omega^{2}{\boldsymbol{\Phi}})]= \bar{{\mathbf{M}}}^{-1}\bar{{\mathbf{Q}}}. \end{aligned}$$

(29b)

In this case, the Jacobian matrix becomes

$$ \boldsymbol{\mathfrak{f}}_{\mathbf{x}} = \frac{\partial\mathbf{f}(\mathbf{x})}{\partial\mathbf{x}} = \begin{bmatrix} {\mathbf{0}}& \mathbf{I} \\ \frac{\partial(\bar{{\mathbf{M}}}^{-1}\bar{{\mathbf{Q}}})}{\partial{\mathbf{q}}} & \frac{\partial(\bar{{\mathbf{M}}}^{-1}\bar{{\mathbf{Q}}})}{\partial\mathbf{v}} \end{bmatrix} , $$

(30)

and it can be approximated by

$$\begin{aligned} \boldsymbol{\mathfrak{f}}_{\mathbf{x}} &\simeq \begin{bmatrix} {\mathbf{0}}& \mathbf{I} \\ \boldsymbol{\mathfrak{F}}_{\mathbf{x}}^{21} & \boldsymbol{\mathfrak{F}}_{\mathbf{x}}^{22} \end{bmatrix} \end{aligned}$$

(31a)

$$\begin{aligned} \boldsymbol{\mathfrak{F}}_{\mathbf{x}}^{21} &= -\bar{{\mathbf {M}}}^{-1} ( \mathbf{K} +\omega^{2}{\boldsymbol{\Phi}}_{{\mathbf{q}}}^{\mathrm {T}}\alpha{ \boldsymbol{\Phi}}_{{\mathbf{q}}}+ 2{\boldsymbol{\Phi}}_{{\mathbf {q}}}^{\mathrm{T}}{ \boldsymbol{\Phi}}_{{\mathbf{q}}{\mathbf{q}}}\dot{\mathbf{v}}) \end{aligned}$$

(31b)

$$\begin{aligned} \boldsymbol{\mathfrak{F}}_{\mathbf{x}}^{22} &= -\bar{{\mathbf {M}}}^{-1} [ \mathbf{C} +{\boldsymbol{\Phi}}_{{\mathbf{q}}}^{\mathrm{T}}\alpha( \dot{\boldsymbol{\Phi}}_{{\mathbf{q}}}+2\zeta\omega{\boldsymbol{\Phi}}_{{\mathbf{q}}})]. \end{aligned}$$

(31c)

Finally, the correction becomes

$$\begin{aligned} \dot{\mathbf{q}}-\mathbf{v}+\mathcal{K}_{1}( \mathbf{h} ( {\mathbf{x}} )- \mathbf{o} ) &= {\mathbf{0}} \end{aligned}$$

(32a)

$$\begin{aligned} \bar{{\mathbf{M}}}\ddot{\mathbf{v}}-\bar{{\mathbf{Q}}}+\bar {{\mathbf{M}}}\mathcal{K}_{2}( \mathbf{h} ( {\mathbf{x}} )- \mathbf{o} ) &= {\mathbf{0}}. \end{aligned}$$

(32b)

As in the previous method, the trapezoidal rule is the chosen integrator. Once included in the formulation, the equations can be solved by the Newton–Raphson method, with the approximated tangent matrix being

Both methods were tested and compared in the simple mechanical problem depicted in Fig. 1. The methodology consists in employing a simulation of the mechanism as ground truth, obtaining the measurements of sensors from the simulation (in this case, the distance between point A and point 2). This first simulation is considered the prototype. A second simulation is the model, which represents the MB model of the prototype. In a real application, the model can be affected by several uncertainties. Hence, the authors included a known error in the force models: the gravity force in the model was 1 $\textrm{m/s}^{2}$ lower than in the prototype. Finally, the last simulation is the observer, which corresponds to the model corrected, by means of the EKF, with the sensor information coming from the prototype. With this strategy, it is easy to evaluate the accuracy of the estimator by comparing the results of each simulation. This methodology is very commonly employed, so hereafter it will be referred to as the three-simulation method.

Fig. 1

Four-bar mechanism with spring-damper element employed in [8]

The tests yielded good results. The estimators were robust with respect to sensor noise and errors in physical parameters, initial position and actuation readings. However, the matrix-R method exhibited a more efficient behavior. The penalty method had the problem that the penalty terms were not capable of ensuring the constraint satisfaction under the large forces introduced by the observer, even though it observed correctly the measured distance. It can be seen in Eq. (32a), (32b) that the value of the Kalman gain is in conflict with $\bar{{\mathbf{M}}}$, and therefore with the value of the penalty factor $\alpha$. Incrementing the penalty factor implies an increment of the penalty forces which opposes to constraint violations but, at the same time, increases the value of the correction terms coming from the EKF. Therefore, increasing the value of the penalty factor to guarantee constraint satisfaction is worthless.

After the publication of the work presented in [8], it was found in [9] that the observer becomes less stable, accurate, and efficient as higher derivatives are measured: replacing position sensors by acceleration sensors, for example, reduced the performance of the filter. This demands either to reduce the integration time step or to increase the value of the measurement noise covariance to keep an acceptable behavior. Moreover, less accurate results were obtained when the measured variable is not a generalized coordinate of the problem since a simpler expression of Jacobian matrix was used due to the difficulties of obtaining the exact expression.

In a posterior paper [10], the matrix-R method was applied to develop an observer for a real car. However, to improve the efficiency, the observer algorithm that combines the equations of motion and the integrator was reformulated. The duplication of the problem size was suppressed. A nonlinear algebraic system of equations was obtained with the positions as primary variables (velocities were eliminated). The problem size was therefore reduced to the number of coordinates (fourteen in this case): chassis translation and rotation, motion of the four suspensions, and the rotation of the wheels.

Two maneuvers were executed: an acceleration ramp and a double lane change. The tests were run for three computational simulations following the three-simulation method: the prototype, the model (including an error in the vehicle mass of 100 kg more with respect to the prototype), and the observer. The tests were performed considering two scenarios: clean sensors and noisy sensors. In both cases, the observer provided an excellent convergence with the prototype for a time step of integration of 1 ms. Larger time step sizes, such as 5 ms, produced acceptable convergence of the observer with the prototype, although a constant discrepancy at several observed magnitudes was obtained (vertical coordinate of the chassis center of mass and chassis pitch angle). From the efficiency point of view, the observer was far from achieving real-time performance. This was mainly due to the high number of Newton–Raphson iterations required to converge at each time step of integration.

4 Sigma-point Kalman filters: SPKFs

Section 3 has shown that obtaining the transition matrix of KFs when using an MB model is complex. In addition, trying to solve simultaneously the dynamics of the system and the observer equations is not always a successful solution. These issues could be avoided by employing another completely different approach: the sigma-point Kalman filter (SPKF). This is a family of KFs that propagates a set of deterministically chosen weighted sample points, called sigma points, through the nonlinear function of the system dynamics. The sample points capture at least the first two moments (the mean and the variance) of the prior and posterior (after propagation through the nonlinear function) Gaussian random variables that characterize the states. Through this approach, the propagation of the state variables must be computed as many times as sigma points are defined. A general introduction to this family of filters can be found in [33].

This method was first explored in combination with MB formulations in [43]. In this paper, two sigma-points KFs, i.e., the unscented Kalman filter (UKF) and the spherical simplex unscented Kalman filter (SSUKF), were tested and compared with the CEKF combined with the matrix-R method. The difference between these two SPKFs is the number of sigma points to be propagated and the way of obtaining these sigma points.

4.1 Unscented Kalman filter: UKF

The UKF is a filter for nonlinear systems presented by Wan and Van der Merwe in [64]. The first step of the UKF is the calculation of the set of $n_{sp}=(2 l +1)$ sigma points, $l$ being the dimension of the state vector. The unchanged state constitutes the zeroth sigma point. The rest of the points can be calculated by means of the square-root decomposition of the covariance matrix of state estimation uncertainty:

$$\begin{aligned} \boldsymbol{\chi} _{k-1}(0) = & {\hat{\mathbf{x}}} ^{+}_{k-1} \end{aligned}$$

(34)

$$\begin{aligned} \boldsymbol{\chi} _{k-1}(i) = & {\hat{\mathbf{x}}} ^{+}_{k-1} + \zeta\left( \sqrt{ \mathbf{P} ^{+}_{k-1}} \right)_{i}, \; i = 1,\ldots, { l }, \end{aligned}$$

(35)

$$\begin{aligned} \boldsymbol{\chi} _{k-1}({ l }+i) = & {\hat{\mathbf{x}}} ^{+}_{k-1} - \zeta\left( \sqrt{ \mathbf{P} ^{+}_{k-1}} \right)_{i}, \; i = 1, \ldots , { l }, \end{aligned}$$

(36)

where $\sqrt{.}$ is the matrix square root using the lower triangular matrix of the Cholesky decomposition, $\boldsymbol{\chi} _{k-1}(i)$ stands for its $i$th sigma point, $\zeta= \sqrt{{ l }+\lambda}$, $\lambda= \alpha^{2} \left( { l } + \kappa\right)$, $\alpha$ and $\kappa$ are user-defined tuning parameters, with $0 < \alpha\leq1$, and $\kappa$ is the scaling factor, usually set to zero. The parameter $\alpha$ sets the spread of sigma points around the mean of the estimates. Then, these samples are transformed via the corresponding function (in this case, an integration step of the MB simulation):

$$ \boldsymbol{\chi} _{k}(i) = \mathbf{f} ( \boldsymbol{\chi} _{k-1}(i)). $$

(37)

Next, the mean and covariance of the resulting set of estimations are calculated:

$$\begin{aligned} {\hat{\mathbf{x}}} ^{-}_{k} & = {\mathrm{E} \left[ \mathbf{f} ( {\hat{\mathbf{x}}} _{k-1}, \mathbf{w} _{k-1})\right]} \approx\sum_{i=0}^{n_{sp}-1} W_{i}^{m} \boldsymbol{\chi} _{k}(i) \end{aligned}$$

(38)

$$\begin{aligned} \begin{aligned} \mathbf{P} ^{-}_{k} & = \mathrm{E} \left[( \boldsymbol{\chi} _{k} - {\hat{\mathbf{x}}} _{k}^{-})( \boldsymbol{\chi} _{k}- {\hat{\mathbf{x}}} _{k}^{-})^{\mathrm{{T}}} \right] \\ & \approx\sum_{i=0}^{n_{sp}-1} W_{i}^{c} \left( \boldsymbol{\chi} _{k}(i)- {\hat{\mathbf{x}}} ^{-}_{k}\right)\left( \boldsymbol{\chi} _{k}(i)- {\hat{\mathbf{x}}} ^{-}_{k} \right)^{\mathrm{{T}}} + \boldsymbol {\varSigma }^{P} , \end{aligned} \end{aligned}$$

(39)

where $W_{0}^{m} = \lambda/\left({ l }+\lambda\right)$, $W_{0}^{c} = W_{0}^{m} +\left( 1 - \alpha^{2} + \beta\right)$, $W_{i}^{c} = W_{i}^{m} = 1/\left[ 2 \left( { l } + \lambda \right)\right]$, $\beta$ being a secondary scaling factor used to emphasize the weighting on the zeroth sigma point for the covariance calculation. The selection of the weights $W_{i}^{m}$ and $W_{i}^{c}$ is done according to the rules proposed in [33].

In case that new information from the sensors is available, the measurement update is performed. The Kalman gain matrix is calculated employing the following expressions:

$$\begin{aligned} \begin{aligned} \boldsymbol{\mathcal{K}} _{k} & = \mathrm{E} \left[( {\mathbf{x}} _{k} - {\hat{\mathbf{x}}} _{k}^{-})( \mathbf{y} _{k}-\hat{ \mathbf{y} }_{k}^{-})^{\mathrm{{T}}}\right] \times \mathrm{E} \left[( \mathbf{y} _{k} - \hat{ \mathbf{y} }_{k}^{-})( \mathbf{y} _{k}- \hat{ \mathbf{y} }_{k}^{-})^{\mathrm{{T}}}\right]^{-1} \\ & = \mathbf{P} _{ {\mathbf{x}} _{k} \mathbf{y} _{k}} \mathbf{P} _{ \mathbf{y} _{k} \mathbf{y} _{k}} = \sum_{i=0}^{n_{sp}-1} W_{i}^{c} \left( \boldsymbol{\chi} ^{-}_{k}(i)- {\hat{\mathbf{x}}} ^{-}_{k}\right)\left(\boldsymbol{\mathcal{Y}}^{-}_{k}(i)- \hat{ \mathbf{y} }_{k}^{-}\right)^{\mathrm{{T}}} \\ & \times\sum_{i=0}^{n_{sp}-1} W_{i}^{c} \left( \boldsymbol{\mathcal{Y}}^{-}_{k}(i)-\hat{ \mathbf{y} }^{-}_{k}\right) \left(\boldsymbol{\mathcal{Y}}^{-}_{k}(i)-\hat{ \mathbf{y} }_{k}^{-} \right)^{\mathrm{{T}}}, \end{aligned} \end{aligned}$$

(40)

$\boldsymbol{\mathcal{Y}}^{-}_{k}(i)$ being the observations of the $i$th sigma point, which are used to obtain the predicted measurements $\hat{ \mathbf{y} }_{k}^{-}$. For this purpose, similarly to the prediction phase, the weighted means of the estimates are propagated through the measurement sensitivity matrix

$$\begin{aligned} \boldsymbol{\mathcal{Y}}^{-}_{k}(i) = \mathbf{h} _{k}\left( \boldsymbol{\chi} _{k}(i)\right) \end{aligned}$$

(41)

$$\begin{aligned} \hat{ \mathbf{y} }_{k}^{-} = \sum_{i=0}^{n_{sp}-1} W_{i}^{m} \boldsymbol{\mathcal{Y}}^{-}_{k}(i). \end{aligned}$$

(42)

Finally, using the Kalman gain matrix, the state and covariance matrix can be corrected:

$$\begin{aligned} {\hat{\mathbf{x}}} ^{+}_{k} = & {\hat{\mathbf{x}}} ^{-}_{k} + \boldsymbol{\mathcal{K}} _{k} ( \mathbf{o} _{k}- \hat{ \mathbf{y} }^{-}_{k}) \end{aligned}$$

(43)

$$\begin{aligned} \mathbf{P} _{k}^{+} = & \mathbf{P} _{k}^{-} - \boldsymbol{\mathcal{K}} _{k} \mathbf{P} _{ \mathbf{y} _{k-1} \mathbf{y} _{k-1}} \boldsymbol{\mathcal{K}} ^{\mathrm{{T}}}_{k}. \end{aligned}$$

(44)

Once the update is complete, a new set of sigma points can be generated. However, if there are concerns of computational cost, the current sigma points $\boldsymbol{\chi} _{k}(i)$ can be reused to save computational effort at the cost of sacrificing accuracy [55].

4.2 Spherical simplex unscented Kalman filter: SSUKF

The SSUKF was first presented in [22]. While the structure and the equations are the same as in the UKF, the difference relies on the number and the way of defining the sigma points. In this case, the number of sigma points is $n_{sp}=( l +2)$. This leads to a lower number of function evaluations, reducing the computational cost.

The new set of sigma points is built using the following algorithm. Without loss of generality, it is assumed that the state vector is ${\mathbf{x}} = {\mathbf{0}}$. In this case, the sigma points are obtained starting from the first component of the state, as follows: $\boldsymbol{\chi} _{0}^{1}=0, \boldsymbol{\chi} _{1}^{1}=- \frac{1}{\sqrt{2w_{1}}}, \boldsymbol{\chi} _{2}^{1}= \frac{1}{\sqrt{2w_{1}}}$, where the superindex 1 indicates that these sigma points are only considered up to the first state.

For the following states $\mathit{j=2,\ldots, l }$, the sigma points include the ones obtained in the previous step, but are completed adding one extra component and one additional sigma point for every state, according to the following equations:

$${\mathit{\chi }}_i^j=\{\begin{array}{cc}\left[\begin{array}{c}{\mathit{\chi }}_0^{j-1}\\ 0\end{array}\right]& \text{for}i=0,\\ \left[\begin{array}{c}{\mathit{\chi }}_i^{j-1}\\ \frac{1}{\sqrt{j(j+1)w_1}}\end{array}\right]& \text{for}i=1,\dots ,j,\\ \left[\begin{array}{c}{\mathbf{0}}_{j-1}\\ \frac{1}{\sqrt{j(j+1)w_1}}\end{array}\right]& \text{for}i=j+1.\end{array}$$

(45)

The sigma points used for the SSUKF are calculated from $\boldsymbol{\chi} _{i}^{ l }$ obtained at the end of this process. Since it was assumed that ${\mathbf{x}} = {\mathbf{0}}$, the actual sigma points for a general case would be $\boldsymbol{\chi} _{i} = {\hat{\mathbf{x}}} + \boldsymbol{\chi} _{i}^{ l }$. In these expressions, the weight of the zeroth sigma point $\mathit{w_{0}}$ is predefined by the user in the domain $\mathit{0 \leq w_{0} \leq1}$. The value for the weight of the remaining sigma points is $\mathit{w_{i}} = \mathit{w_{1}}= (1-\mathit{w_{0}})/( l +1)$. All the points lie on a hypersphere whose radius is $\sqrt{ l }/(1-\mathit{w_{0}})$, with the exception of the zeroth point, which is at the center.

4.3 Implementation and performance

These two formulations were implemented to observe the movement of the five bar mechanism depicted in Fig. 2, whose parameters and the characteristics of its sensors were experimentally determined. The three-simulations method was followed. The matrix-R method was employed for the MB dynamics. The observers compared were the CEKF, the UKF, and the SSUKF, all with the trapezoidal rule integrator (TR) as integrator for the MB problem and the SSUKF with a second-order Runge-Kutta integrator (RK2) as integrator. The aim of the work presented in [43] was to evaluate the performance of the filter in terms of accuracy and efficiency when using implicit or explicit integrators. It is commonly accepted that explicit integrators are less stable than implicit integrators. However, since the system is being corrected by the observer, this disadvantage can be overcome.

Fig. 2

Five-bar mechanism employed in [43]

It is worth noting that, in the case of CEKF, the state vector has to be duplicated as explained in Sect. 3. In the case of sigma-point filters, this duplication is unnecessary.

In the case of SPKFs, the vector of independent accelerations $\ddot{\mathbf{z}}$ has been chosen in [43] as the state vector. The set of sigma point is calculated and propagated through the nonlinear discrete-time system function (the MB model is integrated for each sigma point). Each sigma point is a vector of independent accelerations $\hat{\ddot{\mathbf{z}}}$, which is used to build the vectors of independent positions $\mathbf{z}$ and velocities $\dot{\mathbf{z}}$ by means of the integrator.

The tests performed covered two different situations. The first one corresponds to the case that the integrator time step $\varDelta t _{i}$ and the sampling time of the sensors $\varDelta t _{s}$ are the same and equal to 2 ms. In the second case, the integrator time step and the sampling time are different, being of 2 ms and 6 ms, respectively.

Table 1 provides the consumed CPU time (having as reference the actual duration of the maneuver) and the root mean square error (RMSE) obtained by the different observers, where the error is the difference between the predicted and actual measurements.

Table 1 CPU times and RMSE

As it can be observed, when the integrator time step and the sampling time are the same, the most accurate filter is the CEKF with an RMSE slightly superior to the noise standard deviation ($10^{-3}\text{ rad}$). However, if the sample time of the sensors is greater than the integration time step, the RMSE of the CEKF increases dramatically compared to that of the other filters. An increase of the sampling time step implies that the filter lacks information of the real mechanism and cannot accurately follow the real movement. Consequently, the CEKF is not a competent alternative for multi-rate situations, while SPKFs provide a more accurate solution in these cases. On the other hand, SPKFs present lower accuracy for the case of equal time step of integration and sampling time, mainly due to the fact that they have correction only in accelerations, while the CEKF has corrections in velocities and accelerations. It should be noted that it is possible to include velocities in the state vector of SPKFs, thus obtaining corrections in velocities and accelerations at the cost of increasing the computational time.

4.4 Other implementations

In [63], a new implementation of the UKF was presented. In this case, the state vector was composed by the independent coordinates and their velocities (${\hat{\mathbf{x}}} ^{\mathrm{{T}}}=\left[ {\hat{\mathbf{z}}} ^{\mathrm{{T}}}, {\hat{\dot{\mathbf{z}}}} {}^{\mathrm{{T}}}\right]$), instead of the accelerations vector, as described in Sect. 4.3. This new approach is slower than the previous one, but it improves the accuracy with respect to the CEKF.

Recently, [35] presented an implementation for flexible mechanisms with this same composition of the state vector. The paper proposed the coupling of a floating frame of reference formulation with the state vector of the UKF.

5 Discrete-time extended Kalman filter: DEKF

In [63], a discrete version of the EKF and the matrix-R method was presented. The main difference between the CEKF and the estimators working in discrete time steps, is that the filter is formulated following two separated stages: state transition (also known as prediction or time update) and state update (also known as state correction or measurement update). While the state transition relies on integrating the dynamic equations of the system, the state update consists in including the information from sensors or observations. It should be noted that in the CEKF both stages are smoothly fused together.

Starting with the prediction stage, the EKF equations in their most generic form are

$$\begin{aligned} {\hat{\mathbf{x}}} ^{-}_{k} =& \mathbf{f} ( {\hat{\mathbf{x}}} ^{+}_{k-1} ) \end{aligned}$$

(46)

$$\begin{aligned} \mathbf{P} ^{-}_{k} =& {\mathbf{f}_{\mathbf{x}}} \mathbf{P} ^{+}_{k-1} {\mathbf{f}_{\mathbf{x}}} ^{\mathrm {{T}}} + \boldsymbol {\varSigma }^{P} , \end{aligned}$$

(47)

where $\mathbf{f} (\cdot)$ stands for the transition model of the system and ${\mathbf{f}_{\mathbf{x}}}$ is its Jacobian matrix with respect to the states ${\mathbf{x}}$.

Regarding Eq. (46), the transition matrix is expressed by the matrix-R method, as in the CEKF. Therefore, Eq. (18) to Eq. (21) are used again. If the state vector is defined as ${\hat{\mathbf{x}}} ^{\mathrm{{T}}}=\left[\hat{\mathbf{z}}^{\mathrm{{T}}}, \hat{\dot{\mathbf{z}}}^{\mathrm{{T}}}\right]$, Eq. (21) becomes

$$ \begin{bmatrix} \mathbf{ \dot{\mathbf{z}} } \\ \mathbf{ \ddot{\mathbf{z}} } \end{bmatrix} = \begin{bmatrix} \mathbf{ \dot{\mathbf{z}} } \\ \bar{{\mathbf{M}}}^{-1}\bar{{\mathbf{Q}}} \end{bmatrix} . $$

(48)

The development of the discrete-time extended Kalman filter (DEKF) differs from the generic EKF equations at this point. If the numerical integration of the MB system is performed by means of the forward Euler method with time step $\varDelta t$, the integrator can be expressed in a form that fulfills the requirements of the EKF transition function:

$$\begin{aligned} {\hat{\mathbf{x}}} ^{-}_{k} = \mathbf{f} ( {\hat{\mathbf{x}}} ^{+}_{k-1} ) \quad\Rightarrow \quad\left[ \textstyle\begin{array}{c} {\hat{\mathbf{z}}} _{k} \\ {\hat{\dot{\mathbf{z}}}} _{k} \end{array}\displaystyle \right] = \left[ \textstyle\begin{array}{c} { {\hat{\mathbf{z}}} }_{k-1} + \varDelta t {\hat{\dot{\mathbf{z}}}} _{k-1} \\ { {\hat{\dot{\mathbf{z}}}} }_{k-1} + \varDelta t \hat{\ddot{\mathbf{z}}} _{k-1} \end{array}\displaystyle \right] . \end{aligned}$$

(49)

Thus, the Jacobian of the transition model ${\mathbf{f}_{\mathbf{x}}}$ has a fairly simple structure:

$$\begin{aligned} {\mathbf{f}_{\mathbf{x}}} \equiv\frac{\partial \mathbf{f} }{\partial {\hat{\mathbf{x}}} } = \frac{\partial}{\partial\{ {\hat{\mathbf{z}}} , {\hat{\dot{\mathbf{z}}}} \} } \left[ \textstyle\begin{array}{c} { {\hat{\mathbf{z}}} } + \varDelta t { {\hat{\dot{\mathbf{z}}}} } \\ { {\hat{\dot{\mathbf{z}}}} } + \varDelta t \hat{\ddot{\mathbf{z}}} \end{array}\displaystyle \right] = \left[ \textstyle\begin{array}{c@{\quad}c} {\mathbf{I}}_{ g } & \varDelta t {\mathbf{I}}_{ g } \\ {\mathbf{0}}_{ g \times{ g }} & {\mathbf{I}}_{ g } \end{array}\displaystyle \right] , \end{aligned}$$

(50)

where $g$ is the number of DOFs of the system.

Regarding the discrete plant covariance matrix $\boldsymbol {\varSigma }^{P}$ appearing in Eq. (47), it stands for the additional uncertainty of the new state ${\hat{\mathbf{x}}} _{k}$, physically attributable to unmodeled forces and errors in the parametrization of the mechanism (bars lengths, inertia values, etc.), and to integration errors.

The second stage of the DEKF method, the update, incorporates the sensor readings (when available) to improve the estimate according to the following equations:

$$\begin{aligned} \tilde{\mathbf{y}} _{k} =& \mathbf{o} _{k} - \mathbf{h} ( {\hat{\mathbf{x}}} ^{-}_{k} ) \end{aligned}$$

(51)

$$\begin{aligned} \boldsymbol {\varSigma } _{k} =& \mathbf{h}_{\mathbf{x}} {}_{k} \mathbf{P} ^{-}_{k} \mathbf{h}_{\mathbf{x}} {}_{k}^{\mathrm {{T}}} + \boldsymbol {\varSigma }^{S} \end{aligned}$$

(52)

$$\begin{aligned} \boldsymbol{\mathcal{K}} _{k} =& \mathbf{P} ^{-}_{k} \mathbf{h}_{\mathbf{x}} {}_{k}^{\mathrm{{T}}} \boldsymbol {\varSigma } _{k}^{-1} \end{aligned}$$

(53)

$$\begin{aligned} {\hat{\mathbf{x}}} ^{+}_{k} =& {\hat{\mathbf{x}}} ^{-}_{k} + \boldsymbol{\mathcal{K}} _{k} \tilde{\mathbf{y}} _{k} \end{aligned}$$

(54)

$$\begin{aligned} \mathbf{P} ^{+}_{k} =& ({\mathbf{I}}_{2g} - \boldsymbol{\mathcal{K}} _{k} \mathbf{h}_{\mathbf{x}} {}_{k} ) \mathbf{P} ^{-}_{k}. \end{aligned}$$

(55)

The innovation covariance matrix $\boldsymbol {\varSigma } _{k}$ represents the uncertainty in the system state projected via the sensor function $\mathbf{h}_{\mathbf{x}} {}_{k} \mathbf{P} ^{-}_{k} \mathbf{h}_{\mathbf{x}} {}_{k}^{\mathrm{{T}}}$, plus an additional Gaussian noise originated at the sensor itself $\boldsymbol {\varSigma }^{S}$. Small values of $\boldsymbol {\varSigma } _{k}$ mean that the observation introduces useful information to constrain the estimation of the system state. By evaluating the Kalman gain, the estimation of the mean and covariance are updated in Eq. (54) and Eq. (55), respectively.

In [63], this method was applied to the observation of a four-bar mechanism equipped with IMUs and compared with the UKF described in Sect. 4.4. The state vector in both filters was composed by the independent coordinates and their velocities (${\hat{\mathbf{x}}} ^{\mathrm{{T}}}= \left[ {\hat{\mathbf{z}}} ^{\mathrm{{T}}}, {\hat{\dot{\mathbf{z}}}} {}^{\mathrm{{T}}}\right]$). In the UKF, once the sigma points are obtained, they are transformed with a forward Euler transition function identical to that of previous filters, and the predicted mean ${\hat{\mathbf{x}}} ^{-}_{k}$ and covariance $\mathbf{P} ^{-}_{k}$ are estimated from them. A similar process applies to the propagation of the uncertainty in observations, taking into account both the uncertainty in the system state and the sensor noise ($\boldsymbol {\varSigma }^{P}$ and $\boldsymbol {\varSigma }^{S}$). The two filters used provided good results in terms of accuracy (the RMSE found when estimating the crank angle of the mechanism was 1.15 deg for the DEKF and 1.16 deg for the UKF). However, the DEKF proved to be considerably faster in terms of computational efficiency.

A more developed version of the DEKF, including input force estimation, is presented in [37]. To estimate the input forces, they are modeled as a random walk and included in the state vector. This approach is also referred to as augmented DEKF (ADEKF).

In the work presented in [37], the subsystem global modal parametrization methodology is used to obtain an efficient MB simulation. With this methodology, a complex mechanism is divided into simpler subsystems, and some terms required for the simulation and estimation are precomputed. An exponential integrator is used for the discretization of the equations of motion. Therefore, the program execution is faster because some terms are calculated by interpolation of the precomputed coefficients. The expressions of the derivatives required for the implementation of the method are also provided. The method was tested with a planar half car model, achieving good results, but only for short duration of the tests due to the limitations of the sensors considered, which led to a nonobservable system.

The ADEKF has been also applied in more recent works. Such is the case of [45], where the ADEKF is employed to estimate the loads in the center of a wheel and the strain field on a vehicle suspension test rig. The estimation is made based on a flexible MB model of the suspension system, which relies on the use of a penalty conditioned formulation to achieve a set of ODEs. This approach is afterwards generalized in [1], so that it can be used with the Lagrange multipliers formulation. Finally, in [3], the ADEKF is applied to a slider-crank mechanism. The MB model is reduced from natural coordinates to minimal coordinates through a deep learning approach. In this way, the equations of the model are transformed into a set of ODEs so that they can be combined with the ADEKF equations.

6 Estimators in dependent coordinates

Previous estimators employ independent coordinates, which entails the resolution of the MB position problem at every time step with a high computational cost. For this reason, several alternatives to employ dependent coordinates by including the constraints into the KF were explored. These algorithms were presented and implemented in [54].

6.1 Smoothly constrained Kalman filter: SCKF

The Smoothly constrained Kalman filter (SCKF) is the application of the algorithm described in [16] to an MB model. In this method, the state ${\mathbf{x}}$ is built with the whole MB vectors of coordinates and velocities, ${\mathbf{q}}$ and $\dot{\mathbf{q}}$, respectively. The SCKF transition function is built assuming the forward Euler integrator

$$\begin{aligned} {\hat{\mathbf{x}}} ^{-}_{k} = \mathbf{f} ( {\hat{\mathbf{x}}} ^{+}_{k-1} ) \quad\Rightarrow \left[ \textstyle\begin{array}{c} {\hat{{\mathbf{q}}}}_{k} \\ {\hat{\dot{\mathbf{q}}}}_{k} \end{array}\displaystyle \right] = \left[ \textstyle\begin{array}{c} {\hat{{\mathbf{q}}}}_{k-1} + \varDelta t {\hat{\dot{\mathbf{q}}}}_{k-1} \\ {\hat{\dot{\mathbf{q}}}}_{k-1} + \varDelta t {\hat{\ddot{\mathbf{q}}}}_{k-1} \end{array}\displaystyle \right] , \end{aligned}$$

(56)

where the vector of dependent accelerations ${\ddot{\mathbf {q}}}_{k-1}$ is calculated from the dynamic equations of the system, (1a), (1b). Thus, the Jacobian matrix of the transition model is

$$ {\mathbf{f}_{\mathbf{x}}} \equiv \frac{\partial \mathbf{f} }{\partial\{ \hat{{\mathbf{q}}}, \hat{\dot {\mathbf{q}}}\} } = \left[ \textstyle\begin{array}{c@{\quad}c} {\mathbf{I}}_{ n } & \varDelta t {\mathbf{I}}_{ n } \\ {\mathbf{0}}_{{ n }\times{ n }} & {\mathbf{I}}_{ n } \end{array}\displaystyle \right] , $$

(57)

and the covariance matrix is updated as

$$ \mathbf{P} _{k}^{-} = {\mathbf{f}_{\mathbf{x}}} \mathbf{P} _{k-1}^{+} {\mathbf{f}_{\mathbf{x}}} ^{\mathrm {{T}}} + \boldsymbol {\varSigma }^{P} . $$

(58)

After the prediction, the measurement update is undertaken, but considering only the measurements coming from the sensors:

$$\begin{aligned} \boldsymbol{\mathcal{K}} _{k,0} =& \mathbf{P} ^{-} \mathbf{h}_{\mathbf{x}} {}_{k}^{\mathrm{{T}}}( \mathbf{h}_{\mathbf{x}} {}_{k} \mathbf{P} ^{-} \mathbf{h}_{\mathbf{x}} {}_{k}^{\mathrm{{T}}} + \boldsymbol {\varSigma }^{S} )^{-1} \end{aligned}$$

(59)

$$\begin{aligned} {\hat{\mathbf{x}}} _{k,0}^{+} =& {\hat{\mathbf{x}}} _{k}^{-} + \boldsymbol{\mathcal{K}} _{k,0} ( \mathbf{o} _{k} - \mathbf{h} ( {\hat{\mathbf{x}}} _{k}^{-})) \end{aligned}$$

(60)

$$\begin{aligned} \mathbf{P} ^{+}_{k,0} =& ({\mathbf{I}}_{2n} - \boldsymbol{\mathcal{K}} _{k,0} \mathbf{h}_{\mathbf{x}} {}_{k} ) \mathbf{P} ^{-}_{k}. \end{aligned}$$

(61)

Until this point, the SCKF algorithm is the same as the conventional EKF. The difference is that the states are not expected to fulfill the constraints. Hence, an iterative process has to be started to impose the position and velocity constraints as if they were additional measurements. Although the constraints are perfect measurements (they must be perfectly fulfilled to a known value), virtual noise is added to them in order to ease the convergence of the problem. Without this noise, the perfect fulfillment of a constraint might impede the modification of the coordinates required to satisfy the remaining constraints. This behavior is a consequence of the nonlinear nature of the constraint equations commonly used in MB models. The covariance matrix of the virtual noise added to the constraints is known as weakening matrix, and it is calculated as follows:

$$ \boldsymbol{\xi} _{0} = \tilde{\alpha} \begin{bmatrix} {\boldsymbol{\Phi}}_{\mathbf{x}} \\ \dot{\boldsymbol{\Phi}}_{\mathbf{x}} \end{bmatrix} \mathbf{P} _{k,0}^{+} \begin{bmatrix} {\boldsymbol{\Phi}}_{\mathbf{x}} \\ \dot{\boldsymbol{\Phi}}_{\mathbf{x}} \end{bmatrix} ^{\mathrm{{T}}}, $$

(62)

where $\tilde{\alpha}$ is a tuning parameter, and $\boldsymbol{\Phi}_{\mathbf{x}}$ and $\boldsymbol{\dot{\Phi}}_{\mathbf {x}}$ are the Jacobian matrices of the constraints at position and velocity levels with respect to the current states, respectively. As said before, this weakening matrix contains virtual noise to be added to the MB constraints to ease the convergence of the problem. The iterative update is as follows:

$$ \boldsymbol{\mathcal{K}} _{k,i} = \mathbf{P} _{k,i-1}^{+} \begin{bmatrix} {\boldsymbol{\Phi}}_{\mathbf{x}} \\ \dot{\boldsymbol{\Phi}}_{\mathbf{x}} \end{bmatrix} + \left( \begin{bmatrix} {\boldsymbol{\Phi}}_{\mathbf{x}} \\ \dot{\boldsymbol{\Phi}}_{\mathbf{x}} \end{bmatrix} \mathbf{P} _{k,i-1}^{+} \begin{bmatrix} {\boldsymbol{\Phi}}_{\mathbf{x}} \\ \dot{\boldsymbol{\Phi}}_{\mathbf{x}} \end{bmatrix} ^{\mathrm{{T}}} + \boldsymbol{\xi} _{i-1}\right)^{-1} $$

(63)

$$ {\hat{\mathbf{x}}} _{k,i+1}^{+} = {\hat{\mathbf{x}}} _{k,i}^{+}- \boldsymbol{\mathcal{K}} _{k,i} \begin{bmatrix} \boldsymbol{\Phi} ( {\hat{\mathbf{x}}} _{k,i}^{+}) \\ \boldsymbol{\dot{\Phi}}( {\hat{\mathbf{x}}} _{k,i}^{+}) \end{bmatrix} $$

(64)

$$ \mathbf{P} _{k,i+1}^{+} = \left({\mathbf{I}}_{2n} - \boldsymbol{\mathcal{K}} _{k,i} \begin{bmatrix} {\boldsymbol{\Phi}}_{\mathbf{x}} \\ \dot{\boldsymbol{\Phi}}_{\mathbf{x}} \end{bmatrix} \right) \mathbf{P} _{k,i}^{+}\left({\mathbf{I}}_{2n}- \boldsymbol{\mathcal{K}} _{k,i} \begin{bmatrix} {\boldsymbol{\Phi}}_{\mathbf{x}} \\ \dot{\boldsymbol{\Phi}}_{\mathbf{x}} \end{bmatrix} \right)^{\mathrm{{T}}} + \boldsymbol{\mathcal{K}} _{k,i} \boldsymbol{\xi} _{i} \boldsymbol{\mathcal{K}} _{k,i}^{\mathrm{{T}}} $$

(65)

$$ \boldsymbol{\xi} _{i+1} = \boldsymbol{\xi} _{i}e^{-\tilde{\beta}}, $$

(66)

$\tilde{\beta}$ being another tuning parameter. This iterative process is performed until the position constraints ${\boldsymbol{\Phi}}$ and velocity constraints $\dot{\boldsymbol{\Phi}}$ fit the desired tolerance.

One of the drawbacks of this method is that the measurement model is applied before the constraints are imposed. Hence, depending on the expression of the measurement model, additional errors may arise from its use when the constraint equations are not fulfilled. The other problem is that part of the corrections provided by the sensors might be undone when the constraints are applied.

6.2 Discrete-time iterated extended Kalman filter with perfect measurements: DIEKFpm

The discrete-time iterated extended Kalman filter with perfect measurements (DIEKFpm) is an expansion of the standard discrete-time iterated extended Kalman filter (DIEKF) [61] developed to cope with constraints in its state space by employing the so-called perfect measurements [62]. The key idea consists in augmenting the vector of observations to include virtual observations that reflect the fulfillment of the kinematic constraints in both positions and velocities. The difference with the SCKF is that in the DIEKFpm both the actual measurements and the perfect measurements are applied simultaneously. Moreover, all the corrections are applied from the a priori estimation. Therefore, although iteratively, the perfect measurements are only applied once, but improving the linearization error at every iteration. Although one should aim for a perfect fulfillment of the constraints, a small noise is considered for the perfect measurements to ease the convergence of the algorithm, for the same reason that the weakening matrix was used on the SCKF. Apart from these differences, this method is similar to the SCKF.

The state vector of this estimator comprises the MB model coordinates and their derivatives (${\mathbf{x}} ^{\mathrm{{T}}} = \left[ {\mathbf {q}}^{\mathrm{{T}}} , \dot{\mathbf{q}}^{\mathrm{{T}}} \right]$). The augmented observation model $\mathbf{h} '( {\hat{\mathbf{x}}} )$ is defined as the concatenation of the real sensors $\mathbf{h} ( {\mathbf{x}} )$ and the kinematic constraints in position and velocity, such as $\mathbf{h} '( {\mathbf{x}} )^{\mathrm{{T}}} = [ \mathbf{h} ( {\mathbf{x}} )^{\mathrm{{T}}}\ { \boldsymbol{\Phi}}( {\mathbf{x}} ) ^{\mathrm{{T}}} \ \dot{\boldsymbol{\Phi}}( {\mathbf{x}} )^{ \mathrm{{T}}} ]$. This affects the calculation of the innovation (or “residual”), which must compare the actual sensor readings and current constraint errors with their predictions. For all time steps $k$ and iteration index $i$, the predicted values of the constraints are always zero:

$$ \tilde{\mathbf{y}} _{k,i} = \begin{bmatrix} \mathbf{o} _{k} \\ {\mathbf{0}}_{2m \times1}\end{bmatrix} - \mathbf{h} '( {\hat{\mathbf{x}}} _{k,i}) = \begin{bmatrix} \mathbf{o} _{k} - \mathbf{h} ( {\hat{\mathbf{x}}} _{k,i}) \\ - {\boldsymbol{\Phi}}( {\hat{\mathbf{x}}} _{k,i}) \\ - \dot{\boldsymbol{\Phi}}( {\hat{\mathbf{x}}} _{k,i}) \end{bmatrix} , $$

(67)

where $m$ is the length of the constraints vector. The adjective perfect that names this method comes from the assumption that there is no error source in the virtual observations. However, in practice, some small noise is added to the extended sensor covariance matrix to improve the convergence of the filter, and this noise is reduced at every iteration until the desired constraint fulfillment is achieved.

These methods provided acceptable accuracy with some of the sensors, but they are more difficult to tune than the methods in independent coordinates because of the additional parameters that must be adjusted.

7 Error-state estimators

The sigma-point Kalman filters showed a remarkable advantage from the implementation point of view: they can make use of existing MB implementations without making significant changes to the MB algorithm. However, this comes at the cost of a high computational load. The error-state estimators (also known as indirect estimators) arose as an alternative to the conventional KFs to enable the use of existing MB simulation algorithms inside a KF without having to modify the MB equations. Therefore, any MB formulation and integrator could be used. This algorithm, referred to as error-state extended Kalman filter (errorEKF), was first presented in [55] for MB models, although this type of algorithm is commonly used for other applications such as the integration of inertial sensors [49].

7.1 Error-state extended Kalman filter: errorEKF

This approach consists in combining an MB model, which can have any desired formulation and integrator, with a KF whose states are the position and velocity errors of the coordinates representing the DOFs of the MB model

$$\begin{aligned} {\mathbf{x}} ^{\mathrm{T}}=\left[ \varDelta \mathbf{z} ^{\mathrm{T}} , \varDelta \dot{\mathbf{z}} ^{\mathrm{T}} \right]. \end{aligned}$$

(68)

During the prediction stage, the MB model is integrated. The states of the KF at the prediction stage are null (it is assumed that the MB model is not having any systematic deviation from the reality). The covariance matrix of the estimation error is also updated. The model for this propagation assumes that the main source of errors comes from the acceleration predicted by the MB model so that the uncertainty of velocity and position estimations grows with time if corrections are not available. The equations of the propagation phase are as follows:

$$\begin{aligned} {\hat{\mathbf{x}}} ^{-}_{k} =& {\mathbf{0}} \\ \end{aligned}$$

(69)

$$\begin{aligned} \mathbf{P} ^{-}_{k} =& {\mathbf{f}_{\mathbf{x}}} \mathbf{P} ^{+}_{k-1} {\mathbf{f}_{\mathbf{x}}} ^{\mathrm {T}} + \boldsymbol {\varSigma }^{P} , \end{aligned}$$

(70)

where the Jacobian matrix of the transition model ${\mathbf{f}_{\mathbf{x}}}$ is the same as that used in the DEKF method (Eq. (50)).

After that the correction phase is started using the following equations:

$$\begin{aligned} \tilde{\mathbf{y}} _{k} =& \mathbf{o} _{k} - \mathbf{h} ( {\mathbf{q}}_{k}, \dot {{\mathbf{q}}}_{k} ) \end{aligned}$$

(71)

$$\begin{aligned} \boldsymbol {\varSigma } _{k} =& \mathbf{h}_{\mathbf{x}} {}_{k} \mathbf{P} ^{-}_{k} \mathbf{h}_{\mathbf{x}} {}_{k}^{\mathrm {{T}}} + \boldsymbol {\varSigma }^{S} \end{aligned}$$

(72)

$$\begin{aligned} \boldsymbol{\mathcal{K}} _{k} =& \mathbf{P} ^{-}_{k} \mathbf{h}_{\mathbf{x}} {}_{k}^{\mathrm{{T}}} \boldsymbol {\varSigma } _{k}^{-1} \end{aligned}$$

(73)

$$\begin{aligned} {\hat{\mathbf{x}}} ^{+}_{k} =& {\mathbf{0}}+ \boldsymbol{\mathcal{K}} _{k} \tilde{\mathbf{y}} _{k} \end{aligned}$$

(74)

$$\begin{aligned} \mathbf{P} ^{+}_{k} =& ({\mathbf{I}}_{2g} - \boldsymbol{\mathcal{K}} _{k} \mathbf{h}_{\mathbf{x}} {}_{k} ) \mathbf{P} ^{-}_{k}. \end{aligned}$$

(75)

As it can be seen, the equations are very similar to those of the correction phase in the DEKF method. The differences come when the virtual sensors have to be evaluated. In this method, the virtual sensors are evaluated using the variables of the MB model instead of the states of the filter, as shown in Eq. (71). The other difference can be seen in Eq. (74) since the estimated state after the prediction phase ${\hat{\mathbf{x}}} ^{-}$ is always null.

After this stage of the filter, with the MB model already integrated, the position and velocity errors of the coordinates representing the DOFs of the MB model are estimated. Therefore, the last task is to use this information to correct the MB model. To do so, it is required that the corrections fulfill the constraints of the MB model at position and velocity level. This can be achieved by incrementing the value of the DOF coordinates with the estimated errors and, later, solving the kinematic position and velocity problems. Although this process would provide a perfect fulfillment of the constraints, the position problem is not linear, and therefore it has to be solved iteratively. Since the corrections are made every time the measurements are available, they are expected to be small. Therefore, as an alternative for the position correction, a linearization of the position problem can be applied:

$$ {\boldsymbol{\Phi}}_{{\mathbf{q}}}\varDelta\hat{{\mathbf{q}}}= {\mathbf {0}}\quad \Rightarrow\quad\hat{{\mathbf{q}}}= {\mathbf{q}}+ \varDelta\hat {{\mathbf{q}}}. $$

(76)

In this case, the increments applied to the vector of coordinates must fulfill Eq. (76), which can be solved as a kinematic velocity problem [15], in which the velocities of the DOF coordinates are replaced with the position errors estimated by the Kalman filter. This method provides an acceptable level of constraint fulfillment in most cases, especially if the multibody simulation used jointly with this filter can correct the kinematics at the following simulation steps.

The advantage of this approach is that, since the position problem is linearized, it can be solved faster and in a more predictable time span, which is important when considering real-time implementations of the algorithm. The corrections at velocity level can still be applied at the DOF coordinates and, after that, the velocity problem can be solved without excessive time penalty since it is linear.

After applying the estimated errors to correct the MB model, the estimated error of the MB model is null, and a new time step can be started.

The simplified flow diagram of this algorithm is shown in Fig. 3.

Fig. 3

Simplified flow diagram of a time step of the errorEKF

7.2 Using the complete Jacobian matrix of plant function: errorEKF_EJ

In Sect. 7.1, the Jacobian matrix of the transition model ${\mathbf{f}_{\mathbf{x}}}$ ignores the relation between the errors in the positions, velocities, and acceleration. This is a very simple approach and can provide accurate results in many cases, but it can also produce a lack of observability. In [56], it was shown that, under certain sensor configurations, the simplified version of the errorEKF loses observability. However, its counterpart with the complete Jacobian matrix, referred to as errorEKF_EJ, provides an observable system in more cases. In the examples presented in [56], a four-bar and a five-bar linkage were studied. It was shown that, when using only velocity sensors at their cranks, the systems were observable using the errorEKF_EJ, but they were not when using the errorEKF. The only difference between the two methods is that the Jacobian matrix of the transition model in the errorEKF_EJ includes the derivatives of the acceleration with respect to the position and velocity, as follows:

The expressions of $\frac{\partial\varDelta \hat{\ddot{\mathbf{z}}} }{\partial \mathbf{z} }$ and $\frac{\partial\varDelta \hat{\ddot{\mathbf{z}}} }{\partial \dot{\mathbf{z}} }$ are provided in [13, 56] and are not included here for the sake on conciseness.

The advantages of including these terms are that the accuracy is increased and the system is observable in more complex cases than the simplified errorEKF with only a slightly increased computational cost. However, the implementation of this algorithm is more complex, and a deep understanding of the MB formulation used is required to derive the required extra-terms. Therefore, it is less likely that this method can be implemented if there is no access to the MB simulation algorithm. Although the required derivatives could be computed numerically, it is not considered a practical option because it entails a high computational cost, which increases with the size of the system.

7.3 Force estimation using indirect observers: errorEKF_FE

Both the errorEKF and the errorEKF_EJ assume that the input forces are accurately known. However, in some applications, the force characterization is not good enough, or the source of the force might be even unknown. For example, in the case of a vehicle, the tire force can be unknown due to the variation of the friction coefficient between the road and the tire. In addition, aerodynamic forces due to the wind can be completely unknown if the only sensors available are those generally used in commercial vehicles. In these cases, it can be useful to add the input force estimation to the previous algorithms. In addition to the force estimation itself, this would help to improve the position and velocity estimations when the force models are inaccurate, or when at least part of the forces are unknown.

In [56], another extension of the errorEKF is presented, but adding force estimation. This method, called errorEKF_FE, adds the acceleration error of the DOF coordinates as part of the states so that the state of the filter is

$$\begin{aligned} {\mathbf{x}} ^{\mathrm{T}}=\left[ \varDelta \mathbf{z} ^{\mathrm{T}} , \varDelta \dot{\mathbf{z}} ^{\mathrm{T}}, \varDelta \ddot{\mathbf{z}} ^{\mathrm{T}}\right]. \end{aligned}$$

(78)

If a forward Euler integrator is assumed for the transition model and a random walk model is supposed for the acceleration error, then the complete Jacobian matrix of the transition model would result as follows:

Apart from using a different state vector and, consequently, a different Jacobian matrix of the transition model, the equations for the prediction and correction phases of the KF are the same as in the errorEKF and the errorEKF_EJ methods. The correction of the MB model, however, has some differences which are explained hereafter.

Once the correction process is finished, the positions and velocities are corrected as in the previous indirect methods. For the acceleration correction, the kinematic acceleration problem is solved. In addition, to improve the acceleration prediction for the following integration steps, the forces need to be corrected. If only the accelerations were corrected, then a mismodeled force would always produce a deviation from the true behavior of the system, thus leading to a biased estimator. Therefore, the additional forces which would be required to compensate for the acceleration error are calculated and applied in the following time steps.

Errors in velocity-dependent accelerations and forces are expected to be fixed when the velocities are corrected. Consequently, the only remaining forces to be corrected are those directly related to the acceleration error. They can be calculated as follows:

$$ \varDelta{{\mathbf{Q}}^{i}} = \bar{{\mathbf{M}}} \varDelta{ \hat{\ddot{\mathbf{z}}} }, $$

(80)

where $\varDelta{{\mathbf{Q}}^{i}}$ is the error of the generalized forces vector corresponding to the independent coordinates.

Since the acceleration errors happen due to unmodeled or mismodeled forces, this force error should be added to the known forces and to the previously estimated forces. This way, the errorEKF_FE provides also an estimation of the forces. However, if force sensors are not used, this force estimation is performed in open loop. Therefore, modeling errors, in particular bad characterizations of mass or inertia, could lead to biased force estimations.

As a general rule, this method cannot provide more information about the source of the force errors so that the estimated errors can be simply added to the generalized forces vector. However, in some particular problems, it is possible to have more information about the source of force errors. For example, in the case of a road vehicle, it is very likely that one of the main sources of error comes from the tire forces. In these cases, if this method is applied, it is advisable to project the force errors over the most likely error sources, as in [47], where the errors of the generalized forces are projected and applied as if they were applied forces at the tires.

These indirect estimators can be tailored to specific problems. For example, in [21] a hydraulically actuated system is studied. In this work, the hydraulic equations are added to those of the MB models. The states of the filter are the position and velocity errors of the MB model and the errors in the pressures of the hydraulic system.

7.4 Reformulation of the indirect methods as direct filters

The indirect observers were formulated as error-state observers because the aim was to use them with already existing MB models with minimal changes to the MB implementation, and this strategy seemed a natural choice for this approach. However, the indirect approach might be more confusing than the direct approach at the first glance because the states of filter are not variables of the multibody model.

In this section, the same algorithms described in Sect. 7.1 are presented using a direct formulation, which implies minimal changes. The final implementation shows that the computational cost and the results are the same. The direct approach only differs in the composition of the state vector: instead of the tracking errors of the DOF coordinates, the state vector of the direct version of the filter is composed by the positions and velocities of the DOFs (and the accelerations, if the method with input force estimation is considered). As in the errorEKF, the propagation of the states can be performed using any MB formulation. This means that the system can be modeled in dependent or independent coordinates, and also that implicit integrators can be used to solve the dynamics of the system.

The first stage of the filter consists in integrating the dynamics of the MB model, obtaining the independent coordinates and velocities (and also the independent accelerations in the methods with force estimation). This phase also constitutes the propagation of the states, which are now a subset of the variables calculated with the multibody simulation, ${\mathbf{x}} ^{\mathrm{T}} = \left[ \mathbf{z} ^{\mathrm{T}}, \dot{\mathbf{z}} ^{\mathrm{T}} \right]$ or ${\mathbf{x}} ^{\mathrm{T}} = \left[ \mathbf{z} ^{\mathrm{T}}, \dot{\mathbf{z}} ^{\mathrm{T}} , \ddot{\mathbf{z}} ^{\mathrm{T}}\right]$, if the force estimation is pursued. Therefore, Eq. (69) is not used any more. After that, the covariance matrix of the estimation error is propagated using the same equations as in the indirect filters (Eq. (70)).

This leads to a simplification of the Jacobian matrix of the transition model because the integrator used for the MB simulation can be different from the one used for the propagation of the covariance matrix. For example, the MB dynamics can be integrated using the trapezoidal rule, while the covariance matrix can be propagated using a forward Euler integrator. As explained in [17], this approximation is acceptable in nonlinear systems, where the state propagation may be performed by numerical integrators or more complex algorithms, as in MB dynamics, while the Jacobian matrix of the transition model is only used for the propagation of the covariance matrix of the estimation error, which has lower accuracy requirements.

After the propagation phase is finished, if there are measurements available, the correction phase is undertaken. In this phase, the equations employed are again the same of the indirect filters (Eq. (71) to Eq. (75)). The only difference is that the states of the filter are variables of the MB system instead of the tracking errors of those same variables and, hence, Eq. (74) becomes

$$ {\hat{\mathbf{x}}} ^{+}_{k} = {\hat{\mathbf{x}}} ^{-} + \boldsymbol{\mathcal{K}} _{k} \tilde{\mathbf{y}} _{k}. $$

(81)

At this point, the correction phase of the KF is finished. The estimated values of the positions and velocities of the DOF coordinates of the MB system after the correction are obtained in the state vector. The next stage of the filter consists in applying the new states to the MB system so that the MB model matches the estimation of the KF. In the case of the filter with input force estimation, the states would also include the correct accelerations of the DOF coordinates.

For the filters without force estimation, the kinematic position and velocity problems can be solved. However, the position problem is iterative, which can be time consuming. Therefore, the same linearization process applied to the errorEKF methods can be applied here.

In order to do that, it is needed to obtain the correction, which has to be applied to all the coordinates of the MB model. As in the indirect formulation of the filter, this can be calculated from the difference of the values of the DOF coordinates provided by the MB model at the prediction step and the estimation provided by the filter after the correction phase $\varDelta {\hat{\mathbf{z}}}$. This is the magnitude provided at the correction phase when the Kalman gain multiplies the innovations (the last term of equation Eq. (81)). From this value, the constraints shown in Eq. (76) are applied to obtain the approximated corrections for all the coordinates at position level.

As for the correction of the velocities, since this problem is linear, it can be solved exactly just by solving the kinematic velocity problem with the estimated velocity of the DOF coordinates as the input data.

Regarding the problem with force estimation, the correct accelerations for the whole set of coordinates can be calculated by solving the kinematic acceleration problem, using again the estimated accelerations of the DOFs as the problem input.

Finally, to obtain the correction for the generalized forces, it is required to calculate the increment of the accelerations needed to go from the values predicted by the MB model to the final estimated values $\varDelta \hat{\ddot{\mathbf{z}}}$. As in the position case, these values are the Kalman corrections corresponding to the accelerations. The forces are calculated using Eq. (80), and they are used later in the same way as in the errorEKF with force estimation method.

As said at the introduction of this section, the direct version of the indirect methods provides exactly the same results and the same computation cost as the indirect methods. Hence, both can be used for the same applications, depending on the preferences of the reader.

8 Kinematic estimators

These methods were introduced in [39] and extended to the estimation of forces by means of a two-stage estimator in [40]. Afterwards, the estimator was employed for flexible problems in [41] and validated in a complex real problem, as is the estimation of the digging forces on an excavator in [42]. Properly, they do not address the MB problem as stated in Eq. (1a), (1b). The basic idea is to employ kinematic models, based on kinematic constraint equations, and a proper set of measurable kinematic variables to estimate other unmeasured kinematic variables.

In this approach, the system is modeled by means of the matrix-R formulation, repeated here for the sake of clarity. A suitable set of $g$ independent coordinates $\mathbf{z}$ (which are the same in number as the DOFs of the mechanism) is established, as well as a set of $n$ dependent coordinates ${\mathbf{q}}$ to be measured at some order of derivative. A set of $n$ algebraic constraint equations relating the dependent and the independent coordinates is defined as

$$ {\boldsymbol{\Phi}}\left({\mathbf{q}}, \mathbf{z} \right) = {\mathbf{0}}. $$

(82)

This equation is a set of nonlinear equations in variables $\mathbf{z}$ and ${\mathbf{q}}$ and, if the constraints are scleronomous, it does not depend explicitly on time. Differentiating it with respect to time leads to the following dependent velocity and acceleration expressions:

$$ \dot{\mathbf{q}}= \mathbf{R} \dot{\mathbf{z}} $$

(83)

$$ \ddot{\mathbf{q}}= \mathbf{R} \ddot{\mathbf{z}} + \dot{ \mathbf{R} } \dot{\mathbf{z}} . $$

(84)

It is interesting to note that these are the matrix-R expressions seen in Eq. (18) and Eq. (19). In this case, Eq. (82), Eq. (83), and Eq. (84) define the kinematic model of the system.

The state vector is defined as

$$\begin{aligned} {\mathbf{x}} ^{\mathrm{{T}}}=\left[ \mathbf{z} ^{\mathrm{{T}}}\; \dot{\mathbf{z}} ^{\mathrm{{T}}} \right]. \end{aligned}$$

(85)

An input vector $\mathbf{u}$ is used including, at least, $g$ independent measured accelerations. Thus, the continuous expression for the MB system is defined as

$$ {\dot{\mathbf{x}}} = \begin{bmatrix} \dot{\mathbf{z}} \\ \ddot{\mathbf{z}} \end{bmatrix} = \begin{bmatrix} \dot{\mathbf{z}} \\ ( \mathbf{R} ^{\mathrm{{T}}} \mathbf{R} )^{-1} \mathbf{R} ^{\mathrm{{T}}} [ \mathbf{u} - \dot{ \mathbf{R} } \dot{\mathbf{z}} ] \end{bmatrix} , $$

(86)

where the model input $\mathbf{u}$ is the $n$-dimensional vector of the sensed accelerations, $\mathbf{u} = \ddot{\mathbf{q}}$ ($n > g$). The accelerations $\ddot{\mathbf{q}}$ play, in the kinematic estimation, the same role as the forces (or torques) in the traditional state observers based on dynamic models, where the input vector collects the external actuation and disturbance forces. A final remark is that, since matrix-R depends on the chosen independent coordinates $\mathbf{z}$, this election compromises the existence of the model through the invertibility of $( \mathbf{R} ^{\mathrm{{T}}} \mathbf{R} )^{-1}$.

Regarding the output vector $\mathbf{y}$, the number of the independent measured variable should be at least equal to the number of system DOFs. A set of sensors ensuring adequate observability should include as many nonredundant position measurements as the number of DOFs. Such measurements are able to capture the zero-frequency dynamics and, hence, prevent estimation drifts. The work presented in [39] showed that it is possible to employ as measurements the same input vector $\mathbf{u}$ considered at the prediction stage of the filter.

As a discrete expression for the filter, the authors use the following expression:

$$ {\mathbf{x}} _{k} = {\mathbf{x}} _{k-1} + \varDelta t \sum_{i=1}^{\nu} \beta \kappa_{i}, \ \kappa_{i}=\mathbf{f}_{c} \left( {\mathbf{x}} _{k-1}+ \varDelta t \sum_{j=1}^{\nu}\lambda_{ij}\kappa_{j} \right), $$

(87)

where the parameters $\beta$, $\lambda_{ij}$, and $\nu$ are particular to the specific discretization scheme adopted.

The aim of the work presented in [39] is to estimate accelerations. For this purpose, the state vector is augmented with the acceleration, together with some relations involving variables of a greater derivative order, as the jerk. Three options are proposed:

• Employ a random walk model for the accelerations.

• Embed in the system model a set of first-order difference equations $\psi$, representing the numerical differentiation, in the presence of noise.

• Use a numerical derivative with model uncertainty for the acceleration.

This approach was validated by means of two examples: a slider-crank mechanism and a two-DOFs planar mechanism, obtaining precise estimations of the kinematic variables, including the derivatives of the state.

In [40], the authors analyzed also the estimation of forces including a second stage. The force estimation was performed by means of a disturbance observer [44, 50]. More recently, an application to the estimation of the digging forces of an excavator was developed in [42]. In this work, the authors employed an EKF for the force estimation stage.

In [11], a purely kinematic EKF was used for human motion reconstruction using optical capture. The algorithm presented in this work assisted the process of automatic marker labeling and improved the robustness of the motion capture process, dealing efficiently with optical marker occlusions and with reflections.

9 Parameter estimation

In most situations, the system under study cannot be characterized with accuracy, leading to uncertainties in the parameters which define the system. For instance, some parameters might be prone to change during the operation of the system. Other parameters might differ from the manufacturer information due to tolerances or wear of the material. These uncertainties can affect the performance of the estimator and, therefore, reduce the accuracy of the state and input estimations.

Contrary to state estimators, there is less research on parameter estimation. Parameter estimation is more difficult because the relationships between the measurements commonly available and the value of the parameters are usually not straightforward. In addition, due to the high amount of parameters required to define a mechanical system, trying to estimate all of them is usually expensive or unfeasible from a computational point of view [5]. Hence, in most applications, only the most relevant parameters are estimated.

Parameter estimation has been addressed in the literature following two different approaches. On the one hand, parameters can be estimated by augmenting the state vector with them. On the other hand, parameters can be estimated using an independent KF, which is executed in parallel with the KF that estimates the states. This approach is also known as dual Kalman filter.

In the MB field, there are some works addressing parameter estimation. In [52, 53], parametric and external uncertainties of MB models were considered through the generalized polynomial chaos theory. This work was later continued in [5] in combination with an EKF. In this case, the state of the KF is augmented with the parameters that are estimated. The polynomial chaos theory is later used for estimating the covariance matrices required by the EKF.

In [26], an EKF is also augmented with the parameters of the system. The complexity of the approach relies on the nonlinearities of the parameters since it is difficult to obtain their derivatives. As a solution, the terms of the Jacobian matrix of the EKF related to the parameters are derived through a curve-fitting method.

There are other approaches to estimate parameters together with the states. In [38], a two-state estimator for automobile side-slip angle is developed. The tire forces and side-slip angle are estimated through an EKF. Since those variables are highly influenced by the tire characteristics, a nonlinear least-squares estimator is used to determine the tire parameters. Both estimators are executed independently, sharing relevant information at a certain frequency (it might be at every time step or at a lower frequency).

A similar approach is followed in [47], where a dual KF is employed for estimating the states, parameters, and inputs of a vehicle. In this case, an MB model of the vehicle is combined with an errorEKF_FE to estimate the states and tire forces of the vehicle. Due to the importance of parameters, such as the vehicle mass and the tire-road friction coefficient, a UKF is used for their estimation. The UKF provides a better accuracy than the EKF when the relationships between parameters and measurements are highly nonlinear, as in this case. In addition, the UKF does not require the development of an explicit Jacobian matrix of the transition model, which would have been complex in this situation. Since there are only two parameters to be estimated, the computational cost of the UKF is not very significant in this particular example. In this dual filter approach, the UKF performs the parameter estimation at every time step, and then the errorEKF_FE estimates the states and forces based on the newest parameter estimation available.

10 Plant noise and measurement noise estimation

One of the requirements for the optimal performance of the KF is the exact knowledge of the statistical properties of the system and the measurements [31]. Although the EKF is not optimal, it also benefits from a good characterization of the noise. This information is gathered in the covariance matrices of the system and measurements, presented in Eq. (3) and Eq. (6) as $\boldsymbol {\varSigma }^{P}$ and $\boldsymbol {\varSigma }^{S}$. However, in most real applications, it is not possible to accurately know the values of both matrices. Usually, the covariance matrices are user-defined tunning parameters. Although the KF may be able to perform satisfactory estimations under these uncertainties in many applications, its robustness cannot be guaranteed. In addition, large estimation errors can occur [14]. Adaptive Kalman filtering (AKF) stands out as a solution for systems with unknown noise properties. The purpose of these methods is to reduce the errors derived from inaccurate noise statistics by adapting the KF to the real data [31].

One of the first works using a method for estimating the noise covariance matrices is presented in [31]. This method is based on analyzing the innovation sequence of the KF, which is Gaussian white noise for an optimal filter. It can be classified as a correlation method: a set of equations is derived relating the system parameters to the observed autocorrelation function [32]. The work shows that, following this approach, the estimations of the covariance matrices are asymptotically normal, unbiased, and consistent.

In [34], the maximum likelihood (ML) principle is used to derive the equations of an adaptive KF based also in the innovation sequence. This method has been applied in [46], combining the ML estimation of the covariances matrices with an errorEKF with force estimation based on MB models.

There are other approaches for AKF, such as the variational Bayesian (VB). The VB has been applied in [57] for estimating the measurement covariance matrix. In this method, the state vector of the filter is augmented with the covariance of the noise of the measurements. However, the VB method cannot be used to estimate the covariance noise of the plant. The VB defines a dynamic model for the evolution of the noises, which is usually approximated by an inverse-gamma or inverse-Wishart distribution for the measurement. However, both distributions fail when representing the plant noise due to its variable behavior [6, 29]. Hence, the uncertainties on the plant noise can reduce the accuracy of the solution. As an alternative, in [19], the prediction error covariance matrix is estimated instead of the plant noise covariance. However, it still needs a nominal value of the plant noise covariance matrix at each time step as the prior information of the inverse-Wishart distribution.

The method proposed by Sage and Husa [51] follows a similar approach to the ML since it is also based on the innovation sequence. The main difference is that it estimates the mean of the system noises together with the covariance noise matrices. However, if both the plant and measurement noises are unknown, then this algorithm will result in filter divergence [65]. The method assumes that there are no errors on the estimated noises, which can also result in filter divergences [14].

Although there is no research on the application of the VB and Sage-Husa methods in MB systems, it could be interesting to explore both approaches. The VB does not rely on the innovation sequence and, therefore, it does not need to perform multiple computations over a sliding window. Hence, it could be more computationally efficient. Regarding Sage-Husa, estimating the mean of the system noises could also result in a more accurate estimation of the noise properties.

10.1 Adaptive errorEKF with force estimation: AerrorEKF_FE

The AerrorEKF_FE is presented in [46] and applies the ML to estimate the covariance matrices of the KF. Assuming that the innovation sequence is white Gaussian noise, the maximum likelihood estimates the covariance that best suits the innovation sequence observed. That is the covariance that maximizes the likelihood of observing the innovation sequence of the filter. The likelihood function can be expressed as $L(\boldsymbol{\sigma}^{2}| \tilde{\mathbf{y}} )$, where $\boldsymbol{\sigma}^{2}$ is a vector containing the covariances (the elements of the covariance matrix) and $\tilde{\mathbf{y}}$ the innovation sequence.

The likelihood presented in [34] can be computed as the probability of obtaining a particular innovation sequence under a white Gaussian distribution with unknown covariance $P( \tilde{\mathbf{y}} |\boldsymbol{\sigma}^{2})$. Thus, the method attempts to obtain the covariance which maximizes $P( \tilde{\mathbf{y}} |\boldsymbol{\sigma}^{2})$, being therefore the most probable value of the covariance matrices of the noise.

The set of innovation data increases with time. However, in terms of computational cost, it is not possible to use the full innovation sequence. Moreover, the optimum values for the covariance matrices might change during the operation of the system under study. Hence, the method proposes to select a moving window of the innovation sequence. Assuming that the innovation data of $N$ different time steps are independent (white Gaussian noise), the likelihood can be expressed as

$$ L(\boldsymbol{\sigma}^{2}| \tilde{\mathbf{y}} ) = \prod_{j=1}^{N} P( \tilde{\mathbf{y}} _{j}| \boldsymbol{\sigma}^{2}) = \prod_{j=1}^{N} \frac{1}{\sqrt{(2\pi)^{s} |\boldsymbol {\varSigma }_{j}|}} e^{- \frac{1}{2} \tilde{\mathbf{y}} _{j}^{T} \boldsymbol {\varSigma }^{-1}_{j} \tilde{\mathbf{y}} _{j}} $$

(88)

$\boldsymbol {\varSigma }$ being the covariance matrix ($\boldsymbol {\varSigma }^{S}$ or $\boldsymbol {\varSigma }^{P}$ depending on which one is being estimated), $s$ is the number of measurements per time step, and $|\cdot|$ is the determinant operator.

To maximize Eq. (88), it should be derived with respect to $\boldsymbol{\sigma}^{2}$ and set to zero. However, differentiating Eq. (88) is complex. Hence, it is simplified by taking its natural logarithm:

$$ L(\boldsymbol{\sigma}^{2}| \tilde{\mathbf{y}} ) = -\frac{1}{2}\sum_{j=j_{0}}^{k} \left[ \text{ln} |\boldsymbol {\varSigma }_{j}| + \tilde{\mathbf{y}} _{j}^{T} \boldsymbol {\varSigma }^{-1}_{j} \tilde{\mathbf{y}} _{j} + c_{j} \right], $$

(89)

where $c_{j}$ is a constant term independent of the covariances $\boldsymbol{\sigma}^{2}$. Maximizing the previous equation and after manipulating the equation with the expressions of Eq. (47) and Eq. (52) leads to

$$ \sum_{j=j_{0}}^{k} \text{tr}\left\{ \left[\boldsymbol {\varSigma }^{-1}_{j} - \boldsymbol {\varSigma }^{-1}_{j} \mathbf{y}_{j} \mathbf{y}^{T}_{j} \boldsymbol {\varSigma }^{-1}_{j} \right] \left[ \frac{\partial \boldsymbol {\varSigma }^{S} _{j}}{\partial\sigma^{2}_{k}} + \mathbf{h}_{\mathbf{x}} {}_{j} \frac{\partial \boldsymbol {\varSigma }^{P} _{j-1}}{\partial\sigma^{2}_{k}} \mathbf{h}_{\mathbf{x}} {}_{j} \right] \right\} = 0, $$

(90)

where $k$ is the time step in which the covariance matrix is estimated and $j$ is the counter inside the estimating window.

To obtain independent expressions for $\boldsymbol {\varSigma }^{P}$ and $\boldsymbol {\varSigma }^{S}$, certain assumptions are made. To derive $\boldsymbol {\varSigma }^{P}$, it is considered as a diagonal matrix and $\boldsymbol {\varSigma }^{S}$ is supposed to be known and independent of the estimated parameters $\boldsymbol{\sigma}$. The same assumptions can be applied to derive the expression for estimating $\boldsymbol {\varSigma }^{S}$. Hence,

$$\begin{aligned} \boldsymbol{{}\hat{\varSigma}}{}^{P} _{k} &= \frac{1}{N} \sum_{j=j_{0}}^{k} \left[\varDelta {\mathbf{x}} _{j} \varDelta {\mathbf{x}} ^{T}_{j} + \mathbf{P} _{j}^{+} - {\mathbf{f}_{\mathbf{x}}} {}_{j} \mathbf{P} _{j-1}^{+} {\mathbf{f}_{\mathbf{x}}} {}_{j}^{T} \right] \end{aligned}$$

(91)

$$\begin{aligned} \boldsymbol{{}\hat{\varSigma}}{}^{S} _{k} &= \frac{1}{N} \sum_{j=j_{0}}^{k} \left[ \tilde{\mathbf{y}} _{j} \tilde{\mathbf{y}} ^{T}_{j} - \mathbf{h}_{\mathbf{x}} {}_{j} \mathbf{P} _{j}^{-} \mathbf{h}_{\mathbf{x}} {}_{j}^{T} \right], \end{aligned}$$

(92)

where $\varDelta {\mathbf{x}}$ is the state correction sequence, which can be calculated as

$$\begin{aligned} \varDelta {\mathbf{x}} _{k} = {\hat{\mathbf{x}}} ^{+}_{k} - {\hat{\mathbf{x}}} ^{-}_{k}. \end{aligned}$$

(93)

Depending on the version of the KF used, more constraints can be added to the final shape of the plant covariance matrix, improving the convergence of the adaptive counterpart of the solution. For example, if the errorEKF_FE is used, then the shape of the covariance matrix of the system is [56]

where $\text{diag} \left(\boldsymbol{\hat{\sigma}}{}^{2}\right)$ is a diagonal matrix containing the estimated variances of the plant noise at acceleration level.

Finally, this method cannot guarantee that the estimated covariance matrices are semidefinite positive, which could lead to errors in the filter. In [36], it is proposed to set the negative values of the estimated matrix to their absolute value. In addition, as stated earlier, this method relies on the assumption that the innovation sequence is white Gaussian noise. However, there are systems which have colored noise where this assumption is no longer true.

Results presented in [46] show that, through this method, the algorithm converges to a solution which minimizes the error in the estimations independently of the initial estimation of the covariance noise matrices. However, when estimating both the plant and measurements covariance matrices, the filter showed divergence issues in some of the use-cases presented in [46] due to the available sensors. Regarding the efficiency, estimating the noise covariance matrices through the ML leads to an increment on computational cost, which should be considered when real-time purposes are intended.

11 Colored noise

The KF approaches are developed for dynamic systems corrupted by white noise. However, there are real systems whose plant and/or measurement noises are autocorrelated, and hence the KF estimations can be less accurate. The solution to this issue can be accomplished by applying a shaping filter [4]. This kind of filters were first applied to MB models in [48] and is extended in this work. In this case, a Markov model fed by white noise is used. This noise model uses an internal state, which can be included in the state vector and estimated by the filter.

11.1 ErrorEKF with force estimation and a shaping filter: errorEKF_FE_SH

The model assumed by an EKF can be expressed as follows:

$$ {\mathbf{x}} _{k} = \mathbf{f} ( {\mathbf{x}} _{k-1}) + \omega, $$

(95)

where $\omega$ is the noise of the plant or MB model. The exact value of the noise is unknown, but it is assumed to be white Gaussian noise with a covariance matrix $\boldsymbol {\varSigma }^{P}$.

In practical applications, however, it is common that the noise is not white. For instance, if the plant of the system is an MB model with some incorrect parameters, it is expected that many predictions will have a systematic bias, and therefore the noise will be time-correlated.

To add this information to the filter, a shaping filter can be added estimating the noise of the MB, and the system plant becomes

$$\begin{aligned}& {\mathbf{x}} _{MB_{k}} = \mathbf{f} ( {\mathbf{x}} _{MB_{k-1}}) + \omega_{k-1} \end{aligned}$$

(96)

$$\begin{aligned}& \omega_{k} = \mathbf{W} \omega_{k-1} + \xi, \end{aligned}$$

(97)

where $\mathbf{W}$ is a diagonal matrix with the values of the weighting factors $W_{i}$, and $\xi$ is the white Gaussian noise of the colored noise $\omega$. In this model, the noise applied to the multibody model is no longer white, but comes from a model corrupted by white Gaussian noise, in this case, a Gauss–Markov model. The weighting factors $W_{i}$ can be calculated as

$$ W_{i} = e^{-\frac{ \varDelta t }{\tau}}, $$

(98)

where $\varDelta t$ is the time step of the simulation and $\tau$ is the correlation time, which is difficult to know for the MB plant noise. Therefore, $W_{i}$ is estimated by analyzing the correlation of the innovation sequence of the filter in an online process. Since the available data increase with time, it is proposed to define a moving window over the innovation sequence. Hence, $W_{i}$ is updated based only on the newest innovation data.

If the systems of equations Eq. (96) and Eq. (97) are combined in one system, the new augmented state of the filter would be

$$ {\mathbf{x}} _{aug}=\left[ \textstyle\begin{array}{c} {\mathbf{x}} _{MB} \\ \omega \end{array}\displaystyle \right]. $$

(99)

The propagation of the filter uses Eq. (96) and Eq. (97) for the state and the following equation for the covariance matrix of the estimation error:

$$ \mathbf{P} _{k} = {\mathbf{f}_{\mathbf{x}}} _{aug} \mathbf{P} _{k-1} {\mathbf{f}_{\mathbf{x}}} _{aug}^{\mathrm{{T}}}+ \boldsymbol {\varSigma }^{P} $$

(100)

with

$${{\mathbf{f}}_{\mathbf{x}}}_{aug}=\left[\begin{array}{cc}{\mathbf{f}}_{\mathbf{x}}& \mathbf{I}\\ \mathbf{0}& \mathit{W}\end{array}\right].$$

(101)

In this work, this method is applied to an errorEKF_FE. As it is shown in Eq. (94), the covariance matrix of the plant noise for this filter only has noises in the diagonal terms corresponding to the accelerations. When the shaping filter is applied, these noises are set to zero (because they are already included in the plant model), and now the only terms on the covariance matrix are those corresponding to the Gauss–Markov model, as follows:

$$ \boldsymbol {\varSigma }^{P} = \left[ \textstyle\begin{array}{c@{\quad}c} {\mathbf{0}}& {\mathbf{0}} \\ {\mathbf{0}}& \boldsymbol {\varSigma }^{P} _{\omega} \end{array}\displaystyle \right]. $$

(102)

In this work, the value of $\boldsymbol {\varSigma }^{P} _{\omega}$ is obtained through a previous offline process. Following the three-simulation method, the model is integrated at each time step using as previous values of the coordinates the ones from the prototype. The error signal can be derived by difference of the coordinates obtained from this integration of the model and the coordinates obtained from the prototype. This signal is later analyzed to obtain the values of $\mathbf{W}$ and $\boldsymbol {\varSigma }^{P} _{\omega}$ that fit the noise. In a real scenario, the value of $\boldsymbol {\varSigma }^{P} _{\omega}$ should be adjusted based on a trial and error procedure or by using an AKF.

A similar procedure can be followed if the measurement noise is colored. In this case, the state vector should be augmented with the measurement noise such as

$$ {\mathbf{x}} ^{{\mathrm{{T}}}}=\left[ \textstyle\begin{array}{c} {\mathbf{x}} _{MB} \\ v\end{array}\displaystyle \right], $$

(103)

where the noise would be modeled as

$$ v_{k} = \mathbf{W} v_{k-1} + \zeta, $$

(104)

$\mathbf{W}$ being a weighting factor and $\zeta$ the white noise of the estimated $v$.

There could be applications where both the plant and the measurement noises are colored. In these situations, the previous equations can be applied together as in the use-case presented in [30].

As an example, the solution for plant colored noise is applied on a four-bar linkage (Fig. 4a) and on a five-bar linkage (Fig. 4b). The MB model is defined in natural coordinates using the augmented Lagrangian index-3 (ALI3P) formulation [7] to solve the kinematics and dynamics of the system. The simulations consist in letting the mechanisms move freely under the effect of gravity.

Fig. 4

Mechanisms employed in this work

The tests performed for evaluating the presented solution for systems with plant colored noise follow the three-simulation method described in Sect. 3. All the simulations are executed in MATLAB^® environment using the open-source toolbox MBDE.¹ Thus, three MB models of each mechanism are employed to replicate a real scenario through simulation. All the simulations are executed at a frequency of 200 Hz. In addition to the error of 1 m/s² in the gravity value, there is an initial offset of $\pi/16\text{ rad}$ in the crank angle position of the model with respect to the initial position of the prototype.

The tests are also performed for different sensor configurations. They are selected following the work presented in [56] to carry out a reliable comparison of the results. Regarding the estimator, the errorEKF_FE is also employed in [56]. Hence, the equations for colored plant noise presented in this section can be properly evaluated. The four-bar and five-bar linkages are instrumented with the same type of sensors. However, since the five-bar linkage has two DOFs, the number of sensors is duplicated in this mechanism. The sensor models are provided in [56]. The four considered configurations are listed next:

• Encoders in the cranks of each mechanism for measuring the DOF coordinates.

• Gyroscopes in the cranks for measuring the angular rates of the DOF coordinates.

• Gyroscopes in the couplers of the mechanisms to obtain angular rates that are not directly related with the DOF coordinates.

• Pair of accelerometers at the end of the cranks, in such a manner that there is one sensitive axis parallel and another perpendicular to each crank.

Figure 5 shows the results obtained for two of the use-cases tested: the four-bar linkage with accelerometers at the cranks and the five-bar linkage with gyroscopes in the couplers. The remaining use-cases can be evaluated by the reader by accessing to the open-source toolbox MBDE. The results shown in Fig. 5 correspond to the estimations made by the observer with two different filters: the errorEKF_FE and the errorEKF_FE_SH, which is the errorEKF_FE combined with the shaping filter. Regarding the forces estimated, it can be seen how the addition of the shaping filter improves the accuracy of the errorEKF_FE. However, the most interesting result is that the shaping filter improves the whiteness of the innovation sequence. As it can be seen in Figs. 5b and 5d, the standalone version of the errorEKF_FE shows an innovation sequence with a lack of low frequencies. Meanwhile, complementing the errorEKF_FE with the shaping filter leads to an innovation sequence with similar levels of all frequencies, meaning that it is closer to white noise. It should be remarked that the proposed approach requires an initial period of time to converge to the proper values of the noise.

Fig. 5

Comparison of results between the errorEKF and the errorEKF combined with the shaping filter presented in this work

From the results, it can be concluded that including a shaping filter leads to the whiteness of the innovation sequence, which might result in more accurate estimations. If the observer already has a white innovation sequence, adding a shaping filter may not have effects on the estimations.

Finally, it should be pointed out that the shaping filter could be also combined with the adaptive filters presented in Sect. 10. Since the AKF presented in this work relies on the whiteness of the innovation sequence of the filter, the shaping filter might help to improve the accuracy and performance of the estimator.

12 Benchmarking and discussion

To provide a broader perspective on the methods described in this paper, ten of the methods described before are tested, using the three-simulation method applied to the four-bar mechanism shown in Fig. 4a. Gravity is the single force acting on the mechanism. All the methods are implemented in MATLAB^® using the open-source MBDE library. As in the previous section, the simulations are executed at a frequency of 200 Hz. The mechanism playing the role of the model has a gravity value which is 1 m/s² lower than that of the prototype and, also, the initial position of the crank is deviated by $\pi/16\text{ rad}$ with respect to the true initial position of the mechanism.

This initial position error serves as a practical verification of the observability of the system: if the observer can correct the initial offset, it means that the system is observable for the conditions tested.

Three different sensors (one at a time) are evaluated for these tests:

• Encoder measuring the angle of the crank.

• Gyroscope measuring the angular rate of the crank.

• Gyroscope measuring the angular rate of the coupler.

The measurements of the sensors are generated from the prototype, and a sequence of pseudorandom white Gaussian noise is added to mimic the behavior of actual sensors. The same sequence of pseudorandom noise was used in all of the tests.

The results of the tests can be seen in Fig. 6. Notice that Figs. 6a to 6d use a logarithmic scale. Figure 6a shows the position error of ${\hat{\mathbf{z}}}$ in tests of 10 s. Figure 6b and Fig. 6c show the results at velocity and acceleration level, respectively. Since there is an initial position error, some configurations of the observer take some time until the initial error is corrected. Therefore, an additional plot is included in Fig. 6d, showing the position error without taking into account the first 2 s of the tests, which is the time in which the transient occurs.

Fig. 6

Comparison of results between the estimators analyzed in this work

Starting with the tests having an encoder on the crank, all the methods achieved reasonable good results, although the CEKF provided worse accuracy than the other methods at position level. Since the MB model has one DOF, and there is a sensor at position level, it is not a surprise that the system is observable. The error of the CEKF was 0.0246 rad, while all the other methods achieved an accuracy between 0.0050 and 0.0057 rad. If the transient at the beginning is not taken into account, then the position RMSE for the CEKF is reduced to 0.0159 rad, while it does not change for the other methods. It is worth noticing that the RMSE of the sensor used is 0.0176 rad (due to the pseudorandom noise sequence used). All the methods provide a lower steady-state error than the noise of the sensor used to correct the model. All the methods showed similar trends in velocity and acceleration, with all the discrete methods providing more accuracy than the CEKF. Note that many of the methods compared here do not estimate accelerations directly, but they are taken from the corrected MB model for this comparison. Only the methods with force estimation (errorEKF_FE, errorEKF_ FE_SH, and AerrorEKF) have a direct acceleration estimation.

When studying the behavior of the different observers with a gyroscope on the coupler, some more differences arise. In this case, it is not obvious at first sight that the system will be observable. Since the only available sensor is at velocity level, it could be reasonable to think that the position would not be observable. However, the angular rate of the coupler is not independent of the position of the crank. In fact, for the mechanism considered here, even if the crank were rotating at constant speed, there would be two positions for which the angular rate of the crank would be null. This information is provided by the kinematics of the system. Therefore, all of the methods studied here can correct the initial position error and provide accurate estimations with only a gyroscope on the crank. The accuracy provided by this sensor configuration is lower than that provided by the previous one if the complete maneuver is considered. However, if the initial transient is removed, the accuracy with this sensor is greater than with the encoder for most of the methods tested, with the exceptions of the DEKF, the SCKF, and the DIEKFpm. This improvement is particularly remarkable for the errorEKF and all its derived methods. The reason is that the correction of the initial position error takes longer with this sensor configuration, but once corrected, the estimation is better than that achieved with the encoder in most of the cases.

However, it must be kept in mind that this is a particular result for this mechanism and for the specific motion studied here. For instance, if the mechanism is stopped, all the systems would become unobservable, since the coupler will have null angular rate at any position of the crank. Therefore, no position information could be retrieved with a velocity sensor under this particular situation.

Finally, when considering a gyroscope on the crank, the task is more challenging. In this case, the kinematics of the mechanism allows any angular rate of the crank at any position of the mechanism. Therefore, the kinematic constraints cannot help in achieving the observability of the system. However, the acceleration of the system is related to the absolute position of the mechanism. Hence, the discrete systems with the exact Jacobian (errorEKF_EJ, errorEKF_FE, errorEKF_FE_SH, and AerrorEKF_FE) and the UKF can still correct the initial position error and provide useful estimations. Methods with force estimation provide better results in this test. The discrete methods with simplified Jacobian, both in independent coordinates (DEKF and errorEKF) and dependent coordinates (SCKF and DIEKFpm), cannot correct the initial position error, keeping it approximately constant throughout the whole simulation. However, the variance of the estimation error grows under this situation, so it is expected that the system will get unstable at some point in longer simulations. The continuous-time extended Kalman filter (CEKF) was not able to provide any estimation with this sensor configuration.

Since some of the possible applications of these types of estimators might require real-time execution, the computational cost required to run these methods is relevant. Although this benchmark was run in MATLAB^®, which is not suitable for real-time implementations, the computational cost comparison of the methods provides an idea of their relative efficiency. It can be seen that the slowest methods are the CEKF and the UKF. On the other hand, the errorEKF and the SCKF are the fastest methods, with all the other discrete-time extended Kalman filter methods having a slightly higher computational cost. Since these programs have been run on a computer with a conventional operating system, several runs of the same algorithm may yield slightly different computational costs. This comparison shows the mean CPU time values of four simulations, providing an indication of the most efficient methods.

From other point of view, it should be taken into account that, despite the higher computational cost of the AerrorEKF_FE and the errorEKF_FE_SH with respect to the errorEKF_FE, these two filters provide additional benefits. The AerrorEKF_FE obtains automatically the value of the plant noise, avoiding the time spent in tuning the filter before the execution, which is usually a tedious process. The errorEKF_FE_SH allows to characterize the noise in those cases where the plant and/or measurement noises are autocorrelated (colored noise), reducing the error of the estimation of the filter in those cases. Therefore, the increase of computational cost with both methods may be a good trade-off in particular applications due to the additional benefits they provide.

12.1 Filter tuning

All the Kalman filters have several parameters that condition their estimations. At least, they depend on the covariance matrices of the plant noise $\boldsymbol {\varSigma }^{P}$, the sensor noise $\boldsymbol {\varSigma }^{S}$, and the estimation error assumed initially $\mathbf{P} _{0}$. Although all these parameters have a clear physical meaning when all the assumptions of the Kalman filter are fulfilled, in many practical Kalman filter implementations, some of them are either unknown or the filter is applied in conditions that do not fit the assumptions made in the development of the Kalman filter. Therefore, in practice, one or more of these parameters are treated as tuning parameters, which are adjusted by a trial-and-error procedure. In addition, some of the methods have additional parameters to adjust, such as tolerances in methods with iterative parts. In this section, all the parameters used are discussed.

The initial covariance matrix $\mathbf{P} _{0}$ used in this work is a diagonal matrix with a value of 0.0076 for all the diagonal elements. This value accommodates the initial estimation error due to the initial position error assumed in the tests presented here. In the case of the errorEKF_FE_SH, since the state vector is augmented with the plant noise, the initial covariance matrix $\mathbf{P} _{0}$ is augmented with the new terms related to the plant noise estimation. In this case, a value of 0.001 was used.

The sensors used in this work are ideal sensors modeled in the prototype (referring to the three-simulation method), but corrupted by a sequence of pseudorandom noise. Since this sequence has known statistics, the covariance matrices of the sensor noise $\boldsymbol {\varSigma }^{S}$ can be determined. These matrices are diagonal for all the methods in independent coordinates (in this case, since only one sensor is used in the tests, they are 1 by 1 matrices). The standard deviation of the noise considered in this work is $17.453\cdot10^{-3}\text{ rad}$ for the encoder and $983.943\cdot10^{-6}$ rad/s for the gyroscope. The values used in the covariance matrix are these values squared.

The methods in dependent coordinates presented in this work use the constraints as measurements to impose the constraint fulfillment, as shown in Eq. (64) and Eq. (67). The two methods presented here (SCKF and DIEKFpm) use a weakening scheme to favor the convergence of the constraints. The part of the measurement matrix for the SCKF is explained in Eq. (62) to Eq. (66), where two tuning parameters $\tilde{\alpha}$ and $\tilde{\beta}$ are used. The values used in this work were $\tilde{\alpha} = 0.1$ and $\tilde{\beta} = 10$. Again, these coefficients were adjusted by trial and error. As for the DIEKFpm, a diagonal covariance matrix is used in this case. The variance value applied to all the constraints was 0.001. Then, at every iteration, this variance was divided by the Euler’s number $e$ so that the noise was reduced to impose the constraints to the desired level. For these two methods, the iterations were performed until the norm of the constraints vector (including both position and velocity constraints) reached a value under 0.001.

Finally, the main parameter to adjust is the plant noise covariance matrix for the discrete systems, and the power spectral density matrix of the system noise for the continuous method. This parameter represents the accuracy achieved by the model plant when tracking the prototype. In this work, it is assumed that the main source of uncertainty comes from the acceleration because the integration of position and velocity is usually much more accurate than the force models. Therefore, filters with acceleration estimation use a covariance matrix for the plant noise which has only values on the diagonal terms corresponding to the accelerations with value $\boldsymbol{\sigma}^{2}$. The resulting matrix has the following structure:

Since this is a discrete noise, it should be increased if the time step is also increased. The CEKF also uses the same approach because the noise has the same units that the derivatives of the states although, in this case, the noise is continuous, and therefore it is characterized by its power spectral density at acceleration level $\boldsymbol{q}_{c}$. For this reason, it remains constant independently of the time step used for the integration of the system. The structure of the power spectral density matrix of the system noise is as follows:

For the discrete-time methods in independent coordinates and filters without acceleration estimation, the covariance matrix of the plant noise is calculated from their continuous counterparts using Van Loan’s method [18] so that it can be expressed as a function of the power spectral density of continuous acceleration noise, resulting in the following structure:

Finally, the discrete methods with dependent coordinates use a more complex approach. The covariance matrix of the plant noise is built starting from the power spectral density of the continuous noise of the independent accelerations and applying Van Loan’s method to get its corresponding discrete noise. After that, a matrix like Eq. (107) is obtained. The blocks outside the diagonal are neglected and set to zero. The blocks in the diagonal contain the noise covariances for the DOF coordinates, but the noise covariances of the dependent coordinates have to be obtained. In this case, the authors sought for a noise matrix which allowed to change the values of the dependent coordinates to fulfill the constraints, but without affecting too much to the position of the DOF coordinates, to avoid degrading the accuracy of the estimation. With this in mind, the variance of every DOF coordinate (the diagonal term of the covariance matrix) is set to the same value that it would have in a method in independent coordinates. Then, the remaining values of the diagonal of the covariance matrix are set to values much greater than the ones used for the DOF coordinates. These values can be denoted as $\boldsymbol{\sigma}_{b}^{2} \gg \boldsymbol{q}_{c}$. Finally, the terms coupling every DOF coordinate with the dependent coordinates are scaled using matrix-R, which contains the velocity relationship between independent and dependent coordinates. Therefore, for the position block, the values out of the diagonal for the covariances corresponding to positions are calculated as

$$ \boldsymbol {\varSigma }^{P} {}_{{\mathbf{q}}cov} = \mathbf{R} _{dep} \text{diag} \left( \boldsymbol{q}_{c} \right) \frac{ \varDelta t ^{3}}{3}, $$

(108)

where $\mathbf{R} _{dep}$ is the part of matrix $\mathbf{R}$ corresponding to the dependent coordinates.

For the velocity block, the values out of the diagonal can be calculated as

$$ \boldsymbol {\varSigma }^{P} {}_{\dot{\mathbf{q}}cov} = \mathbf{R} _{dep} \text{diag} \left ( \boldsymbol{q}_{c} \right) \varDelta t . $$

(109)

If it is assumed that the DOF coordinates are the last part of the coordinate vector, the structure of the position block of the plant covariance matrix would become

Finally, the structure of the complete plant noise covariance matrix is

The values of the plant covariance matrices were adjusted by trial an error, using the innovation spectrum as a guide to increase or decrease the value of the plant noise. When the spectrum of the innovation sequence has a uniform amplitude for all the frequencies, it means that the noises are properly adjusted. The value of $\boldsymbol{q}_{c}$ used for all the discrete methods without acceleration estimation in this work was $9.162 \cdot10^{-2}$. The methods with dependent coordinates used $\boldsymbol{\sigma}_{b}^{2} = 1$. The errorEKF_FE used a value for $\boldsymbol{\sigma}^{2}$ of $2.291 \cdot10^{-3}$. The AerrorEKF used the same value as the methods without acceleration estimation. Even if this value did not make sense for this observer, its adaptive capability was put to the test by providing a wrong initial value for its plant covariance matrix. The covariance matrix achieved by this method varies continuously depending on the system motion. However, this matrix reaches values of the same order of magnitude as those tuned by trial and error. Regarding the CEKF, the plant noise value $\boldsymbol{q}_{c}$ used was 0.73303. Finally, for the errorEKF_FE_SH, the plant noise value was of $2.3428 \cdot10^{-3}$. The plant noise covariance matrix structures defined in this section assisted in this time-consuming task.

With respect to the window sizes of the AerrorEKF and the errorEKF_FE_SH, both were adjusted by trial and error. The window sizes do not have to be the same because they represent different concepts in both filters. As a rule of thumb, large window sizes lead to smooth estimations. However, they can also limit the capacity of the filter to adapt to sudden changes. Hence, the window size should be selected attending to the nature of the maneuver. The main idea is to avoid the effects of past events that do not have relation with the current state of the mechanism. In this work, the window size for the AerrorEKF was of 50 samples, while in the errorEKF_FE_SH it was of 500 samples.

There are some other parameters that are particular to each method, and they could potentially affect the final results. These parameters do not exist on all the methods. Even when they serve a similar purpose, they can have different meanings, and they are not comparable. In fact, most of the following parameters are particular to one or few methods, and there is not an equivalent parameter on the other algorithms. In general, the parameters were adjusted to provide the best performance possible to every estimation algorithm while making the methods robust enough to be able to cope with all the different configurations tested here without changing the parameters from test to test. The CEKF employs the trapezoidal rule as the integrator, and the tolerance imposed for its convergence is of $10^{-5}$ for the equation Eq. (25). In the case of the UKF, the trapezoidal rule was also used. In this case, a tolerance of $10^{-10}$ in the norm of the position increment between two consecutive iterations is used as the stopping condition of the integrator. In the methods in which a kinematic position problem is solved iteratively (UKF, and DEKF), the tolerance used for the norm of the constraints is $10^{-13}$. This was also the value used in all the methods for the initial position problem at the beginning of the simulations. The methods in dependent coordinates employed a tolerance of $10^{-3}$ for the norm of the kinematic constraints (both position and velocity constraints are included here). Although a lower tolerance would have been desired, the nonlinear nature of the multibody constraints impedes a better convergence. Finally, all the methods derived from the errorEKF used an augmented Lagrangian of index 3 multibody formulation with projections and trapezoidal rule as the integrator. In this case, the Lagrange multiplier employed had a value of $10^{9}$, and the dynamic tolerance for the fulfillment of the equations of motion was $10^{-10}$. All the magnitudes used internally in the code are expressed using SI units.

It is worth noting that the simpler methods, namely, the DEKF, SCKF, and the DIEKFpm, in the implementation used here employ the forward Euler integrator both for the propagation of the multibody equations and for the propagation of the covariance matrix of the estimation error. In the case of the UKF, since the propagation of the covariance matrix of the estimation error is done by means of the unscented transform, the system matrix is not used, and an implicit integrator can be used. In this case, the trapezoidal rule integrator was used. In the case of the estimators of the errorEKF family, the forward Euler integrator is still used for the propagation of the covariance of the estimation error, but a different integrator can be used for the multibody model. In this case, the augmented Lagrangian of index 3 with projections and the trapezoidal rule was used. This formulation is efficient and also imposes the kinematic constraints, which might not be exactly fulfilled after the estimation errors are fed back to the multibody model. Finally, the CEKF is also used with a trapezoidal rule integrator as it was first introduced in the multibody literature.

13 Conclusions

The relevance of Kalman filtering in industry has been increasing during the last decades. The use of Kalman filters allows to gather more information of a system than that measured with physical sensors. In addition, multibody dynamics is also a tool widely used to perform accurate simulations in industrial applications. Combining both methods can offer an improved solution for estimating variables of any system with high accuracy, thus reducing the amount of physical sensors required for monitoring a particular system.

During the last two decades, a huge effort has been made by the multibody community to combine Kalman filters and multibody models. It is not trivial to combine the equations of the Kalman filter, which are first-order linear differential equations in independent coordinates, with the multibody formulations, which are second-order highly nonlinear differential equations in either dependent or independent coordinates. This motivated a great research effort to achieve reliable, efficient, and accurate formulations combining both techniques.

In this work, a comprehensive review of all the methods combining multibody models with Kalman filters is presented. The research on this topic started with the continuous-time extended Kalman filter (CEKF), which derived to the discrete-time extended Kalman filter (DEKF), looking for a reduced implementation complexity together with higher stability of the estimator. However, both methods require a modification of the multibody equations to fit the Kalman filter structure. Focusing on the reduction of the coupling between Kalman filter and multibody implementations, the sigma-point Kalman filters (SPKFs) were tested. This approach allows us to use the most suitable multibody formulation with independence of the Kalman filter equations. However, it entails a high computational cost, making this approach unsuitable for real-time applications, especially for systems with a high number of degrees of freedom. Versions of the Kalman filter being used with multibody formulations in dependent coordinates were also explored, offering a solution with low computational cost, although less robust and more difficult to tune than the methods in independent coordinates. Indirect versions of the discrete-time extended Kalman filter appeared later, offering a compromise between low computational cost and easiness of implementation together with robustness. Finally, some estimators based on the kinematics of the multibody system were also developed.

Furthermore, to increase the accuracy of the aforementioned solutions, the Kalman filter was extended with the estimation of parameters which showed a high level of uncertainty. In addition, Kalman filters require also to accurately know the statistical properties of the noise of the system under study and of the sensors employed, which are assumed to behave as white Gaussian noise. Due to the difficulties for setting these statistical characteristics, adaptive versions of the Kalman filter were developed. For the cases in which the noise of the system and/or the measurements does not fulfill the requisite of being white Gaussian, a new filter, the errorEKF_FE_SH, has been presented in this work, showing satisfactory results.

Finally, ten of the described approaches have been tested in a simulation environment. A comparison among the ten algorithms has been made in terms of accuracy and computational cost. The results can be useful to determine which is the most suitable approach for a given application. In particular, the UKF is the most versatile and robust solution: the filter equations are totally independent from the MB formulation. However, its higher computational demand compared to the other methods might hinder real-time implementations of the UKF. If real-time performance is required, then the filters belonging to the errorEKF family are the most suitable. They offer a compromise between accuracy and easiness of implementation while allowing real-time performance.

To conclude, this review summarizes the efforts of the multibody community to combine Kalman filters with multibody models, aiming to provide an accurate solution for the estimation problem, thus increasing also the field of application of multibody dynamics. This work can serve as a guide for researchers interested in using observers based on multibody dynamics. Furthermore, it can be used as a starting point for new developments of Kalman filters, which may improve the current state of the art of these methods.