1 Introduction

Modern mechanical system solutions are becoming increasingly dependent on sensing technologies. For example, both onroad and offroad heavy mobile machinery is equipped with numerous sensors for monitoring and control purposes. In this regard, the reliability of the sensors and the quality of the measurement signals become critical. Reliable sensing is especially important for health- and safety-critical applications. Research has shown that the quality of measurement data can be enhanced by the use of state-estimation algorithms [1], which form the topic of this paper.

The use of multibody system dynamics, together with state-estimation algorithms, offers an approach to estimate the behavior of a mechanical system [2]. Within multibody dynamics, state-estimation algorithms have been used in estimation of vehicle dynamics [3, 4], for systems with hydraulic actuators [5], and in railway applications [6]. Kalman-filter-based techniques, in particular, can be seen as a valuable approach since they provide an optimal solution for the linear estimation problem, given that the uncertainties of both the system model and the measurements are known [7]. However, the original Kalman filter cannot be applied directly to nonlinear systems such as multibody systems, and nonlinear variants have to be used instead [8]. Of the many possible variants, the extended Kalman filter [1] and the unscented Kalman filter [9] are commonly employed for multibody models, as in [10].

The extended Kalman filter was first introduced in the 1960s for state estimation of the spacecraft-navigation problem [11]. Application of the extended Kalman filter to multibody system models was pioneered over a decade ago in [12]. In general, Kalman filters are based on two models: a state-transition model that determines the dynamical behavior of the system and a state-update model that is based on the statistical properties of the system. In the case of the continuous extended Kalman filter (CEKF), the state-transition and the state-update models are seamlessly fused together, whereas for the discrete extended Kalman filter (DEKF), they are considered as two separate stages [13]. In the state-transition stage of the DEKF, the a priori values of the state variables and their covariances are evaluated based on their values at the previous time step and the control applied during the time step. Correspondingly, in the state-update stage, the a priori values of state variables are corrected based on the measurement data, and the a posteriori values of the state variables and covariances are obtained.

Currently, a fundamental approach has been to combine the extended Kalman filter with an inherently nonlinear multibody system model by using different trajectories for the integration of state variables and covariances. In the case of CEKF, this is performed by combining the nonlinear equations of motion and the linear Kalman filter equations into a set of nonlinear equations. The resultant nonlinear equations can be solved using iterative integration techniques [12], such as an implicit single-step trapezoidal rule [14]. Correspondingly, the evolvement of the covariances is evaluated using the tangent trajectory of the nonlinear system. Another approach presented in the literature is the use of the error-state extended Kalman filter, where simulation of the system and incorporation of the measurements are separated from each other [15]. In this approach, the state space is modified by using the errors between the simulated output and measured output as EKF states. This results in an a priori estimate of the state vector to be located in the origin of the state space, which simplifies the state-transition stage.

The discrete extended Kalman filter has been proposed in some studies [13, 16] to avoid the need for computationally expensive integration techniques. In this method, the state-transition model is often simplified by assuming constant accelerations through the simulation time interval and using a modified version of the forward Euler method for the state-transition model [13, 16]. However, the approach can overly simplify the state-transition model in the case of large acceleration variations within a time step, since the assumption of constant acceleration through a time step is not valid.

An interesting approach using an exponential integration scheme in the forward dynamics is presented in [17], where exponential integration is used for simulation of a pendulum. Later, the approach is also applied in force estimation using the discrete extended Kalman filter [18]. In a recent study, exponential integration is used for the simulation of stiff viscoelastic contacts of a multibody system [19]. In the study, the linear contact effect is integrated with an exponential integration scheme, while the nonlinear dynamics are integrated using a forward Euler integration scheme [19]. As stated in [17], exponential integration has a long tradition in control engineering [20] [21], where computational efficiency is of great interest. However, exponential integration schemes seem to be somewhat overlooked in the multibody dynamics literature.

The objective of this study is to introduce a novel method for the state-transition model of the discrete extended Kalman filter (DEKF) for application with multibody systems. The aim is to create an accurate state-transition model for the DEKF by using the linearized equations of motion together with an exponential integration scheme. Unlike [17], this paper shows how exponential integration is employed for the multibody equations of motion resultant from the coordinate-partitioning method. Moreover, the present study extends the work in [18] by including symbolic computations from [22], discretization of the continuous time-frame noise components, comparisons to forward Euler-based methods, and by combining exponential integration to the classical coordinate-partitioning method.

Based on energy-balance analysis of the numerical examples in this study, the proposed procedure is found to be more accurate and more numerically stable than forward Euler-based discretization approaches. The proposed method utilizes the computational synergies of integration of the state variables and integration of the covariances to be based on the same linearized system model, which brings advantages over other Kalman-filter technologies. Moreover, the proposed procedure derives the fundamental steps from the nonlinear continuous model to the linearized discrete system model and shows the underlying assumptions behind the different approximations. The stability enhancement of the state-transition model that is achieved using the novel procedure will open up new application areas for the DEKF, such as problems including large linear stiffness.

The paper is organized as follows: Sect. 2 presents the formulation of a nonlinear state-space model for a multibody system, Sect. 3 presents the linearization and discretization procedures for the nonlinear state-space model, and Sect. 4 shows the synergies that the novel formulation uses in the Kalman-filter framework. These sections are followed by numerical examples (Sect. 5) and the conclusion (Sect. 6).

2 Multibody systems

The first step in a state-estimator design is to define the underlying mathematical model of the system (or plant). In the case of multibody dynamics, the plant model is a mathematical description of interconnected bodies. It is important to note that the proposed estimator methodology is not developed specifically for a multibody formulation. However, the selected multibody formulation should produce the second time derivatives of the selected set of coordinates as an explicit function of the coordinates themselves and their first time derivatives. Moreover, the chosen set of coordinates should be linearly independent, meaning that they are only coupled by the dynamics of the system.

In this study, the set of independent coordinates is formed using the generalized global coordinates (also referred to as the reference-point coordinates) and a classical coordinate-partitioning approach. First, a system is considered consisting of \(N_{b}\) interconnected bodies described by a set of \(N_{q}=6N_{b}\) coordinates. The system kinematics is constrained with \(N_{m}\) constraint equations that allow \(N_{f}\) degrees of freedom. The constraint equations are assumed to be scleronomic and holonomic. Using the coordinate-partitioning method with dependent coordinates as presented in [23], the generalized accelerations \(\ddot{\mathbf{q}}\) can be evaluated as:

$$ \begin{bmatrix} \boldsymbol{\Phi}_{\mathbf{q}} \\ \mathbf{R}^{\mathrm{T}}\mathbf{M} \end{bmatrix} \ddot{\mathbf{q}}= \begin{bmatrix} \mathbf{c} \\ \mathbf{R}^{\mathrm{T}}\mathbf{Q} \end{bmatrix} , $$
(1)

where \(\boldsymbol{\Phi}\in \mathbb{R}^{N_{m} \times 1}\) is the constraint vector, \(\boldsymbol{\Phi}_{\mathbf{q}}\in \mathbb{R}^{N_{m} \times N_{q}}\) is the Jacobian of the constraints, \(\mathbf{R}\in \mathbb{R}^{N_{q} \times N_{f}}\) is the velocity-transformation matrix, \(\mathbf{Q}\in \mathbb{R}^{N_{q} \times 1}\) is the vector of external generalized forces, and \(\mathbf{M}\in \mathbb{R}^{N_{q} \times N_{q}}\) is the mass matrix of the system. The vector \(\mathbf{c}\) is the negation of the second time derivative of constraints with zero accelerations. In the case of scleronomic constraints, vector \(\mathbf{c}\) can be evaluated as \(\mathbf{c}=-\dot{\boldsymbol{\Phi}}_{\mathbf{q}}\dot{\mathbf{q}}\) [23]. The velocity transformation matrix \(\textbf{R}\) can be solved as [23]:

$$ \begin{bmatrix} \mathbf{S}&\mathbf{R} \end{bmatrix} = \begin{bmatrix} \boldsymbol{\Phi}_{\mathbf{q}} \\ \textbf{B} \end{bmatrix} ^{-1}, $$
(2)

where \(\mathbf{S}\in \mathbb{R}^{N_{q} \times (N_{q}-N_{f})}\), and \(\mathbf{B}\in \mathbb{R}^{N_{f} \times N_{q}}\) is a constant Boolean matrix each row of which represents a mapping from the complete set of coordinates to a respective independent coordinate. According to [24], the equations of motion in terms of independent accelerations can be written as:

$$ \ddot{\mathbf{z}}=(\mathbf{R}^{\mathrm{T}}\mathbf{M}\mathbf{R})^{-1} \mathbf{R}^{\mathrm{T}} (\mathbf{Q}-\mathbf{M}\mathbf{S}\mathbf{c}) \equiv \bar{\textbf{M}}^{-1}\bar{\textbf{Q}}, $$
(3)

where \(\ddot{\mathbf{z}}\in \mathbb{R}^{N_{f} \times 1}\) is the vector of independent accelerations. Although the matrix \(\mathbf{S}\) does not have a clear physical interpretation, the matrix-vector product \(\mathbf{Sc}\) does, as it represents the solution of generalized accelerations with zero independent accelerations [23]. Using a notation where the independent velocities are \(\mathbf{w}\equiv \dot{\mathbf{z}}\) and constructing a state vector \(\mathbf{X}\in \mathbb{R}^{2N_{f} \times 1}\) from the independent positions and velocities, the state space of the system can be written as:

$$ \dot{\textbf{X}}\equiv \begin{bmatrix} \dot{\textbf{z}} \\ \dot{\textbf{w}}\end{bmatrix} = \begin{bmatrix} \textbf{w} \\ (\mathbf{R}^{\mathrm{T}}\mathbf{M}\mathbf{R})^{-1}\mathbf{R}^{ \mathrm{T}} (\mathbf{Q}-\mathbf{M}\mathbf{S}\mathbf{c}) \end{bmatrix} \equiv \textbf{f}(\textbf{X}), $$
(4)

where \(\mathbf{f}\) is the function defining the nonlinear state space of the system.

Methods to solve the independent positions and velocities using Eq. (4) are discussed in the following sections. However, the resultant independent positions and velocities still need to be mapped into dependent positions and velocities to update the matrices \(\mathbf{R}\) and \(\mathbf{S}\) and the vector \(\mathbf{c}\) accordingly. The dependent velocities can be mapped explicitly using the velocity-transformation matrix \(\mathbf{R}\) as a mapping [23]:

$$ \dot{\mathbf{q}}=\mathbf{R}\dot{\mathbf{z}}. $$
(5)

However, the position problem cannot be solved explicitly but requires an implicit solution of the roots of the constraint-vector elements. In this study, the position problem is solved using the well-known Newton–Raphson iteration technique as:

$$ \textbf{q}_{h+1}^{d}=\textbf{q}_{h}^{d}-[(\boldsymbol{\Phi}_{\mathbf{q}}^{d})^{-1}]_{h}[ \boldsymbol{\Phi}]_{h}, $$
(6)

where \(h\) refers to the index of iteration, \(\mathbf{q}^{d}\) to the dependent part of the complete set of coordinates, and \(\boldsymbol{\Phi}_{\mathbf{q}}^{d}\) to the respective columns of the Jacobian of the constraint vector. The initial guess for the position problem is crucial for fast convergence. When considering a system with scleronomous constraints and assuming the \(\mathbf{R}\) matrix does not change rapidly inside a time step, an approximation of \(\Delta \mathbf{q}\approx \mathbf{R}\Delta \mathbf{z}\) can be concluded from Eq. (5). Using this approximation, the initial guess for the position problem of Eq. (6) can be calculated as:

$$ [\mathbf{q}_{(h=0)}]_{k+1}=\mathbf{q}_{k}+\mathbf{R}_{k}[\mathbf{z}_{k+1}- \mathbf{z}_{k}], $$
(7)

where \(k\) is the index of the time step.

3 Linearized discrete state-transition model

In general, nonlinear differential equations cannot be solved in closed form and a numerical integration scheme needs to be used. The integration methods used can be divided into explicit and implicit methods, where implicit methods require application of an iterative algorithm. On the other hand, it should be noted that many of the advanced explicit methods are so-called multistage methods, such as Runge–Kutta methods [25], where the function to be integrated is evaluated multiple times within a time step similarly to iterative algorithms. This creates a challenge for computationally critical applications because of the recurring function evaluations and the difficulty of forecasting the necessary computational time in the case of an iterative algorithm.

An alternative way to solve the problem is to evaluate a tangent frame of the function. In this approach, the tangent frame represents the instantaneous linear approximation of the behavior of the nonlinear function. The transformation to the tangent frame enables the use of discrete linear control theory methods to explicitly solve the differential equations with a single-point exponential integration scheme.

3.1 State-space model linearization

A common linearization approach in control theory is to find the equilibrium point for the system and perform linearization near that point [21]. However, the resultant model is valid only in the near neighborhood of that equilibrium point. For this reason, an approach is presented here where an arbitrary state vector can represent an artificial equilibrium point by introducing a virtual actuation \(\mathbf{U}_{v}\). The multibody system, modeled with the nonlinear state-space model (4) \(\dot{\mathbf{X}}=\mathbf{f(X)}\), can be augmented with a null-valued virtual control vector \(\mathbf{U}_{v}\in \mathbf{0}^{2N_{f} \times 1}\) as:

$$ \dot{\textbf{X}}=\textbf{f}(\textbf{X})+\mathbf{U}_{v}\equiv \mathbf{g}( \mathbf{X},\mathbf{U}_{v}), $$
(8)

where \(\mathbf{g}\) is the augmented nonlinear state-space model. It is important to note that an arbitrary selection of \(\mathbf{U}_{v}\) leads to a nonphysical model, because the velocities can be controlled independently from the accelerations. However, as long as \(\mathbf{U}_{v}=\mathbf{0}\), Eq. (8) is equal to Eq. (4). Now, the system \(\mathbf{g}\) can be defined to have an equilibrium point at (\(\mathbf{X}=\mathbf{X}_{ref}\), \(\mathbf{U}_{v}=\mathbf{U}_{v,ref}\)) as:

$$ \dot{\textbf{X}}_{ref}=\textbf{f}(\textbf{X}_{ref})+\mathbf{U}_{v,ref}=0 \xrightarrow[]{}\mathbf{U}_{v,ref}=-\textbf{f}(\textbf{X}_{ref}), $$
(9)

where \(\mathbf{X}_{ref}\) can be arbitrarily chosen. The linearization around the fixed equilibrium point can be evaluated by introducing small deviations \(\mathbf{x}\) and \(\mathbf{u}_{v}\) from the equilibrium point as:

$$ \dot{\textbf{X}}_{ref} + \dot{\mathbf{x}} = \mathbf{g}(\textbf{X}_{ref} + \mathbf{x},\mathbf{U}_{v,ref} + \mathbf{u}_{v}), $$
(10)

which can be linearized as:

$$\begin{aligned} \mathbf{g}(\textbf{X}_{ref} + \mathbf{x},\mathbf{U}_{v,ref} + \mathbf{u}_{v}) \approx \mathbf{g}(\mathbf{X}_{ref},\mathbf{U}_{v,ref}) + \frac{\partial \mathbf{g}}{\partial \mathbf{X}}\Bigr\rvert _{( \mathbf{X}_{ref},\mathbf{U}_{v,ref})}\mathbf{x}+ \frac{\partial \mathbf{g}}{\partial \mathbf{U}_{v}}\Bigr\rvert _{( \mathbf{X}_{ref},\mathbf{U}_{v,ref})}\mathbf{u}_{v}, \end{aligned}$$
(11)

where, given that \(\dot{\textbf{X}}_{ref} = \mathbf{g}(\mathbf{X}_{ref},\mathbf{U}_{v,ref}) = \mathbf{0}\), one may write:

$$ \dot{\mathbf{x}}\approx \frac{\partial \mathbf{g}}{\partial \mathbf{X}}\Bigr\rvert _{( \mathbf{X}_{ref},\mathbf{U}_{v,ref})}\mathbf{x}+ \frac{\partial \mathbf{g}}{\partial \mathbf{U}_{v}}\Bigr\rvert _{( \mathbf{X}_{ref},\mathbf{U}_{v,ref})}\mathbf{u}_{v}, $$
(12)

where:

$$\begin{aligned} \mathbf{x}&=\mathbf{X}-\mathbf{X}_{ref} \end{aligned}$$
(13)
$$\begin{aligned} \mathbf{u}_{v}&=\mathbf{U}_{v}-\mathbf{U}_{v,ref} \end{aligned}$$
(14)
$$\begin{aligned} \frac{\partial \mathbf{g}}{\partial \mathbf{X}}\Bigr\rvert _{( \mathbf{X}_{ref},\mathbf{U}_{v,ref})}&= \frac{\partial \mathbf{f}}{\partial \mathbf{X}}\Bigr\rvert _{ \mathbf{X}_{ref}} \end{aligned}$$
(15)
$$\begin{aligned} \frac{\partial \mathbf{g}}{\partial \mathbf{U}_{v}}\Bigr\rvert _{( \mathbf{X}_{ref},\mathbf{U}_{v,ref})}&=\mathbf{I}. \end{aligned}$$
(16)

By substituting the expressions from Eqs. (9), (14), (15), and (16) into Eq. (12), the linearization simplifies to a standard form of a linear time-invariant (LTI) system:

$$ \dot{\textbf{x}}=\boldsymbol{\mathcal{A}}\textbf{x}+ \boldsymbol{\mathcal{B}}\textbf{u}_{v}, $$
(17)

where:

$$\begin{aligned} \boldsymbol{\mathcal{A}}&= \frac{\partial \textbf{f}(\textbf{X})}{\partial \textbf{X}} \Bigr\rvert _{\textbf{X}_{ref}}, \end{aligned}$$
(18)
$$\begin{aligned} \boldsymbol{\mathcal{B}}&=\mathbf{I}, \end{aligned}$$
(19)
$$\begin{aligned} \mathbf{u}_{v}&=\mathbf{f}(\mathbf{X}_{ref}). \end{aligned}$$
(20)

Using the definition of the nonlinear state-space model of Eq. (4), the Jacobian matrix of \(\mathbf{f(X)}\) with respect to state vector \(\mathbf{X}\) can be written as [26]:

$$\begin{aligned} \dfrac{\partial \textbf{f}(\textbf{X})}{\partial \textbf{X}}= \begin{bmatrix} \dfrac{\partial \dot{\mathbf{z}}}{\partial{\mathbf{z}}}&& \dfrac{\partial \dot{\mathbf{z}}}{\partial \dot{\mathbf{z}}} \vspace{5pt} \\ \dfrac{\partial \ddot{\mathbf{z}}}{\partial{\mathbf{z}}}&& \dfrac{\partial \ddot{\mathbf{z}}}{\partial \dot{\mathbf{z}}} \end{bmatrix}= \begin{bmatrix} \mathbf{0}&&\textbf{I} \\ \dfrac{\partial (\bar{\textbf{M}}^{-1}\bar{\textbf{Q}})}{\partial \textbf{z}}&& \dfrac{\partial (\bar{\textbf{M}}^{-1}\bar{\textbf{Q}})}{\partial \dot{\textbf{z}}} \end{bmatrix}\equiv \begin{bmatrix} \boldsymbol{\mathcal{A}}_{11}&\boldsymbol{\mathcal{A}}_{12} \\ \boldsymbol{\mathcal{A}}_{21}&\boldsymbol{\mathcal{A}}_{22} \end{bmatrix}. \end{aligned}$$
(21)

3.2 Discretization using finite-series expansion

A linear continuous-time state-space model can be transformed into its discrete-time equivalent using the zero-order hold (ZOH) discretization method as described in [27]. In this approach, the control is assumed to be constant through a discrete time interval. The assumption of ZOH is valid for the model presented by Eq. (17), since the control \(\mathbf{u}_{v}\) is constant in the tangent frame and, accordingly, it is constant through the discretization time interval as [27]:

$$\begin{aligned} {{\textbf{x}}_{k+1}}=\boldsymbol{\mathcal{F}}\mathbf{x}_{k}+ \boldsymbol{\mathcal{G}}\textbf{f}(\textbf{X}_{ref}), \end{aligned}$$
(22)

where:

$$\begin{aligned} \boldsymbol{\mathcal{F}}&=\mathbf{I}+\boldsymbol{\mathcal{A}}\Delta t \boldsymbol{\Psi} , \end{aligned}$$
(23)
$$\begin{aligned} \boldsymbol{\mathcal{G}}&=\boldsymbol{\Psi}\Delta t \boldsymbol{\mathcal{B}}, \end{aligned}$$
(24)
$$\begin{aligned} \boldsymbol{\Psi} &=\sum _{n=0}^{\infty} \frac{\boldsymbol{\mathcal{A}}^{n}\Delta t^{n}}{(n+1)!}, \end{aligned}$$
(25)

and \(\Delta t\) is the size of the discretization time step. It is important to note that for the sake of compactness, the notation \(\boldsymbol{\mathcal{A}}\equiv \boldsymbol{\mathcal{A}}(\textbf{X}_{ref})\) is used here.

Now, Eq. (22) can be converted back to the original state space using Eq. (13) as:

$$ {{\textbf{X}}_{k+1}-{\textbf{X}}_{ref}}=\boldsymbol{\mathcal{F}}({ \textbf{X}}_{k}-{\textbf{X}}_{ref})+\boldsymbol{\mathcal{G}}\textbf{f}( \textbf{X}_{ref}). $$
(26)

This discretization represents the exact solution of the nonlinear ODE inside the tangent trajectory of the ODE limited only by the accuracy of the approximation of \(\boldsymbol{\Psi}\). Therefore, the new linearization should be performed on each time step, since using the previous linearization equates to doubling the length of the time step. When the linearization is updated on each time step, the reference-state vector can be expressed as \(\mathbf{X}_{ref}=\mathbf{X}_{k}\), producing a state-transition model as:

(27)

The same result is obtained in [17] with a slightly different derivation. To demonstrate the different terms of the transition model (Eq. 22), the matrices \(\boldsymbol{\mathcal{F}}\) and \(\boldsymbol{\mathcal{G}}\) can be written with an approximation order of \(n=1\) in Eq. (25). In this work, this is referred to as the second-order approximation since both \(\boldsymbol{\mathcal{F}}\) and \(\boldsymbol{\mathcal{G}}\) include second powers of the time step. With this order of approximation, the matrices can be written as:

$$\begin{aligned} \boldsymbol{\mathcal{F}}&=\left [ \textstyle\begin{array}{c@{\quad}c@{\quad}|@{\quad}c@{\quad}c} \mathbf{I}+\dfrac{\partial \ddot{\mathbf{z}}}{\partial \mathbf{z}} \dfrac{\Delta t^{2}}{2}&&& \dfrac{\partial \ddot{\mathbf{z}}}{\partial \dot{\mathbf{z}}} \dfrac{\Delta t^{2}}{2}+\mathbf{I}\Delta t \\ \hline &&& \\ \left ( \mathbf{I}\Delta t+ \dfrac{\partial \ddot{\mathbf{z}}}{\partial \dot{\mathbf{z}}} \dfrac{\Delta t^{2}}{2}\right ) \dfrac{\partial \ddot{\mathbf{z}}}{\partial \mathbf{z}}&&& \mathbf{I}+ \dfrac{\partial \ddot{\mathbf{z}}}{\partial \mathbf{z}} \dfrac{\Delta t^{2}}{2}+ \dfrac{\partial \ddot{\mathbf{z}}}{\partial \dot{\mathbf{z}}} \left ( \dfrac{\partial \ddot{\mathbf{z}}}{\partial \dot{\mathbf{z}}} \dfrac{\Delta t^{2}}{2}+\mathbf{I}\Delta t\right ) \end{array}\displaystyle \right ], \end{aligned}$$
(28)
$$\begin{aligned} \boldsymbol{\mathcal{G}}&=\left [ \textstyle\begin{array}{c@{\quad}c@{\quad}|@{\quad }c@{\quad}c} \mathbf{I}\Delta t&&&\mathbf{I}\dfrac{\Delta t^{2}}{2} \\ \hline &&& \\ \dfrac{\partial \ddot{\mathbf{z}}}{\partial \mathbf{z}} \dfrac{\Delta t^{2}}{2}&&& \dfrac{\partial \ddot{\mathbf{z}}}{\partial \dot{\mathbf{z}}} \dfrac{\Delta t^{2}}{2}+\mathbf{I}\Delta t \end{array}\displaystyle \right ]. \end{aligned}$$
(29)

The state-transition matrix \(\boldsymbol{\mathcal{F}}\) can also be found in the literature [13]. The matrix blocks \(\boldsymbol{\mathcal{F}}_{11}\) and \(\boldsymbol{\mathcal{F}}_{12}\) of Eq. (28) coincide with the results obtained in [13]. The terms \(\boldsymbol{\mathcal{F}}_{21}\) and \(\boldsymbol{\mathcal{F}}_{22}\) are, however, different, since they are obtained in [13] as \(\boldsymbol{\mathcal{F}}_{21}=(\partial \ddot{\mathbf{z}}/\partial{ \mathbf{z}})\Delta t\) and \(\boldsymbol{\mathcal{F}}_{22}=\mathbf{I}+(\partial \ddot{\mathbf{z}}/ \partial \dot{\mathbf{z}})\Delta t\). The reason for this difference is the higher-order crosscoupling of accelerations, velocities, and positions in the present study.

3.3 Partial derivatives of the equations of motion using analytical solutions

The analytical solutions for the partial derivatives of independent accelerations with respect to independent positions and velocities were originally developed in [22] and further discussed in [15]. However, for the convenience of the reader, they are reproduced here. The Jacobian of independent accelerations with respect to the independent coordinates (term \(\boldsymbol{\mathcal{A}}_{21}\) in Eq. 21) can be expressed as:

∂ z ¨ ∂ z = − ( R T M R ) − 1 a ¯ − ( R T M R ) − 1 ∂ ( R T M R ) ∂ z ( R T M R ) − 1 Q ¯ ,
(30)

where

$$ \dfrac{(\mathbf{R}^{\mathrm{T}}\mathbf{M}\mathbf{R})}{\partial \mathbf{z}}=( \mathbf{R}_{\mathbf{z}}^{\mathrm{T}}\mathbf{M}\mathbf{R}+\mathbf{R}^{ \mathrm{T}}\mathbf{M}_{\mathbf{z}}\mathbf{R}+\mathbf{R}^{\mathrm{T}} \mathbf{M}\mathbf{R}_{\mathbf{z}}), $$
(31)

and \(\bar{\mathbf{a}}\equiv -\bar{\mathbf{Q}}_{\mathbf{z}}\) is the partial derivative of the projected vector of generalized forces with respect to independent coordinates. Correspondingly, the Jacobian of the independent accelerations with respect to the independent velocities (term \(\boldsymbol{\mathcal{A}}_{22}\) in Eq. 21) can be expressed as:

$$ \dfrac{\partial \ddot{\mathbf{z}}}{\partial \dot{\mathbf{z}}}=-( \mathbf{R}^{\mathrm{T}}\mathbf{M}\mathbf{R})^{-1}\bar{\mathbf{b}}, $$
(32)

where \(\bar{\mathbf{b}}\equiv -\bar{\mathbf{Q}}_{\dot{\mathbf{z}}}\) is the partial derivative of the projected vector of generalized forces with respect to independent velocities. The matrices \(\bar{\mathbf{a}}\) and \(\bar{\mathbf{b}}\) can be presented as:

$$\begin{aligned} &\bar{\mathbf{a}}\equiv - \dfrac{\partial \bar{\mathbf{Q}}}{\partial{\mathbf{z}}}=-( \bar{\mathbf{Q}}_{\mathbf{q}}-\bar{\mathbf{Q}}_{\dot{\mathbf{q}}} \mathbf{S}\dot{\boldsymbol{\Phi}}_{\mathbf{q}})\mathbf{R}, \end{aligned}$$
(33)
$$\begin{aligned} &\bar{\mathbf{b}}\equiv - \dfrac{\partial \bar{\mathbf{Q}}}{\partial \dot{\mathbf{z}}}=- \bar{\mathbf{Q}}_{\dot{\mathbf{q}}}\mathbf{R}, \end{aligned}$$
(34)

where:

(35)
(36)

In Eq. (35), \(\mathbf{a}\equiv -\mathbf{Q}_{\mathbf{q}}\) can be considered as a stiffness matrix of the system and correspondingly in Eq. (36), \(\mathbf{b}\equiv -\mathbf{Q}_{\dot{\mathbf{q}}}\) can be considered as a damping matrix of the system. In Eq. (35), the partial derivatives of \(\mathbf{R}\) and \(\mathbf{Sc}\) with respect to \(\mathbf{q}\) can be expressed as:

(37)
(38)

The last calculation step in the derivation is to find the partial derivatives \(\mathbf{c}_{\mathbf{q}}\) and \(\mathbf{c}_{\dot{\mathbf{q}}}\) in Eqs. (36) and (38). These partial derivatives can be found as:

(39)
(40)

3.4 Lower-order approximations

To analyze the accuracy of the proposed discretization method, it is compared with two different lower-order approximation methods, both of which are called forward Euler methods in the literature. To distinguish between these two methods, they are named in this study as the Forward Euler and the Augmented Forward Euler method. The original Forward Euler can be derived from Eqs. (23–25) by using the approximation order of \(n=0\). A state-transition model equivalent to the resultant model is used in the framework of DEKF in [28] and [29]. In this approximation, the partial derivatives naturally disappear from matrix \(\boldsymbol{\mathcal{G}}\). However, the partial derivatives may not be taken into account in evaluation of matrix \(\boldsymbol{\mathcal{F}}\). Here, it is presented in a form where they are neglected. Thus, the matrices \(\boldsymbol{\mathcal{F}}\) and \(\boldsymbol{\mathcal{G}}\) can be written as:

$$\begin{aligned} \boldsymbol{\mathcal{F}}&= \begin{bmatrix} \mathbf{I}&&\mathbf{I}\Delta t \\ \mathbf{0}&&\mathbf{I} \end{bmatrix}, \end{aligned}$$
(41)
$$\begin{aligned} \boldsymbol{\mathcal{G}}&= \begin{bmatrix} \mathbf{I}\Delta t && \mathbf{0} \\ \mathbf{0}&&\mathbf{I}\Delta t \end{bmatrix}. \end{aligned}$$
(42)

In the Augmented Forward Euler scheme proposed in [16] and [13], the forward Euler is applied to the acceleration term of the previous time step producing the velocity of the current time step. Consequently, the position of the current time step can be evaluated as a trapezoid of known velocities at the previous and current time steps. This model can be derived from Eqs. (28) and (29) by assuming the partial derivatives of accelerations to be zero. This approximation produces a matrix \(\boldsymbol{\mathcal{F}}\) identical to Eq. (41). However, the matrix \(\boldsymbol{\mathcal{G}}\) differs from the one presented in Eq. (42) and can be expressed as:

$$\begin{aligned} \boldsymbol{\mathcal{G}}&= \begin{bmatrix} \mathbf{I}\Delta t && \mathbf{I}\dfrac{\Delta t^{2}}{2} \\ \mathbf{0}&&\mathbf{I}\Delta t \end{bmatrix}. \end{aligned}$$
(43)

4 Discrete extended Kalman filter applied to an instantaneously linear system

The discrete extended Kalman filter (DEKF) is similar to the original linear discrete Kalman filter (DKF); the only difference being that the linear state-space model changes as a function of states. For this reason, the equations derived for the DKF are also applicable in the case of DEKF. The equations shown in this section are heavily based on the derivations shown in [21]. However, due to the different field of study, the idea is briefly reproduced here focusing on the practical implications in the context of multibody systems. Additionally, the necessity of a state-transition model for the incorporation of measurements is demonstrated.

4.1 Discrete extended Kalman filter

Equation (17) describes the instantaneous multibody system dynamics in the standard form of the linear time-invariant (LTI) system. A standard (LTI) state-space model can be augmented by adding noise components to the system model and forming an expression for the measurement vector \(\mathbf{y}\):

$$ \left . \begin{aligned} \dot{\mathbf{x}}&=\boldsymbol{\mathcal{A}}\mathbf{x}+ \boldsymbol{\mathcal{B}}\mathbf{u}+\boldsymbol{\mathcal{B}}_{1} \boldsymbol{\mathcal{W}} \\ \mathbf{y}&=\mathbf{Hx}+\boldsymbol{\mathcal{V}} \end{aligned} \, \right \}, $$
(44)

where \(\mathbf{H}\) is the measurement matrix, \(\boldsymbol{\mathcal{W}}\) is the plant noise vector, \(\boldsymbol{\mathcal{V}}\) is the measurement noise vector, and matrix \(\boldsymbol{\mathcal{B}}_{1}\) is the mapping of the plant-noise components to the time derivatives of the state variables. The plant noise \(\boldsymbol{\mathcal{W}}\) and measurement noise \(\boldsymbol{\mathcal{V}}\) vectors can be assumed to be white noise with power spectral densities of \(\mathcal{R}_{\mathrm{wpsd}}\) and \(\mathcal{R}_{\mathrm{vpsd}}\), respectively. The discrete equivalent system of Eq. (44) can be presented as:

$$ \left . \begin{aligned} \textbf{x}_{k+1}&=\boldsymbol{\mathcal{F}} \textbf{x}_{k}+ \boldsymbol{\mathcal{G}} \textbf{u}_{k} +\boldsymbol{\mathcal{G}}_{1} \boldsymbol{\mathcal{W}}_{k} \\ \textbf{y}_{k}&=\textbf{H} \textbf{x}_{k}+\boldsymbol{\mathcal{V}}_{k} \end{aligned} \, \right \}, $$
(45)

where \(\text{cov}(\boldsymbol{\mathcal{W}}_{k})=\mathcal{R}_{w}\) and \(\text{cov}(\boldsymbol{\mathcal{V}}_{k})=\mathcal{R}_{v}\) and matrix \(\boldsymbol{\mathcal{G}}_{1}\) determines the influence of process-noise components on the system states. The explicit definition of matrix \(\boldsymbol{\mathcal{G}}_{1}\) and \(\mathcal{R}_{w}\) can be avoided by defining their counterparts in continuous time. In the case of multibody systems, it is often practical to assume that the system kinematic relationships are accurately defined, leading to the process noise affecting only the acceleration level. Consequently, matrix \(\boldsymbol{\mathcal{B}}_{1}\) can be written as:

$$ \boldsymbol{\mathcal{B}}_{1}= \begin{bmatrix} \mathbf{0} \\ \mathbf{I} \end{bmatrix} . $$
(46)

The discrete plant-noise covariance matrix \(\boldsymbol{\Sigma}^{P}\) is defined as:

Σ P = G 1 R w G 1 T = ∫ 0 Δ t F ( τ ) B 1 R wpsd B 1 T F T ( τ ) d τ = ∫ 0 Δ t [ F 12 ( τ ) F 22 ( τ ) ] R wpsd [ F 12 ( τ ) F 22 ( τ ) ] T d τ .
(47)

The realization of this integral depends on the order of approximation of \(\boldsymbol{\mathcal{F}}\). However, when using the approximation order of \(n=0\) in Eqs. (23) and (25) and the definition of \(\boldsymbol{\mathcal{A}}_{12}=\mathbf{I}\) in Eq. (21), the plant covariance matrix can be written as:

$$ \boldsymbol{\Sigma}^{P}_{k}= \begin{bmatrix} \boldsymbol{\Sigma}^{P}_{k(11)}&\boldsymbol{\Sigma}^{P}_{k(12)} \\ \boldsymbol{\Sigma}^{P}_{k(21)}&\boldsymbol{\Sigma}^{P}_{k(22)} \end{bmatrix} , $$
(48)

where the entries are:

$$\begin{aligned} \boldsymbol{\Sigma}^{P}_{k(11)}&= \mathcal{R}_{\mathrm{wpsd}} \frac{\Delta t^{3}}{3} \end{aligned}$$
(49)
$$\begin{aligned} \boldsymbol{\Sigma}^{P}_{k(12)}&=\mathcal{R}_{\mathrm{wpsd}} \frac{\Delta t^{2}}{2}+\mathcal{R}_{\mathrm{wpsd}} \boldsymbol{\mathcal{A}}_{22}\frac{\Delta t^{3}}{3} \end{aligned}$$
(50)
$$\begin{aligned} \boldsymbol{\Sigma}^{P}_{k(21)}&=\mathcal{R}_{\mathrm{wpsd}} \frac{\Delta t^{2}}{2}+\boldsymbol{\mathcal{A}}_{22}\mathcal{R}_{ \mathrm{wpsd}}\frac{\Delta t^{3}}{3} \end{aligned}$$
(51)
$$\begin{aligned} \boldsymbol{\Sigma}^{P}_{k(22)}&=\mathcal{R}_{\mathrm{wpsd}}\Delta t+ \left (\mathcal{R}_{\mathrm{wpsd}}\boldsymbol{\mathcal{A}}_{22}+ \boldsymbol{\mathcal{A}}_{22}\mathcal{R}_{\mathrm{wpsd}}\right ) \frac{\Delta t^{2}}{2}+\boldsymbol{\mathcal{A}}_{22}\mathcal{R}_{ \mathrm{wpsd}}\boldsymbol{\mathcal{A}}_{22}\frac{\Delta t^{3}}{3}. \end{aligned}$$
(52)

Unlike the plant noise, the sensor noise is often considered to be independent of the discretization time step. Thus, the discrete covariance \(\mathcal{R}_{v}\) can be directly used as a tuning parameter of the filter.

The Kalman filter for the system can be described using the state-transition model (27) as:

$$ \hat{\textbf{X}}_{k+1}=\bar{\textbf{X}}_{k+1}+ \boldsymbol{\mathcal{K}}_{k+1}[\textbf{Y}_{k+1}-\textbf{h}( \bar{\textbf{X}}_{k+1})], $$
(53)

where:

$$ \bar{\textbf{X}}_{k+1}=\boldsymbol{\mathcal{G}}_{k} \textbf{f}( \hat{\mathbf{X}}_{k})+\hat{\mathbf{X}}_{k}. $$
(54)

In the above equations, the vector \(\bar{\textbf{X}}_{k+1}\) represents the estimate after state transition, \(\hat{\textbf{X}}_{k+1}\) is the estimate after state update, \(\boldsymbol{\mathcal{K}}_{k+1}\) is the Kalman gain, \(\mathbf{Y}_{k+1}\) is the vector of measurements, and \(\mathbf{h}()\) is the measurement function. The evolution of the Kalman gain, the covariance matrix before measurement \(\textbf{P}_{k+1}^{-}\), and the covariance matrix after measurement \(\textbf{P}_{k+1}^{+}\) can be calculated using the following set of equations [1]:

(55)
(56)
(57)

where, in the case of the nonlinear measurement function \(\mathbf{h}()\), \(\mathbf{H}\) is the Jacobian of \(\mathbf{h}()\) with respect to \(\mathbf{X}\) evaluated at the reference point \(\mathbf{X}=\mathbf{X}_{ref}\).

5 Numerical examples

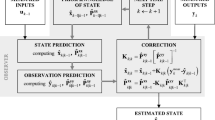
The algorithm of the discrete extended Kalman filter (DEKF) using the state-transition structure proposed in this paper is depicted in Fig. 1. In the figure, the step from the previous time step to the current time step is denoted by the unit time delay, \(z^{-1}\) blocks. Thus, calculation of the current time step starts by definition of the generalized coordinates \(\mathbf{q}\) and independent velocities \(\dot{\mathbf{z}}\) calculated at the previous time step. In this paper, the main objective is the development of the state-transition model, which is illustrated by the gray blocks in Fig. 1. For this reason, the numerical example also tests the accuracy of this part, while the blocks Covariance update and Correction are neglected. However, it is important to note that the state-transition matrix \(\boldsymbol{\mathcal{F}}\) calculated in the Discretization block is also crucial for the correction part of the estimator. This synergy is one of the advantages of the introduced method.

Fig. 1
figure 1

Functional block diagram of proposed algorithm

Full size image

For the sake of simplicity, two variations of the classical closed-loop four-bar mechanism are selected as numerical examples. In the numerical examples, the forward dynamics of the system is analyzed when the system is assumed to be affected by gravity.

5.1 Numerical example 1: configuration with gravity forces only

In the first numerical example, a classical four-bar mechanism affected by gravity is investigated. The mechanism is depicted in Fig. 2 and the system’s physical properties are given in Table 1. The gravitational force acts downwards in Fig. 2. The bodies are modeled as slender beam-like rigid bodies and all joints attached to points A–D are assumed to be ideal revolute type. The rotation of the first body \(\theta _{1}\) is chosen as an independent coordinate and its initial value is set to be \(\pi /3\). The system is simulated for 10 seconds using both the state-transition model proposed in Sect. 3.2 with the second-order approximation and with the lower-order state-transition models presented in Sect. 3.4. To analyze the effect of the time step, the system is simulated with two different time steps, 1 ms and 10 ms.

Fig. 2
figure 2

Four-bar mechanism in the first numerical example

Full size image
Table 1 Parameters used in the numerical example
Full size table

5.2 Numerical example 2: configuration with additional spring

In the second numerical example, the structure of the four-bar mechanism is modified by splitting Body-2 into two separate bodies at its center and attaching the resultant bodies together with a revolute joint. Additionally, a rotational spring with a spring constant \(k=5000\) kN m/rad is attached to this joint. The modified configuration is depicted in Fig. 3, where the additional joint is located at point E. As a result of this modification, the number of degrees of freedom of the system is increased from 1 to 2 and consequently one more independent coordinate is needed. The additional independent coordinate is chosen to be the rotation of the left part of Body-2, denoted as \(\theta _{21}\). This angle is initialized to be \(\theta _{21}=0.4\) rad.

Fig. 3
figure 3

Four-bar mechanism with a spring

Full size image

5.3 Numerical results

The performance of the proposed method is analyzed using two criteria: accuracy and computational efficiency. Energy balance is used as a measure of the method accuracy and mean time to compute one transition step in the MATLAB environment (tic command) as a relative measure of computational cost.

5.3.1 Numerical example 1: numerical results

In Figs. 4a and 4b, the energy balance is presented as a sum of potential and kinetic energies of the system. The energy balance is shifted so that it has initially the value of zero. In Figs. 4a and 4b, a two-sided logarithmic y-axis is used where the dashed horizontal line represents all the values with equal or smaller magnitude than the ± signed value on the \(y\)-axis.

Fig. 4
figure 4

Energy-balance comparison with different integration schemes

Full size image

5.3.2 Numerical example 2: numerical results

The energy balance of the second numerical example is shown in Figs. 5a and 5b. The energy balance is calculated as a sum of the potential energies of the gravitational forces and the spring force and the kinetic energy of the system. In Fig. 5b, the energy-balance graphs of the Augmented Forward Euler and Forward Euler go beyond the edges of the figure. Outside the figure, their respective values extend to infinity within 10 time steps, whose peaks are here ignored for illustrative reasons. To investigate the effect of the Taylor-series approximation order \(n\), the system is simulated with \(n\) varying from 1 to 4.

Fig. 5
figure 5

Energy-balance comparison with different integration schemes

Full size image

To investigate the ability of the simulation to track the fast vibration resulting from the spring force, the relative angle between the left and right parts of the split Body-2 is presented in Figs. 6a and 6b for the first second of the simulation. Also, a ground-truth solution for the vibration is provided using the MATLAB ode45 solver [30]. These figures show that at the beginning of the simulation, the solutions with Forward Euler-based discretization methods start to diverge from the solution obtained by the ode45 nonlinear solver, while the Taylor-series-based method provides consistent results. The figures also show that the diverging behavior is amplified with a larger time step.

Fig. 6
figure 6

Relative angle of rotational spring with different integration schemes

Full size image

5.3.3 Computational efficiency

The computational times of the analyzed methods are shown in Fig. 7. The hardware used in the computations was a HP ZBook Power G8 with an 11th Generation Intel Core i7-11800H processor. The evaluation time in the MATLAB environment varies quite considerably and is not fully deterministic, meaning that the length of the maximum evaluation time can differ significantly between the repeating executions of the same simulation. For this reason, the mean value of evaluation time is considered here as it is not as prone to vary between the executions.

Fig. 7
figure 7

Average computational time per time step

Full size image

Additionally, computational times required to calculate the nonlinear state-space function \(\mathbf{f}\) and its Jacobian were analyzed. The average computational times required for these calculations were 0.14 ms and 0.26 ms per time step for numerical examples 1 and 2, respectively, covering over 85% of the total computational time.

6 Conclusion

This study introduced a novel method for the forward integration of a multibody system. The method is based on the use of a linearized state-space model for application with the discrete extended Kalman filter. The proposed approach aims to increase simulation accuracy compared to forward Euler-based methods. Moreover, the method systematizes the formation of the system matrices.

The study shows that the dynamics of a multibody system with holonomic and scleronomous constraints can be analyzed using an instantaneously linear system model. It is further shown that the proposed method can be numerically more advanced when compared with forward Euler-based integration methods. However, the computational cost of the proposed method with the specific implementation studied is significantly larger than with the forward Euler-based methods.

The computational efficiency results obtained in this study can be considered insufficient to draw a definitive conclusion regarding the method’s suitability for industrial use. The main reasons for this are the use of a high-level programming language (MATLAB), the relatively low level of complexity of the numerical examples, the hardware used in the computations, and nonoptimalities in the computer implementation. Nevertheless, the results show elements that can be considered promising in terms of final applications. First, the doubling of degrees of freedom between numerical examples 1 and 2 resulted in doubled computational cost, which can be considered a moderate increase. Secondly, and more importantly, the results show that most of the computational time of the proposed method is used in the linearization procedure. This, in turn, indicates low computational cost for the time integration if the exact Jacobian has already been calculated for the state estimator, as in [15].

The results of the study indicate that even though the calculation of the partial derivatives of the acceleration terms causes an increase in the computational cost, it significantly enhances the accuracy of the linearized model. Moreover, it is seen that the effect of these partial derivatives is even more dramatic when investigating a system that includes linear force elements (a linear spring in the case example). The energy-balance analysis of the second numerical example (Figs. 5a and 5b) shows poor numerical stability for the system with the forward Euler-based methods, whereas the Taylor-series-based approximation produces a more stable solution. This difference can be explained by the different assumptions behind the approximations. In the forward Euler-based methods, the acceleration terms are assumed to be constant throughout the time step, while in the Taylor-series approximation, only linearity is assumed within a time step. Consequently, the Taylor-series approximation does not suffer large acceleration changes within a time step, providing that the changes can be well defined by a set of linear differential equations.

The great difference in the numerical stability between the different integration schemes in the second numerical example is hypothesized as being caused by the vibrations of the added rotational spring. The vibration phenomenon was further investigated by inspecting the amplitude propagation of the relative angle of the rotational spring during the first second of the simulation. The results show that when using the forward Euler-based methods, the amplitude of the relative angle of the joint to which the spring is attached starts to increase immediately after the simulation starts. On the contrary, the vibration amplitude of the spring remains more stable with the Taylor-series-based method. Moreover, this effect is significantly amplified with a longer time step.

The poor energy balance of Forward Euler-based methods can be also explained through the stability theorem of linear systems. Forward Euler integration has the property of mapping certain eigenvalues of a stable continuous-time system onto unstable eigenvalues of the corresponding discrete-time system [21]. In particular, the problem of instability created by discretization is severe for undamped vibrating systems, where the eigenvalues lying on the imaginary axis are always mapped onto unstable eigenvalues of the discrete-time system regardless of the sampling period. This local instability of the fast eigenvalues of the linearized dynamics can explain the poor energy balance of the Forward Euler-based approximations, although, in general, the stability of a nonlinear system can not be analyzed through its stability in a locally linearized domain.

The introduced method poses numerous research questions for the future. More research is needed to test the proposed method in implementations of the Kalman filter and with systems with a level of complexity similar to final applications. Other important aspects in final applications would be to consider actuations of multibody systems, contacts, and flexible bodies. The authors plan to extend the procedure for hydraulically actuated systems, as has previously been done in the case of the indirect Kalman filter [5]. For contact modeling, one possible approach would be to model the contact forces as unknown external forces and use the force-estimation methodology as in [18]. Moreover, it would be interesting to analyze the motion of flexible bodies using the proposed state-transition method.